Computational fluid dynamics assisted characterization of parafoveal hemodynamics in normal and diabetic eyes using adaptive optics scanning laser ophthalmoscopy

Abstract

Diabetic retinopathy (DR) is the leading cause of visual loss in working-age adults worldwide. Previous studies have found hemodynamic changes in the diabetic eyes, which precede clinically evident pathological alterations of the retinal microvasculature. There is a pressing need for new methods to allow greater understanding of these early hemodynamic changes that occur in DR. In this study, we propose a noninvasive method for the assessment of hemodynamics around the fovea (a region of the eye of paramount importance for vision). The proposed methodology combines adaptive optics scanning laser ophthalmoscopy and computational fluid dynamics modeling. We compare results obtained with this technique with in vivo measurements of blood flow based on blood cell aggregation tracking. Our results suggest that parafoveal hemodynamics, such as capillary velocity, wall shear stress, and capillary perfusion pressure can be noninvasively and reliably characterized with this method in both healthy and diabetic retinopathy patients.

1. Introduction

As the worldwide prevalence of diabetes mellitus continues to increase, diabetic retinopathy (DR) remains the most common vascular complication in diabetic patients [1]. The chronic hyperglycemic state of diabetes results in pathological alterations of retinal microvascular structures and blood flow abnormalities. Currently, despite advances in the treatment, DR remains the leading cause of visual loss in working-aged people worldwide [2,3]. New approaches are necessary in order to best understand how to prevent vision loss from diabetic eye complications, particularly in the early stages of this disease.

The fovea centralis, nourished in part by a network of small caliber retinal capillaries, is the area of the retina responsible for sharp central vision and visual detail. This foveal capillary network supplies nutrients and oxygen and disposes of cellular byproducts to maintain neural retinal function [4]. Central retinal function depends greatly on the foveal microcirculation. However, this network is compromised in many diabetic patients by chronic hyperglycemia, which leads to structural alterations in the capillaries and changes in blood flow, even in early stages of diabetes [5]. If left untreated, these changes can lead to substantial, sometimes irreversible vision loss in diabetic patients.

Given the importance of the parafoveal capillary network, the ability to visualize and assess subtle alterations in this portion of the retinal vasculature, even before visual loss has occurred, is critical for a full understanding of the association between early structural pathology and later functional impairments. Current standard retinal imaging techniques, such as optical coherence tomography (OCT), color fundus photography or fluorescein angiography (FA) are widely used to provide information on healthy and diseased vascular structures [6]. However, these technologies fail to visualize the finest capillary network due to limited imaging resolution, or involve the invasive use of contrast agents, which may be associated with the risk of adverse reactions [7,8]. More importantly, the aforementioned techniques do not generally provide information about parafoveal capillary hemodynamics, which may be essential for best prediction of future development of vascular pathology over the chronic course of diabetes.

Several authors have worked on the characterization of the blood flow changes associated with DR disease progression. An early example is the work by Mendívil et al. who prospectively compared blood flow velocity in the various ocular vessels (ophthalmic artery, posterior ciliary arteries, central retinal vessels, and vortex veins) between proliferative DR (PDR) patients and age-matched controls [9]. Their results show a statistically significant reduction in blood velocity in the DR patients. In a series of subsequent studies, Burgansky-Eliash et al. confirmed these findings in the retinal arterioles and venules of nonproliferative DR (NPDR) patients but found the opposite trend in the patients with early diabetes mellitus that do not show clinical signs of DR [5,10]. These findings speak in favor of a model where hemodynamic changes precede structural alterations of the retinal vasculature in DR. All the above-mentioned studies focus on measuring blood flow on retinal arterioles, venules or capillaries of relatively large caliber due to the resolution limitations associated with imaging the parafoveal region. More recently, Arichika et al. used adaptive optics scanning laser ophthalmoscopy (AOSLO) to measure the velocity of erythrocyte aggregation flowing in the parafoveal region and found a statistically significant increase in NPDR patients compared to PDR and control groups [11]. An additional limitation of these studies is that they focus exclusively on the analysis of blood velocity but not other important hemodynamic variables such as wall shear stress (WSS). There exists mounting evidence (see [12,13] and references therein) that WSS is a key player in both developmental and pathological vascular processes. Indeed, it has been suggested that pathologically enhanced WSS could be behind the suppression of endothelial pro-survival factors seen in DR [14].

In this study, we used AOSLO with computational fluid dynamics (CFD) in order to construct computational blood flow models capable of recapitulating the hemodynamic environment (blood velocity, WSS, and perfusion pressure) of the smallest capillaries in the parafoveal region of the retina. We hypothesize that our flow models will provide similar results to in vivo blood velocity measurements obtained by tracking blood cell aggregation (BCA, mostly individual slow-moving leukocytes followed by a cluster of erythrocytes) visible in the AOSLO scans [11] and present BCA tracking data for the capillary networks assessed in this study for flow model validation purposes. Finally, we show that the proposed methodology is applicable, with similar degree of accuracy, to both diabetic and nondiabetic subjects. We conclude that our approach enables detailed hemodynamic characterization of the parafoveal region beyond what is directly observable experimentally and that it can provide valuable information in order to establish the relationship between early hemodynamic changes and DR disease progression.

2. Methods

2.1 Study participants recruitment

In the study, eyes were classified into two groups: diabetic and nondiabetic (control). The control group included four eyes from three healthy, nondiabetic study participants with no history of ocular or systemic diseases. The diabetic group included four eyes from three additional participants, all with type 1 diabetes of duration from 19 to 29 years. Two eyes had mild NPDR, one eye had severe NPDR and one eye had quiescent PDR. Pupil dilation was performed on all diabetic participants 20 minutes before imaging. No pupil dilation was performed on healthy control participants, but during imaging, the room light was turned off to ensure maximum pupil size. In the non-dilated control group, the pupil size was ≥5 mm in order to maintain image quality. Participant’s demographics are shown in Table 1. Except for the participant with severe NPDR, who had hypertension, all other participants had blood pressure within normal limits on the day of the study visit. Both the severe NPDR and PDR participants were on lipid lowering medications. The study was approved by the Joslin Diabetes Center Institutional Review Board and was consistent with the Declaration of Helsinki.

Table 1. Study Eye and Participant Demographics.

Eye	Age (yrs.)	Sex	Group	HbA1c* (%)	Diabetes Duration (yrs.)	DR Status	IOP* (mmHg)	Visual Acuity
1	37	F	Diabetes	8.6	19	Mild NPDR	15	20/20
2	37	F	Diabetes	8.6	19	Mild NPDR	15	20/20
3	35	F	Diabetes	8.1	29	Quiescent PDR	14	20/16
4	25	F	Diabetes	8.0	20	Severe NPDR	18	20/16
5	32	M	Control	Not measured	N/A	N/A	12	20/20
6	32	M	Control	Not measured	N/A	N/A	11	20/20
7	31	M	Control	Not measured	N/A	N/A	17	20/20
8	31	F	Control	Not measured	N/A	N/A	11.5	20/20

*HbA1c = Hemoglobin A1c (normal range 4% - 5.6%, 5.7% - 6.4% indicates increased risk of diabetes, 6.5% or higher indicates diabetes), measured within 3 months of the study visit. IOP = Intraocular pressure.

2.2 Imaging system setup

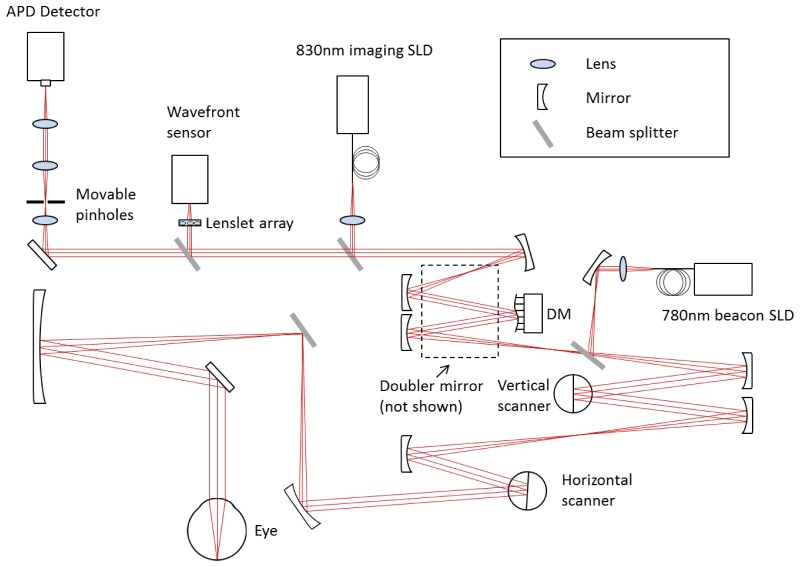
The AOSLO used in this study was a modified version of the Indiana system described previously [15]. The schematic layout of the system is shown in Fig. 1. The AOSLO uses two superluminescent diodes (SLD) for imaging and wavefront sensing, with central wavelengths of 830 nm and 780 nm respectively (BLM-S-830 and BLM-S-780, Superlum, Ireland). A micro-electro-mechanical system deformable mirror (DM, Multi-DM, Boston Micromachines Corp., Cambridge, MA, USA) was used to provide wavefront correction. The DM has an active area of 4.95 mm × 4.95 mm and 12 × 12 actuators with a maximum stroke of 5.5 µm. The system uses doubler mirrors to amplify the usable stroke of the DM [16] (the beam path for the doubler is not shown in Fig. 1 for the sake of simplicity). The maximum beam size at the exit pupil is 6.5 mm. Based on theoretical calculations, this AOSLO system is capable of compensating for >90% of the optical aberrations from an eye with clear media and a dilated pupil, achieving ~2.5 µm resolution.

Fig. 1.

AOSLO system schematic layout (not to scale).

Return light from the retina passes through a confocal aperture that is optically conjugated to the retinal plane. The apertures vary in size and are mounted on a 3-axis motorized stage (MT3-Z8, Thorlabs, NJ, USA). The stage allows precise positioning of the apertures for different imaging modes. In the study, we used two imaging modes: 3 × Airy disk aperture for confocal imaging when the aperture was placed in the center position, and 10 × Airy disk aperture for multiply scattered light imaging (also known as pinhole offset imaging [17]). The pinhole is displaced at negative 5 Airy disk diameters in both the X and Y directions away from the center regardless of vessel orientation. The axial resolution for the multiply scattered light imaging mode is approximately 150 µm with the large confocal pinhole.

2.3 Light safety

The AOSLO output power at the cornea is 183µW for the imaging SLD, and 67µW for the wavefront sensing SLD. The SLD on/off state is modulated with the resonance mirror. The SLD is on during the fore-scan of the resonance mirror, and is at the off state on the back-scan to reduce light exposure time. Superluminescent light levels on the retina are at least five times below the safety thresholds set by the American National Standards Institute ANSI Z136.1 [18].

2.4 Image processing and luminal surface reconstruction

50-frame videos (29 frames/sec, 1.75° × 1.75° area) were captured, aligned and averaged with a custom-made MATLAB (The MathWorks, Inc., Natick, MA, USA) program. Motion contrast perfusion maps were then generated to highlight the parafoveal capillary network. This motion contrast technique is similar to what was used by Tam et al. [19], but with the AOSLO focus set at the plane of the retinal vasculature using multiply scattered light imaging [17] rather than at the plane of the photoreceptors for direct visualization of BCA movement and more precise rendering of the vessel lumen boundaries. Ten frames with the largest intensity variations were selected from the 50 frame video to calculate the perfusion map on a pixel-by-pixel basis. These perfusion maps were then manually montaged to form 5° × 5° greyscale images, with approximately 20% overlap to ensure accurate image alignment. Fine alignment errors from image montaging were minimized by utilizing the “Auto-Blend Layers (Panorama)” function in Photoshop (CS6, Adobe Systems, Inc., San Jose, CA, USA).

Frangi filtering [20] (as implemented in the ImageJ software package) was applied to the images to enhance tubular structures followed by global image thresholding. Manual editing was performed by a trained grader to correct errors in the vascular structure such as discontinuities in the vessel network after image thresholding. The resulting binary masks were used to reconstruct a three-dimensional (3D) model of the luminal surface of the vessels based on the methodology previously described in [21]. Briefly, binary masks were processed with MATLAB in order to compute the graph associated with the image skeleton, calculate vessel radii (lumen width from perfusion maps divided by 2) along the network, and register radii to the graph.

The computed graph underwent two automatic post-processing operations to remove artifacts introduced during imaging and manual editing: caliber normalization and vessel crossing correction. Caliber normalization involved enforcing a minimum vessel diameter of 6 µm. This operation was performed in order to remove artificial narrowing, which would otherwise result in inaccurate portrayal of vessel segments of high resistance, artificially reducing flow upstream/downstream from them. This, in turn, would affect the values of WSS computed by the flow model. Second, vessel crossing correction involved applying a transformation to the network graph to account for the fact that the AOSLO scans were two-dimensional (2D) projections of a 3D vascular network and therefore graph nodes with four incident edges corresponded to vessels running past each other at different depths. These nodes can be easily identified in the network graph and the four incident edges can be paired up based on the intersecting angles they define. Each of these pairs of edges was then translated in opposite directions (assigned randomly) along the axis perpendicular to the 2D projection. Enough distance between the two resulting segments was ensured, based on the radii computed, to avoid contact. Finally, a 3D triangulation of the luminal surface was generated based on the corrected network graph and radii with the software package VMTK (Orobix srl).

2.5 Blood flow simulation

Briefly, blood flow was modeled according to the Navier-Stokes equations for generalized Newtonian incompressible fluids. Let $\text{Ω}$ be a three-dimensional domain with boundary $\partial \text{Ω}$. For $\mathit{x}\in \text{Ω}\cup \partial \text{Ω}$ and time $\mathit{x}\in \text{Ω}\cup \partial \text{Ω}$

$$\begin{array}{c}\nabla ·\mathit{v}=0\\ \rho \left(\frac{\partial \mathit{v}}{\partial t}+\mathit{v}·\nabla \mathit{v}\right)=-\nabla P+\nabla ·\text{T},\end{array}$$

where $\rho$ is the density, $\mathit{v}\left(\mathit{x},t\right)$ is the velocity, $P(\mathit{x},t)$ is the pressure, $\text{T}(\mathit{x},t)$ is the deviatoric part of the stress tensor

$$\begin{array}{c}{\text{T}}_{i,j}=2\eta {\text{S}}_{ij}\\ {\text{S}}_{ij}=\frac{1}{2}\left(\frac{\partial v_j}{\partial x_i}+\frac{\partial v_i}{\partial x_j}\right),\end{array}$$

and $\eta (\dot{\gamma })$ is the dynamic viscosity, which depends on the shear rate

$$\dot{\gamma }=\sqrt{2S_{ij}{S}_{ij}},$$

where $i,j=1,2,3$ and summation over repeated indices is assumed.

Let $\partial {\text{Ω}}_{w,i,o}$ be the wall, inlet, and outlet parts of the domain boundary, such that $\partial \text{Ω}=\partial {\text{Ω}}_w\cup \partial {\text{Ω}}_i\cup \partial {\text{Ω}}_o$. The problem is closed with the following initial condition

$$v\left(\mathit{x},0\right)=0, \mathit{x}∊\overline{\Omega },$$

and boundary conditions

$$\begin{array}{c}\mathit{v}=0, \mathit{x}∊\partial {\text{Ω}}_w,\\ P\hat{\mathit{n}}-\frac{\eta }{\rho }\nabla \mathit{v}·\hat{\mathit{n}}=P_o\hat{\mathit{n}} , \mathit{x}∊\partial {\text{Ω}}_o,\\ \mathit{v}\left(\mathit{x},t\right)={\mathit{v}}_i\left(r\right), \mathit{x}∊\partial {\text{Ω}}_i , t>0,\end{array}$$

where $\hat{n}\left(\mathit{x}\right), \mathit{x}∊\partial \text{Ω}$, is the boundary normal vector, $P_o\left(t\right)$ is the reference pressure at the outlet, and ${\mathit{v}}_i$ is the velocity at the inlet as a function of the distance to vessel centerline, $r$, under the vessel circular cross-section assumption.

In order to construct computational blood flow models of the capillary networks under study, we require for each imaged eye: a) a definition of the flow domain $\text{Ω}$ (e.g. the previously described reconstruction of the network luminal surface), b) a characterization of blood flow at the boundaries of the domain (i.e. inlets, outlets, and vessel walls), i.e. ${\mathit{v}}_i, P_o$ and c) an appropriate blood rheological model, $\eta$.

The inlets and outlet of the network are the closed surfaces defined by the open ends of the vessels that connect the subset of the retinal vasculature imaged to the rest of the cardiovascular system. The arteriolar/venular identity of the inlets/outlets was determined by registration to a 100° wide field fundus photograph (see Fig. 2).

Fig. 2.

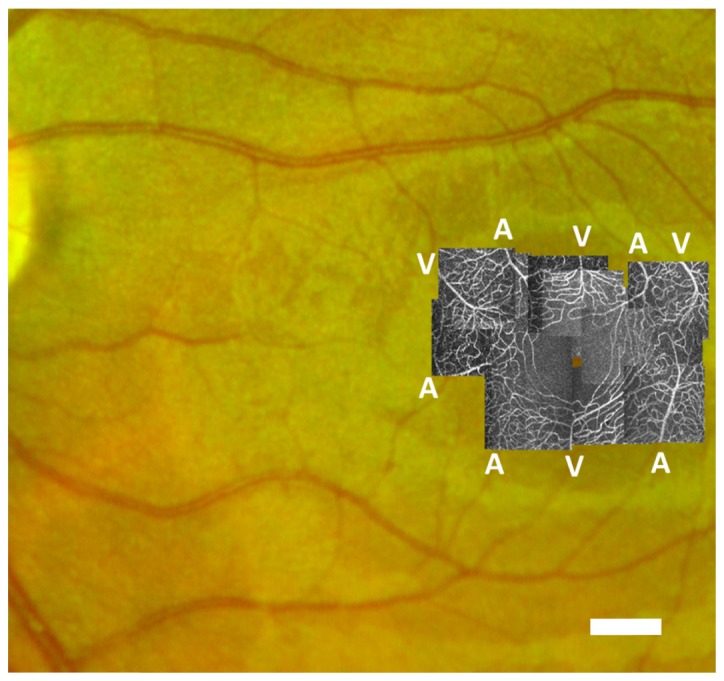
AOSLO perfusion maps montaged at fovea over fundus photograph. Control group case (Eye #5). Scale bar = 500 µm.

Blood flow was assumed to be steady and a constant flow rate was imposed at the inlets of the model. A reference pressure $P_o=0$ mmHg was set at the outlets and therefore the computed pressure field P should be interpreted as a pressure difference with regards to the network outlets. Given the technical difficulty of measuring ${\mathit{v}}_i$ in vivo on the participants of our study, we approximated it based on existing literature [10]. In the study by Burgansky-Eliash et al., the authors measured blood velocities in the arterioles and venules that feed and drain the parafoveal region of the retina. Measurements were classified in three groups according to vessel caliber (<10 µm, 10-20 µm, >20 µm), which were consistent with our own measures of vessel caliber. The study characterized NPDR and control eyes separately and found that arteriolar velocity (and therefore flow rate) depends on vessel caliber in both groups. Building on these results, our procedure for approximating ${\mathit{v}}_i$ is as follows. Given the radius R_i of any given inlet i, we define the inlet centerline velocity V_max as the mean velocity given in Table 4 of [10] for the relevant eye type and vessel caliber subgroups. We use the NPDR measurements in [10] for all our DR flow models, irrespectively of disease stage. The velocity profile at the inlet i is given by

$${\mathit{v}}_i\left(r\right)=V_{\max }\left(1-\frac{r^2}{{R_i}^2}\right) \hat{\mathit{n}},$$

i.e. a parabolic velocity profile, assuming vessel circular cross-section. Blood velocity is taken to be zero at the vessel walls (i.e. no-slip boundary condition). Flow simulations were run with the computational fluid dynamics software package HemeLB ([21], https://github.com/UCL/hemelb). Details regarding the validation of the numerical solver are provided in [21] and [22]. Convergence of the steady-state flow simulations was checked according to the criterion described in Eq. (4).4) of [21] with a relative tolerance of 1e-5.

At a constitutive level, blood is a dense suspension of cells in an aqueous medium known as blood plasma. This configuration leads to complex rheological properties such as the shear thinning and Fåhræus-Lindqvist effects [23]. It is often argued that in larger vessels, these effects are secondary. However, when modeling blood flow in capillaries, they must be taken into account in order to correctly capture the changes in blood viscosity occurring along the capillary beds under study. In the current work, we use the Carreau-Yasuda shear-thinning rheology model parameterized with human data as presented in [24]. See Section 4 for a discussion on the limitations of this approach.

HemeLB was used to compute high-resolution estimates of pressure, velocity, and WSS across the parafoveal capillary networks under study. On average, over 600,000 data points were generated across each vascular network. Simulations were run using 48 cores of ARCHER, UK’s national supercomputing service (http://www.archer.ac.uk). Each simulation took around 10 minutes to complete. Flow visualizations were generated with Paraview (Kitware, Inc.) and post-processing of the results was performed with custom-made Python scripts.

2.6 Flow simulation validation strategy

Several authors have reported the presence of BCA visible as bright, mobile particles followed by a dark trail in AOSLO scans when the focal plane was set at the cone layers [11,25]. In our study, we took advantage of this AOSLO feature, but with a shift of focus to the vessel layer for the validation of the reconstructed blood flow models. In particular, we hypothesized that our flow models would be able to predict the flow velocity of the BCA found in specific locations of the parafoveal capillary network.

We used the multiple scattered light imaging mode to directly capture the motion of BCA at the vessel layer, as shown in Fig. 2. The measurement of the BCA velocity is performed in three steps. First, we identify the location of a BCA in a vessel segment with sequential frames at a fixed frame rate (29 frames/sec). Second, we follow the BCA movement trajectory along the capillary and measure the trajectory path length using ImageJ in those sequential frames. The trajectory path length is adjusted based on an individualized conversion factor calculated from each participant’s axial length measured by IOLMaster (Carl Zeiss Meditec, Inc., Dublin CA, USA). Third, the velocity is determined by using the trajectory path length measured in the previous step divided by the time elapsed over the succession of the frames. 2-6 BCA locations were identifiable in each parafoveal network, with 32 vessel segments in total. In order to reduce error, the velocity of the BCA was calculated based on an average of 3 repeated measurements.

We use the following procedure to compare the measured BCA velocity with the flow model results. First, using a custom-made MATLAB graphical tool, we obtain the coordinates of an arbitrary number of equidistant points along the centerlines of each of the paths defined by the travelling BCA. Then, using a custom-made Python script, we obtain the velocity value predicted by the flow model at each of those points, average them, and compare this average value with the BCA velocity values estimated from the AOSLO scans.

3. Results

3.1 Image acquisition and processing

Figure 2 presents the AOSLO perfusion map of an eye in the control group overlaid against a standard fundus image. The AOSLO standard deviation perfusion map technique provides much higher resolution than the associated fundus photograph and successfully resolves the parafoveal vasculature to a level of detail suitable for the segmentation of individual vessels. In contrast, the larger field of the associated fundus image allows the determination of the arteriolar/venular nature of the parafoveal network inlets/outlets by tracing these vessels back towards their origin at the optic nerve.

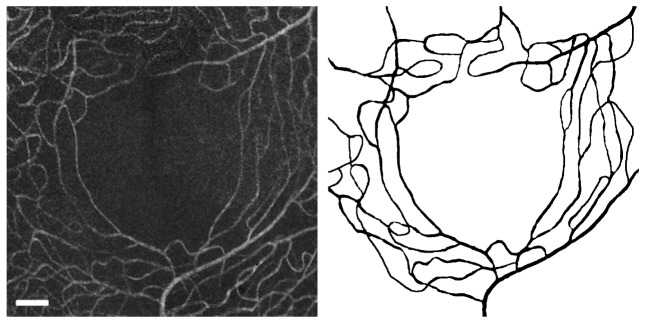
The left panel of Fig. 3 shows the central 5° × 5° of the perfusion map in Fig. 2. A number of arterioles and venules radially approach the fovea to feed/drain the innermost capillaries. In the parafoveal region, capillaries are organized concentrically with the innermost ring being approximately 250 µm from the center of the foveal avascular zone. The innermost capillaries are organized in a single layer and then start to form overlapping anterior and posterior plexuses as they move further away from the fovea.

Fig. 3.

Parafoveal capillary network from control group (Eye #5). Left: central 3 ° × 3° of the capillary network (Auto-Blended in Photoshop). Right: segmentation results from AOSLO image with the same field of view. Scale bar = 100µm.

The right panel of Fig. 3 presents the results of our segmentation workflow applied to the previous image. We found that application of the Frangi filter allowed enhancement of tubular structures in the image such that, following filter application, most background noise could be removed by thresholding. This approach does, however, still require manual correction by a trained retinal image grader in order to correct discontinuities and artificial narrowing of vessels, especially in regions where the signal-to-noise ratio is low. This manual intervention is time consuming and may present a challenge for reproducibility.

3.2 Flow model construction and simulation

Figure 4 shows the 3D luminal surface reconstruction generated from the binary mask in Fig. 3. The close-up view on the right panel shows one of the vessel crossings corrected using the algorithm described in Section 2.4.

Fig. 4.

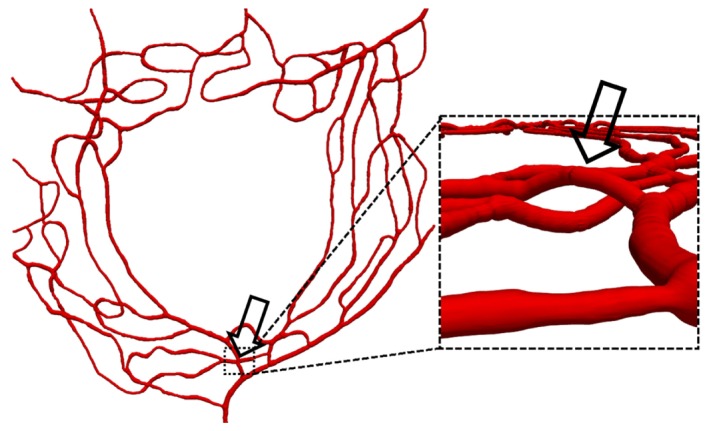
3D view of the reconstructed luminal surface with close-up of one of the corrected vessel crossings (indicated by the arrow).

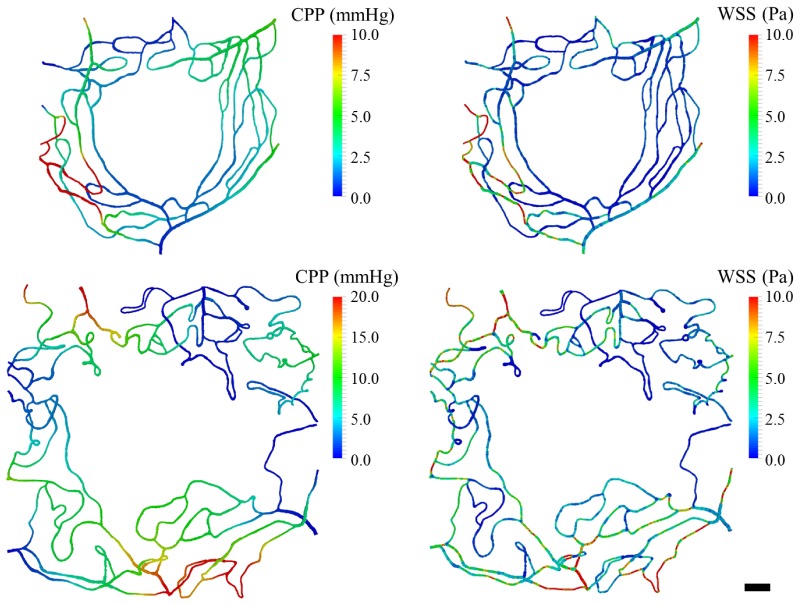
Capillary perfusion pressure (CPP) and WSS maps of one control (Eye #5) and one DR (Eye #4, Severe NPDR) case are shown in Fig. 5. In the left panel, CPP is defined, at any given point, as the pressure difference with respect to the network outlets. The right panel in the same figure plots the WSS magnitude on the luminal surface of the vessels. We observe how feeding arterioles experience the highest magnitudes of WSS in the domain, which is consistent with the experimental observations of [26]. In addition, we observe that WSS gradients correlate with vessel narrowing and branching points.

Fig. 5.

CPP and WSS map from a control (Eye #5, top panel) and DR case (Eye #4, bottom panel). Left panel: CPP across the network (defined as the pressure difference with respect to the network outlets). Right panel: WSS magnitudes across the network. Scale bar = 100µm.

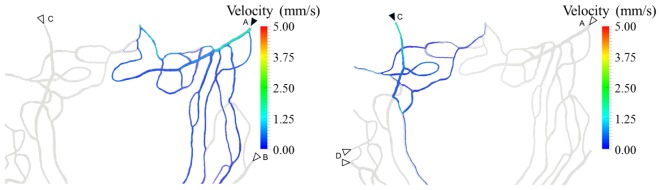
Figure 6 highlights the subsets of the network in Eye #5 perfused by two different inlets (labelled with solid arrow heads). In the left panel, it can be observed how the superior, temporal quadrant is almost exclusively perfused by inlet A, with some contribution from B but none from C. In the right panel, we observe a similar pattern in the superior, nasal quadrant, which is almost exclusively perfused by inlet C, with some contribution from D but none from A. In this particular subject, we observe a clear spatial affinity between the innermost parts of the network and the neighboring feeding arterioles.

Fig. 6.

Subsets of the network from Eye #5 directly perfused by two of the dominant inlets (solid arrowheads) in the superior half of the parafoveal region (left and right panel, respectively). Colored streamlines define the path followed by the bloodstream starting at each of the inlets labeled with solid arrowheads. Additional neighboring inlets are labeled with empty arrowheads. Streamlines were computed based on the simulation results with the Paraview (Kitware Inc.) software.

3.3 Velocity, WSS and CPP results

Table 2 presents the computed mean ± SD values of velocity, WSS, and CPP from each data set. Mean velocity ranges from 0.51 to 0.85 mm/s, mean WSS ranges from 1.67 to 2.71 Pa, and mean CPP ranges from 3.67 to 6.92 mmHg.

Table 2. Summary statistics of the main hemodynamic variables of interest for all the flow models developed. Velocity, wall shear stress magnitude (WSS), and capillary perfusion pressure (CPP).

Eye	Velocity (mm/s)	WSS (Pa)	CPP (mmHg)
1	0.58 ± 0.88	1.72 ± 2.12	4.14 ± 2.85
2	0.82 ± 1.51	2.71 ± 4.35	6.00 ± 8.29
3	0.76 ± 1.12	2.69 ± 3.11	6.92 ± 8.27
4	0.85 ± 1.18	2.69 ± 2.98	7.00 ± 5.76
5	0.51 ± 0.84	1.67 ± 2.50	3.67 ± 4.49
6	0.75 ± 1.13	2.49 ± 2.99	6.45 ± 5.96
7	0.80 ± 1.17	2.33 ± 2.34	6.48 ± 4.51
8	0.85 ± 1.09	2.32 ± 2.29	5.33 ± 3.78

3.4 Blood velocity validation

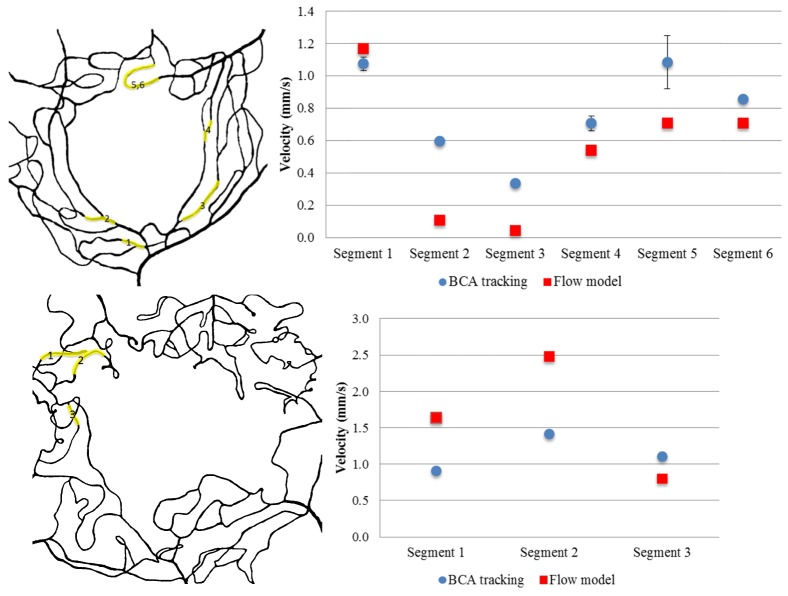
In order to validate our flow models, the computed blood velocity, Vel_m, by the model and the BCA velocity, Vel_a, were compared. Mean Vel_m was 0.80mm/s, whereas the mean Vel_a was 0.71mm/s, both of which are well within the expected range for blood velocity in capillaries of this size caliber [25,27]. The mean difference between Vel_m and Vel_a was 0.11mm/s. For individual eyes, values for Vel_m approximated those obtained for Vel_a (see Fig. 7 for example). Of the 32 vessel segments where velocity was estimated, 44% differed by < 0.5 fold, 69% by < 0.75 fold and 97% by < 1 fold. No statistically significant differences were seen in Vel_m and Vel_a variability between DR vs. control eyes or between eyes with varying DR severity. Detailed velocity results calculated from the two methods are shown in Table 3.

Fig. 7.

Top left panel: BCA tracking vessel segments in Eye #5. Top right panel: Velocity results comparison between BCA tracking and flow model in Eye #5. Bottom left panel: BCA tracking vessel segments in Eye #4. Bottom right panel: Velocity results comparison between BCA tracking and flow model in Eye #4. Highlighted segments are where path with visible BCA.

Table 3. Comparison on velocity between BCA tracking vs. flow model.

Eye	No. of segments	Vela (mm/s)				Velm (mm/s)
		Minimum	Maximum	Mean ± SD		Minimum	Maximum	Mean ± SD
1	5	0.53	0.89	0.64 ± 0.15		0.14	0.54	0.38 ± 0.18
2	2	0.61	0.76	0.69 ± 0.11		0.42	0.48	0.45 ± 0.05
3	4	0.60	1.28	0.99 ± 0.32		0.10	0.50	0.34 ± 0.32
4	3	0.91	1.42	1.14 ± 0.26		0.80	2.48	1.70 ± 0.84
5	6	0.34	1.09	0.78 ± 0.29		0.04	1.17	0.55 ± 0.42
6	4	0.66	1.09	0.82 ± 0.19		0.09	0.72	0.34 ± 0.31
7	4	0.38	0.74	0.62 ± 0.16		0.39	1.18	0.84 ± 0.40
8	4	0.72	0.79	0.76 ± 0.04		0.06	3.14	1.12 ± 1.43

Measurement variability when determining vessel segment length is inevitable. We tried to minimize this type of error by using the mean value of three independent measurements at each vessel segment. On average, the standard deviation of the three measurements was 5 pixels, which was equivalent to a Vel_a uncertainty of ± 0.14 mm/s (Vel_a standard deviation error bar shown in Fig. 7 for each segment. Some error bars are invisible due to minimal variation between measurements. Vel_m error bars are not shown because the values are from deterministic computer simulations, which don’t account for the sources of variability). When quantifying moving object using AOSLO with raster scanners, velocity errors due to the flow direction and eye motions are also expected [28]. Due to the randomness of the vessel orientation and the curvature, as well as the stabilization in the image post-processing, the up-mentioned error were not included in this study. Our mean values of the Vel_m and Vel_a were consistent with mean BCA velocity values (0.32 to 1.16 mm/s) that were reported by researchers who used blue-field entoptic phenomenon [27], by researchers who used AOSLO for BCA velocity measurement (0.77 to 2.10 mm/s) Fig. 8 [25], and by researchers who recently used AOSLO multiply scattered light mode with dual-channel scanning technique on erythrocytes velocity measurement (0.82 to 1.88 mm/s) [29].

Fig. 8.

Example of BCA tracking in 5 sequential frames in Eye #5, Segment #3 (Fig. 7 top left panel). Frame rate 29 Hz (Visualization 1 ^{(5.9MB, AVI)} ).

4. Discussion

In this study, we have demonstrated that the AOSLO motion contrast processing technique [19] allows non-invasive assessment of the human parafoveal capillary network with sufficient resolution for computational blood flow modeling. This approach enables, for the first time, detailed hemodynamic characterization of these vessels, which are of paramount importance for sharp central vision and are often compromised in diabetic patients. The velocities estimated in study eyes by the computational modeling approach fall well within the range of previous blood flow estimates for capillaries of this caliber and are similar to velocity measurements obtained by direct visualization of BCA within the same vessel segments, suggesting that this is a valid method for noninvasive determination of blood flow in the parafoveal capillary network.

No significant difference between blood velocity was found between diabetic and nondiabetic eyes in this small cohort, but this preliminary, feasibility study was not specifically powered to detect differences between these groups. Although the small sample sizes of this study do not allow the drawing of definitive conclusions about differences in blood velocity, WSS or CPP between diabetic versus nondiabetic eyes, we anticipate that the proposed methodology could provide valuable information in order to establish the relationship between early hemodynamic changes and DR disease progression in future studies recruiting larger sample sizes.

We performed validation of our flow models based on AOSLO BCA tracking. Our results demonstrate a modest correlation between model predictions and BCA tracking results. Our mean BCA velocity was 0.71 mm/s. The reconstructed flow models predicted a mean velocity of 0.80 mm/s in the same segments where the BCA were found. This predicted value lies within the range previously reported in the literature [25,27,29]. We also note that the measured BCA velocity is only a surrogate for the typical blood velocity at a given point in the network. This is due to the fact that, in the BCA, leukocytes have a typical size similar to or in excess of the diameter of the vessels that they flow in, therefore they are slowed down due to friction with the endothelium. Indeed, it has been argued [11] that this is the reason why erythrocytes cluster upstream from them and become visible in the AOSLO scans. Furthermore, dark tails in [11] tend to disappear when the BCA reach larger vessels, possibly due to the ability of erythrocytes to overtake slower moving particles or the removal of the spatial constraints that slow down BCA in capillaries. In a recent reference [29], the authors have demonstrated erythrocyte tracking using a dual-beam raster-scan imaging system in the retinal capillary. This is a promising technique that might directly assess or further confirm capillary hemodynamics as estimated by computational modeling.

The main limitations of the study are related to image processing, luminal surface reconstruction, and blood flow simulation. With respect to image processing, the process of perfusion map stitching proved technically challenging, since vessel continuity had to be preserved to a high degree of accuracy. Furthermore, there was a substantial degree of variability in the luminosity levels of each individual map. This difficult semi-automated vessel recognition and segmentation required a highly skilled operator to correct vessel discontinuities. We applied an assumption of a 6 µm minimal vessel diameter to help correct for artificial narrowing and discontinuity seen most frequently in the smallest vessels. This approach may potentially reduce differences due to pathologic narrowing less than 6 µm in some eyes and can be refined further in later investigations. Finally, in order to be able to simulate flow with the current approach, only completely closed networks could be isolated from the AOSLO scans. This introduces a degree of uncertainty since some segments have to be excluded if they appeared blind at one of their ends. It will be critical to address this issue in future studies to best understand how selecting a portion of the vessel network impacts the estimation of WSS and CPP values, particularly at the boundaries of the selected area. With regards to luminal surface reconstruction, our current approach considers the lumen to be a smooth surface and does not account for microstructures like the glycocalyx, which have been shown to play an important role in microvascular hemodynamics [30] and are often compromised on type-1 diabetic patients [31].

The authors believe that recent advances in imaging technology could help ameliorate these issues. Rosen et al. have successfully combined AOSLO and FA in order to further increase the imaging resolution and signal to noise ratio [32–34], which could help to address some of the image processing challenges previously discussed. In such systems, a blue channel (~488nm) light source was added for the fluorescein excitation, while maintaining the capability correcting the ophthalmic aberrations from the cornea and lens to reach theoretical limited imaging performance. However, it should be noted that the inclusion of a blue light source makes the imaging procedure more difficult for patients to comfortably tolerate. More importantly, the time and the light level or exposure must be strictly controlled according to the ANSI standard for the safe use of laser, and should be below both the photochemical and the thermal maximum permissible exposure limits, limiting the time that can be spent imaging with blue light. Besides light safety concerns, adverse reactions to the fluorescein contrast agent are well documented. Although these are rarely severe, they further limit the use of FA for some patients.

Another promising approach to speed up the extraction of vessel network is optical coherence tomography (OCT) angiography. OCT angiography was first introduced by Huang et al. in 2014 [35], and it quickly gains attention from the ophthalmology community. It uses erythrocyte movement against the static feature as intrinsic contrast to provide perfusion information of the retinal vessel network without fluorescent dye injections. It is particularly useful in evaluation of age-related macular degeneration (AMD) and DR by revealing both neovascularization as well as areas of vascular non-perfusion [36,37]. Several current available OCT angiography systems (e.g. AngioVue by Optovue, and AngioPlex by Zeiss) provide volumetric macular scans consist of 3 × 3 mm with a 1.6 mm depth in less than 3 seconds, comparing to ~10 minutes for FA. OCT angiography also gives good depth resolution to acquire en face images of the superficial capillary plexus, deep capillary plexus and outer retina choriocapillaris with reasonably good separation of the layers. In theory, OCT angiography is an excellent candidate for use in retinal vessel network hemodynamics modeling due to its quickness and large field of view. However, our preliminary work using OCT angiography images (results not shown here) indicates that it is challenging to generate full parafoveal network models that include the smallest, most central retinal capillaries, due to the limited spatial resolution (10µm/pixel with OCT angiography comparing to 1µm/pixel on the AOSLO). Nevertheless, we believe that OCT angiography will be well suited for this modeling technique, if the resolution is enhanced in the future (as with multi-MHz A-scan rates OCT that has been reported [38]).

With regards to our approach to blood flow simulation, the main limitations are the use of non-patient specific boundary conditions and a homogeneous shear-thinning rheology model. For the former, it is currently not possible to extract from the AOSLO scans the all required information to define flow rates at individual inlets and outlets of the model. Thus, we decided to compute those flow rates based on published results of typical blood velocities in retinal vessels of similar caliber obtained with the Retinal Function Imager imaging modality [10]. In future work, we will explore the feasibility of using the BCA velocity measurements to infer the flow rates at the inlets and outlets. For the latter, although the shear-thinning properties of blood were taken into account, our rheology model fails to capture some of the non-Newtonian properties of blood that arise from the particle suspension nature of blood (e.g. the Fåhræus–Lindqvist effect). Several authors have shown that it is possible to simulate blood as a suspension of deformable particle flowing in plasma and have studied the errors introduced by the homoegenous approximation [39–41]. In future work, we will evaluate whether this approach is computationally tractable when applied to complex parafoveal networks such as the ones reconstructed in the current study.

5. Conclusion

Despite their potential utility for DR assessment, no experimental measurements of the main parafoveal hemodynamic variables, other than capillary velocity, are available. In this study, we have successfully characterized the parafoveal hemodynamics in diabetic and healthy human eyes by incorporating high-resolution AOSLO imaging and CFD modeling. Capillary velocity, WSS and CPP, were computed in eyes ranging across multiple severity levels of DR. Modeling results from computed blood velocity were compared to in vivo velocity measurements based on BCA tracking. To our best knowledge, this is the first time that these three variables have been reported in the human parafoveal region. In summary, the combination of non-invasive imaging technology and advanced computer modeling allows evaluation of the central retina in vivo, providing quantitative insight into the hypothesized relationship between hemodynamics and disease progression. In the future, the computational modeling approach described here may be compatible with other imaging technologies such as AOSLO-FA and OCT angiography which may further extend the capabilities of this technique.

Funding

National Eye Institute (1R01EY0-24702-01, 2R44EY-16295-04A1); Juvenile Diabetes Research Foundation (2-SRA-2014-264-M-R, 17-2011-359); Eleanor Chesterman Beatson Childcare Ambassador Program Foundation Grant; Massachusetts Lions Eye Research Fund; UK Consortium on Mesoscale Engineering Sciences (UKCOMES)(EP/L00030X/1).