Human skull translucency: post mortem studies

Abstract

Measurements of optical translucency of human skulls were carried out. An incandescent light source and a CCD camera were used to measure the distribution of light transmitted through the skull in 10 subjects post-mortem. We noticed that intra-individual differences in optical translucency may be up to 100 times but inter-individual translucency differences across the skull reach 10⁵ times. Based on the measurement results, a “theoretical” experiment was simulated. Monte-Carlo calculations were used in order to evaluate the influence of the differences in optical translucency of the skull on results of NIRS measurements. In these calculations a functional stimulation was done, in which the oxyhemoglobin and deoxyhemoglobin concentrations in the brain cortex change by 5μM and −5μM respectively. The maximal discrepancies between assumed hemoglobin concentration changes and hemoglobin concentration changes estimated with Monte-Carlo simulation may reach 50% depending of the translucency of the skull.

1. Introduction

Near infrared spectroscopy (NIRS) is a technique being developed and applied for diagnosis of a brain perfusion disorders as well as neurophysiological studies [1, 2]. The technique is based on measurements of changes in absorption of a tissue and makes use of spectral properties of hemoglobin allowing to estimate changes in its concentration [1, 3]. In brain studies the measurements are typically carried out in reflectance geometry; a light source and a detector are positioned on a surface of a head at defined separation, which is usually between 2cm and 5cm [4]. Several techniques of NIRS were proposed: continuous-wave [5], frequency-domain [6] or time-resolved [7, 8] and successfully applied for examination of brain tissue oxygenation. In many studies the imaging approach was tested, in which the signals originating from different regions on a head were analyzed [9]. However, it is well known, that the cerebral oxygenation changes measured by NIRS technique are influenced by optical signals from extracerebral layers (skin, skull) [10, 11].

Recently, in parallel with NIRS technique, the diffuse correlation spectroscopy (DCS) is developed intensively. This method is also based on analysis of light diffusely reflected from the tissue. By analysis of the laser speckles fluctuations the DCS allows to monitor the changes in cerebral blood flow [12]. Moreover, methods allowing for assessment of the brain perfusion based on assessment of inflow and washout of ICG were proposed [13, 14]. These methods were based on monitoring of diffuse reflectance or fluorescence light excited in the dye circulating in the brain [15–18].

The optical signals measured by NIRS and DCS depend strongly on optical properties of the extracerebral tissue layers. The optical properties of tissues, in particular absorption coefficients of skull bones reported by many research groups varied significantly (from 0.007 mm⁻¹ to 0.024 mm⁻¹ @ 800 nm) [19–24]. This may result from uncertainty of measurement techniques, but may also suggest that differences in optical properties of the skull between subjects are large. The inhomogeneity of the overlaying tissue layers significantly influence the depth of light penetration, thus leading to differences in sensitivity profiles of the measured signals [25] and possibly affecting cerebral oxygenation or perfusion measurements performed by multichannel systems.

The problems related to inhomogeneities of the extracerebral tissues may limit accuracy and usefulness of the optical techniques, which are currently extensively applied in variety of clinical applications [26] and in neuroscience research. In human subjects large inter-individual differences in amplitude of the optical signals measured on the surface of the head at fixed source-detector separation can be observed.

In this paper, we analyzed optical inhomogeneity of human adult skulls. We obtained experimentally the spatial distributions of the translucency of the skulls. These distributions were used for estimation of the variability of absorption of a skull post mortem. Furthermore, the influence of the skull absorption distributions on NIRS optical signals measured on the surface of the head in diffuse reflectance geometry was analyzed with the use of Monte-Carlo simulations. It will be shown, that differences in skull translucency might strongly affect continuous-wave NIRS measurements.

2. Methods

2.1 Instrumentation

Spatial distributions of the translucency of the human skulls were imaged in series of experiments carried out on skulls obtained from cadavers. The skulls were illuminated from below with incandescent light source, through the mask of a shape of a skull covered with tracing paper. The size of the mask was however smaller than the skull itself, its height was 13 cm and width 10 cm. The mask was covered with a sheet of tracing paper, which acted as an optical diffuser. The light source applied was 75 W bulb (Osram, Germany) model Classic A 75 W 230 V E27 of color temperature of 2700 K and luminous flux of 935 lm. During the experiment the skull was placed above the light source and light transmitted through the skull (I₁) was imaged from the top, with the use of Nikon D700 digital camera (Nikon, Japan) equipped with 17-35/2.8 lens (Nikkor, Japan). Resolution of the obtained images was 4256 × 2832 pixels. For calibration purposes, images of the light distribution of the illuminator (I₀) were recorded. The idea of the experiment is presented in Fig. 1.

Fig. 1.

Idea of the experiment. Panel A: skull transmittance measurements; Panel B: background measurements; Panel C: result of dividing images of transmittance and background.

The measurements were carried out at fixed f-number = 8, defined as the ratio of the lens's focal length to the diameter of the entrance pupil. The sensitivity of the digital sensor, described by the exposure index and defined according to ISO standard was set to 1000. The skulls were photographed at different exposure times in order to use the whole dynamic range of the CCD element.

2.2 Data analysis

The images of distribution of light were acquired in 14-bit NEF format (Nikon Electronic Format). After conversion to DNG format (Digital Negative) further image processing was carried out in MatLab environment. Both NEF and DNG are lossless compressions, however the second one is easier to process in MatLab environment. During the analysis, both I₁ and I₀ images were transformed from M × N RGB Bayer matrix into M/2 × N/2 matrix by extraction of the red component. In the analysis we focused on the red component only, because the study is related to NIRS technique, which uses the light from red and near infrared region. The spectral response of the red-sensitive Nikon camera sensor is in the range between 550 nm and 950 nm. Furthermore, the images were normalized considering differences in exposure times. Subsequently, obtained images were cropped by the mask of illuminator and divided by each other. Resulting images were presented in logarithmic scale giving changes in translucency in orders of magnitude (log₁₀ (I₁/I₀)).

2.3 Subjects

Spatial distributions of the translucency of the skull were obtained for 10 different subjects, (8 males and 2 females) (Table. 1). The age of the subjects at time of death varied from 21 to 81 years; The skulls thickness was measured at 5 different positions, at the edge of the skull-top. The thickness of the one across all subjects varied from 3 mm to 12 mm. The thickness was measured with a caliper. The exact values are given in Table 1, the 2 numbers represent minimal an maximal values of 5 measured thicknesses.

Table 1. Subjects’ details. Skull thickness represents minimal and maximal values of thicknesses measured at 5 locations at the edge of the skull-top.

Subject	1	2	3	4	5	6	7	8	9	10
Gender	M	F	M	M	M	M	M	M	F	M
Age	48	60	67	70	49	81	47	84	25	21
Skull thickness [mm]	5-10	7-8	3-5	6-8	6-9	5-7	4-6	3-5	5-12	5-7

The skull was prepared during a standard autopsy procedure in the Forensic Medicine Department of the Medical University of Warsaw. The overlaying tissues were carefully removed and afterwards the top part of a skull of height of around 6 cm was cut-off from the head and immediately used for examination of translucency. The soft tissues and the blood were carefully, mechanically removed from the skull trying to avoid any damage of the bone. However, it cannot be excluded that some tissues, especially deoxygenated blood, are still present in the skull structure.

2.4 Monte-Carlo simulations

In order to assess influence of the skull inhomogeneity on the continuous-wave NIRS (CW-NIRS) measurements we simulated an experiment, in which photons are travelling from a source to a detector in the reflectance geometry. The simulations were based on a 4-layer model consisting of a scalp, a skull, a cerebrospinal fluid (CSF) and a brain (described in details in Table 2). The absorption coefficient of the skull was assumed to vary according to the variability of the translucency of the skull. The absorption coefficients of the skull (minimal, typical and maximal) are assessed based on skulls translucency measurements presented in this work.

Table 2. Optical properties of the layered-model of a human head applied in Monte-Carlo simulations: μ′_s – reduced scattering coefficient, μ_a – absorption coefficient, n – refractive index. Skull inhomogeneities are calculated based on skull translucency changes measured for the 8th subject.

Head model layer		μ′s / mm−1		μa / mm−1		n / -	thickness / mm
		@ 750 nm	@ 850 nm	@ 750 nm	@ 850 nm
Scalp		1.30		0.0125	0.0180	1.4	3
skull	Minimal (25th percentile)	1.20		0.0055	0.0080	1.4	7
	Typical			0.0082	0.0118
	Maximal (75th percentile)			0.0111	0.0159
CSF		1.00		0.0025	0.0041	1.4	2
brain	Rest	1.25		0.0156	0.0200	1.4	∞
	ΔCHbO2 = 5μM ΔCHb = −5μM			0.0146	0.0204

The typical optical properties of the tissue layers were assumed according to values presented by Prahl [27]. Considering the Beer-Lambert law, it was assumed that the measured attenuation of light transmitted through a skull A = ln(I₀/I₁) is linearly related to its absorption coefficient μ_a. Assuming that a mean value of the measured light attenuation corresponds to the typical absorption coefficient of the skull, the minimal and maximal values of the skull absorption coefficient were assessed as the 25th and 75th percentiles of the skull translucency distribution, respectively. The brain layer absorption coefficients at the 750 nm and 850 nm wavelengths were assumed for a rest state with a typical brain absorption values according to literature [27]. For a stimulation state the changes in concentration of oxygenated and deoxygenated hemoglobin were assumed to be + 5 μM and −5 μM, respectively. Similar values of hemoglobin concentrations were observed during motor cortex stimulation [28, 29]. Reduced scattering coefficients μ′_s of the head layers do not vary significantly between both wavelengths [27]. Thus, the one constant of μ′_s was set during the simulations at both wavelengths. The skull thickness was set to 7 mm, which was the mean value of measured skull thicknesses of all subjects.

Simulations were carried out utilizing the time-resolved Monte-Carlo code allowing for tracking of photons in a layered turbid medium [30, 31]. The source was defined as a circle with 2 mm diameter located in the center on the surface of the layered medium. The detectors are concentrically located around the source. The ring shaped detectors are 4 mm thick. Two source-detector separations were assumed: 3 cm and 4 cm (internal radius of the ring shaped detector). Results of the simulations are scaled by the area of the detector and width of the detection time-gate in order to present the results in the fluence rate units m⁻²s⁻¹. Furthermore, the fluence rate is converted into the number of detected photons, which can be measured by a time-resolved detection system based on TCSPC electronics. Recently reported algorithm, allowing for conversion the fluence rate into the number of detected photons with assumption of the typical wavelength dependent responsivity of the detection system (s(750nm) = 0.05e-6 m²sr, s(850nm) = 0.03e-6 m²sr) and the integration time (t_meas = 0.1 s), was used in these calculations [32].

The number of detected photons N_rest and N_stim correspond to the intensity of the reemitted light in a rest condition and during a stimulation, respectively. A relative change in the number of detected photons caused by the skull inhomogeneities is calculated as:

$$\delta N^{\text{min/max}}=\left(N_{\text{rest}}^{\text{min/max}}-N_{\text{rest}}^{\text{typical}}\right)/N_{\text{rest}}^{\text{typical}}$$ (1)

where min, max and typical refer to the variability of the skull absorption coefficient. Influence of the skull inhomogeneity on the contrast to noise ratio CNR_N was investigated. The contrast represents change in the number of detected photons caused by the change in hemoglobin concentrations in the brain induced by the stimulation. The CNR_N is calculated as follows:

$$CNR=\left(N_{\text{stim}}-N_{\text{rest}}\right)/\sqrt{N_{\text{rest}}}$$ (2)

where the square root of the number of detected photons in rest conditions represents the Poisson photon noise at the detector. The relative changes of the CNR caused by differences in skull translucency were estimated considering the minimal and maximal values of the skull absorption coefficient:

$$\delta CN{R}^{\text{min/max}}=\left(CN{R}^{\text{min/max}}-CN{R}^{\text{typical}}\right)/CN{R}^{\text{typical}}$$ (3)

where superscripts min, max and typical refer to the CNR^min, CNR^max and CNR^typical calculated for minimal, maximal and typical values of a skull absorption coefficient.

3. Results

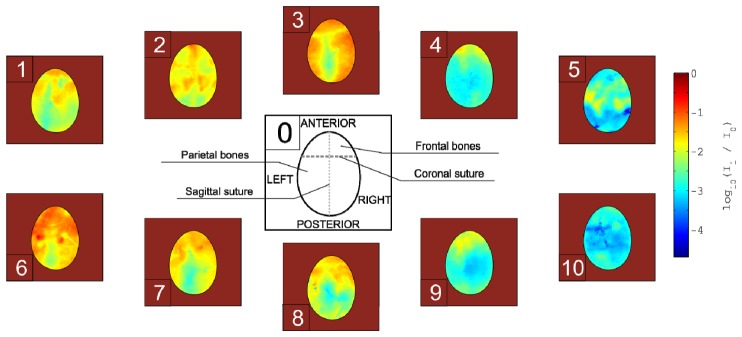
In Fig. 2 the distributions of translucency of the skulls for 10 different subjects were presented. The intersubject translucency differences across the skull varies up to 10⁵ times. The intra-individual differences in translucency are up to 2 orders of magnitude.

Fig. 2.

Spatial distributions of translucency presented for 10 different subjects (panels from 1 to 10). Panel 0 shows a simplified construction of the skull having Latin nomenclature used in the text.

In few subjects, the lowest translucency can be observed in an area of a sagittal suture. In many cases, the sagittal suture is a line of symmetry between translucency of left and right parietal bone. The high difference between the translucency in parietal bones and frontal bones can be also observed. Interesting fact is that the sutures, both coronal and sagittal, are not necessarily characterized with a lower translucency.

In Fig. 3, the histograms of the translucency of 10 skulls are presented. The average histogram is marked with a thick black line. The translucency varies between around −3.5 to around −1.0. It can be easily observed, that there are 2 characteristic peaks of translucency at around −2.8 and at around −1.7. Our results suggest, that the investigated skulls can be divided into 2 groups. The groups are distinguished by a dominant of high or low translucency within the observed skull surface. The histograms correspond with distributions of translucency presented in Fig. 2. The skulls with dominating yellow color (in Fig. 2) in translucency distributions are those with maximum of translucency at −1.7 and skulls in which the distributions of translucency appear more blue are those with the maximum at −2.8.

Fig. 3.

Histograms of skull translucency for 10 different subjects. Averaged histogram was marked with the thick black line.

4. Results of Monte-Carlo simulations

In order to estimate the influence of differences in skull translucency, measured within this work, on CW-NIRS measurements we carried out series of Monte-Carlo simulations. A motor cortex stimulation experiment was simulated, in a 4-layer head model, for 3 different absorption coefficients of the skull. The assumed absorption coefficients result directly from the skull translucency measurements as described in Section 2.4.

The series of simulations were carried out, in which the changes in hemoglobin concentration evoked by a functional brain stimulation were modeled. Three scenarios were applied in which different variability of a skull absorption coefficient was considered: A – minimal, B – typical and C – maximal. The scenarios and utilized optical properties are shown in Fig. 4 and Table 2 respectively.

Fig. 4.

Idea of the Monte-Carlo simulations based on 4-layer model (scalp, skull, CSF, brain). A, B and C – scenarios of brain cortex stimulation experiments in which minimal, maximal and typical values of skull absorption coefficient were assumed.

The variability of absorption coefficient of the skull was assessed using data collected for subject number 8. This subject was chosen due to the highest variability in the skull translucency to show the highest impact on fNIRS measurements. For this case the minimal, maximal and typical (representing mean value of the μ_a) skull absorption coefficients were calculated.

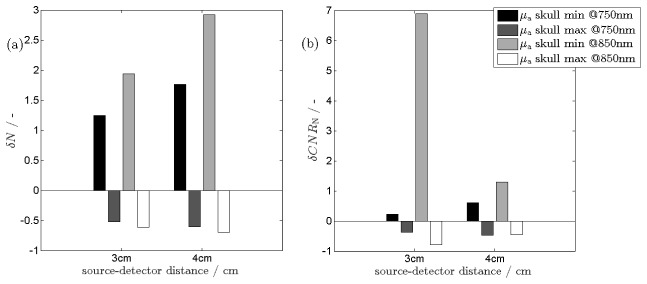
Influence of the skull inhomogeneity on the number of photons detected at the rest state and the contrast to noise ratio are shown in Fig. 5. Furthermore, the relative changes in number of detected photons for minimal and maximal values of the absorption coefficient of the skull in respect to its typical value and the relative changes in contrast to noise ratio are presented in Fig. 6(a) and 6(b) respectively.

Fig. 5.

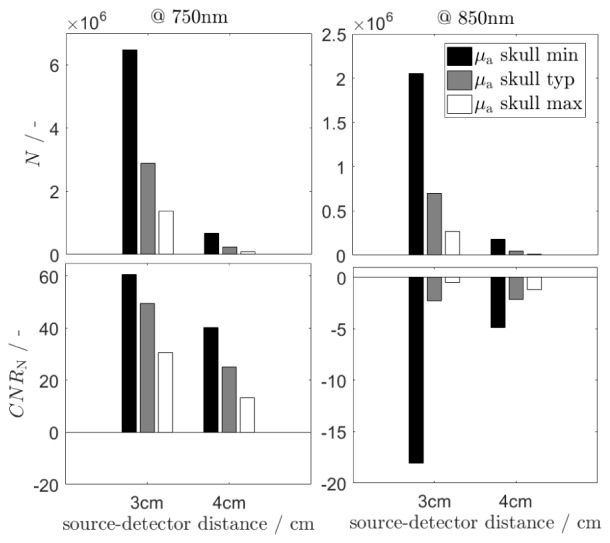
The number of detected photons N at the rest state and the contrast to noise ratio CNR at 2 wavelengths for minimal, typical and maximal values of the skull absorption coefficient. The number of detected photons results from Monte-Carlo stimulation and the contrast to noise ratio is calculated according to Eq. (2).

Fig. 6.

Relative changes in the number of detected photons at 2 wavelengths for minimal and maximal absorption coefficient of the skull in respect to its typical value (a) and the relative changes in contrast to noise ratio (b). The δN (δCNR_N) values were calculate using Eq. (1) and (3) respectively.

It can be observed, that the number of detected photons and consequently contrast-to-noise ratios are highly affected by the skull inhomogeneity. As expected, the number of detected photons is significantly higher when the skull absorption coefficient is minimal than for the typical μ_a skull value, both for 3 cm and 4 cm source-detector separations and at both wavelengths. In general, the differences in number of photons reemitted from the tissue caused by the skull absorption inhomogeneity is higher at 4 cm source detector separation. The values of δCNR_N are higher when the assumed skull absorption coefficient is minimal for both considered wavelengths. Although, a high difference in CNR between minimal and maximal value of the skull absorption coefficient is observed especially for 3 cm source-detector separation and for 850 nm wavelength.

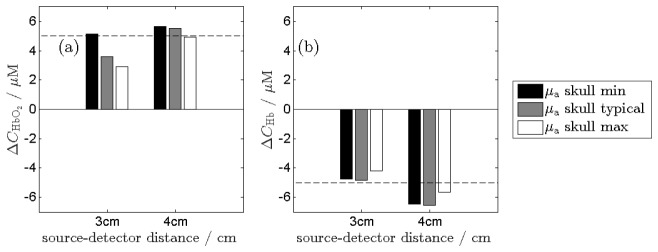
The influence of the skull inhomogeneity on results of calculation of the hemoglobin concentration changes within the brain using the NIRS technique was investigated. Results of the assessment of the hemoglobin changes are presented in Fig. 7. The ΔC_HbO2 oxygenated and ΔC_Hb deoxygenated hemoglobin concentration changes are calculated using the modified Beer-Lambert law and hemoglobin extinction coefficients taken from Prahl [33]. The hemoglobin changes were assessed based on Monte-Carlo, as described in details in Section 2.4, for assumed change in hemoglobin concentration in the brain cortex layer. The realistic mean path lengths of the photons travelling from the source to the detector were obtained from results of the Monte-Carlo simulations.

Fig. 7.

Influence of the skull inhomogeneity on results of calculation of hemoglobin concentration changes based on the NIRS technique: (a) changes in oxyhemoglobin concentration ΔC_HbO2 and (b) changes in deoxy-hemoglobin concentration ΔC_Hb calculated from the results of Monte-Carlo simulations carried out for three assumed values of μ_a of the skull. The assumed changes in oxygenated and deoxygenated hemoglobin within the brain tissue are + 5 μM and −5 μM, respectively.

Results presented in Fig. 7 show discrepancies between calculated and assumed hemoglobin concentration changes which are not larger than −2.1 μM for HbO₂ and −0.80 μM for Hb at 3 cm and + 0.65 μM for HbO₂ and + 1.6 μM for Hb at 4 cm.

5. Discussion and conclusions

We imaged distributions of translucency of human skulls in 10 cadavers and observed their high spatial inhomogeneity. Both, intra- and inter-individual changes in translucency across the skull are observed. In few cases larger attenuation of light is observed along the sagittal suture. It might be related to the fact, that the skull is thicker along the sutures [34]. Many researchers try to avoid this region in optical brain oxygenation or perfusion measurements also because of potential influence of the blood flow in superior sagittal sinus located below [11]. Furthermore, Strangman et al. [35], reported the results of modeling the influence of the skull thickness on the NIRS system sensitivity based on Monte-Carlo simulations together with MRI head model. The differences in the NIRS sensitivity presented in that report, for example lower sensitivity at an inferior frontal region and higher sensitivity at an occipital region, correlate well with the translucency measurements presented in our study. Unfortunately, the measurement of the skull thickness distribution across the whole skull was impossible, thus the analysis of correlation between the skull thickness and its translucency was not carried out.

Many parameters, like absorption and scattering coefficients, thickness, skull geometry, skull structure etc., may influence the translucency measurements. In the presented study, the most realistic measurements of the skull translucency were used in order to assess the impact of the skull inhomogeneity on the NIRS results. We observed, that in many cases the translucency distribution is not symmetrical along the sutures. Also large differences in the translucency of the skull can be noted between spots located symmetrically on both hemispheres.

Large differences in histograms of the translucency of the skulls were also observed. When the inhomogeneity of the optical translucency of the skull is large, the histogram is flattened whereas the histograms with large peaks reflect more homogenous skull structure. The histogram of the mean skull translucency consisting of 2 peaks suggests, that there are two typical translucency values (maxima at −1.7 and −2.8) which influence the individual distributions.

The differences in optical translucency of the skull lead to large differences in optical signals measured in different subjects and at different spots on the surface of the head. The obtained histograms show that differences of 2 orders of magnitude in translucency of the skull can be observed depending on optodes location on the head. Similar results based on cadaver studies were presented by Jagdeo et al. [36]. Considering that photons must pass the skull twice, while travelling from the source to the detector, the differences in skull inhomogeneity influence even more significantly the number of photons collected on the surface of the head. In reality, the skull is covered with soft tissues and a net of blood vessels that supply these tissues influencing the measured signals as well [37]. Absorption of light, by hemoglobin of high concentration present in these vessels, may cause additional strong inhomogeneity of the reemitted light distribution. The results of this study may partially explain the problems with comparison of multi-spot optical measurements carried out on the head of adult humans with the use of NIRS systems.

The skull inhomogeneities lead also to significant differences in contrast-to-noise ratio of the measured NIRS signals as shown in Fig. 5(b) and Fig. 6. Obtained results show that the influence of the inhomogeneity of the skull on the CNR_N depends on the wavelength of the applied light. The uncertainty of the assessment of the attenuation caused by inhomogeneity of the skull absorption influence the results of hemoglobin concentration assessment. At 3 cm source-detector separation the change in oxyhemoglobin (ΔC_HbO2) obtained using Beer-Lambert formula is underestimated when the maximal values of skull absorption coefficients were considered. For minimal skull absorption coefficient the oxyhemoglobin change is close to correct value. At 4 cm source-detector separation the estimation is within 15% error margins. By contrast, it can be observed that the change in deoxyhemoglobin (ΔC_Hb) is estimated properly for 3 cm source-detector separation. At 4 cm separation the deoxyhemoglobin change is overestimated. Results obtained at source-detector separation of 4 cm reveal less sensitivity of the signals to differences in skull absorption properties, what is in accordance with [35].

Obtained results of the Monte-Carlo simulations showed, that assessment of the brain oxygenation carried out at source-detector separation of 3 cm and shorter is strongly influenced by the skull inhomogeneity whereas at larger source-detector separation this influence is smaller.

The problems related to the influence of the skull inhomogneity on amplitudes of measured diffuse reflection signals as well as results of estimation of hemoglobin concentrations are particularly relevant when the measurements concern not only single spot data acquisition but also multi-spot monitoring of cerebral oxygenation or perfusion.

Funding

Studies financed by National Science Center project number 2011/03/B/ST7/02576.