Abstract
We present a novel active-passive path-length encoded (APPLE) swept source Doppler optical coherence tomography (DOCT) approach, enabling three-dimensional velocity vector reconstruction of moving particles without prior knowledge of the orientation of motion. The developed APPLE DOCT setup allows for non-invasive blood flow measurements in vivo and was primarily designed for quantitative human ocular blood flow investigations. The system’s performance was demonstrated by in vitro flow phantom as well as in vivo retinal vessel bifurcation measurements. Furthermore, total retinal blood flow – a biomarker aiding in diagnosis and monitoring of major ocular diseases such as glaucoma, diabetic retinopathy or central/branch retinal vein occlusion – was determined in the eyes of healthy human volunteers.
OCIS codes: (170.0170) Medical optics and biotechnology, (110.4500) Optical coherence tomography, (170.3340) Laser Doppler velocimetry, (170.2655) Functional monitoring and imaging, (170.4470) Ophthalmology
1. Introduction
Label-free visualization and quantification of blood flow in vivo is a rapidly emerging application in the field of biomedical imaging. A vast variety of pathologic effects are associated with alterations in blood flow. Thus, a further improved understanding of hemodynamics will aid in the diagnosis and treatment monitoring in various fields like neurology [1], dermatology [2] or ophthalmology.
Especially in ophthalmology, various major diseases such as glaucoma, diabetic retinopathy (DR) or central/branch retinal vein occlusion (C/BRVO) are directly linked to alterations in ocular blood flow (OBF) [3, 4]. In particular, total retinal blood flow (TRBF) is considered to be a significant biomarker for diagnostic and monitoring purposes of ocular disease development and progression [5–7]. However, although different approaches to quantify OBF [8] and determine TRBF [9, 10] in vivo have already been published, the gold standard is yet to be defined.
Optical coherence tomography (OCT), which was introduced 25 years ago [11], and in particular its functional extension Doppler (D) OCT [12–14] previously proved to be strong candidates. In addition to purely intensity based OCT, DOCT enables flow measurements by exploiting the phase shift introduced by movement of backscattering particles. In living biological tissue, DOCT is essentially used for blood perfusion investigations. Besides the qualitative approach of additional functional image contrast in OCT angiography (OCTA) [15, 16], DOCT allows for quantitative velocity and flow evaluation [17].
Previously reported DOCT approaches can in general be divided into two sub-groups – single-channel and multi-channel techniques.
Single-channel techniques may only obtain the axial velocity component of the moving erythrocyte, therefore they are dependent on additional structural data or information about flow orientation. Post-processing algorithms are used to extract the three-dimensional (3D) vessel geometry.
Wang et al. [10] reported absolute blood flow measurements using two concentric circumpapillary scans of slightly different radii to calculate the vessel orientation. This double-circle scanning pattern technique was applied for TRBF investigations in healthy humans as well as in patients suffering from glaucoma, DR or BRVO [6, 7, 18, 19]. However, for this approach even small errors in vessel orientation estimation result in a significant change in the measured flow. The error is most pronounced if the optical axis is almost perpendicular to the direction of flow (which is mostly true for circumpapillary scans) [20].
High-speed acquisition of large 3D data sets was proposed as another possibility for 3D velocity vector reconstruction of retinal blood flow [21–23]. However, acquisition of large 3D data sets is not very favorable in terms of computational storage and run time.
A first multi-channel approach was introduced for flow phantom investigations by implementing bi-directional illumination using a Wollaston prism [24]. Another technique divides a single sampling beam into multiple components using thickness-sectored glass delay plates to achieve path-length encoded, angle-resolved Doppler images [25, 26].
Werkmeister et al. [27] pursued a dual-beam approach – first reported for zebrafish larvae investigations [28] – for human in vivo application to measure retinal blood flow. Still, one angle of vessel orientation was missing and had to be extracted manually from en face data. By the integration of a rotating Dove prism to adjust the dual-beam plane continuously during each cycle of the circular scanning pattern around the optic nerve head (ONH), TRBF could be retrieved [29]. Furthermore, integration of a retinal vessel analyzer and rotatable beams for orthogonal detection planes in a dual-beam system were reported [30]. Nevertheless, all dual-beam approaches intrinsically lack the ability for 3D velocity vector reconstruction without any prior knowledge of flow orientation or very sophisticated dual-beam plane alignment.
Our group recently introduced a three-beam spectral domain (SD) approach to overcome this shortcoming [31]. The reported technique relied on velocity measurements along three independent directions and enabled TRBF measurements in healthy volunteers [32]. However, by employing three light sources and three separate spectrometers to realize the three-beam DOCT approach, the system’s complexity was high. In addition, possible deviations between the beams regarding the locations they illuminated are not to be recognized with this method, although these may influence the precision of the velocity measurement.
In this paper, we present a new method for reconstruction of the 3D velocity vector of moving particles that solves the addressed problems. The approach is based on a concept previously introduced for speckle reduction in swept source (SS-) OCT [33]. The velocity measurement along one direction is realized by an active illumination/detection channel (as in standard DOCT). However, the velocity components along two other linearly independent directions are obtained by two additional passive detection-only channels. Furthermore, the system’s complexity is greatly reduced by the combination of swept source technology and the principle of path-length encoding [34, 35], which enables interferometric signal acquisition with a single detector. We demonstrate the concept of active-passive path-length encoded (APPLE) DOCT by in vitro measurements on a flow phantom as well as in vivo measurements in the eyes of healthy human volunteers.
2. Methods
2.1 Experimental setup
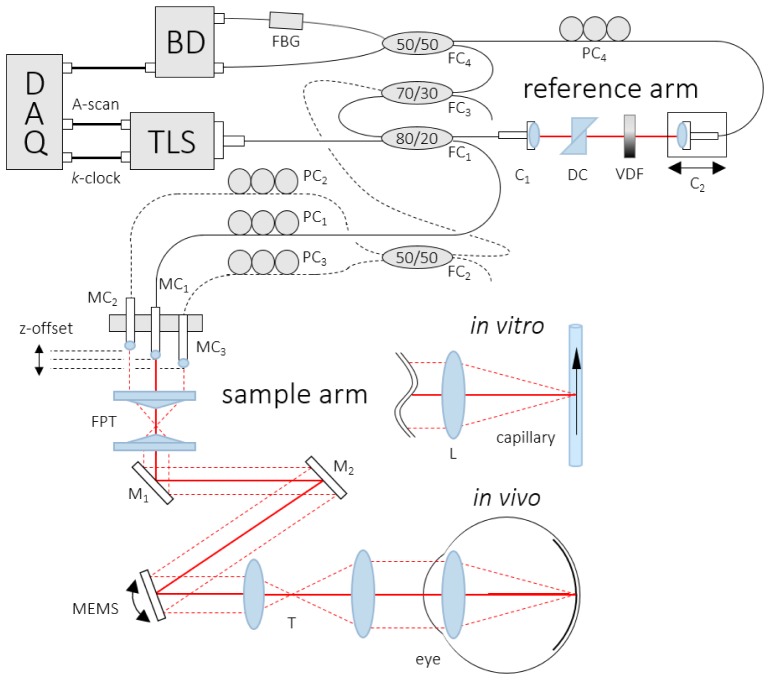
The APPLE DOCT system features a similar equilateral triangle beam geometry as previously reported by Trasischker et al. [31]. However, the new approach uses only one active illumination/detection beam/channel while employing two additional passive detection-only channels to simultaneously probe the target. Thus, only the detection beam geometry is similar to the previous setup, cf. Fig. 1. The yellow double arrow indicates the active channel – illuminating and probing the sample (here a perfused glass capillary) at the same time. The two pink arrows represent the respective passive channels – only probing the sample. It should be clarified here that the setup is not limited to the equilateral triangle beam configuration. Any arbitrary triangle beam geometry can be chosen, as long as three linearly independent measurement orientations are guaranteed. As previously shown [31, 32], knowledge of both the beam separation distances and the focal length of the focusing lens provides all required information to determine the beam geometry matrix (BGM) – which relates the exact geometry of the three channels to the coordinate system of the instrument – and hence the three components of the 3D velocity vector of the sampled moving particle (cf. section 2.3).
Fig. 1.
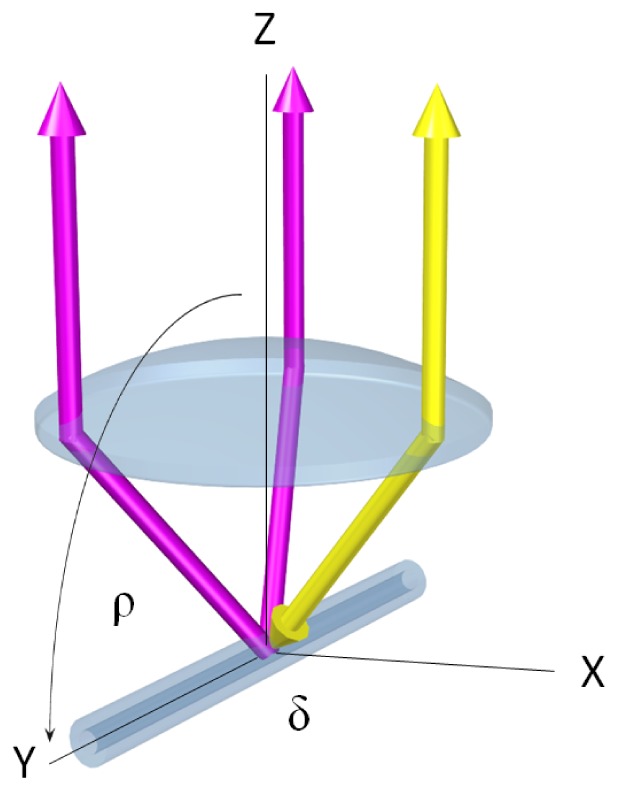
Scheme of pyramidal detection beam geometry for APPLE DOCT. Yellow double arrow: active illumination/detection channel. Pink arrows: passive detection-only channels. Sample: perfused glass capillary (in vitro flow phantom, cf. ‘Results’ section). Rotation of capillary in reference to optical axis along angle δ (orthogonal plane) and angle ρ (parallel plane).
We used a commercially available short cavity wavelength tunable laser source (Axsun Technologies, Inc.; 1060 Swept Laser Engine) centered at λ0 = 1045 nm with a bandwidth of Δλ = 100 nm. The sweep rate was 100 kHz with a duty cycle of ~50%. The source’s integrated k-clock was used to sample the spectral data at equal intervals in k-space.
The experimental setup – depicted in Fig. 2 – is based on a single-mode (SM) fiber-based Mach-Zehnder interferometer. The first fiber coupler (FC1) (all FC: AC Photonics, Inc.) divides the light emitted by the tunable laser source (TLS) at a split ratio of 80/20 into reference (80%) and sample beam (20%). Through the active channel, the light is guided in the sample arm to a miniature fiber collimator (MC1) (OZ Optics, Ltd; f = 2.61 mm; beam diameter ~500 μm, full divergence angle ~2.5 mrad). An in-house designed single block brass mount, which holds two more miniature fiber collimators (MC2, MC3), is used to align all three collimators parallel in an equilateral triangle geometry (side length: 4.4 mm). This narrow separation allows the sharing of all optical elements in the beam path among all three channels. The collimated beam is directed through a facet prism telescope (FPT), which is built up by a pair of custom made three-facet prisms and is used to further decrease the separation of the three channels on the scanning unit [36].
Fig. 2.
Scheme of the APPLE DOCT setup: TLS – tunable light source, FC – fiber coupler, PC – polarization controller, C – collimator, DC – dispersion compensation, VDF – variable density filter, MC – miniature fiber collimator, FPT – facet prism telescope, M – mirror, MEMS – 2D scanning mirror, T – telescope, L – lens, FBG – fiber Bragg grating, BD – balanced amplified photodetector unit, DAQ – data acquisition board.
From the FPT the beam is directed via two stationary mirrors (M1, M2) onto a dual-axis gimbal-less MEMS mirror (Mirrorcle Technologies, Inc.; diameter: 3.6 mm; mechanical tilt angle: −6.5° to 6.5°), which is employed for 2D scanning [36]. Compared to a pair of 1D galvo scanners, the integration of a 2D MEMS mirror significantly reduces the vignetting effect caused by physical separation of the scanning mirrors as well as the phase drift introduced by off-pivot scanning. M1 and M2 are introduced to realize a fairly small angle of incidence (AOI) of the beam onto the MEMS mirror to minimize geometrical scanning distortions [37]. From the scanning mirror, the light is guided through a 50/80 telescope (T) to alter the beam separation from ~1.1 mm to ~1.8 mm (measured by a beam profiler) which allows for penetration of the undilated human pupil at low light conditions for the active illumination/detection as well as the two passive detection-only channels. Considering beam diameters of ~0.8 mm, the minimally required pupil aperture was calculated to be ~3 mm. However, the larger the pupil aperture, the less subject-motion sensitive was the signal intensity. In the in vivo scenario, the illuminating beam was further focused onto the retina by the refractive optics of the human eye. In the in vitro scenario, an additional focusing lens (L; f = 30 mm) was used.
Light scattered back from the sample was not only coupled back into the active channel, but also into the two passive channels (cf. dashed lines in Fig. 2). Thus, we were able to probe the sample from two additional orientations to realize the same pyramidal detection beam geometry as in [31], but this time with only one illuminating beam. In comparison to previous work, the beam power no longer needs to be divided among three illuminating beams to satisfy laser safety regulations. In accordance to the maximum permissible exposure (MPE) limits [38], ocular exposures were 1.85 mW or less (same beam powers for in vitro investigations).
The three MCs are mounted in a way that different offsets in z-direction are obtained. Via this modification, path-length encoding of each interference pattern in the acquisition signal is achieved. Through adjustments of the z-offset among the MCs, the respective interference pattern can be shifted in imaging depth with respect to each other. In comparison to the previous SD-OCT prototype [31], the reduced sensitivity roll-off of the swept source system – which is roughly about 1–2 dB for an imaging range of approximately 3.7 mm in air – is crucial, since three path-length encoded images need to be displayed simultaneously without overlapping.
In the reference arm a fiber collimator (C1) directs the light through two identical N-BK7 glass prisms (DC) to compensate for dispersion mismatch between sample and reference arm. A variable density filter (VDF) is used for optical power adjustments before a second collimator (C2) couples the light into another SM fiber. Finally, the light traveling through the reference arm and the backscattered light from the sample arm are recombined at a 50/50 FC (FC4). Prior to that, the two passive sample arm channels are simply merged at a 50/50 FC (FC2) before being recombined with the active channel at a 70/30 FC (FC3; 70%: recombined passive channels; 30%: active channel). To enable polarization matching between all three sample arm channels and the reference arm, polarization control paddles (PC1 – PC4) were integrated.
The light of both outputs of FC4 is guided to a dual balanced amplified photodetection unit (BD) (Thorlabs, Inc., PDB 460C). One of the two beams traverses a fiber Bragg grating (FBG) (Advanced Optics Solutions GmbH; λ0 = 1060 nm; Reflectivity = 31.8%; Δλ = 0.096 nm). The FBG generates a calibration signal that is used in a post-processing step to compensate for phase fluctuations between A-scans that typically occur with the employed type of swept sources [39] (the central reflection wavelength of the FBG (λ0 = 1060 nm) was chosen due to availability; an FBG with λ0 at one end of the laser sweep would have been preferred).
The axial resolution of the system was measured to be ~7 μm in air (corresponding to an axial resolution of ~5 μm on the retina, assuming a refractive index of 1.4). The beam diameter of the active beam after T was 0.8 mm, corresponding to ~32 μm transverse resolution for retinal imaging. The interference patterns were detected with a bandwidth of 200 MHz before being digitized with a variable frequency of up to 350 MHz (max. k-clock frequency) at 12-bit resolution via a PCIe DAQ board (AlazarTech, Inc.; ATS9350).
For the applied illumination power of 1.85 mW, the measured sensitivity in the active channel using a mirror and attenuators in the sample arm was ~92 dB. The shot noise limit (SNL) was calculated to be ~95.5 dB. The lower sensitivity compared to other SS-OCT systems employing the same light source is caused by the additional FCs integrated in the sample arm. The reason for the 3.5 dB difference to the theoretic SNL can be attributed to the non-flat spectral response of the used FCs. As previously reported [40], this problem can be overcome by a symmetrical Michelson interferometer setup, which compensates for the spectral dependence of the coupling ratio at a cost of 3 dB – because of an additional 50/50 FC. However, our APPLE DOCT approach does not support a symmetrical Michelson interferometer setup. The sensitivity of the two passive channels could not be obtained in the same way as for the active channel. Instead, the sensitivity in the passive channels was estimated from a comparison of intensity signal-to-noise ratio (SNR) values observed in the active and passive channels of retinal OCT scans. The average SNR in 5 selected regions within the rather uniformly backscattering retinal nerve fiber layer (RNFL) was measured to be 25.7 dB for the active channel. For the respective passive channels we measured 23.6 dB and 23.4 dB. The average SNR was ~2 dB lower in the passive channels, yielding a sensitivity of ~90 dB (this comparison potentially suffers from limitations caused by sensitivity roll-off, by non-isotropic angular scattering properties of the RNFL, as well as by optical aberrations varying with scan location [33]).
Prior to the measurements, tip and tilt of the three MCs had to be aligned in a way to have the passive channels aim at the same focal position as the active channel. For this alignment step, all three channels were activated. Additionally, the fiber path-lengths were matched, in order to minimize dispersion discrepancies among the respective channels.
2.2 Determination of the 3D velocity vector
The light backscattered from a moving sample – in our case a red blood cell (RBC) – obtains a phase shift Δφ between two successive A-scans, which is directly proportional to the axial velocity component (velocity component parallel to the beam) vp of the moving sample [17].
| (1) |
In Eq. (1), is the unit vector in beam direction, λ0 denotes the central wavelength of the illuminating light, n represents the refractive index of the medium and T is the time period between successive measurements (A-scans). Since only the velocity component parallel to the sampling beam vp can be measured, additional information about the orientation of flow is necessary to calculate the absolute flow velocity vabs:
| (2) |
with α representing the Doppler angle.
The challenge of determining the unknown Doppler angle can be solved by using three independent beams that simultaneously probe the sample from different angles [31]. This method provides a linear equation system consisting of three equations and three unknowns:
| (3) |
| (4) |
This system of linear equations has a unique solution and thus the 3D Cartesian velocity vector components, andcan be determined.
In case of the use of passive detection-only channels, the composition of the obtained phase shift Δφ and the definition of the Doppler angles need to be reconsidered. Equation (1) can be rewritten as follows:
| (5) |
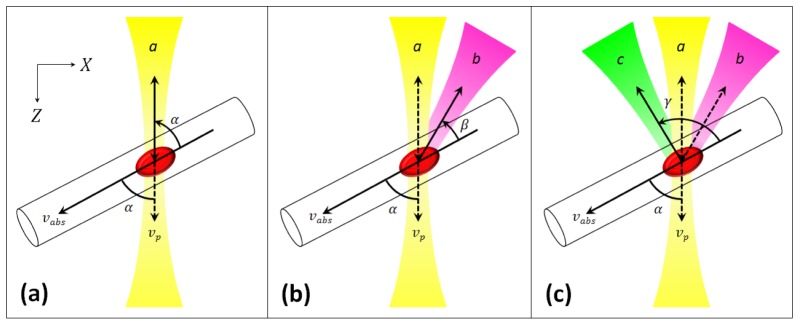
whereindicates the length in particle movement direction within time period T. Considering Eq. (5), it becomes obvious that Δφ originally is a compound of two identical terms (indicated by the first factor 2), each proportional to the cosine of the Doppler angle. The case that both terms are equal only holds true if illumination and detection take place from the same direction a ( = same Doppler angle α), which is the case for the active illumination/detection channel:
| (6) |
If now – as indicated in Fig. 3 – the illumination still takes place from direction a, but the sample is probed from direction b (angle β), Δφab reads:
| (7) |
For the second passive channel, probing the sample from direction c (angle γ), we obtain a similar equation for Δφac:
| (8) |
To eventually end up with the phase shifts Δφaa, Δφbb and Δφcc, which are required to solve the same linear equation system calculations as in [31], Eqs. (6)–(8) can be utilized to express the desired variables:
| (9) |
| (10) |
Thus, APPLE DOCT enables to obtain the three phase shifts Δφaa, Δφab and Δφac, which already hold all the information necessary to extract the 3D velocity vector of the moving sampled particle.
Fig. 3.
Schematic illustration of APPLE principle for DOCT: vp – axial velocity vector component, vabs – 3D velocity vector, α – Doppler angle, a – illumination/detection direction, β – first passive detection (p. d.) angle, b – first p. d. direction, γ – second p. d. angle, c – second p. d. direction. (a) Illumination and detection from same direction. (b) Additional p. d. channel from second direction. (c) Further additional p. d. channel from third direction.
2.3 Post-processing, flow evaluation and in vivo measurement requirements
At first, standard Fourier domain (FD-) OCT data post-processing (mean spectrum subtraction, numerical dispersion compensation, FFT) was performed on the recorded raw data. Due to slight length differences among the optical fibers of the respective channels, numerical dispersion compensation could not be done within a single step but had to be performed for each channel independently. Since the information for all three channels was depth encoded within one A-scan, three windows, each containing one channel, were used to provide independent numerical dispersion compensation.
The phase reference signal generated by the FBG – which resembles a steep spike (~3 pixels FWHM) in the balanced spectrum – introduced line artefacts in the Fourier transformed amplitude part of the raw data. This was compensated for by cutting out ± 3 pixels of the FBG induced peak and interpolating this portion of the recorded spectrum. However, by applying interpolation the true original signal content could not be reconstructed for the ± 3 pixels. This interpolation introduced a slight additional ripple in the noise floor after the FFT, which might be a further explanation for the deviation between measured and calculated sensitivity. This sacrifice in terms of signal conservation had to be made in order to compensate the mentioned phase fluctuations between A-scans.
The next step was to calculate the phase difference tomograms for each channel by taking the difference of the phase signal between corresponding pixels of adjacent A-scans. Only pixels above an empirically chosen intensity threshold (~2.5 times the intensity noise level) were taken into account for generation of the phase difference tomograms. In addition, further post-processing steps had to be performed, differing for each of the three respective measurement types – in vitro flow phantom, in vivo retinal bifurcation and in vivo TRBF measurements.
The phase difference tomograms suffered from inherent phase shifts introduced by the MEMS scanning mirror (and additionally eye-motion in the in vivo scenario). The scanner-introduced phase difference background is dependent on the scanning protocol. For a linear scan pattern (in vitro and in vivo bifurcation measurements) a constant phase offset, and for a circular scan pattern (in vivo TRBF measurements) a sinusoidal phase offset can be observed. Therefore, different phase offset subtraction algorithms were applied for different scanning protocols.
For the in vitro measurements a histogram-based method was used to determine this scanner-introduced phase offset [41]. A reference/baseline measurement with static conditions in the flow phantom was employed to determine the scanner-introduced phase shift. All static pixels in the phase difference tomogram were taken into account for a phase histogram, which was used to determine the constant phase offset for subtraction. For the in vivo bifurcation measurements the same histogram-based method was employed. This time a vessel-free static tissue area was evaluated to determine the scanner-introduced phase shift.
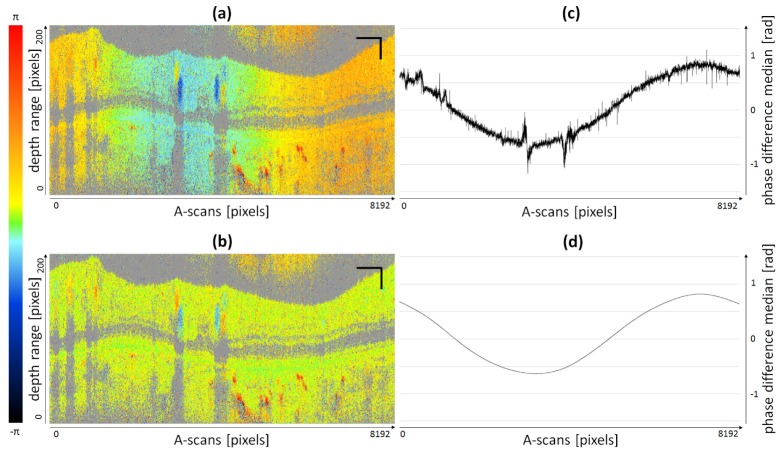
In case of the circular scan pattern employed for the in vivo TRBF measurements, a sinusoidal phase offset was introduced by the scanner, cf. Fig. 4. In order to compensate for this offset, we applied an improved algorithm adopted from previously published work [23, 32]. Each channel and every phase difference B-scan were corrected independently. Every A-scan was evaluated separately to determine the median of all phase difference pixels available (pixels below the intensity threshold were omitted). Thus, a so-called phase offset curve (Fig. 4(c)) was calculated for every single B-scan. For in vivo measurements, phase offsets cannot be attributed to scanning patterns exclusively. Eye-motion may also add to observed phase offsets. Nevertheless, the unprocessed phase offset curve already shows an approximately sinusoidal shape which indicates a primary dependence of the phase offset on the circular scanning pattern. However, especially at vessel locations (non-static tissue) the sinusoidal shape is distorted significantly. The raw phase offset curve was smoothed by a cubic spline fitting algorithm resulting in an almost sinusoidally shaped phase offset curve (Fig. 4(d)). Every A-scan was then corrected for the corresponding value of the smoothed curve. Figures 4(a) and 4(b) show an uncorrected and a phase offset corrected phase difference B-scan, respectively.
Fig. 4.
Illustration of phase offset correction for circular scanning pattern: (a) Non-corrected B-scan (8192 A-scans). (b) Phase offset corrected B-scan. (c) Unprocessed phase offset curve (median of all available pixels per A-scan). (d) Smoothed cubic spline fit of unprocessed phase offset curve. Scale bars: 1 mm (horizontally), 0.1 mm (vertically).
After phase offset correction for each B-scan, the phase difference B-scans were averaged in complex space. In case of the flow phantom investigations, registration of respective B-scans was unnecessary. For the in vivo measurements, the B-scans needed to be registered first. Only selected (manually) rectangular regions of interest (ROI) around a vessel (only vessels with diameter > 50 μm) were registered by hand in reference to the center position of the respective vessel [32]. For the blood flow evaluations, only B-scans within one cardiac cycle were averaged (~40 B-scans (1024 A-scans each, 50% scanning duty cycle) for the bifurcation measurements, ~10 circular B-scans (8192 A-scans each) for TRBF measurements at a subject heart rate (HR) of ~75 bpm). The exact number of B-scans was determined according to the easily observable systolic peaks in the cross-sectional phase difference images of arteries.
In this paper, the procedure to calculate the geometry corrected Cartesian velocity components from the averaged phase difference velocity profiles deviates from the previously reported ones [31, 32]. In [32], the BGM – calculated from knowledge of both the beam separation distances and the focal length of the focusing lens (respective, the refractive optics of the human eye) – is used to solve the three corresponding equations for each pixel separately. Thus, geometry-corrected velocity profile graphs in x-, y- and z-direction are obtained. Thereafter, the geometry-corrected profiles are integrated over the cross-section area and hence one final mean velocity component per Cartesian direction is obtained. In the present work, we perform integration over the cross-sectional profiles before correcting for geometry. Thus, we end up with only three non-geometry-corrected mean velocity components, which afterwards can be used together with the known BGM to calculate the geometry-corrected velocity components. Therefore, only one (compared to former hundreds) matrix multiplication needs to be performed, which largely reduces computational efforts. The cross-sectional integration area was adjusted manually to the borders of each averaged velocity profile with regards to height and width under the constraints of an elliptical shape. Additionally, Haindl et al. [32] introduced an extended BGM calculation algorithm to compute separate BGMs for every single A-scan, since scanning the active sampling beam alters the beam geometry, which, if not corrected for, would result in systematic errors in the 3D velocity vector calculation. As reported previously [31], for a linear scan pattern and small scanning angle (<2.5°), this error can be neglected. Hence, the effect of a changing beam geometry as a function of the scan angle was not considered for the in vitro as well as the in vivo bifurcation measurements. Due to larger angles (~8°–10°) in the circular scanning mode, the small angle, linear scanning approximation was no longer applicable for the in vivo TRBF investigations. Since in this work, integration over the cross-sectional velocity profiles was already applied before the geometry correction, the proposed method needed to be adapted. For each vessel, only one BGM was determined instead of obtaining different BGMs for every A-scan along the lateral extension of the respective vessel. This single BGM corresponds to the central A-scan of the vessel’s lateral extension. Hence, computation time could significantly be decreased by reducing the amount of matrix multiplication operations.
From the 3D velocity vector data, the blood flow Q was determined as follows:
| (11) |
The vessel diameter D was obtained manually from the averaged parabolic phase difference profiles. A mean diameter was calculated from five individual measurements in axial direction assuming a group index of blood of ~1.34. Since the vessel diameter D enters quadratically in Eq. (11), the blood flow calculation is highly sensitive to corresponding changes.
The data acquisition and post-processing was carried out using custom-developed LabView code on an Intel i7 CPU at 3.2 GHz with 24.0 GB RAM.
In vivo measurements were performed in 6 healthy subjects (age: 26–34) after informed consent was obtained. The study was approved by the institutional ethics committee and is in agreement with the tenets of the Declaration of Helsinki. For each volunteer, the axial eye length was determined by partial coherence biometry [42] (Zeiss IOL Master) to allow calculation of the appropriate BGM. The pupil of the subject’s eye was positioned one focal distance from the second telescope lens, using a standard head rest adjustable in x-, y- and z-direction. At this pupil position, the amplitude of beam movement due to scanning was minimal. A simple low-cost video camera – still sensitive enough to visualize the scanning beam at λ0 = 1045 nm – was utilized for correct alignment of the pupil. An adjustable fixation target was displayed to the contralateral eye of the subject to change the imaging location on the retina. Furthermore, an en face online preview generated from OCT data was employed to help locate the desired retinal measurement position while having the scanning beam performing a raster scan pattern.
The linear scanning protocols for the in vitro flow phantom measurements were 704 × 1024 × 150 (depth pixels × A-scans × B-scans) for ~4° scanning angle, the same as for the in vivo retinal bifurcation measurements (the evaluated ROIs (capillary or vessel cross-sections) were centered in the B-scan plane so the previously discussed <2.5° beam geometry approximation for linear scanning could be applied). For the circumpapillary scanning of the in vivo TRBF measurements, 704 × 8192 × 25 for ~8°–10° were used.
3. Results
3.1 In vitro flow phantom measurements
A glass capillary (inner diameter = 300 μm) was used as a flow phantom to demonstrate the capability of our system for quantitative flow measurements. The glass capillary was perfused via a medical injection pump (MGVG Combimat; adjustable flow range: 1.7–3200 μl/min; resulting in mean velocities for parabolic flow of 0.4–750 mm/s) to guarantee constant and reproducible flow rates. The capillary, which was perfused by a scattering fluid – milk diluted with water (ratio: 1:1) – was fixed to a special mount in order to provide alignment along three degrees of freedom to demonstrate absolute quantitative flow measurements and 3D velocity vector reconstruction independently of flow orientation. For the measurements, as depicted in Fig. 1, the capillary was rotated in planes parallel (varying angle ρ) and orthogonal (varying angle δ) to the optical axis.
In Fig. 5, one can observe an exemplary path-length encoded B-scan of a capillary perfusion measurement. The intensity (Fig. 5(a)) as well as the phase difference image (Fig. 5(b)) of the same data set are depicted next to each other (each image is 50-times averaged). Both images contain three cross-sections of the capillary, where the active illumination/detection channel is indicated by yellow stars, whereas the two passive detection-only channels are indicated by pink stars. Each image was cropped to 320 A-scans × 550 depth pixels for the present illustration. The strong reflections, visible in both the intensity and the phase difference image, are attributed to the inner and outer glass surfaces of the capillary. The large gray areas in the phase difference image are due to thresholding of the intensity data (all sub-threshold intensity pixels were set to gray). In Fig. 5(b) the parabolic shaped flow profiles are well noticeable in all three capillary cross-sections. The phase offset introduced by the MEMS scanning mirror was not yet compensated in the phase difference data of Fig. 5(b).
Fig. 5.
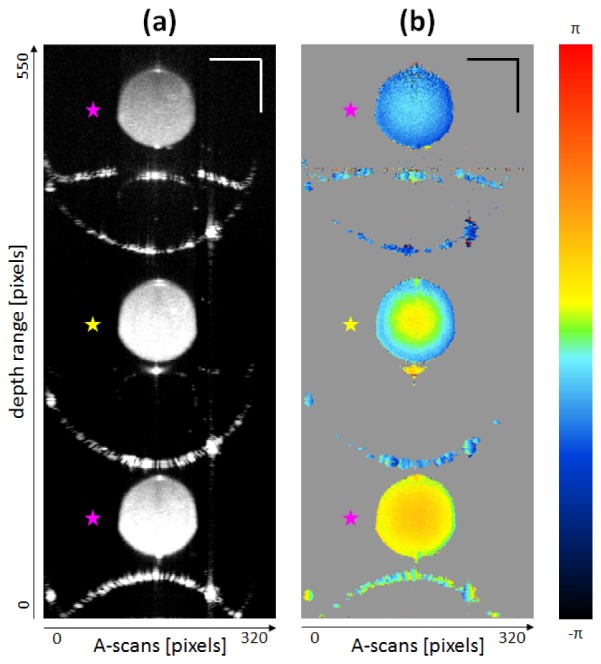
Imaging results from in vitro flow phantom measurements: δ = 90°, ρ = 90°; constant flow 6.94 μl/s; 50-times averaged. Cropped B-scans – yellow stars indicate active illumination/detection channel, pink stars indicate passive detection-only channels. (a) Intensity image. (b) Phase difference image. Scale bars: 200 μm.
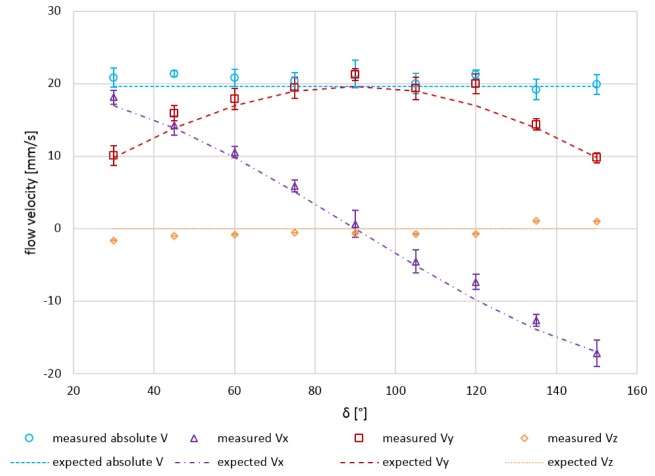
In a first experiment, the 3D velocity vector reconstruction was investigated in the plane orthogonal to the optical axis (x-y-plane). The angle δ was altered from 30° to 150° in steps of 15°. The constant flow mean velocity over the whole parabolic shaped profile was set to 19.65 mm/s. The measured velocity components in x-, y-, and z-direction for varying angles δ are plotted in Fig. 6. The measured velocity values – averaging was applied only over 10 consecutive B-scans here – were in good agreement with the expected/calculated components (error bars indicate ± one standard deviation). The mean residual for the measured absolute velocity (|V|) was 1.0 mm/s (accuracy) and the mean standard deviation was 1.2 mm/s (precision). Since very strong specular reflections from the outer surface of the capillary appeared for ρ = 90°, the capillary needed to be tilted slightly out of the x-y-plane. This tilt results in small systematic deviations of the measured from the expected values, visible in the graph especially for the flow velocity in z-direction which ideally should be zero.
Fig. 6.
Quantitative in vitro flow phantom measurement results: Expected vs. measured velocity vector components Vx, Vy, Vz and |V| for varying angles δ (30°–150° in steps of 15°; orthogonal plane) at a constant mean flow velocity of 19.65 mm/s (10-times averaged). Error bars indicate ± one standard deviation.
In a similar second experiment, the capillary was rotated in the plane parallel to the optical axis (y-z-plane) altering the angle ρ from 90° to 72°. The measurement conditions were identical to the first experiment (constant flow mean velocity = 19.65 mm/s; averaging over 10 consecutive B-scans) and also the measured velocity values showed again very good agreement in comparison to the expected/calculated components (data not shown).
In a third experiment, the 3D velocity vector reconstruction was investigated for varying injection pump flows – ranging from 0.27 to 5.00 μl/s – for fixed angles δ and ρ (δ = 90°, ρ = ~90°). The measured velocity components in x-, y-, and z-direction for varying injection pump flows are plotted in Fig. 7. The measured velocity components were again in good agreement with the expected/calculated components. The mean residual for the measured absolute velocity (|V|) was 1.3 mm/s (accuracy) and the mean standard deviation was 1.6 mm/s (precision).
Fig. 7.
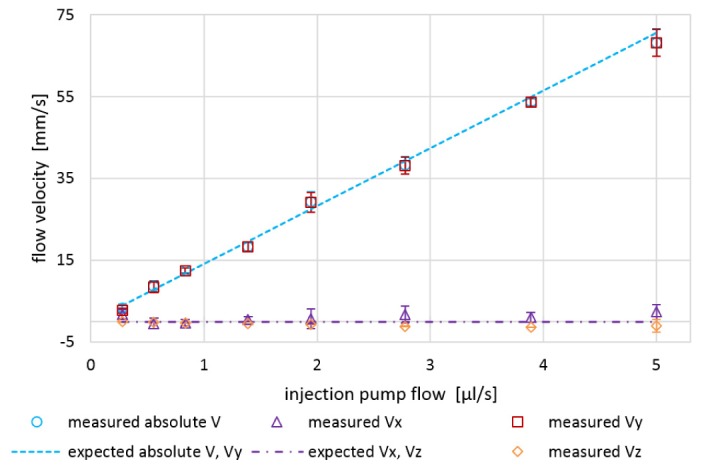
Quantitative in vitro flow phantom measurement results: Expected vs. measured velocity vector components Vx, Vy, Vz and |V| for varying pump flows (0.27–5.00 μl/s) at fixed angles δ = 90° and ρ = 90° (10-times averaged). Error bars indicate ± one standard deviation.
3.2 In vivo retinal bifurcation measurements
Since the in vitro measurements yielded promising results, the next step was to perform in vivo measurements in eyes of healthy human subjects.
Two different types of in vivo measurements were conducted. At first, a verification experiment for demonstrating the performance of the system in vivo was performed. Retinal vessel bifurcations were investigated regarding their respective in- and outflows. The total volumetric inflow of the trunk vessel had to match the summed volumetric outflows of the two daughter vessels. For these preliminary in vivo measurements, linear B-scans were acquired at three locations surrounding a retinal bifurcation.
In total, measurements of three bifurcations in three eyes of three healthy human volunteers were evaluated quantitatively. Table 1 presents the measured Cartesian velocity vector components (Vx, Vy, Vz), the absolute mean flow velocity (|V|), the vessel diameter (D) as well as the respective flow values (Q). Total mean in- and outflow to and from the retinal bifurcation are calculated (discrepancies: 4%–11%).
Table 1. Quantitative evaluation of in vivo retinal bifurcation measurement results: Comparison of absolute in- and outflow to and from three retinal vessel bifurcations in three eyes of three healthy human volunteers.
| Vx [mm/s] | Vy [mm/s] | Vz [mm/s] | |V| [mm/s] | D [mm] | Q [μl/min] | ∑OUT [μl/min] | IN/ ∑OUT | ||
|---|---|---|---|---|---|---|---|---|---|
| EYE 1 | IN | −2.92 | −13.05 | −8.22 | 15.70 | 0.15 | 16.68 | 17.96 | 0.93 |
| OUT 1 | 10.40 | −35.04 | 5.09 | 36.90 | 0.09 | 13.14 | |||
| OUT 2 | 2.82 |
−19.70 |
−3.57 |
20.22 |
0.07 |
4.82 |
|||
| EYE 2 | IN | −1.12 | 26.88 | 4.90 | 27.34 | 0.10 | 13.60 | 12.21 | 1.11 |
| OUT 1 | 1.94 | 21.76 | −1.90 | 21.93 | 0.08 | 7.81 | |||
| OUT 2 | −1.48 |
18.10 |
−3.35 |
18.46 |
0.07 |
4.40 |
|||
| EYE 3 | IN | −1.27 | 19.58 | −6.58 | 20.70 | 0.13 | 17.61 | 18.43 | 0.96 |
| OUT 1 | 3.53 | 24.62 | −3.44 | 25.11 | 0.11 | 14.49 | |||
| OUT 2 | 7.05 | 14.94 | 0.01 | 16.52 | 0.07 | 3.94 |
3.3 In vivo TRBF measurements
For the second type of in vivo measurements – to quantify TRBF – circumpapillary scanning was employed. Since the retinal blood circulation presents a closed system in terms of in- and outflow with a common source/sink at the optic disc, a circular scan pattern around the ONH allows for TRBF measurements. In order to align the subject’s eye utilizing the fixation target, a raster scan pattern was applied to help center the ONH in the en face projection online preview. At the preferred position, the scanning pattern was switched to a circle with a diameter corresponding to a field of view of ~8°–10°. Readjustments of the eye fixation position, necessary due to subject movement, could also be made in circular scanning mode by the trained operator.
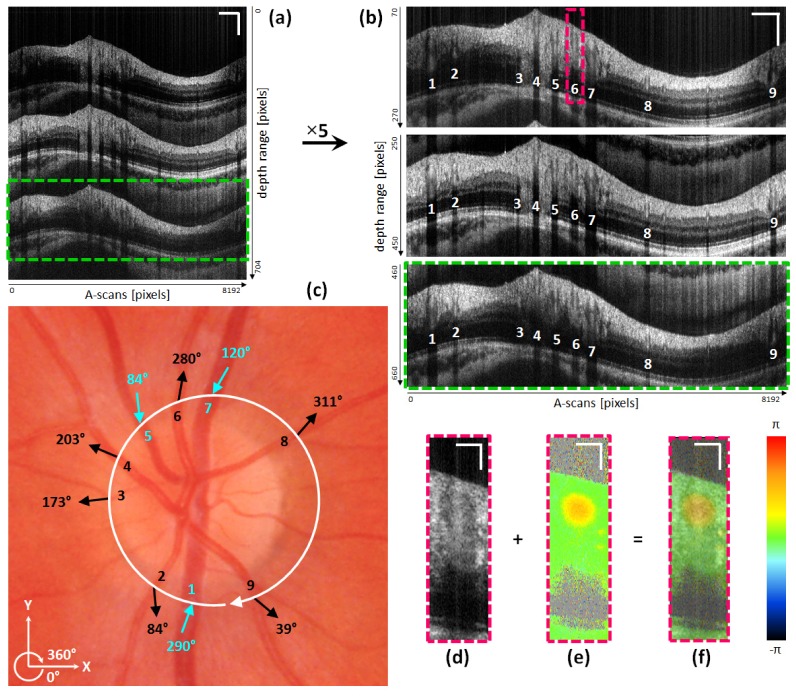
Figure 8 shows exemplary images recorded during a TRBF measurement in the eye of a healthy volunteer. A single path-length encoded circular intensity B-scan is depicted in Fig. 8(a). Additionally, cropped and 5-times averaged circular intensity B-scans for each channel are shown in Fig. 8(b) (white numbers indicate evaluated vessels). Figure 8(c) indicates one circular scan of the active beam around the ONH via the white circle in a fundus photo. Only vessels with a measured diameter larger than 50 μm were evaluated. The numbers inside the circle indicate the evaluated vessels, whereas the small arrows on the outside present the measured flow orientations. Figure 8(d)-8(f) depict a cropped ROI of one of the passive channels containing an artery (No. 6) to illustrate intensity (Fig. 8(d)) and phase difference image results (Fig. 8(e)) as well as a transparent overlay of both (Fig. 8(f)).
Fig. 8.
Illustration of TRBF measurements and OCT image results: (a) single path-length encoded circular OCT intensity B-scan of circumpapillary scan of the eye of a healthy volunteer. (b) Circular OCT intensity B-scans (5-times averaged) for all three channels (active: middle image; passive: upper and lower image). White numbers indicate vessels accounted for TRBF determination. (c) ONH centered color fundus photo. White circular arrow indicates the beam path of the active channel. Numbers, arrows and angular values indicate the respective vessels as well as their orientation of blood flow (veins: turquoise; arteries: black). (d) Cropped circular intensity OCT B-scan of vessel ROI of passive channel. (e) Phase difference image of same ROI as in (d). (f) Transparent overlay of (d) and (e). Scale bars (a), (b): 1 mm (horizontally), 0.2 mm (vertically). Scale bars (d), (e), (f): 100 μm.
In Table 2, the quantitative evaluation results for the TRBF investigation of the same eye as depicted in Fig. 8 can be observed. For every artery/vein the Cartesian velocity components (Vx, Vy, Vz), the absolute mean flow velocity (|V|), the angle of flow orientation within the plane orthogonal to the optical axis (δ), the diameter (D) as well as the respective flow values (Q) are indicated.
Table 2. Quantitative evaluation of in vivo TRBF measurement results: Measured velocity components in x-, y- and z-direction (Vx, Vy, Vz), absolute mean flow velocity value (|V|), vessel orientation (δ), vessel diameter (D) and flow rate (Q) of three veins (V) and six arteries (A) in one eye of a healthy human volunteer.
| # | A / V | Vx [mm/s] | Vy [mm/s] | Vz [mm/s] | |V| [mm/s] | δ [°] | D [μm] | Q [μl/min] |
|---|---|---|---|---|---|---|---|---|
| 1 | V | 5.87 | 16.29 | 1.87 | 17.42 | 290 | 158 | 20.51 |
| 2 | A | 0.75 | −7.09 | 0.99 | 7.20 | 84 | 87 | 2.57 |
| 3 | A | −4.95 | −0.65 | −1.10 | 5.11 | 173 | 55 | 0.74 |
| 4 | A | −11.97 | 5.06 | 2.30 | 13.20 | 203 | 119 | 8.50 |
| 5 | V | 0.91 | −8.00 | 0.48 | 8.07 | 84 | 111 | 4.65 |
| 6 | A | 4.28 | 22.34 | 2.85 | 22.92 | 281 | 119 | 15.18 |
| 7 | V | −8.84 | −15.65 | 0.44 | 17.98 | 120 | 150 | 19.10 |
| 8 | A | 18.37 | 20.95 | 3.90 | 28.13 | 311 | 87 | 11.92 |
| 9 | A | 6.32 | −5.17 | −1.61 | 8.32 | 39 | 79 | 4.14 |
Total venous blood flow (three vessels) can be summed up to 44.26 μl/min, while total arterial blood flow (six vessels) can be summed up to 43.05 μl/min. In Table 3, the total respective venous and arterial blood flow as well as the respective flow ratio of two further evaluated eyes are listed.
Table 3. Quantitative evaluation of in vivo TRBF measurement results: Comparison of total venous Qv and total arterial retinal blood flow Qa in three eyes of three healthy human volunteers.
| Total Qv [μl/min] | Total Qa [μl/min] | Total Qv / Total Qa | |
|---|---|---|---|
| EYE 1 | 44.26 | 43.05 | 1.03 |
| EYE 2 | 49.18 | 48.12 | 1.02 |
| EYE 3 | 44.96 | 42.86 | 1.05 |
Since only three eyes of three healthy human volunteers were investigated for their TRBF, a detailed statistical analysis would be inappropriate. However, the respective flow ratios for all three eyes are fairly close to unity, which demonstrates the system’s ability to quantify TRBF. Additionally, the TRBF values (for veins and arteries) for the three evaluated eyes (between 42 and 50 μl/min) were found to be within the range of previously reported TRBF data [18, 19, 23, 32].
4. Discussion
The introduced APPLE approach for DOCT enables quantification and orientation reconstruction of flow in 3D, without the necessity of prior information of the direction of motion. We tested the system’s performance in vitro on a flow phantom and found good agreement between measured and expected flow velocity values. In principle, the technique can be applied to any sample (biomedical or not) comprising moving particles. In this paper we demonstrate its capabilities for in vivo application in the demanding ophthalmic environment by investigating OBF and determining TRBF in the eyes of healthy subjects.
In comparison to our previous three-beam approach [31], system complexity is greatly reduced. This is achieved by a combination of an active/passive channel approach and the principle of path-length encoding. The active/passive channel concept eliminates the need of multiple light sources and was already proposed for the use of DOCT [33]. One additional benefit of the applied method is that the detected signal in all three channels intrinsically results from one identical backscattering location. Corresponding multi-beam approaches incorporating more than one active illumination/detection channel focused onto a mutual spot, have no means of determining whether their backscattering locations match perfectly. Optical aberrations introduced by the eye may lead to a displacement between multiple active beams on the retina. Using passive channels, these aberrations would cause a reduced backscattering signal. This has previously been observed in retinal imaging with larger scanning angles [33]. In this case, active realignment of the passive detection-only channels needs to be implemented in order to compensate for these aberrations. However, in our experiments – including imaging of the ONH region in six healthy (3 for bifurcation measurements, 3 for TRBF measurements) subjects – we did not encounter any general signal losses in the passive channels as long as the subject’s pupil was well aligned. This might be due to the small scanning angels (up to max. ~10°) that were used in our study. Nevertheless, it was found that signal intensity for the passive channels was more prone to fluctuations for altering scan locations of a circular B-scan than for the active channel, where very stable signal intensity was observed (cf. Fig. 8(a)-8(b)). In some areas (pronounced especially in the RNFL) signal intensity of the passive channels even surpassed the one of the active channel, while in other areas signal intensity was somewhat lower. This effect, on the one hand, might indeed be attributed to optical aberrations introduced by the eye. On the other hand, potential non-isotropic angular scattering properties of the retina – previously reported in directional OCT studies [43] – might cause similar effects. More detailed investigations will be required to better understand the origin of this effect.
The concept of path-length encoding enables a further simplification of the system as the number of detectors and DAQ channels can be reduced to one each. This however, requires an OCT system that offers low sensitivity drop with depth. Thus, path-length encoding is only reasonable applicable for swept source setups. The presented system (sensitivity roll-off ~1–2 dB for 3.7 mm in air) provides sufficient imaging range to visualize three retinal B-scans simultaneously. However, path-length encoding can become problematic in the presence of pathologies such as retinal detachments. In these cases the axial extension of the retina can exceed the imaging range of each channel which results in overlapping images. The implementation of long coherence length swept sources such as VCSEL [44] or akinetic light sources [45] might overcome this limitation, as these provide a larger imaging depth without significant loss of sensitivity. Nevertheless, this would result in the need for detection of a higher frequency bandwidth.
Another advantage of SS-OCT technology is the elimination of fringe/phase washout arising in SD-DOCT at lower A-scan rates [46]. While in SD-OCT high flow velocities cause low signal intensities mainly the axial resolution will be affected in SS-OCT. Although such high flow velocities may result in large phase values (depending on the angle of observation) and consequently in phase wrapping, corresponding techniques to recover the true phase values can be applied in post-processing.
On the other hand, phase stability is a quite controversially discussed topic when it comes to a comparison between SD- and SS-DOCT. Apart from akinetic swept sources [47], many commercially available swept sources (including the one used here) suffer from intrinsic phase instabilities due to trigger fluctuations. Several groups have addressed this problem with a variety of modifications [48, 49]. We achieved satisfying results by employing an FBG to correct for sweep trigger fluctuations [39].
Because of limited availability of swept sources in the 800 nm regime, we choose to switch to the 1050 nm region for our new swept source approach (in comparison to our previous SD system [31] centered at λ0 = 840 nm). The use of longer wavelengths enhances the penetration depth in retinal tissue [50] and thus may be beneficial in patients with media opacities [51]. As such, the system can hence be used to investigate choroidal blood flow beneath the strongly scattering retinal pigment epithelium (RPE). The detection of sub-RPE phase changes, as observable in Fig. 4, is very promising. Thus, future research may also target investigations of choroidal perfusion.
TRBF may further evolve into a significant biomarker in patients suffering from ocular diseases such as glaucoma, DR, or C/BRVO. Critical for the extraction of this parameter from DOCT data is the determination of the vessel diameter D, because it enters quadratically in the flow calculation (cf. Eq. (11)). Due to the pulsatile nature of especially the retinal arteries, the registration and averaging of respective B-scans might introduce systematic errors in D. In addition, it remains unclear whether 10–12 measurement points during a single heart cycle are sufficient to average out the pulsatile behavior. Certainly, further investigations concerning this issue need to be performed. An additional problem for TRBF determination arises for eyes where the circumpapillary scan pattern intersects entangled vessels. In such cases TRBF might not be evaluable because of shadowing of vessels located atop of each other in an acquired circular B-scan. Finally, our post-processing algorithms for TRBF determination are tailored to parabolically shaped velocity profiles. As known from recent work [52], especially for vessel areas close to bifurcations a distorted velocity profile can sometimes be observed.
5. Conclusion
In this work, we presented a novel approach for non-invasive quantitative blood flow investigations in vivo. This active-passive path-length encoded (APPLE) DOCT method is based on swept source technology and features a single active illumination/detection and two passive detection-only channels. We demonstrated the system’s performance with in vitro flow phantom and in vivo retinal bifurcation measurements. Furthermore, the ability to quantify the biomarker TRBF in humans was shown. Alterations in TRBF may be associated with a variety of major ocular diseases like glaucoma, DR or C/BRVO. Thus, it is a future aim of this work to investigate eyes of patients suffering from such pathologies. Moreover, the APPLE principle holds the potential for application in non-ophthalmic research areas like cerebral or dermatologic optical imaging.
Disclosures
All authors – none.
Acknowledgments
We are grateful to Magdalena Baratsits and Philipp K. Roberts, Department of Ophthalmology at the Medical University of Vienna, for providing color fundus photos and performing axial eye length measurements. We would also like to acknowledge Harald Sattmann and Franz Beck for electro technical and Andreas Hodul for technical workshop assistance. Furthermore, we wish to thank Lara M. Wurster, Marco Augustin, Matias Salas, Stanislava Fialová, Laurin Ginner, René Werkmeister, Florian Beer, Danielle J. Harper, Pablo Eugui and Antonia Lichtenegger for their assistance and helpful discussions.
Funding
This work was supported by the Austrian Science Fund (FWF; grant number: P26553-N20).
References and links
- 1.Detre J. A., Leigh J. S., Williams D. S., Koretsky A. P., “Perfusion imaging,” Magn. Reson. Med. 23(1), 37–45 (1992). [DOI] [PubMed] [Google Scholar]
- 2.Cracowski J. L., Minson C. T., Salvat-Melis M., Halliwill J. R., “Methodological issues in the assessment of skin microvascular endothelial function in humans,” Trends Pharmacol. Sci. 27(9), 503–508 (2006). [DOI] [PubMed] [Google Scholar]
- 3.Flammer J., Orgül S., Costa V. P., Orzalesi N., Krieglstein G. K., Serra L. M., Renard J.-P., Stefánsson E., “The impact of ocular blood flow in glaucoma,” Prog. Retin. Eye Res. 21(4), 359–393 (2002). [DOI] [PubMed] [Google Scholar]
- 4.Durham J. T., Herman I. M., “Microvascular modifications in diabetic retinopathy,” Curr. Diab. Rep. 11(4), 253–264 (2011). [DOI] [PubMed] [Google Scholar]
- 5.Grunwald J. E., Riva C. E., Baine J., Brucker A. J., “Total retinal volumetric blood flow rate in diabetic patients with poor glycemic control,” Invest. Ophthalmol. Vis. Sci. 33(2), 356–363 (1992). [PubMed] [Google Scholar]
- 6.Wang Y., Fawzi A. A., Varma R., Sadun A. A., Zhang X., Tan O., Izatt J. A., Huang D., “Pilot study of optical coherence tomography measurement of retinal blood flow in retinal and optic nerve diseases,” Invest. Ophthalmol. Vis. Sci. 52(2), 840–845 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hwang J. C., Konduru R., Zhang X., Tan O., Francis B. A., Varma R., Sehi M., Greenfield D. S., Sadda S. R., Huang D., “Relationship among visual field, blood flow, and neural structure measurements in glaucoma,” Invest. Ophthalmol. Vis. Sci. 53(6), 3020–3026 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schmetterer L., Garhofer G., “How can blood flow be measured?” Surv. Ophthalmol. 52(2 Suppl 2), S134–S138 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Garcia J. P. S., Jr, Garcia P. T., Rosen R. B., “Retinal blood flow in the normal human eye using the canon laser blood flowmeter,” Ophthalmic Res. 34(5), 295–299 (2002). [DOI] [PubMed] [Google Scholar]
- 10.Wang Y., Bower B. A., Izatt J. A., Tan O., Huang D., “In vivo total retinal blood flow measurement by Fourier domain Doppler optical coherence tomography,” J. Biomed. Opt. 12(4), 041215 (2007). [DOI] [PubMed] [Google Scholar]
- 11.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Fujimoto J. G., “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang X. J., Milner T. E., Nelson J. S., “Characterization of fluid flow velocity by optical Doppler tomography,” Opt. Lett. 20(11), 1337–1339 (1995). [DOI] [PubMed] [Google Scholar]
- 13.Chen Z., Milner T. E., Dave D., Nelson J. S., “Optical Doppler tomographic imaging of fluid flow velocity in highly scattering media,” Opt. Lett. 22(1), 64–66 (1997). [DOI] [PubMed] [Google Scholar]
- 14.Izatt J. A., Kulkarni M. D., Yazdanfar S., Barton J. K., Welch A. J., “In vivo bidirectional color Doppler flow imaging of picoliter blood volumes using optical coherence tomography,” Opt. Lett. 22(18), 1439–1441 (1997). [DOI] [PubMed] [Google Scholar]
- 15.Makita S., Hong Y., Yamanari M., Yatagai T., Yasuno Y., “Optical coherence angiography,” Opt. Express 14(17), 7821–7840 (2006). [DOI] [PubMed] [Google Scholar]
- 16.Wang R. K., Jacques S. L., Ma Z., Hurst S., Hanson S. R., Gruber A., “Three dimensional optical angiography,” Opt. Express 15(7), 4083–4097 (2007). [DOI] [PubMed] [Google Scholar]
- 17.Leitgeb R. A., Werkmeister R. M., Blatter C., Schmetterer L., “Doppler optical coherence tomography,” Prog. Retin. Eye Res. 41(100), 26–43 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang Y., Lu A., Gil-Flamer J., Tan O., Izatt J. A., Huang D., “Measurement of total blood flow in the normal human retina using Doppler Fourier-domain optical coherence tomography,” Br. J. Ophthalmol. 93(5), 634–637 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tayyari F., Yusof F., Vymyslicky M., Tan O., Huang D., Flanagan J. G., Hudson C., “Variability and repeatability of quantitative, Fourier-domain optical coherence tomography Doppler blood flow in young and elderly healthy subjects,” Invest. Ophthalmol. Vis. Sci. 55(12), 7716–7725 (2014). [DOI] [PubMed] [Google Scholar]
- 20.Peterson L. M., Gu S., Jenkins M. W., Rollins A. M., “Orientation-independent rapid pulsatile flow measurement using dual-angle Doppler OCT,” Biomed. Opt. Express 5(2), 499–514 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Michaely R., Bachmann A. H., Villiger M. L., Blatter C., Lasser T., Leitgeb R. A., “Vectorial reconstruction of retinal blood flow in three dimensions measured with high resolution resonant Doppler Fourier domain optical coherence tomography,” J. Biomed. Opt. 12(4), 041213 (2007). [DOI] [PubMed] [Google Scholar]
- 22.Wehbe H., Ruggeri M., Jiao S., Gregori G., Puliafito C. A., Zhao W., “Automatic retinal blood flow calculation using spectral domain optical coherence tomography,” Opt. Express 15(23), 15193–15206 (2007). [DOI] [PubMed] [Google Scholar]
- 23.Baumann B., Potsaid B., Kraus M. F., Liu J. J., Huang D., Hornegger J., Cable A. E., Duker J. S., Fujimoto J. G., “Total retinal blood flow measurement with ultrahigh speed swept source/Fourier domain OCT,” Biomed. Opt. Express 2(6), 1539–1552 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Davé D. P., Milner T. E., “Doppler-angle measurement in highly scattering media,” Opt. Lett. 25(20), 1523–1525 (2000). [DOI] [PubMed] [Google Scholar]
- 25.Pedersen C. J., Huang D., Shure M. A., Rollins A. M., “Measurement of absolute flow velocity vector using dual-angle, delay-encoded Doppler optical coherence tomography,” Opt. Lett. 32(5), 506–508 (2007). [DOI] [PubMed] [Google Scholar]
- 26.Ahn Y.-C., Jung W., Chen Z., “Quantification of a three-dimensional velocity vector using spectral-domain Doppler optical coherence tomography,” Opt. Lett. 32(11), 1587–1589 (2007). [DOI] [PubMed] [Google Scholar]
- 27.Werkmeister R. M., Dragostinoff N., Pircher M., Götzinger E., Hitzenberger C. K., Leitgeb R. A., Schmetterer L., “Bidirectional Doppler Fourier-domain optical coherence tomography for measurement of absolute flow velocities in human retinal vessels,” Opt. Lett. 33(24), 2967–2969 (2008). [DOI] [PubMed] [Google Scholar]
- 28.Iftimia N. V., Hammer D. X., Ferguson R. D., Mujat M., Vu D., Ferrante A. A., “Dual-beam Fourier domain optical Doppler tomography of zebrafish,” Opt. Express 16(18), 13624–13636 (2008). [DOI] [PubMed] [Google Scholar]
- 29.Blatter C., Coquoz S., Grajciar B., Singh A. S., Bonesi M., Werkmeister R. M., Schmetterer L., Leitgeb R. A., “Dove prism based rotating dual beam bidirectional Doppler OCT,” Biomed. Opt. Express 4(7), 1188–1203 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Doblhoff-Dier V., Schmetterer L., Vilser W., Garhöfer G., Gröschl M., Leitgeb R. A., Werkmeister R. M., “Measurement of the total retinal blood flow using dual beam Fourier-domain Doppler optical coherence tomography with orthogonal detection planes,” Biomed. Opt. Express 5(2), 630–642 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Trasischker W., Werkmeister R. M., Zotter S., Baumann B., Torzicky T., Pircher M., Hitzenberger C. K., “In vitro and in vivo three-dimensional velocity vector measurement by three-beam spectral-domain Doppler optical coherence tomography,” J. Biomed. Opt. 18(11), 116010 (2013). [DOI] [PubMed] [Google Scholar]
- 32.Haindl R., Trasischker W., Wartak A., Baumann B., Pircher M., Hitzenberger C. K., “Total retinal blood flow measurement by three beam Doppler optical coherence tomography,” Biomed. Opt. Express 7(2), 287–301 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Klein T., André R., Wieser W., Pfeiffer T., Huber R., “Joint aperture detection for speckle reduction and increased collection efficiency in ophthalmic MHz OCT,” Biomed. Opt. Express 4(4), 619–634 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Iftimia N., Bouma B. E., Tearney G. J., “Speckle reduction in optical coherence tomography by “path length encoded” angular compounding,” J. Biomed. Opt. 8(2), 260–263 (2003). [DOI] [PubMed] [Google Scholar]
- 35.Wang B., Yin B., Dwelle J., Rylander H. G., 3rd, Markey M. K., Milner T. E., “Path-length-multiplexed scattering-angle-diverse optical coherence tomography for retinal imaging,” Opt. Lett. 38(21), 4374–4377 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Haindl R., Trasischker W., Baumann B., Pircher M., Hitzenberger C. K., “Three-beam Doppler optical coherence tomography using a facet prism telescope and MEMS mirror for improved transversal resolution,” J. Mod. Opt. 62(21), 1781–1788 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hafez M., Sidler T., Salathe R.-P., “Study of the beam path distortion profiles generated by a two-axis tilt single-mirror laser scanner,” Opt. Eng. 42(4), 1048–1057 (2003). [Google Scholar]
- 38.International Electrotechnical Commission, “Safety of laser products – Part 1: Equipment classification and requirements,” IEC-60825–1(2), (2014).
- 39.Choi W., Potsaid B., Jayaraman V., Baumann B., Grulkowski I., Liu J. J., Lu C. D., Cable A. E., Huang D., Duker J. S., Fujimoto J. G., “Phase-sensitive swept-source optical coherence tomography imaging of the human retina with a vertical cavity surface-emitting laser light source,” Opt. Lett. 38(3), 338–340 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Klein T., Wieser W., Eigenwillig C. M., Biedermann B. R., Huber R., “Megahertz OCT for ultrawide-field retinal imaging with a 1050 nm Fourier domain mode-locked laser,” Opt. Express 19(4), 3044–3062 (2011). [DOI] [PubMed] [Google Scholar]
- 41.Yang V. X. D., Gordon M. L., Mok A., Zhao Y., Chen Z., Cobbold R. S. C., Wilson B. C., Alex Vitkin I., “Improved phase-resolved optical Doppler tomography using the Kasai velocity estimator and histogram segmentation,” Opt. Commun. 208(4–6), 209–214 (2002). [Google Scholar]
- 42.Hitzenberger C. K., “Optical measurement of the axial eye length by laser Doppler interferometry,” Invest. Ophthalmol. Vis. Sci. 32(3), 616–624 (1991). [PubMed] [Google Scholar]
- 43.Lujan B. J., Roorda A., Knighton R. W., Carroll J., “Revealing Henle’s fiber layer using spectral domain optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 52(3), 1486–1492 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Grulkowski I., Liu J. J., Potsaid B., Jayaraman V., Lu C. D., Jiang J., Cable A. E., Duker J. S., Fujimoto J. G., “Retinal, anterior segment and full eye imaging using ultrahigh speed swept source OCT with vertical-cavity surface emitting lasers,” Biomed. Opt. Express 3(11), 2733–2751 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bonesi M., Minneman M. P., Ensher J., Zabihian B., Sattmann H., Boschert P., Hoover E., Leitgeb R. A., Crawford M., Drexler W., “Akinetic all-semiconductor programmable swept-source at 1550 nm and 1310 nm with centimeters coherence length,” Opt. Express 22(3), 2632–2655 (2014). [DOI] [PubMed] [Google Scholar]
- 46.Hendargo H. C., McNabb R. P., Dhalla A.-H., Shepherd N., Izatt J. A., “Doppler velocity detection limitations in spectrometer-based versus swept-source optical coherence tomography,” Biomed. Opt. Express 2(8), 2175–2188 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chen Z., Liu M., Minneman M., Ginner L., Hoover E., Sattmann H., Bonesi M., Drexler W., Leitgeb R. A., “Phase-stable swept source OCT angiography in human skin using an akinetic source,” Biomed. Opt. Express 7(8), 3032–3048 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yamanari M., Lim Y., Makita S., Yasuno Y., “Visualization of phase retardation of deep posterior eye by polarization-sensitive swept-source optical coherence tomography with 1-microm probe,” Opt. Express 17(15), 12385–12396 (2009). [DOI] [PubMed] [Google Scholar]
- 49.Braaf B., Vermeer K. A., Sicam V. A. D. P., van Zeeburg E., van Meurs J. C., de Boer J. F., “Phase-stabilized optical frequency domain imaging at 1-µm for the measurement of blood flow in the human choroid,” Opt. Express 19(21), 20886–20903 (2011). [DOI] [PubMed] [Google Scholar]
- 50.Považay B., Bizheva K., Hermann B., Unterhuber A., Sattmann H., Fercher A., Drexler W., Schubert C., Ahnelt P., Mei M., Holzwarth R., Wadsworth W., Knight J., Russell P. S., “Enhanced visualization of choroidal vessels using ultrahigh resolution ophthalmic OCT at 1050 nm,” Opt. Express 11(17), 1980–1986 (2003). [DOI] [PubMed] [Google Scholar]
- 51.Esmaeelpour M., Považay B., Hermann B., Hofer B., Kajic V., Kapoor K., Sheen N. J. L., North R. V., Drexler W., “Three-dimensional 1060-nm OCT: choroidal thickness maps in normal subjects and improved posterior segment visualization in cataract patients,” Invest. Ophthalmol. Vis. Sci. 51(10), 5260–5266 (2010). [DOI] [PubMed] [Google Scholar]
- 52.Aschinger G. C., Schmetterer L., Doblhoff-Dier V., Leitgeb R. A., Garhöfer G., Gröschl M., Werkmeister R. M., “Blood flow velocity vector field reconstruction from dual-beam bidirectional Doppler OCT measurements in retinal veins,” Biomed. Opt. Express 6(5), 1599–1615 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]