The Moses–Littenberg meta-analytical method generates systematic differences in test accuracy compared to hierarchical meta-analytical models

Abstract

Objective

To compare meta-analyses of diagnostic test accuracy using the Moses–Littenberg summary receiver operating characteristic (SROC) approach with those of the hierarchical SROC (HSROC) model.

Study Design and Setting

Twenty-six data sets from existing test accuracy systematic reviews were reanalyzed with the Moses–Littenberg model, using equal weighting (“E-ML”) and weighting by the inverse variance of the log DOR (“W-ML”), and with the HSROC model. The diagnostic odds ratios (DORs) were estimated and covariates added to both models to estimate relative DORs (RDORs) between subgroups. Models were compared by calculating the ratio of DORs, the ratio of RDORs, and P-values for detecting asymmetry and effects of covariates on DOR.

Results

Compared to the HSROC model, the Moses–Littenberg model DOR estimates were a median of 22% (“E-ML”) and 47% (“W-ML”) lower at Q*, and 7% and 42% lower at the central point in the data. Instances of the ML models giving estimates higher than the HSROC model also occurred. Investigations of heterogeneity also differed; the Moses–Littenberg models on average estimating smaller differences in RDOR.

Conclusions

Moses–Littenberg meta-analyses can generate lower estimates of test accuracy, and smaller differences in accuracy, compared to mathematically superior hierarchical models. This has implications for the usefulness of meta-analyses using this approach. We recommend meta-analysis of diagnostic test accuracy studies to be conducted using available hierarchical model–based approaches.

What is new?

Key findings

• •The Moses–Littenberg model for meta-analyzing diagnostic test accuracy data on average generates lower estimates of test accuracy in comparison to the hierarchical summary ROC method for meta-analysis.
• •Substantial differences in results of investigations of heterogeneity between models are produced, both for estimates of the size of the effect and its statistical significance.

What this adds to what was known?

• •Our findings support and extend those of a previous empirical comparison of methods, further raising concerns around the use of the results of Moses–Littenberg meta-analyses in clinical practice.

What is the implication and what should change now?

• •Evidence for current recommendations for the preferential use of hierarchical models for diagnostic test meta-analyses is provided and should further encourage their uptake.

1. Introduction

There is a considerable body of systematic reviews and meta-analyses of diagnostic test accuracy (DTA) in the public domain [1], [2]. Meta-analysis allows more precise estimation of test accuracy, can provide a stronger comparison of the accuracy of different tests compared to a single study, and allows the inevitable variability between studies to be quantified and formally investigated, as and when there is sufficient cause to suspect clinical or methodological variability [3], [4]. The statistical pooling of test accuracy studies presents an added level of complexity over and above that presented by trials of therapeutic interventions. Accuracy is usually quantified by two related statistics (sensitivity and specificity) rather than one, and meta-analysis must allow for the trade-off between the two. Approaches to DTA meta-analysis include separate pooling of sensitivity and specificity estimates, the linear regression approach to estimating summary receiver operating characteristic (SROC) curves developed by Moses and Littenberg (referred to here as Moses–Littenberg) [5], [6], and methods based on hierarchical models [7], [8], [9], [10], [11].

The theoretical limitations and advantages of the different meta-analytical approaches are well documented [12], [13], [14]. Although the Moses–Littenberg approach accounts for the bivariate nature of the data and the inverse correlation between sensitivity and specificity, it does not appropriately model within- and between-study variability to account for the uncertainty in the estimates, such that confidence intervals and hypotheses tests from the model are possibly invalid and summary operating points are hard to estimate. The hierarchical models preserve the bivariate nature of test accuracy data in terms of both model parameterization and interpretation, accounting for the correlation between sensitivity and specificity; they appropriately weight studies to account for within-study variability; and use a random-effects approach to account for between-study variability. They also allow estimation of the diagnostic odds ratio (DOR) and an average operating point in terms of sensitivity–specificity pair, with associated confidence and prediction regions.

The hierarchical models have been recommended for DTA meta-analyses by the Cochrane Collaboration since 2007 [3]. However, the Moses–Littenberg model was used in 43% of 760 meta-analyses of diagnostic or predictive accuracy published between 1987 and 2009 and made up 86% of all meta-analyses that used ROC approaches to synthesis [15]. A survey of 100 DTA meta-analyses published between September 2011 and January 2012 found that over half continued to pool studies using either simple linear regression-based SROC analysis or a univariate approach, and not the preferred hierarchical models [16]. Three-quarters of corresponding authors for 24 of the reviews using these “traditional” approaches believed the approach to be “currently recommended” and 71% “believed that the method yielded precise estimates” [16]. Meta-analyses undertaken before this period are even more likely to have used the mathematically inferior models [1], [2].

Available empirical studies examining the impact of choice of meta-analytic model on overall results have reached conflicting conclusions, noting that hierarchical models produce different results to simpler models [14] or suggesting that conclusions may not differ [17], [18]. None of these studies considered possible effects on investigations of heterogeneity, such as looking at differences between tests or subgroups.

Given the widespread use of the Moses–Littenberg meta-analysis model, there is a need to identify and quantify any potential differences in estimates of test accuracy and in investigations of sources of heterogeneity. The complexity of the hierarchical models and their omission from commonly used meta-analytical software programs [19] further compounds the need to determine the degree to which results might be affected by the choice of approach. Our objective was to empirically compare the Moses–Littenberg and hierarchical SROC (HSROC) approaches for the overall synthesis of DTA data and for the investigation of sources of heterogeneity using a large sample of systematic reviews.

2. Methods

2.1. Identification, extraction, and analysis of systematic review data

Existing test accuracy systematic reviews were identified from the Database of Abstracts of Reviews of Effects, the HTA database of the Cochrane Library, and the MEDION database of systematic reviews. The cohort we analyzed has been partially reported on previously [1] and includes reviews published between 2000 and 2005 that presented sufficient information to allow the construction of a 2 × 2 contingency table comparing a test to a reference test for at least five primary studies. Systematic reviews had to include at least five studies and report at least one study-level covariate. One reviewer assessed whether reviews met these criteria. All subgroups in the data set contained at least three studies.

Data on the experimental test and target disorder, the 2 × 2 contingency table data, and data on any potential spectrum-related sources of heterogeneity per study were extracted independently by two reviewers. Disagreements were resolved by consensus or referral to a third reviewer.

2.2. Meta-analytical methods

Three alternative meta-analytical methods were considered, two formulations of the Moses–Littenberg model with different study weighting, and the HSROC model.

The Moses–Littenberg model was fitted as originally described [5], [6]. The approach involves computing the logit-transforms of sensitivity and the complement of specificity and undertaking a linear regression of the difference between them (D, or the log of the DOR) on the sum (S, a measure of the proportion that are test positive, which is a proxy for test threshold) to estimate an intercept parameter α and a slope parameter β. A summary ROC curve is derived from the fitted regression line. The test of the significance of the slope β is used to determine whether there is evidence that the DOR varies with the threshold parameter S, which implies that the summary ROC curve has an asymmetric shape. Differences between subgroups in the log DOR can be investigated by adding indicator variables as covariates. The parameter estimates for these are the log relative DOR (RDOR) comparing the DOR between the subgroups. Inclusion of interactions between each covariate and the S parameter allows for different shaped curves in each subgroup. We fitted models with and without the interaction term. The regression intercept term estimates the log of the DOR at the Q* point, where sensitivity is equal to specificity. We used the DOR value at this point in accuracy comparisons, but as it may lie outside the results of the observed studies, we also made comparisons of the DOR estimated at the mean value of S which will be central to the observed study results. We fitted the Moses–Littenberg model giving equal weight to all studies (denoted “E-ML”), and weighting each study (denoted “W-ML”) by the inverse variance of the log DOR, in accordance with standard practice [12]. A standard zero-cell correction (the addition of 0.5 to every cell of a 2 × 2 table that contains at least one zero) was used to avoid divide by zero errors.

Two versions of the hierarchical model are commonly used for meta-analysis, the HSROC, and the bivariate models, which have been shown to be mathematically equivalent for single-test meta-analyses but to estimate different parameters in investigations of heterogeneity [14]. We chose the HSROC model for comparison with the Moses–Littenberg models as both estimate RDOR in heterogeneity investigations. We fitted the HSROC model proposed by Rutter and Gatsonis [7], [8] which is based on a latent-scale logistic regression model [20], [21]. The HSROC model assumes that there is an underlying ROC curve in each study with parameters α and β which characterize the accuracy and asymmetry of the curve, in a similar way to the α and β parameters in the linear regression method of Moses and Littenberg. The parameter α estimates log DOR at the Q* point and the significance of the shape term β can be used to assess whether a symmetric or asymmetric curve best fits to observed data. The model has a third parameter θ related to the proportion test positive—its value is equivalent to the values of S/2 in the Moses–Littenberg model. An average value for θ is estimated by the model, which allows identification of an average operating point on the summary ROC curve central to the observed data. The model is fitted at two levels. At the first level, the proportions test positive in the reference standard positive and negative groups are modeled assuming they follow a binomial distribution, whereas at the second level, variation between studies is modeled assuming normal distributions for log DOR (α) and the positivity threshold parameter (θ). To investigate heterogeneity using the HSROC model, we fitted parallel SROC curves by adding the covariate as a term to both the accuracy and threshold parts of the model (such that the shape of the SROC curves is determined using the whole set of studies). We also fitted models that included a covariate as a third term in the shape part of the model, to allow for variation in differences in log DOR with threshold (allowing the SROC curves to have different shapes; nonparallel).

2.3. Comparison of meta-analytic models

We compared the performance of each Moses–Littenberg regression model with the results of the HSROC model first for a simple meta-analysis by

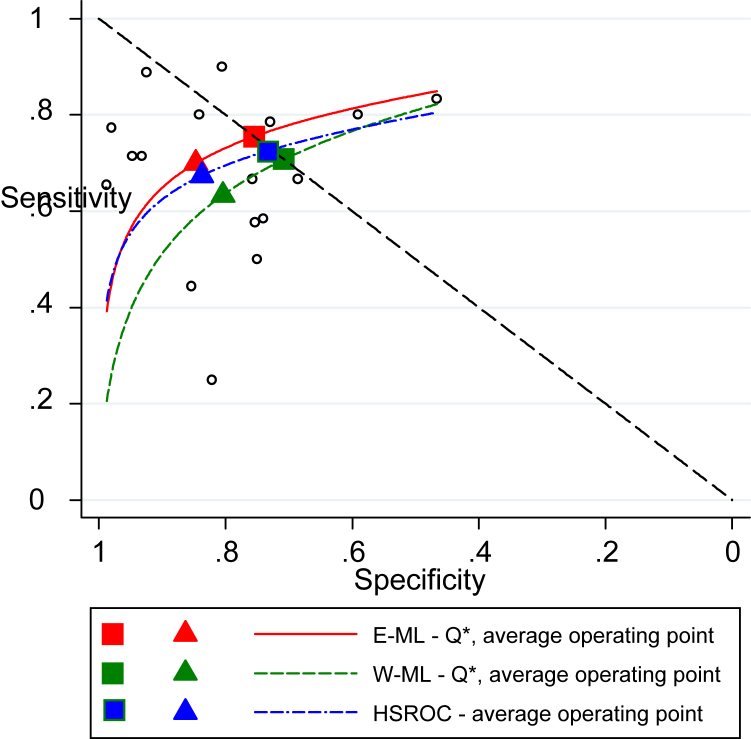
• (1)comparing DOR estimates by computing the ratio of DOR from the Moses–Littenberg models compared to the HSROC model at the central point in the data (which is the equivalent of the average operating point) and at the Q* value (the point where sensitivity = specificity) (sample SROC curves from each model shown in Box 1);
• (2)comparing the detection of SROC curve asymmetry between the Moses–Littenberg and HSROC models by comparing P-values from Wald tests for the β term in both models;

Box 1. Sample SROC curves estimating using Moses–Littenberg and HSROC models.

Abbreviations: Average operating point, DOR point on the SROC curve near to the center of the data using mean threshold; DOR, diagnostic odds ratio; E-ML, equal-weight Moses–Littenberg; HSROC, hierarchical SROC; Q*, DOR plotted at point on SROC curve where sensitivity = specificity; SROC, summary receiver operating characteristic; W-ML, Moses–Littenberg model weighted by inverse variance of D.

Estimates using data from Scheidler et al. [22].

and then in investigations of heterogeneity contrasting two subgroups,

• (3)comparing estimates of the RDOR between the Moses–Littenberg models and the HSROC model again at the central point in the data and at Q*; and
• (4)comparing the significance of the difference in DOR between the models estimated by comparing P-values from Wald tests for the log RDOR terms in both models.

For the Moses–Littenberg model, we identified the central point in the data as being at the mean value of S, whereas for the HSROC model, we identified it as being at the average operating point. For the comparison of subgroups, the RDOR can be less than or greater than one; summary statistics were standardized to code the subgroups such that the HSROC model always estimated an RDOR greater than one.

We additionally investigated how differences in DOR between the models vary according to predefined aspects of (1) magnitude of accuracy, (2) prevalence of zero cells, (3) variation in threshold (based on values for 'S' from the Moses–Littenberg model).

The Moses–Littenberg analyses were performed in STATA (StataCorp. 2013. Stata Statistical Software: Release 13. College Station, TX: StataCorp LP.), and the HSROC model was carried out using the PROC NLMIXED command in SAS (SAS 2012, version 9.3; SAS Institute, Cary, NC, USA).

3. Results

3.1. Search results

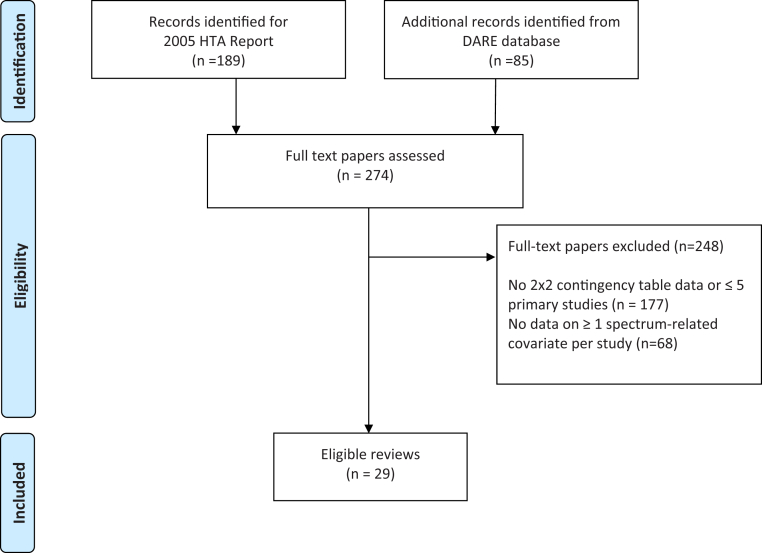
The search identified 97 systematic reviews of test accuracy that presented sufficient data to complete 2 × 2 contingency tables per study (Fig. 1). Information on at least one covariate per study was presented in 29 reviews; however, the HSROC model would not converge for three of the data sets (occasional nonconvergence of the HSROC model, particularly when there are few studies or when all studies sit on one of the boundaries of SROC space is a recognized phenomenon [23]). The comparisons between models are therefore based on 26 data sets with a total of 55 spectrum-related covariate investigations (Supplementary Table 1/Appendix at www.jclinepi.com). The HSROC model could not be completed for nine covariate investigations (for one parallel curve SROC comparison, for four nonparallel curve SROC comparisons, and for four covariates using both parallel and nonparallel SROC curves), either due to insufficient numbers of studies in at least one of the subsets (for five of the nine covariates) or the studies exhibited exceptionally high specificities with varying sensitivities. The median number of studies per review was 16 (interquartile range [IQR] 12, 26); median sample sizes of studies within each review ranged from 20 to 7,575.

Fig. 1.

Flowchart of the review selection process. DARE, Database of Abstracts of Reviews of Effects.

3.2. Comparison of diagnostic odds ratios

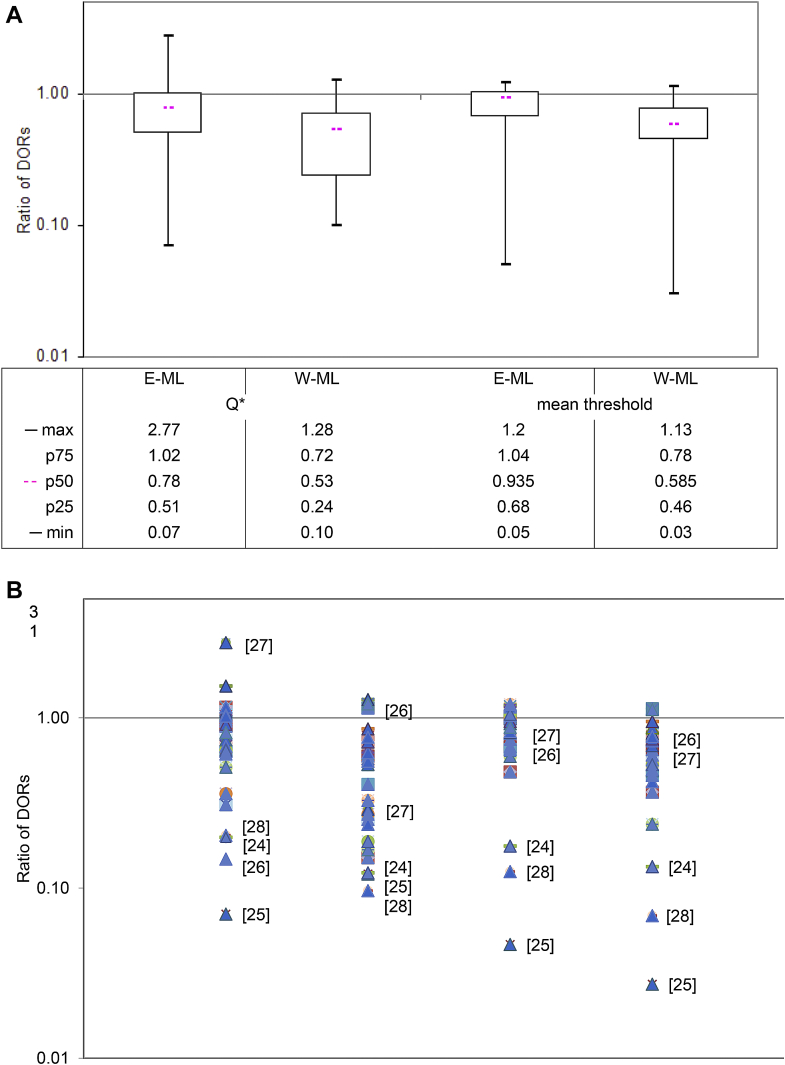
Estimates of the DOR from the Moses–Littenberg methods were on average lower than those of the HSROC model. Evaluated at the Q* point, the “E-ML” model estimates of the DOR were a median of 22% lower (IQR 49% lower to 2% higher) than those from the HSROC model, whereas estimates from the “W-ML” model were a median of 47% lower (IQR 76% lower to 28% lower). Differences between models were smaller at the central threshold, but still showed lower estimates for the Moses–Littenberg models on average: 7% lower (IQR 32% lower to 4% higher) for “E-ML” and 42% lower (IQR 64% lower to 22% lower) (Fig. 2A).

Fig. 2.

Comparison of diagnostic odds ratios: ML models vs. HSROC model. (A) Box and whisker plots of ratio of DORs between models (HSROC model estimate as reference). (B) Scatter plot of ratio of DORs between models (HSROC model estimate as reference). [ ] Denotes reference number for five reviews responsible for most of the extreme differences of DOR. DOR, diagnostic odds ratio; E-ML, equal-weight Moses–Littenberg; HSROC, hierarchical SROC; max, maximum ratio of DORs; mean threshold, point on the SROC curve near to the center of the data; min, minimum ratio of DORs; ML, Moses–Littenberg; p75, ratio of DORs at the 75th percentile; p50, ratio of DORs at the 50th percentile (median); p25, ratio of DORs at the 25th percentile; Q*, point on SROC curve where sensitivity = specificity; SROC, summary receiver operating characteristic; W-ML, Moses–Littenberg model weighted by inverse variance of D.

We categorized the meta-analyses according to their DOR estimate from the HSROC model, the percentage of studies with zero cells in 2 × 2 tables, and the range of the threshold parameter S (Table 1). We noted greater discrepancy between the methods when DORs were high and with increasing percentages of zeros in 2 × 2 tables. There was no clear relationship with the range of the threshold parameter.

Table 1.

Stratified comparison of diagnostic odds ratio (DOR) estimates

Number of reviews	Comparison of DORs at mean thresholda
	E-ML model vs. HSROC model	W-ML model vs. HSROC model
	Median ROR [IQR]	Median ROR [IQR]
Overall (n = 26)	0.94 [0.68, 1.04]	0.59 [0.46, 0.78]
By size of DORb
DOR < 35, n = 9	0.99 [0.88, 1.16]	0.78 [0.60, 0.95]
DOR 35–100, n = 10	1.00 [0.83, 1.05]	0.53 [0.42, 0.69]
DOR > 100, n = 7	0.62 [0.30, 0.75]	0.42 [0.16, 0.59]
By % zero cellsc
<5%, n = 10	1.01 [0.88, 1.05]	0.79 [0.53, 0.88]
5–10%, n = 8	1.02 [0.94, 1.11]	0.63 [0.50, 0.74]
>10%, n = 8	0.62 [0.30, 0.72]	0.42 [0.16, 0.63]
By range in ‘S’d
3 to <6, n = 7	0.82 [0.48, 1.03]	0.75 [0.37, 0.79]
6 to <8, n = 14	0.90 [0.68, 1.00]	0.53 [0.49, 0.75]
≥8, n = 5	1.05 [0.99, 1.16]	0.57 [0.42, 0.73]

Abbreviations: E-ML, equal-weight Moses–Littenberg; W-ML, weighted Moses–Littenberg; HSROC, hierarchical summary receiver operating characteristic; ROR, ratio of DORs between models; median ROR, ROR at the median; IQR, interquartile range in ROR from 25th to 75th percentile; DOR, diagnostic odds ratio.

^aEach Moses–Littenberg model is compared to the HSROC model (denominator).

^bThe stratification by DOR is based on the HSROC overall pooled estimate at mean threshold.

^cNumber of zero false-positive and false-negative cells as a percentage of the total number of cells per analysis.

^dBased on values for ‘S’ from Moses–Littenberg model, where S = logit(sensitivity) + logit(1 − specificity).

A wide range in results was observed for all model comparisons with both higher and lower estimates for Moses–Littenberg models compared to HSROC models (Fig. 2B). The five reviews responsible for most of the extreme differences of DOR all had studies with very high or close to perfect sensitivity [24], [25] and/or specificity [26], [27], [28] (Supplementary Fig. 1/Appendix at www.jclinepi.com). The lack of data points near to Q* for these reviews illustrates the unreliability of DORs estimated at this point. The three data sets that produced extreme values in all analyses were removed in a sensitivity analysis [24], [25], [28]; differences in DOR estimates between Moses–Littenberg and HSROC models remained for both the “E-ML” and “W-ML” model comparisons (the overall range in RORs being 0.48–1.20 and 0.24–1.13, respectively) (analysis not shown).

3.3. Comparison of SROC curve shape

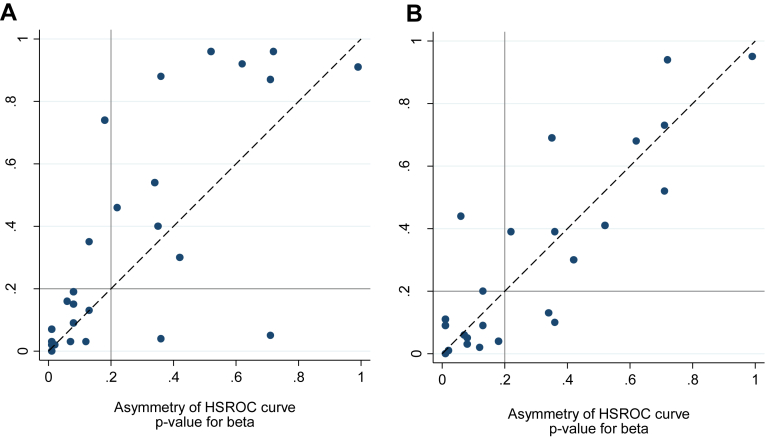
Fig. 3 shows broad but imperfect agreement between the HSROC and Moses–Littenberg models in terms of tests of the asymmetry of the SROC curve. Taking P < 0.20 as providing moderate to strong evidence of curve asymmetry, SROC curve asymmetry was identified for 14 of the 26 data sets using the HSROC model and 12 data sets for each of the Moses–Littenberg models, with four and three reviews showing disagreement for the “E-ML” and “W-ML” models, respectively.

Fig. 3.

Comparison of test of statistical significance of SROC curve asymmetry. (A) E-ML model vs. HSROC model. (B) W-ML model vs. HSROC model. HSROC, hierarchical SROC; E-ML, equal-weight Moses–Littenberg; SROC, summary receiver operating characteristic; W-ML, Moses–Littenberg model weighted by inverse variance of D.

3.4. Comparison of estimates of RDOR in heterogeneity investigations

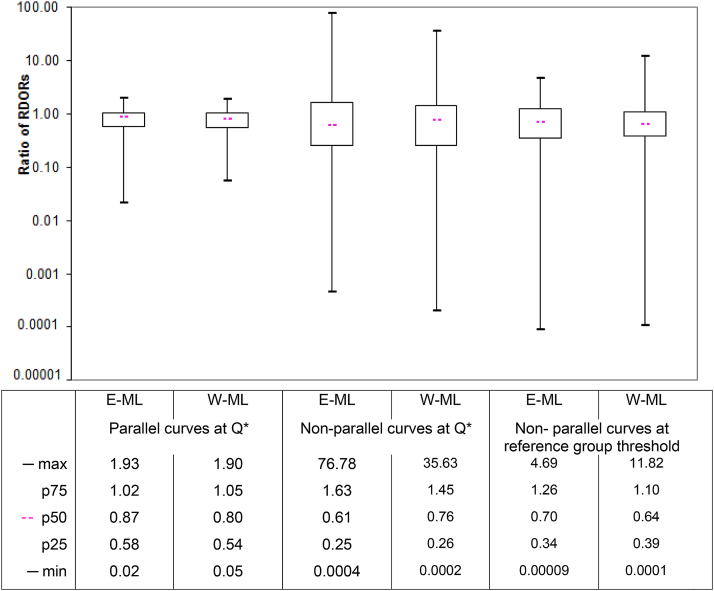
Estimates of RDOR from heterogeneity investigations were on average considerably lower when estimated by the Moses–Littenberg models compared to the HSROC model (Fig. 4). When estimated assuming parallel SROC curves, RDOR values (median [IQR]) were 13% lower [42% lower to 2% higher] for the “E-ML” model and 20% lower [46% lower to 5% higher] for the “W-ML” model. Including interaction terms to allow for nonparallel SROC curves substantially increased both the average difference and the range of differences when evaluated both at the Q* point and the central point.

Fig. 4.

Ratio of relative DORs (RDORs) between models (HSROC model estimate as reference). DOR, diagnostic odds ratio; E-ML, equal-weight Moses–Littenberg; HSROC, hierarchical SROC; max, maximum ratio of DORs; min, minimum ratio of DORs; nonparallel curves, RDORs between study subgroups estimated allowing SROC curves to have different shapes (nonparallel); parallel curves, RDORs between study subgroups estimated assuming SROC curves have same shape (parallel); p75, ratio of DORs at the 75th percentile; p50, ratio of DORs at the 50th percentile (median); p25, ratio of DORs at the 25th percentile; Q*, point on SROC curve where sensitivity = specificity; RDOR, relative diagnostic odds ratio; reference group threshold, RDOR estimated at the point on the SROC curve near to the center of the data in the reference group; SROC, summary receiver operating characteristic; W-ML, Moses–Littenberg model weighted by inverse variance of D.

3.5. Comparison of the statistical significance of sources of heterogeneity

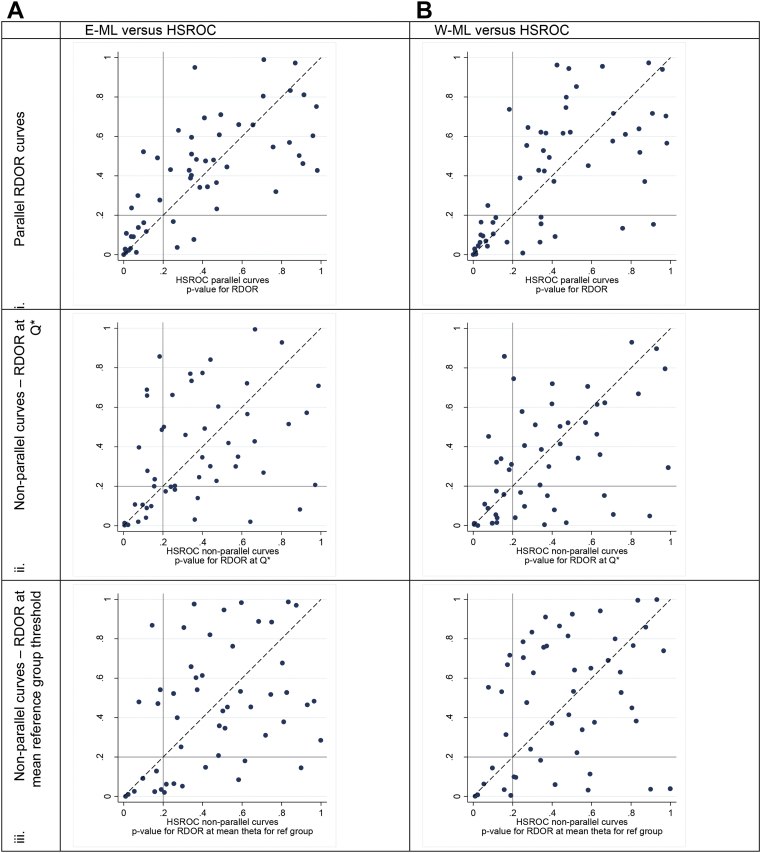
There was poor agreement in the statistical significance of the covariate investigations between Moses–Littenberg and HSROC models with the P-value comparison points scattered widely around the plots (Fig. 5). Disagreements appeared worse for the models with nonparallel SROC curves.

Fig. 5.

Comparison of tests of statistical significance for difference in accuracy. E-ML, equal-weight Moses–Littenberg; HSROC, hierarchical SROC; Q*, point on SROC curve where sensitivity = specificity; RDOR, relative diagnostic odds ratio; SROC, summary receiver operating characteristic; W-ML, Moses–Littenberg model weighted by inverse variance of D.

4. Discussion

We found that the simpler Moses–Littenberg models produced lower estimates of DOR accuracy in comparison with the more complex HSROC model, with median differences of 22% and 47% for unweighted and weighted models at Q*, but with wide interquartile and overall ranges for the differences. The greatest differences were observed when the Moses–Littenberg model was weighted by the inverse variance of lnDOR, where the overall pooled DOR was over 100, and where there were a high proportion of zero cells; situations where the mathematical limitations of Moses–Littenberg method creates misleading estimates.

The weighted Moses–Littenberg model uses the approximate asymptotic standard error of the log DOR in allocating study weights. We have previously shown (in the context of funnel plots and tests for publication bias [29]) that the estimate of the standard error depends on the lnDOR for values of DOR which are greater than one, leading funnel plot based tests such as the Begg and Egger tests to overestimate the frequency of sample size–related effects. The same relationship will affect the estimates of standard errors for larger DOR, most often leading to overestimation of standard errors at higher DOR, so that an inverse variance–weighted meta-analysis will lead to underestimation of overall accuracy.

Zero-cell corrections are used in the Moses–Littenberg model when sensitivities or specificities of 100% are observed, also when the DOR is typically high. Adding 0.5 to each cell of every 2 × 2 contingency table that contains zero false positives or false negatives always creates a downward effect on the estimate of the DOR. The magnitude of effect will be greater in studies with smaller sample sizes in the disease positive and disease negative groups.

There was some disagreement in detection of SROC curve asymmetry between models, but the asymmetry detected was rarely statistically significant with either model. Many of our analyses contained few studies; thus, few of the meta-analyses will have had enough power to detect asymmetry.

Of importance, we observed substantial differences for investigations of heterogeneity, both in terms of the estimates of the size of the effect (RDOR) and their statistical significance. In line with their performance for single-test meta-analyses, Moses–Littenberg methods on average generated lower between group differences in accuracy compared to the HSROC model. The failure of the ML models to account for both within- and between-study variability compromises the models' ability to estimate standard errors used to assess statistical significance, leading to a notable lack of agreement in the statistical significance of relative diagnostic odds ratios. Inferences drawn from covariate investigations using the Moses–Littenberg models can therefore potentially be highly spurious. These findings have implications for meta-analyses that compare tests as well as those which investigate the performance of a single test in subgroups of studies.

Our results support and extend those of previous empirical comparisons (one using a very large data set [15]) showing that SROC curves produced by the simpler Moses–Littenberg model can appear similar to those produced by more rigorous methods but can in some cases diverge [14], [15]; neither of these comparisons compared average operating points on the SROC curves however, and neither compared the results of heterogeneity investigations. Although our data set has shown that although in some circumstances there may be little difference on average between methods, the variability observed around the average indicates the potential for large differences in test accuracy, both in the overall result of the meta-analysis and, perhaps more crucially, with the addition of covariates to the models.

Our comparison of models is subject to a number of limitations. Studies in our cohort were published between 2000 and 2005 with screening for inclusion conducted by only one reviewer. However, given that our purpose was to illustrate the potential effect across a number of data sets rather than to reach a conclusion around the accuracy of a given test, the potential for reviewer bias is limited. Furthermore, the currency of the review cohort has no impact on the statistical models used or external validity of our results as there is no reason to consider that the relationships between the methods would differ in more recent studies. In terms of the statistical analyses, heterogeneity was common and the number of studies per meta-analysis was typical but low, with a median of 16 (range 7–46). These factors will have contributed to some of the extreme results observed but many review authors will nevertheless make the decision to meta-analyze studies in these circumstances.

Furthermore, we focused on comparing DORs rather than sensitivity and specificity estimates as the DOR is the natural parameter of both the Moses–Littenberg and HSROC models. This facilitated the comparison between models to be illustrated with a single parameter; however, the DOR is not as intuitive as other measures of test accuracy. When we looked at summary estimates of sensitivity and specificity at the average operating point and at Q*, the ML model produced at least one estimate in the order of 5% to 9% lower than the HSROC model in 12 of the 26 reviews, and 10% to 23% lower than the HSROC model for 8 of the 26 reviews. Only one review produced an estimate that was higher than that observed from the HSROC model (for the E-ML estimate of sensitivity). Although the differential effects on sensitivity and specificity vary from case to case, the directional “bias” that we observed for the ML model in the DOR comparisons was supported by the comparisons of sensitivities and specificities, with differences large enough to mislead.

The strength of this study was the number of data sets available for reanalysis. Further investigation, for example, using simulated data, might be able to identify circumstances under which the Moses–Littenberg methods more closely approximate those of the HSROC method. Although there are more limited software options for fitting hierarchical models than the Moses–Littenberg models, requiring programs that fit mixed linear (or nonlinear for the HSROC) logistic models, support for fitting these models in SAS, STATA, R (https://www.r-project.org/), and WinBUGS (http://www.mrc-bsu.cam.ac.uk/software/bugs/), is now available such that they should be the preferred approach [30], [31]. Although convergence problems with the HSROC and bivariate model are encountered when there are few studies, fitting HSROC models with fewer parameters (e.g., setting variance parameter estimates to zero, or assuming symmetrical SROC curves) has been found to be a preferable approach.

We have provided empirical evidence that supports current recommendations advocating the use of hierarchical approaches to the statistical synthesis of test accuracy data [30], [31]. Ongoing efforts to extend the scope of the models [32], [33], [34] and to make them more accessible [35], [36], [37] should help to increase their uptake in future systematic reviews.

These findings raise concerns about the clinical use of existing reviews that have used the Moses–Littenberg approach. We have demonstrated that not only the pooled results might be misleading, but also conclusions drawn from models where covariates have been added may be unreliable. This finding applies not only to investigations of heterogeneity but also to comparisons of the accuracy of two or more tests where test covariates are added to the models in the same way as for sources of heterogeneity. The problem may not be considered as serious where investigations are considered exploratory but is of real concern where comparisons between tests are made with the aim of informing the selection of tests for use in clinical practice. Our results also potentially call into question the conclusions from seminal meta-epidemiology articles that have used the Moses–Littenberg model to provide the basis for our understanding of the biases in operation in test accuracy studies [2], [38], [39].

There are a huge number of systematic reviews of diagnostic tests now in the public domain, many of which have used less than optimal approaches to the synthesis of test accuracy data. We have demonstrated the potential for drawing misleading inferences from meta-analyses adopting the Moses–Littenberg model and recommend that caution is used when considering their use. Our findings support and encourage the future uptake of hierarchical models for diagnostic test meta-analyses.