k-space sampling optimization for ultrashort TE imaging of cortical bone: Applications in radiation therapy planning and MR-based PET attenuation correction

Abstract

Purpose:

The ultrashort echo-time (UTE) sequence is a promising MR pulse sequence for imaging cortical bone which is otherwise difficult to image using conventional MR sequences and also poses strong attenuation for photons in radiation therapy and PET imaging. The authors report here a systematic characterization of cortical bone signal decay and a scanning time optimization strategy for the UTE sequence through k-space undersampling, which can result in up to a 75% reduction in acquisition time. Using the undersampled UTE imaging sequence, the authors also attempted to quantitatively investigate the MR properties of cortical bone in healthy volunteers, thus demonstrating the feasibility of using such a technique for generating bone-enhanced images which can be used for radiation therapy planning and attenuation correction with PET/MR.

Methods:

An angularly undersampled, radially encoded UTE sequence was used for scanning the brains of healthy volunteers. Quantitative MR characterization of tissue properties, including water fraction and R2^∗ = 1/T2^∗, was performed by analyzing the UTE images acquired at multiple echo times. The impact of different sampling rates was evaluated through systematic comparison of the MR image quality, bone-enhanced image quality, image noise, water fraction, and R2^∗ of cortical bone.

Results:

A reduced angular sampling rate of the UTE trajectory achieves acquisition durations in proportion to the sampling rate and in as short as 25% of the time required for full sampling using a standard Cartesian acquisition, while preserving unique MR contrast within the skull at the cost of a minimal increase in noise level. The R2^∗ of human skull was measured as 0.2–0.3 ms⁻¹ depending on the specific region, which is more than ten times greater than the R2^∗ of soft tissue. The water fraction in human skull was measured to be 60%–80%, which is significantly less than the >90% water fraction in brain. High-quality, bone-enhanced images can be generated using a reduced sampled UTE sequence with no visible compromise in image quality and they preserved bone-to-air contrast with as low as a 25% sampling rate.

Conclusions:

This UTE strategy with angular undersampling preserves the image quality and contrast of cortical bone, while reducing the total scanning time by as much as 75%. The quantitative results of R2^∗ and the water fraction of skull based on Dixon analysis of UTE images acquired at multiple echo times provide guidance for the clinical adoption and further parameter optimization of the UTE sequence when used for radiation therapy and MR-based PET attenuation correction.

1. INTRODUCTION

Hybrid MR technologies, such as MRI/PET and combined MRI/Linac systems, are currently emerging modalities attracting much attention in the diagnostic imaging and radiation-oncology communities.^1–4 These integrated solutions leverage the exquisite soft-tissue contrast of MR as well as advanced MR applications including real-time image guidance and multiparametric imaging, e.g., diffusion and perfusion for treatment planning and anatomical localization.^2,5–7 Despite much promise, many technical challenges remain, including designing methods for PET attenuation correction (AC) and radiation therapy planning (RTP) which, in the past, have relied on CT to provide attenuation or density information.^8,9 Methods for AC and RTP using MR are complex because the MRI signal intensity is not directly related to the tissue electron density but rather to the presence of hydrogen atoms and their local environment.

Various approaches have been used for MR-based AC (MRAC) and RTP, including both atlas matching and tissue classification schemes with specialized pulse sequences.^10–13 Although there are perhaps fewer technical challenges using atlas-based approaches rather than with individualized tissue classification methods, atlas-based approaches have limited clinical value because of the inter-patient and even intra-patient variations in anatomy and physiology caused by disease pathology and also due to medical interventions such as surgery and radiation therapy. Conventional MRI sequences pose dramatic limitations for distinguishing cortical bone from air due to the extremely short T2^∗ relaxation times of bone,¹⁴ which has been shown to be an important tissue type for both AC and RTP.^14,15 In fact, MR-based attenuation correction methods that ignore cortical bone¹⁵ have been shown to lead to as much as a 37% error in radioactivity concentration or SUV measured in PET images.¹⁶

Regarding the specific use of MR in RTP, MR provides outstanding soft-tissue contrast, thus allowing delineation of tumor and normal structures in a way that cannot be done with CT. Consequently, MR is performed in addition to CT imaging which is used for calculation of the radiation dose. Owing to cost savings and a better patient experience, there is interest in performing the dose calculation based on the MR and in avoiding CT.^17–19 Currently, however, a number of technical challenges make this method impractical for routine clinical use. The manual segmentation of bone and other tissue is labor-intensive,^18,19 and automatic segmentation cannot reliably differentiate air from bone.¹⁷ Thus, there is a demand for an imaging method that achieves excellent bone-to-air contrast within a clinically practical acquisition time duration. Furthermore, the method would be applicable in the generation of MR-based, digitally reconstructed radiographs (DRRs) that could replace the portal images which are currently used for treatment verification.^17,20,21

Regarding the use of MR images for PET attenuation correction, recent literature reports indicate that the ability to differentiate air and bone remains the most challenging issue.²² Preliminary studies have suggested differentiating cortical bone, air, and soft tissue using dual- or triple-echo, ultrashort echo-time (UTE) sequences which have already achieved promising results.^23,24 However, a thorough investigation of the MR signal properties of cortical bone is lacking due to the difficulty of acquiring a sufficient number of sampling points of short echo times in order to capture the T2^∗ decay. In addition, as the human skull consists of multiple layers of water- and fat-rich structures, the scale of which is beyond the resolution of clinical MRI, a subvoxel analysis of the voxel signal contribution using the Dixon type of water/fat separation is needed in order to provide more detailed information regarding UTE signal evolution with echo times.²⁵ As most existing segmentation algorithms for UTE images are based on empirical thresholding schemes or on a statistical clustering boundary between different tissue types,^12,23,24 an in-depth investigation of the MR signal characteristics of cortical bone and its difference from that of soft tissue is essential in order to improve the robustness of segmentation algorithms. Furthermore, and most importantly, the current acquisition times for UTE are prohibitively long for routine clinical imaging and, in addition, the optimal TE necessary to adequately differentiate cortical bone from air has not yet been systematically evaluated. Therefore, it is clinically necessary to develop new acquisition strategies that reduce the scan time while also achieving maximal contrast among different tissue types.

In our study, we attempted to systematically evaluate the MR characteristics of cortical bone signal decay using a radial encoding, multiacquisition, UTE sequence with six different echo times. We then proposed and demonstrated the feasibility of using a reduced sampling method that could substantially shorten the acquisition time of a dual-echo UTE sequence. The data sets are compared for their ability to differentiate cortical bone from air and soft tissue, the ability to generate bone-enhanced images to differentiate cortical bone from air in sinus cavities of the human head, and their MR image quality.

2. MATERIAL AND METHODS

2.A. Volunteers

MRI scans were performed on six healthy volunteers using the scanner best suited for the two applications studied. Four volunteers were scanned on a Philips Achieva 3.0T TX system (Philips Healthcare, the Netherlands) using an 8-channel, birdcage coil which is the setup used for Philips brain PET/MR workflow. Multiple TEs were acquired during multiple acquisitions of the UTE sequence for quantitative characterization of bone. The additional two volunteers were scanned on a Philips Ingenia 3T system (Philips Healthcare, the Netherlands) using a digital 16-channel, phased-array coil, which is the setup used extensively for whole brain radiotherapy planning. On the Ingenia scanner, a free induction decay (FID) signal and a gradient echo were collected within a single acquisition at a UTE and in-phase TE, respectively. These data were used to generate bone-enhanced images that could be useful for RTP and MRAC. The protocol was reviewed and approved by our institutional review board, and a written informed consent was obtained from all volunteers.

2.B. MRI sequence for characterizing cortical bone signal decay

To capture the ultrashort T2^∗ decay of the MR signal in cortical bone, an ultrashort TE on the order of 100 μs is required in order to receive the signal, which is often difficult to achieve. A center-out radial readout sequence that encodes the FID, as described by Stehning et al.,²⁶ is capable of meeting this requirement and was used on the 3T Achieva scanner. FID images were collected at multiple TEs (0.1, 0.2, 0.4, 0.8, 1.6, and 2.3 ms) from multiple acquisitions in order to evaluate the T2^∗ decay of different tissue components. Each TE was acquired with a TR = 6.8 ms so as to ensure a consistent readout scheme across all acquisitions. For each series of TEs, angular sampling rates of 100%, 75%, 50%, and 25% were applied, thus resulting in scan times of 172, 129, 86, and 43 s for each TE, respectively, for the separate acquisitions. The detailed imaging parameters are summarized in Table I.

TABLE I.

MR sequence parameters.

Parameter	Value on 3T Achieva	Value on 3T Ingenia
Total scan duration (s)	172, 129, 86, and 43	219, 146, and 73
Sampling rate (%)	100, 75, 50, and 25	75, 50, and 25
Sequence type	UTE with FID readout	UTE with FID and echo readout
TR (ms)	6.8	5.2
TE (ms)	0.1, 0.2, 0.4, 0.8, 1.6, and 2.3	0.1 and 2.3
Acquisition bandwidth (Hz)	1735	1328
Acquisition orientation	Axial	Axial
Field of view (mm)	220 × 220 × 220	250 × 250 × 250
Acquisition voxel size (mm)	2 × 2 × 2	1.5 × 1.5 × 1.5
Excitation type	Nonselective 3D isotropic	Nonselective 3D isotropic
Flip angle (deg)	15	10

2.C. MR characterization of the human skull

In order to quantitatively assess the MR properties of the skull, including T2^∗ (or R2^∗ = 1/T2^∗) and the water and fat fraction, a Dixon type approach was used to model the signal intensity into water and fat components.^25,27 Specifically, we assumed different T2^∗ decay constants for the water and fat components

$${\displaystyle W=w{e}^{-R_{2W}^{\ast }\times \mathrm{TE}},}$$

$${\displaystyle F=(1-w)e^{-R_{2F}^{\ast }\times \mathrm{TE}},}$$ (1)

in which W and F represent the magnitude of normalized water and fat components within an individual voxel, TE is the echo time, and $R_{2W}^{\ast }$ and $R_{2F}^{\ast }$, respectively, represent the R2^∗ decay rates of water and the fat components. The water fraction defined as W/(W + F) represents the percentage contribution to the signal from the water component. The magnitude of superimposed water and fat signals, considering their distinct Larmor frequencies at 3 T, can be written as

$${\displaystyle S\left(\mathrm{TE}\right)=\sqrt{W^2+F^2+2\cdot W\cdot F\cdot cos\alpha },}$$ (2)

where α = π⋅TE/1.15 ms is the phase difference between water and fat at the acquisition time.

A least-squares fitting program was built using matlab (The Mathworks, Natick, MA, Version R2013b) to perform constrained, nonlinear fitting for the independent parameters, w, $R_{2W}^{\ast }$, and $R_{2F}^{*}$, based on the voxelwise signal intensity data acquired at different TEs. An intensity-based mask, leveled to intensity of background noise, was applied to exclude areas outside of the imaging subject and air cavity from data fitting. A positivity constraint was applied to each parameter. Furthermore, in order to avoid a fat–water swapping effect in the parameter estimates, an inequality constraint was applied to ensure that the $R_{2W}^{\ast }$ was smaller than or equal to $R_{2F}^{*}$ in order to improve the robustness of the estimation.²⁸

2.D. Development of a fast, dual-echo sequence for clinical imaging

To address the fundamental challenge of differentiating bone from air, a dual-echo sequence with TEs of 0.1 ms (FID) and 2.3 ms (in-phase gradient echo) was developed on a 3T Philips Ingenia scanner. To minimize the total scan time, both readouts were acquired within a single TR. The FID was acquired using a center-out radial readout.²⁹ Gradients were then used to refocus an echo at the in-phase TE of 2.3 ms which was acquired with the same radial encoding but starting at the final frequency that encoded the FID.²⁹ All data were reconstructed using vendor-supplied algorithms. The algorithm included regridding the data to Cartesian space prior to transforming the data to image space. To increase the clinical utility of this method, we also investigated the effect of undersampling the total amount of data collected in order to shorten the total scan time. The acquisition times to collect the total dual-echo sequence for 75%, 50%, and 25% sampling schemes were 219, 146, and 73 s, respectively, the last of which was a fourfold reduction in scan time compared to 300 s for the fully sampled acquisition. The detailed imaging parameters are summarized in Table I.

2.E. MRI acquisition and reconstruction details

In general, the 3D radial sampling as described by Stehning et al.²⁶ was used for data acquisition in which the 100% sampling rate was defined as the number of phase encode steps required in order to achieve the same image volume and the spatial resolution equivalent to acquisition using a Cartesian readout. Angular undersampling was achieved by uniformly reducing the sampling points on the k-space surface. A fast sinc gridding function was used to map the radially sampled k-space data into Cartesian coordinates, and a quadratic weighting function³⁰ was applied to compensate for the nonuniform nature of radial sampling before image reconstruction using the 3D Fourier transform. No additional postfiltering was applied for image smoothing.

2.F. Image processing and image quality analysis

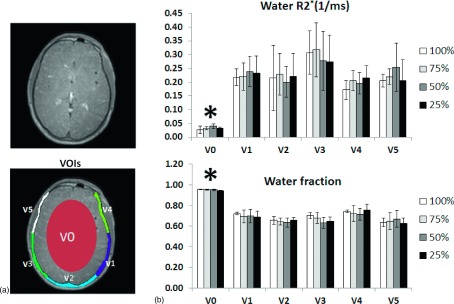
Rigid-body registration was performed on different images for each study subject so as to eliminate any misregistration caused by possible subject movement between acquisitions. For volume-of-interest (VOI) based analysis, VOIs were defined on the images with a 75% sampling rate and a 0.1 ms TE for each individual study subject and were then propagated to other images with different sampling rates, echo times, and parametric maps. Specifically, the axial slice across the middle of the frontal sinus was selected for the VOI definition. Skull was manually delineated based on the images acquired using the 75% sampling rate and the 0.1 ms echo time. The skull base was further evenly divided into five separate areas [Fig. 2(a)], i.e., V1–5. Soft tissue VOI (V0) was manually defined by selecting central brain tissue within the image. The mean value and standard deviation (SD) of the fitted R2^∗ and water fraction were calculated for pixels within each of the six VOIs. To evaluate the impact of the sampling rate on the image noise, a homogeneous region was manually selected in brain soft tissue from 0.1 ms images, with the mean/SD of the signal intensity representing the signal-to-noise ratio (SNR) characteristics of different sampling rates. Visual evaluation of the detailed structure of cortical bone in the original images and the fitted parametric maps was performed to assess the image quality of UTE images as well as the measured MR properties with a low sampling rate.

FIG. 2.

(a) Representative slice and VOI definition for quantitative analysis with one brain and five skull volumes. (b) Fitted water R2^∗ and the water fraction using a two-component model within defined VOIs. Both the R2^∗ value and the water fraction within V1 to V5 are significantly higher than those within brain V0 (p < 0.05). There are no statistically significant differences in the R2^∗ or water fraction from V1 to V5 versus brain. Asterisk indicates p < 0.01.

2.G. Quantitative assessment of bone-enhanced images at different sampling rates

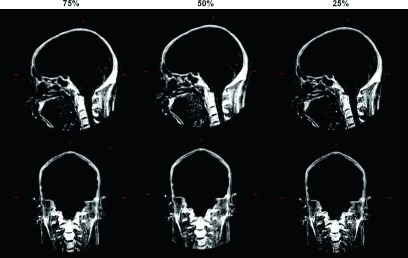
As the direct input for potential RTP and MRAC applications, bone-enhanced MR images were created from weighted subtraction of images acquired at TE = 0.1 and 2.3 ms, respectively. The subtraction weight was selected in order to minimize the signal intensity of soft tissue in the bone-enhanced image. For different sampling rates, i.e., 75%, 50%, and 25%, the same VOIs that enclose the skull and sinus cavity (air) were manually drawn on an axial slice through the center of the frontal sinus by a radiation oncologist. The signal intensity of bone-enhanced images within different osseous structures was compared with that of air in order to evaluate the impact of undersampling on the image contrast between bone and air, which are otherwise difficult to differentiate using traditional imaging sequences.

2.H. Statistics and data analysis

Statistical analyses were conducted using Excel (Microsoft, Seattle, WA) or matlab. The paired t-test and repeated measures ANOVA were used for hypothesis testing.

3. RESULTS

3.A. UTE brain images at different TEs

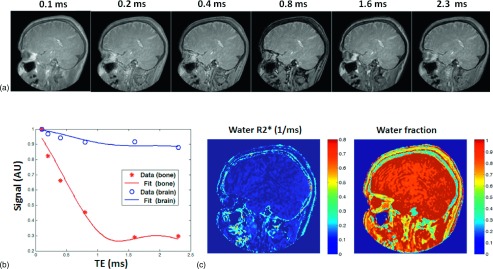
Representative UTE images at different TEs acquired using the 75% sampling rate are displayed in Fig. 1(a). Figure 1(b) is a representative signal-intensity evolution together with corresponding two-component model fit curves in separate skull and soft tissue voxels. With the increase of echo time from 0.1 to 2.3 ms, the soft-tissue signal amplitude is retained, whereas there is rephase and in-phase modulation in fat-rich skull and skin tissue. In addition, due to the proton-density-weighted nature of the UTE sequence, the MR signal from skull is significantly lower compared to that of the surrounding soft tissue. However, within those images with a sufficiently short-echo time, the skull yields a stronger signal due to acquisition before much of the T2^∗ decay. Representative parametric maps of the water R2^∗ (=1/T2^∗) and the water fraction are shown in Fig. 1(c) and reveal a detailed delineation of the multilayer MR signal feature in the skull. They also confirm that the skull exhibits a significantly shorter T2^∗ (or faster R2^∗ relaxation rate) compared to that of soft tissue. It is worth noting that due to the strong susceptibility effect at the skin–air interface, the skin surface also has a fast R2^∗.

FIG. 1.

(a) Representative radial encoding ultrashort TE images from a healthy volunteer show the signal in the cortical bone, the highest at the shortest TE and markedly decreasing with TE, whereas the signal in most other tissues is relatively constant. (b) Two-component fitting of experimental data in soft tissue and cortical bone quantitatively shows the signal of skull decreases more rapidly than that of brain. (c) Representative fitting results of water R2^∗ and the water fraction using a two-component MR signal model in the same subject show that the water component of skull generally has the fastest R2^∗ among tissues and that approximately 60% of the signal in skull is attributed to protons in water.

3.B. Quantitative characterization of cortical bone

Figure 2(a) shows the results of manual segmentation of the skull into five equiangular volumes, i.e., V1–V5, with an additional VOI, V0, defined at the center of the brain. Figure 2(b) shows the distribution of the water R2^∗ as well as the water fraction of the VOIs for the study subjects with the mean depicted by column height and the SD by error bars. No significant difference of the R2^∗ or water fraction was detected in any of the VOIs across the different sampling rates, thus demonstrating the preserved MR properties in the sampled acquisition despite the significantly reduced scanning time. However, both the R2^∗ value and the water fraction within V1–V5 are significantly higher than those within soft-tissue V0 (p < 0.05). There are no statistical differences in the R2^∗ or water fraction from V1 to V5, thus demonstrating the similar MR characteristics within different skull VOIs.

3.C. Effect of the sampling rate on noise

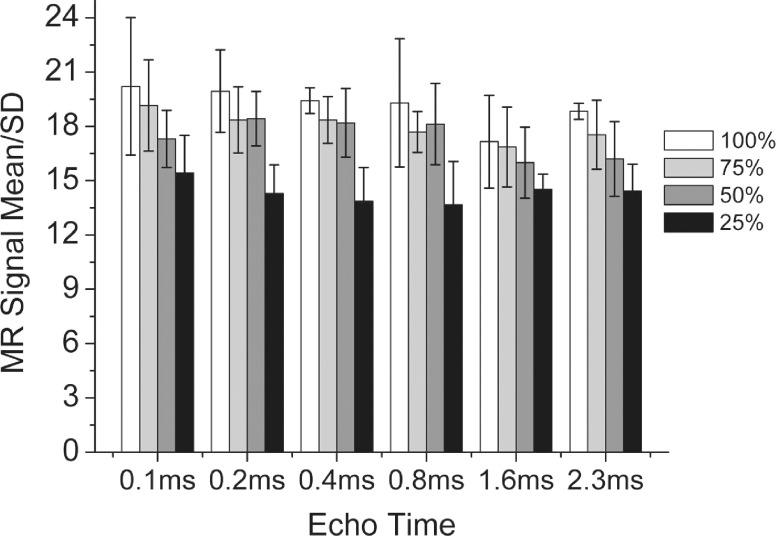
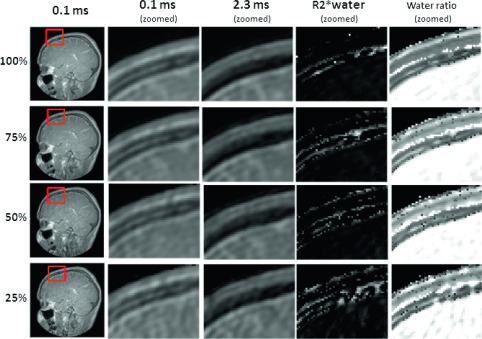
The noise levels of images acquired at different sampling rates are presented in Fig. 3. The signal amplitude of UTE scans for long T2^∗ tissue, i.e., soft tissue, are essentially proton-density-weighted with little or no dependence on the TE and no statistically significant difference between the measured noise levels for TEs from 0.1 to 2.3 ms for a given sampling rate. Signal/SD had a slight tendency to decrease from 20 to 15 with decreases in the sampling rate from 100% to 25%, although the effect was not statistically significant. The left column of Fig. 4 shows the representative images, i.e., TE = 0.1 and 2.3 ms, used to assess the effect of the sampling rate. The second and third columns show zoomed views of a region enclosing the skull as well as no visually appreciable compromise of image quality as the sampling rate was decreased to 75% and 50% and perhaps had a minor impact at 25% even though the total scan times were reduced by as much as fourfold in proportion to the sampling rate. Also shown in Fig. 4 are the parametric images which demonstrate that the reduced sampling rate has minimal, if any, impact on the MR signal in soft tissue and skull.

FIG. 3.

MR SNR measured as the mean/SD in the homogeneous soft-tissue area for different echo times and undersampling rates. Undersampling achieved an increase in acquisition speed without a statistically significant decrease in SNR.

FIG. 4.

Image quality evaluation of UTE, the in-phase echo image, fitted water R2^∗, and water fraction images at different undersampling rates. Relative to 100% sampling, there is no visually conspicuous increase in noise or decrease in spatial resolution in the UTE (0.1 ms) or in the in-phase (2.3 ms) image, a decrease in the sampling rate to 75% and 50%.

3.D. Bone-enhanced imaging and bone detectability

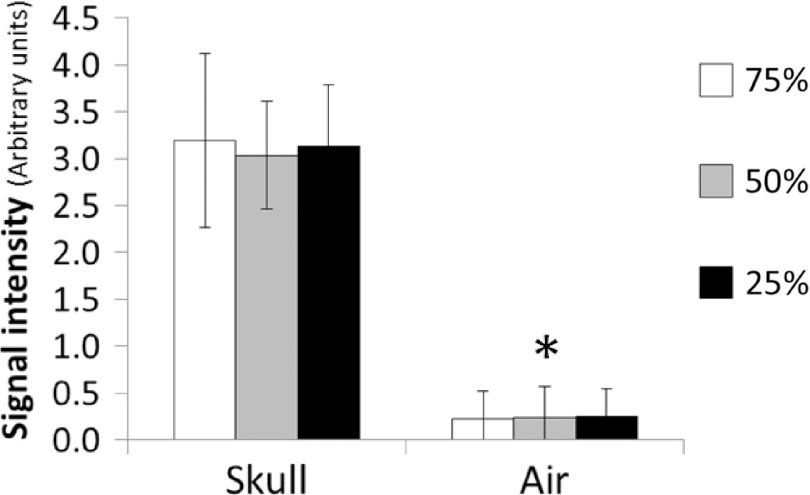
The bone-enhanced images demonstrated visual positive contrast for bone under all sampling rates (Fig. 5). Quantitative analysis (Fig. 6) confirmed that skull exhibited approximately 13-fold greater signal than that of air. The signal intensity of the same tissue type at different radial sampling rates did not differ significantly, while the signal intensity in skull was significantly higher (p < 0.01) than that of frontal sinus (i.e., air) under all sampling rates.

FIG. 5.

Sagittal and coronal slices of bone-enhanced images of different sampling rates. Good visualization of bone is preserved as the sampling rate is decreased.

FIG. 6.

Means and standard deviations of the signal intensities for skull and frontal sinus (air). The standard deviations are the standard deviations among the voxels for different tissue types and the sampling rates. The signal intensity in skull and sinus are statistically different, *p < 0.01.

4. DISCUSSION

We evaluated the MR properties of skull at 3 T using a radial-encoding UTE sequence with angular sampling at a reduced rate. The major findings of this study are (1) the R2^∗ of human skull is more than ten times greater than the R2^∗ of soft tissue; (2) multicomponent R2^∗ fitting is necessary in order to accurately determine the MR characteristics of human skull as the water fraction in human skull is 60%–80% which is significantly less than the >90% water fraction in brain tissue; (3) the reduced angular sampling rate of the UTE trajectory achieves acquisition durations in proportion to the sampling rate, and in as short as 25% of the time for full sampling, while preserving unique MR contrast within the skull at the cost of a minimal increase of noise level; and (4) high-quality, bone-enhanced images can be generated using the reduced sampled UTE sequence with little compromise in image quality or loss of contrast between bone and air, and with as low as a 25% sampling rate.

To our best knowledge, this is the first study to report quantitative measurement of the water fraction and water R2^∗ relaxation properties within the living human skull at 3 T. These findings are helpful in order to further improve the UTE sequence for applications such as RTP and MRAC of the human brain. In general, the motivation for using the UTE sequence to separate bone from soft tissue is the fact that bone exhibits a dramatically more rapid T2^∗ decay than that of soft tissue. However, most of the two-echo UTE sequences, in which TEs are usually selected as the shortest echo time that the scanner can acquire as well as the in-phase echo time, do not accurately determine the R2^∗ as they fail to include the MR signal contribution from fat. In addition, due to the hardware limitations, such as magnetic gradient strength and slew rate, it is impossible to acquire a sufficient number of echoes on the order of 0.1 ms for clinical imaging resolution. Therefore, we used multiacquisition and Dixon type analysis for accurate characterization of the water fraction and the R2^∗ of different tissues. This facilitates the selection of the best TE but is not necessary in order to generate bone-enhanced images which could otherwise be created by acquiring images at the best ultrashort echo time and an in-phase echo time. Compared to soft tissue, there is a relatively high fat content within the medullary bone of the skull, which might be considered as an additional feature that could help to distinguish bone from soft tissue. Furthermore, TE could be selected as there is a joint effect of T2^∗ relaxation and water–fat phase cancellation at a shorter echo time than the in-phase time (2.3 ms at 3 T). Because the spatial resolution is too low to resolve the inner and outer table of the human skull and the enclosed medullary bone, we implemented a water/fat, two-component model with an independent R2^∗ relaxation rate as proposed by Bydder et al.²⁸ It is notable that the value of the water R2^∗ measured in our study using the two-component model is less than the R2^∗ of cortical bone fitted through a single exponential decay within the knee.³¹ This difference might be attributable to differing tissue composition, such as density and mineral deposition of cortical bone in different body parts subjected to different physical stresses. Moreover, because of the unique multilayer structure of the skull, MR imaging with the current resolution is prone to partial volume averaging which results in a lower R2^∗ than for pure cortical bone.

One major limitation for most radial-encoding imaging sequences is their incompatibility with parallel imaging techniques, which in turn leads to prohibitively long scan times. For a 3D radial readout acquisition scheme, k-space is uniformly sampled during the readout gradient in radial directions with starting points evenly sampled on the k-space sphere. Such a sampling scheme results in a highly redundant sampling near the center of k-space domain due to aggregated sampling trajectories within this region. Specifically, the number of samples in the k-space is proportional of the radius of k-space r, while the volume is proportional to r³. Therefore, the sampling density is r⁻²-dependent. Radial-encoding offers a unique opportunity to perform uniformly reduced sampling rates along angular orientations. Specifically, reducing the total number of trajectory lines through the center of the k-space, while preserving the sampling frequency along each line, significantly reduces the total scan time. Importantly, the low-frequency components of k-space are relatively unaffected by undersampling as the low frequency is otherwise highly oversampled during regridding of the radial sampled k-space frequencies into Cartesian coordinates for Fourier reconstruction. As for the high-frequency components, the skipped k-space frequencies lead to a homogeneous, noiselike texture in the image background.²⁶ As demonstrated by the phantom imaging results previously reported by Stehning et al.,²⁶ even though radial undersampling leads to a violation of the Nyquist criterion, spherical symmetry helps to preserve the spatial resolution. Violating Nyquist also leads to aliasing energy widely spread over the image rather than focused in space. Radial undersampling uniformly reduces the sampling density at all frequencies; as the low-frequency components in k-space that determines the overall image intensity and contrast is densely oversampled in radial acquisition, they are less prone to undersampling compared to high-frequency components. Moreover, because of the quadratic weighting of k-space during the regridding of radial sampled data into the Cartesian coordinate, the classical relationship between scan time and the signal-to-noise ratio, $\mathrm{SNR}\propto \sqrt{\mathrm{ScanTime}}$, does not apply to undersampling in radial encoding. As demonstrated in our study, even though the 25% sampling rate speeds up scanning by a fourfold factor, the associated increase in noise level is 30% or less, which is consistent with previous reports regarding the phantom image.²⁶ As one of the major obstacles preventing the ultimate clinical adoption of UTE for radiation-oncology planning and MR-based attenuation correction is the long scan time, the reduced sampling strategy presented here could be used to facilitate the immediate transition of UTE imaging from research into clinical practice.

Because of the dramatically different attenuation properties of bone and air, both of which yield similar low-signal intensity in traditional MR sequences, it is extremely difficult to perform threshold-based segmentation on these MR images. As reported previously regarding UTE images,²³ the difference between FID and later echo images, the so-called bone-enhanced image, generates positive contrast between bone and air. In conjunction with the measured significant difference in T2^∗ relaxation between bone and other brain soft tissue, the multiecho UTE image offers a multiparametric input so that advanced algorithms can effectively distinguish different tissue types. Based on our experimental observation, the T2^∗ contrast is preserved according to different sampling rates between bone and soft tissue, while the signal-intensity contrast in the bone-enhanced image is preserved between bone and air. Therefore, the 25% sampling rate with a scan speed of up to four times is feasible for providing UTE images with sufficient quality for RTP and MRAC.