Stereovision to MR image registration for cortical surface displacement mapping to enhance image-guided neurosurgery

Abstract

Purpose:

A surface registration method is presented to align intraoperative stereovision (iSV) with preoperative magnetic resonance (pMR) images, which utilizes both geometry and texture information to extract tissue displacements as part of the overall process of compensating for intraoperative brain deformation in order to maintain accurate neuronavigational image guidance during surgery.

Methods:

A sum-of-squared-difference rigid image registration was first executed to detect lateral shift of the cortical surface and was followed by a mutual-information-based block matching method to detect local nonrigid deformation caused by distention or collapse of the cortical surface. Ten (N = 10) surgical cases were evaluated in which an independent point measurement of a dominant cortical surface feature location was recorded with a tracked stylus in each case and compared to its surface-registered counterpart. The full three-dimensional (3D) displacement field was also extracted to drive a biomechanical brain deformation model, the results of which were reconciled with the reconstructed iSV surface as another form of evaluation.

Results:

Differences between the tracked stylus coordinates of cortical surface features and their surface-registered locations were 1.94 ± 0.59 mm on average across the ten cases. When the complete displacement map derived from surface registration was utilized, the resulting images generated from mechanical model updates were consistent in terms of both geometry (1–2 mm of model misfit) and texture, and were generated with less than 10 min of computational time. Analysis of the surface-registered 3D displacements indicate that the magnitude of motion ranged from 4.03 to 9.79 mm in the ten patient cases, and the amount of lateral shift was not related statistically to the direction of gravity (p = 0.73 ≫ 0.05) or the craniotomy size (p = 0.48 ≫ 0.05) at the beginning of surgery.

Conclusions:

The iSV–pMR surface registration method utilizes texture and geometry information to extract both global lateral shift and local nonrigid movement of the cortical surface in 3D. The results suggest small differences exist in surface-registered locations when compared to positions measured independently with a coregistered stylus and when the full iSV surface was aligned with model-updated MR. The effectiveness and efficiency of the registration method is also minimally disruptive to surgical workflow.

1. INTRODUCTION

Fiducial registration¹ before craniotomy is the standard practice in image-guided neurosurgery to rigidly transform the patient’s head in physical space in the operating room (OR) into image space defined by the subject’s preoperative magnetic resonance (pMR) scans. Real-time neuronavigation systems based on fiducial registration have been widely used for surgical guidance, and their performance influences surgical outcomes and patient survival.^2–4 Unfortunately, intraoperative brain deformation significantly degrades the accuracy of image guidance when only pMR is employed because tissue movement can be large and has a dynamic, complex, and typically case-dependent pattern.^5,6 To compensate for intraoperative shift, both linear elastic and nonlinear biomechanical models have been developed to estimate whole-brain deformation from which model-updated MR (uMR) images are produced, and the accuracy and performance have been evaluated in clinical cases.^7–16 Since brain shift is case-dependent, intraoperative data can be acquired (e.g., using tracked pointer tools,¹⁴ ultrasound,^10,17 intraoperative MR (iMR),^11,18,19 stereovision,^20,21 and laser range scanners^22,23) to partially sample the tissue motion during a specific surgery, and the resulting information can guide the model estimation process through data inversion (e.g., to minimize model-data misfit^9,10). We have adopted a consolidation-based finite element model for soft tissue deformation⁷ that assimilates intraoperatively acquired cortical surface displacements in a least squares inversion using an adjoint equations method (AEM),¹⁰ which is solved with a steepest gradient descent (SGD) algorithm.⁹ The sparsely sampled displacement data can be derived through image coregistration between pMR and intraoperative images that represent the “undeformed” and “deformed” tissue states, respectively.²⁴ Because the sparse data are actively assimilated into the computations of whole-brain deformation, the accuracy of the image coregistration directly impacts the fidelity of the model-computed uMR and, ultimately, the overall accuracy of uMR-guided neuronavigation.

Before the dura is opened, the brain deforms minimally, whereas after dural opening, its deformation is unpredictable—the brain may collapse due to CSF loss, but the extent depends on the orientation and position of the head, the size of the craniotomy, etc., or the brain may distend from the release of intracranial pressure and stress concentrations from a space-occupying mass. As a result, neuronavigation based on pMR can become inaccurate even at the start of a case. To account for brain deformation due to dural opening, cortical surface movement can be recorded before and after durotomy. Imaging techniques to capture the surface motion include intraoperative stereovision (iSV)^20,21 and laser range scanning.^22,23 These methods acquire both geometry and texture information which can be used to register the two brain surfaces (i.e., before and after dural opening); however, the registration is challenged by the lack of surface features before the dura is opened. Typically, methods that utilize texture information have focused on later stages of surgery after the cortex is exposed when features such as blood vessels appear on the brain surface,^21,23 whereas registration between surfaces pre- and postdural opening is less well studied.

As a result, geometry-based methods are commonly used to extract surface displacements due to dural opening, for example, with iterative closest-point (ICP) algorithms.^20,22 ICP methods, along with other geometry-based schemes such as closest-point distance (CPD)²⁵ which do not utilize texture information, do not capture brain movement accurately, especially when lateral shifts occur. An alternative approach registers pMR with the iSV surface directly and was first studied for frameless patient registration based on natural anatomical landmarks.^26–28 These methods are still geometry based, and, therefore, do not provide completely accurate registration. Miga et al.²² combined ICP and mutual information (MI) registrations where the latter takes advantage of the image features provided by pMR to incorporate the effects of any global lateral shift of the brain that may have taken place. Here, the ICP registration essentially finds a rigid 3D transformation based on geometry, whereas the MI registration incorporates a rigid 2D transformation based on image features. The combination corrects for global shift of the brain surface but does not otherwise account for localized nonrigid distortions that may occur.

In this paper, we report a new surface registration approach to align iSV with pMR images and extract surface sparse data as part of the overall process of compensating for intraoperative brain deformation. Compared to existing surface registration techniques in the literature, our approach utilizes both geometry and texture information from iSV which corrects for global shift as well as local nonrigid movement of the brain, whereas existing techniques either only rely on geometry information or do not account for local nonrigid movement. The surface registration incorporates lateral shift of the cortical surface through a sum-of-squared-difference (SSD) rigid registration and then includes local nonrigid deformation through a block matching method (BMM). The lateral shift and local movement are combined to specify a 2D displacement field that is further transformed into 3D via stereopsis and is subsequently employed in a biomechanical brain deformation model^9,10,29 to produce uMR. Here, we present displacement results obtained from the surface registration technique and assess their accuracy by comparing locations of surface-registered features with independent position measurements obtained with a tracked stylus. We also infer the validity of the displacement maps by using them to generate uMR views that are compared with full iSV acquisitions of the deformed brain surface in terms of geometry as well as texture.

2. MATERIALS AND METHODS

2.A. Surgical cases

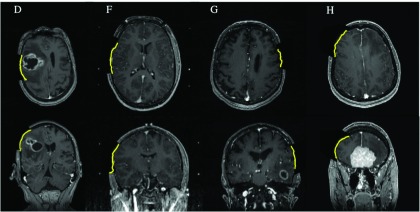
To demonstrate application of the image registration technique and to assess its fidelity in measuring parenchymal surface deformation immediately after dural opening, ten (N = 10) patient cases undergoing brain tissue resection were evaluated. Subject age, gender, and type of lesion are provided in Table I.

TABLE I.

Summary of patient information.

Patient ID	Age	Gender	Type of lesion
A	59	F	Anaplastic oligoastrocytoma
B	18	F	Epilepsy
C	83	M	Glioblastoma
D	68	F	Metastatic carcinoma
E	39	F	Arteriovenous malformation
F	24	M	Epilepsy
G	69	M	Glioblastoma
H	62	F	Meningioma
I	35	M	Meningioma
J	78	F	Metastatic carcinoma

2.B. Patient registration and stereovision system

pMR images of the patient’s head (T1-weighted, 512 × 512 × 120 with voxel size of 0.4688 × 0.4688 × 1.5 mm or 256 × 256 × 120 with voxel size of 0.9375 × 0.9375 × 1.5 mm) were acquired (typically 2–6 h prior to surgery) and registered in the OR with a commercial navigation system (S7^® StealthStation^® Medtronic, Louisville, CO). The iSV system consisted of two charge-coupled device (CCD) cameras (Flea2 from Point Grey Research, Inc., Richmond, BC, Canada) that were attached to one of the binocular ports on the operating microscope (OPMI Pentero^® Carl Zeiss Surgical GmbH, Oberkochen, Germany). The extrinsic and intrinsic camera parameters of the iSV system were calibrated prior to surgery using Tsai’s algorithm³⁰ to determine the projection matrix required to reconstruct a 3D surface from two 2D stereo views. The technical details of stereovision reconstruction have been published previously²⁰ and are briefly summarized here for completeness.

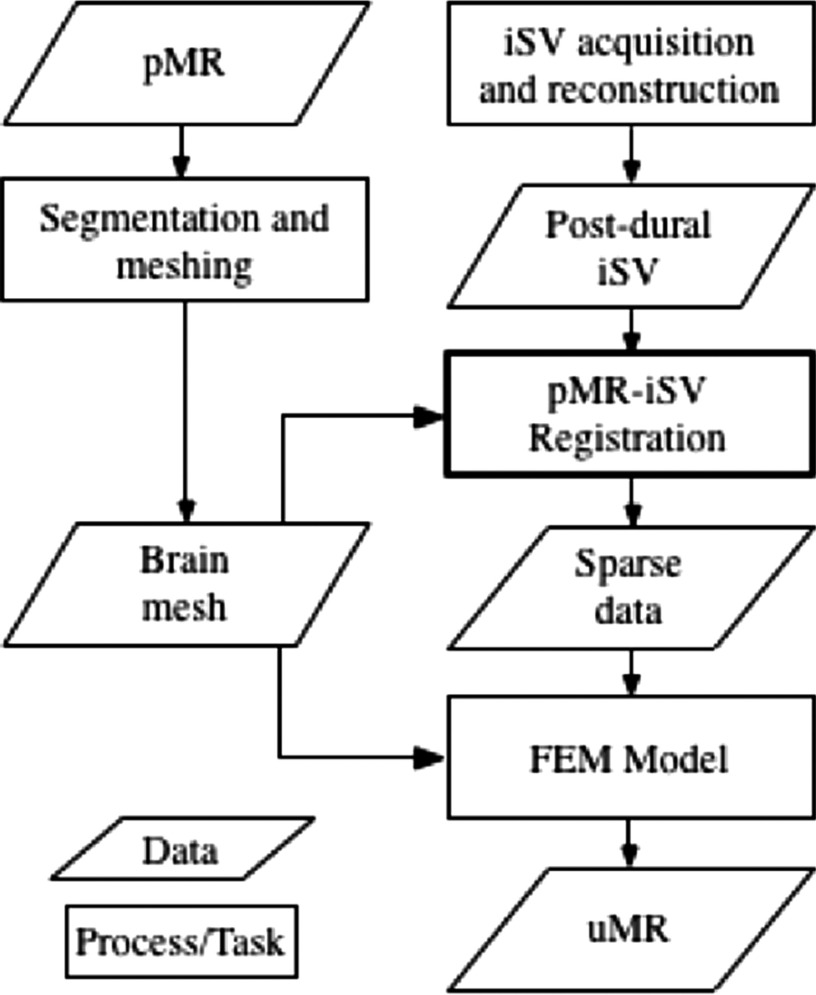
First, images of the cortical surface acquired by the iSV cameras were rectified based on calibrated parameters to correct for image distortion and to simplify the calculation of stereo correspondence. Stereo correspondences for a subset of sampling points (typically ∼200 K) were determined by finding matching points in the left and right rectified images³¹ from which the depths of those points were calculated through triangulation. A texture intensity-encoded 3D profile of the surface was recovered and was subsequently transformed into MR image space. The overall accuracy of the stereovision tracking system has been reported to be 0.9–1.1 mm.³¹ After dural opening, an iSV image pair of the exposed cortical surface was acquired, and a pMR-encoded texture map was generated using a projection approach as described in Sec. 2.C. Then, the MR-encoded texture map was registered with the iSV-based texture map. The 2D displacements were transformed into 3D and assimilated into a biomechanical model, where the resulting whole-brain deformation field was used to transform the pMR images into the model-updated MR-uMR. A flowchart of the biomechanical brain deformation modeling process is shown in Fig. 1.

FIG. 1.

Flowchart of the brain deformation modeling process.

A sterilized tracked stylus similar to the one used to rigidly register the operative field to the navigation system at the start of a case was available during surgery. This tool was used to localize a dominant feature on the cortical surface after dural opening in each case as a way of obtaining an independent estimate of the ground-truth position of this feature (subject to tracking system errors) in the global OR coordinate system against which the surface-registered location of the same feature was compared as a form of validation and accuracy evaluation of the surface registration technique.

2.C. MR-encoded texture map

A challenge in registering iSV data before dural opening is the lack of distinct image features at this surgical stage (because the dural membrane covers the feature-rich cortical surface). We overcome the no-iSV-image-features limitation by utilizing pMR to provide anatomical structures such as vessels and sulci on the surgical surface, similar to previously described technique.²² In Ref. 22 the location of the resection surface was identified in the MR images based on presurgical plans, and the MR-encoded texture map was generated using a ray-casting algorithm and intensity averaging of 3–5 voxels. Our technique transforms the iSV surface and segmented brain into a local coordinate system, directly finds the craniotomy location by projecting the iSV surface onto the segmented brain, and generates the MR-encoded texture map using interpolation. Specifically, in our technique, a brain surface was generated from the level-set segmented parenchyma^32,33 and together with the postdural opening iSV surface was transformed into a local coordinate system where sampling points on the iSV surface were projected along the average surface normal onto the segmented brain surface to create a point cloud that geometrically matched the pMR brain surface. A MR-encoded texture (intensity) map was then generated by interpolating pMR intensities based on the projection point locations and replacing all pixel intensities in the corresponding rectified iSV image with those interpolated from pMR.

Clearly, the accuracy of the MR-encoded texture map depends on the projection point locations on the undeformed parenchymal surface and, hence, the brain segmentation accuracy (e.g., a “hole” in the MR-encoded texture map may result if the corresponding projection point falls outside the brain volume). We increased the search depth for interpolation as a practical approach to ensure all landmarks on the parenchymal surface were included. Specifically, the predural opening surface was successively shifted along the surface normal in 0.1 mm increments for a total of 1 mm. At each step, a MR-encoded surface was similarly interpolated, and the intensities for each sampling point were averaged to create a final MR equivalent textured surface for subsequent analysis (null intensities were excluded from the averaging when the corresponding point fell outside the segmented brain volume).

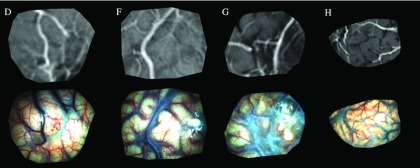
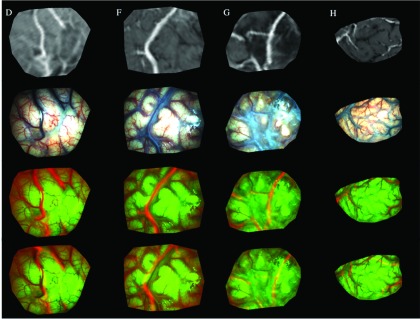
As representative examples, Fig. 2 illustrates MR-encoded texture maps (top row) and their corresponding postdural opening iSV rectified images (bottom row) produced from patient cases D, F, G, and H, respectively. Because the MR-encoded texture map was generated by replacing image intensities on the iSV surface, identical image dimensions and resolution (between the MR texture map and the iSV image) were maintained so that image-based registration methods were readily applied.

FIG. 2.

MR-encoded texture maps (top row) and corresponding postdural opening iSV surface images (bottom row) from patient cases D, F, G, and H.

2.D. Two-step image registration

To estimate brain deformation at the cortical surface after dural opening, we developed a two-step registration method to account for global shift (rigidly in the first step) and local movement (nonrigidly in the second step) of the cortical surface due to parenchymal collapse and/or distention postdurotomy.

2.D.1. Step 1: Rigid registration of global shift

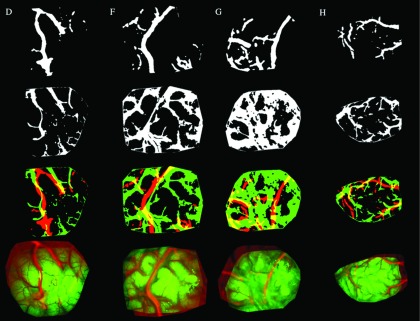
We opted to include only the dominant features that are present in both the iSV and pMR-encoded texture maps and applied SSD registration, accordingly, to minimize effects from specular artifacts that can occur in iSV (and which do not have corresponding features in the MR-encoded texture map). The MR-encoded and corresponding rectified iSV texture maps were first converted to binary images using Otsu’s method, which effectively retained the dominant features shared by the two image modalities. The binary images were registered rigidly by maximizing the overlapping regions using SGD to minimize SSD. The resulting displacement field was then applied to the MR-encoded grayscale image in order to account for the presence of any global shift. Figure 3 illustrates the initial binary image extractions from the iSV and MR-encoded texture maps and the resulting rigid SSD registrations for the same set of patient cases shown in Fig. 2.

FIG. 3.

SSD rigid registration applied to binary iSV and MR-encoded texture maps that highlight the dominant features of the exposed cortical surfaces in patient cases D, F, G, and H (first through fourth columns, respectively). Top row: binary MR-encoded texture maps; second row: binary iSV surface images; third row: binary image overlays before registration; fourth row: rigidly registered binary MR-encoded texture maps overlaid on iSV.

2.D.2. Step 2: Nonrigid registration of local movement

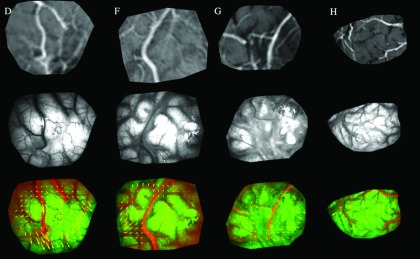
After compensating for global shift of the brain surface in the first rigid registration step, major vessels appearing in the predural opening MR-encoded texture map are aligned with their counterparts in the postdurotomy iSV image (see Fig. 3, fourth row). A block matching method was then applied to the gray-scale images to account for local nonrigid displacement. Specifically, the rigidly aligned grayscale MR-encoded image was divided into small blocks of average size 100 × 100 pixels (block size varied from case to case depending on the field-of-view of the region of interest), and MI registration²² was applied to align each block with its corresponding grayscale postdurotomy iSV image. The step size of the BMM is different from the block size. The former is defined as the distance between neighboring block centers and controls the density of extracted sparse data. The step size was typically 50 pixels in both horizontal and vertical directions, which leads to an average of ∼200 sparse data points, depending on the size of craniotomy in the image. The step size was set to be smaller than the block size, and as a result, overlapping regions occur in neighboring blocks, which help to maintain continuity in the displacement map between neighboring blocks. Figure 4 illustrates these results for the same set of patient cases shown in Figs. 2 and 3.

FIG. 4.

Example outcomes from the block matching method to detect local nonrigid deformation occurring between the pre- and postdural views of the brain surface for patient cases D, F, G, and H (in columns 1–4, respectively). Top row: rigidly aligned grayscale MR-encoded texture map; second row: grayscale iSV texture map after dural opening; third row: block-match MI-registered MR and iSV images with resulting displacement vectors overlaid.

2.E. 3D displacements

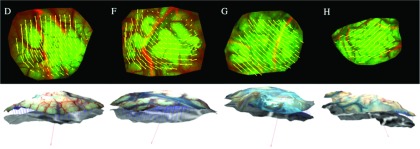
The global and local displacements generated from each of the two registrations were combined to specify a complete 2D displacement map between the pre- and postdural opening brain surfaces as shown in Fig. 5. Because correspondence between iSV and MR-encoded texture maps at each pixel was known, and the spatial locations for these pixels were also available from iSV, 3D displacements were computed³⁴ (see vectors in bottom row of Fig. 5) and indicate both lateral shift and distention of the cortical surface of the brain.

FIG. 5.

Transformation of displacement vectors from 2D (arrows in top row) to 3D (arrows in bottom row). Vector in each image in the bottom row indicates the gravitational direction. Columns correspond to patients D, F, G, and H, respectively.

2.F. Data analysis

To estimate the accuracy of our surface registration approach, we compared the location of a dominant feature in the registered surface images with its position in tracking system coordinates by having the surgeon touch the physical feature with a tracked sterile stylus as a means of providing an independent measurement of its location. To minimize feature localization error, the dominant vessel junction visible in both the MR-encoded and iSV texture maps and accurately identified and localized in the surgical field with a stylus probe was used in each case. The surface registration accuracy was estimated as the distance between the locations of these features in the registered surface images and their positions acquired with the tracked stylus.

As a second form of evaluation that invoked data from the entire coregistered image surface, we used the full surface displacement map generated by the surface registration technique as sparse data in our computational model to generate uMR views from which uMR-encoded texture maps were generated and compared against the corresponding postdural opening iSV data. Here, we considered both geometry (represented by data-model mismatch) and texture (represented by alignment of specific surface features) in the evaluation. To form the uMR volume, a subject-specific brain mesh was created and appropriate boundary conditions and interior forcing conditions were assigned²⁹ according to their locations (e.g., craniotomy, brainstem, saturated and unsaturated parenchyma contact, and fixed positions as described in Ref. 35). We determined the computational cost associated with each major step in this procedure and present qualitative assessment of the surface registration by (1) aligning uMR with the iSV surface in 2D cross-sections and (2) generating uMR-encoded texture maps and aligning them with the corresponding iSV projections in the same local coordinate system. In addition, we demonstrate that our registration technique is superior to the ICP algorithm in an illustrative patient case. Finally, we tabulate displacement components based on the gravitational vector to investigate the extent to which they are correlated with the direction of gravity.

3. RESULTS

3.A. Point-probe accuracy evaluation

To estimate the accuracy of our surface registration algorithm, surface features in ten (N = 10) clinical patient cases were evaluated. Specifically, for each patient, a dominant vessel junction visible in the MR-encoded texture map was identified and its undeformed location in MR image space was saved. After iSV image acquisition postdurotomy, the intraoperative location of the vessel junction was recorded with a tracked stylus once visible on the exposed cortical surface. Table II summarizes the point-to-point differences in the two locations for ten patient cases.

TABLE II.

Summary of point-probe accuracy (in mm) of surface registration based on tracked probe tip locations sampled at vessel junctions on the cortical surface.

Case #	A	B	C	D	E	F	G	H	I	J
Accuracy (mm)	1.32	1.40	2.16	1.69	1.67	2.80	1.38	3.02	1.89a	2.07

^aIn case I, a second dominant vessel junction was evident and yielded nearly identical results (SD ± 0.06).

3.B. Model-updated MR accuracy evaluation

To assess the validity of the full surface registration, model computations driven by the complete displacement maps were evaluated in terms of the model-data misfit (RMS error between model estimates and measured displacements), which was typically 1–2 mm (see Table IV).

TABLE IV.

Summary of surface displacements and model results in ten clinical cases.

Case ID	Location	Craniotomy size (cm)	D3d(mm)	DL(mm)	θ(deg)	Misfita (mm)
A	Right frontal	4.72 × 3.77	5.35 ± 1.25	1.61 ± 0.82	58.91	1.53
B	Left temporal	4.88 × 4.45	5.78 ± 0.60	4.85 ± 0.25	51.86	1.95
C	Right temporal	4.69 × 4.43	4.97 ± 0.35	4.55 ± 0.39	93.56	1.18
D	Right frontal	4.86 × 4.50	8.44 ± 1.43	4.23 ± 1.56	9.16	1.67
E	Right frontal	4.89 × 4.77	4.03 ± 1.81	2.17 ± 0.44	3.80	1.89
F	Right parietal	4.88 × 3.85	8.27 ± 2.17	3.30 ± 1.68	77.21	1.93
G	Left temporal	4.74 × 3.79	9.41 ± 1.96	5.16 ± 1.16	33.31	2.08
H	Right frontal	10.20 × 3.08	9.79 ± 1.12	6.44 ± 0.96	138.19	1.37
I	Right frontal	4.89 × 4.65	6.36 ± 2.64	0.97 ± 0.50	136.34	2.11
J	Right frontal	3.50 × 3.05	6.24 ± 1.52	1.30 ± 0.06	103.56	1.69

^aRMS error between model estimates and measured displacements.

To further evaluate the results of the model computations, uMR images were compared to the reconstructed iSV surface in terms of both geometry and texture. For example, Fig. 6 shows uMR slices overlaid with postdurotomy iSV surfaces (line) from selected cases (patients D, F, G, and H). The alignment between the iSV and uMR surfaces indicates consistent assimilation of the iSV data into the model estimates.

FIG. 6.

Model-updated MR images overlaid with iSV surface (lines) for subjects D, F, G, and H (in columns 1–4, respectively). See Table III for the average misfit error.

In addition, MR-encoded texture maps of the postdural iSV surfaces were generated from the uMR volume with the same technique used to generate pMR-encoded texture maps (see Sec. 2.B). Specifically, since the iSV surface may not align with the parenchymal surface in uMR exactly, it was translated along the surface normal direction for 1–2 mm (depending on the misfit on the surface) in increments of 0.1 mm to produce surfaces that were averaged to create the uMR-encoded texture map. Figure 7 shows example results where the top row contains uMR-encoded texture maps after model compensation, the second row presents rectified iSV images after dural opening, and the third row displays an RGB overlay of the two views. The features (e.g., vessels) in the uMR-encoded texture map align well with those in iSV after model compensation. For comparison, the bottom row displays a RGB overlay of pMR-encoded and iSV-based texture maps where the features are poorly registered without the model compensation.

FIG. 7.

Validation of model results by comparing uMR-encoded texture map with the corresponding iSV-based texture map for subjects D, F, G, and H (in columns 1–4, respectively). Top row and second row show the uMR-encoded and iSV texture maps, respectively. Third row contains an overlay of the two views. In comparison, bottom row shows an overlay of pMR-encoded and iSV-based texture maps before nonrigid surface registration.

3.C. Computational efficiency

Computational efficiency was based on algorithms executed on a Linux computer (2.33 GHz, 16G RAM) with 12 CPUs in matlab (matlab R2012b, the Mathworks, Natick, MA). The registration algorithms, including SSD- and MI-based registrations, were implemented in c ++ through the Insight Segmentation and Registration Toolkit³⁶ (ITK, version 3.10) and were compiled as files executable from within matlab. The MI-based block matching method was executed using the parallel computing toolbox in matlab, allowing 12 single-threaded registrations to be performed simultaneously. The brain deformation model was implemented in fortran. All computational times were measured from within matlab using a stopwatch timer function. The total computational time for pMR–iSV registration was typically 1–2 min, including projection, but the actual time depended on the image size, displacement magnitude, and parameters used for registration. Whole-brain displacements were estimated using SGD typically with 50 iterations as the model-data misfit does not change significantly after 50 iterations (see Ref. 9 for relationship between model-data misfit and the number of iterations). The computational cost of these solutions depended on the FE mesh size and was less than 3 min. The computed whole-brain displacement field was then used to deform pMR images and produce uMR which required about 15 s. Table III lists the major steps involved in estimating brain deformation immediately after dural opening, and their approximate (typical) computational times. Most computationally intense work (e.g., SSD- and MI-based registrations and the biomechanical model) was implemented in c ++ or fortran to improve the computational efficiency. Some of the work was implemented in matlab with computational time in order of seconds, which can potentially be implemented in c or a similar language to further improve the computational efficiency in clinical settings.

TABLE III.

Steps in estimating brain deformation immediately after dural opening and their approximate computational times.

Step	Computational time
Segmentation	5 min
Meshing	30 s
iSV surface reconstruction	1 min
iSV–pMR registration	1–2 min
Other inputs (e.g., boundary conditions)	1 min
Model computation (50 iterations)	3 min

3.D. Analysis of clinical results

To study the deformation patterns that occurred during surgery, the displacements obtained from the pMR to iSV surface registrations from each clinical case were analyzed. Specifically, the average surface normal was computed, and the extracted 3D displacements were decomposed into their components parallel with the surface normal (indicating brain distention or collapse) and perpendicular to the surface normal (indicating lateral shift). The gravitation vector was similarly decomposed into its parallel and perpendicular components to the surface normal. The magnitude of 3D displacements (D_3d) and the magnitude of lateral components (D_L) were quantified. The angle (θ) between the lateral component of gravitation and the average lateral displacement was also computed to investigate the relationship between lateral shift and gravitation.

Case information on craniotomy size (long and short axis), computed magnitude of 3D displacements (mean ± standard deviation) and computed magnitude of 2D lateral shift (mean ± standard deviation), angle θ, and final model-data misfit are reported in Table IV. After dural opening 3D brain deformation at the craniotomy varied from 4.03 to 9.79 mm, whereas the lateral shift varied from 0.97 to 6.44 mm.

Correlation between the amount of lateral shift and various factors was studied further using the Kendall rank correlation coefficient, where the Kendall’s tau (τ) assesses the association of two data sets, and a p-value was reported to test the hypothesis that the two data sets were independent.³⁷ If two sets of measurement quantities are statistically independent, a τ approximate to zero is expected, and the p-value indicates the significance of the correlation. The results show that lateral shift of the brain was not significantly correlated with gravitation (τ = − 0.11, p = 0.73 ≫ 0.05). Indeed, four out of ten patient cases show θ > 90°, indicating lateral shift in the opposite direction to gravitation. The magnitude of lateral shift was also not necessarily related to craniotomy size (τ = 0.20, p = 0.48 ≫ 0.05).

4. DISCUSSION

Estimating intraoperative cortical movement during open-cranial neurosurgery is an important element of compensating for brain deformation in the OR. First, the information can be integrated into a biomechanical model to compute whole-brain displacement and generate uMR views as illustrated in this paper. Here, the specific model we applied is adapted from linearly elastic consolidation to simulate soft tissue deformation, and comparisons of its performance relative to other biomechanical models when supplied the same surface displacements as inputs would be interesting to consider in future. Second, intraoperative surface deformation can be evaluated directly without being integrated into a biomechanical model as a tool for assessing the extent of brain shift and the concomitant degradation in the initial preoperative image registration throughout the course of a complete procedure. Various approaches have been developed to track intraoperative cortical surface motion between different stages of surgery using microscope video sequences or stereovision.^21,23,38 In these studies, the later-stage displacement maps need to be registered to the undeformed cortical surface in pMR, requiring an initial registration to be established between pMR and the first cortical surface acquisition, which our approach conveniently (and accurately) provides.

We solved the problem of surface registration between iSV and pMR for displacement mapping by generating pMR-encoded texture maps that are in the same 2D coordinate system as the iSV data and registering the two images with SSD rigid registration followed by BMM nonrigid registration. Unlike registrations that solely depend on surface geometrical information (e.g., ICP), our technique incorporates both geometry and texture intensity. Independent measurements of feature (vessel junctions) point coordinates with a tracked stylus show that the corresponding surface-registered locations are very similar. Specifically, Table II shows an overall difference in feature locations of 1.94 ± 0.59 mm relative to the probe which is comparable to the other errors expected in the underlying image registration and tracking system. Indeed, differences in the two locations (stylus vs surface-registered) are a result of errors in the surface registration technique modulated by errors in the original fiducial registration, and stylus tracking and feature localization errors, which are on the same order.

Stereovision is an important intraoperative imaging technique that captures the cortical surface noninvasively with high spatial resolution and without interruption to surgical workflow. Nonetheless, surface displacements can be obtained directly by using a stylus tracked by the associated navigation system (e.g., StealthStation). For example, Garlapati et al.¹⁴ identified feature points in the pMR volume to define their undeformed locations, selected the same points in the OR by touching them with a tracked stylus to determine their deformed positions, and used the difference between homologous points as a surface displacement map for input to a biomechanical model for brain deformation compensation. Unfortunately, feature identification with a tracked stylus can be time consuming and may be disruptive to surgical flow, whereas stereovision is noninvasive and the acquisition occurs within ∼1–2 s for a high resolution surface. More importantly, point-by-point feature identification is subject to additional localization errors, in both pMR images and on the actual cortical surface, and only the few discrete features (N < 10) that can be accurately located in pMR images and appear on the exposed cortical surface can be used (e.g., vessel junctions). As a result, very few displacement points can be extracted depending on the size of the craniotomy and the richness of features on the cortical surface. In a previously published study, Ji et al.⁹ showed that model-data misfit has a statistically significant decrease with increasing amounts of sparse data (see Ref. 9 for detailed relationship between number of sparse data points and model-data misfit). Since one important purpose of obtaining surface deformation is to extract surface displacement data as part of the overall process of compensating for intraoperative brain deformation, a large number of data points (N = ∼ 200) are preferred, making point-by-point stylus-probe acquisition of surface displacements cumbersome and impractical in the OR. Here, we only used the probe approach as a means of obtaining independent measurements to validate our iSV results. We also used step size in the block matching method to control the density of the resulting displacement field, i.e., the amount of sparse data, and selected a typical value of 50 pixels in both horizontal and vertical directions, leading to an average of ∼200 sparse data, which is sufficiently large for accurate model estimations.

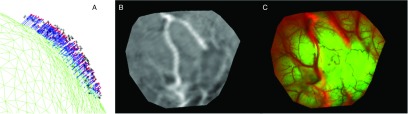
When we incorporated the full 3D displacement field into a biomechanical model to produce uMR views, the subsequent uMR-encoded texture map aligned well with the iSV results acquired after dural opening, which indicates fidelity and self-consistency in our registration approach and model results. Figure 8 shows an example (patient D) of model results generated from sparse displacement data extracted by an ICP distance algorithm.^22,25 Here, the displacement field essentially represents rigid-body motion and does not capture the presence of lateral brain shift or nonrigid surface deformation. When the uMR-encoded texture map resulting from the model assimilation of this data is overlaid on the iSV image, the major vessel appearing near the center of the field-of-view is not well aligned, even though the final model-data misfit is reported to be an acceptable 1.71 mm, comparable to the MR voxel size (typically with diagonal of 2.0 mm) and registration error. Thus, approaches that only utilize geometry information, such as ICP, may not reliably extract sparse displacement data and, therefore, could lead to inaccurate results because they fail to incorporate any of the image texture information that is also available.

FIG. 8.

Extracted sparse data (A) and model results [(B) and (C)] using an ICP registration algorithm. In (A), sparse displacement data (vectors) are produced by registering the pMR parenchymal surface (grid) with the postdural opening iSV surface (crosses), and red points represent the registered brain surface. In (B), the uMR-encoded texture map is generated from the model deformation results produced by using the displacement data in (A). In (C), the uMR-encoded texture map is overlaid on the iSV texture image after displacement data assimilation and reveals considerable surface misalignment from lateral brain shift that has not been captured by the ICP registration.

In work by Joldes et al.,¹⁹ surface registration between pMR and iMR was achieved with an algorithm that combines curvature with image registration. Similar to our approach, Joldes’s algorithm also utilizes both geometry and texture to register cortical features, i.e., sulcal patterns, accurately. Both techniques first convert the 3D surface registration into a simplified 2D registration by projecting surfaces onto a 2D grid, use readily available 2D image registration algorithms to extract the 2D displacements, and convert the 2D displacements into 3D space. In Joldes’s method, undeformed and deformed cortical surfaces were segmented from pMR and iMR, respectively, and were represented through Gaussian curvature. The 2D projection images were directly registered with a B-Spline scheme. The approach can potentially be applied to register successive iMR acquisitions from different surgical stages for later-stage brain deformation compensation. The accuracy of Joldes’s displacement mapping method was evaluated through synthetically generated data and was measured as the difference between the known and recovered displacements in 2D space (and found to be 0.29 ± 0.23 mm on average, 1.6 mm maximum). While the reported accuracy is impressive, some aspects of the overall approach (e.g., image processing, conversion into 3D space) were not applied and, therefore, were not evaluated from an accuracy perspective. As a second approach to validation, Joldes et al. assimilated the algorithm’s measured displacements into a biomechanical model to produce uMR, and the surface contour at the craniotomy from uMR matched well with iMR. However, quantitative results from these clinical cases, which are likely to suffer from additional errors from steps in the displacement mapping algorithm that were not considered using synthetically generated data, were not reported. In comparison, our technique directly captures intraoperative cortical surfaces from stereovision. The accuracy we report here (1.94 ± 0.59 mm) is subject to a number of factors beyond the 2D registrations such as systematic error from the stereovision system [∼1 mm (Ref. 31)], and stylus tracking and feature localization errors. Compared with iMR, iSV does not reveal subcortical features, and therefore, the projection image cannot be directly registered with pMR using nonrigid registration algorithms such as B-Splines because of differences in the image data. As a result, common features such as vessels were segmented for an initial alignment to compensate for the global shift, and a second block matching method using MI registration was applied to detect local movement, thus leading to the longer computational times (∼1–2 minutes vs seconds using Joldes’s approach). However, iSV introduces minimal disruption to surgical workflow, offers much higher spatial resolution than iMR, and is, therefore, able to resolve features that are not visible in MR (e.g., fine vessels). Although the registration between pMR and iSV is limited by the resolution of MR, registration between iSV surfaces during later stages of surgery can be performed at a higher resolution,³⁸ where an initial alignment between pMR and iSV is necessary and crucial to registering later iSV-generated displacement maps with the originally undeformed brain.

On the other hand, limitations in our technique still exist. First, it only applies to open-cranial surgeries where blood vessels or other features are present in both the iSV and pMR image data. Although blood vessels can often be found, the iSV and pMR image quality may significantly influence the effectiveness of the method. For example, iSV images may contain artifacts resulting from light reflections or blood on the brain surface can mask the features of interest. If only smaller blood vessels exist on the exposed cortical surface, the pMR-encoded texture map generated by averaging 1–2 mm of MR voxels may blur/distort these features significantly. In addition, pMR-encoded texture maps may capture subsurface vessels that are not evident in the iSV data, and additional manual segmentation to exclude such vessels may be required. Finally, registration between iSV and pMR is only applicable at the beginning of surgery, i.e., before tissue resection occurs, when tracking brain surface motion is important for estimating brain shift. We have developed other techniques to register iSV images acquired at different temporal stages of surgery,³⁸ and we can track brain tissue motion throughout the case by incorporating these procedures.

In this paper, we also analyzed certain characteristics of the surface displacements and uMR results from the ten clinical cases. Compared with the existing literature, the displacement magnitudes agree with other reports^5,39 and ranged from 4.03 to 9.79 mm. The correlation between surface displacements and gravity, however, is different from some findings in the literature. Our results indicate a weak correlation between lateral shift and gravity, whereas other data⁵ indicate that most of the displacement takes place in the direction of gravity (likely because the iSV surfaces were acquired immediately after dural opening in this study and before gravitational sag becomes the dominant effect). Because all ten patients in our study suffered from brain lesions, immediate brain distention occurred postdurotomy, i.e., immediately after dural opening due to the presence of a space-occupying mass, instead of collapse resulting from CSF loss and gravitational forces as reported elsewhere.^5,39 Brain distention does not necessarily correlate with gravity, but after some time, the brain surface often starts to collapse from fluid loss.

5. CONCLUSION

Durotomy can cause significant brain shift that compromises the accuracy of image guidance based on preoperative images. The brain deformation patterns are case-specific and difficult to predict prior to surgery. Modeling methods provide effective and efficient tools to estimate brain deformation caused by dural opening and when combined with intraoperative data produce model-updated MR volumes that maintain registration accuracy for image guidance. We have developed a method that registers intraoperative stereovision surfaces with preoperative MR images to extract displacement maps that are further assimilated into a brain deformation model to compute a whole-brain displacement field. The iSV–pMR registration method utilizes both texture and geometry information and compares favorably (<2 mm difference on average) with feature coordinate locations acquired independently with a tracked stylus. The model results also agree well with the fully reconstructed iSV surface in terms of both geometric shape and feature texture, and the process generates a well aligned and self-consistent model-updated MR volume. We demonstrate the effectiveness and efficiency of surface registration technique in ten patient cases and show that the MR updates can be computed within 10 min and with minimal interruption to surgical workflow. This suggests the method is a viable approach for brain shift compensation in the OR, especially after dural opening when tissue deformations of 0.5–1 cm are common.