Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2016 Nov 9;118(1):88–95. doi: 10.1038/hdy.2016.108

DNA sequence diversity and the efficiency of natural selection in animal mitochondrial DNA

J James 1, D Castellano 2, A Eyre-Walker 1,*
PMCID: PMC5176113  PMID: 27827387

Abstract

Selection is expected to be more efficient in species that are more diverse because both the efficiency of natural selection and DNA sequence diversity are expected to depend upon the effective population size. We explore this relationship across a data set of 751 mammal species for which we have mitochondrial polymorphism data. We introduce a method by which we can examine the relationship between our measure of the efficiency of natural selection, the nonsynonymous relative to the synonymous nucleotide site diversity (πN/πS), and synonymous nucleotide diversity (πS), avoiding the statistical non-independence between the two quantities. We show that these two variables are strongly negatively and linearly correlated on a log scale. The slope is such that as πS doubles, πN/πS is reduced by 34%. We show that the slope of this relationship differs between the two phylogenetic groups for which we have the most data, rodents and bats, and that it also differs between species with high and low body mass, and between those with high and low mass-specific metabolic rate.

Introduction

Variation in effective population size between species is expected to have two important effects on molecular evolution. First, the higher the effective population size (Ne), the greater the efficiency of natural selection in that population (Kimura, 1984). This is because with increasing Ne, stochastic changes in allele frequencies have a proportionally lower impact, and therefore deleterious mutations are more likely to be removed (Popadin et al., 2007; Corbett-Detig et al., 2015). Second, the greater the Ne, the higher the level of neutral genetic diversity, with the level of neutral genetic diversity in a population determined by the product of Ne and the neutral mutation rate (Kimura, 1984; Charlesworth, 2009). We therefore expect neutral nucleotide diversity and the efficiency of selection to be correlated, as both are influenced by Ne. This prediction is well supported by a number of recent studies in both nuclear (Galtier, 2015) and mitochondrial DNA (mtDNA) (Piganeau and Eyre-Walker, 2009).

We can also make a specific prediction about the relationship between neutral genetic diversity and the efficiency of selection. If all synonymous mutations are neutral, we expect the nucleotide diversity at synonymous sites, πS, to be equal to 4Neμ. If we assume that all nonsynonymous mutations are deleterious, although some may be sufficiently weakly selected that they are effectively neutral, we expect πN, the nonsynonymous nucleotide site diversity, to be influenced by the mutation rate, the effective population size and the distribution of fitness effects (DFE). Assuming the DFE is a gamma distribution, we expect πN to be equal to 4Neμ k Ne−β, where β is the shape parameter of the gamma distribution of fitness effects and k is a constant that depends upon the mean strength of selection (Welch et al., 2008). Hence, πN/πS=kNe−β, and log(πN/πS) and log(πS) are expected to be linearly correlated to each other with a slope of −β if Ne and μ are uncorrelated and if the DFE, and hence k, remains constant with changing Ne.

Here we test whether this prediction is upheld in mtDNA using polymorphism data from 751 mammals. We explore and quantify the relationship between neutral genetic diversity (synonymous site diversity (πS)) and the efficiency of selection (the ratio of nonsynonymous to synonymous site diversity (πN/πS)) in mammalian mitochondria, using a new method. We compare the slope of the log-transformed relationship with the shape parameter estimated from the site frequency spectra under the assumption that the DFE is a gamma distribution. We also investigate whether the relationship between πN/πS and πS differs between phylogenetic groups and according to demographic and life-history parameters.

Materials and methods

Data set

Our data set was constructed by downloading sequences from MamPol, a database of mammalian polymorphisms (Egea et al., 2007). Only protein-coding, mtDNA was used in this study. Sequences for each species were concatenated where possible, to produce longer alignments, and then aligned using Geneious version 7.0.6 (Kearse et al., 2012). We analysed the alignments using our own software to produce polymorphism estimates, and where available, we added life-history and demographic data to the species in our data set, using information from the PanTHERIA database (Jones et al., 2009). Our complete data set contains 751 mammal species for which we have polymorphism data.

Relationship between πN and πN/πS

We use πS, synonymous nucleotide site diversity, as a measure of neutral genetic diversity, and πN/πS, the ratio of nonsynonymous to synonymous nucleotide site diversity, as a measure of the efficiency of natural selection. These summary statistics are used, rather than raw counts of numbers of polymorphisms, to correct for the fact that the species in the data set had variable numbers of sequenced loci, and that the sequences used were of different lengths.

Synonymous polymorphisms are used to calculate both πS and πN/πS, and hence we expect there to be a negative correlation between these variables just through sampling error. Therefore, we removed the statistical non-independence between the variables by first dividing synonymous polymorphisms into three groups by randomly sampling from a hypergeometric distribution. We then used each group to calculate πS1, πS2 and πN/πS3, respectively. This is analogous to dividing each sequence into thirds (Smith and Eyre-Walker, 2002; Piganeau and Eyre-Walker, 2009). As we were interested in the relationship between log(πN/πS) and log(πS), we needed to ensure there were no cases in which either πN or πS were zero; however, removing species in which πS or πN/πS was zero would result in biased results. In addition, individual measurements of πS and πN/πS will be subject to a large degree of sampling error. Therefore, to overcome these problems we first ranked species by πS1, and based on this ranking the species were divided into evenly sized groups. Average πS2 and πN/πS3 values were calculated for each group. We then ran ordinary least squares regression between the log-transformed values of these averages.

Correcting for phylogenetic non-independence

To ensure that our results are not due to phylogenetic non-independence, we used paired-independent comparisons (Harvey and Pagel, 1991). Using DNA-based phylogenetic literature, we identified 186 sister pairs of species in our data set, where sister pairs are defined as sharing a common ancestor to the exclusion of all other species in the data set. We then repeated our method as before, using the ratio of πS1 between species in a pair to rank and group pairs, and calculating the average ratio of πS2 and πN/πS3 between species in a pair over each group. We then considered the relationship between the log of the average ratios of πS2 and πN/πS3.

Simulations

To investigate the performance of our method we ran two sets of simulations. In the first we used SFS_code (Hernandez, 2008) to simulate loci with no intralocus recombination, but with free recombination between loci. We ran simulations of loci of three different lengths: 1, 1000 and 10 000 codons. The number of loci simulated was reduced as the length of the loci was increased, such that we simulated 100 loci 1 codon long, 10 loci 1000 codons long and 3 loci 10 000 codons long. The synonymous sites in these codons were assumed to be neutral and the nonsynonymous mutations to be deleterious and drawn from a gamma distribution. In each simulation the population size was set to 5000 but the arithmetic mean value of Ns and the value of Nμ were changed to reflect changes in N (that is, we take advantage of the fact that increasing s and μ x-fold is equivalent to increasing the population size by x-fold because population genetic behaviour depends on the product of the effective population size and the other parameters). We set the mean Ns and Nμ to be 100 and 0.001, 500 and 0.005, 1000 and 0.01, 2000 and 0.02, 4000 and 0.04 and 8000 and 0.08, respectively (note that because of background selection the effective population size was not equal to the census population size). We simulated data under three different shape parameters for the gamma distribution: 01, 0.3 and 0.5. Each simulation was run for 15N generations for the population to equilibrate before the population was sampled, and for each combination of parameters a number of iterations were run, such that for each parameter combination at least 1000 synonymous polymorphisms were sampled (the exception was the set of simulations with 10 000 codons run with Nμ=0.08 that were only run once as they ran so slowly; in these cases at least 100 synonymous polymorphisms were sampled).

In the second set of simulations we investigated the statistical properties of the method, and in particular our scheme for combining data from different species and/or genes. In each simulation we had 500 species, each of which had 1000 synonymous sites. We sampled effective population sizes from a gamma distribution with a shape parameter βN, arbitrarily and without loss of generality, setting the expected value of Ne to one (the absolute value of Ne is not important in this context, as what matters is how the proportion of effectively neutral mutations changes with Ne, and this is independent of the absolute value). The expected number of synonymous polymorphisms (Ps) and nonsynonymous polymorphisms (Pn) for species i were calculated as E (Psi)=E (Ps) Nei and 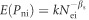Inline graphic where βs is the shape parameter of the distribution of fitness effects, and k is a constant that normalises the expected values of Pn such that E (Pn)=0.2 E (Ps), approximately the pattern that is observed in our data. The simulated values of Pn and Ps were generated by sampling from a Poisson distribution with the expected values as given above. The method then proceeded as detailed previously. We investigated the effects of altering the size of the groups, the average number of synonymous polymorphisms, variation in Ne and the shape parameter of the DFE. For each combination of parameters, we ran the simulation 100 times. Throughout our analyses we use ordinary least squares regression, but we also investigated the use of standard major axis regression in our simulations.

Calculating the DFE

In order to calculate the DFE of mitochondrial mutations, we combined the synonymous and nonsynonymous site frequency spectra (SFS) across species. We cannot calculate the DFE for individual species, first, because mitochondria are inherited in a clonal manner that can make the SFS highly erratic and, second, because the majority of species have too few polymorphisms to allow us to make a reliable estimate of the DFE. We therefore combined SFS data across species in the data set using the method of James et al. (2016); this method weights the data for each species equally to produce an overall nonsynonymous and synonymous SFS for the data set. We then inferred the DFE by fitting a gamma distribution to the ratio of nonsynonymous to synonymous polymorphism at each frequency category of the SFS using least squares. Full details of the method are given in James et al. (2016). This method required each species in the data set to have a common number of sampled individuals: we therefore produced data sets in which the number of individuals (n) for each species was resampled down to a common number. We produced two resampled data sets, one in which n=5 and one in which n=11; however, the sequence data are otherwise identical to that used in the previously described methods. Any species that did not have a minimum of n sampled individuals was excluded from the data sets, and therefore our data sets subsampled to 5 and 11 individuals contained 564 and 256 species, respectively. We again fitted regression models to the subsampled data sets, randomly splitting synonymous polymorphisms into three groups and calculating average values of πS and πN/πS over groups of species as before.

To test whether the shape parameter of the DFE, as inferred from the SFS, was different from the slope of the regression between log(πN/πS) and log(πS) we bootstrapped the data by species 100 times, in each re-estimating the shape parameter of the DFE using the resultant SFS, and the slope of the relationship between log(πN/πS) and log(πS).

Results

We have investigated the relationship between a measure of the efficiency of natural selection, log(πN/πS), and diversity, log(πS), in mammalian mitochondria, using a polymorphism data set of 751 species. If there is free recombination, the DFE is gamma distributed and the effective population size, Ne, is uncorrelated to mutation rate, μ, then this relationship is expected to be linear with a slope equal to the shape parameter of the gamma distribution (Welch et al., 2008). However, it is not straightforward to investigate this relationship for three reasons. First, for many of our species either πN or πS is zero and hence one of our two statistics is undefined; however, to exclude these species will bias our results. Second, there will be a degree of variable error and ‘noise' in our individual measurements of πN and πS. Third, log(πN/πS) and log(πS) are not statistically independent; we therefore expect there to be a negative correlation between log(πN/πS) and log(πS) simply because of sampling error in πS that arises because we have sequences of finite length. To overcome these problems, we randomly split the synonymous polymorphisms into three independent groups, using each to calculate a separate value of πS. We used the first estimate of πS to rank and group species, the second value as our estimate of πS for the group and the third value to calculate πN/πS. 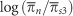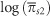We ran ordinary least squares regression between the Inline graphic and Inline graphic where the means are for each group of species. Using this method reduces the variance in our data set, such that the smaller the number of groups the greater the reduction in variance.

Simulating the method

To investigate the properties of the method we ran two sets of simulations. In the first we investigated the population genetics of the method; in particular, we were interested in ascertaining whether linkage affected the predictions determined under the assumption of free recombination. We simulated loci with 1, 1000 and 10 000 codons. There was free recombination between loci but no recombination within a locus. Synonymous mutations were assumed to be neutral and nonsynonymous mutations to be deleterious and drawn from a gamma distribution. We altered the population size over nearly two orders of magnitude from a mean Ns value of 100 and an Nμ value of 0.001 to values of 8000 and 0.08 respectively (where s is the strength of selection and μ is the mutation rate). We simulated data under three different shape parameters: 0.1, 0.3 and 0.5.

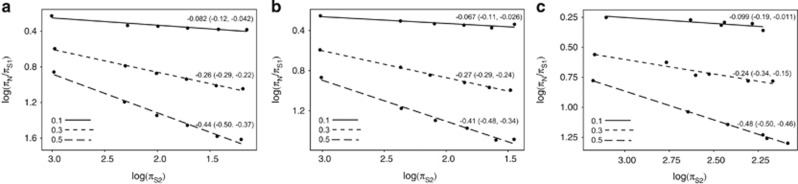
The results are shown in Figure 1, where log(πN/πS) is plotted against log(πS). Despite the fact that there is considerable background selection in some of the simulations, such that background selection reduces synonymous diversity by more than 10-fold in the simulations with 10 000 codons and high Nμ values, the slope of the relationship between log(πN/πS) and log(πS) is close to that expected (Figure 1). However, there is a slight but significant tendency to underestimate the slope. This underestimation does not depend on linkage.

Figure 1.

Figure 1

Open in a new tab

The relationship between log(πN/πS) and log(πS) in simulated data when each non-recombining locus contains (a) 1 codon, (b) 1000 codons and (c) 10 000 codons. In each panel the lines from top to bottom show the results for different shape parameters of the DFE: 0.1, 0.3 and 0.5. The slope of a least squares regression and its confidence interval are given next to each line.

In the second set of simulations we sought to investigate the statistical properties of the method and in particular whether our method of combining data from different species and/or genes gave biased estimates. To do this we ran simulations in which we generated the number of nonsynonymous (Pn ) and synonymous (Ps) according to our model, analysing the resulting data according to the method detailed above—that is, splitting the synonymous polymorphisms into three groups, and considering regressing log(PN/PS) against log(PS) using ordinary least squares regression. We consider the relationship between log(PN/PS) and log(PS) rather than log(πN/πS) and log(πS) because theory predicts the relationship should be the same (Welch et al., 2008) and simulating the numbers of polymorphisms rather than the diversity is more straightforward.

Our simulations suggest that the method is unbiased when the shape parameter of the gamma distribution is very small—that is, when there is no expected relationship between log(PN/PS) and log(PS) (see Table 1). However, the method can either be upwardly or downwardly biased when the shape parameter of the gamma distribution is greater than zero (Table 1). When there is relatively little variation in Ne (higher values of βNe) and relatively few synonymous polymorphisms, then the method tends to estimate the slope to be shallower than it should be. This bias can be ameliorated by using large groups of species/genes, but was not helped by using standard major axis regression; this led to a dramatic overestimation of the slope (data not shown). The bias in underestimating the slope is not surprising; the ability to estimate the relationship between log(PN/PS) and log(PS) will depend upon the relative magnitudes of the variation in Ne and the sampling error in PS; when the latter dominates the former then it is difficult for the method to determine which species/genes have high or low Ne. Surprisingly, the method can also estimate the slope to be slightly steeper than it should be when there is substantial variation in Ne and few synonymous polymorphisms. However, so long as the mean number of polymorphisms per species/gene is reasonable (on average >8), and there is moderate variation in Ne then the method is largely unbiased if large groups of species/genes are used (see Table 1). The bias is not likely to be very large in our data set as the average number of synonymous polymorphisms is quite large (∼16) and we have substantial variation in PS (we estimate βNe to be 1.5 assuming all the variation in PS is due to variation in Ne).

Table 1. The mean slope estimated from 100 simulated data sets under various parameter combinations.

βs E(Ps) βNe Group size Mean slope (s.e.)
0.001 2 1.5 10 −0.04 (0.02)
  4     0.03 (0.01)
  8     0.02 (0.01)
  16     0.00 (0.01)
  32     0.01 (0.01)
  2   20 0.03 (0.03)
  4     0.01 (0.02)
  8     0.02 (0.01)
  16     −0.00 (0.01)
  32     0.01 (0.00)
  2   50 −0.00 (0.04)
  4     0.02 (0.02)
  8     0.01 (0.01)
  16     0.00 (0.01)
  32     −0.01 (0.00)
  2 0.1 50 0.00 (0.02)
  4     0.01 (0.01)
  8     0.00 (0.01)
  16     0.00 (0.00)
  32     0.01 (0.00)
  2 10 50 0.08 (0.07)
  4     −0.05 (0.05)
  8     −0.01 (0.04)
  16     0.00 (0.00)
  32     0.01 (0.00)
0.5 2 1.5 10 −0.26 (0.03)
  4     −0.40 (0.01)
  8     −0.44 (0.01)
  16     −0.46 (0.01)
  32     −0.48 (0.00)
  2   20 −0.33 (0.03)
  4     −0.45 (0.02)
  8     −0.45 (0.01)
  16     −0.46 (0.01)
  32     −0.49 (0.00)
  2   50 −0.54 (0.05)
  4     −0.53 (0.02)
  8     −0.48 (0.01)
  16     −0.48 (0.01)
  32     −0.49 (0.00)
  2 0.1 50 −0.58 (0.01)
  4     −0.54 (0.01)
  8     −0.52 (0.01)
  16     −0.49 (0.00)
  32     −0.49 (0.00)
  2 10 50 −0.01 (0.07)
  4     −0.22 (0.06)
  8     −0.36 (0.04)
  16     −0.44 (0.02)
  32     −0.47 (0.01)
Open in a new tab

Abbreviations: βs, the shape parameter of the distribution of fitness effect (DFE); βNe, shape parameter of the gamma distribution sampled to produce effective population sizes; E(Ps), the average number of synonymous polymorphisms.

The last column gives the mean and s.e. of the slope from simulation run.

Overall relationship between log(πN/πS) and log(πS)

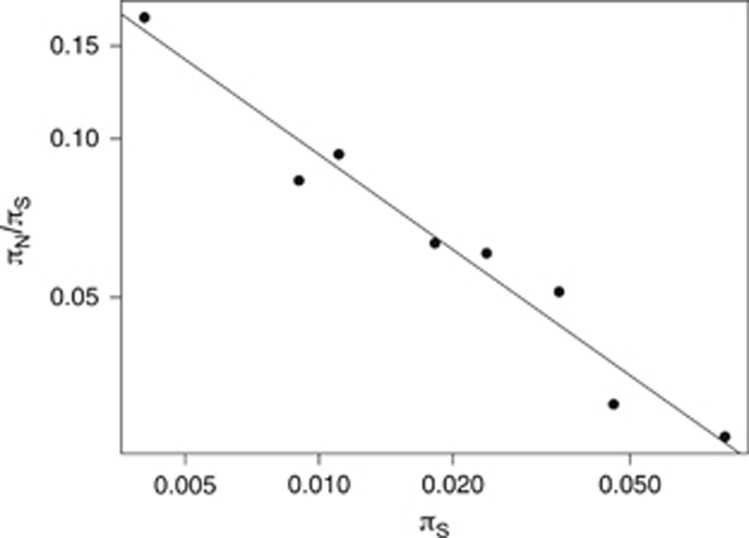
Across the entire mammalian mitochondrial data set, we find that log(πN/πS) is almost perfectly linearly related to log(πS) after grouping species into eight groups (Figure 2). The correlation is highly significant (Pearson's R=−0.98, P<<0.001). The slope of the relationship is −0.60 (s.e.=0.050) (Figure 2), and this means that if diversity doubles the proportion of effectively neutral substitutions is reduced by 1–2−0.60=34%. Similar results are obtained if we use 10, 20, 30 40 and 50 groups (Supplementary Table 1), with the correlation remaining highly significant (P<<0.005) for all numbers of groups. However, as the number of groups increases there is a trend for the slope of the line to become shallower. This is in accordance with the results of our simulations: as the number of groups increases, the lower the number of synonymous polymorphisms per group and the greater the bias in our method towards underestimating the slope.

Figure 2.

Figure 2

Open in a new tab

The relationship between πN/πS and πS in mammalian mitochondrial DNA. Plotted on a log scale.

Correcting for phylogenetic non-independence

The correlation between log(πN/πS) and log(πS) is not due to phylogenetic non-independence between species. Using paired-independent contrasts, we repeated our analysis (exploring the correlation between the log of the ratio of πN/πS and the log of the ratio of πS for each species pair, again dividing species into 8 groups) and found a linear correlation of slope −0.60 (s.e.=0.067) that is identical to that of our nonpaired data set. The correlation was also highly significant (Pearson's R=−0.96, P=0.00011). Similar results are obtained when using 10, 20 and 30 groups (results not shown).

Taxonomic groups

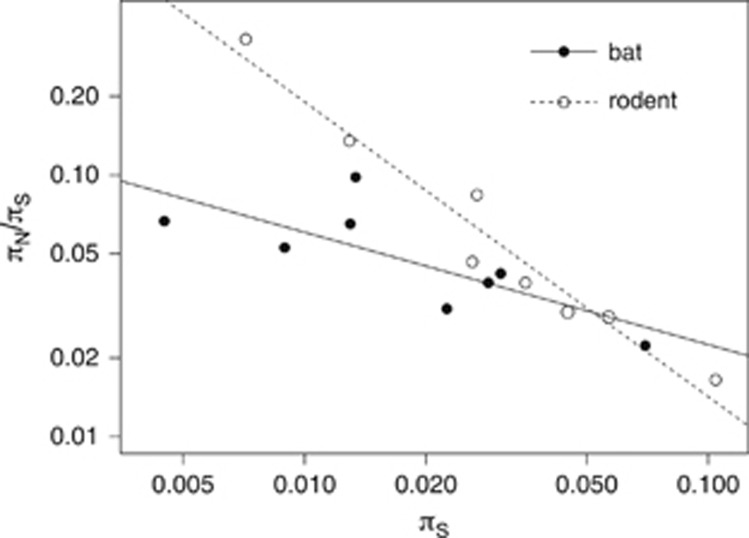
There are a number of reasons why the relationship between log(πN/πS) and log(πS) might differ between species. To investigate this question we compared the two groups represented by the largest number of species in the data set, bats (Chiroptera) and rodents (Rodentia) (178 and 226 species, respectively). These are the two most species-rich groups of mammals. Results are shown in Figure 3. Although the correlation remains significant and negative in both bats and rodents, in rodents the slope of the line is far steeper (slope=−1.13, s.e.=0.10; intercept=−2.97, s.e.=0.16) than in bats (slope=−0.43, s.e.=0.15; intercept=−2.08, s.e.=0.26.) a difference that is statistically significant (P=0.0022). Again, this result holds if we use 10 and 20 groups, although the difference is not significant with 30 groups (results not shown). Hence, although πN/πS is substantially lower in bats than rodents, the efficiency of selection does not increase as rapidly with increasing πS in bats as it does in rodents.

Figure 3.

Figure 3

Open in a new tab

Comparison of the relationship between πN/πS and πS of bats (Chiroptera) and rodents (Rodentia). Plotted on a log scale.

Life-history and demographic traits

We also investigated whether we could detect any influence of life-history or demographic traits on the relationship between log(πN/πS) and log(πS). We looked at three traits: body mass, species range size and mass-specific metabolic rate (that is, resting metabolic rate divided by body mass). We ranked the species by the trait in question, and split the species into two evenly sized groups depending on the ranking. We then used the method as described previously (grouping the species into eight) to investigate the correlation of log(πN/πS) and log(πS) separately for each group. Therefore, we have an estimate of the relationship for those species in which the life-history trait is low, and an estimate for those species in which the life-history trait is high. Results are shown in Table 2 and Figure 4. Of the species in our data set, we have 567 with body mass estimates, 588 with range area estimates and 157 species with mass-specific metabolic rate estimates.

Table 2. Comparisons of the regression slope and intercept for different life-history traits.

Trait Low High Sig.
  Slope Intercept Slope Intercept  
Mass-specific metabolic rate −0.49 −2.03 −1.32 −3.36 0.037
Mass −0.91 −2.81 −0.36 −1.77 0.012
Range −0.50 −2.09 −0.46 −2.08 0.74
Open in a new tab

The species were always split into eight groups in this analysis. The slope and the intercept of the regression line for each life-history trait are given. The relationship between πS and πN/πS was statistically significant for all the above subsets of the data, with P<0.05. The linear models for species with high and low values of the life-history trait were compared using an analysis of variance (ANOVA) test, the significance (Sig.) level of which is given in the last column.

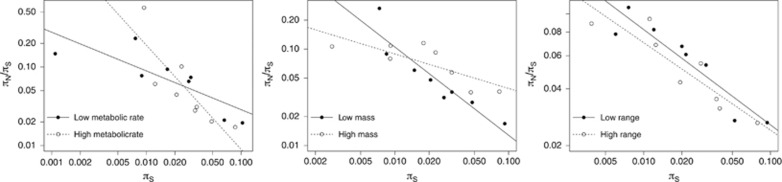
Figure 4.

Figure 4

Open in a new tab

The influence of life-history and demographic traits on the relationship between πN/πS and πS. We consider whether the relationship is different for species with a higher value of a given trait as opposed to a lower value. From left to right, the traits considered are: mass-specific metabolic rate (referred to as ‘metabolic rate' in the figure legend, ml O2 −1h−1 g−1), body mass (g) and range size (km2). Plotted on a log scale.

We found that two of the life-history traits we considered had a significant effect on the regression slope of log(πN/πS) and log(πS). The largest difference in regression slope was found to be between mammals with high and low mass-specific metabolic rates: the slope was steeper for mammals with high rates, such that πN/πS decreases more rapidly with increasing πS in mammals with high as opposed to low mass-specific metabolic rates. We also found that the slope of the regression line was significantly different between mammals with low body mass and mammals with high body mass, with smaller mammals having a steeper regression line. Range size, on the other hand, did not appear to influence the relationship between log(πN/πS) and log(πS).

We also investigated the interaction of body mass and mass-specific metabolic rate on the regression slope between log(πN/πS) and log(πS). In this analysis we increased the number of groups used in the regression to 20. The interaction term was not significant for mass-specific metabolic rate (interaction term=−1.81, P=0.21, such that if the value of log(πS) increases by 1, the slope of the interaction between log(πN/πS) and log(mass-specific metabolic rate) decreases by the value of the term), but was significant for body mass (interaction term=−0.13, P=0.022). However, using higher numbers of groups removes the statistical significance of this interaction.

Comparison of the slope with the shape of the DFE

If the DFE is a gamma distribution then the relationship between log(πN/πS) and log(πS) should be linear with a slope equal to the negative value of the shape parameter. Our analysis above suggests that the relationship between log(πN/πS) and log(πS) is linear, but is the slope equal to the shape parameter? To investigate this we used an independent method to estimate the shape parameter of the DFE. We subsampled the sequences for each species down to a common number of sequences (n=5 and n=11) and combined the site frequency spectra in a manner that weights every species equally, and then estimated the DFE by fitting a gamma distribution to the ratio of nonsynonymous to synonymous polymorphisms at each frequency category of the SFS, using the method of James et al. (2016). We then conducted our analysis of the relationship between log(πN/πS) and log(πS) on the resampled data sets as before. To test whether the estimate of the shape parameter, as inferred from the SFSs, was significantly different to the negative value of the slope of the relationship between log(πN/πS) and log(πS), we bootstrapped the data by species 100 times. The results are shown in Table 3. We found that our estimates for the shape parameter of the gamma distribution was considerably and significantly smaller than the negative value of the slope of the regression line between log(πN/πS) and log(πS) for both 5 and 11 sample data sets (t-test: P<<0.001 for both data sets, where the alternative hypothesis is that the true difference in means is less than 0). This is particularly striking considering that simulations indicate our regression method may estimate the slope to be shallower than it should be.

Table 3a. Estimates of the DFE.

No. of chromo. Shape Lower CI Upper CI S Lower CI Upper CI
5 0.45 0.21 0.56 1120 289 34 400
11 0.44 0.34 0.57 1890 574 12 200
Open in a new tab

Abbreviations: CI, confidence interval; DFE, distribution of fitness effect.

The first column gives the number of chromosomes (chromo.) sampled for each species in the data set. The shape parameter of the gamma distribution of fitness effects is given in the ‘shape' column, and the estimated strength of selection is given in the S column. CIs for each variable are labelled as ‘Lower CI' and ‘Upper CI'.

Discussion

The relationship between πN/πS and πS is of considerable biological interest. There are few estimates of Ne available, and hence πS is commonly used as a proxy for Ne. However, the extent to which πS is related to measures of selective constraint was not previously known. Here we show that log(πN/πS) and log(πS) are strongly negatively and linearly correlated in mammalian mitochondria, so that as neutral genetic diversity doubles, the efficiency of selection also increases, resulting in a 34% reduction in the number of effectively neutral polymorphisms.

Life-history traits affected the slope of the relationship between log(πN/πS) and log(πS): we find that the slope of the relationship is greater in species with high as opposed to low mass-specific metabolic rates; therefore, with increasing genetic diversity, the increase in selective constraint is greater in species with high metabolic rates. We also find that the slope of the relationship between log(πN/πS) and log(πS) is shallower for species with high as opposed to low body mass. This may be because of a correlation between the two life-history traits: species with low body mass are known to have higher mass-specific metabolic rates (Schmidt-Nielsen, 1984; Suarez, 1992). We also find that the relationship between log(πN/πS) and log(πS) is shallower in bats than in rodents. This does not appear to be driven by differences in life-history traits: the bats and rodents in our data set have very similar mass-specific metabolic rates (t-test P-value=0.88, mean mass specific metabolic rate is 1.45 for rodents and 1.43 for bats), and although bats were found to be significantly smaller than rodents (t-test P-value<0.0001, mean mass=196.7 g for rodents, 30.7 g for bats), this would have been expected to generate the opposite pattern in terms of the relationship between log(πN/πS) and log(πS).

There are a number of reasons why the slope of the relationship between log(πN/πS) and log(πS) might differ between bats and rodents, and between species with high and low body mass and metabolic rate. It might be that the DFE differs between the two groups, or alternatively it might be that the relationship between πS and Ne differs; for example, in some groups Ne and the mutation rate per generation might be negatively correlated (Lynch, 2010). There might also be differences in how the strength of selection changes with Ne between different taxonomic groups and species with different life-history traits, that is, the parameter k in the equation πN/πS=kNe−β, which is related to the strength of selection, may also be a function of Ne. To differentiate between these possibilities, we estimated the DFE from the SFSs for each group. The results are presented in Table 4. The estimate of the shape parameter of the DFE from the SFS is very similar in bats and rodents (although the s.e. values associated with the estimates are also large), suggesting that the difference in the slope between log(πN/πS) and log(πS) is not due to differences in the shape of the DFE between bats and rodents, but is probably due to either different relationships between πS and Ne or differences in how the k parameter changes with Ne in the two groups. For example, if k were to increase with increasing Ne in bats but not rodents, the slope of the relationship between log(πN/πS) and log(πS) would be shallower for bats. This might occur because of the metabolic demands of flight that could result in a more rapid increase in a higher mean strength of selection on bat mitochondria with increasing Ne. There is some evidence to support this possibility: for example, there are signs of adaptive mitochondrial evolution on the common ancestral lineage of bats, but not rodents (Shen et al., 2010). In addition, Shen et al. (2009) have found a relationship between flight ability and the strength of selective constraint in bird mitochondrial DNA. However, there is also evidence to suggest that patterns of molecular evolution are different between these two groups, which may suggest a difference in the relationship between πS and Ne. For example, Nabholz et al. (2008) have found that synonymous substitution rates are considerably lower in bats than in rodents: this could be because of lower mutation rates or longer generation times in bats than in rodents. In contrast, the shape parameter of the DFE estimated from the SFS mirrors the difference in slopes between high and low body mass and high and low metabolic rate, although in only the data set in which n=5 is the difference significant. It might therefore be that the DFE differs between groups with different body sizes and metabolic rates.

Table 4. Estimates of the DFE for different taxonomic and life-history groups.

Group n Shape Sig.
Rodents 5 0.51 (0.25) NS
Bats 5 0.46 (0.13)  
Rodents 11 0.66 (0.11) NS
Bats 11 0.59 (0.35)  
High body mass 5 0.13 (0.095) <0.01
Low body mass 5 0.73 (0.16)  
High body mass 11 0.37 (0.11) NS
Low body mass 11 0.59 (0.19)  
High metabolic rate 5 0.71 (0.30) 0.01
Low metabolic rate 5 0.059 (0.083)  
High metabolic rate 11 0.70 (0.28) NS
Low metabolic rate 11 0.23 (0.076)  
Open in a new tab

Abbreviations: DFE, distribution of fitness effect; NS, not significant.

The group of species for which the DFE was calculated is given in the first column. The second column gives the number of individuals sampled for each species in the data set. The shape parameter of the DFE, with the s.e. of the estimate in brackets, is given in the ‘shape' column. The significance (Sig.) level of the difference in the DFE between the groups is given in the last column.

Our results depart from the theoretical prediction that the slope of the relationship between log(πN/πS) and log(πS) is the same as the (negative) shape parameter of the DFE, as estimated from the SFS, with the shape parameter of the gamma distribution being significantly smaller than the slope of the regression line. There are a number of possible reasons for this. First, as Welch et al. (2008) note, if the DFE does not follow a gamma distribution, then the above predictions may not hold. Although the DFE is most commonly modelled as a gamma distribution (Piganeau and Eyre-Walker, 2003; Eyre-Walker et al., 2006; Eyre-Walker and Keightley, 2007; Boyko et al., 2008), some studies have found support for alternative distributions, such as the log normal (Loewe and Charlesworth, 2006), the normal (Nielsen and Yang, 2003) and the bimodal beta distribution (Kousathanas and Keightley, 2013). However, the relationship between log(πN/πS) and log(πS) is linear, consistent with the DFE being a gamma distribution; if it were log normal, for example, the relationship should show curvature (Welch et al., 2008).

Second, it has been suggested that a negative relationship exists between Ne and μ, the mutation rate per site per generation. This is because in populations with larger effective population sizes, natural selection is more efficient, and hence should be more able to reduce the mutation rate μ (Lynch, 2010). This introduces a negative interaction between genetic diversity and the efficiency of selection that will tend to make the slope of the relationship between log(πN/πS) and log(πS) steeper. However, the importance of this effect remains unclear: although some studies have found evidence to suggest that there is a negative correlation between Ne and μ (Piganeau and Eyre-Walker, 2009; Lynch, 2010; Cutter et al., 2013), the theory predicts a relatively small effect of Ne on μ that could be masked by the impact of other influences on μ, such as rate of sperm production and exposure to mutagens (Gao et al., 2016). In addition, the theory suggests that the mutation rate of a species is reduced as far as possible by selection, with genetic drift preventing selection from further reducing the rate (Lynch, 2011). However, mutation rates vary widely between species, with some exceeding the upper limit predicted by this theory by orders of magnitude (Martincorena and Luscombe, 2013).

Third, selection on synonymous codons may influence the slope of log(πN/πS) and log(πS). Synonymous sites are commonly assumed to be neutrally evolving; however, codon usage bias in nuclear genes has been reported in a number of species, including Saccharomyces pombe, Caenorhabditis elegans, Drosophila and Arabidopsis (Duret and Mouchiroud, 1999; Hershberg and Petrov, 2008; Kanaya et al., 2011). Selection on synonymous sites is thought to occur in order to maximise translational efficiency by matching transfer RNA abundances (Kanaya et al., 2011) and to improve mRNA stability (Chamary and Hurst, 2005). (Although not relevant to mtDNA, selection on synonymous sites may also maintain accurate splicing of mRNA (Carlini and Genut, 2006).) If selection for optimal codons also reduces the number of nonsynonymous polymorphisms, this will tend to make the slope of the relationship between log(πN/πS) and log(πS) steeper than that predicted by the shape of the distribution of fitness effects. However, if selection on synonymous codons only affects synonymous polymorphisms, then it is expected to affect diversity and the efficiency of selection equally and therefore will not influence the slope of the relationship. In addition, the strength of selection in animals with low Ne may not be sufficient to select for optimal codon usage, and there is little evidence that selection acts on synonymous sites in mammals, or indeed vertebrates, that are thought to have relatively small effective population sizes (Duret, 2002; Kanaya et al., 2011; although see Chamary et al., 2006). Jia and Higgs (2008) found that mitochondrial codon usage evolution is dominated by mutational effects.

Fourth, as was previously mentioned, there could be a relationship between the k parameter and Ne across species. We make the assumption that the strength of selection, included in k, and the shape of the DFE remain constant as Ne changes; however, this is unlikely to be the case (although there is evidence to suggest that the strength of selection can be nearly independent of Ne in some evolutionary scenarios (Charlesworth, 2013)). It may be that generally there is a negative relationship between k and Ne across the species in our data set: this would result in making the slope of the relationship steeper than that predicted by the shape parameter of the gamma distribution.

Finally, hitchhiking may have an important influence on the relationship between genetic diversity and the efficiency of selection. It has been demonstrated across a broad range of species that hitchhiking and background selection remove more neutral diversity in species with larger census population sizes (and hence larger effective population sizes) (Corbett-Detig et al., 2015). Hitchhiking will result in a loss of genetic diversity and a reduction in Ne at linked sites. However, not all types of site will be affected equally by hitchhiking. Deleterious variants segregate at low frequencies in populations, and therefore are expected to reach their equilibrium frequencies relatively rapidly after a linked selection event. Neutral and advantageous variants on the other hand segregate at higher frequencies in populations, and hence linked selection will result in a proportionally smaller loss of diversity for deleterious than for neutral or advantageous sites. Because selection on linked sites reduces both the efficiency of selection and the level of neutral genetic diversity, we expect the overall effect to be a steeper slope of the relationship between log(πN/πS) and log(πS) than that predicted by the shape parameter of the DFE, which is the average taken across all species. This is perhaps the most likely explanation of our results: mtDNA undergoes minimal recombination, and as such selection on linked sites will have a large impact on molecular evolution, increasing the slope between log(πN/πS) and log(πS) (Birky and Walsh, 1988; Castellano et al., 2015). Furthermore, it has been recently shown that mtDNA undergoes adaptive evolution in animals (James et al., 2016).

Data archiving

All polymorphism estimates, life-history data and sequence alignments used in this analysis can be found at: https://dx.doi.org/10.6084/m9.figshare.3084205.v1.

Table 3b. Regression slope and intercept estimates.

Data set Slope Upper CI Lower CI Intercept Upper CI Lower CI
5 −0.63 −0.38 −0.79 −2.34 −1.96 −2.61
11 −0.74 −0.37 −0.91 −2.54 −2.01 −2.81
Open in a new tab

Abbreviation: CI, confidence interval.

The first column gives the number of individuals sampled for each species in the data set. The slope and the intercept of the regression line are given. CIs for each variable are labelled as ‘Upper CI' and ‘Lower CI'.

Acknowledgments

We thank the editor and two anonymous reviewers for their comments during the revision of this manuscript. Funding for this study was provided by the University of Sussex and NERC, Grant Number NE/L502042/1.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Information
Click here for additional data file. (61.7KB, docx)

References

  1. Birky CW, Walsh JB. (1988). Effects of linkage on rates of molecular evolution. Proc Natl AcadSci USA 85: 6414–6418. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Boyko AR, Williamson SH, Indap AR, Degenhardt JD, Hernandez RD, Lohmueller KE et al. (2008). Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet 4: e1000083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Carlini DB, Genut JE. (2006). Synonymous SNPs provide evidence for selective constraint on human exonic splicing enhancers. J Mol Evol 62: 89–98. [DOI] [PubMed] [Google Scholar]
  4. Castellano D, Coronado-Zamora M, Campos JL, Barbadilla A, Eyre-Walker A. (2015). Adaptive evolution is substantially impeded by Hill–Robertson interference in Drosophila. Mol Biol Evol 33: 442–455. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chamary JV, Parmley JL, Hurst LD. (2006). Hearing silence: non-neutral evolution at synonymous sites in mammals. Nat Rev Genet 7: 98–108. [DOI] [PubMed] [Google Scholar]
  6. Chamary JV, Hurst LD. (2005). Evidence for selection on synonymous mutations affecting stability of mRNA secondary structure in mammals. Genome Biol 6: R75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Charlesworth B. (2009). Fundamental concepts in genetics: effective population size and patterns of molecular evolution and variation. Nat Rev Genet 10: 195–205. [DOI] [PubMed] [Google Scholar]
  8. Charlesworth B. (2013). Stabilizing selection, purifying selection, and mutational bias in finite populations. Genetics 194: 955–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Corbett-Detig RB, Hartl DL, Sackton TB. (2015). Natural selection constrains neutral diversity across a wide range of species. PLOS Biol 13: e1002112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cutter AD, Jovelin R, Dey A. (2013). Molecular hyperdiversity and evolution in very large populations. Mol Ecol 22: 2074–2095. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Duret L. (2002). Evolution of synonymous codon usage in metazoans. Curr Opin Genet Dev 12: 640–649. [DOI] [PubMed] [Google Scholar]
  12. Duret L, Mouchiroud D. (1999). Expression pattern and, surprisingly, gene length shape codon usage in Caenorhabditis, Drosophila, and Arabidopsis. Proc Natl Acad Sci USA 96: 4482–4487. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Egea R, Casillas S, Fernández E, Senar MA, Barbadilla A. (2007). MamPol: a database of nucleotide polymorphism in the Mammalia class. Nucleic Acids Res 35 (Suppl 1): 624–629. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Eyre-Walker A, Keightley PD. (2007). The distribution of fitness effects of new mutations. Nat Rev Genet 8: 610–618. [DOI] [PubMed] [Google Scholar]
  15. Eyre-Walker A, Woolfit M, Phelps T. (2006). The distribution of fitness effects of new deleterious amino acid mutations in humans. Genetics 173: 891–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Galtier N. (2015). Adaptive protein evolution in animals and the effective population size hypothesis. PLoS Genet 12: e1005774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gao Z, Wyman MJ, Sella G, Przeworski M. (2016). Interpreting the dependence of mutation rates on age and time. PLoS Biol 14: e1002355. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Harvey PH, Pagel M. (1991) The Comparative Method in Evolutionary Biology. Oxford University Press: Oxford. [Google Scholar]
  19. Hernandez RD. (2008). A flexible forward simulator for populations subject to selection and demography. Bioinformatics 24: 2786–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hershberg R, Petrov DA. (2008). Selection on codon bias. Annu Rev Genet 42: 287–299. [DOI] [PubMed] [Google Scholar]
  21. James JE, Piganeau G, Eyre-Walker A. (2016). The rate of adaptive evolution in animal mitochondria. Mol Ecol 25: 67–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jia W, Higgs PG. (2008). Codon usage in mitochondrial genomes: Distinguishing context-dependent mutation from translational selection. Mol Biol Evol 25: 339–351. [DOI] [PubMed] [Google Scholar]
  23. Jones KE, Bielby J, Cardillo M, Fritz SA, O'Dell J, Orme CDL et al. (2009). PanTHERIA: a species-level database of life history, ecology, and geography of extant and recently extinct mammals. Ecology 90: 2648. [Google Scholar]
  24. Kanaya S, Yamada Y, Kinouchi M, Kudo Y, Ikemura T. (2011). Codon usage and tRNA genes in Eukaryotes: correlation of codon usage diversity with translation efficiency and with CG-dinucleotide usage as assessed by multivariate analysis. J Mol Evol 53: 290–298. [DOI] [PubMed] [Google Scholar]
  25. Kearse M, Moir R, Wilson A, Stones-Havas S, Cheung M, Sturrock S et al. (2012). Geneious Basic: an integrated and extendable desktop software platform for the organization and analysis of sequence data. Bioinformatics 28: 1647–1649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kimura M. (1984) The Neutral Theory of Molecular Evolution. Cambridge University Press: Cambridge, UK. [Google Scholar]
  27. Kousathanas A, Keightley PD. (2013). A comparison of models to infer the distribution of fitness effects of new mutations. Genetics 193: 1197–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Loewe L, Charlesworth B. (2006). Inferring the distribution of mutational effects on fitness in Drosophila. Biol Lett 2: 426–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lynch M. (2010). Evolution of the mutation rate. Trends Genet 26: 345–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lynch M. (2011). The lower bound to the evolution of mutation rates. Genome Biol Evol 3: 1107–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Martincorena I, Luscombe NM. (2013). Non-random mutation: The evolution of targeted hypermutation and hypomutation. Bioessays 35: 123–130. [DOI] [PubMed] [Google Scholar]
  32. Nabholz B, Glémin S, Galtier N. (2008). Strong variations of mitochondrial mutation rate across mammals- the longevity hypothesis. Mol Biol Evol 25: 120–130. [DOI] [PubMed] [Google Scholar]
  33. Nielsen R, Yang Z. (2003). Estimating the distribution of selection coefficients from phylogenetic data with applications to mitochondrial and viral DNA. Mol Biol Evol 20: 1231–1239. [DOI] [PubMed] [Google Scholar]
  34. Piganeau G, Eyre-Walker A. (2003). Estimating the distribution of fitness effects from DNA sequence data: implications for the molecular clock. Proc Natl Acad Sci USA 100: 10335–10340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Piganeau G, Eyre-Walker A. (2009). Evidence for variation in the effective population size of animal mitochondrial DNA. PLoS One 4: e4396. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Popadin K, Polishchuk LV, Mamirova L, Knorre D, Gunbin K. (2007). Accumulation of slightly deleterious mutations in mitochondrial protein-coding genes of large versus small mammals. Proc Natl Acad Sci USA 104: 13390–13395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Schmidt-Nielsen K. (1984) Scaling. Why Is Animal Size So Important?. Cambridge University Press: Cambridge. [Google Scholar]
  38. Shen Y-Y, Liang L, Zhu ZH, Zhou WP, Irwin DM, Zhang YP. (2010). Adaptive evolution of energy metabolism genes and the origin of flight in bats. Proc Natl Acad Sci USA 107: 8666–8671. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Shen YY, Shi P, Sun YB, Zhang YP. (2009). Relaxation of selective constraints on avian mitochondrial DNA following the degeneration of flight ability. Genome Res 19: 1760–1765. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Smith NGC, Eyre-Walker A. (2002). Adaptive protein evolution in Drosophila. Nature 415: 1022–1024. [DOI] [PubMed] [Google Scholar]
  41. Suarez RK. (1992). Hummingbird flight: sustaining the highest mass-specific metabolic rates among vertebrates. Experientia 46: 565–570. [DOI] [PubMed] [Google Scholar]
  42. Welch JJ, Eyre-Walker A, Waxman D. (2008). Divergence and polymorphism under the nearly neutral theory of molecular evolution. J Mol Evol 67: 418–426. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (61.7KB, docx)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES