Uncovering the genetic signature of quantitative trait evolution with replicated time series data

Abstract

The genetic architecture of adaptation in natural populations has not yet been resolved: it is not clear to what extent the spread of beneficial mutations (selective sweeps) or the response of many quantitative trait loci drive adaptation to environmental changes. Although much attention has been given to the genomic footprint of selective sweeps, the importance of selection on quantitative traits is still not well studied, as the associated genomic signature is extremely difficult to detect. We propose ‘Evolve and Resequence' as a promising tool, to study polygenic adaptation of quantitative traits in evolving populations. Simulating replicated time series data we show that adaptation to a new intermediate trait optimum has three characteristic phases that are reflected on the genomic level: (1) directional frequency changes towards the new trait optimum, (2) plateauing of allele frequencies when the new trait optimum has been reached and (3) subsequent divergence between replicated trajectories ultimately leading to the loss or fixation of alleles while the trait value does not change. We explore these 3 phase characteristics for relevant population genetic parameters to provide expectations for various experimental evolution designs. Remarkably, over a broad range of parameters the trajectories of selected alleles display a pattern across replicates, which differs both from neutrality and directional selection. We conclude that replicated time series data from experimental evolution studies provide a promising framework to study polygenic adaptation from whole-genome population genetics data.

Introduction

The discovery of molecular markers not only provided the first key insights into the selective forces operating in natural populations, but also uncovered the complexity of real data. Since then, a wealth of theoretical and experimental approaches have been proposed to trace the signature of adaptation in the genome of natural populations (Lewontin and Krakauer, 1973; Tajima, 1989; Kim and Stephan, 2002; Sabeti et al., 2002; Akey et al., 2002; Nielsen, 2005). Despite this considerable effort, our understanding of adaptive processes in local populations is still limited to a few, probably not representative, examples. The reasons for this discrepancy are not clear, but it has been cautioned that the simple model of a beneficial allele sweeping through a population until fixation may be the exception rather then the rule (Pritchard and Di Rienzo, 2010; Pritchard et al., 2010). Multiple alleles at the same locus may be selected (soft sweep; Hermisson and Pennings, 2005), resulting in a barely recognizable genomic signature. One further explanation for the dearth of clear signals of genomic adaptation builds on the genetic architecture of adaptive traits. Assuming that multiple loci contribute to the trait in a given environment, a sudden environmental change may result in frequency changes at all these loci. With many loci contributing to the trait, the impact of each of them is modest and requires only small to moderate allele frequency changes (Pritchard et al., 2010; Le Corre and Kremer, 2012; Berg and Coop, 2014). These small adaptive frequency changes are difficult to distinguish from genetic drift, making this mode of adaptation almost impossible to detect from molecular data.

Probably the most promising approach to study quantitative trait adaptation is the combination of different signals. This could be the signal from enriched gene sets in annotated biological pathways (Daub et al., 2013), coordinated shifts of alleles contributing to a trait of interest (Latta, 1998; Le Corre and Kremer, 2012; Bourret et al., 2014), associations of contributing alleles with the focal phenotype (Stephan et al., 2015) or correlations of contributing allelic variation with environmental or geographical variables in divergent populations (Hancock et al., 2011; Günther and Coop, 2013; Berg and Coop, 2014; Mathieson et al., 2015).

We propose an alternative approach to study the genomic signature of quantitative trait adaptation: replicated time series data in an ‘Evolve and Resequence' (E&R, Turner et al., 2011) framework allow us to distinguish signatures of quantitative trait adaptation from selective sweeps and genetic drift. In contrast to selective sweeps, the genomic signature of selection on a quantitative trait after a recent shift in optimum has not been studied to a comparable extent. Previous studies have established expectations for equilibria in quantitative trait evolution (Barton, 1989; Bürger and Gimelfarb, 1999; Pavlidis et al., 2012). These are, however, not directly applicable to genomic signatures of adaptation in experimental evolution studies, where constant population sizes typically do not exceed 1000 and span <100 generations (reviewed in Schlötterer et al., 2015). On the basis of simulations, we highlight characteristic temporal patterns of allele frequency changes for alleles contributing to quantitative trait evolution in typical E&R studies. Then, we discuss how initially parallel allele frequency changes across replicates in combination with different evolutionary fates at later stages provide a genomic response that: (1) is specific to adaptation of quantitative traits, and (2) can be distinguished from neutral patterns and directional selection if a sufficiently large number of replicate populations are studied. Hence, we propose that replicated E&R time series data could be used to uncover the genomic signatures of quantitative trait adaptation.

Materials and methods

Simulations of polygenic adaptation of a quantitative trait

Implementation

Quantitative trait evolution to a new fitness optimum was implemented using forward simulations in diploids assuming random mating and free recombination between loci. The trait z is defined as the sum of effects of n diploid loci with the trait range normalized between zero and one, specified by: z=sum(a_i × x_i) with i ∈ {1 … n} the index of the contributing locus, x_i ∈ {0, 1, 2} the genotype of the i^th contributing locus and a_i the normalized allelic effect size between zero and one of the i^th locus obtained by a_i=a_i'/(2 × sum(a_i')) (a_i' can be any positive numeric vector of length n).

We assume a Gaussian fitness function defined by: fitness=PDF × scalingfac+minfit, with , the Gaussian probability density function, where μ defines the phenotypic optimum within the trait ranging from zero to one and the standard deviation (sd) the spread of the fitness function. The scaling factor, scalingfac, defines the fitness range of all possible phenotypes by 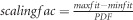with minfit and maxfit, the fitness of the phenotype with the worst and best possible fitness, respectively (Supplementary Figure S1). In every generation the fitness value of each individual influences the probability to contribute gametes to the next generation. Loci in the starting population are in linkage equilibrium.

We evaluated the parameters effective population size (N_e), the number, starting frequencies and effect sizes of contributing alleles, the selection strength and shape of the Gaussian fitness landscape, the duration of the experiment and the number of replicates. For each time point and replicate population we record: (1) frequencies of all contributing alleles, and (2) phenotype/trait values of each individual in the population. Scripts are written in Python and available at http://datadryad.org/ under http://dx.doi.org/10.5061/dryad.c6214.

Simulation parameters

We focus on scenarios with intermediate optimal phenotypes and do not aim to cover the vast parameter space for quantitative trait simulations. Rather, we study a set of examples to illustrate how replicated time series provide a characteristic signature for the identification of quantitative trait adaptation, in particular when redundancy among loci to achieve the intermediate optimum phenotype is moderate. We first describe a characteristic scenario with a small number of equally contributing loci starting from low population frequencies (Table 1). On the basis of these default settings, we modify each parameter one by one to determine the influence on the time series trajectories. Although we do not claim that this small number of loci is representative for E&R experiments, we use this simple example to illustrate the three phase pattern of genomic adaptation and subsequently extend the parameter space to see how general these trajectories are.

Table 1. Default simulation parameter values.

Parameter	Quantitative trait simulation (default values)
Ne	1000
Number of contributing loci	5 (equal contribution)
Starting allele frequencies	All 0.05 (randomly assigned to founder haplotypes)
Effect sizes across loci	Equal (sum of effect sizes across loci is 1, that is, effect sizes of 0.1 of each allele)
Optimum trait value	0.4 (40% of the possible contributing variation)
Fitness landscape and selection strength	Gaussian fitness function with μ=optimum trait value, standard deviation sd=0.2 and minimum, maximum fitness between 0.5 and 1.5 (latter specifies the selection strength)
Genotype-phenotype translation	Heritability of 1, that is, 1:1 mapping from genotype to phenotype
Recombination	Full recombination between contributing loci

Length of the characteristic phases

Although phases can be distinguished by allele frequency trajectories, their transitions are difficult to define based on genomic features only. Hence, we determined the end of phase 1 (directional selection) and phase 3 (termination of stabilizing selection) based on population phenotypes. The end of directional selection (phase 1) is reached when the median population phenotype reaches the optimum phenotype. Phase 3 is terminated when no more genetic variation is segregating in the population, that is, the population phenotypic variance is zero.

Data analysis and visualization

All data analysis and visualization have been performed in R (R Development Core Team, 2008).

Results

Polygenic adaptation to an intermediate trait optimum

Under directional selection (selective sweep model) the fitness optimum of the population is reached after fixation of the causative allele(s). In contrast, adaptation of a quantitative trait to a new, intermediate trait optimum proceeds through allele frequency changes at several loci until the population mean reaches the trait optimum (Figure 1, Supplementary Figure S2). At this point the majority of contributing alleles is typically not fixed but segregates in the population. After this initial directional phase the population is subjected to stabilizing selection maintaining the optimal trait mean while at the same time reducing genetic variation.

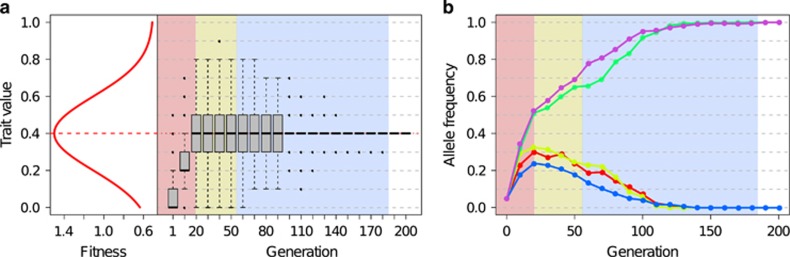
Figure 1.

Quantitative trait adaptation of a single population to a new intermediate trait optimum. The simulations were performed using the default parameter settings, that is, 5 unlinked loci with equal effect sizes (that is, 0.1 for each allele) and starting frequencies of 0.05, N_e=1000 and a Gaussian fitness function with mean 0.4, standard deviation of 0.2 and fitness ranges from 0.5 to 1.5 (for details see Table 1). (a) The Gaussian fitness function and the change in the population phenotype (=trait value) during adaptation to the new trait optimum in a single simulation. (b) The corresponding trajectories of all five loci contributing to the quantitative trait. Directional selection predominates until the population mean has reached the new optimum (phase 1, red shading). Subsequently stabilizing selection reduces the phenotypic variance in the population along with the contributing segregating variation (phases 2 and 3, yellow and blue shading, respectively).

This phenotypic pattern is also manifested on the genomic level with the trajectories of alleles contributing to the focal trait following three characteristic phases (Figure 1b): Immediately after the population has been exposed to a new environment, all segregating loci that contribute to the trait experience a directional change in frequency (phase 1, directional selection). Once the population approaches the fitness optimum the allele frequency change slows down, which results in plateauing of allele frequencies (phase 2). The outcome of the last phase is stochastic, with the fate of the alleles differing among loci: selected alleles become either fixed or lost, whereas the trait mean remains stable (phase 3). The last two phases based on allelic trajectories correspond to stabilizing selection on the optimum trait value. Depending on the specifics of the underlying genetic architecture, the effective population size (N_e) and the shape of the fitness landscape, these three phases can be more or less clearly pronounced for the contributing alleles (for example, Supplementary Figure S2).

The three phases are also clearly reflected in the phenotype with respect to population variance. Although phase 1 can be clearly distinguished through the change in the mean phenotype, the phenotypic variance (V_P) increases during this phase reaching its maximum at the transition to phase 2 (Supplementary Figure S3). During stabilizing selection with the mean population phenotype being maintained, the phenotypic variance is maximal in phase 2 and is then gradually lost during phase 3. As in our simulations we assumed no environmental effects (heritability=1), the phenotypic variance equals the genetic variance (V_G).

Under stabilizing selection, genetic variation as well as phenotypic variation, is typically lost in a finite number of generations (Barton, 1989). Assuming, however, that no homozygous genotype (that is, homozygous for either allele at each contributing locus) matches the trait optimum (for example, Supplementary Figure S2C), a different outcome can be expected. A single locus remains polymorphic in the population as long as the effective population size is large enough limiting the effect of drift (overdominance). Although we did not explore this scenario, previous work already demonstrated that only a minimal fraction of the contributing loci remains polymorphic under stabilizing selection to an intermediate fitness optimum (Wright, 1935; Barton, 1989; Bürger and Gimelfarb, 1999; Pavlidis et al., 2012).

Signatures of selected quantitative trait loci in E&R studies

In contrast to the study of natural populations, where biological replication is difficult if not impossible, experimental evolution studies provide the opportunity to replicate adaptation to a new fitness optimum. This permits tracing the trajectory of the same quantitative trait locus in multiple replicates throughout the experiment. In particular, when replicate populations are being started from a similar genetic composition, the trajectories of the same locus in different replicates can be instrumental in detecting adaptive quantitative trait loci: The three phases depicted in Figure 1 can also be seen for single locus analyzed across replicate populations (Figure 2). Thus, these three phases provide a characteristic hallmark for a single quantitative trait locus across different replicates. Given the potential of replicated E&R studies to generate a characteristic pattern for adaptive quantitative trait loci, we studied how different parameters affect the trajectories of alleles contributing to a quantitative trait upon a change in trait optimum.

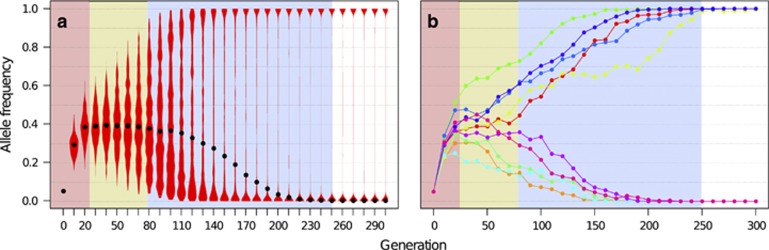
Figure 2.

Trajectories of the same quantitative trait locus in multiple replicates after a change to a new intermediate trait optimum show three distinct phases. Quantitative trait simulations for 500 independent replicates were performed with the default parameter settings, that is, 5 unlinked, free recombining loci with equal effect sizes (that is, 0.1 for each allele) and starting frequencies of 0.05, N_e=1000 and a Gaussian fitness function with mean 0.4, standard deviation of 0.2 and fitness ranges from 0.5 to 1.5 (for details see Table 1). Plots show trajectories of a single locus across replicates. Three phases can be recognized: (1) strong, highly reproducible frequency change in each replicate (red), (2) plateauing (yellow), (3) divergent trajectories with a highly stochastic outcome across replicates (blue). The remaining time period (white) indicates that the focal locus has become monomorphic in each replicate. (a) The trajectory of a single locus in 500 replicate simulations is summarized in violin plots, black dots indicate the median. Note, over time the median returns to zero as with an optimum of 0.4 a focal locus only fixes in 40% of the replicates, whereas the mean allele frequency remains at 0.4. (b) Example trajectories at a single locus in 10 independent replicates.

Effective population size (N _e )

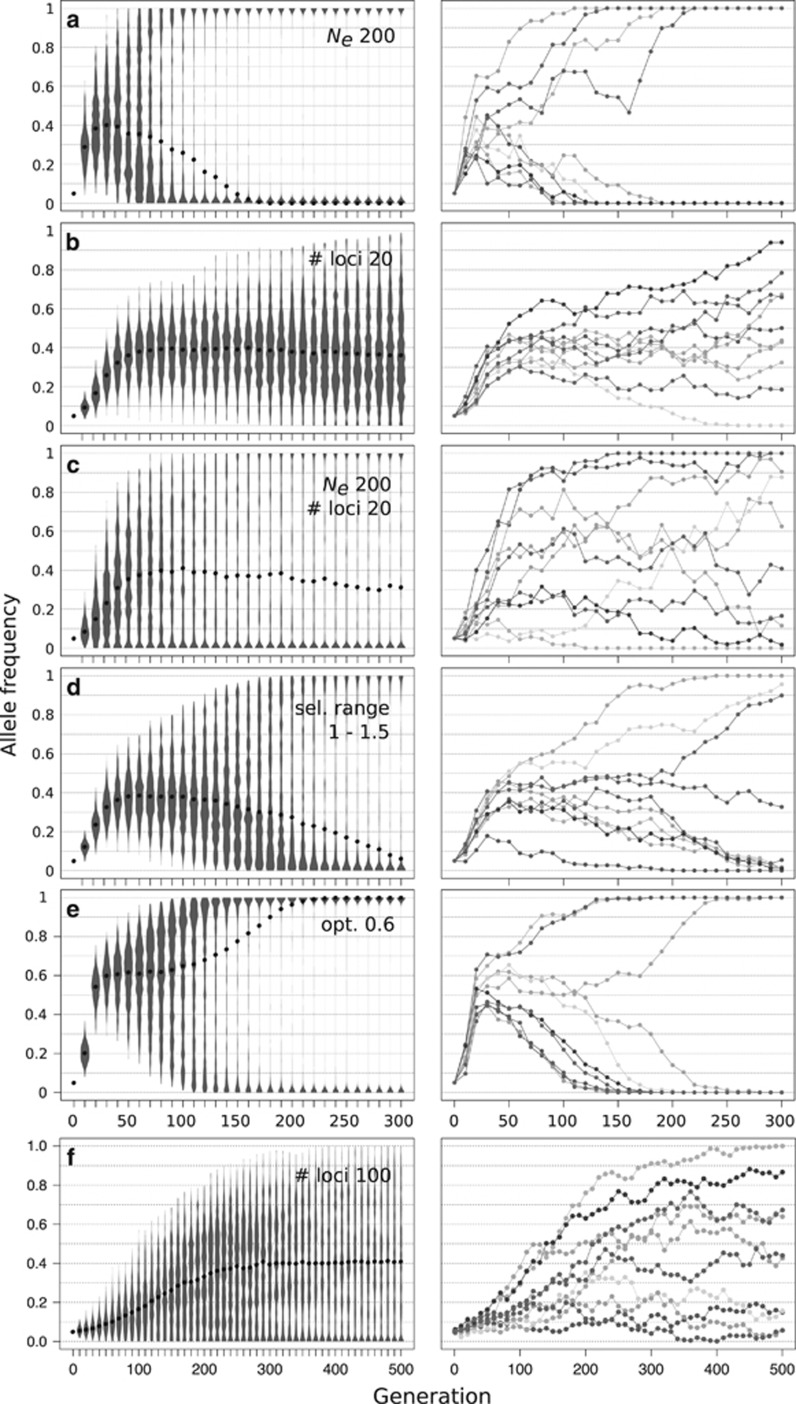
The higher sampling variance of smaller N_e generally increases the stochasticity of the trajectories. This leads to less distinct and shorter duration of all three phases and consequently earlier fixation of all contributing alleles (Figure 2 versus Figures 3a and c; Supplementary Figures S4a and b). Moreover, smaller N_e can lead to a less distinct directional selection phase, where not all alleles show a deterministic increase across replicates (Figure 3b versus Figure 3c, Supplementary Figure S5b).

Figure 3.

Influence of experimental parameters and quantitative trait architecture on the 3 characteristic phases of trait adaptation to a new intermediate trait optimum. Simulations were performed with the default parameters (Table 1). Parameters deviating from the default are shown in the insets (a–f). Left panels summarize the trajectory of a single locus across 500 replicate simulations in violin plots, black dots indicate the median. The right panel shows corresponding example trajectories of a single locus in 10 independent replicates. The modified parameters have a clear influence on the length and/or distinctiveness of the 3 characteristic phases. Note, medians over time indicate the behavior of the majority of loci across replicates at the focal site. Means are expected to remain constant at the frequency corresponding to the optimum phenotype.

Number of contributing loci

Assuming a constant total selection strength, increasing number of loci contributing to the trait reduces the allele frequency changes in a given time interval. With an increasing number of loci all three phases are prolonged (Supplementary Figures S4a and b) and phase 2 and 3 become less distinct from each other (Figures 3b and f). For relatively large effective population sizes this results in a distinct directional selection phase (phase 1) and a clear plateauing of alleles for a few hundred generations (Figure 3b), a signal that is targeted in several approaches to investigate polygenic adaptation (Latta, 1998; Le Corre and Kremer, 2012; Berg and Coop, 2014; Bourret et al., 2014).

If a larger number of contributing loci are combined with a small N_e, the directional selection phase (phase 1) is more difficult to detect based on individual allele frequency trajectories (Figure 3c,Supplementary Figure S2d). With small effect sizes of each individual locus and a large drift component there is a high chance that an individual allele will not respond to selection in the early directional selection phase—particularly when starting from a low frequency. This does not necessarily prevent the population from adaptation to the new phenotypic optimum as, for close optima, a large fraction of alleles subsequently also get lost. However, it results in a less-profound three-phase signature on the genomic level, as well as less differentiation between contributing and neutral alleles based on initial frequency changes (Figure 3c, Supplementary Figure S5b).

Strength of selection

Reducing the total strength of selection, that is, the difference in absolute fitness between an initial individual (with z~0) and an optimally adapted individual (with z=optimum phenotype; see Supplementary Figure S1a versus b), on the trait of interest has a similar effect on the resulting trajectories as increasing the number of contributing loci (Figure 2 versus Figures 3b and d). This is because both factors influence (in this case reduce) the effect on fitness at each contributing locus. Consequently, smaller total selection strength similarly increases the lengths of all phases (Supplementary Figures S4a and b) and individual loci are less likely to respond to selection (Figure 3d).

Distance to the new fitness optimum and shape of the fitness landscape

A greater distance to the new fitness optimum (for example, Supplementary Figures S1a and c) generally increases the expected frequency change at each selected locus and thus the length of the directional selection phase albeit to a far lesser extend than previously discussed parameters (Figure 1 versus Figure 3e, Supplementary Figure S4a). On the other hand, a closer optimum increases the genetic redundancy (Yeaman, 2015), that is, the number of different locus combinations that can achieve the phenotypic optimum. This results in less predictable trajectories of individual loci and among replicate populations.

The distance to the fitness optimum also determines the likelihood of a given allele to become fixed at the end of phase 3. In a replicated E&R experiment, the fate of the focal allele is stochastic, becoming either fixed or lost. Hence, for a trait value optimum of 0.4 (40% of the contributing segregating variation with equal effect sizes or forming 40% of the maximum trait value created by the summed effects of the contributing alleles) a focal allele is lost in 60% of the replicates at the end of phase 3 (Figures 2, 3a–d). In contrast, under scenarios with a trait optimum larger than 0.5 the focal allele fixes in more than half of the replicates and gets lost in the minority of replicates at the end of phase 3 (Figure 3e). More distant phenotype optima result therefore in a large and consistent frequency increase of many loci among replicate populations, providing a clearer signal of selection.

Distribution of effect sizes

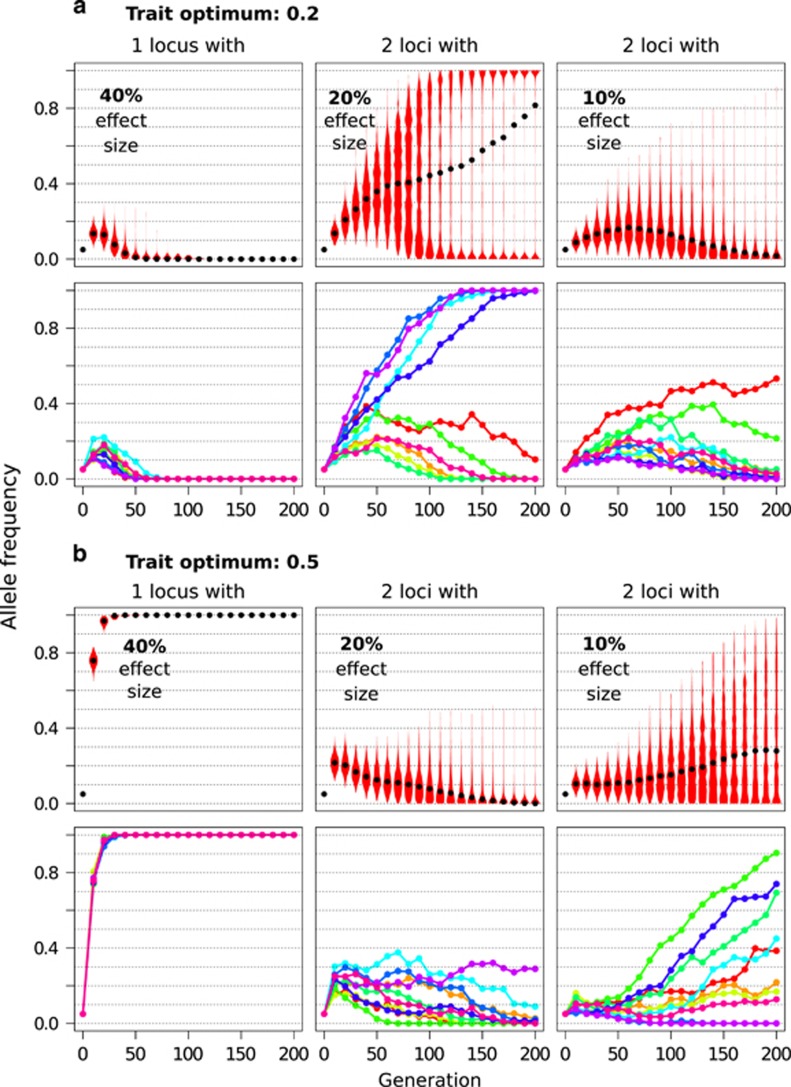
Different effect sizes of the contributing loci influence their dynamics, resulting in a diverse pattern of trajectories of a focal locus among replicates. We illustrate this by simulating two examples of a trait with five contributing loci of three different effect sizes (Figure 4). For each effect size the trajectories are analyzed separately. In these examples the alleles with larger effect sizes increase in frequency, but depending on whether the trait optimum is close (0.2, that is, closer than the effect size of the major locus, Figure 4a) or further away from the starting point (0.5, Figure 4b), alleles become either lost (due to overshooting the of the initially beneficial allele if homozygous) or fixed in all replicates. Thus, replicates are more homogeneous, whereas in this example alleles with smaller effect sizes show more heterogeneity among replicates. In the case of a close optimum, alleles with intermediate effect size resemble the classic pattern shown in Figure 2, with three distinct phases. The alleles with the smallest effect behave very similarly across replicates with a brief increase in frequency followed by a subsequent loss. In the case of a distant fitness optimum, intermediate alleles briefly increase in frequency and subsequently get lost (in a few replicates they remain polymorphic at a low population frequency). Only alleles with the smallest effect increase considerably in frequency in some replicates, whereas in others they become lost or remain at intermediate frequency during the first few hundred generations. Although it is clear that different trait architectures result in different types of trajectories for various effect size combinations, the examples were chosen to illustrate the three possible types of trajectories with respect to replication: (1) concordant trajectories leading to fixation, (2) initially increasing but later diverging trajectories leading to either loss or fixation and (3) concordant increase followed by subsequent loss in all replicates. Remarkably, trajectories of class 2 and 3 are very distinct from neutral alleles or alleles subjected to directional selection. Probably most difficult to distinguish from a selective sweep is the scenario with a distant trait optimum, where the locus with the largest effect size resembles an allele with directional selection. Generally, larger effect alleles have shorter phase lengths than smaller effect alleles as they experience a stronger effect of selection.

Figure 4.

Relative effect sizes of quantitative trait loci affect length and outcome of the three characteristic phases. Quantitative trait simulations were performed with the default parameter settings (Table 1) apart from using unequal effect sizes with 40:20:20:10:10% contribution of the 5 selected loci. The fitness optimum is set to 0.2 (a) and 0.5 (b). Columns correspond to the trajectories of loci with different effect sizes. Upper rows in each panel summarize the distribution for a given locus across 500 simulations in violin plots, black dots indicate the median. Lower rows depict trajectories from 10 replicates at the respective locus. Stronger effect sizes shorten each of the 3 characteristic phases. Depending on the trait optimum, trajectories can vary for each respective effect size.

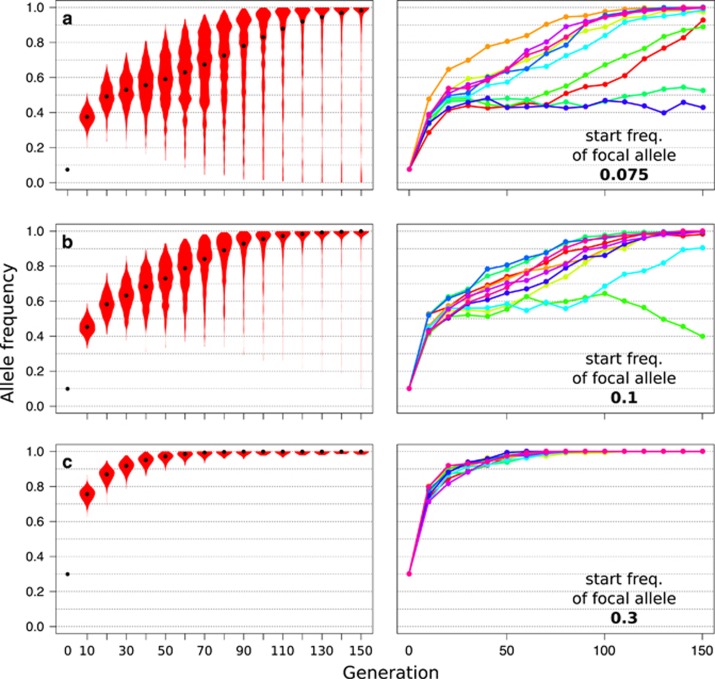
Starting frequency of the focal allele

The starting frequency of the focal allele influences its fate during adaptation to a new trait optimum. Similarly, to alleles under directional selection, selection on a quantitative trait is more effective at an intermediate starting frequency, resulting in a faster frequency increase. Consequently, alleles occurring at a higher frequency are more likely to reach fixation compared with alleles that start from a lower frequency (Figure 5). If the starting frequency of the focal allele is high enough relative to the other contributing loci, this can impede the differentiation between a selective sweep signal and quantitative trait stabilizing selection (for example, Figure 5c).

Figure 5.

The starting frequency of a focal allele affects its dynamics during quantitative trait adaptation. Simulations were performed for default parameter settings (Table 1) apart from the starting frequency of one, i.e. the focal, out of five contributing loci. The modified starting frequencies are specified in the inset (a–c). Plots show the frequency of the focal allele across replicates. The left panel shows the trajectories of 500 replicate simulations summarized in violin plots, black dots indicate the median. The right panel shows individual trajectories of the focal allele for 10 randomly chosen replicates. A higher starting frequency relative to the other contributing alleles increases the probability of fixation of the focal allele.

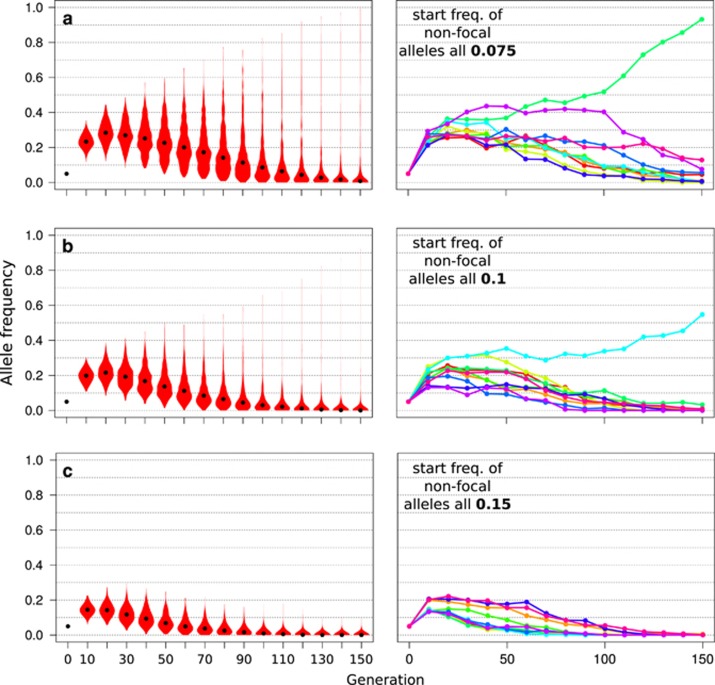
Starting frequencies of the non-focal alleles

The trajectory of a focal allele is also affected by the starting frequencies of the remaining, that is, non-focal, contributing loci. If all non-focal alleles have a higher starting frequency than the focal allele, the focal allele is typically lost after an initial brief increase in all replicates (Figure 6). Moreover, the allele frequency change in the initial phase of frequency increase is less pronounced if the starting frequency of the focal allele is lower than the non-focal alleles. Conversely, a small difference in starting frequencies among contributing loci results in a clear signal of divergent trajectories between replicates in the third phase (Figure 3a).

Figure 6.

Influence of the starting frequencies of non-focal alleles on the trajectories of the focal allele. Simulations were performed for default parameter settings (Table 1) apart from the starting frequency of the remaining four, non-focal alleles contributing to the trait specified in the inset of each subfigure (a–c). Plots show the frequency of the focal allele across replicates. The left panel shows the trajectories of 500 replicate simulations summarized in violin plots, black dots indicate the median. The right panel shows individual trajectories of the focal alleles for 10 randomly chosen replicates. Higher starting frequencies of non-focal alleles reduce the initial increase of the focal allele and increase its probability of subsequent loss.

Discussion

In this report we describe the trajectories of adaptive quantitative trait alleles after a recent environmental change, which results in a new intermediate trait optimum. We identified three characteristic phases that can be observed on the phenotypic as well as the genomic level. In the first phase alleles contributing to the trait change their frequency in a directional manner until the population has reached the new trait optimum. In the second phase (plateauing) only small allele frequency changes can be noticed. Only in the third phase the frequencies of causative alleles change again, resulting in either their fixation or loss. Although these characteristics can be observed in a single adapting population (Figure 1, Supplementary Figure S2), we make the point that similar signatures can be obtained across replicate populations. As these signatures differ qualitatively from both neutral trajectories and alleles under directional selection (sweep model) for a broad parameter range, we propose that E&R studies provide a promising approach to identify adaptive quantitative trait loci.

Polygenic adaptation at a quantitative trait in E&R studies

In natural populations several approaches have been pursued to identify loci involved in quantitative trait adaptation (Hancock et al., 2011; Günther and Coop, 2013; Berg and Coop, 2014; Bourret et al., 2014), however, direct modeling or identification of characteristic quantitative trait signatures in experimental evolution settings has been extremely sparse. Even though several studies specifically selected for quantitative phenotypes that are suggested to have a polygenic basis, the tests applied to detect targets of selection generally assumed directional selection at independent loci (for example, Turner et al., 2011; Remolina et al., 2012; Turner and Miller, 2012); summarized in Schlötterer et al., 2015).

So far, only one simulation study, by Kessner and Novembre (2015), explicitly modeled quantitative trait evolution in an E&R framework. They studied truncating selection, and identified qualitatively different signatures from those of models assuming fixed selection coefficients for all loci (that is, independence of selected loci, compare with: Kofler and Schlötterer, 2013; Baldwin-Brown et al., 2014). These include a faster response of large effect loci and increasing realized selection coefficients of smaller effect loci after fixation of the large effect variants. Those results are, however, not directly comparable to our study as they modeled truncating selection where the trait optimum is set to the most extreme phenotype. In this model, the last two phases of adaptation described in our study (phases 2 and 3) do not exist as all variation contributing to the phenotype becomes eventually fixed (for example, Supplementary Figure S6). In contrast, our study focuses on selection to an intermediate trait optimum, a situation suggested to be predominant in adaptation in natural populations (for example, Pritchard and Di Rienzo, 2010; Kingsolver et al., 2012), for trait examples see (Waser and Price, 1981; Lyon, 1998; Egan et al., 2011), where directional selection is followed by subsequent stabilizing selection.

Most of our analyses focused on a moderate number of loci. Although this does not reflect the classic models of quantitative traits with a large number of loci, we still think that it is reasonable for E&R studies. Many small effect alleles will behave essentially neutrally and cannot be detected given the population sizes of typical E&R studies. Only a few loci with stronger effects will deviate from neutrality and these ones will display the trajectories analyzed in our study. Thus, we consider our assumption of a few contributing loci a legitimate approximation of a quantitative trait architecture.

Laboratory natural versus truncating selection

E&R studies use two different categories of selection regimes, that is, truncating selection and laboratory natural selection. To date, truncating selection is the more frequently used selection regime, where typically the most extreme phenotypes contribute to the next generation (for example, Turner et al., 2011, summarized in Schlötterer et al., 2015). In contrast, in laboratory natural selection individuals are exposed to a new environment, where adaptation proceeds through viability and fertility selection (Orozco-terWengel et al., 2012; Tobler et al., 2014; Burke et al., 2014; Franssen et al., 2015). Although truncating selection is expected to select for the most extreme phenotype, laboratory natural selection favors intermediate, albeit typically unknown, phenotypes increasing fitness in a well-defined environment. We suggest that the characteristic phases of quantitative trait adaptation described in this study are particularly relevant for: (1) laboratory natural selection studies or (2) experimental setups where selection is pursued for an explicit but intermediate phenotype.

Recombination

As the parameter space for polygenic selection is extremely vast including various trait architectures, fitness functions, setups of the founder population and census population sizes, we focused on specific examples to illustrate the general effects of important parameters. Although effects of linkage between contributing loci were not studied, the following effects are expected: as long as linkage between contributing loci exists, dynamics of contributing alleles should effectively follow expectations of a model with fewer loci contributing to the trait, where the effects of both alleles are summed up under additivity. If alleles influencing the trait in the same direction are in positive linkage disequilibrium, initial directional selection will be accelerated compared with the linkage equilibrium scenario, noticeably for the smaller effect allele. By contrast, if opposite effect alleles are initially in positive linkage disequilibrium the speed of adaptation will slow down.

Following trajectories of selected alleles during experimental evolution

Alleles contributing to polygenic adaptation to a new intermediate fitness optimum follow a characteristic pattern that can be partitioned into three phases of adaptation. Importantly, although for directional selection under the classical sweep model unlinked targets of selection are continuously increasing until they become fixed, under the quantitative model studied here, a fraction of the contributing loci ultimately get lost in the adapted population. With the strongest genomic signature of an adaptive quantitative trait coming from the trajectories after the directional phase (phase 1), the importance of time series data is evident. Analyses based on a single time point—particularly of a late evolved generation—may miss crucial information for the identification of contributing loci. If sampled too early, the signature may be confounded with a selective sweep or if sampled too late the frequency increase may be missed (for example, Figures 4 and 6). Using replicated time series data, however, the characteristic signature of adaptive quantitative trait loci under stabilizing selection can be recognized.

Potential and limitations of E&R for the detection of adaptive quantitative trait loci

We showed that a change in the optimum of a quantitative trait results in allele frequency trajectories of contributing alleles which often differ from trajectories expected under neutrality and directional selection (selective sweeps). Nevertheless, we also showed that for some parameters observing the distinction is difficult, if not impossible particularly if the associated allele frequency changes are too small. Hence, it is obvious that the trait signatures cannot be used as a test for selection, as most likely a large number of selection targets are being missed. On the other hand, those loci with a characteristic signature are good candidates for adaptive quantitative trait loci. Thus, it may be possible to detect a quantitative trait signature for a subset of the contributing loci. Although our study showed the specifics of a quantitative trait locus evolving to a new intermediate trait optimum and how they differ from neutrality and classic directional selection (constant selection coefficient), the development of powerful test statistics distinguishing between the alternative scenarios will be an important step to apply our results to experimental data.

Data archiving

All data in the paper were simulated. The simulation scripts are available at http://datadryad.org/ under http://dx.doi.org/10.5061/dryad.c6214.

The authors declare no conflict of interest.