Curvature Forces in Membrane Lipid-Protein Interactions

Abstract

Membrane biochemists are becoming increasingly aware of the role of lipid-protein interactions in diverse cellular functions. This review describes how conformational changes of membrane proteins—involving folding, stability, and membrane shape transitions—potentially involve elastic remodeling of the lipid bilayer. Evidence suggests that membrane lipids affect proteins through interactions of a relatively long-range nature, extending beyond a single annulus of next-neighbor boundary lipids. It is assumed the distance scale of the forces is large compared to the molecular range of action. Application of the theory of elasticity to flexible soft surfaces derives from classical physics, and explains the polymorphism of both detergents and membrane phospholipids. A flexible surface model (FSM) describes the balance of curvature and hydrophobic forces in lipid-protein interactions. Chemically nonspecific properties of the lipid bilayer modulate the conformational energetics of membrane proteins. The new biomembrane model challenges the standard model (the fluid mosaic model) found in biochemistry texts. The idea of a curvature force field based on data first introduced for rhodopsin gives a bridge between theory and experiment. Influences of bilayer thickness, nonlamellar-forming lipids, detergents, and osmotic stress are all explained by the FSM. An increased awareness of curvature forces suggests that research will accelerate as structural biology becomes more closely entwined with the physical chemistry of lipids in explaining membrane structure and function.

The excessive increase of anything causes a reaction in the opposite direction

(Plato, The Republic)

Membrane proteins interact with their aqueous environment as well as the lipid bilayer (1)—they are amphiphiles and are distinguished from the globular and fibrous proteins that have been so conspicuously characterized and studied in the past (2, 3). A greater awareness of the role of membrane lipid-protein interactions in cellular functions (4–7) can profoundly shape our understanding of biology at its confluence with physics and chemistry (8–12). The Janus-like nature of membrane proteins means their interactions with both water and the membrane lipid bilayer (13–15) can affect their actions, as in the case of G-protein–coupled receptors (GPCRs) (16–18), ion channels (12, 19), and transporters (20). Notably, the crystal structures of membrane proteins (21–29) offer profound and tantalizing glimpses into their inner workings. Yet even with the abundance of protein structures that graces the pages and covers of scientific journals, a static depiction simply does not suffice to explain membrane protein function. Cellular membranes are liquid-crystalline ensembles of lipids and proteins (6, 11, 30–35), and so we need to look beyond the crystalline state to more fully grasp their roles in biological phenomena at the molecular and cellular levels (1).

For a number of well-characterized membrane proteins (4, 12, 14, 17, 19, 36–41) and peptides (6, 14, 42–44), structural and functional data point to a significant role of interactions with the membrane bilayer. Which brings us to the following question: so what of the membrane lipids? Are they akin to the chorus of ancient Greek plays—mainly commenting on the dramatic action, though not playing any major character parts? Perhaps they provide an inert backdrop to the activities of membrane proteins and biologically active peptides. Maybe their role is just to function as permeability barriers to ions and polar molecules. Now, concerning biomembranes we are interested in the so-called mesoscopic regime—the system is small enough that it can be treated atomistically (a situation that will become increasingly accessible with faster computers), yet large enough that the correspondence of atomistic-level forces to bulk material properties becomes of interest (see Fig. 1). Thus for membrane lipids it may be useful to ask: does an atomistic approach yield the greatest insight? Or rather does a continuum or material science view more accurately represent the properties underlying membrane protein functions? The answer of course is there is merit to both avenues—the atomistic level and the material science approach—they synergistically reinforce one another. Together they illuminate how natural selection has yielded the characteristic lipid compositions of many biomembranes (45–51).

Figure 1.

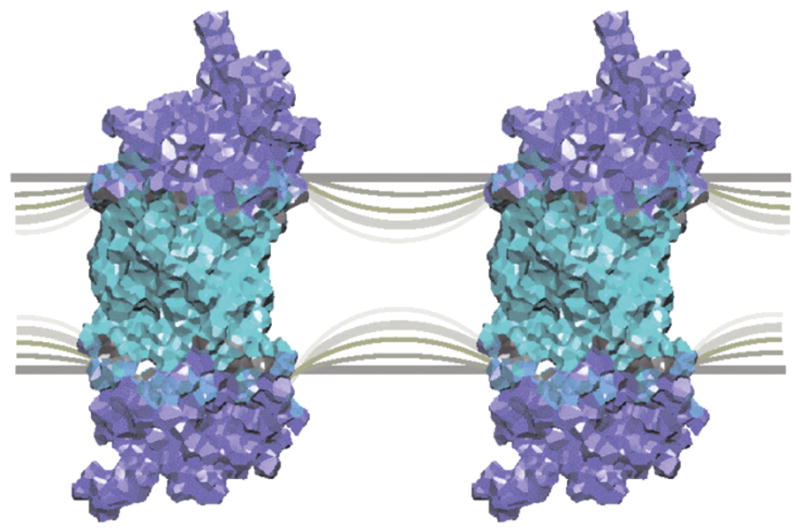
Illustration of mesoscopic approach to membrane lipid-protein interactions formulated in terms of an elastic curvature force field (1). A hybrid view is adopted where rhodopsin is depicted in an all-atom representation (149) embedded within a continuous liquid-crystalline membrane. Curvature deformation (remodeling) competes with hydrophobic matching at the proteolipid boundary and is referred to as frustration (37, 38). Matching of the spontaneous (intrinsic) curvature of a lipid monolayer to the curvature at the proteolipid boundary gives a lipid-mediated force that governs the work of membrane protein conformational changes, as well as their attraction or repulsion within the membrane bilayer. Homeostasis of membrane spontaneous curvature explains the tightly regulated membrane lipid compositions of biomembranes through lipid-protein interactions. (Figure adapted from Ref. (163).) [single column - 2.5 inch width]

LIPID-PROTEIN INTERACTIONS—TWO SCHOOLS OF THOUGHT

Evidently, there are two schools of thought with regard to the functioning of biomembranes. The standard model (31, 52) considers lipid membranes to provide an inert environment for proteins to carry out some of the most ubiquitous functions of life—photosynthesis; oxidative phosphorylation; the generation of nerve impulses; mechanosensation; osmosis; transport of metabolites; the sensing of light, hormones, tastes, and smells; and so forth. In this protein-centered universe, the membrane lipid bilayer allows proteins to sequester ions and polar molecules into cellular compartments. The fluid mosaic model (52) states that membranes constitute a solution of amphipathic membrane proteins within a fluid lipid bilayer solvent. A fluid lipid bilayer naturally serves as a platform for diffusion of membrane proteins (53). Vectorial orientation of membrane proteins and lipids in relation to the cytoplasmic and extracellular-facing monolayers (leaflets) enables transmembrane signaling to occur.

According to Singer and Nicholson (52) “the fluid mosaic structure is… analogous to a two-dimensional oriented solution of integral membrane proteins (or lipoproteins) in the viscous phospholipid bilayer solvent”. The fluid mosaic model considers either weak coupling of lipids to integral membrane proteins, or alternatively strong coupling due to specific lipid-protein interactions involving either the head groups or the acyl chains. It is stated that there is “no significant indication that the association of proteins with the phospholipids of intact membranes affects the phase transitions of the phospholipids themselves” suggesting “the phospholipids and proteins of membranes do not interact strongly; in fact, they appear to be largely independent” (52). Strong coupling due to nonspecific biophysical properties of the lipid bilayer was not considered at that early stage of development of membrane biophysics. On the other hand, characteristic shape transitions due to membrane proteins were clearly established (54).

But the alternative viewpoint—namely, that nonspecific lipid properties are more directly implicated in protein-mediated functions—has steadily gained traction over the years (10, 12, 32, 55). It is now appreciated that lipid-protein interactions do indeed affect the phase transitions of the phospholipids—but not the gel to liquid-crystalline transition as considered by the fluid mosaic model (52). Rather, it is the transition from the lamellar phase to the reverse hexagonal (H_II) (or cubic) phase of membrane phospholipids that is most affected by the proteolipid coupling (56–60). As one example the native retinal rod membranes contain bilayer-forming and nonbilayer-forming lipids (56), yet they are entirely in the fluid, liquid-crystalline (L_α) state (also known as liquid-disordered or l_d phase) near physiological temperature (56, 61). The tendency of lipids to bend is frustrated by the stretching energy of the acyl chains, or equivalently the solvation energy of the proteolipid interface—there is a balance of opposing contributions. Lateral phase separation is absent, and in this membrane system a fluid mosaic bilayer or lipid rafts are unlikely.

More recently, concepts such as curvature matching (1, 62–65) and hydrophobic matching (5, 42, 66–69) of proteins to the lipid bilayer have energized the field of membrane biophysics. They provide a framework for understanding how lipid-protein interactions affect function through chemically nonspecific material properties (38). Yet these same concepts now tend to be enunciated by membrane structural biologists as self-evident—as if they sprang fully formed from the head of the Zeus, much as did Athena, the ancient Greek goddess of wisdom (pp. 201–202 of Ref. (70)). Of course this is not the case—in fact, nothing could be farther from the truth. Rather, the introduction of such ideas stems directly from earlier innovations involving the chemistry and physics of soft materials (a.k.a. nanoscience and nanotechnology). Colloid and interface science—previously considered uninteresting by some membrane biophysicists—is experiencing a striking renaissance as the unity of matter becomes evident for liquid-crystalline colloids and biomembranes (71–73).

BEYOND THE STANDARD MODEL

Here we direct our discussion to structural and cellular biologists who have recently come to appreciate the importance of the membrane lipid bilayer with regard to membrane protein function. The proposal that chemically nonspecific properties of the bilayer directly affect the conformational energetics of integral membrane proteins (1) is based on experimental data first introduced for rhodopsin during the 1980s (36, 37, 56). Related studies of the influences of nonlamellar-forming lipids on the activities of membrane enzymes have appeared starting with Racker in the 1970s and continuing up to the present (14, 74–91). Membrane lipid influences attributable to bilayer deformation have also been established for various ionophoric, antimicrobial, cytotoxic, and fusion peptides (6, 14, 42, 43, 63, 92), as well as for protein folding in membranes (65, 93–96). Lastly, studies of the growth of microorganisms have established a balance between lamellar and nonlamellar lipids that is important for proteins in the membrane (45, 47). How can we begin to unify these fascinating observations?

In fact, this line of research leads directly to the new biomembrane model, called the flexible surface model (FSM). The essential features of the FSM are depicted in Figure 1. A membrane protein interacts with the curvature stress field of the membrane lipid bilayer, which is modeled as a continuous liquid-crystalline material. Deformation or restructuring (remodeling) of the bilayer due to the lipid-protein interactions gives a source of work for membrane protein conformational changes—alternatively, the membrane protein can alter the bilayer curvature of its lipid surroundings. The FSM (1, 37, 38) considers nonspecific properties of the bilayer through an elastic two-way coupling of the lipids to the conformational energetics of membrane proteins. Considering rhodopsin as a prototype, upon light exposure it becomes a sensor of the monolayer spontaneous (intrinsic) curvature, which explains the influences of bilayer thickness, nonlamellar-forming lipids, cholesterol, and osmotic pressure on its activation (13). Matching the curvature at the proteolipid interface to the spontaneous curvature of the membrane lipids gives a lipid-mediated force that yields attraction or repulsion of proteins (crowding) within the membrane bilayer. As a logical extension, cellular growth and homeostasis (47, 48, 97, 98) and the effects of curvature-inducing or sensing proteins and peptides (9, 10, 12, 34, 62, 99–102) are explicable in terms of membrane elasticity. Detailed theoretical analyses have also been described that yield further insight (42, 64, 103–107).

Cellular Membranes in the Mesoscopic Regime

We shall now give a brief synopsis of the concept of elastic membrane curvature deformation aimed at a general chemical or biological readership. We show that by considering the role of the membrane curvature free energy, one obtains a new paradigm for future experimentation. Membrane protein conformational changes and stability (1, 6, 12, 19, 108), folding (94, 96, 109–111), and membrane fusion (44, 112) all can involve curvature deformation of the bilayer. The concept of elastic deformation goes back a long way, of course (113)—at least to the time of Hooke. Displacements of a body from equilibrium are called strain, and are described by a strain tensor. The forces that deform a body are called stresses and involve a corresponding stress tensor. The strain and stress are related through a characteristic modulus that describes the energetic cost of deforming the material, e.g. Young’s modulus in mechanics. That is the underlying basis for introducing the concept of a flexible surface in the analysis of membrane phenomena (114).

One should recognize that application of a material science (or physics) approach to lipid-protein interactions differs fundamentally from the standard model, inasmuch as it entails chemically nonspecific properties that affect biological activity (36, 38). The work of deforming a material establishes a connection to continuum mechanics (113). Historically, such continuum theories have been successful in explaining a multitude of physical phenomena over many years. According to Aristotle: “The continuum is that which is divisible into indivisibles that are infinitely divisible” (115). How short are the distances that we should consider before atomic- or molecular-size effects (35, 106, 116, 117) become important? A notable caveat of elasticity theory is that the distance scale of the forces is large compared to the molecular size. However, at some length the elastic forces begin to emerge from the local interactions (118, 119). Hence for small systems such as membranes, an essential question is the following: is it most insightful to extrapolate the properties from the molecular scale, or rather to begin with the macroscopic system?

A Brief History of Membrane Elasticity

Readers are well served to know the genesis of ideas of membrane lipid elasticity in relation to protein energetics and stability. According to the FSM (1, 37), matching the geometrical deformation of the lipids adjacent to the protein to the spontaneous (intrinsic) monolayer curvature counterbalances the unfavorable hydrophobic mismatch. The anisotropic balance of forces in membranes suggests the possibility of long-range lipid-protein interactions that entail chemically nonspecific material properties of the bilayer (1). Indeed, formulation of the theory of membrane curvature elasticity by Helfrich (114, 120) has found widespread application in the field of surfactant and membrane nanotechnology—we have pointed out the same concepts are applicable to biomembranes (1). Within the surfactant field, the notion of a flexible surface and the associated concepts of minimal surfaces have been fruitfully applied (71, 121–124). Seminal contributions of Scriven (125), Larsson (126), Israelachvili (127), Björn Lindman (128), Håkan Wennerström (122, 124), and their coworkers are encapsulated in the book entitled “The Language of Shape” by Barry Ninham and colleagues (71). For thin films of surfactant or lipid molecules, the curvature free energy and the chain packing (stretching) energy are mutually frustrated (they cannot be minimized simultaneously)—a concept that has proved useful for understanding the polymorphism of both surfactants and membrane lipids (122–124).

Chemically Specific Interactions or Material Properties?

Let us next ask the following question: do the lipid effects on membrane protein activity stem from specific biochemical interactions, or rather are they due to nonspecific material properties of the membranes? In other words: are they peculiar to the various lipid types, or rather to the bilayer itself? And if the latter is applicable, what are the membrane properties that are implicated in protein activity? For rhodopsin, during the 1980s a direct influence of membrane lipids on the conformational energetics of integral membrane proteins was established for the first time (1, 36, 129, 130). The findings were conceptually reviewed (1) in 1994 in a thematic issue on “Functional Dynamics of Lipids in Biomembranes” (131). At that time they were largely unprecedented—today they constitute a paradigm for further experimental study and testing. In fact, the role of nonspecific bilayer properties in modulating the functions of integral membrane proteins (1) is where the FSM clearly departs from the fluid mosaic model.

Yet, with regard to biomembranes, the view concurrently held by many structural biologists until recently was that the membrane lipid bilayer was an inert solvent or scaffold for membrane proteins. Studies of lipid bilayers were deemed boring and uninteresting—the wallpaper of structural biology in comparison to membrane proteins—worse yet, an intellectual backwater according to some. As previously noted by this author (1) “the alternative point of view, namely that the membrane lipid bilayer represents a unique biological material whose properties are closely associated with the functioning of proteins, [was] regarded with skepticism or even disdain by many structural biologists.” On the other hand, research during the 1980s and 1990s uncovered striking influences of the membrane lipid bilayer on the activities of membrane proteins, as notably reviewed by Anthony Lee (4). Properties of the membrane environment associated with the tightly regulated lipid composition were proposed to affect protein function in cellular membranes (1, 4, 10, 36, 38, 47, 77, 78, 80, 81, 97, 129, 130, 132). Membrane lipids were also shown to govern the growth of bacteria (49, 50, 98, 133) and other microorganisms (46, 47). In the work of Lindblom and coworkers it was found that a balance of lamellar- and nonlamellar forming lipids in A. laidlawii (45, 47) was important for the functioning of proteins in the membrane. These findings have had a strong impact on thinking about the roles played by the lipids in membranes (97, 134–136).

Even a cursory examination of the membrane literature shows the standard model has been very influential in its impact on our understanding of membrane structure and dynamics. Perhaps as a result, it is natural for subsequent workers to point out its limitations. But what does the fluid mosaic model really say? According to Singer and Nicholson (52) “the bulk of the phospholipid is organized as a discontinuous fluid bilayer, although a small fraction of the lipid may interact specifically with the membrane proteins.” Hence “the largest portion of the phospholipid is in bilayer form and not strongly coupled to proteins in the membrane”. The emphasis is on average membrane structure, and when dynamics are considered it is mainly in connection to the rotational and lateral diffusion of membrane proteins, such as rhodopsin. Nowhere is it considered that the activities of membrane proteins may entail the bulk membrane lipid bilayer. Rather it is stated: “the phospholipids and proteins…appear to be largely independent”. In cases where phospholipids affect membrane protein function “the interaction might require that the phospholipid contain specific fatty acid chains or particular polar head groups” (52). The standard model overlooks the possibility of considering membrane function in terms of the entire proteolipid membrane assembly, due to interactions of both the membrane proteins and lipids. But note: an active role of bulk membrane lipids would fundamentally alter the way we look at cellular processes at the membrane level. That would entail the introduction of new biological principles and concepts—that is, ones not fully anticipated by current knowledge.

FROM MOLECULES TO INFINITY

Indeed, many years ago this author pointed out that “structure–activity correlations involving liquid-crystalline supramolecular assemblies appear to be rather subtle, and may not involve the more readily seen van der Waals surface of the molecules, as abundantly depicted in standard biochemistry texts and scientific journals” (1). The chemical viewpoint is exemplified by molecular simulations, as evinced by an upsurge of applications to biomembranes that are too numerous to mention individually (35, 116, 117, 137). The physics alternative—namely that of equilibrium mechanics—is that the forces acting on the proteins in membranes are described by classical elasticity theory (113). Quasi-elastic properties of the membrane bilayer are considered to be emergent over the mesoscopic length scale intermediate between the molecular dimensions and the bulk bilayer. Let us next take a closer look at these two different points of view—namely, the molecular and the continuum approaches.

Lipid Polymorphism and Molecular Packing

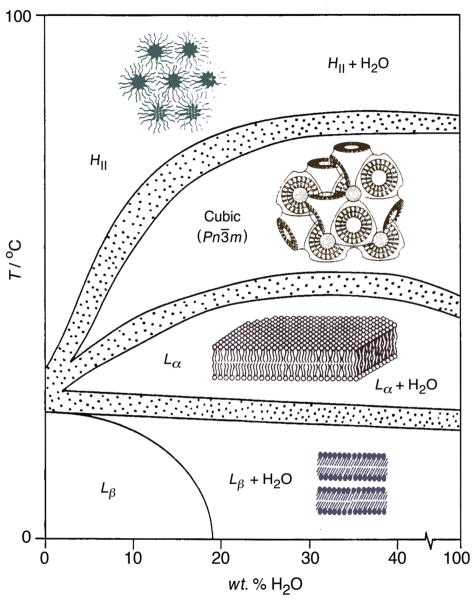
In turns out the canonical lipid bilayer found in biochemistry textbooks is not the only way membrane lipids can organize themselves (123, 138–140). Indeed, it has long been recognized that many biomembranes contain lipids with a tendency to form nonlamellar phases, as emphasized by Cullis and DeKruijff (138). In the case of retinal disk membranes containing rhodopsin, both lamellar and nonlamellar forming lipids are present (56). Homeostatic control (47) of lamellar and nonlamellar-forming lipids (45) also occurs in microorganisms such as A. laidlawii (46) and E. Coli (98, 133). A schematic picture of a temperature-composition phase diagram for a hypothetical phospholipid is shown in Fig. 2. The phase diagram can be readily comprehended in terms of various cuts through the continuous mathematical surface as follows. For a given composition, the sequence of structures with increasing temperature manifests greater repulsive pressure due to the hydrophobic acyl chains as compared to the polar head groups. Transitions from the planar lamellar phase (L_β or L_α) to the bicontinous lipidic cubic phase (Im 3̄m or Pn3̄m) and reverse hexagonal (H_II) phase indicate a more negative spontaneous curvature. Alternatively, for a given temperature increasing the amount water leads to the head groups becoming progressively more hydrated. The sequence from the reverse hexagonal (H_II) and lipidic cubic phases to the lamellar phase is favored due to a less negative spontaneous curvature. According to equilibrium thermodynamics, the phase boundaries (Fig. 2) are described by the Clausius-Clapyeron equation in terms of the standard enthalpy, entropy, and volume changes of the transitions.

Figure 2.

Membrane lipid curvature underlies the temperature-composition phase diagrams of phospholipids. Lipid head groups are indicated by circles and acyl chains by wormlike strings. Hypothetical phase diagram shows the sequence of microstructures with greater tendency to curve towards water as temperature rises; the phase boundaries are described by the Gibbs phase rule. At lower temperatures lamellar microstructures are found where the gel state (L_β; also known as solid-ordered) has trans acyl chains. The lamellar liquid-crystalline state (L_α; also known as liquid-disordered) is found at higher temperature and has liquid-like chains with gauche defects. Further increasing the temperature yields the cubic phase with a curved lipid film draped upon a lattice of cubic symmetry. Lipidic (bicontinuous) cubic phases with zero mean curvature (Pn3̄m based on the Schwarz D-surface; or Im 3̄m based on the Schwartz P-surface, also known as the “plumber’s nightmare”) entail a labyrinth of two nonpenetrating aqueous regions separated by a lipid film; there is no aqueous path from one side to the other. At higher temperature the H_II reverse hexagonal phase (type 2, with negative curvature towards water) involves lipid cylinders whose diameters depend on the water content. Note that distinction in terms of solid-ordered (so), liquid-disordered (ld), and liquid-ordered (lo) phases (rafts) is inapplicable to describing membrane curvature. [single column - 3 inch width]

Lateral Pressure—Water’s Molecularly Thin Interface with Hydrocarbon

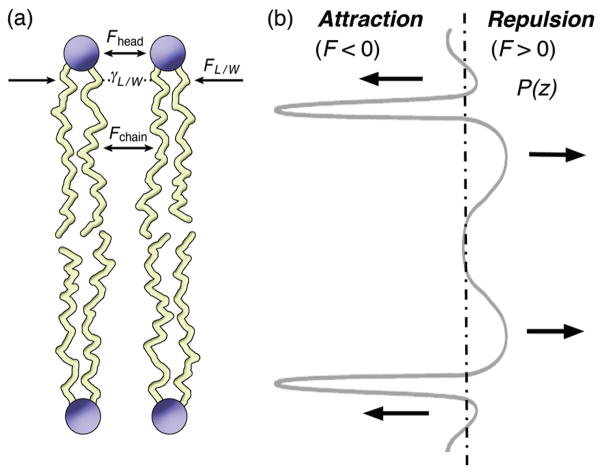
Many readers will appreciate that the structure of matter generally entails a balance of opposing attractive and repulsive forces. Within the lipid head group region, attractive and repulsive interactions act at the polar–nonpolar interface to govern the area per molecule (141–145). Referring now to Fig. 3(a), the attractive forces (F_L/W) lead to a condensation of the lipids described by the surface tension (γ_L/W) due to the interface of the nonpolar acyl groups with water (123). Surface tension is generally associated with a sharp boundary on the order of the size of the interacting groups, in the present case hydrocarbon and water. The positive repulsive pressure is due to short-range steric forces arising from both the head groups (F_head) and the acyl chains (F_chain) above and below the aqueous interface, respectively. For a given head group size, the lipid area constrains the packing of the acyl chains (143) leading to the observed microstructures (see below). The balance of attractive and repulsive forces governs the self-organization and polymorphism of the lipids, together with their remodeling due to membrane biogenesis or external perturbations.

Figure 3.

Phospholipids in different nanostructures embody a balance of forces that governs their assembly and restructuring (remodeling) due to proteins, hydration, or bilayer additives. (a) Depiction of attractive and repulsive forces acting at the level of the polar head groups and the nonpolar acyl chains. Head groups are represented as spheres and acyl chains as wormlike strings. The attractive force (pressure) acting at the aqueous interface (F_L/W) is due to the hydrophobic effect, which counterbalances the repulsive force (pressure) within the head group region (F_head) and the acyl chains (F_chain). (b) Schematic indication of the profile of lateral pressure along the bilayer normal as a function of bilayer depth. The attractive pressure (F_L/W) (negative) involves the surface tension (γ_L/W) of the hydrophobic acyl groups with water; further attractive interactions occur among the head groups and the acyl chains. Above and below the aqueous interface the repulsive pressure (positive) is due to short-range steric forces from both the head groups (F_head) and the acyl chains (F_chain). Note the lateral pressure profile is a heuristic device that does not correspond to any directly measurable experimentally quantity. [single column - 3 inch width]

Next, Fig. 3(b) illustrates how the attractive and repulsive forces are decomposed along the bilayer normal in terms of a lateral pressure profile (123, 134, 135). The attractive (negative) pressure stems mainly from the hydrophobic effect acting at the molecularly thin interface with water. Additional attractive interactions include head group dipole and hydrogen-bonding forces that act in concert with the long-range van der Waals force among the acyl chains of the two monolayers (143). The repulsive (positive) pressure due to the head groups and the acyl chains, Fig. 3(b), counterbalances the attractive pressure as described above. But equilibrium thermodynamics teaches us the lateral tension of bilayers in the absence of osmotic stress is zero. Indeed the following fact is worth noting: the lateral pressure profile is not an experimentally accessible quantity. That is because the integral must be zero for bilayers at equilibrium. So how can the lateral pressure along the bilayer normal be experimentally measured? The answer is that it cannot be measured—it is invisible. Only theoretical MD simulations (116, 117, 137) allow one to establish a correspondence of the lateral pressures to the energetics and stability of membrane proteins, as in the case of rhodopsin (1) or mechanosensitive channels (19).

THE POWER OF CURVATURE

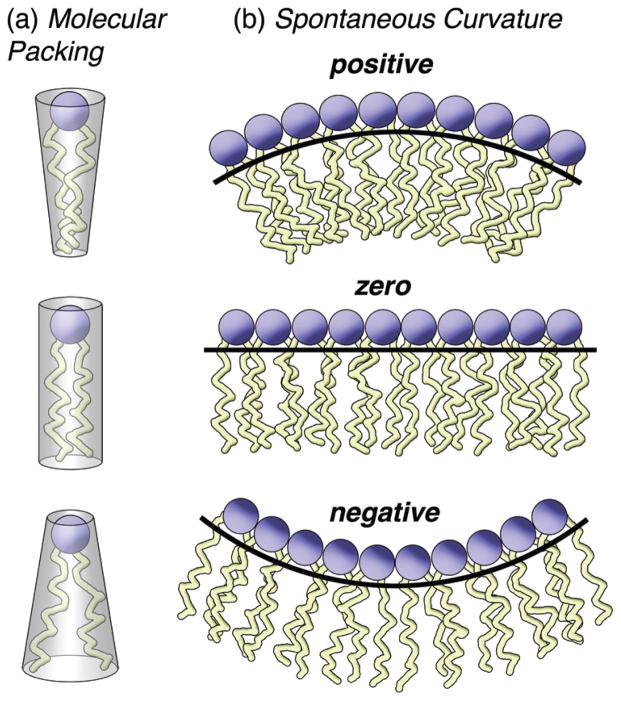
The idea of a balance of opposing forces is also embodied in an earlier explanation for the polymorphism of membrane lipids (123, 138, 139, 146) using a geometric theory for the self-assembly of amphiphiles (73, 127). The studies of Göran Lindblom and coworkers (45, 47) have led to a model in terms of optimal packing of lipids in membranes that is directly related to the curvature energy (48). Such a view exemplifies the chemistry perspective (147), whereby molecular packing is quantitatively related to curvature (148)—either the balance of lamellar and nonlamellar lipids (36) or packing constraints (45, 47) leads to similar conclusions (48). Figure 4(a) shows a chemical view of phospholipids in terms of a molecular packing parameter. The packing of lipids within the aggregate manifests the attractive and repulsive forces acting upon the polar head groups and the nonpolar acyl chains (73). Amphiphiles with a greater head group size relative to the chains, such as gangliosides, lysophospholipids, or single-chain detergents, favor packing into a conical molecular shape on average, Fig. 4(a), top. They tend to form micelles or normal H_I phases, and are analogous to an oil-in-water dispersion (123). Lipids with larger head groups, for instance phosphatidylcholine (PC) whose head group is methylated versus phosphatidylethanolamine (PE), tend to pack on average with a cylindrical molecular shape, Fig. 4(a), middle. They form a planar lipid bilayer (Fig. 2), as abundantly depicted in standard biochemistry texts. Last, those lipids with relatively small head groups compared to the chains, such as PE, prefer to pack into an inverted conical molecular shape on average, Fig. 4(a), bottom. They are able to form the reverse H_II phase (Fig. 2), which is analogous to a water-in-oil dispersion (123, 147). The idea of a molecular packing parameter is also connected to the lateral pressure profile as discussed above, which describes the balance of opposing forces at the level of the lipid polar head groups and the nonpolar acyl chains, see Fig. 3(b).

Figure 4.

Phospholipid form and function involve molecular packing and spontaneous membrane curvature. (a) Schematic illustration of the older view characterized by a molecular packing parameter. Lipids with different head groups and acyl chains are inscribed within their corresponding geometrical shapes. Molecular packing involves the optimal cross-sectional area of the head groups versus the projected acyl chain length and the hydrocarbon volume. Either a frustum of a cone (inverted or upright, top or bottom) or average cylindrical lipid shape (middle) accounts for the diversity of cellular lipids. (b) The new model entails mismatch of the optimal areas of the head groups versus the cross-sectional chain area, thus giving a bending moment for the lipid monolayer. For a membrane bilayer the spontaneous curvature compensates the frustration of the acyl chain packing. Examples are shown where the spontaneous (intrinsic) monolayer curvature is positive (towards hydrocarbon), zero, or negative (towards water). As the optimal head group area becomes progressively smaller vis-à-vis the acyl chains, the spontaneous curvature follows a sequence from positive through zero to negative. The spontaneous monolayer curvature becomes more negative as temperature increases or hydration is less, giving the sequence of nanostructures in Fig. 2. (Figure courtesy of J. Kinnun.) [single column - 2.5 inch width]

But why reckon with an explicit proteolipid membrane (149, 150) if we can forgo an atomistic or molecular perspective? The physics alternative is to regard the membrane lipid bilayer implicitly as a continuous material (151–154). In effect we would like to go beyond flatland—the domain of the lamellar phase. Now, let us imagine we can treat the force balance in terms of a flexible surface. The notion of a long-range spontaneous (intrinsic) monolayer curvature (114, 120) is based on the general theory of elasticity (113). A material science or engineering viewpoint is adopted, whereby chemically nonspecific properties of the lipids play a central role in lipid-protein interactions (37, 38). According to this view, the profile of the lateral pressures gives an intrinsic or spontaneous monolayer curvature, as shown in Fig. 4(b). All of this was pointed out early on (1) in which it was stated that “a related approach is to formulate the balance of forces in terms of the lateral stress profile across the bilayer”. Notably, the spontaneous mean curvature H₀ is not a virtual curvature—it can be experimentally measured for membrane lipids under conditions of dual solvent stress (155). In this regard H₀ is clearly distinguishable from the lateral pressure profile (134, 135, 156).

Shape and Form in Membrane Lipid Function

Perhaps it is worth noting that the curvatures are not implicit; rather they correspond to bending of a neutral (pivotal) plane running beneath the membrane aqueous interface, where the lateral area remains constant. For example, lipids that form nonlamellar phases, such as the H_II phase, have a negative spontaneous curvature H₀. When they are present in a planar bilayer, there is a mismatch of the geometric mean curvature H (which is zero) from the spontaneous curvature H₀. The two monolayers are held together by the hydrophobic effect and packing forces. Curvature mismatch involves the tendency of an individual monolayer of the bilayer to achieve its natural curvature, which is frustrated by the chain packing interactions with the other monolayer. Although a bilayer is flat on average, the two monolayers can still have an inherent tendency to curl. All of these aspects are discussed in several earlier review articles (1, 123, 140).

This curvature energy finds its natural expression in the appearance of nonlamellar structures, such as the reverse hexagonal H_II phase (type 2) of phospholipids, as well as normal hexagonal H_I phases (type 1) for lysolipids and surfactants (Fig. 2). Additional phases with significant curvature can occur, including microemulsions and bicontinuous cubic phases, e.g. corresponding to the gyroid (G), Schwartz diamond (D), and primitive (P) minimal surfaces (where the mean curvature is everywhere zero) that are related through the Bonnet transformation (71). The lipid or surfactant mono- or bilayer is draped upon an infinite periodic minimal surface giving a labyrinth-like system of channels—perhaps analogous to that experienced by Theseus in his encounter with the Minotaur of classical Greek mythology (pp. 1508–1509 of Ref. (70)). This polymorphism can be deciphered using a vocabulary of shape and form (71) that is based on the mathematics of differential geometry. What is most striking, however, is not so much the topology of these fascinating mesophases—but rather the monolayer curvature, which differs from the planar bilayer geometry seen in most biochemistry textbooks.

With these basic precepts in mind, the polymorphism of membrane lipids (see Fig. 2) can now be readily understood by applying the continuum flexible surface model. The spontaneous (intrinsic) monolayer curvature (H₀) can be positive (towards hydrocarbon), zero, or negative (towards water), as shown in Fig. 4(b). When the optimal head group separation exceeds the chains, there is a tendency to curl towards hydrocarbon—the head groups have their greatest exposure to water, as in the case of single-chain surfactants (e.g. lysolipids), as well as glycolipids and gangliosides, as in the top of Fig. 4(b). The positive spontaneous curvature (H₀) is expressed through formation of small micelles or the normal hexagonal (H_I) phase (or elongated wormlike micelles), with the head groups outside and the chains inside the aggregate (oil-in-water dispersion) (not shown). By contrast, lipids with smaller head groups or larger chains, as in the case of double-chain phospholipids, have less exposure to water. They favor a more condensed membrane surface, with a smaller interfacial area per lipid. If the optimal head group separation matches the chains, there is only a small inclination of a monolayer to curl, as in the case of PCs; the spontaneous curvature H₀ is now approximately zero. The planar lipid bilayer is formed as in the standard fluid mosaic model; see the middle of Fig. 4(b). Last of all, lipids with small head groups are even less hydrated, and so they promote a further condensation of the membrane surface. Because the optimal polar head group separation is less than the chains, the lipid monolayer tends to curl towards water, e.g. as occurs in unsaturated and polyunsaturated PEs; now there is a negative spontaneous curvature. Hence the reverse hexagonal (H_II) (or cubic) phases are formed, see the bottom of Fig. 4(b), with the head groups inside and the chains outside the lipid aggregate (water-in-oil dispersion).

THE NEW BIOMEMBRANE MODEL

Our framework for understanding how polymorphism of membrane lipids is connected with their spontaneous curvature (or molecular packing) is based on the flexible surface model (FSM) (1). The lack of molecular specifics is both the weakness and the strength of a continuum picture like the FSM. It adopts a material science approach for understanding membrane lipid-protein interactions at the mesoscopic length scale, falling between the macroscopic membrane dimensions and the atomistic level of the lipids and protein molecules. The new biophysical principle entails curvature matching in contradistinction to purely hydrophobic thickness matching. Accordingly, the spontaneous curvature H₀ is the property that describes the polymorphism and energetics of membrane lipid nanostructures, as well as biological functions of the lipid-embedded proteins. Curvature and hydrophobic matching of the membrane lipid bilayer to the proteolipid boundary accounts for the tightly regulated lipid compositions of cellular membranes in terms of membrane protein activity and stability. Actually the model is not new—it was described many years ago for rhodopsin (36–38), and it has been subsequently reviewed (1, 13). Of course the continuum picture does not preclude a more atomistic view—each approach has its individual merits and limitations (157).

One possibility is to adopt a picture that assumes a continuous membrane film as a basis for interpreting the lipid influences on protein function in terms of material properties, perhaps akin to a composite or an alloy (38). We have previously mentioned that: “it may be plausible to consider the liquid-crystalline bilayers as a material analogous to a composite or metal alloy, whose average properties depend on the composition” (13). Indeed, for rhodopsin it has been demonstrated that lipids modulate a thermodynamically reversible equilibrium between the inactive Meta I state and the active Meta II form (17, 36, 38, 39, 130, 132, 158–162). Lipid substitution experiments show that small lipid head groups such as PE combined with longer unsaturated or polyunsaturated chains forward shift the Meta I–Meta II equilibrium to the active Meta II form. On the other hand, lipids with relatively large PC head groups and shorter fatty acyl chains back shift the Meta I–Meta II equilibrium towards the inactive Meta I state. A specific hypothesis for the effects of nonlamellar-forming lipids on membrane protein function involves a balance of curvature elastic deformation with the hydrophobic solvation energy of the acyl chains (1). We have pointed out that “chemically specific properties of the various lipids are not required, but rather average or material properties of the entire assembly, which may involve the curvature free energy of the membrane lipid-water interface” (1).

Following our original suggestions (36, 56), we have proposed that rhodopsin and other integral membrane proteins act as sensors of the spontaneous (intrinsic) monolayer curvature of the membrane (1, 37, 38)—they exist within the curvature stress field of the lipid bilayer (Fig. 1) (163). The FSM considers a neutral plane, where the curvature deformation (bending) occurs independently of the area strain (intermediate value theorem). Above and below the neutral plane, a compressive (negative) or tensile (positive) strain exists (107). The stress field of the lipids governs the energetics of membrane protein conformations due to their different shapes within the bilayer (163). A balance of attractive and repulsive forces acts upon the embedded protein inclusions, where emphasis is placed on average properties of a long-range nature, e.g. membrane elastic properties (153, 155). Related ideas have been put forth for membrane peptides by Huey Huang (92) and for integral membrane proteins by Olaf Andersen and coworkers (62, 64, 107).

Dealing with Stress—Powered by Curvature

What is the logical basis for the above conclusions, which depart so strikingly from the epitome of the standard fluid mosaic model? Here, we mainly discuss rhodopsin as an embodiment of integral membrane proteins in general. A direct connection of theory with experiment is possible using electronic (UV–visible) spectroscopy, which allows influences of the membrane lipids on the light-induced conformational energetics of rhodopsin to be studied directly (36). From such studies, it has been proposed (1) that “one must significantly revise the standard model for lipid-protein interactions” in which “coupling…to the lateral and/or curvature stresses within the bilayer can provide a source of work, and thus contribute a thermodynamic driving force for the conformational change”. Specific lipids were shown to be sufficient albeit unnecessary for rhodopsin activation—rather, chemically nonspecific material properties of the bilayer lipids are associated with elastic membrane deformation, as formulated by a flexible surface model. For rhodopsin (1) the approach was “to formulate the balance of forces in terms of the lateral stress profile across the bilayer”. As a result, “a curvature elastic stress or frustration exists in one or the other conformational state of the protein”. Moreover: “by enabling a given monolayer of the bilayer to approach its spontaneous curvature, an energetically downhill process, the free energy released can provide a source of work for the MI–MII transition”.

Two Faces of Membrane Lipids

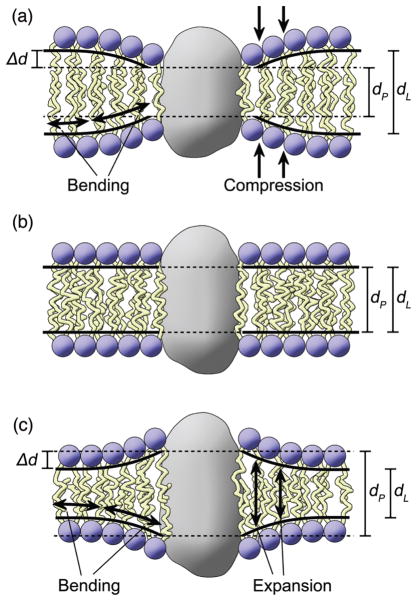
Let us next ask: assuming the standard model may be insufficient, should we be searching for a new biomembrane model? Notably, the FSM is a minimal theory that describes how curvature elastic energy governs membrane protein conformational changes associated with their biological functions. It is conceptually tied to more detailed theoretical treatments (103–105, 164). How are nonlamellar-forming lipids in biomembranes relevant to protein-mediated functions in terms of the spontaneous (intrinsic) membrane curvature? Figure 5 illustrates the role of chemically nonspecific bilayer properties, involving bending of the proteolipid membrane. If deformation of the mean curvature H of the flexible surface (neutral plane) away from the spontaneous mean curvature H₀ occurs, then a strain develops as described by the FSM. The corresponding curvature stress involves the bending modulus κ—together the stress and strain describe the work (free energy) of the elastic membrane remodeling needed to balance the hydrophobic mismatch in the case of rhodopsin. Notably, the influences of nonlamellar-forming lipids (123, 139, 140) on membrane protein function (13, 14, 36, 56, 76–78, 80–82, 85, 86, 89–91) clearly point to an influence of curvature elastic deformation (38) on the energetics of membrane lipid-protein interactions (1, 19, 36, 82, 95, 165). To continue further, applying such a continuum view to biomembranes means there are two interfaces of interest—namely, the lipid/water interface and the protein/lipid interface. All of this was introduced many years ago (38) and was anticipated by earlier work with rhodopsin (36, 56). As a consequence of these two interfaces—one due to interactions of the membrane lipids with water (hydrophobic effect) and the other to the intramembranous protein surface (solvation energy)—small differences in large opposing forces can affect lipid-protein interactions in biomembranes (1, 38, 163). A key prediction of the FSM is that the nonlamellar-forming tendency of the membrane lipids modulates the protein energetics, as first shown experimentally for rhodopsin (1, 36), and subsequently for mechanosensitive ion channels (12, 19).

Figure 5.

Flexible surface model (FSM) for lipid-protein interactions explains lipid-protein interactions by a language of shape (1). Rhodopsin provides a specific example. A mesoscopic hybrid view is shown in which the protein is represented by a continuous surface, whereas the membrane lipids are depicted together with bending of the neutral (pivotal) plane. Hydrophobic coupling involves local compression or expansion of the bilayer adjacent to the proteolipid interface. The FSM relates lipid polymorphism and membrane remodeling to biological function by frustration of the monolayer curvature free energy. Altering the intramembranous hydrophobic surface of the protein affects the solvation energy by the acyl chains, which is balanced by the curvature free energy of the membrane film. Lipids with ≈zero spontaneous curvature H₀ shift the equilibrium towards the inactive Meta I state of rhodopsin; whereas lipids with negative H₀ shift it towards the active Meta II state. Deformation of a fluid membrane away from the monolayer spontaneous curvature frustrates the bending energy, thus producing work for protein conformation changes. The new biomembrane model illuminates how the energetics of membrane proteins depend on material properties of the lipid bilayer. (Figure redrawn from Ref. (1) courtesy of J. Kinnun.) [single column - 2.5 inch width]

Flexible Surface Model for Lipid-Protein Interactions

In its present form, the FSM stems from work conducted in the 1980s and 1990s that is gradually gaining acceptance in the fields of biophysics and structural biology. For rhodopsin it was pointed out that the “lipid composition may be such that it is close to a lamellar–hexagonal phase boundary” (56). According to our experimental studies “interaction of rhodopsin with membrane lipids close to a L_α to H_II (or cubic) phase boundary may thus lead to properties which influence the energetics of conformational states of the protein linked to visual function” (36). Notably the “force imbalance…gives rise to a curvature elastic stress of the lipid/water interface” (1). “Thus chemically specific properties of the various lipids are not required, but rather average or material properties of the entire assembly, which may involve the curvature free energy of the membrane-lipid water interface” (1). It follows that “a flexible surface model explains both the dispersal and activation of rhodopsin in terms of bilayer curvature deformation (strain) and hydrophobic solvation energy. The bilayer stress is related to the lateral pressure profile in terms of the spontaneous curvature and associated bending rigidity” (163). Notably, the FSM is not specific to rhodopsin, which is studied as a prototypical integral membrane protein (31). Whereas the fluid mosaic assumes weak coupling of lipids to integral membrane proteins—or strong coupling due to specific lipid-protein interactions involving the head groups or acyl chains—the FSM entails nonspecific properties of the bilayer, in analogy with a continuum material (1).

CURVATURE FORCES IN ELASTIC MEMBRANE REMODELING

The general framework of the FSM is illustrated in Fig. 5 as an embodiment of the new concepts. It describes a remodeling due to the curvature stress field of the bilayer (1, 106, 163) that is driven by hydrophobic mismatch of the lipid hydrocarbon core to the proteolipid interface. If a change in protein shape occurs, e.g. involving transformation from a cylindrical- to an hourglass- or vase-shaped protein inclusion, then the free energy of the system (comprising protein, lipids, and water) is affected by the membrane bilayer (160). Deformation of the monolayer curvature H away from its spontaneous (intrinsic) curvature H₀ yields a free energy that is balanced (frustrated) by the proteolipid solvation energy due to the amphiphilic environment. A change in curvature free energy due to restructuring of the lipid bilayer or detergent micelle explains the shifting of the Meta I–Meta II equilibrium for rhodopsin. The curvature elastic stress in a given state (e.g. Meta I or Meta II) is approximated by κ|H–H₀|² where the Gaussian (saddle) curvature (114) is neglected in a first approximation. The contribution to the free energy change due to bending of the proteolipid membrane is thus described by two quantities: the bending modulus κ and the monolayer spontaneous curvature H₀.

The author is frequently asked: how could a planar membrane whose actual curvature is zero have a nonzero spontaneous curvature? The answer is that the spontaneous curvature H₀ is the result of a balance of attractive and repulsive forces as a function of depth within the lipid film, i.e. along the lipid molecules (1, 123). It cannot be directly visualized just as the force of gravity or the pressures (stress) acting upon a macroscopic physical object cannot be seen by eye, unless deformation (strain, or in some cases failure) occurs. Yet it should be understood that the spontaneous curvature H₀ is by no means a virtual curvature—it can be experimentally measured (123, 140, 155). Mismatch of the lateral pressures within the head group region and within the hydrocarbon volume gives a bending moment (1) that can be frustrated by the chain packing energy for a lipid bilayer, or the proteolipid solvation energy for a biomembrane.

Frustration of the Curvature Free Energy

Continuing along these lines, bending a surface with no intrinsic curvature gives a curvature free energy. Likewise, flattening a surface with a natural tendency to curve also requires a bending energy. In both cases, the free energy is associated with changes in curvature of the surface. To further grasp the idea of frustration, perhaps a simple analogy is helpful. Let us consider an object that has a natural or intrinsic curvature, such as a soccer (foot) ball or a hat. If it is flattened or squashed flat, then the potential energy is increased, and when it is released the surface springs back to recover its intrinsic curvature (elastic deformation). The case of a bilayer is exactly analogous, where the curvature “frustration” of a monolayer (leaflet) is balanced by the chain packing energy (due to stretching perpendicular to the membrane surface) and vice versa. Although the individual monolayers have a spontaneous curvature (towards either water or hydrocarbon), the contribution from the chain packing free energy can yield a stable bilayer whose geometrical mean curvature is zero.

Bending and Stretching—the Art of Compromise

Referring back to Fig. 5, a flat bilayer (whose monolayer leaflets can have a nonzero intrinsic curvature) can be deformed by the interaction between the proteins and lipids. In accord with the idea of a curvature stress field (1, 106, 163), elastic membrane modeling can occur about polytypic integral membrane proteins with multiple transmembrane helices like rhodopsin. The curvature free energy results from deforming the membrane bilayer away from its monolayer spontaneous curvature H₀ giving a source of work for protein conformational changes. Now if a protein conformational transition entails a change in the lipid curvature free energy—e.g. due to altering the geometrical mean curvature near the proteolipid boundary, or to a change in the monolayer spontaneous curvature—then the new protein state can be stabilized as shown in Fig. 5. Direct experimental evidence is provided by rhodopsin (36, 38), where the Meta I–Meta II equilibrium triggers visual signal transduction via activation of a signal-transducing G-protein (transducin). The Meta I–Meta II equilibrium is known to be promoted by lipids with a tendency to form nonlamellar phases, such as the natural retinal rod lipids having both PE head groups and polyunsaturated acyl chains (36, 56). That is to say—upon light absorption, rhodopsin becomes a sensor of the negative spontaneous curvature of the membrane (36). If the monolayer tends to curve towards water, then an elastic two-way coupling of the protein to the local monolayer curvature can occur (as in Fig. 12 of Ref. (1)). Such ideas also have been put forth with regard to ion channels in membranes (12, 19, 64).

The Rise and Fall of Hydrophobic Mismatch

Skeptics may say the above interpretation in terms of a curvature stress field is baloney—everything is due to the hydrophobic effect (166, 167). Another view that has gained traction in the literature entails hydrophobic matching of the lipid bilayer to the intramembranous proteolipid boundary (5, 66–68, 130, 168, 169). True, there is an influence of bilayer thickness on membrane protein and peptide function (4, 5). Surely consideration of the hydrophobic solvation energy of the protein can suffice to explain the influences of lipid-protein interactions, e.g. in terms of hydrophobicity scales related to protein folding and stability in membranes, as put forth by White and von Heijne as well as other investigators (15, 170–172). Why not just explain the effects of lipid-protein interactions by hydrophobic matching of the lipid bilayer to the protein intramembranous surface? Why is there any need to introduce some new physics beyond what is already established from simpler lipid systems?

The answer is: to minimize the hydrophobic solvation energy, either the bilayer must deform or the protein must deform—e.g. by helical movements as shown by Hubbell et al. (16, 173)—or both must deform. The FSM can be viewed in terms of a curvature remodeling of the membrane bilayer that is driven by hydrophobic mismatch of the lipid hydrocarbon core to the proteolipid interface. Effectively, the membrane deforms up to the point that the total energy cost is minimized (163). Hydrophobic matching entails the intramembranous surface area of the protein that is exposed to the acyl chains of the lipid bilayer versus the fraction exposed to water. Due to collective interactions among the membrane lipids (154), long-range coupling of the lipid and protein molecules extends over several molecular diameters. Experimentally, this coupling is manifested by a dependence of membrane function on the lipid/protein molar ratio (163, 174). An alternative is that collective lipid-protein interactions are explicable in terms of a persistence length for hydrophobic mismatching of the lipids to the proteolipid boundary. Yet the correspondence to experimental observables is not as direct as one would like. Why take a heuristic detour via the persistence length when the directly measurable quantity—the lipid spontaneous curvature—is readily available?

Rhodopsin as a Sensor of Curvature Stress

Let us now come back to the idea (36, 56) that rhodopsin is a sensor of the curvature stress field of the membrane. Most arresting, the simple idea of curvature membrane deformation (36–38) can explain many of the heretofore inexplicable influences of membrane lipids on the Meta I–Meta II equilibrium of rhodopsin (1, 13). The FSM readily explains the influences of bilayer thickness (130), cholesterol (132), and detergents (16, 175) on rhodopsin activation. It offers a minimalist interpretation that is easily appreciated by nonspecialists and specialists alike, and can be developed more quantitatively (64, 106, 107, 176). Lipids with approximately zero spontaneous curvature H₀ shift the equilibrium towards the inactive Meta I state; whereas lipids with negative H₀ shift it towards the active Meta II state. By tipping the balance of the curvature free energy and the proteolipid solvation (packing) energy, the bilayer environment of rhodopsin can selectively stabilize various photoproducts linked to its activation mechanism (1, 13, 161, 162). All of these ideas stem from material science—only the extension to the mesoscopic length scale of membrane lipid-protein interactions is original. The new biophysical principle entails matching the monolayer curvature at the proteolipid interface to the spontaneous curvature of the membrane (1). In analogy to capillary condensation, an attractive or repulsive curvature force occurs between the membrane-embedded protein inclusions that can explain their association or oligomerization in biomembranes (163, 177). For rhodopsin, a curvature elastic stress develops upon photon absorption, which drives formation of an activated ensemble of Meta II substates (178), leading to binding of the G-protein (transducin) and subsequent visual perception. These principles were enunciated and reviewed some years ago (1), yet today they remain equally applicable and constitute a prototype for further experimental testing and study. In fact any process that occurs within the stress field of the membrane can be affected by the curvature free energy of the lipid bilayer (1), such as the membrane protein folding reactions extensively investigated by Engelman and other researchers (15, 94, 109, 110, 179–181). But a more complete account rests upon experimental undertakings that are currently ongoing in various laboratories (96, 182, 183).

WHAT’S NEXT?

To spring fully formed from the head of her father Zeus, the ancient Greek goddess Athena was first conceived by his union with Metis, the goddess of crafty thought—likewise we see that concepts of membrane elastic deformation stem from the union of surface chemistry and physics with structural and cellular biology. Originating from the theory of elasticity, such ideas lead directly through surface chemistry to membrane structural biology. The concept of membrane elastic deformation due to the interplay of lipids and proteins gives a new framework that is subject to further testing and refinement. Integral membrane proteins differ fundamentally from the globular proteins that have been so extensively investigated in the past. Whereas proteins in solution exist in a largely isotropic environment, membrane proteins are subject to anisotropic longer-range elastic forces that govern their distribution, oligomerization, and conformational equilibria. Just as the chorus of an ancient Greek plays an essential role by acting as a non-individualized group of performers, membrane lipids speak with a collective voice to much of cellular biology. Although often overlooked or neglected as the main protein players captivate our attention, the lipids are equally involved with the key processes of life. The new paradigm of membrane curvature forces can thus yield further insights at the intersection of structural and cellular biology with lipid physical chemistry—subjects that are certain to become more closely intertwined in the future.