Single-Molecule Reaction Chemistry in Patterned Nanowells

Abstract

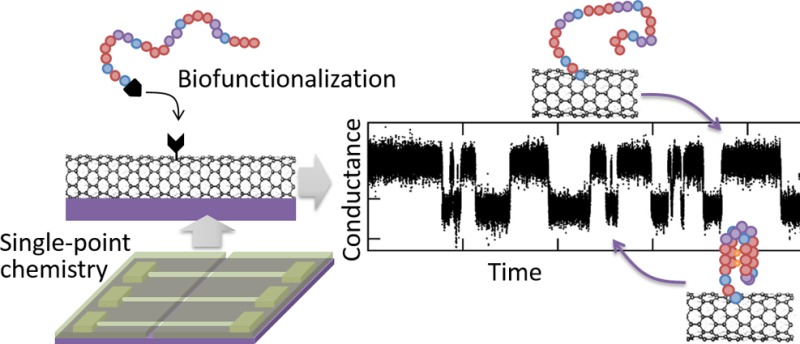
A new approach to synthetic chemistry is performed in ultraminiaturized, nanofabricated reaction chambers. Using lithographically defined nanowells, we achieve single-point covalent chemistry on hundreds of individual carbon nanotube transistors, providing robust statistics and unprecedented spatial resolution in adduct position. Each device acts as a sensor to detect, in real-time and through quantized changes in conductance, single-point functionalization of the nanotube as well as consecutive chemical reactions, molecular interactions, and molecular conformational changes occurring on the resulting single-molecule probe. In particular, we use a set of sequential bioconjugation reactions to tether a single-strand of DNA to the device and record its repeated, reversible folding into a G-quadruplex structure. The stable covalent tether allows us to measure the same molecule in different solutions, revealing the characteristic increased stability of the G-quadruplex structure in the presence of potassium ions (K⁺) versus sodium ions (Na⁺). Nanowell-confined reaction chemistry on carbon nanotube devices offers a versatile method to isolate and monitor individual molecules during successive chemical reactions over an extended period of time.

Reaction chemistry and micro/nanofabrication are two distinct sets of techniques that have evolved independently from one another over the past decades. On one end, synthetic methods developed by chemists have enabled the creation of a wide variety of molecules and macromolecules that find applications in many disparate fields, such as materials science, medicinal chemistry, and environmental chemistry. These chemical reactions were typically developed and optimized on milligram and larger scales, corresponding to populations of more than 10²⁰ molecules. Such large numbers of reacting species produce highly predictable reaction yields, which, combined with purification and analytical techniques, enable the rapid synthesis of highly pure molecules and macromolecules. Nonetheless, it is not clear how traditional synthesis routes translate at the ultrasmall scale, when only a few molecules are involved, as found in emerging confined environments such as nanofluidics and lab-on-chip technology.¹ In parallel to the development of reaction chemistry, the semiconductor industry has been propelled forward by the refinement and miniaturization of microfabrication techniques. In the current state of the art, low-dimensional materials such as nanotubes,² nanowires,³ and 2D van der Waals materials^4,5 are assembled to form miniature electronic devices, and nanolithography methods are used to pattern ultrafine features down to the molecular scale.⁶

Here, we combine together synthetic chemistry and nanofabrication techniques to isolate single-molecule chemical reactions and observe them in real time over extended periods of time. We propose and demonstrate the use of lithographically patterned nanowells to confine chemical reactions to a single point on individual carbon nanotubes, forming what we call a single-molecule probe (see Figure 1). The nanotube serves as a substrate for the chemical reaction tethering the initial single-molecule probe, and the resulting adduct forms a single-molecule field-effect transistor (smFET) that can be used to observe and characterize in real time, through quantized fluctuations in electrical signals,⁷⁻⁹ consecutive individual chemical reactions, molecular interactions, and molecular conformational changes occurring at the probe site.

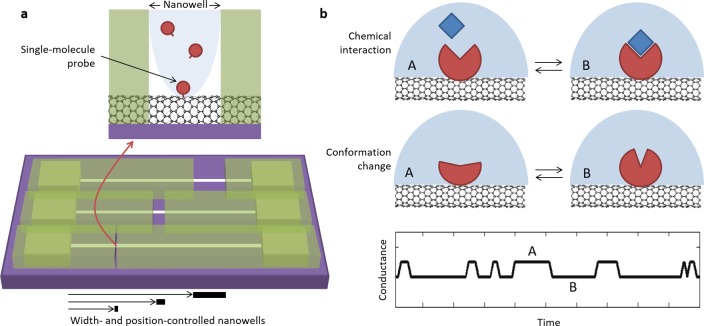
Figure 1.

Single-molecule reaction chemistry. (a) Nanowells of controlled width and position are patterned using high-resolution electron-beam lithography in a thin polymer layer covering carbon nanotube devices. The resulting nanowells confine chemical reactions performed within them, in order to achieve formation of a single-molecule probe. (b) After dissolution of the mask, various consecutive secondary single-molecule reactions can be performed on the initial single-molecule probe, and further molecular interactions (top) and conformational changes (middle) can be monitored in real-time via quantized fluctuations between A and B states in the device electrical conductance (bottom).

Typical chemical reactions performed on carbon nanotube surfaces haphazardly distribute over the entire surface of the nanotube.¹⁰⁻¹² The few approaches able to produce single-point functionalization, such as feedback-controlled oxidation^8,13 or noncovalent assembly,¹⁴ rely on unfavorable statistics that result in minimal control on the position and the yield of the chemistry. Moreover, the necessity to individually monitor each device in feedback-controlled methods imposes throughput limitations in the preparation of devices. Noncovalent approaches also bear time scale limitations in that only short read times are possible due to the instability of the molecule–nanotube coupling. Contrastingly, our approach relies on high-yield covalent chemistry and confinement within nanowells patterned in a thin polymer layer to achieve the formation of stable, isolated functional groups at a set of predetermined positions on an array of carbon nanotube devices (Figure 1a). Here, we demonstrate the functionalization of hundreds of devices in one chemical step, with predictable yields in the number of functional groups as well as unprecedented control over the position of functional sites.

After the initial chemical reaction on the nanotube, the polymer mask can be dissolved, and the remaining functional group acts as a single-molecule probe to support a variety of successive, secondary reactions and interactions with single-molecule resolution. Employing a combination of microfluidics and real-time electronic detection, we demonstrate how to generate and track consecutive chemical reactions, molecular interactions, and molecular conformational changes on the same individual molecule, through changes in the electrical conductance of the nanotube (Figure 1b). In this paper, we present two examples of such secondary reactions: (i) the transient, millisecond scale interaction between a carboxylic acid group on the primary single-molecule probe and a carbodiimide coupling reagent⁷ and (ii) the covalent attachment of a single-stranded DNA onto the primary single-molecule probe and its reversible folding into a well-defined tertiary DNA structure. Specifically, we use a guanine-rich DNA sequence that adopts a unique G-quadruplex fold in the presence of alkali metal cations such as K⁺ or Na⁺ and observe its folding and unfolding in real time. Consistent with previous studies,¹⁵ we find that the folded G-quadruplex structure is more stable in the presence of K⁺ ions versus Na⁺ ions.

Nanowell-Confined Chemistry on Carbon Nanotubes

Nanowell-confined chemistry is developed and optimized using carbon nanotube transistors with a 4 μm channel length between source and drain electrodes. Nanowells, ranging from 5 nm to the full 4 μm channel length, are patterned in a thin polymer layer using high-resolution electron-beam lithography. Details on devices and nanowells fabrication are provided in the Supporting Information. We design the masks to cover the electrodes and to expose only a portion of the nanotube channel as illustrated in Figure 2a. Nanotube segments outside the electrodes are kept fully covered on one side and fully exposed on the other side to act as negative and positive controls, respectively. Figure 2b shows atomic force microscopy (AFM) images of a 4-μm-long nanotube device covered by a mask with a 20-nm-wide nanowell (middle) and the same nanotube after removal of the mask (top). The corresponding height profile in Figure 2b (bottom) reveals a polymer thickness of approximately 70 nm and confirms the position and width of the nanowell (see additional AFM characterization in Supplementary Figure 1). To confirm full-depth opening of the nanowells down to substrate level, we evaporate an 8-nm-thick layer of titanium over test masks with nanowells of various widths. Scanning electron microscopy of the resulting metal lines (shown in Supplementary Figure 2) indicates that the smallest wells that can be reliably fabricated are 20 nm wide. After incubation for ∼24 h in saline buffer, we observe no significant deterioration in the polymer defining the nanowells (see Supplementary Figure 3).

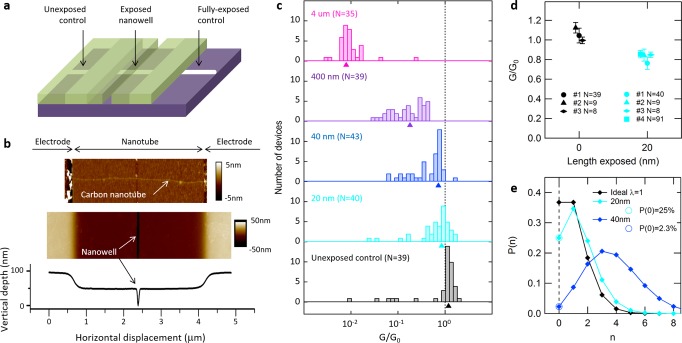
Figure 2.

Effect of nanowell-confined chemistry on carbon nanotube devices. (a) Mask design showing a nanowell of controlled position and width over the device channel. Positive and negative controls are designed outside the device channel using full exposure and full protection of the nanotube, respectively. (b) Atomic force microscopy image showing a carbon nanotube between metallic electrodes (top) and the same device covered with a protecting mask opened with a 20 nm nanowell (middle), along with the corresponding height profile (bottom). (c) Distribution of conductance change G/G₀ after functionalization within nanowells of different widths, compiled on N individual devices from the same nanotube (N_total = 196). Arrows indicate the mean conductance change obtained from a log-normal fit of the distribution. (d) Conductance change and error bars (s.d.) obtained using 20 nm nanowell masks (cyan) compared to control devices (black). Each data point is a N-device average from a different nanotube. (e) Modeled probability of getting a number n of functional groups using small nanowells. Circles represent measured points based on data in panel c; others are extrapolated from a Poisson distribution.

In order to install functional groups on the nanotube sidewall, we perform covalent chemistry inside the nanowells formed in the polymer mask. Aryl diazonium chemistry is chosen because it is a reliable, well-characterized reaction¹⁶ that forms stable adducts.^17,18 This reaction also provides good electronic coupling with the nanotube,¹⁹ and attached single-molecule probe groups can be terminated with reactive functional groups. In this study, the carboxylic acid group is selected to facilitate subsequent bioconjugation.²⁰ We functionalize carbon nanotubes by incubating mask-covered devices for 24 h in an aqueous solution of 4-carboxybenzenediazonium tetrafluoroborate salt (CBDT) (see details on the functionalization protocol in the Supporting Information). AFM profiles taken before and after functionalization confirm the absence of swelling or other alterations in the mask (see Figure 2b and Supplementary Figure 3). After the reaction, we remove the mask by soaking devices in room-temperature acetone, thus making the functional groups available for chemical reactions in organic solvents and with larger, more complex molecules.

We study the statistics of nanowell-confined chemistry by exposing hundreds of devices created from the same, ultralong nanotube to the CBDT reaction (see Supporting Information and Supplementary Figure 4). The width of the nanowells is varied from 20 nm to 4 μm, and some devices are kept fully covered with resist to serve as negative controls. We compare the electrical source–drain conductance before and after functionalization for each device and report the conductance change defined as G/G₀ = G_{Functionalized}/G_Initial at V_DS = 50 mV and V_G = −10 V (see Supplementary Figure 5 for examples of full current–voltage characteristics). Figure 2c shows histograms of the data for each nanowell width on a typical nanotube, as well as the mean conductance change obtained from a log-normal fit of the distributions.^19,21 As expected, the fully exposed devices exhibit a more than an order of magnitude drop in conductance as well as a defect-related D band in their Raman spectra (see Supplementary Figure 6).^19,22−24 As the nanowell width is decreased, the conductance change and D-band intensities also decrease (see Supplementary Figure 7). Unexposed control devices do not show any conductance drop or measurable D band. These observations confirm that functionalization does occur on the nanotube and only inside the nanowell.

In the case of the smallest 20-nm-wide nanowell, we observe a small but consistent conductance change when compared to the unexposed controls (Figure 2d), as tested on four different nanotubes. Mean conductance change is calculated using 8–91 different devices on each nanotube. In contrast to the exposure through large nanowells, where current drops are highly variable for different nanotubes (see Supplementary Figure 7), reaction in 20-nm-wide nanowells generates a reproducible ∼20% average current drop on all tested nanotubes. This difference between large-scale and localized functionalization is likely due to the fact that, in the case of large nanowells, CBDT molecules have a high probability of encountering intrinsic, reactive defects along the nanotube, resulting in inhomogeneous reactions, whereas, in the case of 20 nm-wide nanowells, CBDT molecules have a very low probability of encountering such defects. Consistency in the current drop for small nanowells across different devices and nanotubes suggests that it stems from the creation of a consistent number of functional groups.

The actual number of functional groups is extracted from the population of unreacted devices for each nanowell width. We find that the overlap between the G/G₀ distributions of 20 nm nanowell devices and unexposed control devices is about 1 in 4, which is assigned to the population of unreacted devices. Using a Poisson distribution p(n) = λⁿe^–λ/n! to model the probability p(n) to get a number n of individual functional groups, we first estimate p(0) from the fraction of devices with no or positive change in conductance, then extrapolate to find the average number λ of functional groups. For 20 nm nanowells, we find an average of λ = 1.39 functional groups per device and a population of devices having single-molecule probe attachment of p(n = 1) = 35%, which approaches the λ = 1 theoretical optimum for single-molecule devices illustrated in Figure 2e. In contrast, larger nanowells allow for a wider distribution in the number of functional groups per device, as illustrated by the Poisson distribution calculated for 40 nm nanowells in Figure 2e and by the corresponding broadening of histograms in Figure 2c. Finally, we note that the ∼20% average conductance drop associated with this single-molecule reaction is consistent with recent experimental work on CBDT-induced defects²⁵ and that this value is significantly less in amplitude than that obtained by oxidative defect-mediated single-point approaches,^8,13 in agreement with hybrid density functional theory (DFT)/nonequilibrium Green’s function calculations that predict the oxidative method to generate a greater alteration than a single-point chemical bond.²⁶

Real-Time Detection of Sequential Chemical Reactions

To confirm the presence of a single-molecule functional group and to test the ability of the platform to monitor sequential chemical reactions on this probe, we use an array of ten smFETs functionalized using nanowell-confined chemistry and integrated with a microfluidic platform (see Supporting Information and Figure 3a). Of 10 devices, seven are exposed through 20-nm-wide nanowells using CBDT chemistry (“exposed” devices), and three are designed to be controls by fully covering them with the polymer mask (“unexposed” devices), as summarized in Supplementary Table 1. As before, Raman spectroscopy is used on positive and negative controls to confirm, respectively, the reactivity of the nanotube to the diazonium chemistry and the effectiveness of the protective mask (see Figure 2a). After completing the reaction, five of the exposed devices experience an average drop in conductance of ∼20%, a signature consistent with that obtained above in the statistical analysis for the binding of single-molecule probes. The two other exposed devices show no conductance drop, consistent with remaining not functionalized, as discussed above. These devices are labeled as “functionalized” and “unfunctionalized”, respectively (see Supplementary Table 1). Similarly, all unexposed devices preserve their conductance due to the protection provided by the mask.

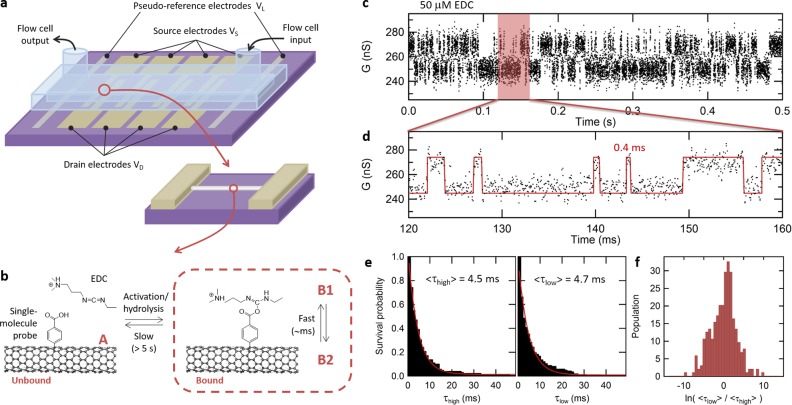
Figure 3.

Real-time sensitivity to secondary reactions on the primary single-molecule probe. (a) Design of smFET devices, including carbon nanotube channel, drain, and source electrodes, as well as pseudoreference electrodes for electrolytic gating in the microfluidic cell. (b) Reaction kinetics between an EDC molecule and a single-molecule carboxyphenyl probe covalently attached on the nanotube. Two levels of kinetics can be observed: slow transition between the unbound and bound states, corresponding to the reversible activation and hydrolysis reactions on the COOH probe, as well as fast kinetics due to fluctuations within a bound COOH/EDC complex. (c) Real-time response of a device in the presence of 50 μM EDC, after baseline correction, showing an active phase with two-state activity characteristic of rapid fluctuations in a single carboxy-EDC adduct (B1/B2 fluctuations). (d) Zoomed region of the trajectory superimposed with an idealized trace obtained from a hidden Markov model, revealing events resolved in the submillisecond range. (e) Survival probability plot for the high- and low-conductance states, fitted with a single-exponential function to obtain average lifetimes ⟨τ_high⟩ and ⟨τ_low⟩. (f) Distribution of ⟨τ_high⟩/⟨τ_low⟩ ratios obtained from multiple, successive, 1-s-long segments of a long trajectory, showing kinetics centered on the symmetric case in which ⟨τ_high⟩ = ⟨τ_low⟩, with a level of heterogeneity in the distribution that is typical of single-molecule experiments.

All devices are immersed in aqueous 2-(N-morpholino)ethanesulfonic acid (MES) buffer solution (100 mM, pH 4.5) in the flow cell, and their drain-source current is measured in real-time using a constant DC applied bias of V_SD = 100 mV and an electrolytic gating potential of V_L = −300 mV, chosen to place the electrostatic potential of the nanotubes between their electrical ON and OFF states (see Supporting Information and Supplementary Figure 8). Under these conditions, all devices exhibit a baseline current of several hundreds of nA with 1/f background noise and no distinguishable activity (see Supplementary Figure 9). The buffer solution is then switched to a 50 μM solution of 1-ethyl-3-(3-(dimethylamino)propyl)carbodiimide (EDC) in aqueous MES buffer (100 mM, pH 4.5). EDC is an activating and dehydrating agent that forms an O-acylisourea derivative of a carboxylic acid.²⁰ These intermediate derivatives hydrolyze quickly in the presence of water with a typical turnover period of 10–100 s in such conditions,^7,27 as illustrated by the slow kinetics between the unbound (A) and bound (B) states in Figure 3b. In presence of EDC, two of the functionalized devices are found to exhibit successive phases of random telegraph noise (RTN) in their conductance, separated by inactive phases as shown in Supplementary Figure 10. Following Goldsmith et al.,⁷ we attribute the inactive phases to the unbound, hydrolyzed state (A) and the active phases with RTN to rapid fluctuations (B1/B2) within a single COOH/EDC complex.

The period of active or inactive phases is observed to be longer than 5 s (see Supplementary Figure 10), which is consistent with the turnover rate of the activation/hydrolysis reaction.^7,27 An example trajectory measured in an active phase is shown in Figure 3c and d, after baseline correction for clarity (see raw trajectories and baseline fit in Supplementary Figure 10).²⁸ The trajectory shows rapid two-state RTN activity, in which dwell times with submillisecond duration can be resolved (see Figure 3d). Using a hidden Markov model, we extract the distribution of dwell times in the high- and low-conductance states and build survival probability plots, presented in Figure 3e. These plots can be fitted with a single-exponential function, indicating simple kinetics with average lifetimes of ⟨τ_high⟩ = 4.5 ms and ⟨τ_low⟩ = 4.7 ms for the high- and low-conductance states, respectively. The similarity between the lifetimes of the two states in that trajectory indicates that both states are almost equally probable, i.e., that the equilibrium constant between B1 and B2 is close to 1. When repeating this analysis on multiple, successive 1-s-long segments, we obtain a distribution of ⟨τ_high⟩/⟨τ_low⟩ ratios centered around the case in which ⟨τ_high⟩ = ⟨τ_low⟩, as presented in Figure 3f. The width of the distribution illustrates a level of heterogeneity in the kinetics which is commonly observed in single-molecule measurements. We also perform several controls to ensure that the active phases with rapid two-state RTN are strictly related to the COOH/EDC adduct (see Supplementary Figure 9). First, the observed two-state RTN disappears after flushing the device with fresh buffer, consistent with the fact that the system remains in the unbound state (A) after the EDC molecule is washed away. In addition, none of the three unexposed devices nor the two unfunctionalized devices exhibit any activity when exposed to EDC (see Supplementary Table 1). Examples of trajectories for these different types of controls are presented in Supplementary Figure 9.

The presence of multiseconds-long inactive and active phases, millisecond-scale fast RTN in the active phase, and heterogeneous kinetics centered on ⟨τ_high⟩ = ⟨τ_low⟩ are all consistent with results reported for the interaction of the EDC molecule with a single carboxylic acid group.⁷ Moreover, the ratio of exposed devices exhibiting this specific signature (2 out of 7) is compatible with the proportion of devices functionalized with a single-molecule probe as derived from the earlier, large-array study. This remarkable agreement obtained from two independent experiments (i.e., the conductance change experiment and the real-time reactivity experiment) corroborates the ability of our nanowell-confined chemical approach to produce single-molecule probes with high and reproducible yields. More practically, the presence of this specific COOH/EDC signature can be used as an indicator to identify, from a large array of devices, the set of devices holding a single-molecule probe, which can be further used as a template to support a variety of other individual molecules, as demonstrated in the following section.

Conformational Dynamics of a Single DNA G-Quadruplex

Finally, we demonstrate the ability of the platform to support a second level of functionalization, by covalently tethering an individual biomolecule to the primary single-molecule probe and measuring its conformational dynamics in real-time. For these experiments, we use a 24-nucleotide, 5′-amino-modified, single-stranded DNA oligomer that models human telomeric DNA in that it is composed of four repeats of the TTAGGG guanine-rich sequence typically found in the terminal, single-stranded, telomeric region of human chromosomes (see Supporting Information for full sequence).²⁹ This sequence can fold into a structure called a G-quadruplex that is comprised of a series of stacked guanine tetrads as illustrated in Figure 4a. Monovalent cations, in particular K⁺ and, to a lesser extent, Na⁺, stabilize the folded form of the G-quadruplex sequence by binding between (K⁺) or within (Na⁺) the plane of the guanine tetrads.^15,30,31 On the same microfluidic-integrated array of ten smFETs described above, we covalently attach the 5′-amino-modified DNA oligomer to the primary single-molecule probe on the carbon nanotube via an amide bond formed using two consecutive chemical reactions, as described in the Supporting Information.

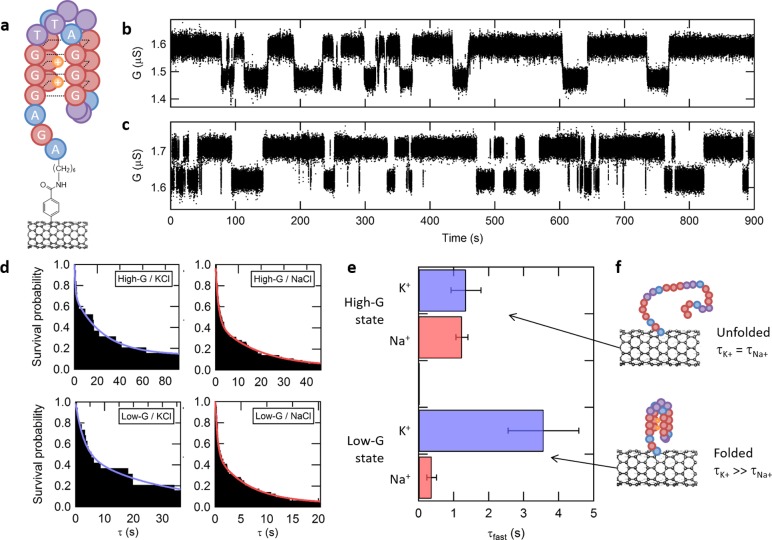
Figure 4.

Single-molecule observation of DNA G-quadruplex folding. (a) Representation of a folded G-quadruplex DNA sequence capturing two K⁺ cations, bound to an initial single-molecule probe on a nanotube. (b–c) Real-time trajectories with baseline correction, showing two-state fluctuations in conductance in the presence of 10 mM KCl or NaCl, respectively. (d) Survival probability plots for each conductance state (high-G/low-G) and each ion type (K⁺/Na⁺) are fitted with a double-exponential kinetic model. (e) Average lifetime ⟨τ_fast⟩ and error bars extracted from the survival plots in panel d for the high-G and low-G states as well as both K⁺ and Na⁺ ions. (f) High-G and low-G conductance states are attributed to the unfolded and folded DNA configurations, respectively. The folded configuration is found to have a longer lifetime in the presence of K⁺ cations than Na⁺.

After functionalization with the DNA oligomer, we measure the conductance of all ten devices in real time and at room temperature, with V_DS = 100 mV and V_L = −300 mV. The conductance of the devices is recorded in real-time for 15 min in Tris-HCl buffer (10 mM, pH 7.5) supplemented with 10 mM KCl. Under these conditions, one device exhibits fluctuations between a low-conductance state (low-G) centered at 1.49 μS and a high-conductance state (high-G) centered at 1.61 μS, as shown in the baseline-corrected trajectory in Figure 4b (raw traces are provided in Supplementary Figure 11). After once again flushing the flow cell thoroughly, we collect real-time data for 15 min and at room temperature in Tris-HCl buffer, supplemented this time with 10 mM NaCl. As observed in the presence of K⁺, the trajectory recorded in the presence of Na⁺ shows fluctuations between a low-G state and a high-G state, respectively centered at conductance values of 1.64 μS and 1.73 μS (Figure 4c). A control experiment recorded using the same device, but in the presence of only the Tris-HCl buffer (i.e., in the absence of K⁺ or Na⁺ ions), does not exhibit such fluctuations, which is consistent with other studies reporting only weak interaction between pristine carbon nanotubes and G-quadruplex DNA.^32,33 Similarly, measurements using an unexposed control device do not exhibit such fluctuations, either in the presence of KCl or NaCl. Each of these controls is presented in Supplementary Figure 12.

In order to rigorously assign the low-G and high-G states to configurations of the G-quadruplex oligomer, we perform a statistical analysis of the transitions between these states. To do so, we use a hidden Markov model as previously described^8,28,34 to calculate the most probable sequence of transitions between the low-G- and high-G states forming the trajectories (i.e., the idealized paths) (see Supporting Information and Supplementary Figure 11). Survival probability plots of the dwell times spent in low-G state prior to transitioning to the high-G state and, conversely, of the dwell times spent in high-G state prior to transitioning to the low-G state are shown in Figure 4d. Consistent with previous single-molecule biophysical studies of G-quadruplex sequences,^15,35,36 each survival probability plot is best described by a double exponential decay function (see Supplementary Figure 13), yielding two characteristic lifetimes (τ_fast and τ_slow) for both the low- and high-G states (see Supplementary Table 2). While the small number of long dwells that predominantly contribute to τ_slow render this lifetime particularly susceptible to the effects of possible missed transitions, the much larger number of short dwells that predominantly contribute to τ_fast render this lifetime significantly resistant to the effects of possible missed transitions (see Supplementary Figure 14). Consequently, τ_fast is a much more robust lifetime measurement and is therefore presented in Figure 4e for each state and each ion type. For the low-G state, we find that τ_fast obtained in the presence of K⁺ is 10 times longer than that obtained in the presence of Na⁺. In contrast, for the high-G state, we find that τ_fast obtained in the presence of K⁺ is within error of that obtained in the presence of Na⁺. Previous studies of G-quadruplex sequences similar to that investigated here have demonstrated that, at any particular monovalent ion concentration, the folded form of the G-quadruplex sequence should be more stable in the presence of K⁺ versus Na⁺, whereas the stability of the unfolded form should be independent of the identity of the ion.³⁷ Given that all of our experiments are conducted at the same monovalent ion concentration and given our finding that K⁺ stabilizes the low-G state by a factor of 10 over Na⁺, whereas the stability of the high-G state is independent of the identity of the ion, we unambiguously assign the low-G and high-G states of the trajectories to the folded and unfolded forms of the G-quadruplex sequence, respectively (see Figure 4f).

We note that the values of τ_fast for both the folded and unfolded forms of the G-quadruplex sequence reported here are in close agreement with the corresponding lifetimes of the folded and unfolded forms of a similar G-quadruplex sequence obtained from single-molecule fluorescence resonance energy transfer (smFRET) studies performed under similar experimental conditions to those used here.¹⁵ In addition, the existence of two classes of dwells (i.e., τ_fast and τ_slow) in both the folded- and unfolded forms of the G-quadruplex sequence is fully consistent with previous smFRET studies of similar G-quadruplex sequences.^15,38 The close correspondence between our results and the results of smFRET studies of analogous G-quadruplex sequences suggests that tethering of the G-quadruplex to the surface of the carbon nanotube device does not impair the folding/unfolding dynamics of the G-quadruplex. This observation validates the use of the smFET devices described here for single-molecule studies of biomolecular folding and structural dynamics. Notably, the label-free-, increased time-resolution-, and expanded observation time aspects of the smFET approach described here should enable investigations of biomolecular folding reactions and dynamic processes that are currently difficult or impossible to investigate using more conventional single-molecule biophysical approaches such as smFRET,³⁹ single-molecule force spectroscopy,⁴⁰ or single-molecule tethered-particle motion⁴¹ approaches.

Conclusions

Nanowell-confined chemistry on carbon nanotube devices provides a versatile platform to support and monitor individual chemical reactions. We obtain a high yield for the attachment of the primary single-molecule probe, and the covalent chemistry ensures strong nanotube-molecule coupling and long-term stability of the adduct. The method is independent of a specific chemical reaction and generalizable to any aqueous nanotube chemistry. It is also easily scalable to the wafer scale, enabling the production of a large number of devices and robust statistical analysis. Once the mask defining the nanowells is removed, the platform supports an even larger variety of reactions and reagents, for instance reactions in organic solvents or bioconjugation with large macromolecules. Successive secondary single-molecule reactions on the same single-molecule probe can be recorded in real time, with submillisecond resolution and for many hours. In particular, this platform can measure the conformational dynamics of individual DNA G-quadruplexes, which are important components of the biological mechanisms underlying cell aging and the proliferation of cancer cells, in that their formation is known to inhibit the replication of the terminal ends of chromosomes.^42,43 More generally, this platform opens routes to investigate a variety of other fundamental chemical mechanisms such as lifetimes of intermediates in catalytic reactions and to improve chemical sensor and lab-on-chip technology with localized functionality.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.6b02149.

• Materials and methods, as well as additional characterization of PMMA masks, devices, functionalization, and real-time data analysis (PDF)

The authors declare no competing financial interest.