A DEEP LEARNING APPROACH FOR CANCER DETECTION AND RELEVANT GENE IDENTIFICATION

Abstract

Cancer detection from gene expression data continues to pose a challenge due to the high dimensionality and complexity of these data. After decades of research there is still uncertainty in the clinical diagnosis of cancer and the identification of tumor-specific markers. Here we present a deep learning approach to cancer detection, and to the identification of genes critical for the diagnosis of breast cancer. First, we used Stacked Denoising Autoencoder (SDAE) to deeply extract functional features from high dimensional gene expression profiles. Next, we evaluated the performance of the extracted representation through supervised classification models to verify the usefulness of the new features in cancer detection. Lastly, we identified a set of highly interactive genes by analyzing the SDAE connectivity matrices. Our results and analysis illustrate that these highly interactive genes could be useful cancer biomarkers for the detection of breast cancer that deserve further studies.

1. Introduction

The analysis of gene expression data has the potential to lead to significant biological discoveries. Much of the work on the identification of differentially expressed genes has focused on the most significant changes, and may not allow recognition of more subtle patterns in the data.^1–6 Tremendous potential exists for computational methods to analyze these data for the discovery of gene regulatory targets, disease diagnosis and drug development.^7–9 However, the high dimension and noise associated with these data presents a challenge for these tasks. Moreover, the mismatch between the large number of genes and typically small number of samples presents the challenge of a “dimensionality curse”. Multiple algorithms have been used to distinguish normal cells from abnormal cells using gene expression.^10–13 Although there has been a lot of research into cancer detection from gene expression data, there remains a critical need to improve accuracy, and to identify genes that play important roles in cancer.

Machine learning methods for dimensionality reduction and classification of gene expression data have achieved some success, but there are limitations in the interpretation of the most significant signals for classification purposes.^14,15 Recently, there have been efforts to use single-layer, nonlinear dimensionality reduction techniques to classify samples based on gene expression data.¹⁶ In similar studies of computer vision, unsupervised deep learning methods have been successfully applied to extract information from high dimensional image data.¹⁷ Similarly, one can extract the meaningful part of the expression data by applying such techniques, thereby enabling identification of specific subsets of genes that are useful for biologists and physicians, with the potential to inform therapeutic strategies.

In this work, we used stacked denoising autoencoders (SDAE) to transform high-dimensional, noisy gene expression data to a lower dimensional, meaningful representation.¹⁸ We then used the new representations to classify breast cancer samples from the healthy control samples. We used different machine learning (ML) architectures to observe how the new compact features can be effective for a classification task and allow the evaluation of the performance of different models. Finally, we analyzed the lower-dimensional representations by mapping back to the original data to discover highly relevant genes that could play critical roles and serve as clinical biomarkers for cancer diagnosis. The performance of these methods affirm that SDAEs could be applied to cancer detection in order to improve the classification performance, extract both linear and nonlinear relationships in the data, and perhaps more important, to extract a subset of relevant genes from deep models as a set of potential cancer biomarkers. The identification of these relevant genes deserves further analysis as it potentially can improve methods for cancer diagnosis and treatment.

2. Background

Classification and clustering of gene expression in the form of microarray or RNA-seq data are well studied. There are various approaches for the classification of cancer cells and healthy cells using gene expression profiles and supervised learning models. The self-organizing map (SOM) was used to analyze leukemia cancer cells.¹⁹ A support vector machine (SVM) with a dot product kernel has been applied to the diagnosis of ovarian, leukemia, and colon cancers.¹¹ SVMs with nonlinear kernels (polynomial and Gaussian) were also used for classification of breast cancer tissues from microarray data.¹⁰

Unsupervised learning techniques are capable of finding global patterns in gene expression data. Gene clustering represents various groups of similar genes based on similar expression patterns. Hierarchical clustering and maximal margin linear programming are examples of this learning and they have been used to classify colon cancer cells.^20,21 K-nearest neighbors (KNN) unsupervised learning also has been applied to breast cancer data.¹²

Due to the large number of genes, high amount of noise in the gene expression data, and also the complexity of biological networks, there is a need to deeply analyze the raw data and exploit the important subsets of genes. Regarding this matter, other techniques such as principal component analysis (PCA) have been proposed for dimensionality reduction of expression profiles to aid clustering of the relevant genes in a context of expression profiles.²² PCA uses an orthogonal transformation to map high dimensional data to linearly uncorrelated components.²³ However, PCA reduces the dimensionality of the data linearly and it may not extract some nonlinear relationships of the data.²⁴ In contrast, other approaches such as kernel PCA (KPCA) may be capable of uncovering these nonlinear relationships.²⁵

Similarly, researchers have applied PCA to a set of combined genes of 13 data sets to obtain the linear representation of the gene expression and then apply a autoencoder to capture nonlinear relationships.²⁶ Recently, a denoising autoencoder has been applied to extract a feature set from breast cancer data.¹⁶ Using a single autoencoder may not extract all the useful representations from the noisy, complex, and high-dimensional expression data. However, by reducing the dimensionality incrementally, the multi-layered architecture of an SDAE may extract meaningful patterns in these data with reduced loss of information.²⁷

3. Materials and Methods

We have applied a deep learning approach that extracts the important gene expression relationships using SDAE. After training the SDAE, we selected a layer that has both low-dimension and low validation error compared to other encoder stacks using a validation data set independent of both our training and test set.²⁸ As a result, we selected an SDAE with four layers of dimensions of 15,000, 10,000, 2,000, and 500. Consequently we used the selected layer as input features to the classification algorithms. The goal of our model is extracting a mapping that possibly decodes the original data as closely as possible without losing significant gene patterns.

We evaluated our approach for feature selection by feeding the SDAE-encoded features to a shallow artificial neural network (ANN)²⁹ and an SVM model.³⁰ Furthermore, we applied a similar approach with PCA and KPCA as a comparison.

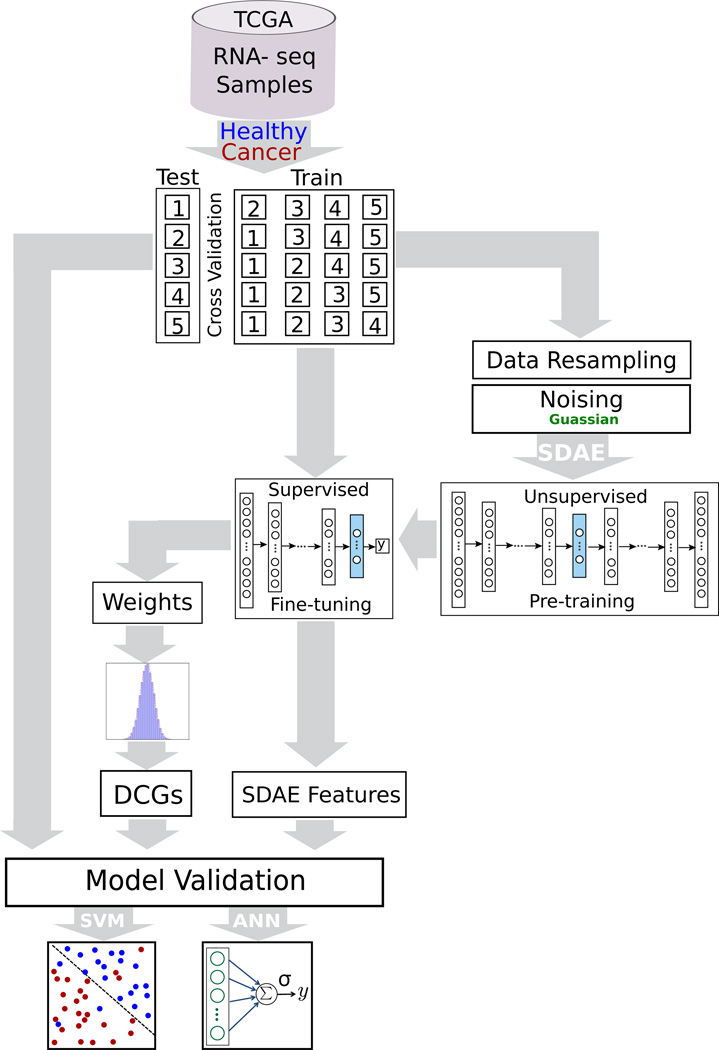
Lastly, we used the SDAE weights from each layer to extract genes with strongly propagated influence on the reduced-dimension SDAE-encoding. These selected “deeply connected genes” (DCGs) are further tested and analyzed for pathway and Gene Ontology (GO) enrichment. The results from our analysis showed that in fact our approach can reveal a set of biomarkers for the purpose of cancer diagnosis. The details of our method are discussed in the following subsections, and the work-flow of our approach is shown in Fig 1.

Fig. 1.

The pipeline representing the stacked denoising autoencoder (SDAE) model for breast cancer classification and the process of biomarkers extraction.

3.1. Gene Expression Data

For our analysis, we analyzed RNA-seq expression data from The Cancer Genome Atlas (TCGA) database for both tumor and healthy breast samples.³¹ These data consist of 1097 breast cancer samples, and 113 healthy samples. To overcome the class imbalance of the data, we used synthetic minority over-sampling technique (SMOTE) to transform data into a more balanced representation for pre-training.³² We used the imbalanced-learn package for this transformation of the training data.³³ Furthermore, we removed all genes that had zero expression across all samples.

3.2. Dimensionality Reduction Using Stacked Denoising Autoencoder

An autoencoder (AE) is a feedforward neural network that produces the output layer as close as possible to its input layer using a lower dimensional representation (hidden layer). The autoencoder consists of an encoder and a decoder. The encoder is a nonlinear function, like a sigmoid, applied to an affine mapping of the input layer, which can be expressed as f_θ(X) = σ(Wx+b) with parameters θ = {W, b}. The matrix W is of dimensions d′ × d to go from a larger dimension of gene expression data d to a lower dimensional encoding corresponding to d′. The bias vector b is of dimension d′. This input layer encodes the data to generate a hidden or latent layer. The decoder takes the hidden representations from the previous layer and decodes the data as closely as possible to the original inputs, and can be expressed as z = g_θ′(y) = σ(W′y + b′). In our implementation, we imposed tied weights, with W′ = W^T. We can refer to the weight matrix W and bias b as θ = {W, b} and similarly θ′ = {W′, b′}.

A SDAE can be constructed as a series of AE mappings with parameters θ₁, θ₂, …, θ_n and the addition of noise to prevent overfitting.¹⁸ In order to get a good representation for each layer, we maximize the information gain between the input layer (modeled as a random variable X from an unknown distribution q(X)) and its higher level stochastic representation (random variable Y from a known distribution p(X|Y ;θ′)). For layer i, we then learned a set of parameters θ_i and ${\theta }_i^{\prime }$ from a known distribution p where q(Y|X) = p(Y|X;θ_i) and also $q(X|Y)=p(X|Y;{\theta }_i^{\prime })$ that maximize the mutual information.¹⁸

This maximization problem corresponds to minimizing the reconstruction error of the input layer using hidden representation. In this construction, the hidden layer contains the compressed information of the data by ignoring useless and noisy features. In fact, the autoencoder extracts a set of new representations which encompass the complex relationships between input variables. The reconstruction error of the input layer using this new representation is non-zero, but can be minimized. In practice, the weights of the model are learned through the stochastic gradient descent (SGD) algorithm.^34,35

Autoencoders extract both linear and nonlinear relationships inherent in the input data, making them powerful and versatile. The encoder of the SDAE decreases the dimensionality of the gene expression data stack-by-stack, which leads to reduced loss of information compared to reducing the dimension in one step.²⁷ In contrast, the decoder increases the dimensionality to eventually achieve the full reconstruction of the original input as close as possible. In this procedure, the output of one layer is the input to the next layer. For this implementation, we used the Keras library with Theano backend running on an Nvidia Tesla K80 GPU.³⁶ Although it is difficult to estimate the time complexity of the deep architecture of the SDAE, with batch training and highly parallelizable implementation on GPUs, training takes a few minutes and testing of a sample is performed in a few seconds.

It is proven in practice that pre-training the parameters in a deep architecture leads to a better generalization on a specific task of interest.¹⁸ Greedy layer-wise pre-training is an unsupervised approach that helps the model initialize the parameters near a good local minimum and convert the problem to a better form of optimization.²⁷ Therefore, we considered the pre-training approach as supposed to achieve smoother convergence and higher overall performance in cancer classification. After starting with the initial parameters resulting from the pre-training phase, we used supervised fine-tuning on the full training set to update the parameters.

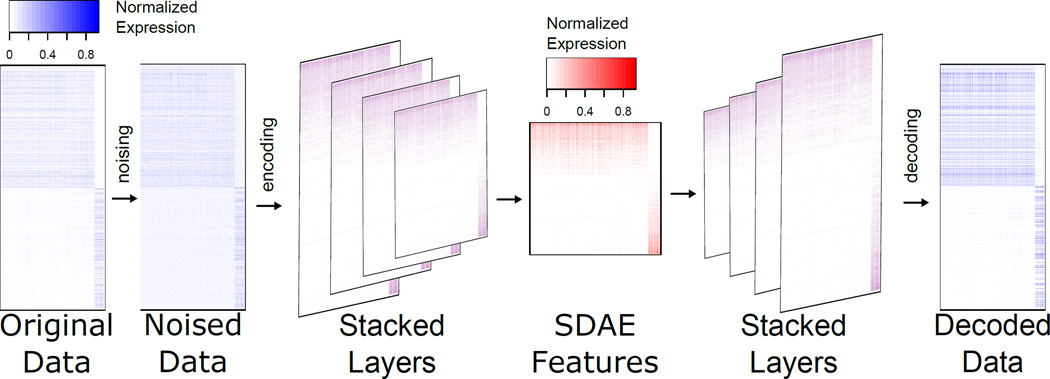
To avoid overfitting in the learning phase (both pre-training and fine-tuning) of the SDAE, we utilized a dropout regularization factor, which is a method of randomly excluding fractions of hidden units in the training procedure by setting them to zero. This method prevents nodes from co-adapting too much and consequently avoids overfitting.³⁷ For the same purpose, we provided partially corrupted input values to the SDAE (denoising). The SDAE is robust, and its accuracy does not change upon introducing noise at a low rate. In fact, SDAE with denoising and dropout can find a better representation from the noisy data. Fig 2 shows the SDAE encoded, decoded, and denoised representations on the subset of genes.

Fig. 2.

SDAE representation using the enriched genes in the TCGA breast cancer. In this depiction for illustrative purposes, the top 500 genes with median expression across cancer samples enriched above health samples, and the top 500 genes with reduced median expression across cancer samples is shown.

3.3. Differentially Expressed Genes

We used significantly differentially expressed genes as a comparison to our SDAE features for cancer classification. First, we computed the log fold change comparing the median expression in cancer tissue samples to that of healthy tissue samples. We then computed a two-tailed p-value using a Gaussian fit, followed by a Benjamini-Hochberg (BH) correction.³⁸ We identified two sets of differentially expressed genes. The first, DIFFEXP0.05 was the 206 genes, 98 upregulated and 118 down-regulated, that were significant at an FDR of 0.05. The second set, DIFFEXP500, contains the top 500 most significant differentially expressed genes (the same dimension as the SDAE features) using the same 2-tailed p-values, containing 244 up-regulated and 256 down-regulated genes.

3.4. Dimensionality Reduction Using Principal Component Analysis

As a second level of comparison, we extracted features using linear PCA to provide a baseline for the performance of linear dimensionality reduction algorithms for our ML models. The same reduced dimensionality of 500 was used. In addition, we used KPCA with an RBF kernel to extract features that by default are of the same dimension as the number of training input samples. For both PCA and KPCA we used an implementation in the scikit-learn package.³⁹

4. Results and Discussion

4.1. Classification Learning

In order to evaluate the effectiveness of our autoencoder-extracted features, we used two different supervised learning models to classify cancer samples from healthy control samples. First, we considered a single-layer ANN with input nodes directly connected to output layers without any hidden units. If we consider the input units as X = (x₁, x₂, …, x_n), the output values are calculated as y = σ(∑_i w_ix_i + b). Second, we considered both an SVM with a linear kernel and with a radial basis function kernel (SVM-RBF). We applied 5-fold cross-validation for to exhaustively split the data into train and test sets to estimate the accuracy of each model without overfitting. In each split, the model was trained on 4 partitions and tested on the 5th, ensuring that training and testing are performed on non-overlapping subsets.

5. Comparison of Different Models

To assess the effectiveness of the SDAE features, we compared their performance in classification to differentially expressed genes and to principal components for different machine learning models. The performance of the SDAE features for classification is summarized in Table 1. The best method varies depending on the performance metric, but on these data the SDAE features performed best on three of the five metrics we considered. The highest accuracy was attained using SDAE features applied to SVM-RBF classification. This method also had the highest F-measure. The highest sensitivity was found for SDAE features as well, but using the ANN classification model. KPCA features applied to an SVM-RBF had higher specificity and precision.

Table 1.

Comparison of different feature sets using three classification learning models.

Features	Model	Accuracy	Sensitivity	Specificity	Precision	F-measure
	ANN	96.95	98.73	95.29	95.42	0.970
SDAE	SVM	98.04	97.21	99.11	99.17	0.981
	SVM-RBF	98.26	97.61	99.11	99.17	0.983
	ANN	63.04	60.56	70.76	84.58	0.704
DIFFEXP500	SVM	57.83	64.06	46.43	70.42	0.618
	SVM-RBF	77.391	86.69	71.29	67.08	0.755
	ANN	59.93	59.93	69.95	84.58	0.701
DIFFEXP0.05	SVM	68.70	82.73	57.5	65.04	0.637
	SVM-RBF	76.96	87.56	70.48	65.42	0.747
	ANN	96.52	98.38	95.10	95.00	0.965
PCA	SVM	96.30	94.58	98.61	98.75	0.965
	SVM-RBF	89.13	83.31	99.47	99.58	0.906
	ANN	97.39	96.02	99.10	99.17	0.975
KPCA	SVM	97.17	96.38	98.20	98.33	0.973
	SVM-RBF	97.32	89.92	99.52	99.58	0.943

6. Deep Feature Extraction and Deeply Connected Genes

Going beyond classification, there is potential biological significance in understanding what subsets of genes are involved in the new feature space that makes it an effective set for the cancer detection. Previous work on cancer detection using a single-layer autoencoder has evaluated the importance of each hidden node.¹⁶ Here, we analyzed the importance of genes by considering combined effect of each stack of the deep architecture. To extract these genes, we utilized a strategy of computing the product of the weight matrices for each layer of our SDAE. The result is a 500 × G dimensional matrix W, where G is the number of genes in the expression data, computed for an n-layer SDAE by

$$W=\prod _{i=1}^n{W}_i.$$

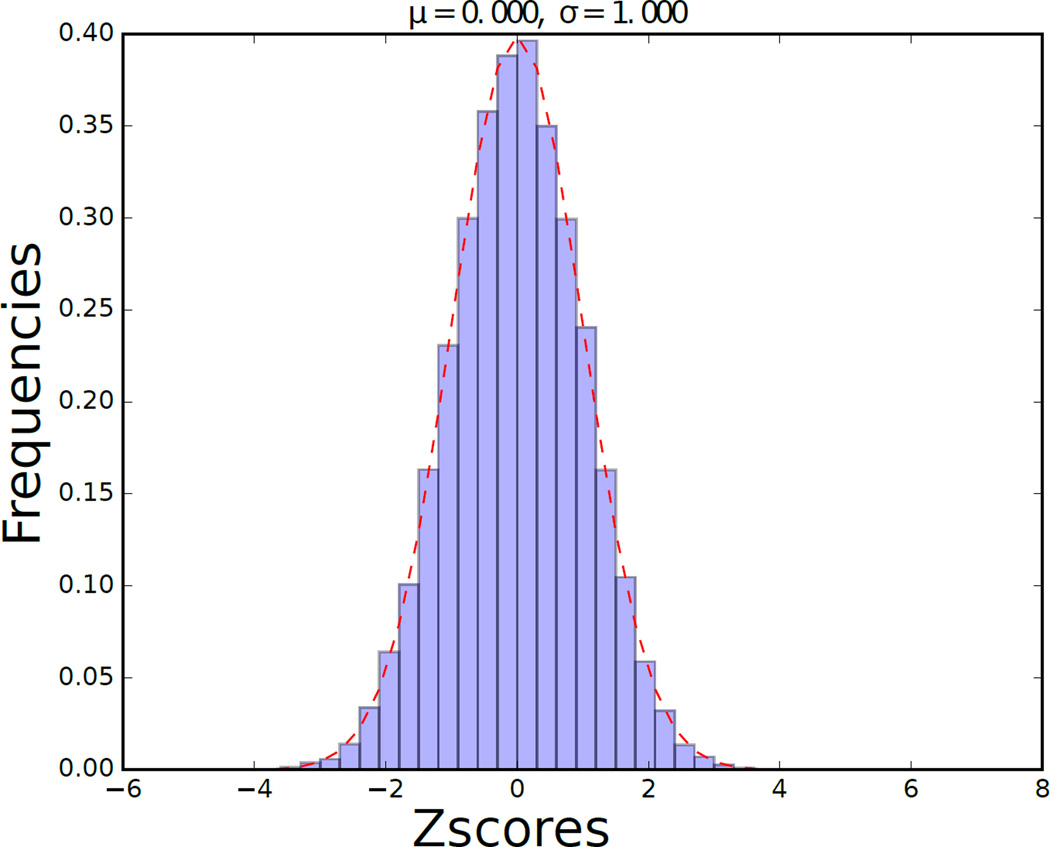
Although the weights of each layer of the SDAE are computed with a nonlinear model, the matrix W is a linearization of the compounded effect of each gene on the SDAE features. Genes with the largest weights in W are the most strongly connected to the extracted and highly predictive features, so we called these genes DCGs. We found that the terms of matrix W were strongly normally distributed (Fig 3). We identified the subset of genes with the most statistically significant impact on the encoding by fitting the distribution of these values in W to a normal distribution, computing a p-value using this fit, and applying a BH correction with an FDR of 0.05.

Fig. 3.

Histogram of z-Scores from the dot product matrix of the weights connectivity of the SDAE.

6.1. Gene Ontology

We examined the functional enrichment of the DCGs through a GO term and Panther pathway analysis. Table 2 presents the statistically-enriched GO terms under “biological process”, and having a Bonferroni-corrected p-value of less than 1e–10. Many of the most significant terms are related to mitosis, suggesting a large number of genes with core functionality that is relevant to cell proliferation. In addition, an analysis of the enrichment of Panther pathways led to a single enriched term, p53 pathway, where we observe 10 genes when 1.34 are expected, giving a p-value of 2.21E-04. P53 is known to be an important tumor-suppressor gene^40–42, and this finding suggests a role of tumor suppressor function in many of the DCGs.

Table 2.

Enriched GO terms associated with DCGs in breast cancer data from TCGA.

GO biological process	Total	Observed	Expected	Enrichment	P-value
cell cycle process (GO:0022402)	1079	100	16.46	6.07	1.12E-45
cell cycle (GO:0007049)	1311	108	20	5.4	3.28E-45
mitotic cell cycle process (GO:1903047)	741	85	11.31	7.52	1.06E-44
mitotic cell cycle (GO:0000278)	760	85	11.6	7.33	7.33E-44
nuclear division (GO:0000280)	470	63	7.17	8.78	1.52E-35
organelle fission (GO:0048285)	492	64	7.51	8.53	1.99E-35
mitotic nuclear division (GO:0007067)	357	56	5.45	10.28	1.34E-34
cell division (GO:0051301)	477	58	7.28	7.97	3.72E-30
chromosome segregation (GO:0007059)	274	46	4.18	11	5.46E-29
sister chromatid segregation (GO:0000819)	176	36	2.69	13.41	7.62E-25
nuclear chromosome segregation (GO:0098813)	230	38	3.51	10.83	3.97E-23
mitotic cell cycle phase transition (GO:0044772)	249	35	3.8	9.21	8.10E-19
mitotic prometaphase (GO:0000236)	99	25	1.51	16.55	1.56E-18
cell cycle phase transition (GO:0044770)	255	35	3.89	9	1.72E-18
regulation of cell cycle (GO:0051726)	943	62	14.39	4.31	2.48E-18
chromosome organization (GO:0051276)	984	63	15.01	4.2	4.15E-18
DNA metabolic process (GO:0006259)	768	52	11.72	4.44	2.67E-15
organelle organization (GO:0006996)	3133	112	47.8	2.34	4.27E-15
mitotic cell cycle phase (GO:0098763)	211	29	3.22	9.01	7.67E-15
cell cycle phase (GO:0022403)	211	29	3.22	9.01	7.67E-15
biological phase (GO:0044848)	215	29	3.28	8.84	1.25E-14
sister chromatid cohesion (GO:0007062)	113	22	1.72	12.76	1.18E-13
cellular resp. to DNA damage stimu. (GO:0006974)	719	48	10.97	4.38	1.27E-13
regulation of cell cycle process (GO:0010564)	557	42	8.5	4.94	2.53E-13
mitotic sister chromatid segregation (GO:0000070)	90	20	1.37	14.56	3.01E-13
cell cycle checkpoint (GO:0000075)	196	25	2.99	8.36	1.09E-11
M phase (GO:0000279)	173	23	2.64	8.71	6.55E-11
mitotic M phase (GO:0000087)	173	23	2.64	8.71	6.55E-11
regulation of mitotic cell cycle (GO:0007346)	461	35	7.03	4.98	1.10E-10
single-organism process (GO:0044699)	12451	253	189.98	1.33	4.67E-10
DNA replication (GO:0006260)	213	24	3.25	7.38	5.74E-10
anaphase (GO:0051322)	154	21	2.35	8.94	6.13E-10
mitotic anaphase (GO:0000090)	154	21	2.35	8.94	6.13E-10
cellular component organization (GO:0016043)	5133	139	78.32	1.77	7.74E-10

6.2. Classification Learning

Finally, we used the expression of the DCGs as features for the ML models previously mentioned. These genes served as useful features for cancer classification, achieving 94.78% accuracy (Table 3). Although these features performed a few percentage points below that of the SDAE features, they still have advantage of being more readily interpreted. Future work is needed to improve the extraction of DCGs to enhance their utility as features for classification.

Table 3.

Cancer classification results using deeply connected genes (DCGs).

Features	Model	Accuracy	Sensitivity	Specificity	Precision	F-measure
	ANN	91.74	98.13	87.15	85.83	0.913
DCGs	SVM	91.74	88.80	97.50	97.25	0.927
	SVM-RBF	94.78	93.04	97.5	97.20	0.951

6.3. Conclusion

In conclusion, we have used a deep architecture, SDAE, for the extraction of meaningful features from gene expression data that enable the classification of cancer cells. We were able to use the weights of this model to extract genes that were also useful for cancer prediction, and have potential as biomarkers or therapeutic targets.

One limitation of deep learning approaches is the requirement for large data sets, which may not be available for cancer tissues. We expect that as more gene expression data becomes available, this model will improve in performance and reveal more useful patterns. Accordingly, deep learning models are highly scalable to large input data.

Future work is needed to analyze different types of cancer to identify cancer-specific biomarkers. In addition, there is potential to identify cross-cancer biomarkers through the analysis of aggregated heterogeneous cancer data.