How to Get Statistically Significant Effects in Any ERP Experiment (and Why You Shouldn’t)

Abstract

Event-related potential (ERP) experiments generate massive data sets, often containing thousands of values for each participant, even after averaging. The richness of these data sets can be very useful in testing sophisticated hypotheses, but this richness also creates many opportunities to obtain effects that are statistically significant but do not reflect true differences among groups or conditions (bogus effects). The purpose of this paper is to demonstrate how common and seemingly innocuous methods for quantifying and analyzing ERP effects can lead to very high rates of significant-but-bogus effects, with the likelihood of obtaining at least one such bogus effect exceeding 50% in many experiments. We focus on two specific problems: using the grand average data to select the time windows and electrode sites for quantifying component amplitudes and latencies, and using one or more multi-factor statistical analyses. Re-analyses of prior data and simulations of typical experimental designs are used to show how these problems can greatly increase the likelihood of significant-but-bogus results. Several strategies are described for avoiding these problems and for increasing the likelihood that significant effects actually reflect true differences among groups or conditions.

It can seem like a miracle when a predicted effect is found to be statistically significant in an event-related potential (ERP) experiment. A typical ERP effect may be only a millionth of a volt or a hundredth of a second, and these effects can easily be obscured the many sources of biological and environmental noise that contaminate ERP data. Averaging together a large number of trials can improve reliability and statistical power, but even with an infinite number of trials there would still be variance due to factors such as mind wandering. All these sources of variance can make it very difficult for a 1 μV or 10 ms difference between groups or conditions to reach the .05 threshold for statistical significance. Consequently, when an experiment is designed to look for a small but specific effect, much care is needed to ensure that the predicted effect will be statistically significant if it is actually present.

On the other hand, it is extraordinarily easy to find statistically significant but unpredicted and unreplicable effects in ERP experiments. ERP data sets are so rich that random variations in the data have a good chance of producing statistically significant effects at some times points and in some electrode sites if enough analyses are conduct. These effects are bogus (i.e., not genuine), but it can be difficult for the researchers, the reviewers of a journal submission, or the readers of a published article to know if a given effect is real or bogus. This likely leads to the publication of a large number of effects that are bogus but have the imprimatur of statistical significance. Estimating how often this happens is difficult, but there is growing evidence that many published results in psychology (Open Science Collaboration, 2015), neuroscience (Button, Ioannidis, Mokrysz, Nosek, Flint, Robinson, & Munafò, 2013), and oncology (Prinz, Schlange, & Asadullah, 2011) are not replicable. Many factors contribute to the lack of replicability, but one of them is what Simmons, Nelson, and Simonsohn (2011) called experimenter degrees of freedom. This is the idea that experimenters can analyze their data in many different ways, and if the methods that experimenters choose are selected after the data have been viewed, this will dramatically increase the likelihood that bogus effects reach the criterion for statistical significance.

Experimenters typically have more degrees of freedom in the analysis of ERP experiments than in the analysis of behavioral experiments, and this likely leads to the publication of many significant-but-bogus ERP findings. The purpose of the present paper is to demonstrate the ease of finding significant-but-bogus effects in ERP experiments and to provide some concrete suggestions for avoiding these bogus effects. Following the approach of Simmons et al. (2011), we will begin by showing how the data from an actual experiment can be analyzed inappropriately to produce significant-but-bogus effects. We will then discuss in detail a common practice—the use of analysis of variance with large numbers of factors—that can lead to significant-but-bogus effects in the vast majority of experiments. We will also provide concrete suggestions for avoiding findings that are statistically significant but are false and unreplicable.

How to Find Significant Effects in Any ERP Experiment: An Example

Our goal in this section is to show how a very reasonable-sounding analysis strategy can lead to completely bogus conclusions. To accomplish this, we took a subset of the data from an actual published ERP study (Luck, Kappenman, Fuller, Robinson, Summerfelt, & Gold, 2009) and performed new analyses that sound reasonable but were in fact inappropriate and led to completely bogus effects. Note that everything about the experiment and re-analysis will be described accurately, with the exception of one untrue feature of the design that will be revealed later and will make it clear that any significant results must be bogus in this re-analysis (see Luck, 2014 for a different framing of these results). Although the original study compared a patient group with a control group, the present re-analysis focuses solely on within-group effects from a subset of 12 control subjects.

Design and Summary of Findings

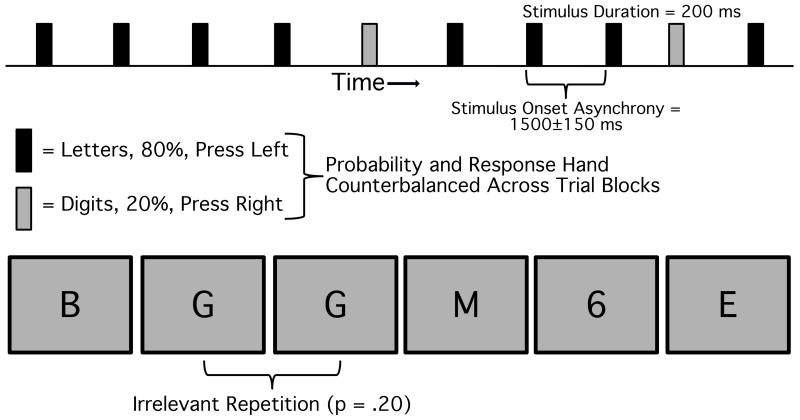
In this study, data were obtained from 12 healthy adults in the visual oddball task shown in Figure 1. Letters and digits were presented individually at the center of the video display, and participants were instructed to press with the left hand when a letter appeared and with the right hand when a digit appeared (or vice versa). The stimuli in a given block consisted of 80% letters and 20% digits (or vice versa), and the task required discriminating the category of the stimulus and ignoring the differences among the members of a given category (i.e., all letters required one response and all digits required the other response). However, unbeknownst to the participants, 20% of the stimuli in the frequent category were exact repetitions of the preceding stimulus (such as the repetition of the letter G in the example shown in Figure 1). The goal of the analyses presented here was to determine whether these frequent repetitions were detected, along with the time course of the differential processing of repetitions and non-repetitions. Previous research has shown that repetitions of the rare category can influence the P3 wave (Duncan-Johnson & Donchin, 1977; Johnson & Donchin, 1980), but the effects of repetitions on individual exemplars of the frequent category are not known.

Figure 1.

Experimental paradigm from the study of Luck et al. (2009). Letters and digits were presented at fixation, with a stimulus duration of 200 ms and a stimulus onset asynchrony of 1500±150 ms. One of these two stimulus categories was rare (20%) and the other was frequent (80%). Participants were instructed to make a left-hand button-press for one category and a right-hand button-press for the other category. Both the rare category and the category-hand response mapping were counterbalanced across trial blocks. The same letter or digit was occasionally presented twice in succession in the frequent category.

The experiment included 800 trials per participant, with 640 stimuli in the frequent category and 160 stimuli in the rare category. Within the frequent category, there were 128 repetitions and 512 non-repetitions for each participant. As has been found many times before, the N2 and P3 waves were substantially larger for the rare category than for the frequent category (see Luck et al., 2009 for a comparison of these waveforms). The present analyses focused solely on the frequent category to determine whether there were any differences in the ERPs for frequent repetitions and frequent non-repetitions. Standard recording, filtering, artifact rejection, and averaging procedures were used (see Luck et al., 2009 for details).

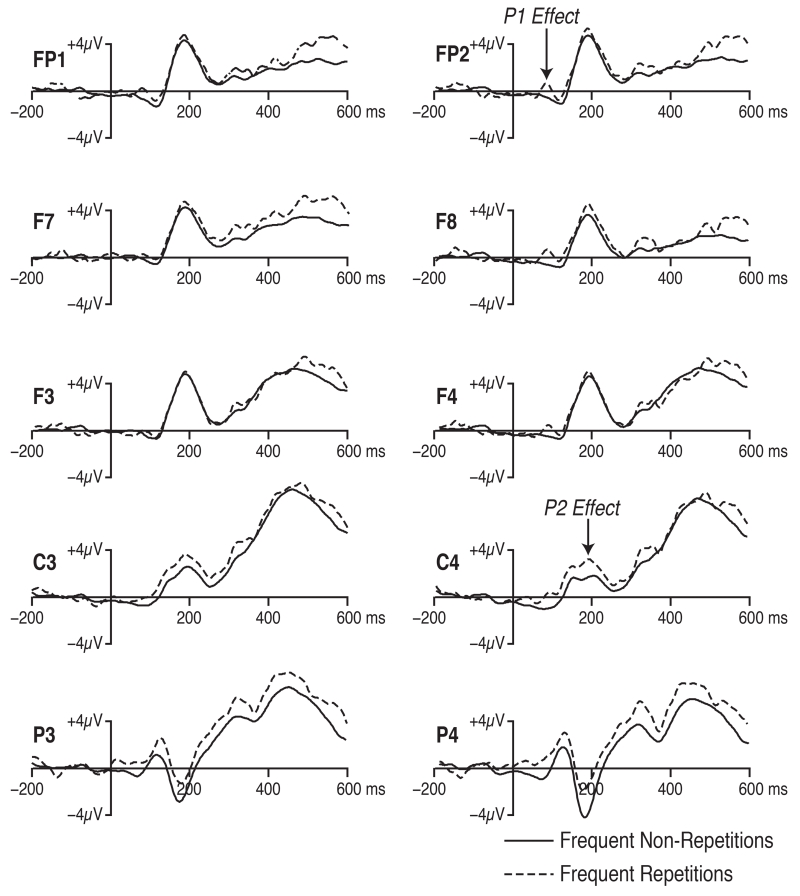
Figure 2 shows the grand average waveforms for the frequent repetitions and the frequent non-repetitions. There were two clear differences in the waveforms between these trial types. First, repetitions elicited a larger P1 wave than non-repetitions, especially over the right hemisphere. Second, repetitions elicited a larger P2 wave at the central and parietal electrode sites. We performed standard analyses to determine whether these effects were statistically significant.

Figure 2.

Grand average waveforms for the frequent repetitions and frequent non-repetitions. Repetitions yielded a larger P2 wave over posterior scalp sites (the P2 effect) and a larger P1 wave over the right hemisphere (the P1 effect).

In these analyses, P1 amplitude was quantified as the mean voltage between 50 and 150 ms poststimulus, and the amplitude measures were analyzed in a three-way analysis of variance (ANOVA) with factors of trial type (repetition versus non-repetition), electrode hemisphere (left versus right), and within-hemisphere electrode position (frontal pole, lateral frontal, mid frontal, central, or parietal). The effect of trial type was only marginally significant (p = .051), but the interaction between trial type and hemisphere was significant (p = .011). Because of the significant interaction, follow-up comparisons were performed in which the data from the left and right hemisphere sites were analyzed in separate ANOVAs. The effect of trial type was significant for the right hemisphere (p = .031) but not for the left hemisphere. These results are consistent with the observation that the P1 at right hemisphere electrode sites was larger for the repetitions than for the non-repetitions.

P2 amplitude was quantified as the mean voltage between 150 and 250 ms poststimulus at the central and parietal electrode sites, and the amplitude measures were again analyzed in an ANOVA with factors of trial type, electrode hemisphere, and within-hemisphere electrode position. The effect of trial type was significant (p = .026), supporting the observation that the P2 was larger for the repetitions than for the non-repetitions at the central and parietal electrodes.

Together, the P1 and P2 results indicate that repetitions of specific exemplars of the frequent category are detected even when this is not required by the task. Further, these results indicate that the repetition happens rapidly (within approximately 100 ms of stimulus onset) and also impacts later processing (ca. 200 ms).

One might be concerned that many fewer trials contributed to the averaged ERP waveforms for the repetition waveforms than for the non-repetition waveforms. However, this is not actually a problem given that mean amplitude, rather than peak amplitude, was used to quantify the components. Mean amplitude is an unbiased measure, which means that it is equally likely to be larger or smaller than the true value and is not more likely to produce consistently larger values in noisier waveforms (see Luck, 2014).

Actual Design and Bogus Results

Although the analyses we have presented follow common practices, and might not be criticized in a journal submission, our analysis strategy was seriously flawed. The statistically significant effects were, in fact, solely a result of random noise in the data. Ordinarily, one cannot know whether a set of significant effects are real or bogus, but we know with completely certainty that any effects involving stimulus repetition in the present experiment were bogus because there was not actually a manipulation of stimulus repetition. This was just a cover story to make the data analysis sound plausible. Instead of manipulating repetitions versus non-repetitions, we randomly sorted the frequent stimuli for each subject into a set of 512 trials that we arbitrarily labeled “non-repetitions” and 128 trials that we arbitrarily labeled “repetitions.” In other words, we simulated an experiment in which the null hypothesis was known to be true: The “repetition” and “non-repetition” trials were selected at random from the same population of trials. Thus, we know that the null hypothesis was true for any effects involving the “trial type” factor, and we know with certainty that the significant main effect of trial type for the P2 wave and the significant interaction between trial type and hemisphere for the P1 wave are bogus effects. This also means that our conclusions about the presence and timing of repetition effects are false.

The problem with our strategy for analyzing this data set is that we used the observed grand average waveforms to select the time period and electrode sites that were used in the analysis. Even though this was a relatively simple ERP experiment, there were so many opportunities for noise to create bogus differences between the waveforms that we were able to find time periods and electrode sites where these differences were statistically significant. There is nothing special about this experiment that allowed us to find bogus differences; almost any ERP experiment will yield such a rich data set that noise will lead to statistically significant effects if the choice of analysis parameters is based on the observed differences among the waveforms.

The Problem of Multiple Implicit Comparisons

This approach to data analysis leads to the problem of multiple implicit comparisons (Luck, 2014): the experimenter is implicitly making hundreds of comparisons between the observed waveforms by visually comparing them and performing explicit statistical comparisons only for the time regions and scalp regions in which the visual comparisons indicate that differences are present. To show how this problem arises, we re-analyzed the data from the aforementioned experiment in a way that makes the problem of multiple comparisons explicit. Specifically, we performed a separate t test at each individual time point and at each electrode site to compare the “repetition” and “non-repetition” waveforms. This yielded hundreds of individual p values, many of which indicated significant differences between the “repetition” and “non-repetition” waveforms. It is widely known that this strategy is inappropriate and leads to a high rate of false positives. If we had tried to publish the results with hundreds of individual t tests and no correction for multiple comparisons, any reasonable reviewer would have cited this as a major flaw and recommended rejection. Indeed, none of the differences remained significant when we applied a Bonferroni correction for multiple comparisons.

Although it is widely understood that performing large numbers of explicit statistical comparisons leads to a high probability of bogus differences, it is less widely appreciated that researchers are implicitly conducting multiple comparisons when they use the observed ERP waveforms to guide their choice of explicit statistical comparisons. This is exactly what we did in the aforementioned experiment: We looked at the grand average waveforms, saw some differences, and decided to conduct statistical analyses of the P1 and P2 waves using specific time ranges and electrode sites that showed apparent differences between conditions. In other words, differences between the waveforms that were entirely due to noise led us to focus on specific time periods and electrode sites, and this biased us to find significant-but-bogus effects in a small number of explicit statistical analyses. Using the grand averages to guide the analyses in this manner leads to the same end result as performing hundreds of explicit t tests without a correction for multiple comparisons—namely a high rate of spurious findings—and yet it is very easy to “get away with” this approach when publishing ERP studies. Similar issues arise in fMRI research (Vul, Harris, Winkielman, & Pashler, 2009).

If we had submitted a paper with the small set of ANOVA results described earlier, we could have told a reasonably convincing story about why we expected that the P1 and P2 waveforms would be sensitive to the detection of task-irrelevant stimulus repetitions (which is known as hypothesizing after the results are known or HARKing – see Kerr, 1998). Moreover, we could have concluded that repetitions are detected as early as 100 ms poststimulus, and it is plausible that the paper would have been accepted for publication. Thus, completely bogus differences that are a result of random variation could easily lead to effects that are convincing and possibly publishable, especially if they are described as “predicted results” rather than post hoc findings.

Thus, an unethical researcher who wishes to obtain “publishable effects” in a given experiment regardless of whether the results are real would be advised to look at the grand averages, find time ranges and electrode sites for which the conditions differ, measure the effects at those time ranges and electrode sites, report the statistical analyses for those measurements, and describe the data as fitting the predictions of a “hypothesis” that was actually developed after the waveforms were observed. However, a researcher who wants to avoid significant-but-bogus effects would be advised to focus on testing a priori predictions without using the observed data to guide the selection of time windows or electrode sites, treating any other effects (even if highly significant) as being merely suggestive until replicated.

How to Avoid Biased Measurement and Analysis Procedures

In this section, we will describe several approaches that can be taken to avoid the bogus findings that are likely to occur if the grand average waveforms are used to guide the measurement and analysis procedures (see Luck, 2014 for additional discussion). First, however, we would like to note that there is a tension between the short-term desire of individual researchers to publish papers and the long-term desire of the field as a whole to minimize the number of significant-but-bogus findings in the literature. Most approaches for reducing the Type I error rate will simultaneously decrease the number of significant and therefore publishable results. Moreover, many of these approaches will decrease statistical power, meaning that the rate of Type II errors (false negatives) will increase as the rate of Type I errors (false positives) decreases. It is therefore unrealistic to expect individual researchers—especially those who are early in their careers—to voluntarily adopt data analysis practices that are good for the field but make it difficult for them to get their own papers published. The responsibility therefore falls mainly on journal editors and reviewers to uniformly enforce practices that will minimize the Type I error rate. The need for editors and reviewers to enforce these practices is one of the key points of the recently revised publication guidelines of the Society for Psychophysiological Research (Keil, Debener, Gratton, Junhöfer, Kappenman, Luck, Luu, Miller, & Yee, 2014).

A Priori Measurement Parameters

When possible, the best way to avoid biasing ERP component measurement procedures toward significant-but-bogus effects is usually to define the measurement windows and electrode sites before seeing the data. However, this is not always possible. For example, the latency of an effect may vary across studies as a function of low-level sensory factors, such as stimulus luminance and discriminability, making the measurement windows from previous studies inappropriate for a new experiment. Also, many studies are sufficiently novel that prior studies with similar methods are not available to guide the analysis parameters. There are several alternative approaches for these cases.

Functional Localizers

One approach, which is popular in neuroimaging research, is to use a “functional localizer” condition to determine the time window and electrode sites for a given effect. For example, an experiment that uses the N170 component to examine some subtle aspect of face processing (e.g., male faces versus female faces) could include a simple face-versus-nonface condition; the timing and scalp distribution of the N170 from the face-versus-nonface condition could then be used for quantifying N170 amplitude in the more subtle conditions. An advantage of this approach is that it can take into account subject-to-subject differences in latency and scalp distribution, which might be more sensitive than the usual one-size-fits-all approach. A disadvantage, however, is that it assumes that the timing and scalp distribution of the effect in the functional localizer condition is that same as in the conditions of interest, which may not be true (see Friston, Rotshtein, Geng, Sterzer, & Henson, 2006 for a description of the potential shortcomings of this approach in neuroimaging).

Collapsed Localizers

A related approach, which is becoming increasingly common, is to use a collapsed localizer. In this approach, the researcher simply averages the waveforms across the conditions that will ultimately be compared and then uses the timing and scalp distribution from the collapsed waveforms to define the analysis parameters that will be used for the non-collapsed data. For example, in an experiment designed to assess the N400 in two different conditions, the data could first be averaged across those two conditions, and then the time range and electrode sites showing the largest N400 activity could be used when measuring the N400 in the two conditions separately. There may be situations in which this approach would be problematic (see Luck, 2014), but it is often the best approach when the analysis parameters cannot be set on the basis of prior research.

Window-Independent Measures

Some methods for quantifying ERP amplitudes and latencies are highly dependent on the chosen time window, and other methods are relatively independent (see Luck, 2014). For example, mean amplitude can vary by a great deal depending on the measurement window, whereas peak amplitude is less dependent on the precise window, especially when the largest peak in the waveform is being measured. Mean amplitude is typically superior to peak amplitude in other ways, however, such as sensitivity to high-frequency noise (Clayson, Baldwin, & Larson, 2013; Luck, 2014). Nonetheless, it may be appropriate to use peak amplitude when there is no good way of determining the measurement window for measuring mean amplitude. Another approach is to show that the statistical significance of a mean amplitude effect doesn’t depend on the specific measurement window (see, e.g., Bacigalupo & Luck, 2015).

The Mass Univariate Approach

Another approach is the mass univariate approach, in which a separate t test (or related statistic) is computed at every time point for every electrode site and some kind of correction for multiple comparisons is applied to control the overall Type I error rate. The traditional Bonferroni correction is usually unreasonably conservative, but a variety of other correction factors are now available (Groppe, Urbach, & Kutas, 2011a; Maris & Oostenveld, 2007) and are implemented in free, open-source analysis packages, such as the Mass Univariate Toolbox (Groppe, Urbach, & Kutas, 2011b) and FieldTrip (Oostenveld, Fries, Maris, & Schoffelen, 2011). These approaches are still fairly conservative, but they may be the best option when no a priori information is available to guide the choice of latency windows and electrode sites.

Mathematical Isolation of the Latent Components

Another approach is to use a method that attempts to mathematically isolate the underlying latent ERP components. For example, techniques such as source localization, independent component analysis, and spatial principal component analysis attempt to quantify the magnitude of the underlying component at each time point, eliminating the need to select specific electrode sites for analysis. Similarly, temporal principal component analysis attempts to quantify the magnitude of the underlying component across each type of trial, eliminating the need to select specific time windows for analysis.

Replication

The final and most important approach is simple, old-fashioned replication. If there is no a priori basis for selecting a time window and set of electrode sites, a second experiment can be run that demonstrates the replicability of the findings with the same analysis parameters. The second experiment will not typically be an exact replication of the first experiment, but will instead add something new (e.g., showing that the results generalize to somewhat different conditions).¹

Do Published Papers Actually Justify Their Measurement Parameters?

According to the latest publication guidelines of the Society for Psychophysiological Research, “measurement windows and electrode sites must be well justified” (Keil et al., 2014, p. 7) using one of the approaches just described or some other clear and compelling method. To assess how well this guideline is being followed, we conducted an informal analysis of the papers published in Psychophysiology during the first six months of 2015. We selected all of the papers that met the following three criteria: 1) Empirical studies (excluding review papers and methodology papers); 2) Focused on ERPs (rather than other psychophysiological measures); 3) Univariate ANOVAs used as the primary statistical approach (so that statistical practices could be assessed in a subsequent section of this paper). Fourteen papers met these criteria for inclusion. Ten of these papers provided a clear a priori justification for the choice of time windows and electrode sites or used methods that are insensitive to or independent of the choice of time windows and electrode sites. However, four of the papers provided no justification or only a vague justification (e.g., an appeal to the literature without citing any specific papers). In some cases, visual inspection of the observed waveforms was explicitly cited as a part of the justification, even though this is exactly what should be avoided in most cases.

Although our analysis of these papers in Psychophysiology was based on a relatively small sample of papers, it does indicate that authors, editors, and reviewers are not always following the requirement that a good justification must be provided for measurement windows and electrode sites. It is also worth noting that 12 of the 14 papers included only a single experiment, making it impossible to assess the replicability of the observed results. Thus, relatively few papers in this journal are using the most powerful approach to demonstrating the robustness of their findings, namely replication.

Factorial ANOVAs and Familywise/Experimentwise Error Rates

Defining Familywise and Experimentwise Error Rates

In addition to the problem of multiple implicit comparisons, ERP studies often involve a problem of multiple explicit comparisons that can be highly problematic but is not usually recognized. Specifically, ERP studies often involve conducting two or more multi-factor ANOVAs, leading to several main effects and interactions that are tested with no correction for multiple comparisons. The probability of a Type I error for one or more effects in a set of related analyses (e.g., the main effects and interactions from a single ANOVA) is called the familywise error rate. For example, each three-way ANOVA used to analyze the experiment shown in Figures 1 and 2 involved seven main effects and interactions, leading to a familywise error rate of over 30%. This means that the chance of obtaining one or more significant-but-bogus results from among the seven effects in each three-way ANOVA was >30% and not the 5% that one might expect.

Similarly, the probability of a Type I error for one or more effects across all the analyses performed for a given experiment is called the experimentwise error rate. Two three-way ANOVAs were reported for this experiment, and the experimentwise error rate was over 50%. In other words, although there were no true effects for any of the 14 main effects and interactions that were assessed in this experiment, the chance of finding at least one significant-but-bogus effect was approximately 50%. Thus, even if we had used a priori time windows and electrode sites, we would have had a 50% chance of finding a significant-but-bogus effect and not the 5% chance that one ordinarily expects. This does not reflect something unique about the experiment shown in Figures 1 and 2; the experimentwise error rate would be approximately 50% for any experiment that was analyzed using two three-way ANOVAs. This problem does not seem to be widely recognized, so we will provide a detailed discussion and some simple simulations to make the problem clear (see also Cramer, van Ravenzwaaij, Matzke, Steingroever, Wetzels, Grasman, Waldorp, & Wagenmakers, 2015).²

Post Hoc Corrections for Multiple Comparisons

Virtually every graduate-level ANOVA course includes a discussion of the problem of multiple comparisons, along with the Bonferroni and Scheffé corrections. Often this is raised in the context of follow-up analyses for factors that contain more than two levels. For example, if Factor A of an experiment has three conditions—A₁, A₂, and A₃—and a significant effect of Factor A is found, follow-up analyses can be conducted to compare A₁ with A₂, to compare A₂ with A₃, or to compare A₁ with A₃. The more such comparisons are performed, the greater is the likelihood that one or more of them will yield a significant-but-bogus result, and the overall probability of a Type I error (i.e., a false positive) will exceed the nominal .05 level. A correction is therefore applied so that the overall probability of a Type I error will remain at the .05 level. However, the standard advice is that a correction is not necessary for planned comparisons.

Although this conceptualization of the problem of multiple comparisons is widely taught, it is much less common for courses to consider the problem of multiple comparisons that arises within a single ANOVA with multiple factors. For example, in a simple 2 × 2 experiment with Factor A and Factor B, the ANOVA will yield three p values: one for the main effect of Factor A, one for the main effect of Factor B, and one for the A × B interaction. If the null hypothesis is true for both of the main effects and the interaction, this analysis provides three opportunities to obtain a significant-but-bogus effect. The likelihood that at least one of these three effects will be significant is not 5%, but is actually close to 14%. However, researchers do not usually provide a correction for multiple comparisons, presumably because the main effects and interactions in an ANOVA are treated as planned rather than unplanned comparisons.

Computing the Familywise and Experimentwise Error Rates

The probability of obtaining one or more significant-but-bogus effects in factorial ANOVA can be computed using simple probability theory. If c independent statistical comparisons are performed, and we call the single-test error rate α_s (typically .05), the combined alpha for the c comparisons will be can be defined as follows:

$$\text{Combined alpha for}\mathit{c}\text{tests}=1-{(1-{\alpha }_{\mathit{s}})}^{\mathbf{c}}$$

For example, if you conduct 3 statistical tests, and the null hypothesis is actually true for all 3, the chance that one or more of the tests will yield a significant result is as follows:

$$\text{Combined alpha for}3\text{tests}=1-{(1-.05)}^3=1-{.95}^3=.14$$

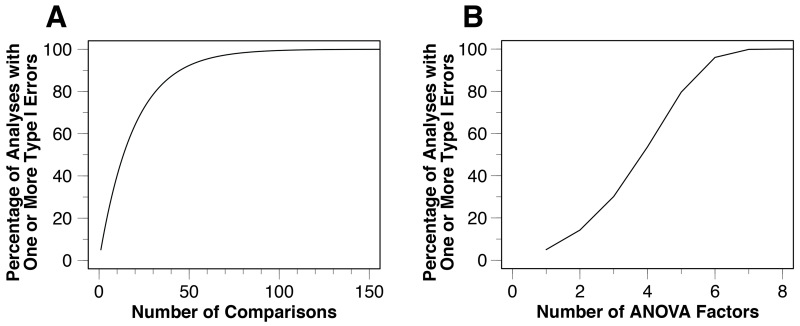
The relationship between the number of statistical tests and combined alpha is shown graphically in Figure 3A. Note that the combined alpha could be either the familywise alpha (when the number of tests used in the equation is the number of main effects and interactions in a single ANOVA) or the experimentwise alpha (when the number of tests used in the equation is the total number of main effects and interactions across all the statistical analyses in an experiment).

Figure 3.

Familywise Type I error rate as a function of the number of statistical comparisons in a set of related tests (A) and as a function of the number of factors in a given ANOVA (B).

The number of independent tests (main effects and interactions) in an ANOVA with f factors is f² − 1, so the equation for determining the familywise alpha level (α_f) for a factorial ANOVA with f factors is as follows:

$$\text{Familywise}\alpha \text{for}\mathbf{ANOVA}\text{with}\mathit{f}\mathbf{factors}=1-{(1-{\alpha }_{\mathit{s}})}^{({\mathbf{f}}^2-1)}$$

For a 3-factor ANOVA, this would give us:

$$\text{Familywise}\alpha \text{for}3-\text{way}\mathbf{ANOVA}=1-{(1-.05)}^{(3^2-1)}=1-{.95}^8=1-.663=.337$$

When multiple ANOVAs are conducted, the total number of statistical tests is simply the sum of the number of tests for the individual ANOVAs. For example, if you conduct an experiment with two 3-way ANOVAs, each ANOVA involves 7 main effects and interactions, leading to 14 total tests that contribute to the experimentwise error. This gives us

$$\text{Experimentwise error for an experiment with}14\text{tests}=1-{(1-.05)}^{14}=.512$$

This relationship between the number of factors and the combined error rate is shown graphically in Figure 3B.

Note that the above equations require the assumption that all of the effects are independent (uncorrelated), which will be approximately correct for null effects. There will be some small correlations as a result of finite sample sizes, so these equations slightly overestimate the true overall alpha rate in most real experiments (Cramer et al., 2015).

Effects of Large Numbers of ANOVA Factors in ERP Research

Researchers do not typically apply a correction for multiple comparisons in factorial ANOVAs, under the implicit assumption that all of the main effects and interactions are effectively planned comparisons. That may be a reasonable assumption in a two-way ANOVA, but it is unlikely that a researcher has a priori hypotheses about all 15 main effects and interactions that are computed for a four-way ANOVA. Moreover, the number of main effects and interactions increases exponentially as the number of factors in the ANOVA increases, and the likelihood of a false positive can become very high. This is illustrated in Table 1 and Figure 3B, which show that the probability of one or more significant-but-bogus effects exceeds 50% in a four-way ANOVA and approaches 100% with a seven-way ANOVA (when the null hypothesis is true for all effects).

Table 1. Number of effects (main effects and interactions) and approximate familywise Type I error rate for ANOVA designs with different numbers of factors.

Number of Factors	1	2	3	4	5	6	7	8
Number of Effects	1	3	7	15	31	63	127	255
Familywise Type I Error Rate	0.05	0.1426	0.3017	0.5367	0.7961	0.9605	0.9985	1.0000

With enough factors in an ANOVA, researchers are virtually guaranteed that at least one effect will be statistically significant. Thus, a researcher who wishes to obtain “something significant” in a given experiment—irrespective of whether the effects are real—would be advised to include as many factors as possible in the ANOVA. However, a researcher who wants to avoid significant-but-bogus effects—and promote real scientific progress—would be advised to include as few factors as possible.

Common approaches to the statistical analysis of ERP experiments tend to lead to very high familywise and experimentwise error rates. These error rates are elevated in many ERP analyses relative to behavioral analyses because each condition of an experiment that yields a single behavioral measurement may yield many ERP measurements because multiple different components may be measured, because the amplitude and the latency may be measured for each component, and because each component may be measured at multiple electrode sites.

This is a very common issue in ERP studies, including our own. To take an extreme example, consider a paper published by Luck & Hillyard (1994a) in Psychophysiology that provided a detailed analysis of several different ERP components in a set of visual search tasks. The analysis of the first experiment alone involved four 5-factor ANOVAs, three 4-factor ANOVAs, and three 3-factor ANOVAs, for a total of 190 individual p values. The experimentwise error rate for an experiment with 190 p values is close to 100%, so it is a near certainty that at least one of the significant effects in that experiment was bogus. Of course, this was an exploratory study, and many of the key effects were replicated in subsequent experiments. Nonetheless, this example demonstrates that it is possible to publish ERP studies with an extremely high experimentwise error rate in a journal that has a reputation for methodological rigor.

To go beyond this single anecdote, we examined the aforementioned set of 14 ERP studies published in Psychophysiology during the first six months of 2015. Three of these 14 papers reported at least one four-way ANOVA (and one of these three papers included 5 four-way ANOVAs, along with 8 two-way ANOVAs). Three additional papers reported between 3 and 5 three-way ANOVAs each. Of the 14 papers, 12 reported at least 10 different statistical tests and the remaining two papers included 6 or 7 statistical tests each. Following standard practice, no correction for multiple comparisons was applied in any of these analyses. This does not mean that the authors of these papers did anything wrong or that their conclusions are incorrect. However, it does demonstrate that the number of independent statistical tests is quite high in the kinds of ERP papers published in this journal.

Simulations of Familywise Error Rates in Factorial ANOVAs

The Simulation Approach

To provide a concrete demonstration of how familywise error rates play out in factorial ANOVAs in a typical ERP study, we simulated a hypothetical experiment in which the late positive potential (LPP) was measured for stimuli with varying emotional content in two different groups of participants (N = 30 per group). The nature of the groups does not matter for this simulation, nor does it matter that the simulation included both between- and within-group effects. The key is that the study is reflects the number of factors that is found in many ERP studies.

In the simulated experiment, participants performed an oddball task in which they viewed photographs and pressed one of two buttons on each trial to indicate whether the photograph showed an affectively positive scene (e.g., a cute baby) or an affectively negative scene (e.g., a dead animal). In half of the trial blocks, positive scenes were frequent (80%) and negative scenes were rare (20%), and this was reversed in the remaining trial blocks. Half of the simulated participants in each group responded with a left-hand buttonpress for the positive scenes and with a right-hand buttonpress for the negative scenes, and this was reversed for the other half (for counterbalancing purposes). Simulated measurements of LPP amplitude were from 18 electrode sites (Fp1, Fpz, Fp2, F3, Fz, F4, FC3, FCz, FC4, C3, Cz, C4, CP3, CPz, CP4, P3, Pz, P4). Following common practice, the data were collapsed across nearby electrode sites to form frontal, central, and parietal electrode clusters. This design yielded four main factors: a between-participants factor of group (patient versus control) and within-participant factors of stimulus probability (rare versus frequent), stimulus valence (positive versus negative), and anterior-posterior electrode cluster (frontal, central, and parietal). There was also a fifth counterbalancing factor of stimulus-response mapping (left versus right hand for positive valence stimuli).

Simulated experiments such as this are valuable in three main ways. First, whereas the true effects are unknown in real experiments, we know the truth (i.e., the population means) in simulations. Second, simulations allow us to see what would happen if we conducted the same experiment many times, allowing us to see how often real effects are found to be statistically significant (the true positive rate) and how often null effects are found to be statistically significant (the false positive rate, which is the same as the Type I error rate). Third, these simulations do not require assumptions about the independence of the statistical tests and therefore provide a more accurate estimate of the false positive rate.

In our simulations, the R statistical package (R Core Team, 2014) was used to generate simulated amplitude and latency values for each participant in each condition (as if they were measured from the averaged ERP waveforms of the individual participants). For the sake of simplicity, the simulated data exactly matched the assumptions of ANOVA: the values were sampled from normal distributions with equal variances and covariances. These assumptions would likely be violated in the LPP experiment, which would likely increase the rate of Type I errors even further (Jennings & Wood, 1976). We examined two different possible patterns of results, and we simulated 10,000 experiments for each of these patterns. In each simulation, we randomly sampled the values for each participant in each condition from the relevant probability distributions and conducted an ANOVA. Following the typical convention, a given effect was classified as statistically significant if the p value for that effect was less than .05 (i.e., the alpha level was set at .05). By asking how often significant effects were obtained across these 10,000 experiments, we can determine the true positive and false positive rates.

Simulation Results for the Case of All Null Effects

In the first set of simulations, there were no true main effects or interactions. The population mean for LPP amplitude was exactly 5 μV at each electrode site in each condition. Likewise, the population mean for LPP latency was 400 ms at each electrode site in each condition. This is clearly unrealistic, because the LPP would ordinarily vary in amplitude and latency across electrode sites, but this simulation allowed us to assess the number of Type I errors that would be found if the null hypothesis were true for all effects (which should approximately match the formulae given earlier). Observed means for each cell of the design are presented for 1 of the 10,000 simulated experiments in Table S1 (available in online supplementary materials). Most of the observed means were fairly close to the true population mean of 5.0 μV, but some differed considerably simply by chance.

In our statistical analyses of the data from each of these simulated experiments, we began by conducting a four-way ANOVA on mean amplitude with the factors described above, excluding the counterbalancing factor (stimulus-response mapping). This led to 15 separate main effects and interactions. Table 2 shows the proportion of experiments in which each main effect and interaction was found to be significant, as well as the proportion of experiments in which one or more effects was found to be significant (the familywise error rate). For any given effect, the probability of a significant effect was very close to 5%, which is exactly what should happen when the null hypothesis is true, given an alpha level of .05. In fact, the probability of Type I error averaged across all main effects was exactly 5.0%. In other words, if you do experiments with four-way ANOVAs, but you look at only one of the effects (e.g., the Group × Probability interaction) and ignore any other significant effects, you will obtain a false positive for this one effect in only 5% of your experiments. However, if you look at all 15 main effects and interactions, the likelihood that at least one of these effects is significant (but bogus) will be much higher. Indeed, we found at least one significant effect in 5,325 of our 10,000 simulated experiments, which is a familywise false positive rate of approximately 53.3% (which is nearly identical to the predicted rate of 53.7%). In other words, even though there were no real effects, more than half of experiments yielded at least one significant-but-bogus effect. Moreover, if we included the counterbalancing variable (stimulus-response mapping) as a fifth factor in the ANOVA, approximately 79.1% of the experiments yielded at least one significant-but-bogus effect.

Table 2. Number and Percentage of Significant Effects (p < .05) for Each Factor Combination in a 4-Way ANOVA of Simulated Data with All Null Main Effects and Interactions.

ANOVA Factor	Number of Simulations with Significant Effects	Percentage of Simulations with Significant Effects
AP	500	5.0%
G	495	5.0%
SP	536	5.4%
SV	503	5.0%
AP × G	497	5.0%
SP × AP	469	4.7%
SP × G	518	5.2%
SP × SV	484	4.8%
SV × AP	499	5.0%
SV × G	516	5.2%
SP × AP × G	479	4.8%
SP × SV × AP	488	4.9%
SP × SV × G	525	5.3%
SV × AP × G	511	5.1%
SP × SV × AP × G	503	5.0%
Average	502	5.0%
Experiments with a Type I Error	5325	53.3%

Note. G = Group, SP = Stimulus Probability, SV = Stimulus Valence, AP = Anterior-Posterior Electrode Cluster.

In a real experiment of this nature, the key result would be a main effect of Group or an interaction between Group and one or more of the other factors. We therefore asked how many of our simulated experiments yielded a significant Group main effect or at least one interaction involving Group. With the four-way ANOVA shown in Table 2, 36.8% of experiments yielded a significant-but-bogus effect involving the Group factor. If we included the counterbalancing factor as a fifth variable, this likelihood rose to 58.5%. Thus, even when we limited ourselves to group-related effects, there was still a high likelihood of obtaining a significant-but-bogus effect.

As revealed by our literature review, many studies include multiple ANOVAs, and this will further boost the likelihood of obtaining a false positive. To demonstrate this, we conducted a four-way ANOVA on peak latency in addition to the four-way ANOVA on mean amplitude. Together, these two ANOVAs yielded 62 main effects and interactions, producing an experimentwise false positive rate of 78.0%. When we added the counterbalancing variable and conducted the amplitude and latency ANOVAs, the experimentwise false positive rate rose further to 95.7%.

Simulation Results for the Case of a Mixture of True and Null Effects

We performed a second set of simulations that was more realistic because it contained some true effects for both LPP amplitude and LPP latency. In this simulation, LPP amplitude was 50% larger for rare stimuli than for frequent stimuli and was progressively larger at more posterior electrode sites, but with no other effects (see Table 3 for the population means). Note, however, that the probability and electrode site effects were proportional rather than additive, as would be true with real ERP data, and this created a probability by electrode cluster interaction (McCarthy & Wood, 1985). For the sake of simplicity, we did not perform a normalization procedure to deal with this interaction. In addition, LPP latency was 25 ms longer in the rare condition than in the frequent condition and was also progressively longer at more posterior electrode sites (see Table 3). The probability effect on latency was greater for rare than for frequent stimuli, producing an electrode cluster by stimulus probability interaction. We again simulated 10,000 experiments with this pattern, running ANOVAs for each simulation.

Table 3. Population Means (amplitude and latency) for Each Combination of Stimulus Probability and Electrode Cluster in the Second Simulation.

Stimulus Probability	Measure	Electrode Cluster
		Frontal	Central	Parietal
Frequent	Amplitude (μV)	2.0	4.0	6.0
	Latency (ms)	400	425	450
Rare	Amplitude (μV)	3.0	6.0	9.0
	Latency (ms)	400	450	500

We first replicated the four-way ANOVA on mean amplitude, which collapsed across the counterbalancing variable. We found that the main effect of probability, the main effect of anterior-posterior electrode cluster, and the interaction between these factors were statistically significant in 100% of the simulated experiments. This is what would be expected, because these were real effects with large effect sizes. The 28 other main effects and interactions were null effects, and each of these effects considered alone yielded a significant effect in approximately 5% of the simulated experiments. When considered together, however, at least one of these 28 null effects was significant in 46% of the experiments (4,629 out of 10,000 experiments). In other words, approximately half the experiments yielded at least one significant-but-bogus effect in addition to the true positive effects. When two ANOVAs were run for each experiment, one for amplitude and one for latency, the experimentwise false positive rate rose to 71.2%. We then added the counterbalancing variable to our analysis, yielding 2 five-way ANOVAs. The experimentwise false positive rate rose even higher to 94.3%. Thus, even under more realistic conditions in which several true effects were present, null effects were statistically significant in a large percentage of the simulated experiments.

Together, these simulations clearly demonstrate that ERP experiments will have a high likelihood of finding significant-but-bogus effects if they involve large numbers of statistical tests as a result of multi-factor ANOVAs, especially if more than one ANOVA is conducted for a given experiment.

Reducing the Familywise and Experimentwise Error Rates

One approach to dealing with the high familywise error rate that occurs in ANOVAs with several factors would be to apply an explicit correction for multiple comparisons. A variety of correction approaches are now available, each with its own assumptions, strengths, and weaknesses (see Groppe et al., 2011a for an excellent discussion). However, mathematical corrections will inevitably decrease the statistical power of an experiment, so this section will describe some alternative approaches.

Reducing the Number of Factors

An alternative solution that does not reduce statistical power is to simply reduce the number of factors in a given ANOVA. For example, factors that are simply used for counterbalancing should be left out of the ANOVA (e.g., the stimulus-response mapping factor in the simulated experiment described in the previous section).

In addition, it is often possible to eliminate factors that are a part of the design but are not necessary for testing the main hypotheses of the study. In the present example, we could eliminate the electrode cluster factor and instead collapse the measures across all the electrode sites (or measure from a single cluster if based on an a priori assumption about the cluster at which the component is present). We reanalyzed the data from our second set of simulations (with the population means shown in Table 3) to determine how well this would reduce the familywise error rate. We simply took the single-participant amplitude measurements from the previous simulation and averaged them across the three electrode clusters (frontal, central, and parietal).³ We then performed a three-way ANOVA for each simulated experiment with factors of group, stimulus probability, and stimulus valence. Because we collapsed across electrode sites, the only true effect in this simulation was the main effect of probability, and we found that this main effect was significant in 100% of the simulations. The only remaining effects tested in the ANOVA were the main effect of group, the main effect of valence, the three two-way interactions, and the three-way interaction. The null hypothesis was true for all six of these effects, and one or more of these effects was significant in 26.8% of the simulated experiments (or 18.7% of experiments if we limited ourselves to Group-related effects). This is still a fairly high familywise error rate, but it is much better than the 53.3% familywise error rate obtained when the same data were analyzed with a 4-way ANOVA (or the 79.1% error rate we obtained with a 5-way ANOVA).

Using Difference Scores to Eliminate Factors from an ANOVA

In the previous example, the number of factors was reduced by average across the levels of one factor (i.e., averaging across the electrode sites). A related approach is to take the difference between two levels of a factor and perform the analyses on these difference scores. In the simulated experiment, for example, the ANOVA could be performed on measurements taken from rare-minus-frequent difference waves, eliminating the stimulus probability factor. When we applied this approach to the present simulation, using a two-way ANOVA to analyze the rare-minus-frequent difference scores after averaging across electrode sites, the familywise error rate dropped to 14.0% of experiments (9.6% if we limited ourselves to Group-related effects).

This difference-based strategy is already widely used in some areas of ERP research. Consider, for example, the N2pc component, which is typically defined as the difference in amplitude between electrode sites that are contralateral versus ipsilateral to a target object in a visual stimulus array. In early studies, the N2pc was analyzed statistically by looking for an interaction between stimulus side and electrode hemisphere (see, e.g., Luck & Hillyard, 1994a, 1994b). To determine whether N2pc amplitude was larger for one condition than for another, it was then necessary to look for a 3-way interaction between condition, stimulus side, and electrode hemisphere. If within-hemisphere electrode site was also included as a factor in in the ANOVA, this required a four-way ANOVA with 15 total main effects and interactions, yielding a familywise Type I error rate of approximately 50%.

Over the years, there has been a clear movement away from this approach. Instead, N2pc amplitude is measured from contralateral-minus-ipsilateral difference waves that have been collapsed across both hemispheres and often collapsed across a cluster of within-hemisphere electrodes as well (Eimer & Kiss, 2008; Hickey, McDonald, & Theeuwes, 2006; Sawaki, Geng, & Luck, 2012). This eliminates three factors from the analysis, often allowing the data to be analyzed with a simple t test or a two-way ANOVA, which dramatically reduces the familywise Type I error rate. The same contralateral-minus-ipsilateral approach is also commonly used for the lateralized readiness potential (Smulders & Miller, 2012) and for contralateral delay activity (Perez & Vogel, 2012). In addition, the mismatch negativity is often measured from rare-minus-frequent difference waves (Alain, Cortese, & Picton, 1998; Javitt, Grochowski, Shelley, & Ritter, 1998; Näätänen, Pakarinen, Rinne, & Takegata, 2004), and the P3 wave is occasionally analyzed this way (Luck et al., 2009; Vogel, Luck, & Shapiro, 1998). Statistical analyses of difference scores were used in several of the 14 papers published in Psychophysiology that were discussed above.

Eliminating unnecessary analyses

Whereas reducing the number of factors within a given analysis reduces the familywise error rate for a given analysis, it is possible to reduce the experimentwise error rate by eliminating unnecessary analyses altogether. For example, analyzing both amplitudes and latencies can double the experimentwise error rate, as will analyzing the data from two components instead of just one. If an experiment is designed to look at, for example, the amplitude of the P3 wave, any significant effects observed for P3 latency or for other components should be treated with caution and described as being exploratory.

Costs and Benefits of Reducing the Number of Factors

The obvious downside of reducing the number of ANOVA factors or the number of measures being analyzed is that a true effect might be missed. However, many of these effects will not be of great scientific interest. For example, hemispheric differences are very difficult to interpret in N2pc studies, so not much information is lost by collapsing across the left and right hemispheres. Other cases may not be so clear, and researchers will always need to balance the importance of avoiding Type I errors with the ability to find unexpected by potentially important effects.

More broadly, ERP researchers should focus their data analyses on the effects that are most important for testing the underlying theory. Many statistics textbooks encourage a hierarchical strategy, in which an omnibus ANOVA with all possible factors is conducted first, followed by follow-up analyses to decompose any significant effects observed in the omnibus ANOVA. This is not a good strategy from the perspective of minimizing the experimentwise Type I error rate. Instead, researchers should focus on the specific main effects and interactions that test the underlying theory, and they should treat any other significant effects as suggestive rather than conclusive. This strategy could also be encouraged by journal editors and reviewers. More generally, a good dose of clear thinking and logic would be an effective treatment for most of the causes of bogus-but-significant results described in this paper.

Replication and the Role of Reviewers and Editors

The most convincing way of demonstrating that a significant result is not bogus is to show that it replicates. Replications take time, and the short-term payoffs are not always very high for individual researchers. However, journal editors and reviewers can, in principle, demand replications of an experiment when the data analysis strategy seems likely to yield a high experimentwise Type I error rate (for more on the issue of replication, see Pashler & Harris, 2012). Replication of ERP results within a single paper does not seem to be as common as might be desired, at least in Psychophysiology, given that only 2 of the 14 papers that were examined in the analyses described earlier included more than a single experiment.

Some studies require a great deal of time and money to conduct (e.g., longitudinal studies, large-N patient studies), and it would be impractical to run a replication before publishing the results. However, most such studies are done as follow-ups to smaller, less expensive studies that can be used to define a priori data analysis parameters. For such studies, journal editors and reviewers should demand that these a priori parameters are well defined and extremely well justified. This has already been specified in the publication guidelines of the Society for Psychophysiological Research (Keil et al., 2014), but widespread adoption will require a change in practice among researchers, editors, and reviewers.

Given the potential for a massive inflation of the Type I error rate in ERP studies given the large number of degrees of freedom in selecting measurement windows and electrode sites, along with the common use of multifactor ANOVAs, it may be time for the field (or at least the journal Psychophysiology) to require that the main findings from every paper be replicated unless the authors make a compelling argument against the need for replication (e.g., because of cost, high statistical power, etc.). This would likely slow down the rate at which papers are published, and it would require an adjustment in our expectations for productivity, but it would probably speed the ultimate rate of scientific progress.