The Central Role of KNG1 Gene as a Genetic Determinant of Coagulation Pathway-Related Traits: Exploring Metaphenotypes

Abstract

Traditional genetic studies of single traits may be unable to detect the pleiotropic effects involved in complex diseases. To detect the correlation that exists between several phenotypes involved in the same biological process, we introduce an original methodology to analyze sets of correlated phenotypes involved in the coagulation cascade in genome-wide association studies. The methodology consists of a two-stage process. First, we define new phenotypic meta-variables (linear combinations of the original phenotypes), named metaphenotypes, by applying Independent Component Analysis for the multivariate analysis of correlated phenotypes (i.e. the levels of coagulation pathway–related proteins). The resulting metaphenotypes integrate the information regarding the underlying biological process (i.e. thrombus/clot formation). Secondly, we take advantage of a family based Genome Wide Association Study to identify genetic elements influencing these metaphenotypes and consequently thrombosis risk. Our study utilized data from the GAIT Project (Genetic Analysis of Idiopathic Thrombophilia). We obtained 15 metaphenotypes, which showed significant heritabilities, ranging from 0.2 to 0.7. These results indicate the importance of genetic factors in the variability of these traits. We found 4 metaphenotypes that showed significant associations with SNPs. The most relevant were those mapped in a region near the HRG, FETUB and KNG1 genes. Our results are provocative since they show that the KNG1 locus plays a central role as a genetic determinant of the entire coagulation pathway and thrombus/clot formation. Integrating data from multiple correlated measurements through metaphenotypes is a promising approach to elucidate the hidden genetic mechanisms underlying complex diseases.

Introduction

Considerable efforts have been invested to evaluate hundreds of genetic variants associated with human traits. Despite these efforts, the loci that have been identified only explain a small proportion of the total phenotypic variance. Thus, there is the question of where the remaining heritability resides. For a complex disease, such as thrombosis, traditional single-trait genetic studies may be unable to detect the pleiotropic effect that a given genetic variant could have on the intermediate phenotypes involved with the disease. In particular, the normal physiological process underlying thrombosis is complex and many of its components are involved in the coagulation and fibrinolysis pathways. These components form a collection of intermediate phenotypes that are generally measured in the study of thrombosis. These intermediate phenotypes may reflect more directly the effects from causal genes than disease status. They are also less genetically complex and more strongly associated with susceptibility loci.

So far, the genetic analyses of thrombosis have been carried out using one or more intermediate traits separately [1–7]. However, if a locus is associated with two or more traits, i.e. it is pleiotropic, a single-trait study may lose the power to detect this pleiotropic effect. However, finding disease risk indexes would contribute to a greater understanding of the pathogenesis of disease, and ultimately will develop better diagnostic, prevention and treatment strategies. In addition, the simultaneous analyses of multiple traits may uncover regulating elements such as master regulators or variants belonging to transcription factor binding sites. Genetic analyses have been performed using aPTT (Activated Partial Thromboplastin Time) as a phenotype to improve the understanding of the biological mechanisms underlying thrombotic disease [8,9]. Although aPTT measures the combined activity of several clotting factors in the intrinsic and common coagulation pathways [10] (including factors FII, FV, FVIII, FIX, FX, FXI and FXII), the present genetic studies on aPTT consider it as an univariate model without considering pleiotropic effects [11]. Another example of exploiting the genetic information of different traits comes from the GAIT (Genetic Analysis of Idiopathic Thrombophilia) Project, where we demonstrated that coagulation factors FVIII and vWF are genetically correlated with thrombotic disease [12]. Also, in a previous study, we identified common variants associated with the plasma levels of several proteins and consequently the risk of thrombosis [13]. However, the pleiotropic effects of loci in the coagulation cascade have not been explored fully.

Both genetic association and linkage research have focused on statistical and computational techniques to investigate the genetic effects between one genotype and one phenotype including polygenic and multiphenotypic approaches. Several strategies have been applied for the analysis of multiple and correlated traits. These can be divided into three categories: p-value correction methods, regression models and data reduction methods. P-value correction methods consist on combining several univariate tests, one for each trait, accounting for the observed correlational structure of the traits [14,15].

Regression models make use of mixed effects models for modelling the covariance structure of the phenotypes, as well as population structure [16]. These two approaches have a limited practical use since with a large number of correlated traits, they require the simultaneous estimation of too many parameters [17]. As an alternative, data reduction methods based on the transformation of the original traits to a reduced number of canonical traits have been proposed [18–20] with the intent of applying the traditional single trait analyses to these new variables. Generally, the canonical variables are obtained through a given mathematical model that transforms the original phenotypic data in a new space of reduced dimensionality where the new coordinate axes (also called components) define new phenotypic quantities obtained synthetically. In particular, Principal Components Analysis (PCA) has been applied for this purpose [17, 21, 22].

In this study, we explore an original methodology to determine the inner correlation within a set of related traits involved in the coagulation cascade, to help understanding the genetic bases of the coagulation cascade consequently of thrombosis risk. We apply Independent Component Analysis, a data reduction method, original in this field, to derive new phenotypic variables, called metaphenotypes, which integrate information regarding the underlying biological variability on the thrombus/clot formation. Then, we take advantage of our GWAS to identify genetic elements influencing these metaphenotypes and their relationship with thrombosis risk.

Materials and Methods

The GAIT Project

The GAIT (Genetic Analysis of Idiopathic Thrombophilia) Project has been described in Souto et al 2000 [13]. Briefly, the GAIT Project included 398 individuals from 21 extended Spanish families (mean pedigree size = 19) [12]. Twelve of these families were selected on the basis of a proband with idiopathic thrombophilia, whereas the remaining nine families were unaffected and selected randomly. The ages of the subjects ranged from <1 to 88 years (mean = 37.7 years) and the male to female sex ratio was 0.85. The study was performed according to the Declaration of Helsinki. All procedures were reviewed by the Institutional Review Board of the Hospital de la Santa Creu i Sant Pau, Barcelona, Spain. Adult subjects gave written consent for themselves and for their minor children.

Genotypes and Data Cleaning

A genome-wide set of 307,984 SNPs was typed for all of the participants using the Infinium^® 317k Beadchip on the Illumina platform (San Diego, CA, USA). Individuals with a low call rate (<0.5%), a too high IBS (>0.95%) and a too high heterozygosity (FDR <1%) were removed from the sample. In addition, markers with a low call rate (<0.95%) and a low MAF (<0.0064%) were discarded also. A total of 34 individuals and 30,793 SNPs were removed from the study. A clean dataset containing n = 364 individuals and 277,191 SNPs was obtained for further analyses. This procedure was implemented in R using the GenABEL package [23].

Phenotypes

Among the 80 phenotypes in the GAIT sample, m = 27 phenotypes involved in the coagulation pathway were selected to study their joint biological activity within this metabolic process. These phenotypes were selected as they are defined in the literature [24]. The original phenotypes are described in S1 Table.

To properly apply the mathematical methods that we used, phenotypic data were freed of missing values. To guarantee this condition, the phenotypic dataset was imputed using a bPCA, a Bayesian method for missing value imputation [25].

“Metaphenotypes” as a Concept

A metaphenotype is defined as a new phenotypic variable obtained synthetically from a set of traits (phenotypes) using a given mathematical model of dimensionality reduction. Metaphenotypes should be able to capture the original structure of the data to describe them as a whole. Therefore, identifying genetic variants related to these metaphenotypes may help to ascertain the genetic bases of the observed variability of the set of phenotypes, here the coagulation pathway.

The coagulation factors in the coagulation cascade show related patterns of activity. It is known that the genes coding for the different coagulation factors share a joint ancestry [13], so there may exist also some regulatory elements jointly regulating their activity. We consider analyzing the 27 coagulation pathway-related phenotypes measured in the GAIT project under the concept of metaphenotypes.

Metaphenotypes are computed from the correlation among factors. There are several algorithms in the literature that are able to decompose the variability under different criteria. We applied an ICA (Independent Component Analysis), an algorithm based on a criterion of minimum shared information. ICA was compared to PCA(Principal Component Analysis) a reference method for studying the genetic association of correlated phenotypes [18, 21].

Statistical Analyses

Both PCA and ICA methods apply a linear transformation to the original phenotypic data and obtain a new system of coordinates of reduced dimensionality, following the expression in Eq 1.

$$X=M\cdot W+E$$ (1)

where X (n × m) are the original phenotypes, M (n × m) are the metaphenotypes and W (m × m) are the weights of the model and E is the error of the model. Note that the metaphenotypes correspond to the axes of the new system of coordinates, and are called “components”. The maximum number of components obtained is the same as the original phenotypes but generally, only a few of them are informative and therefore are taken into account.

The metaphenotypes are determined by the characterization of the weights of this linear transformation, either using PCA or using ICA.

Independent Component Analysis

In ICA, the weights W are optimized to guarantee the statistical independence of the metaphenotypes. The independence of the components is guaranteed by finding W that maximizes the non-gaussianity of the metaphenotypes (M).

Among the several ICA algorithms, the fastICA procedure was applied, using a particular approximation of the negentropy measure for maximizing the nongaussianity [26]. In particular, this method was applied with an optimal number of metaphenotypes (components) of k = 15, according to a criterion based on cross-validation approximations [27]. As other ICA implementations, fastICA previously applies a PCA to the data in order to ensure that the components are uncorrelated. The number of components to be used are then determined from the PCA procedure using a cross-validation model.

Principal Component Analysis

In PCA, the weights W are optimized so that the metaphenotypes capture the maximum covariance existing between the original phenotypes. In this case, the metaphenotypes explore the correlation that exists among the original traits to capture the variability shared by the collection of original phenotypes.

PCA was used as a reference method. By default, PCA obtained as many components as original variables (k = 27).

Differences between PCA and ICA

As the structure of the interrelations among phenotypes is hidden and unknown, both techniques are complementary to unravel the cascade of physiological relationships.

PCA and ICA answer different biological questions.

PCA obtains metaphenotypes that explain the greatest overall variability or correlation between the original phenotypes. In other words, metaphenotypes built with PCA are a new set of indexes of jointly altered levels of the original phenotypes, capturing the common activity of the original phenotypes.

In contrast, ICA was chosen because it obtains metaphenotypes that are statistically independent. Thus, ICA is able to separate the different (independent) sources of variability captured by the original phenotypes. Let us consider the original traits as statistical mixtures of different sources of variability (genetic, environmental, or experimental). If there was a genetic source of variability captured by the set of phenotypes (pleiotropy), the metaphenotypes obtained using ICA will capture it. In other words, ICA is especially useful to detect pleiotropic effects.

Heritability Estimation

The heritabilities of the metaphenotypes were estimated using the variance component method implemented in SOLAR [28]. This method partitions the total phenotypic variance into a proportion due to polygenic (additive) effects and a proportion due to environmental effects. The heritability (h2r) estimates the total variance of a trait due to additive genetic effects.

Genetic Association

Genome-Wide Association Analyses with the SNPs of the GAIT project were performed using a Likelihood Ratio test based on a linear mixed effects (Variance Components) model described in Eq 2.

The model provides a vector of fitted values of the phenotype and an estimate of the variance-covariance matrix for each family [28, 29, 30].

The polygenic mixed model defined in Eq 2 was applied for each metaphenotype M_i with the age and gender co-variables for testing the association as they present a significant correlation with almost all of the metaphenotypes.

$$M_i\sim \mu +{\Sigma }_j{\beta }_j{c}_{ji}+G_i+{\epsilon }_j$$ (2)

where i is the individual index, M_i is the metaphenotype, μ is the overall mean, β_j is the regression coefficient of the j-th covariate, c_ji is the j-th covariate, G_i is the random additive polygenic effect (breeding value) which variance is defined as Φσ_G where Φ is the kinship matrix and σ_G is the additive genetic variance due to polygenes. Finally ε_i are the residuals of the model.

With a comparative purpose, GWAS of the original phenotypes were also computed.

All the p-values where corrected using the Bonferroni critertion, with a significance criterion set at α = 0.05 after adjustment.

Results

A total of 15 metaphenotypes were obtained with our methodology. All of the metaphenotypes showed a significant heritability ranging from 0.15 to 0.7 (Table 1). Significant findings obtained in GWAS are shown in Table 2. To illustrate the relevance of these findings, they were compared with metaphenotypes obtained with a PCA-based approach and with univariate GWAS applied to the original phenotypes. Heritabilities of PCA-based metaphenotypes are shown in S2 Table. Table 2 presents SNPs significantly associated with ICA-based metaphenotypes in comparison with PCA-based metaphenotypes and univariate phenotypes. For two particular SNPs (rs9898 and rs27311672), concordant results were found among the three GWAS approaches. Both SNPs were significantly associated with both an ICA-based and a PCA-based metaphenotype as well as with the univariate phenotypes corresponding to the proteins coded by their respective closest gene (HRG and F12). Concordant ICA-based and PCA-based metaphenotypes were compared as follows. Associations p-values with all the original phenotypes with the SNPs reported in Table 2 are presented in S3 Table.

Table 1. Heritabilities of ICA-based metaphenotypes (components 1 to 15 from the ICA model).

Metaphenotype	h2r
C1	0.48***
C2	0.17*
C3	0.53***
C4	0.15*
C5	0.22*
C6	0.61***
C7	0.24**
C8	0.55***
C9	0.35***
C10	0.7***
C11	0.45***
C12	0.58***
C13	0.32***
C14	0.24***
C15	0.59***

Significant thresholds for heritability estimation:

* <0.05,

**<0.005,

*** <0.0005

Table 2. GWAS significant SNPs for the three approaches (univariate phenotypes, ICA-based metaphenotypes and PCA-based metaphenotypes.

For each SNP, the Chromosome where it is located, its physically closest gene and its MAF are shown as well as the adjusted p-value.

SNP ID	Chr	Gene	MAF	HRG	FXII	P-value
						ICA—C3	ICA—C4	ICA—C5	ICA—C10	PCA—C8	PCA—C9	PCA—C10
rs9898	3	HRG	0.35	1.9 x 10−16		9 x 10−18				1 x 10−07	4.3 x 10−08
rs3733159	3	FETUB	0.34	3.3 x 10−13		6.6 x 10−09
rs1621816	3	KNG1	0.24	1.5 x 10−09		5 x 10−08
rs1403694	3	KNG1	0.32	1.1 x 10−08		6.7 x 10−07
rs17255413	3	BOC	0.007				2.6 x 10−08
rs3113727	4	COL25A1	0.24					3.8 x 10−07
rs27311672	5	F12	0.17		7.6 x 10−36				1.1 x 10−14			1.5 x 10−11

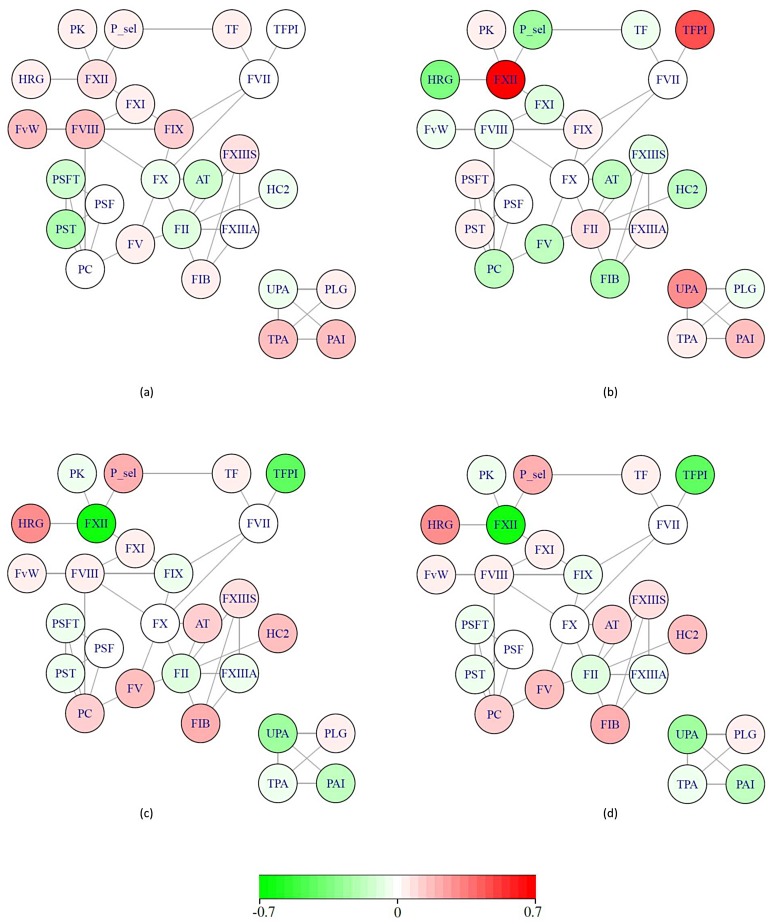
To obtain a clear and interpretable view of metaphenotypes, we plotted them in a simple graph (Fig 1). Non-directed graphs were used to express the existing interaction among the 27 original phenotypes, represented by nodes whose colors represent their weights in the resulting metaphenotype. This is interpretable as the contribution of the original phenotype to the corresponding metaphenotype. Numerical values for the weights are included in S4 and S5 Tables.

Fig 1. Metaphenotype graphical representation using a simple graph.

(a) ICA-based metaphenotype corresponding to the 3^rd component (ICA-C3), (b) ICA-C10, (c) PCA-C9 (d) PCA-C10.

It is observed in Table 2 that ICA and PCA obtained concordant in two cases. For instance, SNPs rs2731672 and rs9898 were significantly associated with metaphenotypes coming from different methodologies.

It is observed that the two metaphenotypes significantly associated with SNP rs2731672 (ICA-C10 and PCA-C10) are influenced clearly by the trait corresponding to the FXII levels (dark nodes in Fig 1.b and 1.d). This SNP is an intergenic variant ~5.8kb upstream of the F12 gene. In both cases the FXII levels have an important loading in the metaphenotypes indicating the variability captured by the metaphenotype is due highly to the variability in the FXII levels. As expected, this SNP was also significantly associated with the FXII levels with the univariate GWAS approach.

The metaphenotypes ICA-C3 and PCA-C9, significantly associated with SNP rs9898 are shown in Fig 1.a and 1.c. SNP rs9898 is a nonsynonymous SNP in exon 5 of the HRG gene. While the PCA-based metaphenotype is oriented clearly to the HRG trait due to the weight of HRG levels in the metaphenotype (dark red HRG node in Fig 1.c), this specific trait does not present a high weighting value in the ICA-based metaphenotype (Fig 1.a).

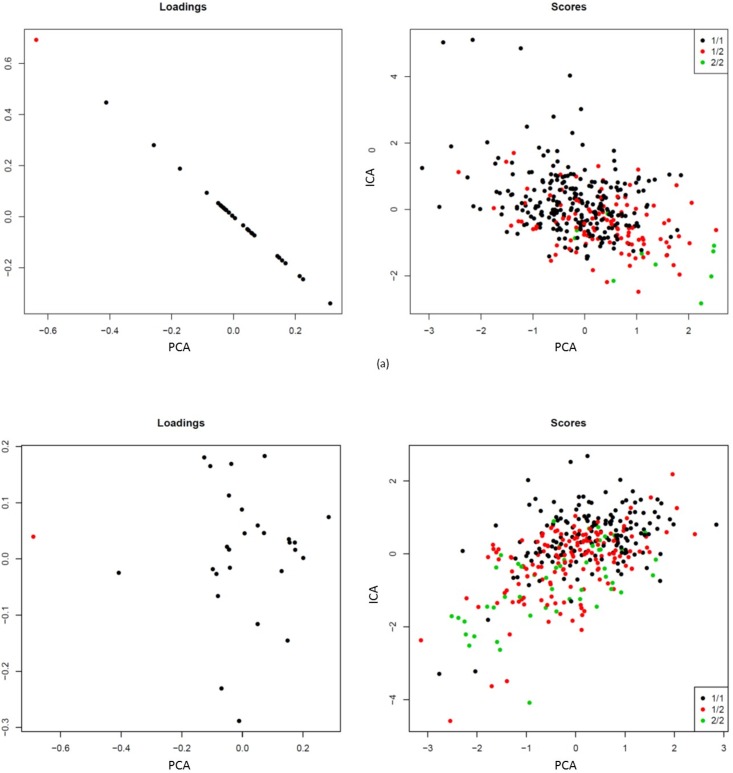
In addition, Fig 2 compares directly both metaphenotypes in terms of their loadings (the weight of each trait on the metaphenotypes) and their scorings (the projection of each individual on the metaphenotypes). For the metaphenotypes associated with SNP rs2731672 (ICA-C10 and PCA-C10) (Fig 2.a), a clear correlation between both loadings and scorings from both metaphenotypes was observed. This confirms that the common variability captured by both metaphenotypes is the same in both cases and is due highly to the variability of the FXII. By contrast, as shown in Fig 2.b, no correlation was observed between the loadings or the scoring of the metaphenotypes associated with SNP rs9898 (ICA-C3 and PCA-C9). This indicates that both metaphenotypes capture different information from the original phenotypes.

Fig 2. Comparison between the metaphenotypes obtained with both PCA and ICA models.

(a) metaphenotype associated with the SNP rs2731672 at the F12 locus and (b) metaphenotypes associated with the SNP rs9898 at the HRG locus.

In addition, the ICA-C3 metaphenotype was significantly associated with three other SNPs (rs3733159, rs1621816 and rs1403694) on Chromosome 3. The former one corresponds to an intronic SNP in the FETUB gene, whereas the latter two are intronic SNPs in the KNG1 gene. It is important to note that KNG1 is located at a distance of around 40Kb from HRG. However, the SNPs rs1621816 and rs1403694 in the KNG1 gene showed a low amount of Linkage Disequilibrium with the SNP rs9898 in the HRG gene (r² = 0.22 and r² = 0.21). These four SNPs showed a significant association with the HRG trait with the univariate GWAS approach.

For the metaphenotypes associated with SNP rs2731672 (Fig 2.a), a clear correlation between both loadings and scorings from both metaphenotypes was observed. This confirms that the common variability captured by both metaphenotypes is the same in both cases and is due highly to the variability of the FXII. By contrast, as shown in Fig 2.b, no correlation was observed between the loadings or the scoring indicating that both metaphenotypes capture different information from the original phenotypes.

Discussion

To date, there are no genetic studies of the coagulation pathway as a whole. Since single-trait genetic studies explain only a small proportion of the phenotypic variability of thrombotic disease, it is prudent to explore other sources of heritability, such as pleiotropy. In our study, we propose a methodology to capture the correlation that exists between a set of intermediate phenotypes involved in the coagulation cascade to elucidate the hidden genetic causes of thrombosis. For doing that, we introduced the concept of metaphenotype consisting on new phenotypic indices that gather the observed variability of a collection of related phenotypes. Metaphenotypes are obtained through mathematical models of data dimensionality reduction. In this study, we applied ICA for the metaphenotype construction. This method is original in this field and was compared to PCA, a reference method for the combined analysis of correlated traits in genetic linkage and association studies^{18, 19, 22}. ICA was chosen because it is especially useful to detect pleiotropy. By contrast, PCA is characterized by being able to capture the common variability existing among the phenotypes. Because they answer different biological questions, both methodologies may be complementary.

Metaphenotypes were obtained from a collection of coagulation-related phenotypes from the GAIT project¹² with the aim of identifying genetic variants underlying the whole biological process of blood coagulation. The final goal was to propose genetic markers as candidate regulators of the coagulation cascade and consequently of thrombosis risk.

Even if metaphenotypes are not intuitively informative, biologically speaking, they may enable the identification of possibly important loci for a more integrated coagulation index and thus be able to characterize the genetic baseline of coagulation function or thrombosis risk. Metaphenotypes can be graphically represented by use of simple graphs (Fig 1) where the original phenotypes involved in their construction are represented by nodes whose colors represent their weights in the resulting metaphenotype. This is interpretable as the contribution of the original phenotypes to the corresponding metaphenotype. In addition, obtaining metaphenotypes with a heritability greater than 50% (Table 1), allows to assume that the variability of these new phenotypic entities may be highly due to genetic variants. This justifies performing GWAS to metaphenotypes.

Results from GWAS with both ICA-based and PCA-based metaphenotypes were concordant in two cases. For instance, SNPs rs2731672 and rs9898 were significantly associated with metaphenotypes coming from different methodologies.

In both cases, we compared graphically the metaphenotype obtained with ICA and the one obtained with PCA (Fig 2).

As shown in Table 2, the SNP rs2731672 in the F12 locus on Chromosome 5 was significantly associated with an ICA-based metaphenotype (p-value of 1.1e^-14) and with a PCA-based metaphenotype (p-value: 1.48x10^-11). It is observed in Fig 1 that both the PCA-based metaphenotype (Fig 1.b) and the ICA-based metaphenotype (Fig 1.d) are influenced clearly by the FXII levels in blood. In addition, Fig 2.a shows a clear correlation between both loadings and scorings of both metaphenotypes. This suggests that the common variability captured by both metaphenotypes is the same in both cases and is due highly to the variability of the FXII. This observation is in agreement with the univariate association between this particular locus (encoding the structural F12 gene) and FXII levels [1]. This result confirms that the ICA method also captures non-pleiotropic effects.

Secondly, SNP rs9898 at the HRG locus at chromosome 3 was significantly associated with an ICA-based (p-value: 9e^-18) and two PCA-based (pvalues: 1e^-07 and 4.3e^-08) metaphenotypes. Comparisons were carried out with the metaphenotype showing a lower p-value. In this case, no correlation was observed between the loadings or the scoring (Fig 2.b). This suggests that both metaphenotypes capture different information of the original traits. Thus, the biological interpretation of the results may be done separately. The univariate GWAS confirmed that SNP rs9898 is associated with Histidine Rich Glycoprotein (HRG) levels, but previous results also reported that it was associated with Activated Prothrombin Time (aPTT) trait and consequently with thrombosis risk [8, 31]. This explains why, as observed in Fig 1.c, the metaphenotype obtained with PCA is oriented clearly to the HRG trait. However, the HRG levels do not have a high weighting value in the metaphenotype obtained using ICA (Fig 1.a). In other words, whereas the metaphenotype obtained with PCA captures the variance due to the more weighted trait (that is HRG), the result obtained through ICA extend our knowledge about the implication of this genetic variant, indicating that this locus has a pleiotropic effect on the set of coagulation-related traits involved with this metaphenotype.

In addition, the same ICA-based metaphenotype, showed a significant association with three other SNPs located in the same genomic region of HRG on chromosome 3 (rs3733159 at the FETUB locus and rs1621816 and rs1403694 at the KNG1 locus). These 3 SNPs were also associated with HRG levels in univariate analyses. The proteins coded by these three genes are Histidine Rich Glycoprotein (HRG), Fetuin-B (FB) and the High Molecular Weight Kininogen (HMWK). All of these proteins are structurally related to a fourth protein, the fetuin A- Heremams Schmide-glycoprotein [32]. Together, they form a subgroup (denoted type 3) within the cystatin superfamily of cysteine inhibitors. Among the several physiological roles associated to type 3 cystatins, the most relevant is the regulation of coagulation and platelet functions, controlled mainly by HRG and kininogen proteins. Furthermore, High-molecular-weight kininogen (HMWK) (encoded by KNG1), as well as coagulation Factor FXII (encoded by F12) are, together with prekallikrein (PK), important constituents of the plasma contact-kinin system. This system was first recognized as a surface-activated coagulation system, also known as the Coagulation Intrinsic Pathway (CIP). CIP is activated when blood or plasma interacts with artificial surfaces. A better understanding of this system may lead to insight into mechanisms for thrombosis and, therefore, the contact-kinin system represents a promising multifunctional target for potential thromboembolic therapies, since blocking of distinct members of the kallikrein-kinin system has the potential to become an effective and safe strategy to combat cardiovascular diseases such as myocardial infarction.

Focusing on SNPs located at the KNG1 locus we observed that SNPs rs1621816 and rs1403694 showed a low degree of linkage disequilibrium with the SNP rs9898 at the HRG locus (r² = 0.22 and r² = 0.21). This indicates that they represent an distinct genetic signal. Thus, it is reasonable to suggest that among the results obtained, the association between SNPs located at the KNG1 locus and an ICA-based metaphenotype may have more relevant biological and clinical implications. Our results indicate that KNG1 plays a relevant role in the CIP not only at a molecular level, but also at a genetic level. This result is particularly interesting since allelic variants in KNG1 were previously associated with risk of thrombosis [33]. Our result strengthens previous conclusions concerning the association of KNG1 with thrombosis suggesting that KNG1 plays a role in the regulation of CIP, even without the influence of the FXI or the FXII levels, since neither FXI nor FXII levels show a specific weight within this metaphenotype (Fig 1.c).

In conclusion, the methodology proposed in this study complemented existing tools for detecting genetic associations in correlated phenotypes. This strategy explores the potential mechanisms and pathways underlying complex diseases and helps to interpret how they are associated with genetic variants. Our approach is based on the assumption that pleiotropy may occur in many complex diseases and more particularly in thrombosis diseases. The proposed mathematical approach is especially addressed to capture several aspects of the correlated activity of a set of original traits, here blood levels of the proteins involved in the coagulation cascade. Applying this original concept helped to identify two candidate SNPs in the KNG1 gene susceptible to have an important role in the genetic regulation of the coagulation pathway as a whole and consequently of thrombosis disease.

Supporting Information

S1 Table. Description of the phenotypes.

(XLSX)

S2 Table. Heritabilities ofPCA-based metaphenotypes (components 1 to 27 from the PCA model).

Significant thresholds for heritability estimation: * <0.05, **<0.005, *** <0.0005.

(XLSX)

S3 Table. P-values of associations of the relevant SNPs of this study with all the original phenotypes.

(XLSX)

S4 Table. Loadings (weights) of the coagulation phenotypes in the obtained ICA-based metaphenotypes.

(XLSX)

S5 Table. Loadings (weights) of the coagulation phenotypes in the obtained PCA-based metaphenotypes.

(XLSX)

Data Availability

All relevant data are within the paper and its Supporting Information files.

Funding Statement

This study was supported by funds from the Instituto de Salud Carlos III Fondo de Investigación Sanitaria PI 11/0184 and PI 14/00582, Red Investigación Cardiovascular RD12/0042/0032 and AGAUR 2009 SGR 1147 from Generalitat de Catalunya. Laura Martin-Fernandez was supported by Ayudas Predoctorales de Formación en Investigación en Salud (PFIS) FI12/00322. This work has been partially supported by the Supported by the Spanish National Grants from Ministry of Economy and Competitiveness with grant TEC2014-60337-R, and the Generalitat de Catalunya, under the grant 2014 SGR 1063. CIBER-BBN is an initiative of the ISCIII.014 SGR 1063. CIBER-BBN is an initiative of the ISCIII. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.