Online Updating of Statistical Inference in the Big Data Setting

Abstract

We present statistical methods for big data arising from online analytical processing, where large amounts of data arrive in streams and require fast analysis without storage/access to the historical data. In particular, we develop iterative estimating algorithms and statistical inferences for linear models and estimating equations that update as new data arrive. These algorithms are computationally efficient, minimally storage-intensive, and allow for possible rank deficiencies in the subset design matrices due to rare-event covariates. Within the linear model setting, the proposed online-updating framework leads to predictive residual tests that can be used to assess the goodness-of-fit of the hypothesized model. We also propose a new online-updating estimator under the estimating equation setting. Theoretical properties of the goodness-of-fit tests and proposed estimators are examined in detail. In simulation studies and real data applications, our estimator compares favorably with competing approaches under the estimating equation setting.

1 Introduction

The advancement and prevalence of computer technology in nearly every realm of science and daily life has enabled the collection of “big data”. While access to such wealth of information opens the door towards new discoveries, it also poses challenges to the current statistical and computational theory and methodology, as well as challenges for data storage and computational efficiency.

Recent methodological developments in statistics that address the big data challenges have largely focused on subsampling-based (e.g., Kleiner et al., 2014; Liang et al., 2013; Ma et al., 2013) and divide and conquer (e.g., Lin and Xi, 2011; Guha et al., 2012; Chen and Xie, 2014) techniques; see Wang et al. (2015) for a review. “Divide and conquer” (or “divide and recombine” or ‘split and conquer”, etc.), in particular, has become a popular approach for the analysis of large complex data. The approach is appealing because the data are first divided into subsets and then numeric and visualization methods are applied to each of the subsets separately. The divide and conquer approach culminates by aggregating the results from each subset to produce a final solution. To date, most of the focus in the final aggregation step is in estimating the unknown quantity of interest, with little to no attention devoted to standard error estimation and inference.

In some applications, data arrive in streams or in large chunks, and an online, sequentially updated analysis is desirable without storage requirements. As far as we are aware, we are the first to examine inference in the online-updating setting. Even with big data, inference remains an important issue, particularly in the presence of rare-event covariates. In this work, we provide standard error formulae for divide-and-conquer estimators in the linear model (LM) and estimating equation (EE) framework. We further develop iterative estimating algorithms and statistical inferences for the LM and EE frameworks for online-updating, which update as new data arrive. These algorithms are computationally efficient, minimally storage-intensive, and allow for possible rank deficiencies in the subset design matrices due to rare-event covariates. Within the online-updating setting for linear models, we propose tests for outlier detection based on predictive residuals and derive the exact distribution and the asymptotic distribution of the test statistics for the normal and non-normal cases, respectively. In addition, within the online-updating setting for estimating equations, we propose a new estimator and show that it is asymptotically consistent. We further establish new uniqueness results for the resulting cumulative EE estimators in the presence of rank-deficient subset design matrices. Our simulation study and real data analysis demonstrate that the proposed estimator outperforms other divide-and-conquer or online-updated estimators in terms of bias and mean squared error.

The manuscript is organized as follows. In Section 2, we first briefly review the divide-and-conquer approach for linear regression models and introduce formulae to compute the mean squared error. We then present the linear model online-updating algorithm, address possible rank deficiencies within subsets, and propose predictive residual diagnostic tests. In Section 3, we review the divide-and-conquer approach of Lin and Xi (2011) for estimating equations and introduce corresponding variance formulae for the estimators. We then derive our online-updating algorithm and new online-updated estimator. We further provide theoretical results for the new online-updated estimator and address possible rank deficiencies within subsets. Section 4 contains our numerical simulation results for both the LM and EE settings, while Section 5 contains results from the analysis of real data regarding airline on-time statistics. We conclude with a brief discussion.

2 Normal Linear Regression Model

2.1 Notation and Preliminaries

Suppose there are N independent observations {(y_i, x_i), i = 1, 2, . . . , N} of interest and we wish to fit a normal linear regression model $y_i={\mathbf{x}}_i^{\prime }\beta +{ϵ}_i$ where ε_i ~ N(0, σ²) independently for i = 1, 2, . . . , N, and β is a p-dimensional vector of regression coefficients corresponding to covariates x_i (p × 1). Write y = (y₁, y₂, . . . , y_N)′ and X = (x₁, x₂, . . . , x_N)′ where we assume the design matrix X is of full rank p < N. The least squares (LS) estimate of β and the corresponding residual mean square, or mean squared error (MSE), are given by $\widehat{\beta }={\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$ and $\mathrm{MSE}=\frac{1}{N-p}{\mathbf{y}}^{\prime }({\mathbf{I}}_N-\mathbf{H})\mathbf{y}$, respectively, where I_N is the N × N identity matrix and H = X(X′X)⁻¹X′.

In the online-updating setting, we suppose that the N observations are not available all at once, but rather arrive in chunks from a large data stream. Suppose at each accumulation point k we observe y_k and X_k, the n_k-dimensional vector of responses and the n_k × p matrix of covariates, respectively, for k = 1, . . . , K such that $\mathbf{y}={({\mathbf{y}}_1^{\prime },{\mathbf{y}}_2^{\prime },\dots ,{\mathbf{y}}_K^{\prime })}^{\prime }$ and $\mathbf{X}={({\mathbf{X}}_1^{\prime },{\mathbf{X}}_2^{\prime },\dots ,{\mathbf{X}}_K^{\prime })}^{\prime }$. Provided X_k is of full rank, the LS estimate of β based on the k^th subset is given by ${\widehat{\beta }}_{n_k,k}={\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-1}{\mathbf{X}}_k^{\prime }{\mathbf{y}}_k$ and the MSE is given by ${\mathrm{MSE}}_{n_k,k}=\frac{1}{n_k-p}{\mathbf{y}}_k^{\prime }({\mathbf{I}}_{n_k}-{\mathbf{H}}_k){\mathbf{y}}_k$, where ${\mathbf{H}}_k={\mathbf{X}}_k{\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-1}{\mathbf{X}}_k^{\prime }$, for k = 1, 2, . . . , K.

As in the divide-and-conquer approach (e.g., Lin and Xi, 2011), we can write $\widehat{\beta }$ as

$$\widehat{\beta }={\left(\sum _{k=1}^K{\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-1}\sum _{k=1}^K{\mathbf{X}}_k^{\prime }{\mathbf{X}}_k{\widehat{\beta }}_{n_k,k}.$$ (1)

We provide a similar divide-and-conquer expression for the residual sum of squares, or sum of squared errors (SSE), given by

$$\mathrm{SSE}=\sum _{k=1}^K{\mathbf{y}}_k^{\prime }{\mathbf{y}}_k-{\left(\sum _{k=1}^K{\mathbf{X}}_k^{\prime }{\mathbf{X}}_k{\widehat{\beta }}_{n_k,k}\right)}^{\prime }{\left(\sum _{k=1}^K{\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-1}\left(\sum _{k=1}^K{\mathbf{X}}_k^{\prime }{\mathbf{X}}_k{\widehat{\beta }}_{n_k,k}\right),$$ (2)

and MSE = SSE/(N − p). Expression (2) is quite useful if one is interested in performing inference in the divide-and-conquer setting, as $\mathrm{var}\left(\widehat{\beta }\right)$ may be estimated by $\mathrm{MSE}{\left({\sum }_{k=1}^K{\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-1}$. We will see in Section 2.2 that both expressions (1) and (2) may be expressed in sequential form that is more advantageous from the online-updating perspective.

2.2 Online Updating

While equations (1) and (2) are quite amenable to parallel processing for each subset, the online-updating approach for data streams is inherently sequential in nature. Equations (1) and (2) can certainly be used for estimation and inference for regression coefficients resulting at some terminal point K from a data stream, provided quantities $({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k,{\widehat{\beta }}_{n_k,k},{\mathbf{y}}_k^{\prime }{\mathbf{y}}_k)$ are available for all accumulation points k = 1, . . . , K. However, such data storage may not always be possible or desirable. Furthermore, it may also be of interest to perform inference at a given accumulation step k, using the k subsets of data observed to that point. Thus, our objective is to formulate a computationally efficient and minimally storage-intensive procedure that will allow for online-updating of estimation and inference.

2.2.1 Online Updating of LS Estimates

While our ultimate estimation and inferential procedures are frequentist in nature, a Bayesian perspective provides some insight into how we may construct our online-updating estimators. Under a Bayesian framework, using the previous k – 1 subsets of data to construct a prior distribution for the current data in subset k, we immediate identify the appropriate online updating formulae for estimating the regression coefficients β and the error variance σ² with each new incoming dataset (y_k, X_k). The Bayesian paradigm and accompanying formulae are provided in the Supplementary Material.

Let ${\widehat{\beta }}_k$ and MSE_k denote the LS estimate of β and the corresponding MSE based on the cumulative data D_k = {(y_ℓ, X_ℓ), ℓ = 1, 2, . . . , k}. The online-updated estimator of β based on cumulative data D_k is given by

$${\widehat{\beta }}_k={({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k+{\mathbf{V}}_{k-1})}^{-1}({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k{\widehat{\beta }}_{n_{k}k}+{\mathbf{V}}_{k-1}{\widehat{\beta }}_{k-1}),$$ (3)

where ${\widehat{\beta }}_0=0,{\mathbf{V}}_k={\sum }_{\ell =1}^k{\mathbf{X}}_{\ell }^{\prime }{\mathbf{X}}_{\ell }$ for k = 1, 2, . . . , and V₀ = 0_p is a p × p matrix of zeros. Although motivated through Bayesian arguments, (3) may also be found in a (non-Bayesian) recursive linear model framework (e.g., Stengel, 1994, p313).

The online-updated estimator of the SSE based on cumulative data D_k is given by

$${\mathrm{SSE}}_k={\mathrm{SSE}}_{k-1}+{\mathrm{SSE}}_{n_k,k}+{\widehat{\beta }}_{k-1}^{\prime }{\mathbf{V}}_{k-1}{\widehat{\beta }}_{k-1}+{\widehat{\beta }}_{n_k,k}^{\prime }{\mathbf{X}}_k^{\prime }{\mathbf{X}}_k{\widehat{\beta }}_{n_k,k}-{\widehat{\beta }}_k^{\prime }{\mathbf{V}}_k{\widehat{\beta }}_k$$ (4)

where SSE_nk,k is the residual sum of squares from the k^th dataset, with corresponding residual mean square MSE_nk,k =SSE_nk,k/(n_k – p). The MSE based on the data D_k is then MSE_k = SSE_k/(N_k – p) where $N_k={\sum }_{\ell =1}^k{n}_{\ell }(=n_k+N_{k-1})$ for k = 1, 2, . . . . Note that for k = K, equations (3) and (4) are identical to those in (1) and (2), respectively.

Notice that, in addition to quantities only involving the current data (y_k, X_k) (i.e., ${\widehat{\beta }}_{n_k,k},{\mathrm{SSE}}_{n_k,k},{\mathbf{X}}_k^{\prime }{\mathbf{X}}_k$, and n_k), we only used quantities (${\widehat{\beta }}_{k-1}$, SSE_k–1, V_k–1, N_k–1) from the previous accumulation point to compute ${\widehat{\beta }}_k$ and MSE_k. Based on these online-updated estimates, one can easily obtain online-updated t-tests for the regression parameters. Online-updated ANOVA tables require storage of two additional scalar quantities from the previous accumulation point; details are provided in the Supplementary Material.

2.2.2 Rank Deficiencies in X_k

When dealing with subsets of data, either in the divide-and-conquer or the online-updating setting, it is quite possible (e.g., in the presence of rare event covariates) that some of the design matrix subsets X_k will not be of full rank, even if the design matrix X for the entire dataset is of full rank. For a given subset k, note that if the columns of X_k are not linearly independent, but lie in a space of dimension q_k < p, the estimate

$${\widehat{\beta }}_{n_k,k}={\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-}{\mathbf{X}}_k^{\prime }{\mathbf{y}}_k,$$ (5)

where ${\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-}$ is a generalized inverse of $\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)$ for subset k, will not be unique. However, both $\widehat{\beta }$ and MSE will be unique, which leads us to introduce the following proposition.

Proposition 2.1

Suppose X is of full rank p < N. If the columns of X_k are not linearly independent, but lie in a space of dimension q_k < p for any k = 1, . . . , K, $\widehat{\beta }$ in (1) and SSE (2) using ${\widehat{\beta }}_{n_k,k}$ as in (5) will be invariant to the choice of generalized inverse ${\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-}$.

To see this, recall that a generalized inverse of a matrix B, denoted by B⁻, is a matrix such that BB⁻B = B. Note that for ${\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-}$, a generalized inverse of $\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)$, ${\widehat{\beta }}_{n_k,k}$ given in (5) is a solution to the linear system $\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right){\beta }_k={\mathbf{X}}_k^{\prime }{\mathbf{y}}_k$. It is well known that if ${\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-}$ is a generalized inverse of $\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)$, then ${\mathbf{X}}_k{\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-}{\mathbf{X}}_k^{\prime }$ is invariant to the choice of ${\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-}$ (e.g., Searle, 1971, p20). Both (1) and (2) rely on ${\widehat{\beta }}_{n_k,k}$ only through product ${\mathbf{X}}_k^{\prime }{\mathbf{X}}_k{\widehat{\beta }}_{n_k,k}={\mathbf{X}}_k^{\prime }{\mathbf{X}}_k{\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-}{\mathbf{X}}_k^{\prime }{\mathbf{y}}_k={\mathbf{X}}_k^{\prime }{\mathbf{y}}_k$ which is invariant to the choice of ${\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-}$.

Remark 2.2

The online-updating formulae (3) and (4) do not require ${\mathbf{X}}_k^{\prime }{\mathbf{X}}_k$ for all k to be invertible. In particular, the online-updating scheme only requires ${\mathbf{V}}_k={\sum }_{\ell =1}^k{\mathbf{X}}_{\ell }^{\prime }{\mathbf{X}}_{\ell }$ to be invertible. This fact can be made more explicit by rewriting (3) and (4), respectively, as

$${\widehat{\beta }}_k={({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k+{\mathbf{V}}_{k-1})}^{-1}({\mathbf{X}}_k^{\prime }{\mathbf{y}}_k+{\mathbf{W}}_{k-1})={\mathbf{V}}_k^{-1}({\mathbf{X}}_k^{\prime }{\mathbf{y}}_k+{\mathbf{W}}_{k-1})$$ (6)

$$SS{E}_k=SS{E}_{k-1}+{\mathbf{y}}_k^{\prime }{\mathbf{y}}_k+{\widehat{\beta }}_{k-1}^{\prime }{\mathbf{V}}_{k-1}{\widehat{\beta }}_{k-1}-{\widehat{\beta }}_k^{\prime }{\mathbf{V}}_k{\widehat{\beta }}_k$$ (7)

where W₀ = 0 and ${\mathbf{W}}_k={\sum }_{\ell =1}^k{\mathbf{X}}_{\ell }^{\prime }{\mathbf{y}}_{\ell }$ for k = 1, 2, . . ..

Remark 2.3

Following Remark 2.2 and using the Bayesian motivation discussed in the Supplementary Material, if X₁ is not of full rank (e.g., due to a rare event covariate), we may consider a regularized least squares estimator by setting V₀ ≠ 0_p. For example, setting V₀ = λI_p, λ > 0, with μ₀ = 0 would correspond to a ridge estimator and could be used at the beginning of the online estimation process until enough data has accumulated; once enough data has accumulated, the biasing term V₀ = λI_p may be removed such that the remaining sequence of updated estimators ${\widehat{\beta }}_k$ and MSE_k are unbiased for β and σ², respectively. Further details are provided in the Supplementary Material.

2.3 Model Fit Diagnostics

While the advantages of saving only lower-dimensional summaries are clear, a potential disadvantage arises in terms of difficulty performing classical residual-based model diagnostics. Since we have not saved the individual observations from the previous (k – 1) datasets, we can only compute residuals based upon the current observations (y_k, X_k). For example, one may compute the residuals e_ki = y_ki – ŷ_ki, where i = 1, . . . , n_k and ${\widehat{y}}_{ki}={\mathbf{x}}_{ki}^{\prime }{\widehat{\beta }}_{n_k,k}$, or even the externally studentized residuals given by

$$t_{ki}=\frac{e_{ki}}{\sqrt{{\mathrm{MSE}}_{n_k,k\left(i\right)}(1-h_{k,ii})}}=e_{ki}{\left[\frac{n_k-p-1}{{\mathrm{SSE}}_{n_k,k}(1-h_{k,ii})-e_{ki}^2}\right]}^{1∕2},$$ (8)

where $h_{k,ii}=\mathrm{Diag}{\left({\mathbf{H}}_k\right)}_i=\mathrm{Diag}{\left({\mathbf{X}}_k{\left({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k\right)}^{-1}{\mathbf{X}}_k^{\prime }\right)}_i$ and MSE_nk,k(i) is the MSE computed from the k^th subset with the i^th observation removed, i = 1, . . . , n_k.

However, for model fit diagnostics in the online-update setting, it would arguably be more useful to consider the predictive residuals, based on ${\widehat{\beta }}_{k-1}$ from data D_k–1 with predicted values ${\check{\mathbf{y}}}_k={({\check{y}}_{k1},\dots ,{\check{y}}_{k{n}_k})}^{\prime }={\mathbf{X}}_k{\widehat{\beta }}_{k-1}$, as ě_ki = y_ki – y̌_ki, i = 1, . . . , n_k. Define the standardized predictive residuals as ${\check{t}}_{ki}={\check{e}}_{ki}∕\sqrt{\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}\left({\check{e}}_{ki}\right)},i=1,\dots ,n_k$.

2.3.1 Distribution of standardized predictive residuals

To derive the distribution of ${\check{t}}_{ki}$, we introduce new notation. Denote $y_{k-1}={({\mathbf{y}}_1^{\prime },\dots ,{\mathbf{y}}_{k-1}^{\prime })}^{\prime }$, and ${\mathcal{X}}_{k-1}$ and ϵ_k–1 the corresponding N_k–1 × p design matrix of stacked X_ℓ, ℓ = 1, . . . , k – 1, and N_k–1 × 1 random errors, respectively. For new observations y_k, X_k, we assume y_k = X_kβ + ε_k, where the elements of ε_k are independent with mean 0 and variance σ² independently of the elements of ϵ_k–1 which also have mean 0 and variance σ². Thus, E(ě_ki) = 0, $\mathrm{var}\left({\check{e}}_{ki}\right)={\sigma }^2(1+x_{ki}^{\prime }{\left({\mathcal{X}}_{k-1}^{\prime }{\mathcal{X}}_{k-1}\right)}^{-1}{x}_{ki})$ for i = 1, . . . , n_k, and $\mathrm{var}\left({\check{\mathbf{e}}}_k\right)={\sigma }^2({\mathbf{I}}_{n_k}+{\mathbf{X}}_k{\left({\mathcal{X}}_{k-1}^{\prime }{\mathcal{X}}_{k-1}\right)}^{-1}{\mathbf{X}}_k^{\prime })$ where ě_k = (ě_k1, . . . , ě_knk)′.

If we assume that both ε_k and ϵ_k–1 are normally distributed, then it is easy to show that ${\check{\mathbf{e}}}_k^{\prime }\mathrm{var}{\left({\check{\mathbf{e}}}_k\right)}^{-1}{\check{\mathbf{e}}}_k\sim {\chi }_{n_k}^2$. Thus, estimating σ² with MSE_k–1 and noting that $\frac{N_{k-1}-p}{{\sigma }^2}{\mathrm{MSE}}_{k-1}\sim {\chi }_{N_{k-1}-p}^2$ independently of ${\check{\mathbf{e}}}_k^{\prime }\mathrm{var}{\left({\check{\mathbf{e}}}_k\right)}^{-1}{\check{\mathbf{e}}}_k$, we find that ${\check{t}}_{ki}$ ~ t_Nk–1–p and

$${\check{F}}_k≔\frac{{\check{\mathbf{e}}}_k^{\prime }{({\mathbf{I}}_{n_k}+{\mathbf{X}}_k{\left({\mathcal{X}}_{k-1}^{\prime }{\mathcal{X}}_{k-1}\right)}^{-1}{\mathbf{X}}_k^{\prime })}^{-1}{\check{\mathbf{e}}}_k}{n_k{\mathrm{MSE}}_{k-1}}\sim F_{n_k,N_{k-1}-p}.$$ (9)

If we are not willing to assume normality of the errors, we introduce the following proposition. The proof of the proposition is given in the Supplementary Material.

Proposition 2.4

Assume that (i) ε_i, i = 1, . . . , n_k, are independent and identically distributed with E(ε_i) = 0 and $E\left({ϵ}_i^2\right)={\sigma }^2$; (ii) the elements of the design matrix ${\mathcal{X}}_k$ are uniformly bounded, i.e., |X_ij| < C, $\forall$ i, j, where C < ∞ is constant; (iii) $\underset{N_{k-1}\to \infty }{\lim }\frac{{\mathcal{X}}_{k-1}^{\prime }{\mathcal{X}}_{k-1}}{N_{k-1}}=\mathbf{Q}$, where Q is a positive definite matrix. Let ${\check{\mathbf{e}}}_k^{\ast }={\Gamma }^{-1}{\check{\mathbf{e}}}_k$, where $\Gamma {\Gamma }^{\prime }\triangleq {\mathbf{I}}_{n_k}+{\mathbf{X}}_k{\left({\mathcal{X}}_{k-1}^{\prime }{\mathcal{X}}_{k-1}\right)}^{-1}{\mathbf{X}}_k^{\prime }$. Write ${\check{\mathbf{e}}}_k^{\ast \prime }=({\check{\mathbf{e}}}_{k_1}^{\ast \prime },\dots ,{\check{\mathbf{e}}}_{k_m}^{\ast \prime })$, where ${\check{\mathbf{e}}}_{k_i}^{\ast }$ is an n_ki × 1 vector consisting of the $({\sum }_{\ell =1}^{i-1}{n}_{k_{\ell }}+1)th$ component through the $\left({\sum }_{\ell =1}^i{n}_{k_{\ell }}\right)th$ component of ${\check{\mathbf{e}}}_k^{\ast }$, and ${\sum }_{i=1}^m{n}_{k_i}=n_k$. We further assume that (iv) $\underset{n_k\to \infty }{\lim }\frac{n_{k_i}}{n_k}=C_i$, where 0 < C_i < ∞ is constant for i = 1, . . . , m. Letting 1_ki be an n_ki × 1 vector of all ones, then at accumulation point k, we have

$$\frac{{\sum }_{i=1}^m\frac{1}{n_{k_i}}{\left(1_{k_i}^{\prime }{\check{e}}_{k_i}^{\ast }\right)}^2}{MS{E}_{k-1}}\stackrel{d}{\to }{\chi }_m^2,as{n}_k,N_{k-1}\to \infty .$$ (10)

2.3.2 Tests for Outliers

Under normality of the random errors, we may use the standardized predictive residuals ${\check{t}}_{ki}$ and F̌_k in (9) to test individually or globally if there are any outliers in the k^th dataset. Notice that ${\check{t}}_{ki}$ and F̌_k can be re-expressed equivalently as

$${\check{t}}_{ki}={\check{e}}_{ki}∕\sqrt{{\mathrm{MSE}}_{k-1}(1+x_{ki}^{\prime }{\left({\mathbf{V}}_{k-1}\right)}^{-1}{x}_{ki})}\text{and}{\check{F}}_k=\frac{{\check{\mathbf{e}}}_k^{\prime }{({\mathbf{I}}_{n_k}+{\mathbf{X}}_k{\left({\mathbf{V}}_{k-1}\right)}^{-1}{\mathbf{X}}_k^{\prime })}^{-1}{\check{\mathbf{e}}}_k}{n_k{\mathrm{MSE}}_{k-1}},$$ (11)

respectively, and thus can both be computed with the lower-dimensional stored summary statistics from the previous accumulation point.

We may identify as outlying y_ki observations those cases whose standardized predicted ${\check{t}}_{ki}$ are large in magnitude. If the regression model is appropriate, so that no case is outlying because of a change in the model, then each ${\check{t}}_{ki}$ will follow the t distribution with N_k–1 – p degrees of freedom. Let p_ki = P (|t_Nk–1–p| > |${\check{t}}_{ki}$|) be the unadjusted p-value and let p̃_ki be the corresponding adjusted p-value for multiple testing (e.g., Benjamini and Hochberg, 1995; Benjamini and Yekutieli, 2001). We will declare y_ki an outlier if p̃_ki < α for a prespecified α level. Note that while the Benjamini-Hochberg (BH) procedure assumes the multiple tests to be independent or positively correlated, the predictive residuals will be approximately independent as the sample size increases. Thus, we would expect the false discovery rate to be controlled with the BH p-value adjustment for large N_k–1.

To test if there is at least one outlying value based upon null hypothesis H₀ : E(ě_k) = 0, we will use statistic F̌_k. Values of the test statistic larger than F(1 – α, n_k, N_k–1 – p) would indicate at least one outlying y_ki exists among i = 1, . . . , n_k at the corresponding α level.

If we are unwilling to assume normality of the random errors, we may still perform a global outlier test under the assumptions of Proposition 2.4. Using Proposition 2.4 and following the calibration proposed in Muirhead (1982) (Muirhead, 1982, page 218), we obtain an asymptotic F statistic

$${\check{F}}_k^a≔\frac{{\sum }_{i=1}^m\frac{1}{n_{k_i}}{\left(1_{k_i}^{\prime }{\check{\mathbf{e}}}_{k_i}^{\ast }\right)}^2}{{\mathrm{MSE}}_{k-1}}\frac{N_{k-1}-m+1}{N_{k-1}\cdot m}\stackrel{d}{\to }F(m,N_{k-1}-m+1),\text{as}{n}_k,N_{k-1}\to \infty .$$ (12)

Values of the test statistic ${\check{F}}_k^a$ larger than F(1 – α, m, N_k–1 – m + 1) would indicate at least one outlying observation exists among y_k at the corresponding α level.

Remark 2.5

Recall that $var\left({\check{\mathbf{e}}}_k\right)=({\mathbf{I}}_{n_k}+{\mathbf{X}}_k{\left({\mathcal{X}}_{k-1}^{\prime }{\mathcal{X}}_{k-1}\right)}^{-1}{\mathbf{X}}_k^{\prime }){\sigma }^2\triangleq \Gamma {\Gamma }^{\prime }{\sigma }^2$, where Γ is an n_k × n_k invertible matrix. For large n_k, it may be challenging to compute the Cholesky decomposition of var(ě_k). One possible solution that avoids the large n_k issue is given in the Supplementary Material.

3 Online Updating for Estimating Equations

A nice property in the normal linear regression model setting is that regardless of whether one “divides and conquers” or performs online updating, the final solution ${\widehat{\beta }}_K$ will be the same as it would have been if one could fit all of the data simultaneously and obtained $\widehat{\beta }$ directly. However, with generalized linear models and estimating equations, this is typically not the case, as the score or estimating functions are often nonlinear in β. Consequently, divide and conquer strategies in these settings often rely on some form of linear approximation to attempt to convert the estimating equation problem into a least square-type problem. For example, following Lin and Xi (2011), suppose N independent observations {z_i, i = 1, 2, . . . , N}. For generalized linear models, z_i will be (y_i, x_i) pairs, i = 1, . . . , N with $E\left(y_i\right)=g\left({\mathbf{x}}_i^{\prime }\beta \right)$ for some known function g. Suppose there exists ${\beta }_0\in {\mathbb{R}}^p$ such that ${\sum }_{i=1}^{N}E\left[\psi ({\mathbf{z}}_i,{\beta }_0)\right]=0$ for some score or estimating function ψ. Let ${\widehat{\beta }}_N$ denote the solution to the estimating equation (EE) $M\left(\beta \right)={\sum }_{i=1}^N\psi ({\mathbf{z}}_i,\beta )=0$ and let V̂_N be its corresponding estimate of covariance, often of sandwich form.

Let {z_ki, i = 1, . . . , n_k} be the observations in the kth subset. The estimating function for subset k is $M_{n_k,k}\left(\beta \right)={\sum }_{i=1}^{n_k}\psi ({\mathbf{z}}_{ki},\beta )$. Denote the solution to M_nk,k(β) = 0 as ${\widehat{\beta }}_{n_k,k}$. If we define

$${\mathbf{A}}_{n_k,k}=-\sum _{i=1}^{n_k}\frac{\partial \psi ({\mathbf{z}}_{ki},{\widehat{\beta }}_{n_k,k})}{\partial \beta },$$ (13)

a Taylor expansion of –M_nk,k(β) at ${\widehat{\beta }}_{n_k,k}$ is given by $-M_{n_k,k}\left(\beta \right)={\mathbf{A}}_{n_k,k}(\beta -{\widehat{\beta }}_{n_k,k})+{\mathbf{R}}_{n_k,k}$ as $M_{n_k,k}\left({\widehat{\beta }}_{n_k,k}\right)=0$ and R_nk,k is the remainder term. As in the linear model case, we do not require A_nk,k to be invertible for each subset k, but do require that ${\sum }_{\ell =1}^k{\mathbf{A}}_{n_{\ell },\ell }$ is invertible. Note that for the asymptotic theory in Section 3.3, we assume that A_nk,k is invertible for large n_k. For ease of notation, we will assume for now that each A_nk,k is invertible, and we will address rank deficient A_nk,k in Section 3.4 below.

The aggregated estimating equation (AEE) estimator of Lin and Xi (2011) combines the subset estimators through

$${\widehat{\beta }}_{NK}={\left(\sum _{k=1}^K{\mathbf{A}}_{n_k,k}\right)}^{-1}\sum _{k=1}^K{\mathbf{A}}_{n_k,k}{\widehat{\beta }}_{n_k,k}$$ (14)

which is the solution to ${\sum }_{k=1}^K{\mathbf{A}}_{n_k,k}(\beta -{\widehat{\beta }}_{n_k,k})=0$. Lin and Xi (2011) did not discuss a variance formula, but a natural variance estimator is given by

$${\widehat{\mathbf{V}}}_{NK}={\left(\sum _{k=1}^K{\mathbf{A}}_{n_k,k}\right)}^{-1}\sum _{k=1}^K{\mathbf{A}}_{n_k,k}{\widehat{\mathbf{V}}}_{n_k,k}{\mathbf{A}}_{n_k,k}^{\mathsf{T}}{\left[{\left(\sum _{k=1}^K{\mathbf{A}}_{n_k,k}\right)}^{-1}\right]}^{\mathsf{T}},$$ (15)

where V̂_nk,k is the variance estimator of ${\widehat{\beta }}_{n_k,k}$ from the subset k. If V̂_nk,k is of sandwich form, it can be expressed as ${\mathbf{A}}_{n_k,k}^{-1}{\widehat{\mathbf{Q}}}_{n_k,k}{\mathbf{A}}_{n_k,k}^{-1}$, where Q̂_nk,k is an estimate of Q_nk,k = var(M_nk,k(β)). Then, the variance estimator is still of sandwich form as

$${\widehat{\mathbf{V}}}_{NK}={\left(\sum _{k=1}^K{\mathbf{A}}_{n_k,k}\right)}^{-1}\sum _{k=1}^K{\widehat{\mathbf{Q}}}_{n_k,k}{\left[{\left(\sum _{k=1}^K{\mathbf{A}}_{n_k,k}\right)}^{-1}\right]}^{\mathsf{T}}.$$ (16)

3.1 Online Updating

Now consider the online-updating perspective in which we would like to update the estimates of β and its variance as new data arrives. For this purpose, we introduce the cumulative estimating equation (CEE) estimator for the regression coefficient vector at accumulation point k as

$${\widehat{\beta }}_k={({\mathbf{A}}_{k-1}+{\mathbf{A}}_{n_k,k})}^{-1}({\mathbf{A}}_{k-1}{\widehat{\beta }}_{k-1}+{\mathbf{A}}_{n_k,k}{\widehat{\beta }}_{n_k,k}).$$ (17)

for k = 1, 2, . . . where ${\widehat{\beta }}_0=0$, A₀ = 0_p, and ${\mathbf{A}}_k={\sum }_{\ell =1}^k{\mathbf{A}}_{n_{\ell },\ell }={\mathbf{A}}_{k-1}+{\mathbf{A}}_{n_k,k}$. With V̂₀ = 0_p and A₀ = 0_p, the variance estimator at the k^th update is given by

$${\widehat{\mathbf{V}}}_k={({\mathbf{A}}_{k-1}+{\mathbf{A}}_{n_k,k})}^{-1}({\mathbf{A}}_{k-1}{\widehat{\mathbf{V}}}_{k-1}{\mathbf{A}}_{k-1}^{\mathsf{T}}+{\mathbf{A}}_{n_k,k}{\widehat{\mathbf{V}}}_{n_k,k}{\mathbf{A}}_{n_k,k}^{\mathsf{T}}){\left[{({\mathbf{A}}_{k-1}+{\mathbf{A}}_{n_k,k})}^{-1}\right]}^{\mathsf{T}}.$$ (18)

By induction, it can be shown that (17) is equivalent to the AEE combination (14) when k = K, and likewise (18) is equivalent to (16) (i.e., AEE=CEE). However, the AEE estimators, and consequently the CEE estimators, are not identical to the EE estimators ${\widehat{\beta }}_N$ and V̂_N based on all N observations. It should be noted, however, that Lin and Xi (2011) did prove asymptotic consistency of AEE estimator ${\widehat{\beta }}_{NK}$ under certain regularity conditions. Since the CEE estimators are not identical to the EE estimators in finite sample sizes, there is room for improvement.

Towards this end, consider the Taylor expansion of –M_nk,k(β) around some vector ${\check{\beta }}_{n_k,k}$, to be defined later. Then

$$-M_{n_k,k}\left(\beta \right)=-M_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)+\left[{\mathbf{A}}_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)\right](\beta -{\check{\beta }}_{n_k,k})+{\check{\mathbf{R}}}_{n_k,k}$$

with Ř_nk,k denoting the remainder. Denote ${\tilde{\beta }}_K$ as the solution of

$$\sum _{k=1}^K-M_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)+\sum _{k=1}^K\left[{\mathbf{A}}_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)\right](\beta -{\check{\beta }}_{n_k,k})=0.$$ (19)

Define ${\tilde{\mathbf{A}}}_{n_k,k}=\left[{\mathbf{A}}_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)\right]$ and assume A_nk,k refers to ${\mathbf{A}}_{n_k,k}\left({\widehat{\beta }}_{n_k,k}\right)$. Then we have

$${\tilde{\beta }}_K={\left\{\sum _{k=1}^K{\tilde{\mathbf{A}}}_{n_k,k}\right\}}^{-1}\left\{\sum _{k=1}^K{\tilde{\mathbf{A}}}_{n_k,k}{\check{\beta }}_{n_k,k}+\sum _{k=1}^K{M}_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)\right\}.$$ (20)

If we choose ${\check{\beta }}_{n_k,k}={\widehat{\beta }}_{n_k,k}$, then ${\tilde{\beta }}_K$ in (20) reduces to the AEE estimator of Lin and Xi (2011) in (14), as (19) reduces to ${\sum }_{k=1}^K{\mathbf{A}}_{n_k,k}(\beta -{\widehat{\beta }}_{n_k,k})=0$ because $M_{n_k,k}\left({\widehat{\beta }}_{n_k,k}\right)=0$ for all k = 1, . . . , K. However, one does not need to choose ${\check{\beta }}_{n_k,k}={\widehat{\beta }}_{n_k,k}$. In the online-updating setting, at each accumulation point k, we have access to the summaries from the previous accumulation point k – 1, so we may use this information to our advantage when defining ${\check{\beta }}_{n_k,k}$. Consider the intermediary estimator given by

$${\check{\beta }}_{n_k,k}={({\tilde{\mathbf{A}}}_{k-1}+{\mathbf{A}}_{n_k,k})}^{-1}(\sum _{\ell =1}^{k-1}{\tilde{\mathbf{A}}}_{n_{\ell },\ell }{\check{\beta }}_{n_{\ell },\ell }+{\mathbf{A}}_{n_k,k}{\widehat{\beta }}_{n_k,k})$$ (21)

for $k=1,2,\dots ,{\tilde{\mathbf{A}}}_0=0_p,{\check{\beta }}_{n_0,0}=0$ and ${\tilde{\mathbf{A}}}_k={\sum }_{\ell =1}^k{\tilde{\mathbf{A}}}_{n_{\ell },\ell }$. Estimator (21) combines the previous intermediary estimators ${\check{\beta }}_{n_{\ell },\ell },\ell =1,\dots ,k-1$ and the current subset estimator ${\widehat{\beta }}_{n_k,k}$, and arises as the solution to the estimating equation ${\sum }_{\ell =1}^{k-1}{\tilde{\mathbf{A}}}_{n_{\ell },\ell }(\beta -{\check{\beta }}_{n_{\ell },\ell })+{\mathbf{A}}_{n_k,k}(\beta -{\widehat{\beta }}_{n_k,k})=0$, where ${\mathbf{A}}_{n_k,k}(\beta -{\widehat{\beta }}_{n_k,k})$ serves as a bias correction term due to the omission of $-{\sum }_{\ell =1}^{k-1}{M}_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)$ from the equation.

With the choice of ${\check{\beta }}_{n_k,k}$ as given in (21), we introduce the cumulatively updated estimating equation (CUEE) estimator ${\tilde{\beta }}_k$ as

$${\tilde{\beta }}_k={({\tilde{\mathbf{A}}}_{k-1}+{\tilde{\mathbf{A}}}_{n_k,k})}^{-1}({\mathbf{a}}_{k-1}+{\tilde{\mathbf{A}}}_{n_k,k}{\check{\beta }}_{n_k,k}+{\mathbf{b}}_{k-1}+M_{n_k,k}\left({\check{\beta }}_{n_k,k}\right))$$ (22)

with ${\mathbf{a}}_k={\sum }_{\ell =1}^k{\tilde{\mathbf{A}}}_{n_k,k}{\check{\beta }}_{n_k,k}={\tilde{\mathbf{A}}}_{n_k,k}{\check{\beta }}_{n_k,k}+{\mathbf{a}}_{k-1}$ and ${\mathbf{b}}_k={\sum }_{\ell =1}^k{M}_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)=M_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)+{\mathbf{b}}_{k-1}$ where a₀ = b₀ = 0, Ã₀ = 0_p, and k = 1, 2, . . . . Note that for a terminal k = K, (22) is equivalent to (20).

For the variance of ${\tilde{\beta }}_k$, observe that $0=-M_{n_k,k}\left({\widehat{\beta }}_{n_k,k}\right)\approx -M_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)+{\tilde{\mathbf{A}}}_{n_k,k}({\widehat{\beta }}_{n_k,k}-{\check{\beta }}_{n_k,k})$. Thus, we have ${\tilde{\mathbf{A}}}_{n_k,k}{\check{\beta }}_{n_k,k}+M_{n_k,k}\left({\check{\beta }}_{n_k,k}\right)\approx {\tilde{\mathbf{A}}}_{n_k,k}{\widehat{\beta }}_{n_k,k}$. Using the above approximation, the variance formula is given by

$${\tilde{\mathbf{V}}}_k={({\tilde{\mathbf{A}}}_{k-1}+{\tilde{\mathbf{A}}}_{n_k,k})}^{-1}({\tilde{\mathbf{A}}}_{k-1}{\tilde{\mathbf{V}}}_{k-1}{\tilde{\mathbf{A}}}_{k-1}^{\mathsf{T}}+{\tilde{\mathbf{A}}}_{n_k,k}{\widehat{\mathbf{V}}}_{n_k,k}{\tilde{\mathbf{A}}}_{n_k,k}^{\mathsf{T}}){\left[{({\tilde{\mathbf{A}}}_{k-1}+{\tilde{\mathbf{A}}}_{n_k,k})}^{-1}\right]}^{\mathsf{T}},$$ (23)

for k = 1, 2, . . . and Ã₀ = Ṽ₀ = 0_p.

Remark 3.1

Under the normal linear regression model, all of the estimating equation estimators become “exact”, in the sense that ${\widehat{\beta }}_N={\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}={\widehat{\beta }}_{NK}={\widehat{\beta }}_K={\tilde{\beta }}_K$.

3.2 Online Updating for Wald Tests

Wald tests may be used to test individual coefficients or nested hypotheses based upon either the CEE or CUEE estimators from the cumulative data. Let $({\breve{\beta }}_k={({\breve{\beta }}_{k,1},\dots ,{\breve{\beta }}_{k,p})}^{\prime },{\breve{\mathbf{V}}}_k)$ refer to either the CEE regression coefficient estimator and corresponding variance in equations (17) and (18), or the CUEE regression coefficient estimator and corresponding variance in equations (22) and (23).

To test H₀ : β_j = 0 at the k^th update (j = 1, . . . , p), we may take the Wald statistic $z_{k,j}^{\ast 2}={\breve{\beta }}_{k,j}^2∕\mathrm{var}\left({\breve{\beta }}_{k,j}\right)$, or equivalently, $z_{k,j}^{\ast }={\breve{\beta }}_{k,j}∕se\left({\breve{\beta }}_{k,j}\right)$, where the standard error $se\left({\breve{\beta }}_{k,j}\right)=\sqrt{\mathrm{var}\left({\breve{\beta }}_{k,j}\right)}$ and $\mathrm{var}\left({\breve{\beta }}_{k,j}\right)$ is the j^th diagonal element of V̆_k. The corresponding p-value is $P(\mid Z\mid \ge \mid z_{k,j}^{\ast }\mid )=P({\chi }_1^2\ge z_{k,j}^{\ast 2})$ where Z and ${\chi }_1^2$ are standard normal and 1 degree-of-freedom chi-squared random variables, respectively.

The Wald test statistic may also be used for assessing the difference between a full model M1 relative to a nested submodel M2. If β is the parameter of model M1 and the nested submodel M2 is obtained from M1 by setting Cβ = 0, where C is a rank q contrast matrix and V̆ is a consistent estimate of the covariance matrix of estimator $\breve{\beta }$, the test statistic is ${\breve{\beta }}^{\prime }{\mathbf{C}}^{\prime }{\left(\mathbf{C}\breve{\mathbf{V}}{\mathbf{C}}^{\prime }\right)}^{-1}\mathbf{C}\breve{\beta }$, which is distributed as ${\chi }_q^2$ under the null hypothesis that Cβ = 0. As an example, if M1 represents the full model containing all p regression coefficients at the k^th update, where the first coefficient β₁ is an intercept, we may test the global null hypothesis H₀ : β₂ = . . . = β_p = 0 with $w_k^{\ast }={\breve{\beta }}_k^{\prime }{\mathbf{C}}^{\prime }{\left(\mathbf{C}{\breve{\mathbf{V}}}_k{\mathbf{C}}^{\prime }\right)}^{-1}\mathbf{C}{\breve{\beta }}_k$, where C is (p – 1) × p matrix C = [0, I_p–1] and the corresponding p-value is $P({\chi }_{p-1}^2\ge w_k^{\ast })$.

3.3 Asymptotic Results

In this section, we show consistency of the CUEE estimator. Specifically, Theorem 3.2 shows that, under regularity, if the EE estimator based on the all N observations ${\widehat{\beta }}_N$ is a consistent estimator and the partition number K goes to infinity, but not too fast, then the CUEE estimator ${\tilde{\beta }}_K$ is also a consistent estimator. The technical regularity conditions are provided in the Supplementary Material. We use the same conditions, (C1)-(C6), as Lin and Xi (2011) with the exception of condition (C4). Instead, we use a slightly modified version which focuses on the behavior of A_n,k(β) for all β in the neighborhood of β₀ (as in (C5)), rather than just at the subset estimate ${\widehat{\beta }}_{n,k}$. (C4’) In a neighborhood of β₀, there exists two positive definite matrices Λ₁ and Λ₂ such that Λ₁ ≤ n^–1 A_n,k(β) ≤ Λ₂ for all β in the neighborhood of β₀ and for all k = 1, ..., K.

We assume for simplicity of notation that n_k = n for all k = 1, 2, . . . , K. The proof of the theorem can be found in the Supplementary Material.

Theorem 3.2

Let ${\widehat{\beta }}_N$ be the EE estimator based on entire data. Then under (C1)-(C2), (C4’)-(C6), if the partition number K satisfies K = O(n^γ) for some 0 < γ < min{1 – 2α, 4α – 1}, we have $P(\sqrt{N}\Vert {\tilde{\beta }}_K-{\widehat{\beta }}_N\Vert >\delta )=o\left(1\right)$ for any δ > 0.

Remark 3.3

If n_k ≠ n for all k, Theorem 3.2 will still hold, provided for each k, $\frac{n_{k-1}}{n_k}$ is bounded, where n_k–1 and n_k are the respective sample sizes for subsets k – 1 and k.

Remark 3.4

Suppose N independent observations (y_i, x_i), i = 1, . . . , N, where y is a scalar response and x is a p-dimensional vector of predictor variables. Further suppose $E\left(y_i\right)=g\left({\mathbf{x}}_i^{\prime }\beta \right)$ for i = 1, . . . , N for g a continuously differentiable function. Under mild regularity conditions, Lin and Xi (2011) show in their Theorem 5.1 that condition (C6) is satisfied for a simplified version of the quasi-likelihood estimator of β (Chen et al., 1999), given as the solution to the estimating equation $Q\left(\beta \right)={\sum }_{i=1}^N[y_i-g\left({\mathbf{x}}_i^{\prime }\beta \right)]{\mathbf{x}}_i=0$.

3.4 Rank Deficiencies in X_k

Suppose N independent observations (y_i, x_i), i = 1, . . . , N, where y is a scalar response and x is a p-dimensional vector of predictor variables. Using the same notation from the linear model setting, let (y_ki, x_ki), i = 1, . . . , n_k, be the observations from the k^th subset where y_k = (y_k1, y_k2, . . . , y_knk)′ and X_k = (x_k1, x_k2, . . . , x_knk)′. For subsets k in which X_k is not of full rank, we may have difficulty in solving the subset EE to obtain ${\widehat{\beta }}_{n_k,k}$, which is used to compute both the AEE/CEE and CUEE estimators for β in (14) and (20), respectively. However, just as in the linear model case, we can show under certain conditions that if $\mathbf{X}={({\mathbf{X}}_1^{\prime },{\mathbf{X}}_2^{\prime },\dots ,{\mathbf{X}}_K^{\prime })}^{\prime }$ has full column rank p, then the estimators ${\widehat{\beta }}_{NK}$ in (14) and ${\tilde{\beta }}_K$ in (20) for some terminal K will be unique.

Specifically, consider observations (y_k, X_k) such that E(y_ki) = μ_ki = g(η_ki) with ${\eta }_{ki}={\mathbf{x}}_{ki}^{\prime }\beta$ for some known function g. The estimating function ψ for the k^th dataset is of the form ψ(z_ki, β) = x_kiS_kiW_ki(y_ki – μ_ki), i = 1, . . . , n_k, where S_ki = ∂_μki/∂_ηki, and W_ki is a positive and possibly data dependent weight. Specifically, W_ki may depend on β only through η_ki. In matrix form, the estimating equation becomes

$${\mathbf{X}}_k^{\prime }{\mathbf{S}}_k^{\prime }{\mathbf{W}}_k({\mathbf{y}}_k-{\mu }_k)=0,$$ (24)

where S_k = Diag(S_k1, . . . , S_knk), W_k = Diag(W_k1, . . . , W_knk), and μ_k = (μ_k1, . . . , μ_knk)′.

With S_k, W_k, and μ_k evaluated at some initial value β⁽⁰⁾, the standard Newton–Raphson method for the iterative solution of (24) solves the linear equations

$${\mathbf{X}}_k^{\prime }{\mathbf{S}}_k^{\prime }{\mathbf{W}}_k{\mathbf{S}}_k{\mathbf{X}}_k(\beta -{\beta }^{\left(0\right)})={\mathbf{X}}_k^{\prime }{\mathbf{S}}_k^{\prime }{\mathbf{W}}_k({\mathbf{y}}_k-{\mu }_k)$$ (25)

for an updated β. Rewrite equation (25) as ${\mathbf{X}}_k^{\prime }{\mathbf{S}}_k^{\prime }{\mathbf{W}}_k{\mathbf{S}}_k{\mathbf{X}}_k\beta ={\mathbf{X}}_k^{\prime }{S}_k^{\prime }{\mathbf{W}}_k{\mathbf{v}}_k$ where v_k = y_k – μ_k+S_kX_kβ⁽⁰⁾; this can be recognized as the normal equation of a weighted least squares regression with response v_k, design matrix S_kX_k, and weight W_k. Therefore the iterative reweighted least squares approach (IRLS) can be used to implement the Newton–Raphson method for an iterative solution to (24) (e.g., Green, 1984).

Rank deficiency in X_k calls for a generalized inverse of ${\mathbf{X}}_k^{\prime }{\mathbf{S}}_k^{\prime }{\mathbf{W}}_k{\mathbf{S}}_k{\mathbf{X}}_k$. In order to show uniqueness of estimators ${\widehat{\beta }}_{NK}$ in (14) and ${\tilde{\beta }}_K$ in (20) for some terminal K, we must first establish that the IRLS algorithm will work and converge for subset k given the same initial value β⁽⁰⁾ when X_k is not of full rank. Upon convergence of IRLS at subset k with solution ${\widehat{\beta }}_{n_k,k}$, we must then verify that the CEE and CUEE estimators that rely on ${\widehat{\beta }}_{n_k,k}$ are unique. The following proposition summarizes the result; the proof is provided in the Supplementary Material.

Proposition 3.5

Under the above formulation, assuming that conditions (C1)-(C3) hold for a full-rank sub-column matrix of X_k, estimators ${\widehat{\beta }}_{NK}$ in (14) and ${\tilde{\beta }}_K$ in (20) for some terminal K will be unique provided X is of full rank.

The simulations in Section 4.2 and Supplementary Material consider rank deficiencies in binary logistic regression and Poisson regression. Note that for these models, the variance of the estimators ${\widehat{\beta }}_K$ and ${\tilde{\beta }}_K$ are given by ${\mathbf{A}}_K^{-1}={\left({\sum }_{k=1}^K{\mathbf{A}}_{n_k,k}\right)}^{-1}$ or ${\tilde{\mathbf{A}}}_K^{-1}={\left({\sum }_{k=1}^K{\tilde{\mathbf{A}}}_{n_k,k}\right)}^{-1}$. For robust sandwich estimators, for those subsets k in which A_nk,k is not invertible, we replace ${\mathbf{A}}_{n_k,k}{\widehat{\mathbf{V}}}_{n_k,k}{\mathbf{A}}_{n_k,k}^{\mathsf{T}}$ and ${\tilde{\mathbf{A}}}_{n_k,k}{\widehat{\mathbf{V}}}_{n_k,k}{\tilde{\mathbf{A}}}_{n_k,k}^{\mathsf{T}}$ in the “meat” of equations (18) and (23), respectively, with an estimate of Q_nk,k from (16). In particular, we use ${\widehat{\mathbf{Q}}}_{n_k,k}={\sum }_{i=1}^{n_k}\psi ({\mathbf{z}}_{ki},{\widehat{\beta }}_k)\psi {({\mathbf{z}}_{ki},{\widehat{\beta }}_k)}^{\mathsf{T}}$ for the CEE variance and ${\tilde{\mathbf{Q}}}_{n_k,k}={\sum }_{i=1}^{n_k}\psi ({\mathbf{z}}_{ki},{\tilde{\beta }}_k)\psi {({\mathbf{z}}_{ki},{\tilde{\beta }}_k)}^{\mathsf{T}}$ for the CUEE variance. We use these modifications in the robust Poisson regression simulations in Section 4.2.2 for the CEE and CUEE estimators, as by design, we include binary covariates with somewhat low success probabilities. Consequently, not all subsets k will observe both successes and failures, particularly for covariates with success probabilities of 0.1 or 0.01, and the corresponding design matrices X_k will not always be of full rank. Thus A_nk,k will not always be invertible for finite n_k, but will be invertible for large enough n_k. We also present results of a proof-of-concept simulation for binary logistic regression in the Supplementary Material, where we compare CUEE estimators under different choices of generalized inverses.

4 Simulations

4.1 Normal Linear Regression: Residual Diagnostic Performance

In this section we evaluate the performance of the outlier tests discussed in Section 2.3.2. Let k* denote the index of the single subset of data containing any outliers. We generated the data according to the model $y_{ki}={\mathbf{x}}_{ki}^{\prime }\beta +{ϵ}_{ki}+b_k\delta {\eta }_{ki}$, i = 1, . . . , n_k, where b_k = 0 if k ≠ k* and b_k ~ Bernoulli(0.05) otherwise. Notice that the first two terms on the right-hand-side correspond to the usual linear model with β = (1, 2, 3, 4, 5)′, x_ki[2:5] ~ N(0, I₄) independently, x_ki[1] = 1, and ε_ki are the independent errors, while the final term is responsible for generating the outliers. Here, η_ki ~ Exp(1) independently and δ is the scale parameter controlling magnitude or strength of the outliers. We set δ ∈ {0, 2, 4, 6} corresponding to “no”, “small”, “medium”, and “large” outliers.

To evaluate the performance of the individual outlier t-test in (11), we generated the random errors as ε_ki ~ N(0, 1). To evaluate the performance of the global outlier F-tests in (11) and (12), we additionally considered ε_ki as independent skew-t variates with degrees of freedom ν = 3 and skewing parameter γ = 1.5, standardized to have mean 0 and variance 1. To be precise, we use the skew t density, $g\left(x\right)=\frac{2}{\gamma +\frac{1}{\gamma }}f\left(\gamma x\right)$ for x < 0 and $g\left(x\right)=\frac{2}{\gamma +\frac{1}{\gamma }}f\left(\frac{x}{\gamma }\right)$ for x ≥ 0, where f(x) is the density of the t distribution with ν degrees of freedom.

For all outlier simulations, we varied k*, the location along the data stream in which the outliers occur. We also varied n_k = n_k* ∈ {100, 500} which additionally controls the number of outliers in dataset k*. For each subset ℓ = 1, . . . , k* – 1 and for 95% of observations in subset k*, the data did not contain any other outliers.

To evaluate the global outlier F-tests (11) and (12) with m = 2, we estimated power using B = 500 simulated data sets with significance level α = 0.05, where power was estimated as the proportion of 500 datasets in which F̌_k* ≥ F(0.95, n_k*, N_{k* –1} – 5) or ${\check{F}}_{k^{\ast }}^a\ge F(0.95,2,N_{k^{\ast }-1}-1)$. The power estimates for the various subset sample sizes n_k*, locations of outliers k*, and outlier strengths δ appear in Table 1. When the errors were normally distributed, notice that the Type I error rate was controlled in all scenarios for both the F test and asymptotic F test. As expected, power tends to increase as outlier strength and/or the number of outliers increase. Furthermore, larger values of k*, and hence greater proportions of “good” outlier-free data, also tend to have higher power; however, the magnitude of improvement decreases once the denominator degrees of freedom (N_{k* – 1} – p or N_{k* – 1} – m + 1) become large enough, and the F tests essentially reduce to χ² tests. Also as expected, the F test given by (11) is more powerful than the asymptotic F test given in (12) when, in fact, the errors were normally distributed. When the errors were not normally distributed, the empirical type I error rates of the F test given by (11) are severely inflated and hence, its empirical power in the presence of outliers cannot be trusted. The asymptotic F test, however, maintains the appropriate size.

Table 1.

Power of the outlier tests for various locations of outliers (k*), subset sample sizes (n_k = n_k*), and outlier strengths (no, small, medium, large). Within each cell, the top entry corresponds to the normal-based F test and the bottom entry corresponds to the asymptotic F test that does not rely on normality of the errors.

Outlier Strength	nk* = 100 (5 true outliers)				nk* = 500 (25 true outliers)
	k* = 5	k* = 10	k* = 25	k* = 100	k* = 5	k* = 10	k* = 25	k* = 100
	F Test/Asymptotic F Test(m=2)				F Test/Asymptotic F Test(m=2)
Standard Normal Errors
no	0.0626	0.0596	0.0524	0.0438	0.0580	0.0442	0.0508	0.0538
	0.0526	0.0526	0.0492	0.0528	0.0490	0.0450	0.0488	0.0552
small	0.5500	0.5690	0.5798	0.5718	0.9510	0.9630	0.9726	0.9710
	0.2162	0.2404	0.2650	0.2578	0.6904	0.7484	0.7756	0.7726
medium	0.9000	0.8982	0.9094	0.9152	1.0000	1.0000	1.0000	1.0000
	0.5812	0.6048	0.6152	0.6304	0.9904	0.9952	0.9930	0.9964
large	0.9680	0.9746	0.9764	0.9726	1.0000	1.0000	1.0000	1.0000
	0.5812	0.6048	0.6152	0.6304	0.9998	1.0000	1.0000	1.0000
Standardized Skew t Errors
no	0.2400	0.2040	0.1922	0.1656	0.2830	0.2552	0.2454	0.2058
	0.0702	0.0630	0.0566	0.0580	0.0644	0.0580	0.0556	0.0500
small	0.5252	0.4996	0.4766	0.4520	0.7678	0.7598	0.7664	0.7598
	0.2418	0.2552	0.2416	0.2520	0.6962	0.7400	0.7720	0.7716
medium	0.8302	0.8280	0.8232	0.8232	0.9816	0.9866	0.9928	0.9932
	0.5746	0.5922	0.6102	0.6134	0.9860	0.9946	0.9966	0.9960
large	0.9296	0.9362	0.9362	0.9376	0.9972	0.9970	0.9978	0.9990
	0.7838	0.8176	0.8316	0.8222	0.9988	0.9992	0.9998	1.0000

Power with “outlier strength = no” are Type I errors.

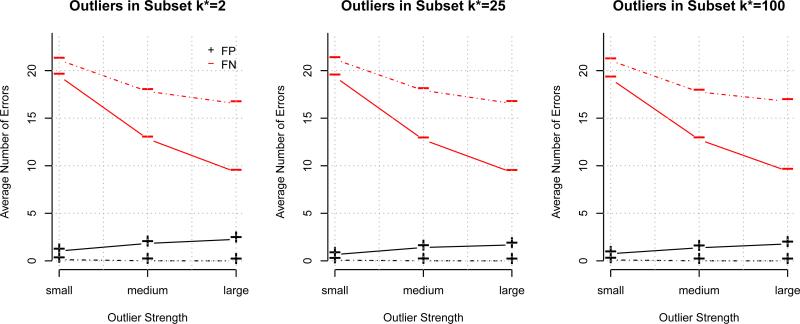
For the outlier t-test in (11), we examined the average number of false negatives (FN) and average number of false positives (FP) across the B = 500 simulations. False negatives and false positives were declared based on a BH adjusted p-value threshold of 0.10. These values were plotted in solid lines against outlier strength in Figure 1 for n_k* = 500 for various values of k* and δ; the corresponding plot for n_k* = 100 is given in the Supplementary Material. Within each plot the FN decreases as outlier strength increases, and also tends to decrease slightly across the plots as k* increases. FP increases slightly as outlier strength increases, but decreases as k* increases. As with the outlier F test, once the degrees of freedom N_{k* – 1} – p get large enough, the t-test behaves more like a z-test based on the standard normal distribution. For comparison, we also considered FN and FP for an outlier test based upon the externally studentized residuals t_k*i from subset k* only. Specifically, under the assumed linear model, t_k*i as given by (8) follow a t distribution with n_k* – p – 1 degrees of freedom. Again, false negatives and false positives were declared based on a BH adjusted p-value threshold of 0.10, and the FN and FP for the externally studentized residual (ESR) test are plotted in dashed lines in Figure 1 for n_k* = 500; the plot for n_k* = 100 may be found in the Supplementary Materials. This ESR test tends to have a lower FP, but higher FN than the predictive residual test that uses the previous data. Also, the FN and FP for the ESR test are essentially constant across k* for fixed n_k*, as the ESR test relies on only the current dataset of size n_k* and not the amount of previous data controlled by k*. Consequently, the predictive residual test has improved power over the ESR test, while still maintaining a low number of FP.

Figure 1.

Average numbers of False Positives and False Negatives for outlier t-tests for n_k* = 500. Solid lines correspond to the predictive residual test while dotted lines correspond to the externally studentized residuals test using only data from subset k*.

4.2 Simulations for Estimating Equations

4.2.1 Logistic Regression

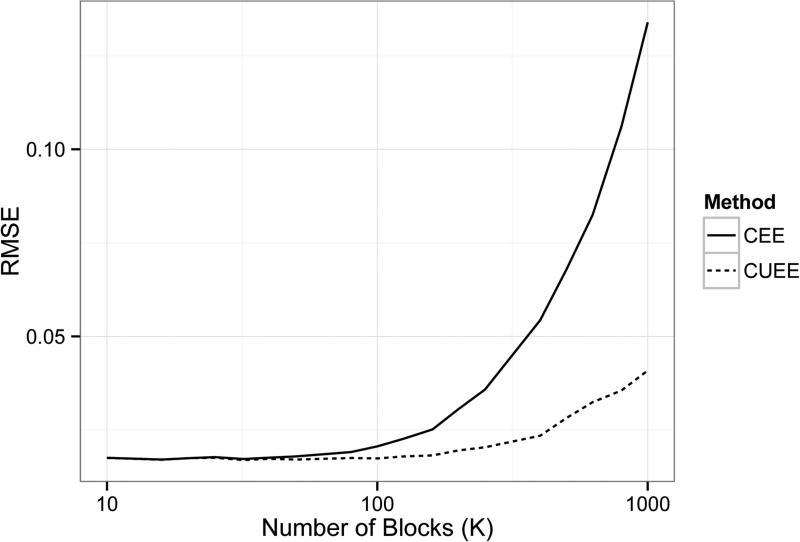
To examine the effect of the total number of blocks K on the performance of the CEE and CUEE estimators, we generated y_i ~ Bernoulli(μ_i), independently for i = 1, . . . , 100000, with $\mathrm{logit}\left({\mu }_i\right)={\mathbf{x}}_i^{\prime }\beta$ where β = (1, 1, 1, 1, 1, 1)′, x_i[2:4] ~ Bernoulli(0.5) independently, x_i[5:6] ~ N(0, I₂) independently, and x_ki[1] = 1. The total sample size was fixed at N = 100000, but in computing the CEE and CUEE estimates, the number of blocks K varied from 10 to 1000 where N could be divided evenly by K. At each value of K, the root-mean squared error (RMSE) of both the CEE and CUEE estimators were calculated as $\sqrt{\frac{{\sum }_{j=1}^6{({\breve{\beta }}_{Kj}-1)}^2}{6}}$, where ${\breve{\beta }}_{Kj}$ represents the j^th coefficient in either the CEE or CUEE terminal estimate. The averaged RMSEs are obtained with 200 replicates. Figure 2 shows the plot of averaged RMSEs versus the number of blocks K. It is clear that as the number of blocks increases (block size decreases), RMSE from CEE method increases very fast while RMSE from the CUEE method remains relatively stable.

Figure 2.

RMSE of CEE and CUEE estimators for different numbers of blocks.

4.2.2 Robust Poisson Regression

In these simulations, we compared the performance of the (terminal) CEE and CUEE estimators with the EE estimator based on all of the data. We generated B = 500 datasets of y_i ~ Poisson(μ_i), independently for i = 1, . . . , N with $\log \left({\mu }_i\right)={\mathbf{x}}_i^{\prime }\beta$ where β = (0.3, −0.3, 0.3, −0.3, 0.3)′, x_ki[1] = 1, x_i[2:3] ~ N(0, I₂) independently, x_i[4] ~ Bernoulli(0.25) independently, and x_i[5] ~ Bernoulli(0.1) independently. We fixed K = 100, but varied n_k = n ∈ {100, 500}.

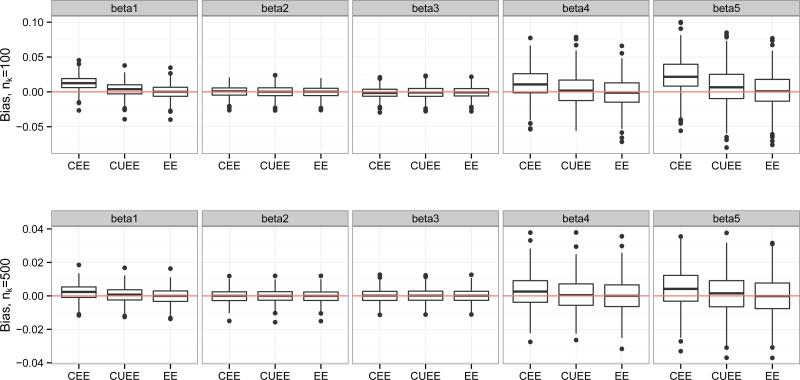
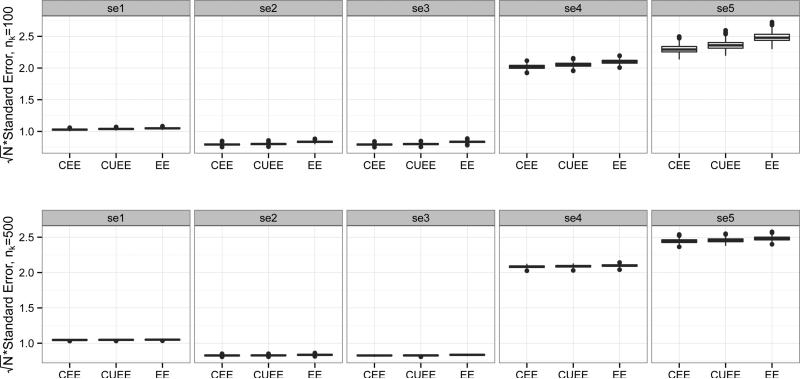
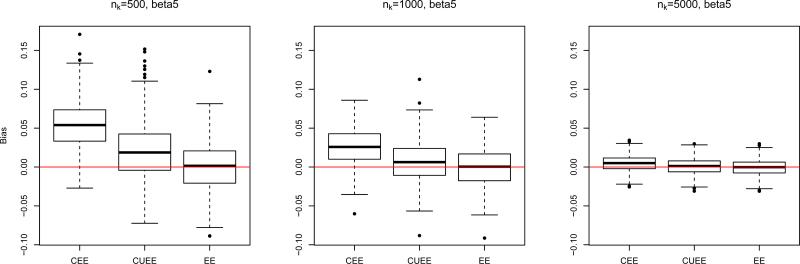
Figure 3 shows boxplots of the biases in the 3 types of estimators (CEE, CUEE, EE) of β_j, j = 1, . . . , 5, for varying n_k. The CEE estimator tends to be the most biased, particularly in the intercept, but also in the coefficients corresponding to binary covariates. The CUEE estimator also suffers from slight bias, while the EE estimator performs quite well, as expected. Also as expected, as n_k increases, bias decreases. The corresponding robust (sandwich-based) standard errors are shown in Figure 4, but the results were very similar for variances estimated by ${\mathbf{A}}_K^{-1}$ and ${\tilde{\mathbf{A}}}_K^{-1}$. In the plot, as n_k increases, the standard errors become quite similar for the three methods.

Figure 3.

Boxplots of biases for CEE, CUEE, EE estimators of β_j (estimated β_j - true β_j), j = 1, . . . , 5, for varying n_k.

Figure 4.

Boxplots of standard errors for CEE, CUEE, EE estimators of β_j, j = 1, . . . , 5, for varying n_k. Standard errors have been multiplied by $\sqrt{K{n}_k}=\sqrt{N}$ for comparability.

Table 2 shows the RMSE ratios, RMSE(CEE)/RMSE(EE) and RMSE(CUEE)/RMSE(EE), for each coefficient. The RMSE ratios for CEE and CUEE estimators confirm the boxplot results as the intercept and the coefficients corresponding to binary covariates (β₄, β₅) tend to be the most problematic for both estimators, but more so for the CEE estimator.

Table 2.

RMSE Ratios of CEE and CUEE with EE

		β 1	β 2	β 3	β 4	β 5
nk = 100	CEE	2.414	1.029	1.036	1.299	1.810
	CUEE	1.172	1.092	1.088	1.118	1.205
nk = 500	CEE	1.225	1.002	1.002	1.060	1.146
	CUEE	0.999	1.010	1.016	0.993	1.057

For this particular simulation, it appears n_k = 500 is sufficient to adequately reduce the bias. However, the appropriate subset size n_k, if given the choice, is relative to the data at hand. For example, if we alter the data generation of the simulation to instead have x_i[5] ~ Bernoulli(0.01) independently, but keep all other simulation parameters the same, the bias, particularly for β₅, still exists at n_k = 500 (see Figure 5) but diminishes substantially with n_k = 5000.

Figure 5.

Boxplots of biases for CEE, CUEE, EE estimators of β₅ (estimated β₅ - true β₅), for varying n_k, when x_i[5] ~ Bernoulli(0.01).

5 Data Analysis

We examined the airline on-time statistics, available at http://stat-computing.org/dataexpo/2009/the-data.html. The data consists of flight arrival and departure details for all commercial flights within the USA, from October 1987 to April 2008. This involves N = 123, 534, 969 observations and 29 variables (~ 11 GB).

We first used logistic regression to model the probability of late arrival (binary; 1 if late by more than 15 minutes, 0 otherwise) as a function of departure time (continuous); distance (continuous, in thousands of miles), day/night flight status (binary; 1 if departure between 8pm and 5am, 0 otherwise); weekend/weekday status (binary; 1 if departure occurred during the weekend, 0 otherwise), and distance type (categorical; ‘typical distance’ for distances less than 4200 miles, the reference level ‘large distance’ for distances between 4200 and 4300 miles, and ‘extreme distance’ for distances greater than 4300 miles) for N = 120, 748, 239 observations with complete data.

For CEE and CUEE, we used a subset size of n_k = 50, 000 for k = 1, . . . , K – 1, and n_K = 48239 to estimate the data in the online-updating framework. However, to avoid potential data separation problems due to rare events (extreme distance; 0.021% of the data with 26,021 observations), a detection mechanism has been introduced at each block. If such a problem exists, the next block of data will be combined until the problem disappears. We also computed EE estimates and standard errors using the commercial software Revolution R.

All three methods agree that all covariates except extreme distance are highly associated with late flight arrival (p < 0.00001), with later departure times and longer distances corresponding to a higher likelihood for late arrival, and night-time and weekend flights corresponding to a lower likelihood for late flight arrival (see Table 3). However, extreme distance is not associated with the late flight arrival (p = 0.613). The large p value also indicates that even if number of observations is huge, there is no guarantee that all covariates must be significant. As we do not know the truth in this real data example, we compare the estimates and standard errors of CEE and CUEE with those from Revolution R, which computes the EE estimates, but notably not in an online-updating framework. In Table 3, the CUEE and Revolution R regression coefficients tend to be the most similar. The regression coefficient estimates and standard errors for CEE are also close to those from Revolution R, with the most discrepancy in the regression coefficients again appearing in the intercept and coefficients corresponding to binary covariates.

Table 3.

Estimates and standard errors (×10⁵) from the Airline On-Time data for EE (computed by Revolution R), CEE, and CUEE estimators.

	EE		CEE		CUEE
	${\widehat{\beta }}_{Nj}$	$se\left({\widehat{\beta }}_{Nj}\right)$	${\widehat{\beta }}_{Kj}$	$se\left({\widehat{\beta }}_{Kj}\right)$	${\tilde{\beta }}_{Kj}$	$se\left({\tilde{\beta }}_{Kj}\right)$
Intercept	−3.8680	1395.65	−3.7060	1434.60	−3.8801	1403.49
Depart	0.1040	6.01	0.1024	6.02	0.1017	5.70
Distance	0.2409	40.89	0.2374	41.44	0.2526	38.98
Night	−0.4484	81.74	−0.4318	82.15	−0.4335	80.72
Weekend	−0.1769	54.13	−0.1694	54.62	−0.1779	53.95
TypDist	0.8785	1389.11	0.7676	1428.26	0.9231	1397.46
ExDist	−0.0103	2045.71	−0.0405	2114.17	−0.0093	2073.99

We finally considered arrival delay (ArrDelay) as a continuous variable by modeling log(ArrDelay − min(ArrDelay) + 1) as a function of departure time, distance, day/night flight status, and weekend/weekday flight status for United Airline flights (N = 13, 299, 817), and applied the global predictive residual outlier tests discussed in Section 2.3.2. Using only complete observations and setting n_k = 1000, m = 3, and α = 0.05, we found that the normality-based F test in (11) and asymptotic F test in (12) overwhelmingly agreed upon whether or not there was at least one outlier in a given subset of data (96% agreement across K = 12803 subsets). As in the simulations, the normality-based F test rejects more often than the asymptotic F test: in the 4% of subsets in which the two tests did not agree, the normality-based F test alone identified 488 additional subsets with at least one outlier, while the asymptotic F test alone identified 23 additional subsets with at least one outlier.

6 Discussion

We developed online-updating algorithms and inferences applicable for linear models and estimating equations. We used the divide and conquer approach to motivate our online-updated estimators for the regression coefficients, and similarly introduced online-updated estimators for the variances of the regression coefficients. The variance estimation allows for online-updated inferences. We note that if one wishes to perform sequential testing, this would require an adjustment of the α level to account for multiple testing.

In the linear model setting, we provided a method for outlier detection using predictive residuals. Our simulations suggested that the predictive residual tests are more powerful than a test that uses only the current dataset in the stream. In the EE setting, we may similarly consider outlier tests also based on standardized predictive residuals. For example in generalized linear models, one may consider the sum of squared predictive Pearson or Deviance residuals, computed using the coefficient estimate from the cumulative data (i.e., ${\tilde{\beta }}_{k-1}$ or ${\widehat{\beta }}_{k-1}$). It remains an open question in both settings, however, regarding how to handle such outliers when they are detected. This is an area of future research.

In the estimating equation setting, we also proposed a new online-updated estimator of the regression coefficients that borrows information from previous datasets in the data stream. The simulations indicated that in finite samples, the proposed CUEE estimator is less biased than the AEE/CEE estimator of Lin and Xi (2011). However, both estimators were shown to be asymptotically consistent.

The methods in this paper were designed for small to moderate covariate dimensionality p, but large N. The use of penalization in the large p setting is an interesting consideration, and has been explored in the divide-and-conquer context in Chen and Xie (2014) with popular sparsity inducing penalty functions. In our online-updating framework, inference for penalized parameters would be challenging, however, as the computation of their variance estimates is quite complicated and is also an area of future work.

The proposed methods are particularly useful for data that is obtained sequentially and without access to historical data. Notably, under the normal linear regression model, the proposed scheme does not lead to any information loss for inferences involving β, as when the design matrix is of full rank, ${\widehat{\beta }}_{n_k,k}$ and MSE_nk,k are sufficient and complete statistics for β and σ². However, under the estimating equation setting, some information will be lost. Precisely how much information needs to be retained at each subset for specific types of inferences is an open question, and an area devoted for future research.