g-Ratio weighted imaging of the human spinal cord in vivo

Abstract

The myelin g-ratio is defined as the ratio of the inner to the outer diameter of the myelin sheath. This ratio provides a measure of the myelin thickness that complements axon morphology (diameter and density) with high specificity for assessment of demyelination in diseases such as multiple sclerosis. Previous work has shown that an aggregate g-ratio map can be computed using a formula that combines axon and myelin density measured with quantitative MRI.

In this work, we computed g-ratio weighted maps in the cervical spinal cord of nine healthy subjects. We utilized the 300 mT/m gradients from the CONNECTOM scanner for estimating the fraction of restricted water (fr) with high accuracy using the CHARMED model. Myelin density was estimated using the lipid and macromolecular tissue volume (MTV) method, derived from normalized proton density (PD) mapping. The variability across spinal level, laterality and subject were assessed using a three-way ANOVA.

The average g-ratio value obtained in the white matter was 0.76 +/− 0.03, consistent with previous histology work. Coefficients of variation of fr and MTV were respectively 4.3% and 13.7%. fr and myelin density were significantly different across spinal tracts (p = 3×10⁻⁷ and 0.004 respectively) and were positively correlated in the white matter (r = 0.42), suggesting shared microstructural information. The g-ratio did not show significant differences across tracts (p=0.6).

This study suggests that fr and myelin density can be measured in vivo with high precision and that they can be combined to produce a map robust to free water pool contamination such as cerebrospinal fluid or veins and weighted by the myelin g-ratio. Potential applications include the study of early demyelination in multiple sclerosis and the quantitative assessment of remyelination drugs.

Graphical abstract

1. Introduction

The white matter of the central nervous system is composed of axons that transmit neuronal information. Most of these axons have a myelin sheath (Hildebrand et al., 1993) that enables faster propagation of action potentials (Rushton, 1951), notably via saltatory conduction (Huxley and Stämpfli, 1949), and higher firing frequency (Perge et al., 2012). Changes in the integrity of the myelin sheath can have dramatic consequences such as paralysis, loss of sensation or chronic pain (Dijkers et al., 2009) depending on the localization of dysfunction in the neuroaxis. Demyelination and/or axonal damage can be induced by neurodegenerative diseases such as amyotrophic lateral sclerosis or after traumatic injury through the process of Wallerian degeneration of the disrupted axons (Raff et al., 2002; Waller, 1850).

Magnetic Resonance Imaging (MRI) is the most widely used imaging modality to diagnose neuropathology (Saba, 2015). Conventional MRI contrasts (T₂- or T₁-weighted) can reveal pathologies such as focal MS lesions or edema and ischemia in spinal cord injury. However, conventional MRI lacks sensitivity to subtle white matter demyelination and degeneration. To overcome these limitations, several novels MRI techniques such as diffusion-weighted imaging or magnetization transfer have been developed to improve our ability to assess microstructure integrity (Saba, 2015). While these advanced techniques increase sensitivity and specificity to white matter microstructure, they are still not entirely specific to particular cellular properties. For instance, reduction of fractional anisotropy from diffusion tensor imaging can be caused by demyelination, axon degeneration, gliosis, edema, lower axon density or cerebrospinal fluid (CSF) contamination (Alexander et al., 2007; Metwalli et al., 2010; Saba, 2015). More advanced diffusion MRI techniques such as diffusion kurtosis imaging (Jensen et al., 2005; Lätt et al., 2008), AxCaliber (Assaf et al., 2008), ActiveAx (Alexander et al., 2010) or NODDI (Zhang et al., 2012), try to disentangle these different pathologic entities by introducing more complex models. Such models can quantify in particular the fraction of restricted water (fr), assumed to be the relative fraction of intra-axonal water in the white matter. This metric appears to be more specific to microstructural changes such as axon degeneration (Adluru et al., 2014; Zhang et al., 2012). However, diffusion-based techniques alone cannot easily distinguish between different sources of axon pathology. For example, an increase of extracellular-space can be caused by edema or axon degeneration, and the ratio of intra- to extracellular diffusion-visible water is independent of absolute myelin content. Complementary measures of myelin density or myelin volume fraction (MVF) can help characterize the integrity of white matter axons. These can be estimated with MRI, using for example quantitative magnetization transfer (Sled and Pike, 2000), myelin water fraction (Mackay et al., 1994) or lipid and macromolecular tissue volume (Aviv Mezer et al., 2013).

By combining MVF with fr it is possible to calculate a map weighted by the myelin g-ratio, which is defined as the ratio of the inner to the outer diameter of the myelin sheath and thus provide a specific marker of demyelination (Stikov et al., 2011). For example, in a case of axonal loss or edema, fr and MVF would decrease, but the g-ratio would remain constant. However, in the case of pure demyelination, axon density (obtained using the formula (1−MVF)*fr) would remain relatively constant while MVF would decrease, resulting in higher g-ratio.

The myelin g-ratio is known to vary between 0.6 and 0.8 in the central nervous system (Chomiak and Hu, 2009; Rushton, 1951), with an optimal value around 0.77 (Chomiak and Hu, 2009). Bigger axons are known to have a relatively thinner myelin sheath, and thus a higher g-ratio (Ikeda and Oka, 2012; Paus and Toro, 2009; West et al., 2015). For a given diameter, however, the myelin g-ratio is relatively constant in the central nervous system and across species (Chomiak and Hu, 2009). It is also associated with sex differences in brain development (Paus and Toro, 2009; Pesaresi et al., 2015), and pathologies such as schizophrenia (Uranova et al., 2001). Measurement of myelin g-ratio using MRI has been demonstrated in the corpus callosum of a macaque and the sensitivity to the g-ratio has been shown using comparison with histology (Stikov et al., 2015b). The feasibility in vivo has been shown in the brain of healthy subjects (Campbell et al., 2014; Mohammadi et al., 2015), as well as in an MS patient (Stikov et al., 2015b).

The goal of this study was to map the myelin g-ratio in the in vivo human cervical spinal cord and study the distribution of the resulting map across different spinal pathways using atlas-based analysis.

2. Methods

Experiments were performed in nine healthy subjects (29 +/− 14 years old, five males), in agreement with the institutional review board of Massachusetts General Hospital (MGH). A written consent was obtained from all subjects. For each subject, two successive protocols were used: a diffusion MRI AxCaliber protocol (Assaf et al., 2008), and a lipid and macromolecular tissue volume (MTV) protocol similar to the one used by Mezer et al. (Aviv Mezer et al., 2013). The total duration of the acquisition was about 30 min.

2.1. Acquisition

MR scans were performed using a dedicated high-gradient (AS302) (Setsompop et al., 2013), 3T MRI scanner (MAGNETOM Skyra CONNECTOM, Siemens Healthcare). The gradients are capable of 300mT/m in each direction (x, y, z) and a maximal slew rate of 200T/m/s (downgraded to 90T/m/s for the diffusion gradients for safety reasons). A custom-made 60-channel phased-array head/neck receive coil was used (Keil et al., 2013). The body coil was used for excitation. The isocenter was set at the level of the mouth.

2.1.1. Diffusion

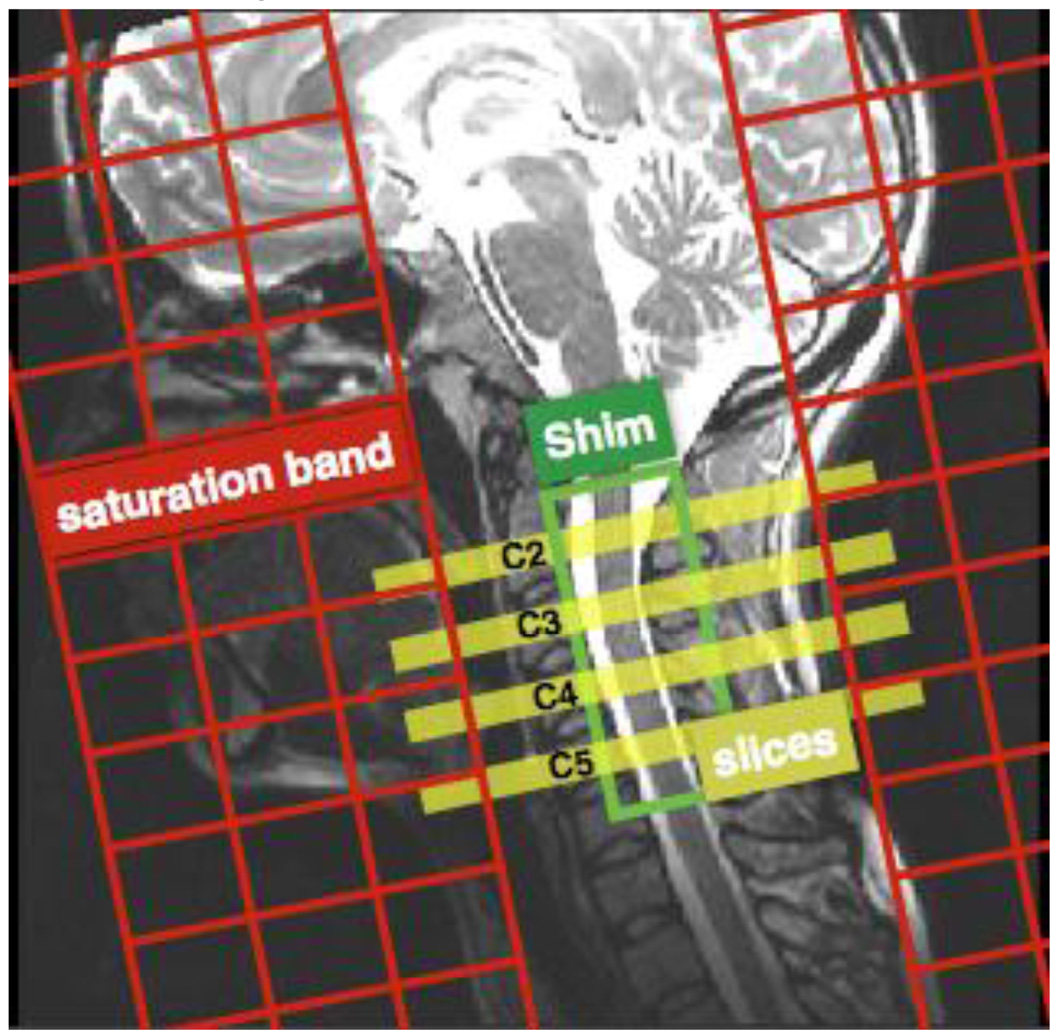
Four axial slices were acquired in an interleaved spatial order, covering C2, C3, C4 and C5 (the gap was adjusted per subject). Slices were placed at the level of the mid-vertebral body, where B0 field is the most homogeneous (Cohen-Adad et al., 2011). Slice thickness was 5mm and matrix size 128×128. The field of view (FOV) was adjusted for each subject in order to have the slice-selection direction oriented along the spinal cord main axis. Second-order shimming was done in a small box encompassing the cervical cord. Field of view in the phase encoding direction (antero-posterior) was reduced using two saturation bands, resulting in an in-plane resolution of 0.8×0.8mm². A single-shot spin-echo echo-planar imaging with monopolar diffusion-encoding was used. Parameters were: TE = 70ms, acceleration of R=2 using GRAPPA reconstruction (Griswold et al., 2002), bandwidth = 1185 Hz/pixel. Effective echo-spacing was 0.49ms. The acquisition was cardiac-gated using an oximeter probe. Two slices were acquired per cardiac cycle, resulting in a repetition time of approximately 2s (forced to be higher than 1.6s to maximize T1 recovery). Effect of T1-weighting caused by partial longitudinal recovery was discussed in (Duval et al., 2015).

Q-space was sampled linearly (from G = 0 to G = √2*300 = 424 mT/m) in four directions perpendicular to the spinal cord XY, X-Y,-XY,-X-Y as in (Duval et al., 2015). In addition, 32 b=0 images were acquired Diffusion parameters were: gradient pulse duration δ = {3 6, 6, 10} ms and diffusion time Δ = {20 20 40 36} ms In total 460 q-space images were acquired per subject. Image acquisition was randomized in order to intersperse high SNR data (used for motion correction) throughout the acquisition.

2.1.2. MTV

Multiple flip angle spoiled gradient echo 3D FLASH images were acquired to measure MTV. Parameters were: TR/TE = 20/2.74 ms, flip angle = {4°, 10°, 20°, 30°}, 20 slices covering C2 to C5, matrix size = 192×192, resolution = 0.8×0.8×5mm³, R=2 acceleration using GRAPPA reconstruction, bandwidth=400 Hz/pixel.

In order to correct for B₁+ inhomogeneity, a B₁ map was estimated using the double angle method (Insko and Bolinger, 1993). A segmented spin-echo EPI sequence was used with the following parameters: TR/TE=3000/19ms, flip angle = {60°, 120°}, 4 slices covering C2 to C5, voxel size = 3×3×5 mm³, matrix size = 64×64.

2.2. Preprocessing

2.2.1. Diffusion

2.2.1.1. Estimation of noise standard deviation

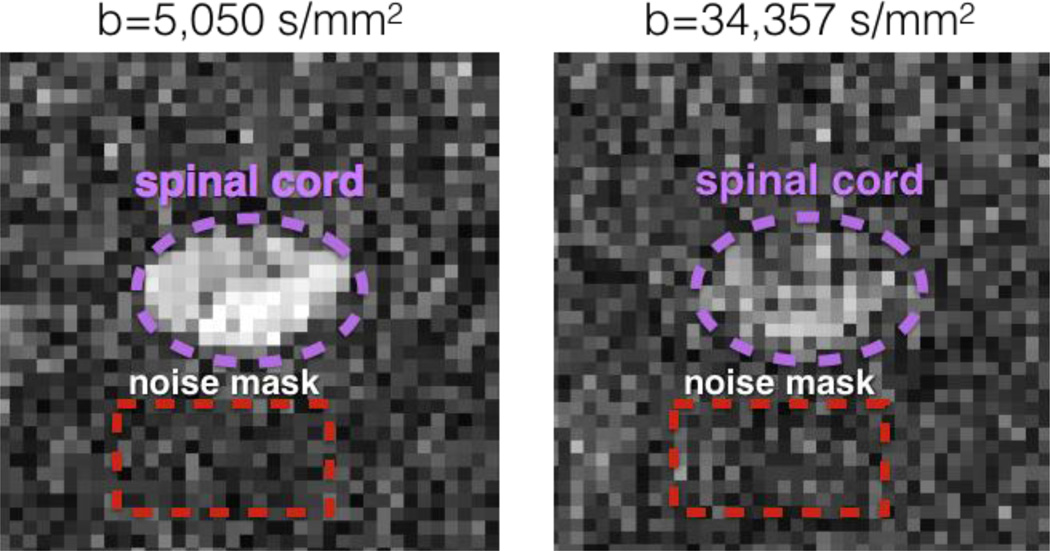
For each subject, noise histogram was estimated on the raw diffusion data within a manually drawn mask showing no signal at high b-value (> 5000 s/mm²) and close to the spinal cord (see figure 2). The noise was estimated at b-value > 5000 s/mm² where signal from fat, muscles or CSF was mostly non-existent This resulted in clean “background voxels” that were not affected by chemical shift, ghosting or aliasing artifact. This noise mask was chosen very close (<1cm) to the spinal cord in order to solve the smooth spatially-dependent noise distribution when using GRAPPA reconstruction (Aja-Fernández et al., 2011).

Figure 2.

Illustration of the noise mask manually drawn on a slice of subject #5 at b = 5,050 s/mm² and b = bmax = 34,357 s/mm². Note that the high diffusion-weighting suppresses signal from CSF and fat, and thus allows to estimate the noise distribution close to the spinal cord.

The noise was assumed to follow a non-central χ distribution (Aja-Fernández et al., 2011), which has three parameters: the standard deviation of the noise σ, the degree of liberty L (representing the effective number of coils) and the non-centrality parameter η (representing the underlying signal). Histogram fitting was done using Matlab¹.

2.2.1.2. Eddy-current and subject motion correction

Eddy-current distortions were corrected using the reversed gradient method (Bodammer et al., 2004). Subject motion was corrected by using a slice-by-slice registration method regularized along the superior-inferior direction (SliceReg) (Cohen-Adad et al., 2015). Images acquired with b-values ranging between 429 and 4000 s/mm² were used to estimate transformations as other images were not reliable (CSF contamination at low b-value and poor SNR on high b-value). The first of these images was used as a reference. Then, a spline regularization along the time dimension was used to correct images acquired at b-value < 429 and b-value > 4000 s/mm² (Duval et al., 2015).

2.2.2. MTV

FLASH images with flip angle 4°, 10° and 30° were registered to the FLASH image with flip angle 20° using SliceReg (Cohen-Adad et al., 2015) and mutual information metric. The B₁+ map obtained using the double-angle method was smoothed using 3D polynomial functions of order 6 and resampled to the FLASH space.

2.2.3. Registration of MTV metrics to diffusion data

The spinal cord was segmented on the MTV and mean diffusion image using PropSeg (De Leener et al., 2014). MTV data were then registered on the diffusion data based on spinal cord segmentations using slice-by-slice affine transformation.

2.3. Metric quantification

2.3.1. Diffusion

Q-space data were analyzed using the two-compartment model CHARMED (Assaf and Basser, 2005). This model assumes two compartments, intra- and extra-axonal, where water molecules present restricted (r) or hindered (h) diffusion. The MRI signal in each voxel is then expressed as:

$$S=S_0(TE,TR)·[(1-\mathit{\text{fr}})·S_h(q,\delta ,\Delta ,Dh)+\mathit{\text{fr}}·S_r(q,\delta ,\Delta ,d)]$$ (1)

with q, δ and Δ the diffusion parameters of the MRI acquisition; Dh, fr and d quantitative metrics describing the tissue; S_h and S_r the signal models of the hindered and restricted compartments.

Dh represents the apparent diffusion coefficient of the hindered diffusion compartment, (1−fr) the fraction of hindered (or extra-axonal) water, Dr the diffusion coefficient of the restricted compartment, fr the fraction of restricted (or intra-axonal) water and d the axon diameter index (Alexander et al., 2010). Axon diameter index is the average axon diameter in a voxel, weighted by the volume of each axon. Throughout the manuscript, we refer to it as axon diameter for simplicity.

S_h was modeled assuming Gaussian diffusion using the Stejskal and Tanner equation (Stejskal and Tanner, 1965) and S_r was modeled using Gaussian phase distribution equation in a cylinder (Wang et al., 1995). The diffusion coefficient in cylinders was set to Dr = 1.4µm²/ms as in (Barazany et al., 2009).

Model fitting was done voxel-by-voxel using the interior-point optimization algorithm (Byrd et al., 2000) included in the Matlab Optimization Toolbox Release 2014a (MathWorks, Inc.). Table 1 shows the fitting parameters with initialization and constraints. Rician likelihood was used in the objective function f in order to account for noise bias during the fitting:

$$f=-\sum \hspace{1em}\mathit{\text{log}}\left(\frac{S_{\mathit{\text{data}}}}{\sigma }\mathit{\text{exp}}\right(-\frac{{S_{\mathit{\text{data}}}}^2+{S_{\mathit{\text{model}}}}^2}{2{\sigma }^2}\left)I_0\right(\frac{S_{\mathit{\text{data}}}{S}_{\mathit{\text{model}}}}{{\sigma }^2}\left)\right)$$ (2)

with S_data the experimental data, S_model the signal computed using equation 1 and σ the standard deviation of the noise evaluated using the method describe in the previous section.

Table 1.

Fitting parameters used in the interior-point algorithm, with initialization and boundaries

fitting parameter	S0	fr	Dh (µm2/ms)	d (µm)
initialization	1	0.3	1	2
boundaries [min, max]	[0, 2]	[0, 1]	[0, 3]	[0, 10]

2.3.2. MTV

Voxel-wise estimation of M0 (product of the coil reception profile and proton density) and T1 were done according to (Fram et al., 1987). B₁+ map was used to estimate the effective flip angle in each voxel (Venkatesan et al., 1998). Reception profile was estimated using the method described in (Mezer et al., 2015; Volz et al., 2012) that uses the linear relationship between T1 and PD to estimate a smooth field in the cord. We assumed no contribution from T₂* relaxation due to the fairly short TE (2.74 ms).

A cerebrospinal fluid mask was computed using (i) estimated T₁ values > 3 s and < 7 s and (ii) a 4mm dilation of the spinal cord segmentation. PD of cerebrospinal fluid (PDCSF) was then averaged in that mask. Finally, MTV was computed as in (Aviv Mezer et al., 2013):

$$\mathrm{M}\mathrm{T}\mathrm{V}=1-(\mathrm{P}\mathrm{D}/\mathrm{P}\mathrm{D}\mathrm{C}\mathrm{S}\mathrm{F})$$ (3)

2.3.3. g-Ratio

The g-ratio weighted metric was computed as in Campbell et al. 2014 (Campbell et al., 2014; Stikov et al., 2015b), assuming that the Myelin Volume Fraction (MVF) is directly related to the Macromolecular Tissue Volume (MTV): MVF = MTV (see discussion). First, Fiber Volume Fraction (FVF) was calculated by combining Diffusion and MTV metrics: FVF = MVF+(1−MTV)*fr. Then, the g-ratio was computed as in (Stikov et al., 2011):

$$g=\sqrt{1-MTV/FVF}$$ (4)

2.4. Effect of spinal cord curvature

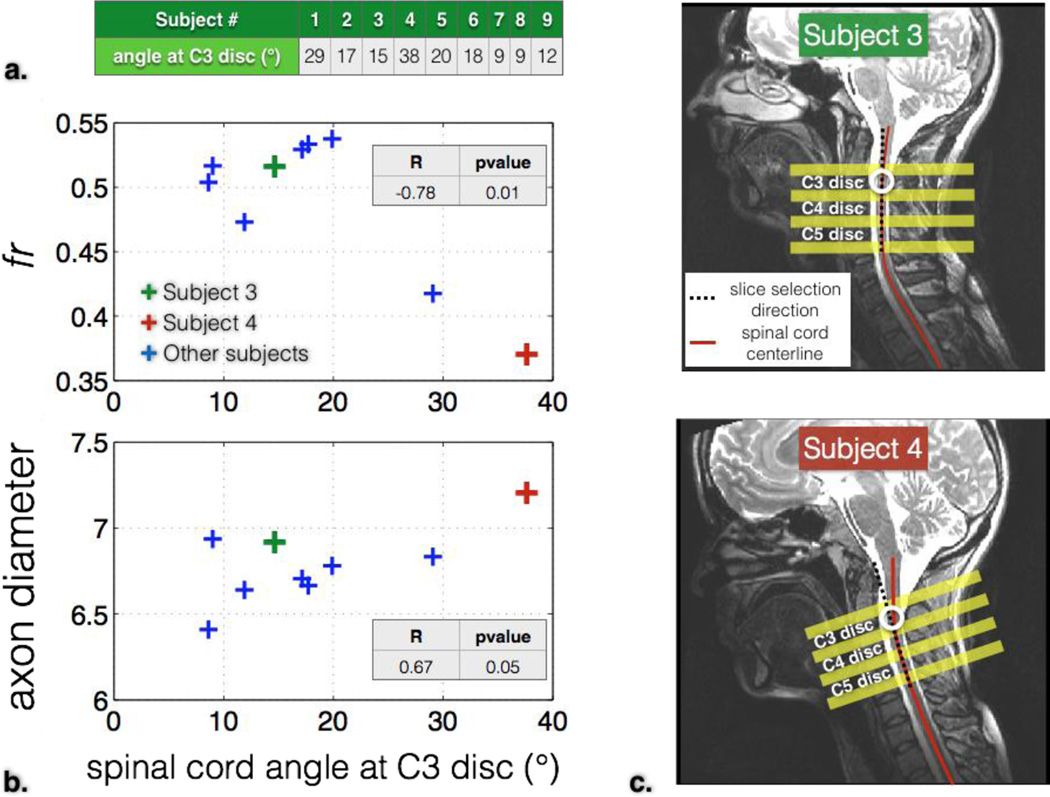
The diffusion protocol assumed that the diffusion-encoding gradients were applied orthogonally to the main running spinal tracts, i.e., orthogonally to the spinal cord axis. Although we made sure that slices were positioned orthogonally to the cord (see figure 1), some subjects exhibited a curved spinal cord and hence a bias on the estimated diffusion metrics might have been present This bias was assessed by computing the Pearson’s coefficient correlation between the error angle (defined as the angle between the slice encoding direction and the cord axis at the C2–C3 disc location) and the diffusion metrics, averaged in the white matter at C2 and C3 levels.

Figure 1.

Slices, shim box and saturation bands position on subject #4.

2.5. Template registration and atlas-based analysis

Registration of Diffusion and MTV metrics to the MNI-Poly-AMU template (Fonov et al., 2014), as well as the extraction of metrics per tract were done using the Spinal Cord Toolbox (SCT)².

In order for the registration procedure to account for the inter-subject variability of gray matter shape, a highly contrasted white/gray matter image was generated from the diffusion data by averaging diffusion-weighted images acquired at b-values between 2,000 s/mm² and 20,000 s/mm² (see figure 5). Throughout the manuscript the term “mean DWI” will be used to define this image. This mean DWI image was then registered to the white matter template of the MNI-Poly-AMU template. Registration was performed slice-by-slice in two steps: (i) initial affine transformation and (ii) diffeomorphic SyN transform (Avants et al., 2008).

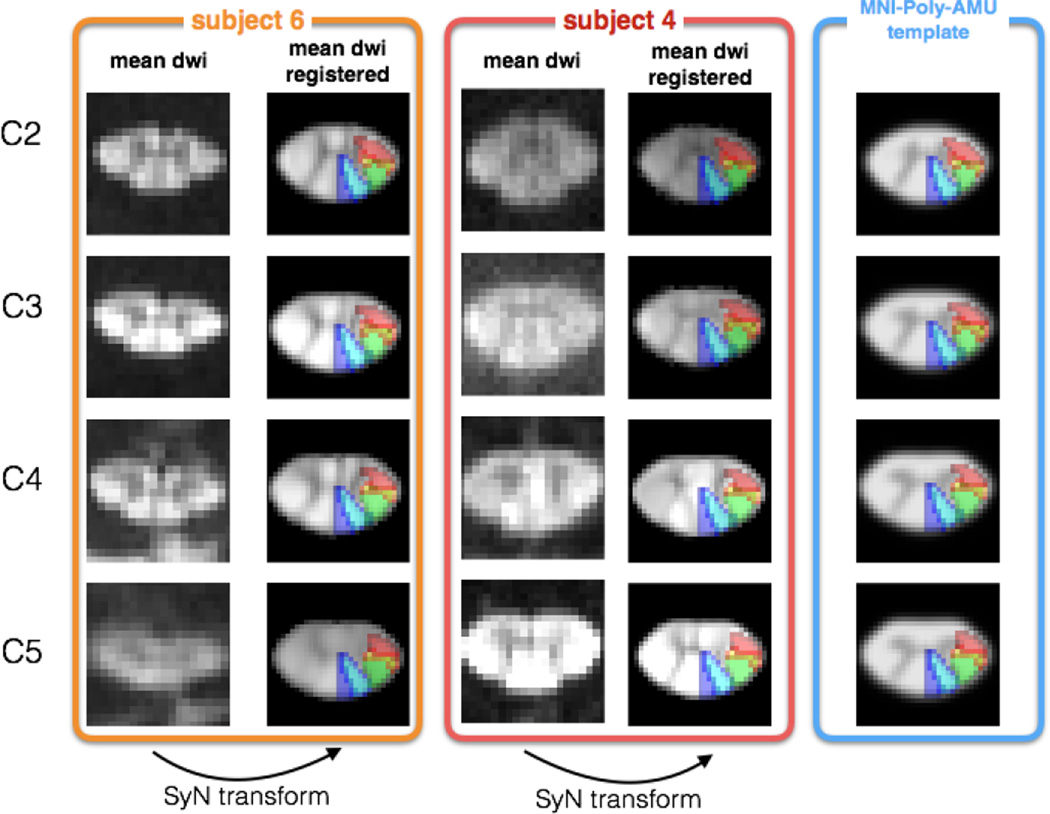
Figure 5.

Registration result of the mean DWI to the template space. Subjects #6 (orange panel) and #4 (red panel) are presented here for illustration purpose. For each subject, the mean DWI was registered to the MNI-Poly-AMU white matter template (Blue panel) using a combination of affine and SyN transformations. Gracilis (blue), cuneatus (cyan), corticospinal (green), rubrospinal (orange) and spinothalamic (red) tracts are overlaid on the registered data for visualization purpose. Note that the mean DWIs shown here were generated using data acquired at b-values between 2,000 s/mm² and 20,000 s/mm² (also see the Methods section).

Quantification of metrics within the white matter and specific spinal pathways was done in the template space using the atlas of white matter tracts (Lévy et al., 2015). Maximum a posteriori method was used to correct for partial volume effect between tracts and between the white matter, the gray matter and the CSF. The following tracts were studied: gracilis, cuneatus, corticospinal, rubrospinal and spinothalamic.

In order to assess the reproducibility of g-ratio, MTV, T₁, Dh, fr and axon diameter a three-way ANOVA analysis was done using the following categories: subject, pathway and laterality (left/right). Significance level was set at p = 0.01.

3. Results

3.1. SNR and noise analysis

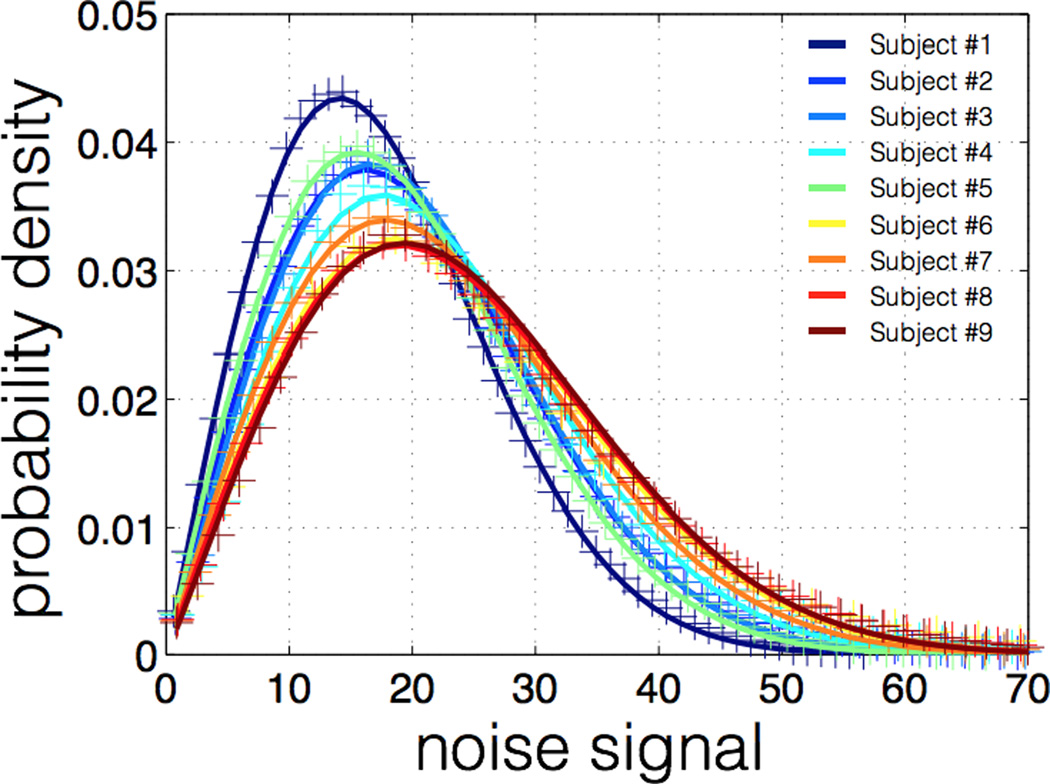
Table 2 shows the average SNR in the spinal cord for each subject at b=0 and bmax, along with fitted parameter L (effective number of coils) of the non-central χ distribution Average NR was 12.7 on b=0 images and 2.1 on images acquired at bmax. Note that this measure of SNR includes both the thermal noise and the physiological noise, hence the relatively low values. The effective number of coils L was always lower than 1.05, which is very close to a Rician distribution (L=1). Fitting results of noise histograms are shown in figure 3. Fitting was very good for all subjects, suggesting a good modeling of the noise.

Table 2.

SNR and L (non-central χ parameter) values for each subject

Subject #	1	2	3	4	5	6	7	8	9
SNR b=0	12.5	10.9	13.8	12.7	18.0	12.4	10.9	9.8	13.2
SNR bmax	1.9	2.3	2.5	2.0	2.8	2.4	2.0	1.7	1.8
L (Effective number of coils)	1.02	1.01	1.05	1.04	1.00	1.00	1.00	1.00	1.03

Figure 1.

Non-central χ fitting of noise histogram for each subject Noise was assessed on images acquired at b > 5,000 s/mm². Noise distribution was found to be Rician (L < 1.05 for all subjects).

3.2. Effect of spinal cord curvature

Figure 4 shows the effect of spinal cord’s angle with respect to the slice encoding direction on diffusion metrics. The error angle was measured at the C3 disc for each subject. Diffusion metrics were averaged in the white matter of vertebral levels C2 and C3. fr was significantly decreased (r=−0.78, p=0.01) for angles over 20°. Axon diameter was significantly correlated with the error angle (r=0.67, p=0.05). The average error angle at C3, C4 and C5 discs was 17°, 12° and 23° respectively.

Figure 4.

Effect of the spinal cord’s angle with respect to the slice-selection direction on diffusion metrics. a. angle values (in degree) for each subject (here, extracted at C3 for illustration purpose). b. Diffusion metrics fr and axon diameter averaged in the white matter (at levels C2 and C3) as a function of spinal cord angle (at C2–C3 disc). c. Illustration of two subjects (#3 and #4) with different spinal cord angle at the C3 disc location.

3.3. Registration

Figure 5 shows the registration result for two different subjects. Although the initial shape of the spinal cord differed significantly between subjects, the SyN transform was able to register both the white and gray matter correctly on the MNI-Poly-AMU template.

3.4. Quantitative MRI metric mapping

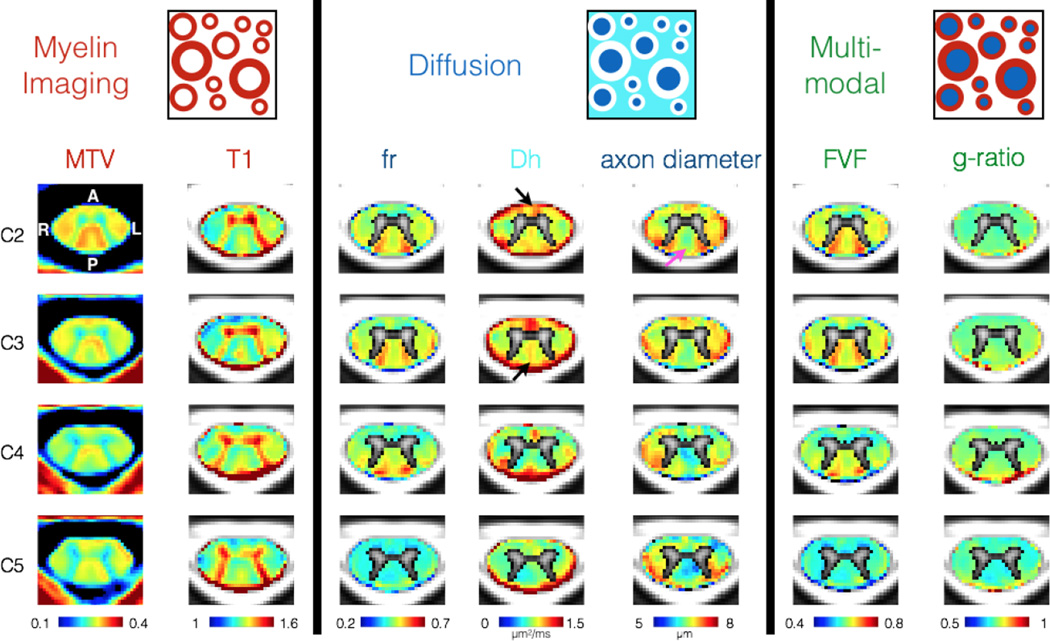
Figure 6 shows the quantitative maps of MTV, T₁, fr, axon diameter, Dh, FVF and g-ratio averaged across all nine subjects. We observe similar trends across slices and across left-right laterality for all metrics. Axon diameter in the gracilis tract was found to increase towards the upper cervical level (pink arrow). fr was similar across slices except at C5 where values were significantly lower (fr = 0.41 at C5 vs fr = 0.48 at C4, T-test gave p-value of 3×10⁻⁴¹). This is partly due to the larger curvature of the spinal cord at this level (23° at C4–C5 disc vs 12° at C3–C4 disc, see previous results). Lower fr at C5 resulted in lower FVF and lower g-ratio at this level. T₁ and MTV were negatively correlated (r = −0.81), consistent with a previous study (Aviv Mezer et al., 2013). fr and MTV were positively correlated (r = 0.42). As expected due to CSF contamination, apparent diffusion coefficient of the hindered compartment (Dh) increased at the periphery of the spinal cord, at the location of the anterior white commissure and at the thin posterior medial sulcus (black arrows on figure 6). All metrics except the g-ratio weighted metric were sensitive to the characteristic variation of microstructure in the posterior column between cuneatus and gracilis tracts. The g-ratio weighted metric was fairly homogeneous within the spinal cord white matter except at the periphery of the spinal cord. The average g-ratio in the white matter was 0.75 +/− 0.03.

Figure 6.

Maps of quantitative MRI metric averaged over nine subjects. Top: schematic cross-section of axons. Left: metrics obtained using MTV protocol. Middle: metrics obtained using diffusion MRI. Right: multimodal metrics combining myelin and diffusion measures. The gray matter was masked using the probabilistic template on metrics where the model isn’t adapted (mainly due to the orientation dispersion of the fibers).

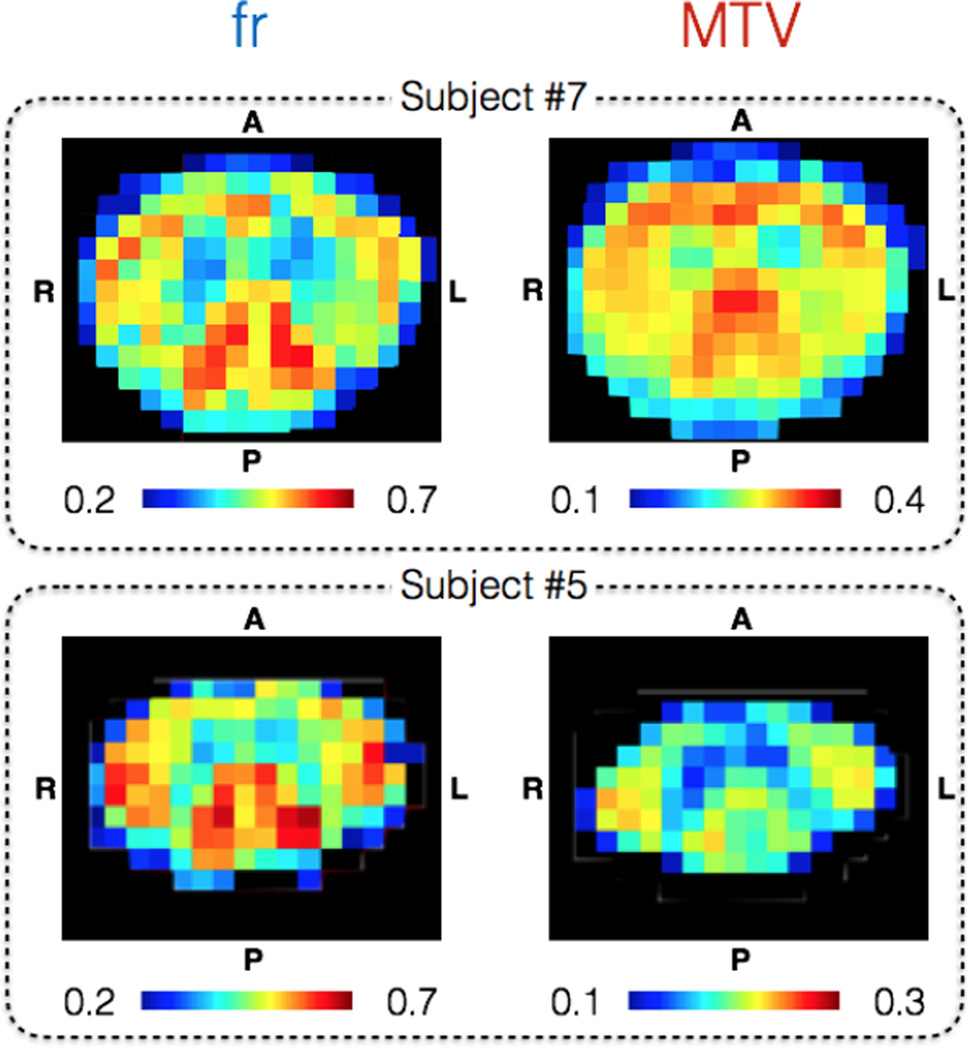
Figure 7 illustrate quality of fr and MTV metrics on an individual basis at slice C3. Even though subjects #5 and #7 present large differences in term of spinal cord shape and cross sectional area, the same pattern can be recognized in the white matter and grey matter. Some discrepancies can be observed between the two subjects, notably in the dorsal part, that we attribute to higher CSF contamination in the smaller spinal cord (subject #5). The high sensitivity of both metrics to microstructure is assessed by the strong contrast between spinal cord tracts, and their high precision by the low level of noise. Note again the apparent positive correlation between fr and MTV metrics in the white matter, this time on individual basis.

Figure 7.

Illustration of the quality of fr (left column) and MTV (right column) at C3 level on two representative subjects: one with a large (subject #7) and another with a small spinal cord (subject #5). The relatively high precision and good sensitivity of these two metrics is suggested by the low level of noise and strong contrast in the white matter, allowing us to distinguish the fasciculus cuneatus and lateral corticospinal tracts, even on a single-subject basis.

In order to prevent the report of biased values due to excessive spinal cord curvature, subjects #1 and #4 as well as slices acquired at C4 and C5 vertebral levels were discarded for all subsequent results.

Table 3 lists normative values of the different quantitative metrics extracted in the white matter (thresholding the probabilistic white matter template by 0.7). For each metric, we extracted the mean value, the standard deviation within the white matter (averaged across subjects), the standard deviation across subjects of the mean white matter values and the resulting coefficients of variation across subjects. Diffusion metrics fr and axon diameter were highly reproducible across subjects (COV = 4% and 3% respectively). A particularly significant variation of MTV, and thus g-ratio, was found between subjects (COV = 14%). Finally, the B1+ variation within the cord averaged across subjects was 1.02 +/− 0.06. The reader is referred to the Discussion section where possible sources of bias are listed.

Table 3.

White matter normative values. Mean value, standard deviation within the white matter (computed per subject and then averaged), the standard deviation across subjects (of the mean white matter values obtained per subject) and the resulting coefficient of variation (COV) across subjects (STD across subjects divided by the mean).

	MTV	T1 (s)	fr	Dh (µm2/ms)	axon diameter (µm)	FVF	g-ratio
mean	0.28	1.29	0.52	1.05	6.72	0.66	0.76
STD in white matter	0.02	0.13	0.04	0.24	0.32	0.04	0.03
STD across subjects	0.04	0.11	0.02	0.13	0.18	0.01	0.04
COV across subjects (%)	13.7	8.3	4.3	12.7	2.7	1.4	5.0

3.5. Tract-by-tract analysis

Figure 8 shows the results of the tract-by-tract analysis for each metric. The three-way ANOVA (tracts, laterality and subjects) showed no significant difference of g-ratio between tracts (p = 0.6). However, both myelin imaging and diffusion imaging metrics showed significant differences between tracts (p < 4×10⁻³ for all metrics). Significant left-right differences were found only for the axon diameter metric, particularly in the rubrospinal and the lateral spinothalamic tracts (further work will assess if this is artefactual or not). Variation of axon diameter between tracts (p = 4×10⁻¹⁰) was more significant than the variation between subjects (p = 2×10⁻⁴), suggesting a particularly good reproducibility of axon diameter measurement across subjects. The same conclusion applies for the metrics fr and Dh with similar variation between tracts and between subjects. Results per tract can be found in supplementary material S1.

Figure 8.

Tract-by-tract analysis of quantitative metrics. Metrics were extracted in five different tracts (color-coded) in the left and right hemispheres of the spinal cord. A three-way ANOVA analysis was done to assess reproducibility across tracts, laterality and subjects.

Based on the resulting F-scores, a post-hoc power analysis was performed in order to have more insights about the population size needed to detect changes across tracts and/or laterality, assuming a statistical power over 99%. To detect changes across tracts for g-ratio, axon diameter, fr, MTV and Dh, the required sample size is respectively 70, 2, 2, 3 and 2. To detect changes across laterality (also for the same metrics), the required sample size is 8, 2, 200, 2 and 4.

4. Discussion

In this work we combined axon and myelin density measures in the spinal cord of nine healthy subjects to derive a metric weighted by the myelin g-ratio. We believe this is the first attempt to measure the g-ratio in vivo in the spinal cord. Although results showed good reproducibility across tracts, slices and laterality left-right, the interpretation of these quantitative metrics needs to be discussed.

4.1. Comparison with histology

To our knowledge, there is very little literature reporting average values of g-ratio in the spinal cord. In their paper, Chomiak and Hu (Chomiak and Hu, 2009) presented an extensive literature review of the measured g-ratio in the CNS: a value of 0.79 has been reported in the spinal cord of mice (Benninger et al., 2006), and values ranging between 0.72 and 0.81 in different part of the CNS (corpus callosum, optic nerve, superior cerebellar peduncle, anterior commissure, internal capsule and brainstem) of a variety of small animals (mouse, rat, murine, guinea pig and rabbit). They also proposed a theoretical optimal g-ratio value of 0.77 in the CNS. (Remahl and Hildebrand, 1982) observed a higher myelination of axons, and thus a lower g-ratio, in the spinal cord compared to the corpus callosum in rodents. This observation is also corroborated by significantly higher myelin water fraction measured with MRI (Kolind and Deoni, 2011). In another study performed in the ventral root of cat spinal cord, g-ratio ranged between 0.6 and 0.7 (Berthold et al., 1983). The g-ratio measured in the present study (0.75 +/− 0.03) is in the same range as that reported by previous histological studies (between 0.6 and 0.81). Abnormal values (g-ratio > 0.85 or < 0.6) were found at the periphery of the spinal cord and are likely caused by low MTV and FVF values due to CSF contamination, and thus unstable values of g-ratio (see equation 4).

As also observed in (Duval et al., 2015), maps of axons diameter are particularly consistent with histology, but should be interpreted with caution. Indeed, values reported in the current paper are known to overestimate the real mean axon diameter because (i) the use of a single diameter model prevented us from correcting for the effect of larger signal contribution from larger axons (Alexander et al., 2010), (ii) axons smaller than ~3µm hit the resolution limit for axon diameter at 300 mT/m (Nilsson and Alexander, 2012) and could be interpreted as axons of ~3µm diameter in the fitting procedure and (iii) the diffusion metrics might be biased by time-dependency of hindered diffusion coefficient Dh (Burcaw et al., 2015; De Santis et al., 2016; Novikov et al., 2014). Note that this last effect could also disturb the fr metric in this study due to the use of variable diffusion time, as it does in models that use the tortuosity approximation (De Santis et al., 2016).

MTV is the complement of the water volume fraction. Due to the use of short TE (2.74ms) the water volume fraction also includes myelin water or any free proton in the tissue (Tofts, 2003). As reviewed by (Tofts, 2003), evaporation or gravimetric technique of post-mortem or biopsy, as well as other MRI proton density studies, show that human white matter is composed of 72.5% water in the brain. A similar value was measured in the spinal cord (Lajtha, 2013, p. 308) and is consistent with the present study: PD = 1 − MTV = 72% in average. The relation between MTV and myelin content is discussed in the next section (4.2).

fr measures the ratio of the intra-axonal water over the MRI visible water content (assuming restriction in axons only). A range of 45 to 60% was proposed in the review paper (Nilsson et al., 2013). By fixing the g-ratio to 0.75, we came across the same range of fr based on the previous literature reporting an intra-axonal volume fraction of 33% estimated from osmium staining histology of the brain (Perge et al., 2009; Stikov et al., 2015c) and spinal cord (Ong and Wehrli, 2010). Those values are in agreement with the values of fr found in this study (0.52 +/− 0.04).

It should be noted that using histology as ground truth has limitations, given the numerous tissue alterations during preparation (tissue shrinkage after fixation, slicing, staining, microscopy resolution, etc.). For instance, histological studies based on optical imaging in the spinal cord (Chin et al., 2004, 2002; Ong et al., 2008) usually overestimate the myelin fraction compared to the axoplasm volume, leading to abnormal values of g-ratio (~0.3), which is likely due to the insufficient spatial resolution of optical imaging. Alternative histology techniques, such as in vivo microscopy of myelin using coherent anti-Stokes Raman scattering (Bégin et al., 2009; Fu et al., 2008), might prove useful in addressing those limitations.

4.2. Myelin versus macromolecular volume fraction

The sensitivity of MTV to myelin has been demonstrated through the relationship of MTV with other quantitative myelin mapping techniques (Aviv Mezer et al., 2013). In particular, MTV correlates with myelin content (r=0.52 in a single subject and r=0.9 using literature data), as measured with quantitative magnetization transfer qMT (Sled and Pike, 2000). Note that qMT has been used to measure myelin content in different g-ratio applications (Stikov et al., 2015b, 2011). The sensitivity of MTV to myelin is also confirmed by (i) lower values in the grey matter (see figure 6), (ii) its sensitivity to demyelination in the spinal cord (Bot et al., 2004; Chong et al., 2016), (iii) its high correlation with myelin stained histology (r² = 0.52) in multiple sclerosis (Mottershead et al., 2003), and (iv) its relation with brain development (Saito et al., 2012).

Like other MRI myelin mapping techniques, MTV has to be calibrated to retrieve the absolute myelin volume fraction from the myelin (or macromolecular)-specific metric. This could be done assuming a linear relationship MVF = a*MTV+b. Interestingly MTV values found in the present study are very close to the volume of the myelin sheath (MVF) in white matter tissue estimated using histology: 25 to 30% in the brain (Mottershead et al., 2003; Perge et al., 2009; Stikov et al., 2015c) and the spinal cord (Ong and Wehrli, 2010) (computed from extra-axonal volume assuming a g-ratio of 0.75). In addition, the relatively small variation of MTV (STD in the white matter = 0.02) measured in the present study is consistent with the small variation of myelin content measured with myelin segmented histology of rat spinal cord (STD across tracts = 0.03) (Harkins et al., 2016), or assessed with myelin stained human spinal cord (Bot et al., 2004; Nijeholt et al., 2001). These observations motivated the assumption MVF = MTV used in the present manuscript. This result is somewhat unexpected because MTV includes macromolecules and lipids present not only in the myelin, but also in glial cells membranes and organelles MTV however doesn’t include the myelin water while MVF does. Similar values between myelin and MTV suggest that the non-myelin macromolecules compensate approximately the myelin water.

Note that the proton density (PD = 1 − MTV) is required in order to measure FVF accurately: FVF = MVF + PD*fr. So far, MRI g-ratio studies that use compartmental diffusion models assumed that PD is the opposite of myelin (1−MVF) (Campbell et al., 2014; Dean et al., 2016; Stikov et al., 2015b), without considering the fraction of macromolecules that are outside the myelin (11 to 14% in healthy tissue). In particular, this assumption could be critical in pathology where the extra-axonal compartment is modified due to glial cell proliferation, in particular microglia, or astrocyte scarring. The acquisition of both PD and myelin content might be an interesting means to increase the specificity of the g-ratio metric. While we considered additional myelin biomarkers, hardware constraints on the body coil of the CONNECTOM scanner prevented us from using magnetization transfer pulse. Further investigations using other myelin-specific techniques, such as multicomponent T₂, are needed.

4.3. Reproducibility of quantitative metrics

Axon diameter and fr were remarkably reproducible across subjects without significant spinal cord curvature with coefficients of variation of 2.7 and 4.3% respectively. Variation between tracts were larger than or similar to the variation between subjects. These findings suggest that axon diameter is very similar between subjects and that these metrics do not depend much on factors such as the coil sensitivity profile, the level of noise, the curvature of the spinal cord within reasonable range (< 20°) and other imaging artifacts that can affect the reproducibility of other metrics. This particularly good reproducibility could be attributed to the use of large diffusion gradient up to √2*300 = 424 mT/m high NR thanks to the custom-made tight fitting 64ch coil, and also to the 2D q-space sampling (orthogonal to the spinal cord axis) that simplifies the white matter modeling with fewer parameters to fit and fewer assumptions. Indeed, the tortuosity model designed for 3D sampling (Alexander et al., 2010) also has some bias (De Santis et al., 2016) and reduced sensitivity to the restricted diffusion coefficient Dr (see discussion in (Duval et al., 2015)). The dependency of axon diameter and fr to the protocol scheme (diffusion parameters G, δ and Δ) will be investigated in future studies Finally we can note that comparison with our previous dataset (Duval et al., 2015), acquired with a different scheme, suggests relatively small variation for fr (see discussion “Comparison with previous work”).

Two subjects exhibited large spinal cord curvature (>20° at C2/C3), which introduced biases in the estimation of diffusion metrics. Although the spinal cord curvature can be accounted for in the diffusion model, large curvature can also lead to a total loss of signal at high b-value due to higher diffusion and lower restriction. This issue could be solved with the development of sequences that enable the acquisition of non-parallel slices, or minimized using specially designed head supports that would enable easier antero-posterior tilting of the head.

Here we used cardiac gating to minimize the effect of CSF flow and cord motion on diffusion scans. While cardiac gating with a relatively short TR (here, TR was set to two cardiac cycles, hence about 2s) was previously shown to have minimum impact on the estimation of fr and fh, it should be mentioned that the CSF having a much longer T₁ than the tissue (0.85 vs. 3.5 s at 3T in the CSF, according to (Clare and Jezzard, 2001; Smith et al., 2008)), its partial recovery might have introduced a bias that needs to be further investigated (Pasternak et al., 2009).

MTV showed a reproducible contrast across tracts (three-way ANOVA, p = 0.004), but also a significant bias across subjects (p = 1×10⁻²⁵) and some inconsistency along the spinal cord (see figure 6) that might be artifactual. This inconsistency along the spinal cord is different from the relative consistency of MTV values in different brain pathways (Aviv Mezer et al., 2013). Several causes could explain these discrepancies. Firstly, flip angle correction using B1+ mapping might have lacked accuracy (see figure 6). Incorrect B1+ mapping could be due to an insufficiently long TR (5s) that led to incomplete longitudinal relaxation of spins (especially in the CSF). Alternative B1+ mapping techniques could be explored, such as actual flip angle (Yarnykh, 2007) or Bloch-Siegert technique (Sacolick et al., 2010). Secondly, the measure of PD in the CSF (PDCSF) used to normalize PD in the spinal cord (see equation 3) might have been affected by flow artifacts (Lisanti et al., 2007) and partial volume effects (e.g., with spinal nerves and epidural fat).

4.4. Comparison with previous work

The diffusion protocol used here was slightly modified compared to our previous study (Duval et al., 2015): the echo time was kept fixed at 70 ms in order to prevent T₂ relaxation effects gradient pulse duration δ was varied between 3 ms (necessary for the acquisition at short diffusion time Δ, as suggested by (Huang et al., 2015)) and 10 ms (necessary for large diffusion encoding (qmax = 0.18 µm⁻¹)). Gaussian Phase Distribution was used here to model the restricted compartment as in the supplementary material S4 of (Duval et al., 2015). Correction of noise bias was improved in the present paper by (i) fitting a non-central χ distribution on noise histogram and (ii) using Rician likelihood in the objective function of the fitting procedure, which could partly explain why axon diameter measurements were more reproducible across subjects in the present study.

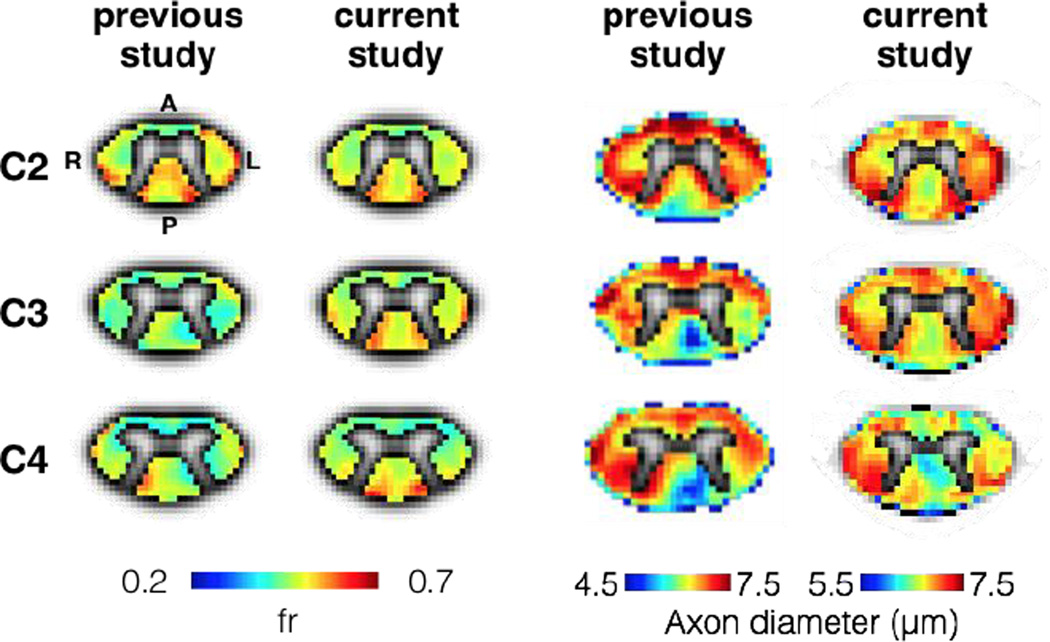
Figure 9 compares the results of axon diameter and fr mapping between (Duval et al., 2015) and the present study. The metric fr was reproducible between both studies (0.52 vs 0.5 in average). Axon diameter mapping however was slightly larger in the present paper (6.72 µm +/− 0.18 µm) than in (Duval et al 2015) (6 14 +/ 0 9µm) While fairly small these differences might be explained by differences between the two studies regarding (i) noise correction algorithm (ii) acquisition protocols or (iii) subject demography (effects of aging, spinal cord area or sex), although the small variation of axon diameter across subjects in the present study (STD = 0.18µm) suggest a small effect of the subject phenotype. A similar contrast between the different tracts can be observed in both studies. For example, the gracilis tract exhibited small and dense axons with increasing diameter towards the rostral direction. Also, both studies show largest axons in the spinocerebellar tract.

Figure 9.

Comparison of axon diameter (left) and fr (right) between (Duval et al., 2015) and the current study (2016). Note that these maps were averaged across five subjects in the previous study (Duval et al., 2015) and seven other subjects in the current study.

The fraction of restricted water measured in the present study (0.52 +/− 0.04) agrees well with NODDI in the human spinal cord white matter (0.57 +/− 0.09) (Grussu et al., 2015). This result shows the consistency of the models between 3D and 2D q-space sampling, as was expected due to the relatively low dispersion of fibers in the spinal cord white matter as measured with NODDI (0.027 +/− 0.003) (Grussu et al., 2015). Values are also in agreement with studies using diffusion data acquired perpendicular to the fibers (fr ≈ 0 5) as explained in (Nilsson et al., 2013). However it should be noted that intracellular volume fraction is often underestimated and can largely differ across methods (Ferezi et al, NIMG, 2015).

MTV values reported in the present paper (0.28 +/− 0.02 in the white matter) are consistent with previous brain studies (between 0.23 and 0.31) (Aviv Mezer et al., 2013; Tofts, 2003). MTV showed very little differences between the spinal cord tracts with a standard deviation in the white matter of only 0.02 (see table 3 and MTV values in supplementary material S1). This small variation (less than 2% variation between white matter ROIs) was also reported using myelin mapping techniques on rat spinal cord white matter using both histology and quantitative magnetization transfer methods (Dula et al., 2010), and on the in vivo human spinal cord using mcDESPOT (Kolind and Deoni, 2011) and inhomogeneous magnetization transfer (Taso et al., 2016).

We notice a negative correlation between the T1 map and the mean axon diameter map (see figure 6) as previously demonstrated in the rodent spinal cord (Harkins et al., 2016). Although the contrast of T1 maps on figure 6 is qualitatively consistent with cervical spinal cord T1 maps found in the literature (Smith et al., 2008), the T1 values were overestimated (1290 +/− 130 ms versus 876 +/− 27 ms). A bias is expected with the variable flip angle T1 mapping method in vivo as shown in (Stikov et al., 2015a). The effect on the MTV metric is unclear: although MTV is normalized with the CSF, the slope of MTV might have been affected by biased T1 values. Future work will address this question by comparing results with MTV values obtained using calibrated T1 from inversion recovery sequence as done in (A. Mezer et al., 2013).

4.5. Interpretation of g-ratio measurements

Based on metric mapping (figure 6) and tract-by-tract analysis (figure 8), both fr and MTV are sensitive to the microstructural differences across spinal tracts. Theoretically however, both metrics present a lack of specificity. Indeed, a decrease of their value can be caused by axonal loss, edema, CSF contamination or demyelination. Combining both metrics via the g-ratio equation (equation 4) aims at disentangling the contributions of confounding factors and extracting only the degree of axon myelination. This would help for instance to understand the complex evolution of multiple sclerosis (MS) lesions: inflammatory cell swelling, demyelination, axon atrophy, astrocyte scarring; all these processes can increase both the intra- and extracellular spaces or reduce myelin content (Franklin, 2002; Frohman et al., 2006), making interpretation of single modality MRI metrics difficult and producing discrepancies between the lesion activity observed with MRI and the patient clinical score (Guttmann et al., 1995; Rovira et al., 2013). The robustness of the g-ratio weighted metric to these different case scenarios will be investigated in future studies. Some assumptions that are necessary for computing the g-ratio might not hold in pathology. For instance, the hindered compartment might become restricted in case of aquaporin-4 deficiency (Badaut et al., 2011) or glial scar formation. Also, the macromolecular content might increase independently from (and not proportionally with, as assumed in “4 2 Myelin versus macromolecular volume fraction”) myelin content due to the proliferation of microglia, migration of astrocytes or by the presence of axonal debris. Additional information, such as Myelin Water Fraction (MWF), might be required to resolve all these case scenarios. Yet, the g-ratio metric computed in the present manuscript is robust to the CSF contamination at the periphery of the spinal cord, suggesting that it can discriminate a pure inflammation scenario from inflammation with demyelination, and thus is expected to bring a gain in specificity compared to the quantitative metrics fr and MTV taken independently.

The g-ratio is known to be fairly homogeneous in the white matter (Chomiak and Hu, 2009; Rushton, 1951), which has been confirmed in the current experiment with fairly low STD of g-ratio across the entire white matter (0.75 +/− 0.03). The underlying source of a homogeneous g-ratio measured with MRI is the correlation found between fr and MTV (r = 0.42, see results section “Quantitative MRI metric mapping“) which will be detailed in the following paragraph.

If we assume a perfectly constant g-ratio, equation 4 can be rewritten in order to express MTV as a function of fr:

$$MTV(\mathit{\text{fr}})=\frac{k*\mathit{\text{fr}}}{(1-k*(1-\mathit{\text{fr}}))}\mathit{\text{with }}k=1-g^2$$ (5)

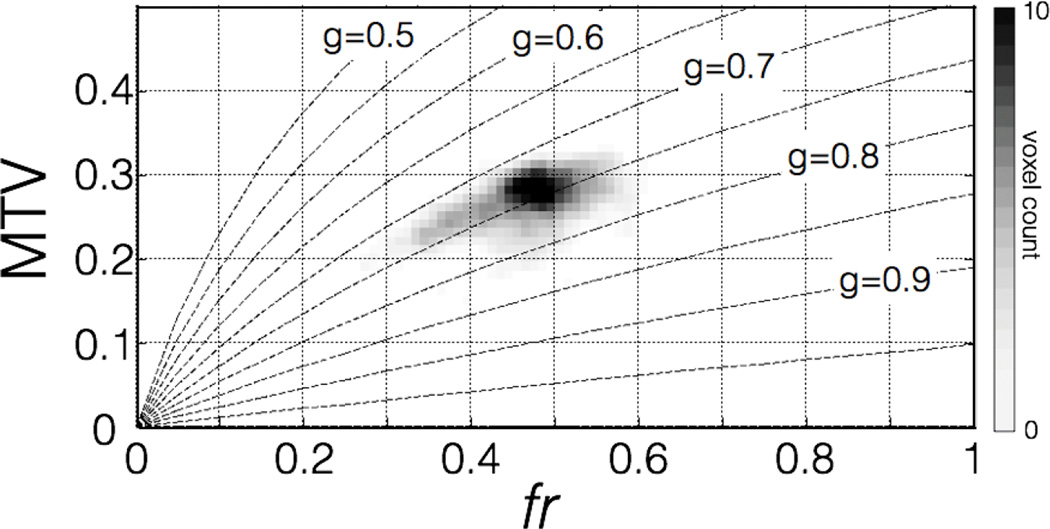
For g ∈ [0,1], this function is increasing monotonically. A homogeneous g-ratio should then be associated with a correlation between MTV and fr metrics, as observed on metrics mapping of figures 6 and 7. Figure 10 shows the voxel-wise comparison of the subject-averaged metrics MTV and fr in the white matter, along with the line of constant g-ratio computed from equation 5, suggesting that both metrics tend to a homogeneous g-ratio for each subject. Note that this figure also gives information on the range of MTV and fr values that would produce abnormal g-ratio values, as well as the precision of g-ratio measurement via the distance separating g-ratio level sets.

Figure 10.

Voxel-wise comparison of subject-averaged MTV and fr metrics in the white matter with lines of constant g-ratio. The grayscale encodes for voxel count. The two different MRI metrics seem to tend toward a constant g-ratio.

g-Ratio values in the gray matter has been masked out voluntarily on Figure 6 to prevent misinterpretation. Indeed, the large orientation dispersion of fibers, as well as the presence of numerous somas and dendrites, limit the interpretation of diffusion metrics acquired with 2D q-space sampling. Note however that the g-ratio appeared homogeneous on the entire cord (data not shown, STD within the cord = 0.03) due to the high correlation between MTV and fr in the entire cord (r = 0.70, p = 10⁻⁸⁰, 548 voxels).

The computation of the myelin g-ratio using equation 4 presents two main limitations. First, it pro ides an “aggregate” g-ratio instead of the average g-ratio in a voxel (Stikov et al., 2011). This metric has been shown experimentally (Stikov et al., 2015c; West et al., 2016) to correlate strongly with the average g-ratio (r = 0.85, p = 0.007) with moderate overestimation (g_aggregate ≅ g_mean + 0.03). Second, we assume a good specificity and accuracy of quantitative MRI metrics fr and MTV. As shown in (Campbell et al., 2016) and discussed in (Dean et al., 2016), this assumption is particularly critical because a lack of accuracy in one of these metrics would imply a poor decoupling of both metrics and thus wrong estimation of g-ratio. A good knowledge of the bias of the quantitative metrics would be required to use g-ratio as a direct measure of the degree of myelination, especially in the pathological white matter. Yet, the accuracy shouldn’t be considered at the expense of the precision. Indeed, the quantitative metrics that we aim to develop are expected to measure subtle changes and should be sensitive to the diversity of microstructure in the white matter tissue.

Results from this study suggest that MTV and fr are particularly precise and sensitive to white matter characteristics, allowing us to detect microstructure differences between white matter tracts on an individual basis (see figure 7 and results of the three-way ANOVA on figure 8). Regarding accuracy, the average fr measured in the present in vivo study are in good accordance with previous ex vivo histological studies as discussed in section “4.1. Comparison with histology” The use of MTV as a surrogate for myelin provided an accurate approximation on healthy tissue with a 1:1 relation, although one has to keep in mind that this might not hold true in the pathological white matter as discussed in section “4.2. Myelin versus macromolecular volume fraction”.

All these evidences suggest that the technique used in this study provides a metric weighted by the myelin g-ratio that is expected to have higher sensitivity and specificity to the integrity of the myelin sheath. The specificity of this metric and its robustness in pathology will be investigated in the future.

5. Conclusion

A metric weighted by the myelin g-ratio can be measured in the in vivo human spinal cord using MRI. Indirect correlation with known histological features, as well as the good reproducibility across tracts of the metrics that are used to compute the g-ratio, suggest a good specificity of these quantitative metrics for the underlying microstructure. These new biomarkers might prove useful for the early diagnosis of demyelination and for assessing the efficiency of new remyelinating drugs.