Abstract
In the last decade, major strides have been made in understanding visual working memory through mathematical modeling of color production responses. In the delayed color estimation task (Wilken & Ma, 2004), participants are given a set of colored squares to remember and a few seconds later asked to reproduce those colors by clicking on a color wheel. The degree of error in these responses is characterized with mathematical models that estimate working memory precision and the proportion of items remembered by participants. A standard mathematical model of color memory assumes that items maintained in memory are remembered through memory for precise details about the particular studied shade of color. We contend that this model is incomplete in its present form because no mechanism is provided for remembering the coarse category of a studied color. In the present work we remedy this omission and present a model of visual working memory that includes both continuous and categorical memory representations. In two experiments we show that our new model outperforms this standard modeling approach, which demonstrates that categorical representations should be accounted for by mathematical models of visual working memory.
Introduction
One of the most exciting recent developments in working memory (WM) research has been the widespread use of delayed estimation tasks (e.g. Bays, Wu, & Husain, 2011; Fougnie & Alvarez, 2011; van den Berg, Shin, Chou, George, & Ma, 2012; Wilken & Ma, 2004; Zhang & Luck, 2008, 2011). In these kinds of tasks, participants study a set of items which can take on any value on a continuum and, after a delay, participants must reproduce the remembered stimulus value as precisely as they can. Thus, delayed estimation tasks are one type of WM task that requires participants to remember the specific studied value in order to perform ideally on the task. This is in contrast to other, more traditional WM tasks in which the memoranda take on a few categorical values, in which case participants only need to remember rough categorical information to perform ideally on the task (e.g. Allen, Baddeley, & Hitch, 2006; Cocchini, Logie, Sala, MacPherson, & Baddeley, 2002; Kane et al., 2004; Saults & Cowan, 2007). The delayed estimation paradigm has produced a great deal of research and has broad theoretical implications. Some authors argue that more traditional WM theories should be updated so as to focus not only on the quantity of information held in WM but also, and perhaps primarily, on the quality of that information (Ma, Husain, & Bays, 2014).
Most of the recent studies that use delayed estimation tasks use mathematical modeling to estimate the precision with which participants can remember the studied features. Mathematical models work by assuming that the data were generated by a specific psychological/statistical process. If that assumption is true, then it is possible to obtain reliable estimates of the parameters of the model, like WM precision, by working backwards from the data. However, if the data were not generated under the assumed model, but the parameters are estimated under that model, then the parameter estimates may be biased or, in the worst case, meaningless. As we will show, the most popular mathematical modeling approach used for color delayed estimation tasks is not appropriate for data from our experiments, which are representative of the common delayed-estimation paradigm. This calls into question both the parameter estimates obtained from that model, across a wide variety of studies, and the theoretical interpretations of cognitive process that follow from these estimates.
In particular, a large portion of the research on WM precision has used the mathematical model used by Zhang and Luck (2008), which we refer to as the ZL (Zhang and Luck) model. Much of the debate based around the ZL model has been focused on whether the data support a discrete (Fukuda, Awh, & Vogel, 2010; Zhang & Luck, 2008) or continuous (Bays, Catalao, & Husain, 2009; van den Berg et al., 2012; Wilken & Ma, 2004) visual working memory resource. The disagreement in the cited literature is related to the interpretation of results rather than the models that generated those results. Given that both sides of the debate use models that are similar or identical to the ZL model, we call the model the “ZL model” not to take a side in this debate but to identify a type of model. Our focus in the present work is not in determining the correct interpretation of results. Rather we seek to determine whether the model used to produce the results accurately accounts for patterns in the data. We use the name “ZL model” only because the model was first proposed by these authors and we lack better shorthand.
As we will show, the main deficiency of the ZL model is that it does not include a mechanism by which information could be stored categorically in WM, rather assuming that all information in WM is stored continuously. By continuously, we mean as a specific value that can vary along a continuum, such as a specific shade of red which can vary continuously within color space. However, it is entirely possible that certain kinds of continuous information can be stored in WM using some kind of categorization (Bae, Olkkonen, Allred, & Flombaum, 2015; Olsson & Poom, 2005; Rouder, Thiele, & Cowan, 2014). For example, colors could be remembered categorically if the studied colors are named and the names maintained using, e.g., covert verbal rehearsal (Donkin, Nosofsky, Gold, & Shiffrin, 2015). As we will show, categorical color representations appear to be heavily used by our participants. We will argue that the ZL model is unable to effectively account for our data, and we propose an alternative model that is more complete.
Research Plan
We used two delayed estimation tasks using colors that varied across a continuous spectrum. A schematic of a single trial is presented in Figure 1. In our first experiment, we manipulated the memory load that participants were placed under by manipulating set size, which is the number of to-be-remembered colors that were presented on each trial. In our second experiment, we fixed the set size to four items and instead manipulated the amount of attentional resources available to participants by varying the cognitive load that participants were placed under. This was done by requiring that the participants perform a secondary task while maintaining the studied colors. The secondary task was a tone discrimination task. Cognitive load was manipulated by varying the number of discriminations that were required during a fixed-length maintenance interval (for more on cognitive load, see Barrouillet, Bernardin, Portrat, Vergauwe, & Camos, 2007; Barrouillet & Camos, 2012; Barrouillet, Portrat, & Camos, 2011). The two manipulations we used in our experiments can be thought to increase task difficulty in different ways. The set size manipulation increases difficulty by requiring participants to maintain a greater number of items in WM. The cognitive load manipulation increases difficulty by reducing the attentional resources available to support memory maintenance. By using these manipulations, we are able to determine which, if either, of the manipulations dynamically impacts the content of visual working memory. The primary parameters of our model provide a mathematical reflection of this impact.
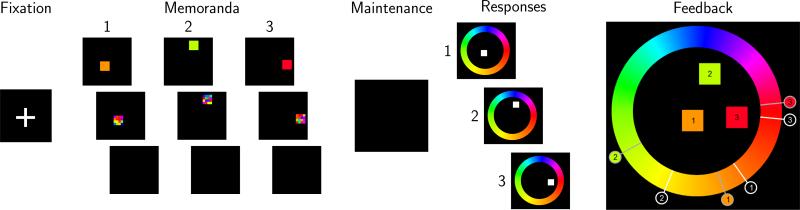
Figure 1.
Schematic of a single trial with 3 stimuli for Experiment 1. Each trial began with a fixation cross, followed by the to-be-studied colors for that trial. Following a maintenance interval, participants made their responses to each of the color stimuli in the order of stimulus presentation. The feedback display showed the studied colors in their locations, with order indicated with numbers. The participant's responses were indicated with white markers and the correct responses were indicated with gray markers with backgrounds filled with the studied color. In this example, for color 3, the correct response is just above the given response. The trial structure for Experiment 2 was very similar, with the main difference being that the maintenance interval contained the secondary tone discrimination task and was longer (6 s).
We analyzed our data using a mathematical model that, as we will show, outperforms the ZL model and offers new insights into the behavior of participants. In our modeling approach, we will focus primarily on three important parameters of WM. The first two primary parameters are the two parameters of the ZL model: the proportion of the studied colors that are stored in WM on a typical trial and the memory precision of these continuously-remembered colors. Our third parameter, a novel component of our model, reflects the proportion of items stored in memory categorically versus continuously. This parameter allows us to determine 1) whether people use categorical representations in delayed color estimation tasks at all and, if 1 is true, 2) whether our task difficulty manipulations cause a trade-off between categorical and continuous memory. There are other secondary parameters that are required for the model to function well, but the three primary parameters are of greatest theoretical importance.
Cognitive Load
One of the novel contributions of the present work is that we examined the effect of cognitive load on performance in a delayed estimation task. This allowed us to test whether important parameters of WM, such as precision, vary with cognitive load. Cognitive load is the proportion of the retention interval which is occupied by a non-maintenance task. In other words cognitive load quantifies how much time is spent on secondary tasks during the retention of a working memory set. Higher cognitive load means more time spent on secondary tasks and less time spent on maintenance.
Although most work using delayed estimation has primarily analyzed the number of representations maintained by manipulating set size (e.g. Bays & Husain, 2008; Zhang & Luck, 2008) and cueing (e.g. Gorgoraptis, Catalao, Bays, & Husain, 2011; Zokaei, Gorgoraptis, Bahrami, Bays, & Husain, 2011), the manipulation of cognitive load holds the primary task constant and varies secondary task requirements. It is an open question whether varying the amount of maintenance time available during retention would affect representations held in visual working memory in the same manner as attempting to remember more items in total. Our manipulation of cognitive load tasks is a first step toward answering this question.
Focus of Attention
The assumption that items in WM are stored in different ways is related to the idea that continuous information is difficult or impossible to maintain through active maintenance (Ricker & Cowan, 2010; Vergauwe, Camos, & Barrouillet, 2014). In contrast to continuous stimulus values, most memory items are naturally categorical. Words, numbers, letters, etc. are all discretely categorical in that they are either remembered or not. A specific color value differs from these discrete examples in that participants can remember color values that are perfectly correct, nearly correct, slightly wrong, very wrong, or anywhere in between. If it is indeed difficult to maintain continuous information, we might expect most memory items to be remembered categorically in delayed estimation tasks. We have previously argued that truly continuous information cannot be actively maintained, but it may also be true that a limited amount of information can be maintained through constant focal attention (Ricker & Cowan, 2010; Vergauwe et al., 2014). Following this theory, if information leaves the focus of attention for more than a few milliseconds, then all continuous information may be lost.
In recent years several authors have put forth strong arguments in favor of a single item focus of attention size (e.g. Garavan, 1998; McElree & Dosher, 1989; Oberauer & Bialkova, 2009). If the focus of attention is required to maintain continuous information and if it can only accommodate a single item, it could explain why only a limited amount of continuous information can be maintained. Following this theory we would expect that no more than a single item would be remembered through the use of continuous item memory on any given trial. Our model, however, does not strictly assume anything about the number of categorical and continuous stimuli that can be remembered in WM, instead allowing the capacities to be freely estimated. On trials using a secondary task, perhaps even fewer items would be remembered on average by using a continuous memory representation because the focus of attention would have to be shared with the secondary task. To anticipate, this pattern of results is found in our data.
Method
Our two experiments share a similar method and were analyzed in the same way, so we present the methods together before moving on to a combined results section. Both experiments were approved by the University of Missouri Campus Institutional Review Board.
Experiment 1
A sample of 12 participants (6 female) with mean age of 19.1 years drawn from an introductory psychology course at the University of Missouri, Columbia took part in the experiment. On each trial, participants were tasked with remembering a sequence of 1, 3, or 5 colors presented at distinct locations on a computer screen. The structure of a single trial is shown in Figure 1. Each trial began with a fixation cross in the center of the screen that was presented for 500 ms. Each color in the sequence was presented as a square for 400 ms. Immediately following each color, a mask made from a 4×4 checkerboard of randomly selected color values was presented for 200 ms, followed by a 200 ms interstimulus interval in which the screen was blank. Following the last item, mask, and interstimulus interval, there was a 1300 ms maintenance interval before the test screen was presented (i.e. there was a 1500 ms delay between the last mask and the test screen). At test, the participant was shown a color ring surrounding the area in which the colors had been presented. The participant was asked to estimate the values of all of the studied colors in order by clicking the color on the ring that corresponded to each studied item. To assist participants, a white square (white was not one of the possible stimulus colors) was presented in the location of the color that they should be reproducing. After each response was made, the white square was moved to the location of the next color that should be reproduced. Because the responses were cued in the order of presentation, each remembered color could be retrieved through its binding with either a unique location or a unique serial position. After the participant had made their final response, they were shown a feedback display that showed 1) the correct colors in their locations, with numbers indicating the order in which the colors had been presented, 2) the locations on the ring that corresponded to these colors, and 3) the participant's responses. Each participant performed 60 trials at each set size for a total of 180 trials. The experimental software was created using CX (Hardman, 2015) and was run on standard desktop PCs with CRT monitors running at a resolution of 1024 by 768 pixels.
The colors we used were full saturation, full brightness colors from the HSB color space, continuously varying in hue. The set of colors used for each trial were selected at random given the constraint that no two colors were allowed to be within 40 degrees of angle from one another during any single trial. The angle corresponded to the location of the color on the response ring. The colors were selected using a function that converts an angle in degrees to a hue. The function warps the hue values in order to control the amount of the resulting color ring that filled with different colors. This function is given by the following system of equations
where AO is the output angle, AI is the input angle, LI and HI are the low and high ends of the input range that AI is in, LO and HO are the low and high ends of the output range corresponding to the input range, HSB(h, s, b) is a function that produces colors given hue (h) in degrees, saturation (s), and brightness (b) values, and CO is the output color. The input range values were 0, 180, 270, and 360 degrees and the output range values were 0, 90, 230, and 360 degrees. As an example, if the input angle AI = 250, then LI = 180 and HI = 270. The output interval endpoints that correspond to the input interval endpoints are then LO = 90 and HO = 230.
After participants finished the WM task, but before they were debriefed, they were given a short questionnaire related to their use of strategy while performing the task. To assess the use of a naming strategy, we asked participants: “How much of the time did you remember the colors by remembering their names? Give your answer on a scale from 1 to 5, where 1 is never, 3 is half of the time, and 5 is always.” To assess strategies related to remembering precise details about colors, we asked the following question: “How often did you remember colors by visualizing the exact colors that you saw?” with the same response scale as the previous question. This questionnaire was not used in Experiment 2.
Experiment 2
In a second experiment, we manipulated cognitive load rather than set size in order to examine the effects of a difficulty manipulation other than set size. A new sample of 24 participants drawn from the same participant pool as Experiment 1 participated in the experiment. Each participant performed 30 trials at each level of cognitive load for a total of 90 trials. Because the set size was 4 and the participants responded to each studied stimulus, there were 120 responses per participant per cognitive load. Except for the details included below, the methodology of Experiment 2 was the same as in Experiment 1.
For this Experiment, the set size was fixed to 4 colors. After the last study item was presented, a 6 s maintenance interval began, during which participants performed a secondary task. The secondary task was to judge whether a single presented tone was the higher or lower of two standard tones that were used throughout the experiment. The participant was instructed to press the up arrow key on standard keyboard if the tone was the high tone or the down arrow key if the tone was the low tone. The tones were sine waves, the frequencies of the low and high tones were 262 Hz and 523 Hz, respectively, and each tone was played for 250 ms. The difficulty of the secondary task was varied over three cognitive load levels by manipulating the number of tone discriminations that were required during each maintenance interval. At the three cognitive load levels, 2, 4, or 6 tone discriminations were required during the maintenance interval, which was the same length regardless of the number of tone discriminations. The first tone was played immediately after the mask for the last color had been removed from the screen and the delay between tones was such that an equal amount of time followed each tone. For example, for 2 tones, the first tone was played for 250 ms, followed by a 2750 ms delay, followed by the next tone for 250 ms, followed by a 2750 ms delay.
In this experiment, audio feedback was provided to participants based on their color memory performance after they had finished making all responses for a trial. There were three feedback sounds: A short melody for good performance, a single tone that increased in frequency for neutral performance, and a single tone that decreased in frequency for poor performance. Positive feedback was received if the average error was less than 20 degrees; neutral feedback was received if the average error was between 20 and 60 degrees; negative feedback was received if the average error was greater than 60 degrees.
The memoranda were the same as in Experiment 1, except for the distribution of colors on the response ring. In this experiment, we sampled the colors from the HSB color space where the hue was equal to the angle on the ring, i.e. the color angle warping function was the identity function: AO = AI. The difference in the distribution of colors between experiments allowed us to examine whether the locations of our participants’ color categories is determined by the color value, which might be expected if participants use a naming strategy, or by the angle on the response ring associated with that color, which might be expected if participants try to maximize the distance between color categories in the response space.
Model
We give here an overview of our model, which is mathematically defined in the Appendix. We made two variants of this model and, to anticipate, we begin be presenting the variant that we end up selecting as our best model.
Between-Item Variant
Our first model variant assumes that each response is based on either categorical or continuous memory representations, but not both. Thus, a single memory-based response cannot reflect a combination of both categorical and continuous information. We call this a between-item mixture model because the mixture of categorical and continuous information occurs between items. Note that we do not assume that it is impossible to have both categorical and continuous information about a single item, just that only one of the two kinds of information is used when making a response. As we will demonstrate, this assumption appears to be supported by the data.
When a color is remembered categorically, we assume that the memory item is simply remembered as a color category and all fine-grained detail about the specific hue of the studied color is lost. The number of categories and the locations of the categories are allowed to vary between participants. It is assumed that the same categories are used regardless of task condition (i.e. set size or cognitive load level). Responses based upon categorical representations are centered upon the color category location. For example, a response based on a color that was put into the red category would tend to be a response centered on a specific shade that represents canonical red to a participant. It is assumed that there will be some amount of noise in this response, perhaps due to imprecise positioning of the mouse by the participant.
Continuously-stored colors are stored with information specific to the precise shade of color that was studied. A response that uses a continuous color is assumed to be centered on the studied color with some amount of error, due to an imperfect representation of the color, motor noise, and/or other factors. Continuous responses are assumed to be unaffected by categorical information (e.g. there is no bias caused by categories near the studied color).
Our model accounts for the possibility that when participants guess, they might guess at the location of one of their color categories. Categorical guesses are assumed to have the same variability around the category location as responses based on a categorical memory. When making a categorical guess, it is equally likely that any of that participant's categories will be chosen. If a participant does not make a categorical guess, the guess is assumed to come from a circular uniform distribution (i.e. any response angle is equally likely).
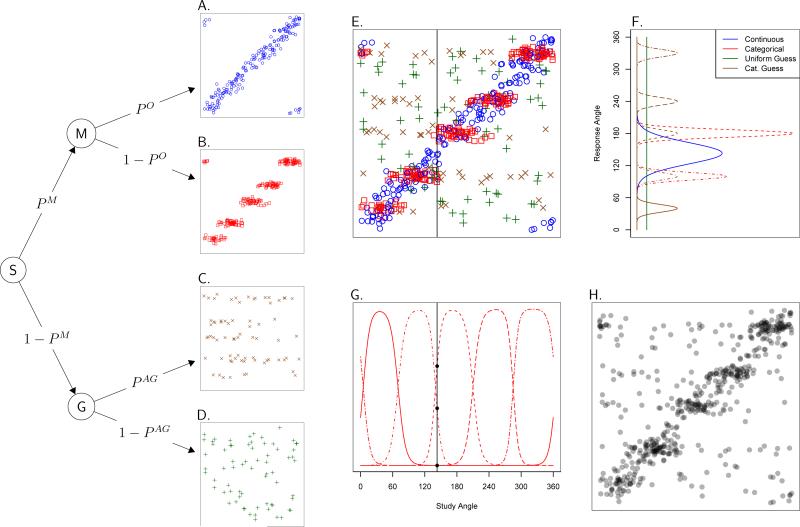
The major components of the model are shown in Figure 2, in which the characteristics of the model are demonstrated using data sampled from an imaginary participant with known parameter values and 5 color categories. There are four types of responses accounted for by the model: continuous memory responses, categorical memory responses, categorical guesses, and uniform guesses. Scatterplots of each of these types of responses are plotted in Panels A through D of Figure 2.
Figure 2.
Multinomial process tree for the model and related plots. For the scatterplots in Panels A to E and H, the x-axis is the study angle and the y-axis is the response angle. The points in those scatterplots are data sampled from an imaginary participant with 5 color categories. Panels A to D show individual response types and Panel E shows the points in Panels A through D in one panel. Panel H shows the same points as Panel E, but without information about the type of the response. Panel F shows the response densities for the different response types for a single study angle, indicated by the vertical line in Panel E. Panel G shows the function that gives the probability that a given study angle will be assigned to the given category.
A multinomial process tree for the model can be seen on the left of Figure 2. Starting from the start node S, the first branch depends on whether or not the participant has the tested item in WM, which happens with probability PM. If the item is in WM, the participant reaches node M. The item in WM may be stored with continuous information, which happens with probability PO, in which case the response distribution in Panel A is reached. With probability 1 – PO, the memory item was categorical in nature and the response distribution in Panel B is reached. If the test item is not in WM, which happens with probability 1 – PM, the participant must guess. A categorical guess happens with probability PAG (“AG” stands for cAtegorical Guess) and a uniform guess happens with probability 1 – PAG, resulting in the response distributions seen in Panels C and D, respectively. As can be seen, the guessing distributions do not depend on the study angle, while the response distributions do.
The response variability in Panel A is controlled by the continuous imprecision parameter, σO. The response variability around category centers in Panel B is controlled by the categorical imprecision parameter, σA, and the locations of the categories are controlled by a set of category center parameters, μ. The variability of categorical guesses around category centers is controlled by the categorical imprecision parameter, σA.
The complete pattern of responses predicted by the model can be seen in Panel E of Figure 2, where the responses from Panels A to D are plotted together in one panel. The same data points are also plotted in Panel H, where information about the type of response represented by each point has been removed to produce a plot resembling the real data (for which we do not know the type of each response). Depending on the type of each response, there are varying probabilities of each response angle being chosen, which are plotted in Panel F of Figure 2. This panel gives a different perspective on the information in Panel E by taking a slice through the response distributions at the study angle marked by the vertical line in Panel E. Thus, the heights of the distributions in Panel F reflect the likelihood that different response angles would be chosen given the study angle.
Studied colors are assumed to be categorized in a probabilistic way, where a given color may not always be categorized in the same way. The function that gives the probabilities that any given study angle would be assigned to each of the 5 color categories of the imaginary participant is plotted in Panel G of Figure 2. The general shape of this function was informed by empirical color-naming data from Bae et al. (2015). In Panel G, different line types indicate different categories. In general, if a studied color is near the center of a category, that category will be selected by the participant nearly all of the time. If a study color is halfway between two categories, either of those categories will be selected with approximately equal probability. For the study color marked with the vertical line in Panel G, it can be seen that the probability that the color would be assigned the two nearby categories is roughly equal, but it is very unlikely for that color would be assigned to any of the more distant categories. Each participant has a category selectivity parameter, σS, that controls how rapidly the probabilities of category assignment transition as the studied color angle moves from one category to another.
All of the parameters of our model are important, but three of the parameters are of primary interest for determining the nature of visual working memory representations. These are 1) the probability that an item is in WM, PM, 2) the precision of continuous WM representations, σO, and 3) the proportion WM representations that are continuous in nature, PO. The first two parameters have the same interpretation as the two parameters of the ZL model, while the third parameter is unique to our model. We allowed these three primary parameters to vary as a function of set size and cognitive load, which will allow us to determine how those task difficulty manipulations impact the most important factors of WM performance. There was no theoretically motivated reason to think that the task difficulty manipulations would affect the secondary parameters, so they were assumed to have the same value regardless of difficulty condition, which had the benefit of constraining model flexibility.
Within-Item Variant
The model we have described above assumes that each response is based on either categorical or continuous memory, but not both. In a recent article, Bae et al. (2015) suggest a model in which each response is based on a mixture of categorical and continuous memory. An assumption here is that participants encode both a categorical and a continuous representation of each item. When a response is required, the two representations are combined in order to take advantage of both sources of information. In this model, all responses are based on a mixture of categorical and continuous information, so we call it a type of within-item mixture model. We decided to investigate the Bae et al. suggestion of within-item use of categorical and continuous memory by participants by creating a variant of our model that uses a within-item mixture of categorical and continuous information.
Our within-item model variant is the same as our between-item model, except that in our within-item variant the meaning of PO changes to the proportion of each response that is based on the continuous memory representation, while 1 – PO is the proportion of that response based on the categorical memory representation. The details of how this changes the model mathematically are described in the Appendix. In the within-item model variant, each response is a weighted average of a categorical and a continuous representation. As a result of this averaging, the within-item model produces qualitatively different data than the between-item model, as is illustrated in Figure 3. In geometric terms, the within-item model produces clusters of responses with a slope between 1, which is the slope of continuous responses, and 0, which is the slope of categorical responses. This intermediate slope arises from the averaging of categorical and continuous representations. The slope of the clusters of responses depends on the relative amounts of categorical and continuous information that are used in each response, which depends on PO. The higher PO is, the more weight is placed on the continuous memory representation and the closer the slopes of the clusters are to 1. The lower PO is, the more weight is placed on the categorical memory representation and the closer the slopes of the clusters are to 0.
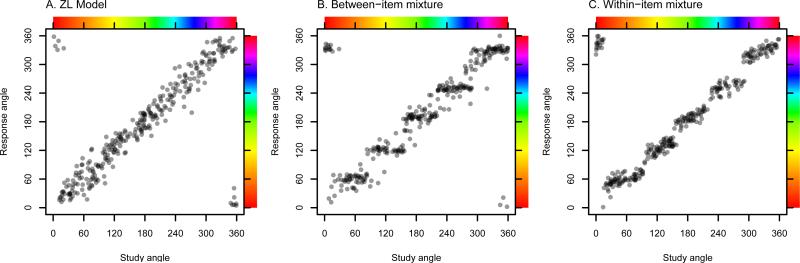
Figure 3.
Data generated from A. the ZL model, B. the between-item variant of our model (the primary model), and C. the within-item variant of our model. No guesses are plotted: Only the memory distributions. For the ZL model, response angles are centered on the studied angle with some error. For the between-item model, responses are either categorical and appear as horizontal steps or continuous and, like the ZL model, are centered around the studied angle. For the within-item model, responses are a mixture of categorical and continuous information, which results in responses that are between the fully categorical flat stair step and the fully continuous line of ideal responding (an intercept of 0 and a slope of 1).
Our within-item model differs in a few ways from the Bae et al. (2015) model. One difference is that in our model the category locations are estimated as part of the parameter estimation procedure, while the Bae et al. model uses category location estimates derived from a separate experimental procedure. Given this difference, the categories used by our model are based on the same task that the other WM parameters are based on. Although unlikely, it is possible that the categories used by participants would differ between tasks, which would result in the category estimates used by our model to be more accurate. An additional difference is that the proportion of each response that is categorical in nature is freely estimated in our model for each participant with the PO parameter. In the Bae et al. model, each is response is based on a constant mixture of categorical and continuous information that does not differ by participant. Thus, there is greater flexibility in our model to account for the potential for participants to differ in how they combine categorical and continuous information in WM. This flexibility, as well as other aspects of our model, may not be desired by some researchers who may instead see advantages of the Bae et al. model for their application. It should be noted that our overarching interest is not to compare our model to the Bae et al. model, but rather to examine the difference between the between-item and within-item assumptions in two variants of our model. By comparing two very similar variants of our model, we avoid having the comparison of the between-item and the within-item assumptions confounded by extraneous differences between our model and the Bae et al. model.
Results
In this section, we will begin by presenting the raw data in scatterplots and describe the patterns seen in the data. We will then compare our two models variants and the ZL model to select the best model. We will then present the parameter estimates we obtained from the winning model, which was the between-item model. Next, we analyze our results from the perspective of the number of categorical and continuous representations remembered by participants (i.e. WM capacity). Finally, we will present some approaches we used to validate our between-item model.
Raw Data
The raw data from the experiments are plotted in Figure 4. This representation was used by Rouder et al. (2014) and allows for a thorough examination of the patterns in the data. Our data show patterns of categorical responding. A “correct” categorical response is a response that is reasonably near the studied value, but which does not depend on the exact studied value. Thus, categorical responses should look like clusters of responses near the line of ideal responding (the line with intercept 0 and slope 1). In practice this looks like a staircase pattern on the scatterplot with each step representing a color category. Correct categorical responses are near the line of ideal responding because they are based on categorical information about the studied color. However, categorical responses are uncorrelated with the specific studied color due to the lack of fine-grained information. A lack of correlation implies that the slope of the best fit line through the responses to each color category should be 0 (i.e. the stairs of the staircase should be level). For example, a studied color in the yellow range of colors would typically be categorized as yellow. When a response for an item in the yellow category is made, that response would be based only on the color category, but not the specific shade of yellow that was studied, because only the category is known.
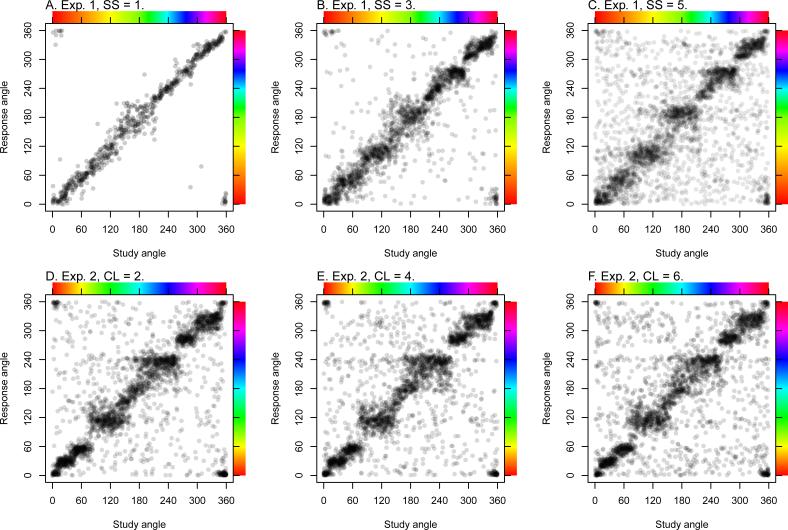
Figure 4.
Scatterplots of data from Experiment 1 (top row) and 2 (bottom row) across manipulations of set size (SS) and cognitive load (CL). Horizontal response bands near the line of ideal responding (intercept 0 and slope 1) are indicative of categorical memory responses. Horizontal response bands that cross the entire space are indicative of categorical guessing.
Of the three predicted patterns of memory responses shown in Figure 3, the aggregated raw data in Figure 4 looks most similar to either the between-item or within-item models. Only at set size 1 in Experiment 1 does responding looks fairly continuous, like the ZL model predictions. The categorical memory responding stair steps appear to be fairly horizontal, which is more in line with our between-item model than our within-item model, but note that it is possible for the within-item model to predict horizontal steps if PO = 0. Thus, it is difficult to distinguish between our two model variants by visual inspection, so we turn to formal modeling to select the best model. Once the best model is selected, we will examine its parameter estimates in detail.
Parameter Estimation
The parameters of the three models were estimated using a Bayesian MCMC approach that was implemented in C++. Details about the specification of the Bayesian model, including priors, can be found in the Appendix. Note that for the parameters that were common between models (including the ZL model), we used the same priors, which were uninformative. For each data set, we ran three parallel chains of 5000 iterations of a Gibbs sampler and verified convergence with the Brooks, Gelman, and Rubin (Brooks & Gelman, 1998; Gelman & Rubin, 1992) diagnostic as implemented in the boa (Smith, 2007) package for R. Convergence was slow for our model variants, so the first 1000 iterations of each chain were discarded as burn-in, then the remaining 4000 iterations per chain were collapsed together for analysis. For two participants in Experiment 2, some of the parameters of the between-item model did not converge according to the convergence diagnostics (the parameters appeared to possibly have bimodal posterior distributions). The analyses were repeated excluding those two participants, but this did not change our results or conclusions, so we elected to keep those participants in the reported analyses.
Model Selection
Comparing the Between- and Within-item Models
We want to know which of our between-item and within-item model variants is the better model. We do not, however, have a fully Bayesian way to compare the model variants, which is due in large part due to the complexities of the models. For an example of the complexity, the category location and category active parameters (see the Appendix for more on these parameters) do not have meaningful posterior means, so measures like the deviance information criterion that require the use of meaningful posterior means cannot be used with our models. Conveniently, however, the between- and within-item variants of our model have the same number of parameters and most of the parameters have the same role in both models. Given the similarities of the model variants, it is reasonable to compare them by simply comparing the likelihoods of the models.
We calculated the likelihood of the model for each participant for each iteration of the MCMC chain, by which we were able to take the parametric uncertainty in the posterior distributions into account. Then, we took the average of the likelihoods across all iterations of the MCMC chain (excluding the burn-in iterations) for each participant. These average likelihoods were compared for the two model variants for each participant. Note that we do not compare the models at each set size or cognitive load because many of the parameters of the models are the same for a participant across all the levels of those factors. As such, comparisons between the variants at each factor level would be dependent on one another, so it is best to perform the comparisons for each participant over all factor levels (participants are also dependent on one another to some extent because we use hierarchical priors on most of the parameters, but the dependence caused by hierarchical priors is smaller than the dependence caused by using the same parameter values for one participant across conditions). Another option would have been to fit the model separately to each set size, but we did not have enough data at each set size to do this (for example, we had only 60 responses at set size 1).
We found that in Experiment 1 the between-item model had a better likelihood for 10 of the 12 participants. In Experiment 2 the between-item model had a better likelihood for 22 out of 24 participants. Thus, there is good support for the between-item mixture model over the within-item model for most of our participants. As such, we will not use the within-item model variant further. Note, however, that we do not believe that this is a final rejection of the within-item assumption, because we have only tested it with our data, which is based on mostly moderately high set sizes. As we indicate in the Discussion, we believe that the within-item assumption may hold under some circumstances, including lower set sizes, and we welcome further research in this area.
Comparing the Between-Item and ZL Models
Now that we have selected the between-item model as the better of our two models, we will compare the between-item model to the ZL model to determine which is the better model. The likelihood-based approach used to compare the within-item and between-item model variants is not applicable here because the between-item model and the ZL model differ substantially in terms of the number of free parameters in the models, which prevents a direct comparison of model likelihoods. Instead, we used an approach based on the fact that the ZL model can be thought of as a simplification of our between-item model. The ZL model assumes that participants make only continuous responses. If that is true, PO in our model should be 1. Thus, it is possible to test the ZL model assumption that participants make only continuous responses by checking whether PO was 1 in our between-item model. If participants make only continuous memory responses, then the added complexity of our model is unnecessary and our model should be discarded in favor of the simpler ZL model. We used a Bayesian hierarchical model with estimated normal distribution prior on PO, which allows us to perform inference on the estimated value of the mean of PO test the ZL model (see the Appendix for more information on the model specification). If PO ≠ 1, then the ZL model can be rejected in favor of our more complex model.
It is difficult to test the value of 1 for the mean of PO because, due to the model specification, PO exists in a latent space on the interval (–∞, ∞). We transformed from the latent space to the manifest probability space with the logit transformation, which means that a probability of 1 corresponds to ∞ in the latent space. It is not possible to test equality with ∞, so we instead tested the hypothesis that the mean of PO = 0.99, which corresponds to a finite value in the latent space. We performed this test using data from Experiment 1 with the Savage-Dickey procedure as suggested by Wagenmakers, Lodewyckx, Kuriyal, and Grasman (2010). The Savage-Dickey procedure involves comparing prior and posterior densities at the point hypothesized to be the true parameter value, with the result of the test being a Bayes factor related to the hypothesis. We found strong evidence that the mean of PO is not 0.99, with a Bayes factor of 3.7 · 1023 in favor of a difference. Due to the model specification, the mean of PO is the mean at set size 5, which was 0.30, indicating high levels of categorical responding. Thus, there is clear evidence that the ZL model, which assumes no categorical memory responding, is not sufficient to account for our data and our between-item model is the best of the three models we compared. Thus, we will go on to interpreting parameter estimates from our between-item model and not present results from either the within-item or ZL models.
Parameter Estimates
Task Condition Effects
The three primary parameters of the between-item model, PM, σO, and PO, were allowed to vary as a function of task condition (set size or cognitive load) through the use of task condition main effect parameters. One of the conditions (the cornerstone condition) had its condition effect parameter set to 0, which means that the condition effects can be interpreted as a difference from the cornerstone condition. The effects of task condition were examined by testing whether the condition effect parameters were equal to 0, which was done using the Savage-Dickey density ratio. The priors on the condition effects were Cauchy distributions with location 0 and a scale that differed for different parameter types (see the prior specifications in the Appendix for more information). Testing any one condition effect is straightforward and comparing two non-cornerstone conditions simply requires calculation of the marginal prior on the difference between two non-cornerstone conditions, which is just the difference between the priors. The difference between two zero-centered Cauchy distributions is a Cauchy distribution with location 0 and scale equal to the sum of the scales of the two distributions. The Bayes factors resulting from the tests of condition effects can be found in Table 1. A Bayes factor greater than 1 is evidence that difference between the conditions is not zero and we will interpret Bayes factors greater than 3 as evidence of a difference. The subscripts on the Bayes factor (BF10) indicate that the alternative hypothesis that there is a difference (denoted 1) is in the numerator and the null hypothesis of no difference (denoted 0) is in the denominator. The ordering of numbers in the subscript indicates numerator or denominator, where the first number indicates which hypothesis is the numerator hypothesis. The Bayes factor reflects evidence in favor of the numerator hypothesis versus the denominator hypothesis, so a larger BF10 gives evidence in favor of the alternative hypothesis of a difference between conditions. The results shown in Table 1 are summarized below.
Table 1.
Effects of Task Condition on the Three Primary Parameters for Both Experiments
| Exp. | Parameter | Comparisona | BF10b |
|---|---|---|---|
| 1 | PM | 1 - 3 | 6.8 · 103 |
| 1 | PM | 1 - 5 | 2.1 · 108 |
| 1 | PM | 3 - 5 | 3.7 · 1012 |
| 1 | σ O | 1-3 | 1.8 · 1012 |
| 1 | σ O | 1-5 | 2.6 · 1013 |
| 1 | σ O | 3-5 | 1.5 · 101 |
| 1 | PO | 1-3 | 2.5 · 106 |
| 1 | PO | 1-5 | 2.8 · 1025 |
| 1 | PO | 3-5 | 7.2 · 100 |
| 2 | PM | 2 - 4 | 1.0 · 100 |
| 2 | PM | 2 - 6 | 3.3 · 105 |
| 2 | PM | 4 - 6 | 4.4 · 102 |
| 2 | σ O | 2-4 | 1.6 · 10–1 |
| 2 | σ O | 2-6 | 2.2 · 10–1 |
| 2 | σ O | 4-6 | 2.8 · 10–1 |
| 2 | PO | 2-4 | 2.9 · 10–2 |
| 2 | PO | 2-6 | 7.2 · 10–2 |
| 2 | PO | 4-6 | 9.6 · 10–2 |
Experiment 1: The set sizes that were compared; Experiment 2: The cognitive loads that were compared.
Bayes factor in favor of the hypothesis that the compared conditions differed.
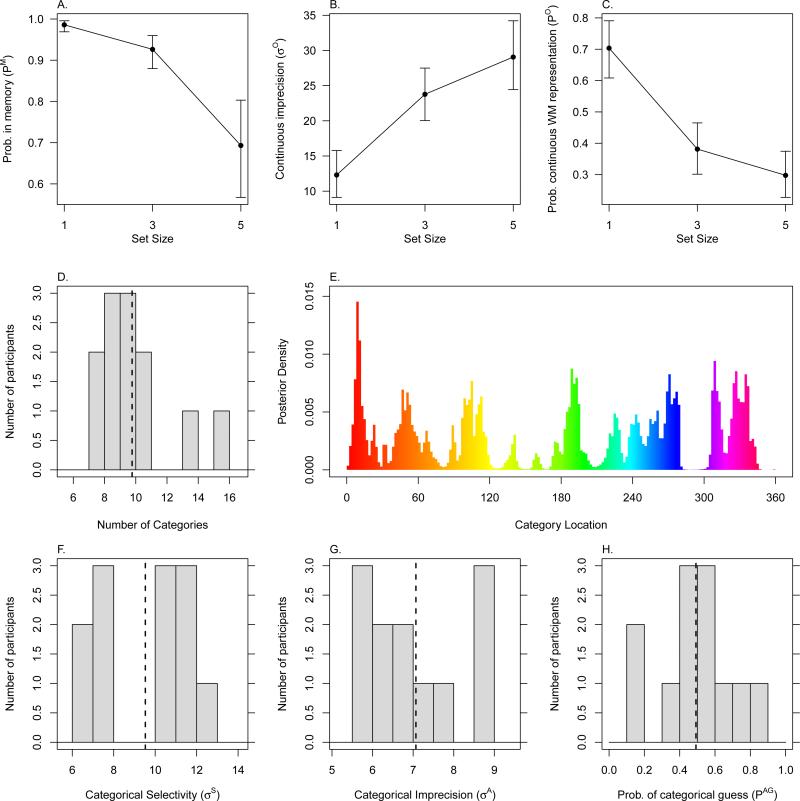
In Experiment 1, there were clear effects of set size for all three of the primary parameters. These differences can be seen in Panels A, B, and C of Figure 5. Like most studies in this area, we found that the probability that an item is in WM decreases as set size increases (e.g. Zhang & Luck, 2008). The proportion of categorical memory responding that is present in the data can be seen in the plots for Experiment 1. At set size 1 (Panel A of Figure 4), very little categorical responding is apparent. At higher set sizes, responses appear to become increasingly categorical in nature. This is visually apparent due to the staircase pattern in the data that becomes more pronounced at higher set sizes. For example, see the cluster of responses near 180 degrees in Panel C of Figure 4. These results suggest that at low memory loads, participants are able to remember precise color information, but that at higher memory loads, most of the colors in WM are stored categorically. The modeling results confirmed the visual inspection: We found that the proportion of responses that were continuous in nature decreased with set size, down to about a third of responses at set size 5.
Figure 5.
Parameter summary from Experiment 1. Error bars in Panels A, B, and C are 95% credible intervals. In the histograms in Panels D, F, G, and H, the dashed vertical line is at the mean. Panel E shows the posterior distributions of category centers collapsed across all participants.
We also found that WM imprecision increased with set size, which is in agreement with some studies (e.g. Bays et al., 2009; van den Berg et al., 2012), but not with some other studies which have found that WM imprecision plateaus past set size 3 (e.g. Zhang & Luck, 2008). Either pattern of data can be predicted by various theories about the structure of WM, but we think that the difference in findings may be related to an issue of statistical power. We fit the ZL model to our data and found ambiguous evidence as to whether memory imprecision increased from set size 3 to set size 5, BF10 = 1.0, with the posterior mean of the difference being 1.2 degrees. With our model we found clear evidence for just such a difference, BF10 = 15. The major difference between our model and the ZL model is that our model separates categorical and continuous memory, which gives our model greater power to selectively detect effects in continuous memory. More importantly, in the ZL model, it is not possible to tell the difference between 1) changes in WM precision and 2) changes in the proportion of categorical responses. In prior studies that used the ZL model, these two changes are confounded.
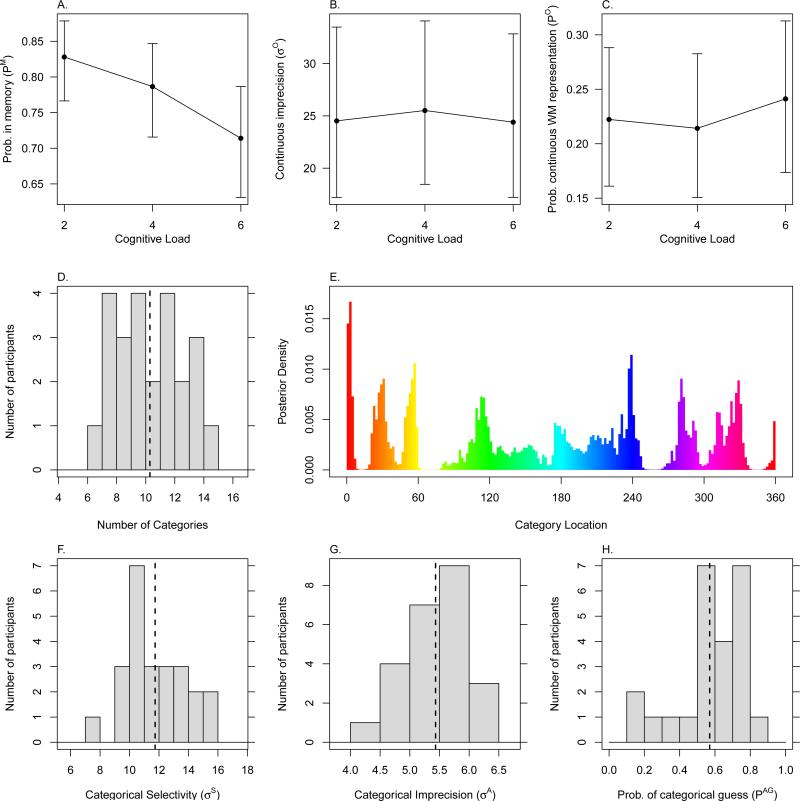
In Experiment 2, there were only effects of cognitive load for PM, with no effect of cognitive load for σO and PO. Plots of these results can be found in Panels A, B, and C of Figure 6. There were only differences for PM between cognitive loads 2 and 6 (BF10 = 3.3 · 105 ) and 4 and 6 (BF10 = 4.4 · 102), with ambiguous evidence related to a difference between cognitive loads 2 and 4 (BF10 = 1). This cognitive load effect on PM is in line with many previous studies that find that cognitive load reduces the amount of information that can be stored in WM, including visuo-spatial information (e.g. Barrouillet et al., 2007; Ricker & Cowan, 2010; Vergauwe, Barrouillet, & Camos, 2009, 2010). However, there was no effect of cognitive load for either σO and PO. This suggests that cognitive load does not differentially affect categorical and continuous information within a memory set. If there was a differential effect, we would expect that PO would change with cognitive load. In addition, the fact that σO does not change with cognitive load indicates that WM precision does not depend on cognitive load. This set of results is interesting because it suggests that cognitive load affects the number of items that can be stored in WM, but not the precision with which those items are known or the proportion of items for which continuous information is known. These results are surprising because it might be expected that cognitive load would be a general effect that would impact all aspects of WM performance, including continuous precision, but that does not appear to the be case.
Figure 6.
Parameter summary from Experiment 2. See the caption of Figure 5 for explanation of the figure elements.
Color Categories
As can be seen in Panel D of Figures 5 and 6, the number of color categories used by participants was consistent across experiments, being near 10 for both experiments. The specific colors that were used by participants as the centers of their categories can be examined in the E panels of Figures 5 and 6. Those panels show the posterior distributions of the category centers collapsed across all participants. Most participants tended to use similar color categories, which can be seen from the fact that the distribution of color categories has strong peaks in a number of locations. If participants all used idiosyncratic color category centers, the distributions in the E panels would be uniform distributions. Some possible names for the eight most commonly used categories are red, orange, yellow, green, cyan, blue, purple, and pink. With the exception of cyan (near 240 degrees in Experiment 1 and 180 degrees in Experiment 2), these color categories are the same categories identified by Rosch (1973) as natural color categories that are easily learned by participants regardless of past exposure to the colors or the participant's native language. Of our 8 categories, cyan is the least-consistently-used category, which is in line with Rosch's results. As the average number of categories used by participants was approximately 10, it seems likely that most of our participants used these 8 categories, plus about 2 more idiosyncratic categories.
As described in the method section, following their experimental session in Experiment 1, participants were asked about their strategy use during the experiment. One participant did not provide answers to the questionnaire. For the question about the use of a color naming strategy, the mean response was 4 (out of a maximum of 5), indicating high levels of color naming as a strategy. For the question about visualizing exact colors, the mean response was 2.36, indicating moderate levels of color visualization. These self-report data suggest that color naming was used as a strategy by participants, which goes along with the finding that participants consistently used easily-named color categories.
Category Parameters
Categorical selectivity, categorical imprecision, and the probability of making a categorical guess had similar values in both of our experiments. Histograms of these parameters can be found in Panels F, G, and H of Figures 5 and 6. The values we obtained for categorical selectivity suggest that participants are quite good at categorizing colors. The simulated participant used to create the data in Figure 2 had σS = 20. Our participants had values of σS nearer to 10, which would make the transitions between categories, as illustrated in Panel G of Figure 2, substantially more abrupt than is pictured, indicating that most colors had a probability near 1 of being assigned to the most likely category. The categorical imprecision, σA, was fairly low (about 6 degrees), which seems reasonable for a response based on a categorical representation. Finally, the probability of a guess being categorical in nature was near 0.5, suggesting that a substantial proportion of guesses are categorical. This is evidence that it is appropriate to include categorical guessing in the model.
Number of Categorical and Continuous Items in WM
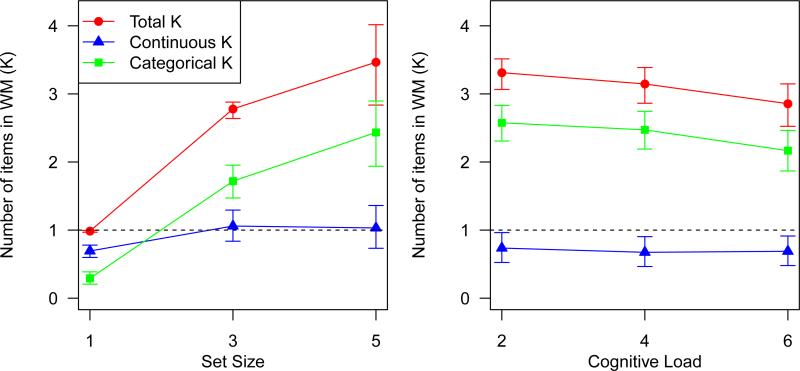
It is possible to examine our results from the perspective of the number of items that can be held in WM, commonly denoted K (e.g. Cowan, 2001). The PM and PO parameters of our model can be used in combination with the set size to calculate the number of continuous and categorical items in WM. The number of continuous items used by participants is given by N · PM · PO, where N is the set size, and the number of categorical items is given by N · PM · (1 – PO). This was done at each set size for Experiment 1 and at each cognitive load for Experiment 2. The results of these calculations are plotted in Figure 7. As can be seen in that figure, the number of items stored with continuous information appears to be approximately 1 in Experiment 1 and near, but below, 1 in Experiment 2.
Figure 7.
Plot of the number of items in working memory by set size (Experiment 1; left panel) or cognitive load (Experiment 2; right panel). The total number of items in working memory is also divided into the categorical and continuous items in working memory. As can be seen, the number of continuous items in working memory is very near to 1 (indicated with the dashed horizontal lines) in Experiment 1 and slightly below 1 in Experiment 2. Error bars are 95% credible intervals.
We tested whether the number of continuous items in WM was equal to 1 using one-sample Bayesian t-tests (Rouder, Speckman, Sun, Morey, & Iverson, 2009) as implemented in the BayesFactor package (Morey & Rouder, 2015) for R (R Core Team, 2015). For Experiment 1, we only used set sizes 3 and 5 in the analysis, because at set size 1, the maximum number of continuous items that could be in WM was 1, which artifactually forces the estimated number of items in WM to be less than or equal to 1. For Experiment 1, there was some evidence that the number of continuous items in WM was 1 at set sizes 3 and 5, BF01 = 3.2. For Experiment 2, there was evidence that the number of continuous items was not 1, BF10 = 104. Thus, in Experiment 1, participants tended to have 1 continuous item in WM, but in Experiment 2 participants sometimes did not maintain a continuous representation.
We did not find any effect of cognitive load on continuous WM precision or the probability that an item was stored continuously. However, as can be seen in Figure 7, the number of continuous items in WM appears to be lower in Experiment 2 than in Experiment 1, which could reflect an effect of the existence of the cognitive load task. Thus, we examined whether having any cognitive load task at all had an effect on WM capacity, which was done by comparing the average of set sizes 3 and 5 in Experiment 1 with the lowest cognitive load condition in Experiment 2 (which had a set size of 4). We found that the total K did not differ (BF10 = 0.43), but that there was some evidence for differences in both categorical and continuous K estimates (BF10 = 2.3 for categorical K and BF10 = 3.2 for continuous K). The means of the total K estimates were 3.05 and 3.20 for Experiments 1 and 2, respectively. The means of the categorical K estimates were 2.02 and 2.45, while the means of the continuous K estimates were 1.04 and 0.75. Although changing the level of cognitive load in Experiment 2 did not affect the proportion of items that were stored categorically or continuously, it appears that the addition of the cognitive load task between Experiments 1 and 2 does change the nature of representations maintained. When a cognitive load task was present, participants stored a greater portion of colors categorically without decreasing the total number of remembered colors. This conclusion has one important confound that should be noted, which is that another difference between Experiments 1 and 2 is the length of the maintenance interval, which was 1.5 s in Experiment 1 and 6 s in Experiment 2. It could be that trace decay of continuous memory representations (Ricker & Cowan, 2010; Ricker, Vergauwe, & Cowan, 2014) provides an alternative explanation for the observed difference, although that does not explain how participants were able to remember the same total number of items.
Model Validation
We performed three different procedures to validate our models. The results of the model validation procedure are reported only for the between-item model, but we also verified that the within-item model was behaving appropriately. The first procedure is verifying that data with only continuous responding is identified as such by our model. The second is verifying that when data is generated by our model, that the model can effectively recover the parameter estimates. The third is checking that the model is able to produce data that looks like the data that was given to the model.
Identifying Fully Continuous Responding
We tested the possibility that the data could have been generated under the ZL model's assumption of fully continuous memory responding but that our model spuriously suggests that there is categorical memory responding present in the data. We did this by simulating data for 20 virtual participants whose behavior matched the ZL model predictions (i.e. all responses were continuous in nature) and then fitting our model to the simulated data. If we find that PO = 1 for the simulated data, it would indicate that our model correctly identifies that the simulated participants are fully continuous in their responding pattern (note that this is essentially the same as testing whether or not the ZL model is appropriate for the data, as we did above). For this simulation, we found that the mean of PO was indistinguishable from 0.99 (BF01 = 5.6), which indicates nearly completely continuous memory responding. This test shows that our model correctly identifies data that contains only continuous responding, proving that if our actual data had contained only continuous responding, then the parameter estimates would have reflected that fact.
Parameter Recovery
We tested the ability of our model to recover the parameter values that were used to generate data similar to our actual data (i.e. with categorical and continuous responding present). To do this, we simulated data from 20 virtual participants with known parameter values. The parameter values were randomly sampled in such a way that the simulated participants had parameter values similar to the actual parameter estimates from our experiments. We included effects of task condition of similar magnitudes to those we found in our experiments for PM, σO, PO. Each simulated participant “performed” a number of trials equal to the actual number of trials used in Experiment 1 at the same 3 set size conditions, resulting in a simulated data set. We then fit our model to the simulated data, which resulted in recovered estimates of the parameters that were used to generate the data. If our model is poorly identified, perhaps due to an excessive number of parameters, then the recovered parameter values would have little relationship with the known parameters that were used to generate the data.
We found that the recovered parameters were strongly related to the known parameter values we used to generate the data. The correlations between the known participant parameters and the posterior mean of the recovered parameters ranged from 0.76 to 0.99. The number of color categories correlated 0.88. The regression slopes ranged from 0.87 to 1.15, where 1 is ideal. The average difference in mean level between the true and recovered parameters was about 2% of the true values. In addition, the differences between task conditions were effectively recovered, with the errors being on the order of 10% of the true values (e.g. a true difference was 2 and the recovered difference was 1.8). It should be remembered that some noise is introduced during the data simulation process, so without a large sample of data, we would not expect to necessarily recover the exact parameter values that were used to generate the data. Our recovered parameters are close enough to the true parameter values that the parameter estimates can be trusted to be reasonably accurate.
Reproducing Data
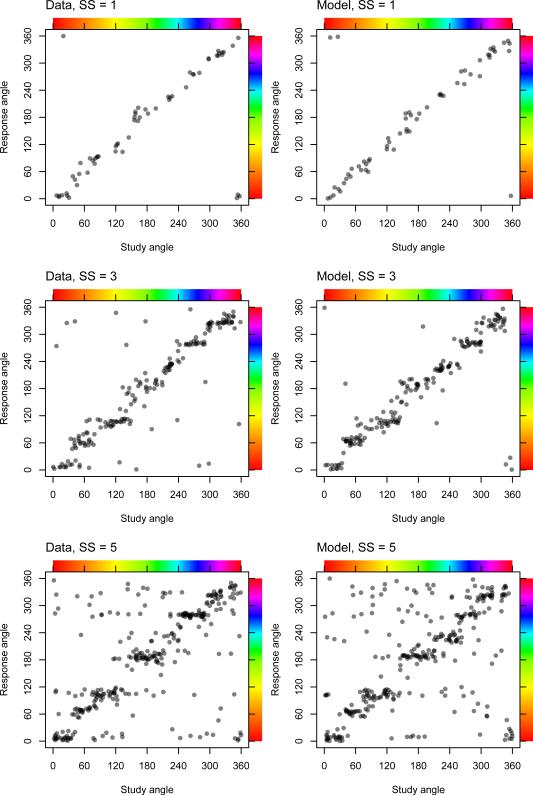
One way to examine the validity of a model is to compare data generated from the fitted model to the real data. Once a participant's parameters have been estimated, data can be generated from the model using those parameter estimates by sampling from the posterior predictive distribution of the data. This sampled data can be compared to that participant's real data to determine whether the model is capable of reproducing the patterns in the data. We show the results of this process for one participant in Figure 8. As can be seen by comparing the left and right columns of scatterplots, the data generated from the model (right column) closely matches the patterns in the real data (left column). These results for the selected participant are fairly typical and support the claim that our model is appropriate for the data.
Figure 8.
Plots of data from one participant in all three set size (SS) conditions of Experiment 1 (left column) and data generated by sampling from the posterior predictive distribution of the model (right column). As can be seen, data sampled from the fitted model effectively captures the primary characteristics of the data.
Discussion
There are a number of important conclusions that can be made on the basis of the novel model we used in this study. These conclusions are related to 1) constraints on models of WM and the data representations used for those models, 2) our finding of a continuous WM capacity of one item, 3) mechanisms of information storage in WM, 4) cognitive load effects, and 5) the color categories used by participants. These issues are discussed in detail below. We also discuss the possibility that our method may have biased participants toward using categorical representations, some ways in which our model could be extended, and other studies that have provided evidence for categorical WM.
Constraints on Models and Data Representations
We found that our model quite effectively accounts for participant data, in contrast to the ZL model. In particular, we found clear evidence that a large proportion of memory responses were categorical in nature. The ZL model does not account for categorical memory responses, which makes it unable to differentiate between changes in WM imprecision and changes in the proportion of categorical responses: A change in the proportion of categorical responses could appear to the ZL model to be a change in WM imprecision. This fact makes the ZL model unsuitable for estimating WM imprecision when categorical memory responding is present in the data. Given this, we believe that the ZL model should not be used to estimate the parameters of WM for color delayed estimation data unless it can be verified to be an appropriate model for a specific data set. To verify this, it would be necessary to show that a data set has no categorical memory responding present, which may be possible to do by looking for clusters of responses, or the absence thereof, such as those that are present in our data. It would, of course, be even better to use a model-based approach to verify the absence of categorical responding.
Although the choice of model is important, the choice of data representation is even more important. In most work using delayed color estimation, the data representation that is modeled is the response error, which is the difference between the study angle and the response angle (e.g. Fougnie & Alvarez, 2011; Zhang & Luck, 2011). Using the response error results in averaging out the categorical memory responses, which are only detectable if raw study and response angles are used. Plotting study and response angles, as we did in Figures 4 and 8, allows for the detection of patterns of categorical responding in the data. These patterns would be lost if response error were plotted instead. Models of response errors cannot reveal the categorical memory responses that we observed in the present work because of this aggregation problem. Even if future researchers do not use our exact model, they should carefully consider whether it is justified to use response errors rather than study/response pairs. Examining memory responses from the perspective of response error is justified as long as the distribution of responses is independent of the studied angle. In that case, nothing is lost by taking the difference between the study and response angle.
Our preceding discussion has focused on how our model has a better fit than the ZL model specifically for categorical memory responses. Here we turn our attention to categorical guesses. In our model, we have to account for the fact that participants may make categorical guesses because we use the raw response angle. Thus, the location of a response relative to a category location is relevant and must be modeled. The ZL model has the computational advantage of being able to account for categorical guesses, or any complex guessing distribution, without having to explicitly model that distribution. It is able to do this because of the fact that it uses a uniform distribution of response errors as the guessing distribution. To illustrate how a uniform distribution of response errors can account for unusual guessing distributions in the raw response space, imagine the extreme case of a participant who always responds at angle 0 when guessing (i.e. at a specific place on the response wheel). Given that the distribution of study angles is uniform, as it is in most experimental designs, the response errors between the guessing angle 0 and the studied angles will also be a uniform distribution. Thus, the ZL model's uniform distribution of response errors can account for a non-uniform distribution of guesses in the response space. This basic logic extends to any guessing distribution, where a guessing distribution for a response is by definition not dependent on the studied angle. Thus, the ZL model is able to account for complex guessing distributions with a simple uniform distribution of guessing response errors. This is a computational advantage for the ZL model, because our model on raw responses must explicitly account for any complexities in the guessing distribution.
Potential Categorization Biases
There are three ways in which it is possible that our method might have led to a greater use of categorical memory representations than might be found in other studies. These are 1) the sequential presentation of stimuli, 2) the use of multiple responses per trial, and 3) the potential for distortions in presented colors. On point 1, we presented colors in serial order, but it is more common for delayed-estimation tasks to present a whole array of stimuli at once (e.g. Fougnie, Asplund, & Marois, 2010; Zhang & Luck, 2008). In our method of presenting colors one at a time, participants might have been encouraged to name each color as it was presented. When colors are presented in a briefly-presented array, participants may not have time to name the colors, which could result in reduced use of categorical memory representations than in our study. On point 2, we had participants respond to every color on each trial, while it is more common to require participants to respond to only one color per trial (e.g Bays et al., 2011; Zhang & Luck, 2008). It is possible that making multiple responses per trial causes output interference that disrupts continuous color memory. In that case, the amount of categorical memory responses we observed in our tasks would be higher than in tasks which only require a single response. In addition, the combination of serial presentation and multiple responses might reduce the amount of continuous memory available due to decay or interference that arises during the delay between study and test for any one item. With shorter study-test delays, more continuous information might be available in WM at test.
On point 3, the colors seen be participants were likely different from those we intended to present. Recent work by Bae, Olkkonen, Allred, Wilson, and Flombaum (2014) demonstrates that standard computer monitors do not always present the color intended by the experimenter, but instead have systematic distortions in the color rendered by the monitor due to hardware and software limitations. As we did not test the accuracy of rendered colors in our study, these distortions may be present in our data. Further, they show that these distortions in color do account for some, but not all, stimulus specific effects. For example, they found that certain colors were associated with higher imprecision than others even when the task required no memory component. In our data, it is hard to see how this could account for our clear finding that people maintain categorical representations. Indeed Bae et al. (2014) did observe color category effects on precision above and beyond the effect of rendering errors in their own work. It may be though that some of the color values that tended to be neglected in our study (yellow-green, purple-blue) had luminance values that causes participants to be less likely to initially attend to the memory stimulus or to that portion of the color wheel. This could result in reinforcing the categorical nature of our findings, but cannot account for the totality of our findings in favor of categorical memories as there was clearly a large range of differing color values presented by the monitor in our study. Additionally, we found evidence that the color categories chosen by participants corresponded to easily-named colors. It seems unlikely that color presentation errors would happen to bias participants toward using easily named-colors because those colors differ substantially in terms of many characteristics, including luminance.
Since our methods may have biased participants to use categorical memory more than more standard methods, it will be important to explore to what extent method influences the amount of categorical memory maintained. Conveniently, our model can be applied to existing data sets to explore this issue. We think it is entirely possible that at least some categorical memory is used by participants in many experimental designs, but this is an empirical question that we would hope would be addressed in future studies.
Continuous WM Capacity of One Item
We found that the number of continuous items used by participants was 1 in Experiment 1 and slightly below 1 in Experiment 2, regardless of set size or cognitive load. One possible explanation for these results is that continuous color information is maintained in a special way by the one-item focus of attention that is postulated by some models of WM (e.g. McElree, 2006; Nee & Jonides, 2013; Oberauer, 2002). When participants were allowed to use attention entirely for maintenance in Experiment 1, they were able to store an average of 1 continuous item in WM. When the attention-demanding secondary task was added in Experiment 2, the average number of continuous items in WM decreased. This could be because the focus of attention, which may be used for the maintenance of continuous colors, is less available for maintenance in the presence of the attention-demanding secondary task. An alternative possibility is that something about the experimental design, such as the serial presentation of stimuli, coincidentally resulted in an average of approximately a single continuous item being held in WM. It could be that different continuous capacity limits would be found with other experimental designs, which should be examined in future research.
In Experiment 1, continuous memory precision decreased as set size increased. This result indicates that even if continuous items are maintained by a specialized WM process, this process is not independent of the amount of information maintained by other processes. Thus, it seems likely that if the single continuous item is maintained by the focus of attention, the focus of attention is also used for maintenance of the categorical items in WM to some extent. Future work examining the relationship between continuous precision of WM and the number of categorical representations maintained in WM should be a high priority.
Mechanisms of WM Storage
We found that 1) the number of items in WM that were continuous in nature was approximately one regardless of set size and 2) about two items in WM were categorical in nature at higher set sizes. These results are consistent with a model of WM in which there are at least two qualitatively distinct, fixed-capacity storage mechanisms in WM. One storage mechanism can maintain about one continuous item and another storage mechanism can maintain about two categorical items. As discussed in the previous section, however, these two potential storage mechanisms do not appear to be independent, which brings into question whether they are in fact different memory systems. Finally, as we have noted, our method may have led participants to use categorical memory more than other methods. It could be that different task demands than were present in this study could cause participants to remember more than one continuous item. As such, we believe that additional evidence from studies with a variety of methods is required before concluding that there are two qualitatively distinct WM systems.
Related to how information is stored in WM, we were interested in whether categorical and continuous information were used separately, as in our between-item model, or in concert, as in our within-item model that we based on the Bae et al. (2015) model. We compared these two possibilities with two variants of our model and found that between-item assumption that categorical and continuous information were used separately was the better assumption for our data. This suggests either 1) that participants do not tend to store information both categorically and continuously, rather storing information in only one of the two forms or 2) that participants do store information in both ways, but do not integrate the information from both forms when making their response, rather just selecting one type of information when responding. Future research may be able to differentiate between these two possibilities. Note that although the between-item model variant was best for our data, there may be some experimental conditions for which a within-item mixture of information would be a better assumption. For example, when a set size of only one or two items is used, participants might store both categorical and continuous information about the items and have sufficient WM resources available to combine those pieces of information at test. Future research could determine if and when a within-item mixture of information occurs.
Cognitive Load Effects
We found that level of cognitive load that participants are placed under only affects the probability that an item was in WM, and not continuous precision or the probability that a response is continuous. Thus, it does not appear that the cognitive load level differentially impacts categorical and continuous representations in WM, instead affecting both kinds of representations equally. However, cognitive load did not affect continuous WM precision at all, which suggests that cognitive load affects only the number, but not the quality, of representations in WM.
We also examined the effect of the mere presence of the secondary task by comparing across experiments. The total number of items in WM was constant between the higher set sizes of Experiment 1 and the lowest cognitive load of Experiment 2, indicating that the addition of the secondary task does not affect the total amount of information in WM. However, the addition of the secondary task caused the number of continuous items to decline and the number of categorical items to increase. This leads to the conclusion that the presence of a secondary task, but not its difficulty, may cause a trade-off between continuous and categorical information. This relates to the idea that the focus of attention is less able to maintain continuous representations when attention is captured by the secondary task. However, another difference between the experiments is that the maintenance interval in Experiment 2 (6 s) was longer than in Experiment 1 (1.5 s), which could have also had an effect on the maintenance of continuous colors. Elsewhere we have proposed that continuous information may decay over time because it cannot be actively maintained, while categorical information does not because it can be actively maintained (Ricker & Cowan, 2010; Vergauwe et al., 2014). Future experiments should focus on disentangling the effects of maintenance interval duration and secondary task cognitive load.
Color Categories
As can be seen in Figures 5 and 6, the colors that people use for category locations are fairly consistent across participants and also across manipulations of the color distribution. The colors that were used for the stimuli differed somewhat between experiments. The clearest difference is that the range of warm colors (red, orange, and yellow) is wider in Experiment 1 than Experiment 2. It might be expected that participants would evenly distribute their color categories around the response ring so as to maximize the angular distance between categories. Another possibility is that participants’ categories are based on location rather than color. Instead, it appears that the categories used by participants tend to focus on a set of eight main colors and that these colors are used regardless of their locations. In addition, seven of the eight color categories used by our participants match those identified by Rosch (1973) as natural color categories. Finally, our participants reported fairly high levels of color naming as a strategy. Thus, our results are clearly suggestive of a color naming strategy, which necessarily leads to categorical rather than continuous WM representations.
Possible Extensions of our Model
Future research could potentially extend our model to answer other theoretically-motivated questions. One such question relates to whether the order of encoding or the order of responding differentially affects categorical or continuous memory. We were unable to examine this issue with our design because responses were always made in the order of stimulus presentation, which fully confounds encoding and response order. Future studies could 1) deconfound encoding and response order and 2) add encoding order or response order effects to our model to examine this issue.
In the version of our model used in this study, we constrained the following parameters to be the same across all task conditions for each participant: the number and location of categories, categorical imprecision, categorical selectivity, and the proportion of categorical guesses. These constraints were reasonable given that 1) the model was complex enough as to require substantial constraint and 2) we did not have clear theoretically motivated reasons to lift these constraints. Future researchers, however, may have sufficient data as to allow a relaxation of model constraints or good reasons to examine a less-constrained model. For example, researchers may be interested in how effectively participants categorize stimuli and would want to examine how the categorical selectivity parameter changes across task conditions. Another example is that it may be possible for participants to use more categories at lower set sizes because they have more resources available to precisely categorize stimuli. We encourage future research on the parts of our model that we constrained, but note that reducing constraint on a model as complex as ours can easily result in a reduction of the identifiability of model parameters.
In this study, we compared the between-item and within-item variants of our model and found that the between-item model had a better fit to the data. Logically, however, the two model variants are not mutually exclusive: Different proportions of responses could be fully categorical, fully continuous, and combined categorical-continuous responses. We attempted to fit such a model, but found that it was not identifiable, possibly due to the amount of data we had per participant, but the exact cause of the unidentifiability is unknown to us. Future researchers could attempt to use such a version of our model with a data set with more responses per participant, with the caveat that identifiability of the parameters must be carefully verified.
Related Work on Categorical Memory Representations
Evidence for categorical representations within visual working memory has recently been provided by several other research groups. Our work is not the first to show evidence for this assertion, but rather provides converging evidence and a sophisticated, agile model. We also apply our model to directly testing the fitness of the ZL model and to several other important questions in the field of working memory, demonstrating the importance of understanding the full data representation. Finally we stress the importance of considering the full dimensionality of the data and not just the response errors. Having discussed the novel contributions of our own work, we now discuss the convergence of our findings with similar findings by other researchers.
In a recent study, Bae et al. (2015) used a delayed color estimation task and found that there was evidence for categorical storage of colors in WM. In this work, Bae et al. asked participants to perform a delayed estimation task and also collected data from a perceptual categorization task in which participants identified the best examples of certain canonical colors and the best exemplars of these colors on a color wheel. They then used these color category estimates as biases, modeling the effect of color categories as biasing responses away from the presented color and toward the category location. For example, when a light blue color was presented the Bae et al. model predicts that the general blue color category would bias the response toward the most relevant category exemplar, likely “blue”, resulting in a remembered color that was darker than the presented color. Our results corroborate their fundamental finding: color categories exist within visual working memory, distorting the expected pattern of responses away from a distribution of errors around the presented stimulus value. Critically, we come to this conclusion on the basis of a model that, as we have discussed, differs substantially from the model of Bae et al. (2015). Still, we think that our model and the model of Bae et al. (2015) share many common features. Both are significant improvements over standard models of response error in the field and incorporate reasonable categorical representations in useful ways. Thus, there is convergence from differing paradigms and model implementations demonstrating the existence of categorical color effects on delayed estimation performance.
The concept of stimulus-specific effects on memory fidelity, whether due to the categorical nature of the stimuli, as we show here (see also Bae et al., 2015; Olsson & Poom, 2005), or to rendering errors (Bae et al., 2014) is an important one that has thus far been neglected in studies of working memory quality. The modeling of response errors while ignoring the presented stimuli leads to improper generalization and aggregation of data. This over-aggregation necessarily leads to improper modeling and erroneous conclusions. This is of critical importance in the field considering the dominance of variable precision models of visual working memory in accounting for delayed estimation data. These models are similar to other continuous resource models of visual working memory (Fougnie, Suchow, & Alvarez, 2012; van den Berg, Awh, & Ma, 2014; van den Berg et al., 2012) in that they propose that a single resource that can be spread over an unlimited number of memory items and that precision decreases as the number of items maintained increases. They go beyond this though and argue that the amount of the central resource available to memory varies from trial to trail and between different items within a trial. This has the effect that different stimuli are assumed to have different amounts of precision within visual working memory. Variable precision models tend to have better fits than other competing models, but the validity of the variable precision assumptions is questionable given the existence of categorical memory states. In addition, variable precision models can support their claim that all responses are based on memory by explaining away what we would call uniformly distributed guesses as instead being very low precision memory responses. This same argument, however, cannot explain categorical guessing because there is no reason for very low precision memory responses to be made at specific category locations in the response space. Thus, categorical guessing bands are evidence against variable precision models (Rouder et al., 2014).
Bae et al. (2014, 2015) and Pratte, Park, Rademaker, and Tong (2015) point out that these models ignore stimulus-specific variance, instead erroneously attributing it to variation in the amount of central resource deployed across stimuli and trials. Colors that are farther away from the center of a categorical representation will have greater measures of imprecision, leading to the appearance of variation in precision across items and trials. This is likely a large part of the model fit success found with variable precision models even though it is not the variance intended to be fit by the model. Our study gives more evidence for the assessment of Bae et al. and Pratte et al., showing that there is stimulus-specific variation due to color categories. Clearly, variable precision models cannot be adequately tested on aggregated error distributions because these distributions obscure stimulus-specific effects. Instead model testing must incorporate stimulus-specific effects such as color category effects in order to discover if there is any latent variability in central resources.
In a recent study, Donkin et al. (2015) found evidence for verbal labeling in a delayed-estimation task with color stimuli. They obtained an estimate of the precision of participants’ verbal labels independently of a main memory task. They then analyzed the memory task data with a model that included a mixture of categorical memory based on the verbal labels and continuous memory. They found that the model performed worse when the verbal labeling component of the model was removed, which is evidence that participants use verbal labeling. Interestingly, Donkin et al. required participants to remember only a single color at a time, yet they still found evidence for verbal labeling. Thus, Donkin et al. provide additional support for the claim that categorical representations of colors are used by participants.
Using a change-detection paradigm, Olsson and Poom (2005) found evidence that visual WM capacities are substantially higher when stimuli are easily categorized. They used this as evidence that visual WM is heavily supported by the use of categorical representations. In particular, they found that for easy-to-categorize stimuli the WM capacity was about 3 items while for hard-to-categorize stimuli the WM capacity was about 1 item. This result suggests that 1) participants take advantage of opportunities to categorize stimuli, which allows more stimuli to be remembered and 2) when participants are unable to categorize stimuli, only a very limited number of continuous stimuli are remembered. These results of Olsson and Poom are similar to our results in which we found a total WM capacity of 3 items, about 1 of which was continuous in nature. Thus, our findings about WM capacity are basically in agreement with Olsson and Poom.
Our findings, however, go far beyond those of Olsson and Poom in that 1) our model accounts for both categorical and continuous representations, whereas the model used by Olsson and Poom cannot separate the two types of representation, 2) because of 1), we are able to estimate the number of both categorical and continuous memory representations at once, while Olsson and Poom could only estimate the total number of representations in WM, and 3) we are also able to estimate the precision of continuous representations in WM, which Olsson and Poom did not do. Finally, one limitation of Olsson and Poom is that their stimulus sets differed in a variety of ways, not just categorizability, which makes it impossible to definitively conclude that the differences in WM capacity they found were due to differences in the use of categorical representations by their participants. In contrast, our results are based on a single stimulus set, which avoids this confound. Thus, our work provides important methodological improvements over Olsson and Poom.
The findings in favor of categorical memories do not appear to be limited to color. In a study using delayed estimation of orientation stimuli, Rouder et al. (2014) found evidence for the use of categorical memory representations and categorical guessing by participants. In their design, the orientations were confined to a range around the top of a circle. In this design, it is natural to categorize studied orientations as left or right of center, which participants appeared to do with some regularity. In addition, guesses were often to the left or right of center. The results of our study indicate that the basic findings of Rouder et al. (2014) extend to color stimuli on a circular space. Thus, we corroborate their finding that participants seem to be categorical in terms of both memory-based responses and guesses.
The strong converging of evidence in favor of categorical memory representations across methodologies points toward categorical responding as a basic cognitive tool in human cognition. There is converging evidence that categorical responding is present in tasks thought to involve purely continuous representations, possibly based upon categorical representations of the perceptual stimuli themselves (Bae et al., 2014) or naming of the stimuli (Donkin et al., 2015). Future research should examine whether categorical responding is present in WM delayed estimation tasks when a variety of stimulus sets are used and how these categories correspond to those found in perception.
Final Conclusions
In this work we have presented a new computational model of visual working memory. This model emphasizes the importance of categorical representations to understanding the nature of human memory performance. Our model is a much better fit to the data collected from two versions of the delayed color estimation task than the widely used ZL model. These tasks were representative of those used in the literature, although there were some differences from the most commonly used designs, as we have explained. An important factor that sets our conclusions apart from past studies is that our conclusions are based on a model that accounts for both the categorical and continuous response patterns that are apparent in the data. Past studies that used response error and the ZL model were unable account for categorical memory responding, which makes their results unreliable if a substantial amount of categorical memory responding was present in their data.
There has been substantial debate over whether visual working memory is based upon fixed slots (Fukuda et al., 2010; Zhang & Luck, 2008) or a variable resource (Bays et al., 2009; Ma et al., 2014). We think that this debate has been hampered by models and data representations that do not capture the true nature of the data. Much of the slots versus resources debate has been based on models which utilize response errors, such as the ZL model. As we have argued, representing the data as response errors distorts the true nature of the data by averaging out the categorical responding present in the data. Thinking of data in their natural form, as study angle and response angle rather than response error, brings one closer to the basic truth of cognition. Here the basic truth is clear: There are multiple kinds of visual working memories, some continuous in nature and others categorical.
Acknowledgments
We received support from Swiss National Science Foundation grant P300P1_154611 to Evie Vergauwe, NIH Grant R01-HD21338 to Nelson Cowan, and a University of Missouri Life Sciences Fellowship to Kyle O Hardman. Thanks go to Nelson Cowan for providing laboratory resources and to Jake Lazaroff for assistance with data collection. Thanks also to Jonathan Flombaum and an anonymous reviewer for helpful comments.
Appendix
Model Specification
Between-Item Variant
The overviews of both model variants are given in the main text. Starting with Equation 1 below, we provide the equations for the basic likelihood function of the between-item model variant. Note that the complete specification of the model requires additional information, such as the priors, that is presented in the following sections. With the obvious substitutions, the following equations can all be combined into one equation, but the parts of the equation are presented separately for clarity.
See Table A1 for a reference for the parameters of the model. For mnemonic purposes, note that “a” is the second letter of “categorical” and “o” is the second letter of “continuous”. Also note that superscripted letters should be thought of as helping to specify the identity of the parameter or variable; there are no variables or parameters in exponents in this model. For example, the σO, σA, and σS parameters are continuous imprecision, categorical imprecision, and category selectivity, respectively.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Table A1.
Symbol Meanings
| Symbol | Meaning |
|---|---|
| S | The study angle in degrees. |
| R | The response angle in degrees. |
| PM | Probability that the tested item is in WM. |
| PO | Probability that a memory item is continuous in nature. 1 – PO is the probability that a memory item is categorical in nature. |
| σ O | Continuous WM imprecision in degrees . Serves the same function as the WM imprecision parameter in the ZL model. |
| μ k | The category center of the kth category. |
| ψ k | An indicator of whether or not the kth category is active, i.e. used by the participant. Is equal 1 if the category is active, 0 otherwise. |
| σ S | Category (in)selectivity. Lower values result in more abrupt transitions between categories for the weights function. |
| σ A | Categorical WM imprecision : Determines how close a categorical response it to the category center. |
| PAG | Probability of a categorical guess (versus a uniform guess). |
| V(x, μ, σ) | Probability density function of the von Mises distribution for observation x with center μ and precision 1/σ2 (i.e., we have parameterized V in terms of, roughly speaking, standard deviation rather than precision). |
Parameters are subscripted as follows: i indexes participant; j indexes condition; k indexes category; t indexes trial within participant and condition. As indicated by the subscripts, μik, νik, , and are the same regardless of which condition a participant is in. Thus, the categories that are used by participants are assumed to be the same in all conditions. In addition, and are not subscripted with k, indicating that they are the same for each category. Thus, the different categories for a participant differ in terms of their location and whether or not they are active, but not σS or σA.
Equation 1 gives L(Rijt|Sijt), the likelihood for a response, R, given the item that was studied, S, and, implicitly, all of the parameters of the model. The equation is a mixture between memory responses and guesses. A memory response happens with probability PM and a guess happens with probability 1 – PM. The likelihood for a memory response is and the likelihood for a guess is .
Equation 2 gives , the likelihood for a memory response. This equation is a mixture of continuous responses, which happen with probability PO, and categorical responses, which happen with probability 1 – PO. is the likelihood for a continuous response and is the likelihood for a categorical response.
Equation 3 gives , the likelihood for a continuous response. is the likelihood of a von Mises density function for the response angle R given the study angle S with imprecision . This part of the model is equivalent to memory responding in the ZL model. Note that von Mises distributions are typically parameterized in terms of precision, κ. We have instead parameterized our von Mises distributions in terms of imprecision, σ, which we define as the square root of the reciprocal of precision: .
Equation 4 gives , the likelihood for a categorical memory response. This equation sums up the likelihoods for the response angles, R, across all of the category locations, μ, weighting the probability that the studied item would have been encoded into that category with the weights function Wijkt(Sijt). The likelihood for the category location nearest the study angle is given the greatest weight, with the weights decreasing as the category locations get farther from the study angle. This likelihood also depends on the imprecision of a categorical response, . If is low (indicating high precision), a high likelihood value will only be assigned to a response that is very near a category location. Note that M is the maximum number of categories a participant can have, which is set to a relatively large constant value before parameter estimation. We chose M = 20, which is safely above the highest number of categories estimated to be used by any of our participants.
Equation 5 gives Wijkt(Sijt), which is the weights function. This function is plotted for all values of S and multiple categories in Panel G of Figure 2. This function gives the relative probability that an item that is in the process of being categorically encoded will be assigned to each of the categories. The weights function is the ratio of the density for the study angle for category k to the sum of the densities across all categories. The denominator scales the result so that the weight is a probability between 0 and 1. The numerator gives a density for the kth category and is highly dependent on the value of νik, which is an indicator parameter for the kth category. νik can be either 0 or 1, where 0 means that the category is inactive and 1 means that the category is active. Note that the number of categories used by participant i is given by . If the category is not active (i.e. νik = 0), there is 0 weight assigned to category k, which has the effect of disallowing study angles from being assigned to that category, which effectively removes the category from this part of the model.
Equation 6 gives , the likelihood for a guess. This equation is a mixture of categorical guesses, which happen with probability PAG, and uniform guesses, which happen with probability 1 – PAG. The likelihood for a categorical guess is and the likelihood of a uniform guess is 1/360.
Equation 7 gives , the likelihood for a categorical guess. For a categorical guess, the probability that the guess is from category k does not depend on the study angle. Thus, each category is given equal weight and the likelihood is the average likelihood across all categories. Like with the weights function, inactive categories are ignored.
Condition Effects
Three of the parameters – PM, PO, and σO – were allowed to vary between conditions, where the conditions were set size in Experiment 1 and cognitive load in Experiment 2. Rather than allowing the parameters to freely vary, we constrained the parameters by assuming that for each parameter, there was a main effect of condition applied to the latent parameters underlying each manifest parameter (see the Priors section below for more information on the latent parameters). The application of the main effect to a latent parameter is represented by the following template for a generic parameter P
where Pij is the manifest parameter for participant i in condition j, TP is a transformation function that converts the latent parameter into a manifest parameter, is the latent parameter for participant i, and is the latent main effect on the parameter for condition j. The transformation function, TP, depends on whether the parameter is a probability parameter, in which the transformation is the inverse logit function, or a standard deviation parameter, in which case the transformation is the max(P, 0.5) function, where P is the parameter.
Because the manifest parameters are the sum of unbounded, latent participant parameters and unbounded condition effects, it is possible for the participant and condition parameters to trade off with one another perfectly. This would result in arbitrarily diffuse posterior distributions that are of no use for inference. We prevented a perfect trade off from occurring by using a cornerstone parameterization in which one of the condition effects was set to 0. We chose to use the last condition (set size 5 and cognitive load 6 for Experiments 1 and 2, respectively).
The parameters that were not able to vary between conditions were μ, ν, σA, σS, and PAG, which is indicated in the likelihood function by the fact that they are not subscripted with j.
Priors
The parameters of the model were estimated using Bayesian MCMC techniques, which requires that priors be specified for the parameters of the model.
Probability Parameters
Several of the parameters of the models are probabilities (PM, PO and PAG) and exist on the interval [0, 1]. Is it not easy to put hierarchical priors on parameters that exist on a finite interval. To simplify the priors, we transformed the manifest probability parameters that exist on the [0, 1] interval into latent parameters that exist on the interval (–∞, ∞) using logit transformation. We then placed hierarchical priors on the latent parameters. The prior on each of the probability parameters is given by the following template in which the generic parameter P is replaced by each of the probability parameters in turn.
| (8) |
| (9) |
| (10) |
| (11) |
The first equation is the manifest to latent transformation. The second equation is the prior on the participant-level parameters. The third and fourth equations are the hierarchical priors on the mean and variance of the prior on .
Standard Deviation Parameters
The standard deviation parameters (σO, σS, and σA) are strictly non-negative and also require some work in order to have simple hierarchical priors placed on them. We used latent standard deviation parameters that exist on the interval (–∞, ∞) that were transformed by taking the maximum of the latent parameter and 0.5 (standard deviations less than 0.5 were prevented because of problems with numerical precision). The prior on each of the latent standard deviation parameters is given by the following template in which the generic parameter S is replaced by each of the standard deviation parameters in turn.
| (12) |
| (13) |
| (14) |
| (15) |
The latent standard deviation parameters were typically far enough from the truncation point (0.5 degrees) that there was very little difference between the latent and manifest parameters.
Condition Effects
The condition effect parameters , , and had moderately informative priors placed on them. Cauchy priors with location 0 were used for each of the parameters, except of course for the parameters of the cornerstone condition, which were set to 0 (i.e. the prior was a point mass on 0). The scale of the Cauchy was 2 for both and and was 5 for . The use of moderately informative, zero-centered priors reflects the fact that our prior belief is that we would expect no effect of condition on the condition effect parameters.
Category Center and Active Parameters
We have the prior belief that if two category centers are very close together, that those category centers do not represent different categories. Rather, it seems more plausible that two very close category centers represent the same category. Thus, our prior on the category centers should push category centers away from one another or deactivate one of them when they are very close together, but not affect them if they are reasonably far apart. This can thought of as a penalty for category location parameters that are too close together. The category centers, μ, and the category active parameters, ν had the following priors placed on them.
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
The parameter σ0μ is set to a constant value (discussed below). In function h (Equation 20), the term νkνk′ evaluates to 0 unless both categories are active. Thus, if either category k or category k′ is inactive, then h evaluates to 1 and has no effect on the value of g. In h, the term V(0, 0, σ0μ) gives the maximum possible density for a von Mises distribution with standard deviation σ0μ. The term V(μk, μk′, σ0μ) gives a density that depends on the distance that the kth category center is from the k′th category center. When the distance between the kth and k′th category centers is 0, μk = μk′, and as a result V(μk, μk′, σ0μ) = V(0, 0, σ0μ), so their ratio equals 1 and h evaluates to 0 (as long as νk = νk′ = 1). Thus, the closer that μk is to other category centers, the less likely that the prior finds μk to be.
As a result of the behaviors of g and h, the prior on μk is a notched distribution with a notch with low density at each μk′. The prior on νk is a Bernoulli distribution, where the probability of a “success” (νk = 1) depends on the value of f, scaled so that the probability of a success and the probability of a failure sum to 1.
In general, g does not integrate to 1 with respect to μk, but there exists some function SF(νk) that scales g so that f integrates to 1 with respect to μk. Because g does not integrate to 1 with respect to μk, that makes it improper. The form of SF is unknown, but it depends on νk (among other things) which means that it is not constant with respect to νk. Because the form of SF is unknown, its value must be estimated, which we did with each evaluation of f. The value of SF was estimated by evaluating g at 50 evenly-spaced values of μk in the interval [0, 360), which we found to provide acceptable precision. Because it is counterintuitive, we note that g may be used as the prior for μk (although we did not do so for the sake of simplicity), but f (and not g) must be used for the prior on νk.
We chose σ0μ = 12 so that there was very little penalty unless the category centers were fairly close together. We found that it is necessary to use priors of the sort we used. When uniform priors on μk and νk were used, all of the possible categories were active nearly all of the time and some category centers were very close to one another (less than 5 degrees), neither of which are reasonable results.
Within-Item Model Variant
Our within-item model variant makes a different assumption about how categorical information is used than our between-item model variant. The within-item variant assumes that 1) if a item is in WM, both categorical and continuous information about that item is available, 2) the categorical and continuous components of each representation contain some amount of noise, and 3) when making a response, the two noisy representations are combined with a weighted average. A supplementary assumption is that the imprecision of categorical memory is the same as the imprecision of categorical guesses.
We will say that the continuous representation is a von Mises random variable denoted y and the categorical representation is a von Mises random variable denoted z. Because y represents continuous information, the location of y (i.e. the center of the distribution) is the location of the studied color. Because z represents categorical information, the location of z is the location of the category that the memory item was put into. The variances of y and z are reflected by the σO and σA parameters, respectively. For a single studied color on a single trial, that color is assigned a category, which determines the location of z. Then, realizations of y and z are taken, with the variance of the realizations depending on σO and σA. Finally, the two realizations are combined by taking a weighted average of the realizations, with the weighting depending on PO: The larger PO is, the more weight is put on the continuous component of WM.
The response made by a participant is a von Mises random variable denoted x. The random variable x is the weighed average of two random variables, y and z. The weighting is controlled by PO and the equation for x is x = WCM((y, z), (PO, 1 – PO)), where WCM is the weighted circular mean function, defined below, which takes into account transitions across 0 degrees. For example, if y = 355 and z = 5, the linear mean is 180, which is incorrect when considering the circular space, but the circular mean is 0, which is correct. The weighted linear mean equation for x would be x = PO y + (1 – PO)z. Thus, in the within-item variant, PO means the proportion of each response that is continuous, whereas in the between-item variant, it meant the probability that a response is fully continuous.
The aforementioned process is the process assumed to be used by participants and is straightforward to simulate. It is more difficult, however, to estimate the parameters of the process by working backwards from the data because the responses, x, are based on the weighted average of two components of WM which are not directly observable: Only the response, and not the process leading to the response, are emitted by participants. Thus, some statistical theory must be applied.
We will make two simplifying assumptions that make this problem statistically tractable. First, given the range of standard deviations observed in our designs, that there is little difference between a circular mean and a linear mean. Second, that the variance of a von Mises distribution, when it is treated as existing in a linear space, is equal to the inverse of the precision of the distribution. On the first assumption, when combining y and z to get x, the model uses a weighted circular mean, the definition for which is given in Equation 24. The weighted linear mean is much simpler to work with, but produces values very similar to the circular mean as long as angular distance between the two values is small enough (less than 100 degrees), which it typically is for our model. The second assumption is related to the fact that, for typical data used with our model, the von Mises distributions are fairly precise, which results in them having very thin tails. If a fairly precise von Mises distribution were to be split at the point opposite from the center of the distribution and unrolled into a linear space, it can be treated as a linear distribution because the tails have effectively 0 density. Little is lost in the circular to linear transformation because the tails are so thin. Once this linearizing is done, the variance of the linearized von Mises distribution is approximately equal to the inverse of the precision of the original distribution. We have verified that both of these assumptions are reasonable in that they are approximately true. Without these assumptions, it would be difficult to perform the required calculations.
With these two assumptions is place, it is straightforward to combine the variances of y and z to get the variance of the distribution of x. When dealing with linear variance, the variance of the weighted sum of two independent random variables is the sum of the variances times to squared weights. By our first assumption, we can use this rule. If the sum is weighted by P, then Var(x) = Var(P · y + (1 – P)z). Because y and z are assumed to be independent,
Following from our second assumption, it is approximately true that and . Equation 25 follows directly. Although Equation 25 provides an approximation for , it is an accurate enough approximation to allow for fairly accurate parameter recovery in simulations in which data is directly generated from the model. The location of x is simply the weighted circular mean of the locations of y and z. Thus, the linearization assumption is used to calculate the variance, but not the location.
The within-item mixture model variant we used is mathematically very similar to the between-item mixture model. The only modification is to replace Equation 2 from the between-item model with the equation for LM below. The rest of the model is unchanged. Given the preceding derivations, the following equations follow in a straightforward way.
| (22) |
| (23) |
| (24) |
| (25) |
Equation 22 gives the likelihood for a single response by taking a weighted average across the categories that the studied item, Sijt, might have been categorized into. The weights function, Wijkt, is the same as used by the between-item model as given in Equation 5. The likelihood of each response is given by the von Mises density function, V, for the response angle, Rijt, the mean response angle, , and the standard deviation of the response . The interesting parts of this equation happen within and , as discussed below.
Equation 23 gives , which is the center of the memory response distribution for an item put into the kth category. It is based on the study angle, Sijt, and the location of the kth category, μijk. These locations are averaged with WCM with weights based on PO, where the weight used for Sijt is PO and the weight used for μijt is 1 – PO.
Equation 24 gives the weighted circular mean function, which produces the angular mean of a vector of angles where the contribution of each angle is weighted by the weight vector . The atan2 function is the arctangent function of two arguments, which uses the signs of the arguments to determine which quadrant the resulting angle is in, which allows it to return a result in the interval [0, 360).
Equation 25 gives , which is the imprecision of the combination of the categorical and continuous WM representations. The logic of this equation was given prior to the equations.
Contributor Information
Kyle O Hardman, University of Missouri.
Evie Vergauwe, University of Geneva, Switzerland.
Timothy J Ricker, College of Staten Island & The Graduate Center, City University of New York.
References
- Allen RJ, Baddeley AD, Hitch GJ. Is the binding of visual features in working memory resource-demanding? Journal of Experimental Psychology: General. 2006;135(2):298–313. doi: 10.1037/0096-3445.135.2.298. doi: 10.1037/0096-3445.135.2.298. [DOI] [PubMed] [Google Scholar]
- Bae G-Y, Olkkonen M, Allred SR, Flombaum JI. Why some colors appear more memorable than others: A model combining categories and particulars in color working memory. Journal of Experimental Psychology: General. 2015;144(4):744–63. doi: 10.1037/xge0000076. doi: 10.1037/xge0000076. [DOI] [PubMed] [Google Scholar]
- Bae G-Y, Olkkonen M, Allred SR, Wilson C, Flombaum JI. Stimulus-specific variability in color working memory with delayed estimation. Journal of Vision. 2014;14(4):1–23. doi: 10.1167/14.4.7. doi: 10.1167/14.4.7. [DOI] [PubMed] [Google Scholar]
- Barrouillet P, Bernardin S, Portrat S, Vergauwe E, Camos V. Time and cognitive load in working memory. Journal Of Experimental Psychology: Learning, Memory, And Cognition. 2007;33:570–85. doi: 10.1037/0278-7393.33.3.570. doi: 10.1037/0278-7393.33.3.570. [DOI] [PubMed] [Google Scholar]
- Barrouillet P, Camos V. As time goes by: Temporal constraints in working memory. Current Directions in Psychological Science. 2012;21:413–419. doi: 10.1177/0963721412459513. [Google Scholar]
- Barrouillet P, Portrat S, Camos V. On the law relating processing to storage in working memory. Psychological Review. 2011;118:175–92. doi: 10.1037/a0022324. doi: 10.1037/a0022324. [DOI] [PubMed] [Google Scholar]
- Bays P, Catalao RF, Husain M. The precision of visual working memory is set by allocation of a shared resource. Journal of Vision. 2009;9(10):1–11. doi: 10.1167/9.10.7. doi: 10.1167/9.10.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays P, Husain M. Dynamic shifts of limited working memory resources in human vision. Science. 2008;321(8):851–4. doi: 10.1126/science.1158023. doi: 10.1126/science.1158023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays P, Wu E, Husain M. Storage and binding of object features in visual working memory. Neuropsychologia. 2011;49(6):1622–1631. doi: 10.1016/j.neuropsychologia.2010.12.023. doi: 10.1016/j.neuropsychologia.2010.12.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks S, Gelman A. General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics. 1998;7:434–455. doi: 10.1080/10618600.1998.10474787. [Google Scholar]
- Cocchini G, Logie RH, Sala SD, MacPherson SE, Baddeley AD. Concurrent performance of two memory tasks: Evidence for domain-specific working memory systems. Memory and Cognition. 2002;30(7):1086–1095. doi: 10.3758/bf03194326. doi: 10.3758/BF03194326. [DOI] [PubMed] [Google Scholar]
- Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences. 2001;24(1):87–185. doi: 10.1017/s0140525x01003922. doi: 10.1017/S0140525X01003922. [DOI] [PubMed] [Google Scholar]
- Donkin C, Nosofsky R, Gold J, Shiffrin R. Verbal labeling, gradual decay, and sudden death in visual short-term memory. Psychonomic Bulletin and Review. 2015;22(1):170–8. doi: 10.3758/s13423-014-0675-5. doi: 10.3758/s13423-014-0675-5. [DOI] [PubMed] [Google Scholar]
- Fougnie D, Alvarez GA. Object features fail independently in visual working memory: Evidence for a probabilistic feature-store model. Journal of Vision. 2011;11(12):1–12. doi: 10.1167/11.12.3. doi: 10.1167/11.12.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fougnie D, Asplund CL, Marois R. What are the units of storage in visual working memory? Journal of Vision. 2010;10(12):1–11. doi: 10.1167/10.12.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fougnie D, Suchow JW, Alvarez GA. Variability in the quality of visual working memory. Nature Communications. 2012;3:1229. doi: 10.1038/ncomms2237. doi: 10.1038/ncomms2237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, Awh E, Vogel EK. Discrete capacity limits in visual working memory. Current Opinion in Neurobiology. 2010;20(2):177–82. doi: 10.1016/j.conb.2010.03.005. doi: 10.1016/j.conb.2010.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garavan H. Serial attention within working memory. Memory & Cognition. 1998;26:263–76. doi: 10.3758/bf03201138. doi: 10.3758/BF03201138. [DOI] [PubMed] [Google Scholar]
- Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statistical Science. 1992;7:457–511. doi: 10.1214/ss/1177011136. [Google Scholar]
- Gorgoraptis N, Catalao RFG, Bays PM, Husain M. Dynamic updating of working memory resources for visual objects. The Journal of Neuroscience. 2011;31:8502–11. doi: 10.1523/JNEUROSCI.0208-11.2011. doi: 10.1523/JNEUROSCI.0208-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardman KO. CX (version 0.1.1) [Computer software] 2015 Retrieved from https://github.com/hardmanko/ofxCX/releases/tag/v0.1.1.
- Kane MJ, Hambrick DZ, Tuholski SW, Wilhelm O, Payne TW, Engle RE. The generality of working memory capacity: A latent-variable approach to verbal and visuospatial memory span and reasoning. Journal of Experimental Psychology: General. 2004;133:189–217. doi: 10.1037/0096-3445.133.2.189. doi: 10.1037/0096-3445.133.2.189. [DOI] [PubMed] [Google Scholar]
- Ma WJ, Husain M, Bays PM. Changing concepts of working memory. Nature Neuroscience. 2014;17(3):347–56. doi: 10.1038/nn.3655. doi: 10.1038/nn.3655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McElree B. Accessing recent events. In: Ross BH, editor. The psychology of learning and motivation. Vol. 46. Academic Press; San Diego: 2006. pp. 155–200. [Google Scholar]
- McElree B, Dosher BA. Serial position and set size in short-term memory: The time course of recognition. Journal of Experimental Psychology: General. 1989;118:346–73. doi: 10.1037/0096-3445.118.4.346. [Google Scholar]
- Morey RD, Rouder JN. Bayesfactor: Computation of bayes factors for common designs [Computer software manual] 2015 Retrieved from http://CRAN.R-project.org/package=BayesFactor (R package version 0.9.12-2)
- Nee DE, Jonides J. Trisecting representational states in short-term memory. Frontiers in Human Neuroscience. 2013;7:196. doi: 10.3389/fnhum.2013.00796. doi: 10.3389/fnhum.2013.00796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oberauer K. Accessing information in working memory: Exploring the focus of attention. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2002;28:411–21. doi: 10.1037/0278-7393.28.3.411. [PubMed] [Google Scholar]
- Oberauer K, Bialkova S. Accessing information in working memory: Can the focus of attention grasp two elements at the same time? Journal of Experimental Psychology: General. 2009;138:64–87. doi: 10.1037/a0014738. doi: 10.1037/a0014738. [DOI] [PubMed] [Google Scholar]
- Olsson H, Poom L. Visual memory needs categories. Proceedings of the National Academy of Sciences. 2005;102(24):8776–8780. doi: 10.1073/pnas.0500810102. doi: 10.1073/pnas.0500810102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pratte MS, Park YP, Rademaker RR, Tong F. Accounting for variable precision in visual working memory reveals a discrete capacity limit.. Paper presented at the Vision Sciences Society; St. Petersburg, FL.. 2015. [Google Scholar]
- R Core Team. R: A language and environment for statistical computing [Computer software manual] Vienna, Austria: 2015. Retrieved from https://www.R-project.org/ [Google Scholar]
- Ricker TJ, Cowan N. Loss of visual working memory within seconds: The combined use of refreshable and non-refreshable features. Journal of Experimental Psychology: Learning Memory and Cognition. 2010;36(6):1355–1368. doi: 10.1037/a0020356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricker TJ, Vergauwe E, Cowan N. Decay theory of immediate memory: From brown (1958) to today (2014). Quarterly Journal of Experimental Psychology. 2014;2006:1–27. doi: 10.1080/17470218.2014.914546. doi: 10.1080/17470218.2014.914546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosch EH. Natural categories. Cognitive Psychology. 1973;4(3):328–350. [Google Scholar]
- Rouder JN, Speckman PL, Sun D, Morey RD, Iverson G. Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin and Review. 2009;16(2):225–237. doi: 10.3758/PBR.16.2.225. doi: 10.3758/PBR.16.2.225. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Thiele JE, Cowan N. Evidence for guessing in working-memory judgments. Paper presented at the 55th annual meeting of the Psychonomic Society. 2014 Nov; [Google Scholar]
- Saults JS, Cowan N. A central capacity limit to the simultaneous storage of visual and auditory arrays in working memory. Journal of Experimental Psychology: General. 2007;136:663–84. doi: 10.1037/0096-3445.136.4.663. doi: 10.1037/0096-3445.136.4.663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith BJ. boa: An r package for mcmc output convergence assessment and posterior inference. Journal of Statistical Software. 2007;21(11):1–37. [Google Scholar]
- van den Berg R, Awh E, Ma WJ. Factorial comparison of working memory models. Psychological Review. 2014;121:121–49. doi: 10.1037/a0035234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Berg R, Shin H, Chou W-C, George R, Ma WJ. Variability in encoding precision accounts for visual short-term memory limitations. Proceedings of the National Academy of Sciences. 2012;109(22):8780–5. doi: 10.1073/pnas.1117465109. doi: 10.1073/pnas.1117465109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergauwe E, Barrouillet P, Camos V. Visual and spatial working memory are not that dissociated after all: A time-based resource-sharing account. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2009;35(4):1012–28. doi: 10.1037/a0015859. doi: 10.1037/a0015859. [DOI] [PubMed] [Google Scholar]
- Vergauwe E, Barrouillet P, Camos V. Do mental processes share a domain-general resource? Psychological Science. 2010;21(3):384–90. doi: 10.1177/0956797610361340. doi: 10.1177/0956797610361340. [DOI] [PubMed] [Google Scholar]
- Vergauwe E, Camos V, Barrouillet P. The effect of storage on processing: How is information maintained in working memory? Journal of Experimental Psychology: Learning, Memory, and Cognition. 2014;40:1072–95. doi: 10.1037/a0035779. doi: 10.1037/a0035779. [DOI] [PubMed] [Google Scholar]
- Wagenmakers E-J, Lodewyckx T, Kuriyal H, Grasman R. Bayesian hypothesis testing for psychologists: A tutorial on the savage-dickey method. Cognitive Psychology. 2010;60(3):158–89. doi: 10.1016/j.cogpsych.2009.12.001. doi: 10.1016/j.cogpsych.2009.12.001. [DOI] [PubMed] [Google Scholar]
- Wilken P, Ma WJ. A detection theory account of change detection. Journal of Vision. 2004;4(8):1120–35. doi: 10.1167/4.12.11. doi: 10.1167/4.12.11. [DOI] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. Discrete fixed-resolution representations in visual working memory. Nature. 2008;453(8):233–235. doi: 10.1038/nature06860. doi: 10.1038/nature06860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. The number and quality of representations in working memory. Psychological Science. 2011;22(11):1434–1441. doi: 10.1177/0956797611417006. doi: 10.1177/0956797611417006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zokaei N, Gorgoraptis N, Bahrami B, Bays PM, Husain M. Precision of working memory for visual motion sequences and transparent motion surfaces. Journal of Vision. 2011;11(14):1–18. doi: 10.1167/11.14.2. doi: 10.1167/11.14.2. [DOI] [PMC free article] [PubMed] [Google Scholar]