Abstract
Quantitative Susceptibility Mapping (QSM) estimates the underlying tissue magnetic susceptibility from the gradient echo (GRE) phase signal through background phase removal and dipole inversion steps. Each of these steps typically requires solving an ill-posed inverse problem and thus necessitates additional regularization. Recently developed single-step QSM algorithms directly relate the unprocessed GRE phase to the unknown susceptibility distribution, thereby requiring the solution of a single inverse problem. In this work, we show that such a holistic approach provides susceptibility estimation with artifact mitigation and develop efficient algorithms that involve simple analytical solutions for all of the optimization steps. Our methods employ Total Variation (TV) and Total Generalized Variation (TGV) to jointly perform the background removal and dipole inversion in a single step. Using multiple spherical mean value (SMV) kernels of varying radii permits high fidelity background removal while retaining the phase information in the cortex. Using numerical simulations, we demonstrate that the proposed single-step methods reduce the reconstruction error by up to 66% relative to the multi-step methods that involve SMV background filtering with the same number of SMV kernels, followed by TV- or TGV-regularized dipole inversion. In vivo single-step experiments demonstrate a dramatic reduction in dipole streaking artifacts and improved homogeneity of image contrast. These acquisitions employ the rapid 3D-EPI and the Wave-CAIPI trajectories for SNR-efficient whole-brain imaging. Herein, we also demonstrate the Multi-Echo capability of Wave-CAIPI sequence for the first time, and introduce an automated, phase-sensitive coil sensitivity estimation scheme based on a 4-second calibration acquisition.
Keywords: quantitative susceptibility mapping (QSM), total variation (TV), total generalized variation (TGV), alternating direction method of multipliers (ADMM), Wave-CAIPI
INTRODUCTION
High-resolution phase images derived from gradient echo (GRE) acquisitions provide a dramatic contrast boost between and within gray matter and white matter, compared to conventional magnitude imaging (1). However, the phase contrast at a particular location stems from non-local effects with contributions from surrounding voxels (2–4). These nonlocal effects make it difficult to robustly relate features in the phase images to the underlying anatomical structures (5). Nonetheless, the same GRE data also lend themselves to Quantitative Susceptibility Mapping (QSM), which estimates the underlying tissue magnetic susceptibility that gives rise to this phase contrast. QSM resolves the confounding non-local bias in the phase images and provides a novel quantitative biomarker in the brain. Susceptibility mapping has already shed light on brain development and aging (6–8), evaluation and monitoring of neurodegenerative and neuro-inflammatory diseases (9–11), and estimation of vessel oxygenation (12–14).
However, QSM estimation from the acquired GRE phase signal entails successive applications of multiple post-processing steps. These steps include phase unwrapping, removal of phase contributions from background sources, and solving an ill-posed inverse problem relating the tissue phase to the magnetic susceptibility distribution (dipole inversion). Efficient phase unwrapping techniques have been developed to resolve the ambiguity due to 2π periodicity of the acquired GRE phase (15,16). The background component of the unwrapped phase, mostly stemming from the air-tissue and air-bone interfaces, is up to two orders of magnitude larger than the tissue component, and thus needs to be removed for the successive processing. Popular background removal techniques include Sophisticated Harmonic Artifact Reduction for Phase data (SHARP, aka Spherical Mean Value (SMV) filtering) (17) and Projection onto Dipole Fields (PDF) (18). Finally, an inverse problem needs to be solved to estimate the underlying susceptibility distribution from the background-removed unwrapped tissue phase. To mitigate the streaking artifacts due to the ill-posed inversion, weighted quadratic smoothing (i.e., ℓ2 penalty on the image gradients) (19,20), weighted Total Variation (TV) (21–25), and Total Generalized Variation (TGV) (26–28) regularized QSMs have been proposed. As these regularized QSMs impose sparsity or smoothness assumptions on the image gradients, streaking artifact mitigation comes at a cost of some amount of image blurring. To prevent both image blurring and streaking artifacts, additional GRE volumes acquired at different head orientations relative to the MRI magnetic field can be used. The combination of these GRE volumes results in an over-determined inverse problem, which can be solved without regularization. This technique is termed Calculation Of Susceptibility through Multiple Orientation Sampling (COSMOS) and yields QSM images with exquisite detail and contrast (5,22,29–31). Despite marked improvement in image quality relative to single-orientation regularized QSMs, multi-orientation QSM comes at a cost of a significant increase in data acquisition time (32).
More recently, a new class of QSM algorithms that directly relate the GRE phase signal to the unknown susceptibility distribution has been proposed (27,28,33–35). By performing the background phase removal and dipole inversion in a single step, these algorithms prevent potential error propagation across successive operations. As a single regularizer acts on both operations, a separate thresholding parameter for SMV background filtering is no longer needed. In (33), a single-step QSM reconstruction technique that combined single-kernel SMV filtering with weighted quadratic smoothing was proposed. By extending the Morphology Enabled Dipole Inversion (MEDI) technique (21–23), a differential QSM method was developed to bypass the phase unwrapping and background phase removal steps (34). Using TGV regularization, a single-step QSM model was developed in (27,28) to mitigate staircasing artifacts often observed in the TV-based reconstructions. This single-step TGV optimization problem was efficiently solved using a primal-dual algorithm that finds a saddle point of general convex-concave problems (36). In (35), multiple SMV kernels were incorporated into the single-step QSM with quadratic smoothing regularization to reduce the loss of cortical phase information.
In this work, we develop a new single-step QSM model that combines the advantages of multiple SMV kernels and variational penalties that consist of TV and TGV regularizations. The main contributions of this work are as follows:
TV- and TGV-regularized single-step QSM with multiple SMV kernels are proposed. Using both numerical and in vivo data, we demonstrate that the proposed single-step QSM methods better mitigate dipole artifacts with improved homogeneity of image contrast than the conventional QSM algorithms that involve multiple sequential post-processing steps.
We introduce the Multi-Echo version of the Wave-CAIPI sequence (30,37) that allows rapid 3D-GRE imaging with high encoding efficiency. The Multi-Echo extension of Wave-CAIPI fully utilizes the repetition time (TR) to sample multiple echoes, which are then combined to improve the magnitude and phase signal-to-noise ratios (SNR). Furthermore, we propose a novel coil sensitivity estimation scheme that is fully automated and allows high quality parallel imaging while preserving the image phase. This relies on a rapid, 4-sec calibration scan, which is followed by phase-sensitive channel compression (38) and ESPIRiT coil sensitivity estimation (39).
Fast solvers for the proposed single-step model are developed based on alternating direction method of multipliers (ADMM) and variable splitting (40–48). Special structures of the matrices in the models are exploited so that all the sub-problems can be solved using closed-form solutions.
Accompanying data and MATLAB implementation are made available at martinos.org/~berkin/TGV_SS_QSM.zip
THEORY
TV- and TGV-Regularized Single-Step QSM with Multiple SMV Kernels
The underlying magnetic susceptibility distribution is conventionally estimated from the GRE phase using multiple sequential post-processing steps. First, the acquired raw phase ϕ is unwrapped (15,16). Then, the background phase is removed to obtain the unwrapped tissue phase ϕu,tissue (17,18). Finally, the following system of linear equations is solved to estimate the underlying susceptibility distribution χ from phis;u,tissue
| (1) |
where d is the spatial dipole kernel, and * denotes the 3-dimensional convolution.
Recently, QSM algorithms that estimate the underlying χ in a single step have been proposed to prevent potential error propagation between the subsequent steps. In this work, we propose to estimate the underlying χ in a single step by solving the following optimization problem
| (2) |
Ψ is the Laplacian unwrapping operator defined as Ψ(ϕ) = Δ−1 · Im(e−jψ · Δe−jψ) where Δ is the discrete Laplacian. hi is an SMV kernel for the ith reliable phase region defined as hi = δ − ρi where δ is a unit impulse, and ρi is a nonnegative radially symmetric, normalized kernel (17). Mi is a diagonal matrix that contains a binary mask for the ith reliable phase region, and R(χ) is a regularizer that imposes prior knowledge on the solution.
The first term of Eq. (2) is the data consistency term that combines phase unwrapping, background phase removal using multiple SMV kernels, and dipole inversion described by Eq. (1). The term Mi (hi * Ψ(ϕ))represents the V-SHARP background phase removal technique, which employs multiple kernels with varying radii (49,50). By using the convolution theorem, we obtain the k-space form of Eq. (2)
| (3) |
where F is the discrete Fourier transform operator, is the dipole kernel in k-space, and Hi is the discrete Fourier transform of hi. The second term in Eqs. (2) and (3) is the regularization term that imposes prior information on the solution. In this work, we propose two types of regularizations, R(χ): TV and second-order TGV. In the discrete setting, TV is defined as TV(χ) = ||Gχ||1 where G is the 3-dimensional gradient operator. The second-order TGV operator is defined as where ℰ is a symmetrized derivative as defined in (26) and in the Appendix. Compared to the quadratic smoothing (i.e., α penalty on the image gradients), both TV and TGV assign relatively less penalty to large degrees of signal variation. As a result, they mitigate noise and artifacts while preserving the edges in the signal. As opposed to TV, which only considers the first-order derivative, the second-order TGV also introduces the information about the second-order derivatives. It has been observed that the staircasing artifacts that often arise in the TV-based reconstructions are mitigated in the TGV-based reconstruction (26–28,51).
The improved models based on the more complicated data consistency term and TV/TGV regularization come at a cost of prolonged computation time. To address this, we propose an efficient solution to Eq. (3) using ADMM with variable splitting in both data consistency and regularization terms. In addition, the special structures of the matrices in the model are also exploited. Consequently, the updates in all the sub-problems can be carried out using closed-form solutions. Please refer to the Appendix and the accompanying MATLAB code for implementation details.
EXPERIMENTAL
Using two numerical brain phantoms, in vivo 3D echo planar imaging (EPI) data, in vivo Multi-Echo Wave-CAIPI data at 3T, and high-resolution in vivo Wave-CAIPI data at 7T, we compared the performances of six different QSM methods with multiple SMV kernels:
- SMV background filtering, followed by quadratic smoothing regularized dipole inversion (V-SHARP L2):
- SMV background filtering, followed by TV-regularized dipole inversion (V-SHARP TV):
- SMV background filtering, followed by TGV-regularized dipole inversion (V-SHARP TGV):
- Single-step QSM with quadratic smoothing regularization (Single-Step L2):
- Proposed: Single-step QSM with TV regularization (Single-Step TV):
- Proposed: Single-step QSM with TGV regularization (Single-Step TGV) :
For all the methods, the GRE phase was unwrapped using a Laplacian-based phase unwrapping algorithm (15,52). For the data set with an anisotropic voxel size, the SMV kernels were scaled accordingly. For V-SHARP L2 and Single-Step L2, the MATLAB built-in preconditioned conjugate gradients (pcg) function was used with the residual tolerance of 0.1%. For the other four methods, ADMM was used with the stopping criterion that iterations were terminated when the solution change between consecutive iterations was less than 1%. For the TGV-based methods, we followed (51) and set α0:α1 = 2:1 to reduce the number of regularization parameters that needed to be tuned. For the numerical phantoms, the regularization parameters were chosen to minimize root-mean-square error (RMSE) of all the methods. For the in vivo data, regularization parameters were selected using the L-curve heuristic (24,53). All parameter values are reported in Table 1. A workstation with 16 Intel Xeon E5-2670 processors and 128 GB of memory was used in all experiments.
Table 1.
Reconstruction parameters of each QSM method. For Numerical Brain Phantom, the reconstruction parameters were reported for the case where we used 5 SMV kernels for all the methods. For 3D-EPI, the reconstruction parameters were reported for the case where we used 5 SMV kernels for the single-step methods and 14 SMV kernels for the multi-step methods.
| Methods | Parameter | Duke Brain Phantom | Numerical Brain Phantom | 3D-EPI | ME Wave-CAIPI @ 3T | High-res Wave-CAIPI @ 7T |
|---|---|---|---|---|---|---|
| V-SHARP L2 | α | 8 × 10−3 | 2 × 10−2 | 2.73 × 10−2 | 2.73 × 10−2 | 5.56 × 10−2 |
|
| ||||||
| V-SHARP TV | α | 4 × 10−4 | 2 × 10−4 | 5.46 × 10−3 | 2.73 × 10−4 | 2.66 × 10−2 |
| μ | 3 × 10−2 | 3 × 10−2 | 3 × 10−3 | 3 × 10−3 | 10−1 | |
|
| ||||||
| V-SHARP TGV | α | 3 × 10−4 | 2 × 10−4 | 4.36 × 10−3 | 2.73 × 10−4 | 2.66 × 10−2 |
| μ0=μ1 | 3 × 10−2 | 3 × 10−2 | 3 × 10−3 | 3 × 10−3 | 10−1 | |
|
| ||||||
| Single-Step L2 | α | 3 × 10−3 | 3 × 10−4 | 2.66 × 10−2 | 2.09 × 10−2 | 6.80 × 10−3 |
|
| ||||||
| Single-Step TV | α | 2 × 10−4 | 7 × 10−5 | 5.46 × 10−3 | 2.69 × 10−4 | 7.00 × 10−3 |
| μ0=μ1 | 3 × 10−2 | 3 × 10−2 | 10−1 | 10−1 | 10−1 | |
|
| ||||||
| Single-Step TGV | α0 | 3 × 10−4 | 6 × 10−5 | 5.46 × 10−3 | 2.69 × 10−4 | 7.00 × 10−3 |
| μ0=μ1=μ2 | 3 × 10−2 | 3 × 10−2 | 10−1 | 10−1 | 10−1 | |
Duke Brain Phantom
A numerical brain phantom based on the segmented Duke model (54) with a spatial resolution of 1 mm3 isotropic was generated with the following susceptibility values (in the SI units): hippocampus = 0.05 ppm, hypothalamus = 0.05 ppm, medulla oblongata = 0.05 ppm, white matter = −0.03 ppm, cerebellum = −0.0065 ppm, pons = −0.0065 ppm, thalamus = −0.0065 ppm, midbrain = −0.0065 ppm, CSF = 0 ppm, and skull = −2.1 ppm. Additional magnetic susceptibility sources at 0.6 ppm were included to resemble subcutaneous fat without the chemical shift effect. In addition, magnetic susceptibility sources at 9.2 ppm were included within the head to mimic internal air in the nasal cavity and ear canal. The resulting phantom was convolved with the dipole kernel to generate the field map, and Gaussian white noise was then added to obtain an RMSE of 2.4% with respect to the noise-free field map. For all methods, background removal was performed using 5 SMV kernels with radii ranging from 1 voxel to 5 voxels, with a step size of 1 voxel.
For the multi-step methods (V-SHARP L2, V-SHARP TV, and V-SHARP TGV), we also reconstructed the susceptibility map from the background-free tissue phase to demonstrate that an error from the background field removal step propagates into the dipole inversion.
Numerical Brain Phantom
A numerical brain phantom with a resolution of 0.94 × 0.94 × 1.5 mm3 was adapted from (28,55) with the following susceptibility values (in the SI units): CSF = 0 ppm, globus pallidus = 0.19 ppm, putamen = 0.09 ppm, red nucleus = 0.07 ppm, substantia nigra = 0.09 ppm, dentate nucleus = 0.09 ppm, caudate nucleus = 0.09 ppm, and cortical gray matter = 0.05 ppm. With this setup, the white matter structures had the magnetic susceptibility values between −0.03 ppm and −0.01 ppm. In addition to the susceptibility sources inside the brain, two additional susceptibility sources were positioned in the region in close proximity to the brain to provide background field intensity and pattern that were similar to those appeared in the in vivo EPI data set (28). The resulting phantom was convolved with the dipole kernel to generate the field map, and Gaussian white noise was then added to obtain an RMSE of 2.4% with respect to the noise-free field map. Different number of SMV kernels with a maximum radius size ranging from 1 voxel to 8 voxels and with a step size of 1 voxel were tested to demonstrate the effect of the kernel size on the reconstructed susceptibility map.
3D Echo Planar Imaging (EPI)
Four-average data were acquired from a healthy volunteer (32 years old, male) with a written informed consent using a 3D EPI sequence (56) at 3T (TimTrio, Siemens Healthcare, Erlangen, Germany) in 57 seconds. Imaging parameters were: field-of-view (FOV) = 230 mm × 230 mm × 176 mm, spatial resolution = 1 mm3 isotropic, TR = 69 ms, echo time (TE) = 21 ms, GRAPPA acceleration factor = 4, partial Fourier along the primary phase encoding direction = 75%, and number of receiver coils = 32. Based on the results obtained from the numerical brain phantom, we observed that using five SMV kernels for the single-step methods gave a good balance between the reduction in RMSE and increase in reconstruction time. Consequently, for the single-step methods, 5 SMV kernels with radii ranging from 1 voxel to 5 voxels and with a step size of 1 voxel were used. Similarly, we observed that using 14 SMV kernels also gave a good tradeoff for the multi-step methods (results not shown), so we used 14 SMV kernels with radii ranging from 1 voxel to 14 voxels and with a step size of 1 voxel for the multi-step methods.
As an additional comparison, we also reconstructed the susceptibility map using the multi-step methods with five SMV kernels to demonstrate the effect of using different reconstruction methods with the same number of SMV kernels for this in vivo dataset.
Multi-Echo Wave-CAIPI at 3T
Wave-CAIPI is a parallel imaging technique that allows highly accelerated acquisition with minimal g-factor noise amplification penalty (37,57). This is achieved through a helical k-space trajectory that increases the distance between the aliasing voxels in sub-sampled acquisitions, thus improving the variation in the coil sensitivity profiles and providing better parallel imaging capability. This acquisition strategy has so far been applied to single-echo 3D-GRE imaging to achieve 9-fold acceleration with near-perfect g-factor performance (37). While Wave-CAIPI largely mitigates the g-factor noise amplification penalty due to parallel imaging reconstruction, the intrinsic penalty on SNR still hampers the achievable image quality. At 9-fold acceleration (R=9), this incurs a 3-fold reduction in the SNR, which would especially be challenging for high-resolution imaging. To mitigate this intrinsic SNR penalty, herein we have extended the Wave-CAIPI acquisition to sample multiple echoes within each TR, thus increasing the effective signal averaging time and boosting the SNR. As detailed below, we also propose a rapid acquisition and processing pipeline for coil sensitivity estimation to provide phase-sensitive, high-quality parallel imaging reconstruction.
Coil sensitivity estimation
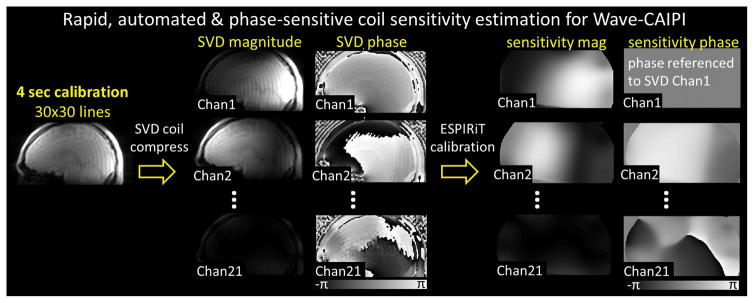
Accurate estimation of coil sensitivities is crucial for successful parallel imaging at high acceleration factors while preserving the object phase. ESPIRiT provides high-fidelity coil sensitivities by estimating the coil profiles that are implicitly used in autocalibrating k-space based parallel imaging methods (39). The phase of the sensitivities, however, is taken to be relative to the first channel (i.e. the first ESPIRiT coil profile which has zero phase). This presents a challenge since the fringe lines, also known as phase singularities, present in the first channel will propagate to the other channels, which will then reflect to the coil combined image. To address this, we employ the virtual body coil concept and obtain a reference channel by applying SVD coil compression (38). At 3T, the dominant singular vector (i.e. the compressed channel with the largest signal) is observed to have slowly varying phase and can replace the body coil acquisition as phase reference. By inputting the dominant singular vector to ESPIRiT as the first channel, we thus achieve automated, phase-sensitive coil sensitivity estimation. At 7T, the wavelength of coil sensitivity patterns is on the order of the subject’s head, and the interaction between the magnetic field and the subject is much higher. These lead to more complicated coil sensitivity profiles. As such, the dominant singular vector may no longer be spatially smooth and phase singularities could become a concern at ultra-high field.
For calibration, we use a low resolution (ky × kz = 30 × 30) 3D-GRE acquisition with short TE/TR = 2 / 3.5 ms. This requires less than 4 sec of scan time, which is then SVD compressed to 21 channels while the compression error remains below 1%. This pipeline is depicted in Figure 1. The same SVD matrix is also applied to the high-resolution undersampled Wave-CAIPI data for coil compression.
Figure 1.
The pipeline of the proposed rapid, automated and phase-sensitive coil sensitivity estimation for Wave-CAIPI.
Multi-Echo Wave-CAIPI acquisition & reconstruction
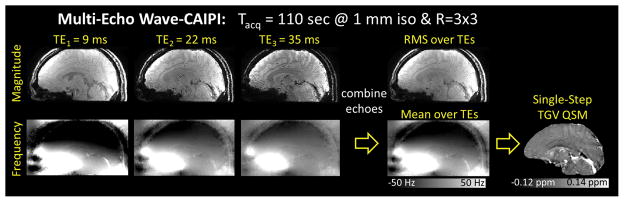
R=3×3 fold accelerated data were acquired from a healthy volunteer (33 years old, male) with a written informed consent using Multi-Echo Wave-CAIPI at 3T (TimTrio, Siemens Healthcare, Erlangen, Germany) in 110 seconds. Imaging parameters were: FOV = 256 mm × 192 mm × 120 mm, spatial resolution = 1 mm3 isotropic, TR = 43 ms, TEs = 9/22/35 ms, bandwidth = 100 Hz/pixel, and number of receiver coils = 32. The undersampled coil-compressed Wave-CAIPI data were reconstructed using generalized SENSE (37,58) with ESPIRiT coil sensitivities. The magnitude images from the three echoes were merged with root-mean-square combination, while the phase images were unwrapped, normalized by their TEs, and then averaged for improved SNR (Figure 2). The combined frequency map was then processed by the QSM algorithms.
Figure 2.
Multi-Echo Wave-CAIPI. The unwrapped phase images were normalized by their TEs and averaged for improved SNR. The resulting combined phase was then processed by the QSM algorithms.
QSM for Multi-Echo Wave-CAIPI
For the single-step methods, five SMV kernels with radii ranging from 1 voxel to 5 voxels and with a step size of 1 voxel were used. For the multi-step methods, background field removal was performed using 14 SMV kernels with radii ranging from 1 voxel to 14 voxels, with a step size of 1 voxel.
High-resolution Wave-CAIPI at 7T
To compare the QSM reconstructions on high-resolution 3D-GRE data, one healthy volunteer (32 years old, male) underwent MR imaging at 7T (Siemens Magnetom) using a 32-channel custom receive array. The imaging protocol included the single-echo Wave-CAIPI sequence (TE/TR = 20/30 ms, 0.5 mm3 isotropic resolution, BW = 100 Hz/px, matrix size = 384 × 512 × 240) with R=3×3, which resulted in a total acquisition time of 5 min. For the single-step methods, 5 SMV kernels with radii ranging from 1 voxel to 5 voxels and with a step size of 1 voxel were used. For the multi-step methods, background removal was performed using 14 SMV kernels with radii ranging from 1 voxel to 14 voxels, with a step size of 1 voxel.
RESULTS
Figures 3 through 8 and Supplementary Figures 1 through 4 show the reconstruction results obtained from the six different QSM algorithms. The reconstruction times were reported in Table 2. Although it has been observed that the staircasing artifacts that often arise in the TV-based reconstructions are mitigated in the TGV-based reconstructions in several applications (26–28,51), we observed that the reconstruction quality of the proposed Single-Step TV and Single-Step TGV methods were comparable in our experiments, as shown in the figures (especially in Supplementary Figure 4).
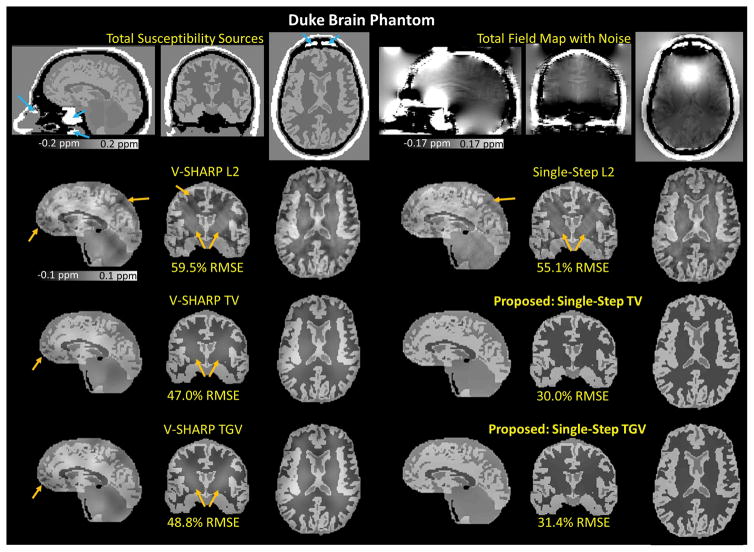
Figure 3.
Duke Brain Phantom. The reconstructed magnetic susceptibility maps obtained from six different QSM algorithms (5 SMV kernels) with their corresponding RMSEs. The blue arrows indicate the magnetic susceptibility sources (9.2 ppm) that mimic internal air in the nasal cavity and ear canal. The orange arrows indicate the apparent remaining dipole artifacts and background phase contamination.
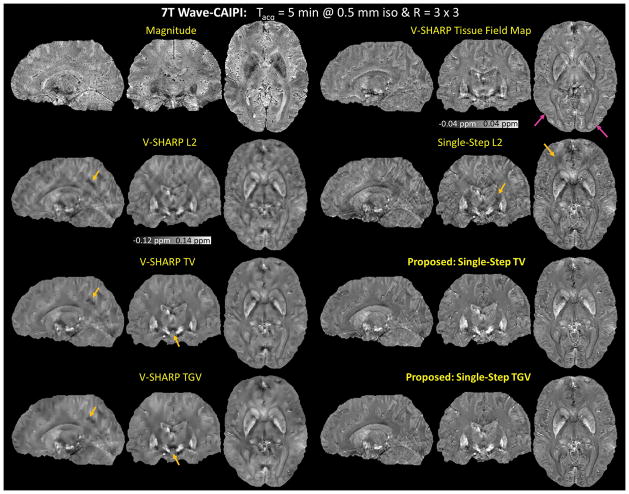
Figure 8.
High-Resolution Wave-CAIPI at 7 Tesla. The proposed methods alleviated the artifacts that were apparent in the other four methods as indicated by the orange arrows. As indicated by the pink arrow in the V-SHARP tissue field map, the cortical regions became blurred after the dipole inversion in the multi-step methods.
Table 2.
Reconstruction time of each QSM method. For Numerical Brain Phantom, the reconstruction times were reported for the case where we used 5 SMV kernels for all the methods. For 3D-EPI, the reconstruction times were reported for the case where we used 5 SMV kernels for the single-step methods and 14 SMV kernels for the multistep methods.
| Methods | Reconstruction time (sec) | ||||
|---|---|---|---|---|---|
| Duke Brain Phantom | Numerical Brain Phantom | ME Wave-CAIPI @ 3T | High-res Wave-CAIPI @ 7T | ||
| V-SHARP L2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.8 |
| V-SHARP TV | 9.5 | 6.0 | 13.5 | 10.3 | 29.9 |
| V-SHARP TGV | 41.3 | 50.5 | 54.9 | 75.0 | 158.1 |
| Single-Step L2 | 111.3 | 101.8 | 25.1 | 30.8 | 205.3 |
| Single-Step TV | 127.8 | 105.8 | 82.9 | 80.5 | 350.6 |
| Single-Step TGV | 243.7 | 189.3 | 258.3 | 200.6 | 870.7 |
Duke Brain Phantom
Using 5 SMV kernels, the RMSEs of the reconstructed susceptibility maps with respect to the true susceptibility distribution were 59.5% for V-SHARP L2, 47.0% for V-SHARP TV, 48.8% for V-SHARP TGV, 55.1% for Single-Step L2, 30.0% for Single-Step TV, and 31.4% for Single-Step TGV. As shown in Figure 3 and Supplementary Figure 1, Single-Step TV and Single-Step TGV better mitigated the background phase contamination and dipole artifacts (indicated by the orange arrows) compared to the other methods.
Applying V-SHARP filtering to the total phase, which had the contributions from both underlying tissue and background components, resulted in the filtered phase that had 49.5% RMSE with respect to the underlying tissue phase. By performing the dipole inversions on the V-SHARP filtered phase, we obtained the susceptibility maps with RMSEs of 59.5% using the quadratic smoothing, 47.0% using TV, and 48.8% using TGV regularizations, with respect to the underlying susceptibility map. Instead of using the V-SHARP filtered phase, we have also performed the dipole inversions on the underlying background-free tissue phase. The RMSEs of the reconstructed susceptibility maps were 19.4%, 5.9%, and 5.9% using quadratic smoothing, TV-, and TGV-regularized dipole inversions, respectively. In this case, the RMSEs of the reconstructed susceptibility maps were much lower than those obtained from the methods that involved V-SHARP filtering. With this comparison, we have demonstrated that an error from the background field removal step propagated into the dipole inversion step.
Numerical Brain Phantom
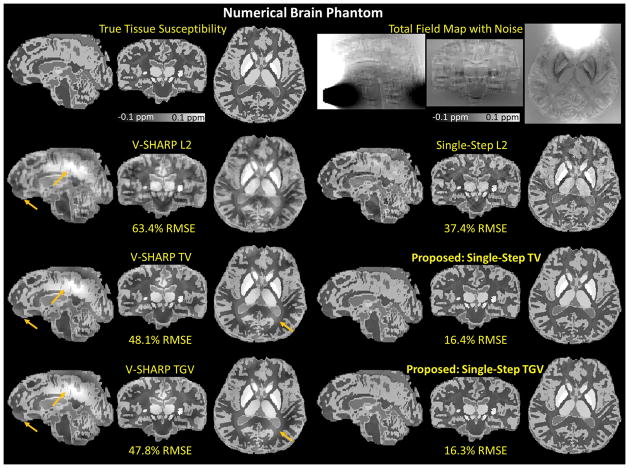
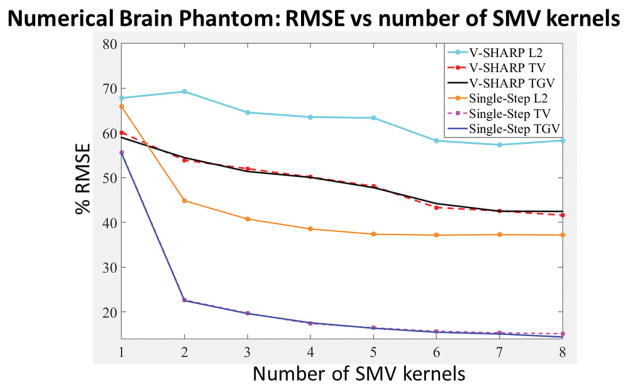
Using 5 SMV kernels, the RMSEs of the reconstructed susceptibility maps with respect to the true susceptibility distribution were 63.4% for V-SHARP L2, 48.1% for V-SHARP TV, 47.8% for V-SHARP TGV, 37.4% for Single-Step L2, 16.4% for Single-Step TV, and 16.3% for Single-Step TGV. The %RMSE for specific regions with respect to the underlying magnetic susceptibility values were reported in Table 3. As shown in Figure 4 and Supplementary Figure 2, Single-Step TV and Single-Step TGV better mitigated the background phase contamination and dipole artifacts (indicated by the orange arrows) compared to the other methods. As shown in Figure 5 and listed in Table 3, both Single-Step TV and Single-Step TGV yielded lower RMSEs compared to the other methods with the same number of SMV kernels.
Table 3.
Numerical Brain Phantom. %RMSEs in specific regions of the reconstructed magnetic susceptibility maps (5 SMV kernels) with respect to the underlying susceptibility values.
| Methods | V-SHARP L2 | V-SHARP TV | V-SHARP TGV | Single-Step L2 | Single-Step TV | Single-Step TGV |
|---|---|---|---|---|---|---|
| ROIs | ||||||
| CSF (0 ppm) | 227.3 | 188.6 | 188.5 | 162.7 | 55.7 | 55.7 |
| globus pallidus (0.19 ppm) | 24.2 | 6.6 | 4.1 | 15.8 | 2 | 1.8 |
| putamen, substantia nigra, dentate nucleus, and caudate nucleus(0.09 ppm) | 32.9 | 14.6 | 13.3 | 19.0 | 4.7 | 4.4 |
| red nucleus (0.07 ppm) | 27.9 | 19.5 | 21.8 | 19.4 | 3.8 | 4.0 |
| cortical gray matter (0.05 ppm) | 60.1 | 41.6 | 41.1 | 34.1 | 14.7 | 15.0 |
| white matter (−0.03 to −0.01 ppm) | 67.5 | 54.8 | 54.7 | 39.3 | 18.8 | 18.4 |
Figure 4.
Numerical Brain Phantom. The reconstructed magnetic susceptibility maps obtained from six different QSM algorithms (5 SMV kernels) with their corresponding RMSEs. Single-Step TV and Single-Step TGV better mitigated the background phase contamination and dipole artifacts (indicated by the orange arrows) compared to the other methods.
Figure 5.
Numerical Brain Phantom. RMSEs of the reconstructed magnetic susceptibility maps obtained from six different QSM algorithms.
3D Echo Planar Imaging (EPI)
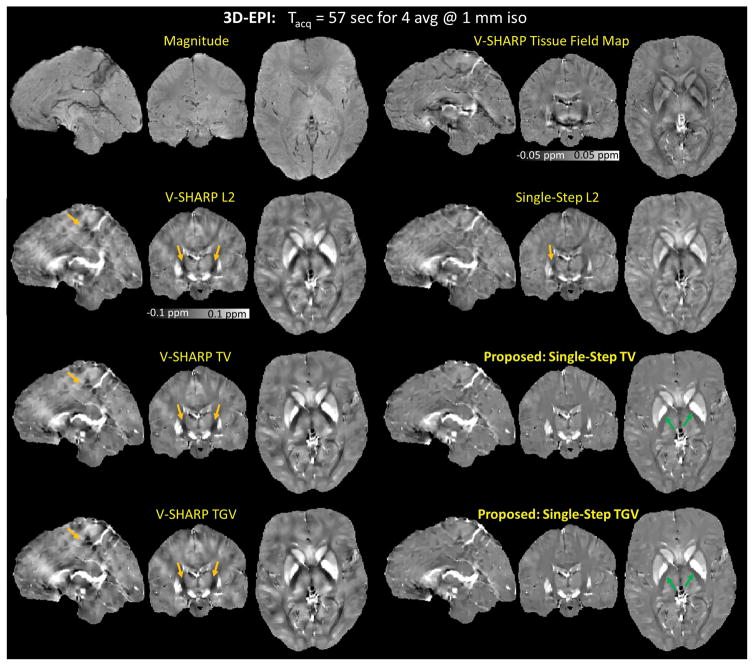
Figure 6 shows the reconstructed susceptibility maps obtained from the multi-step (14 SMV kernels) and single-step (5 SMV kernels) methods. Single-Step TV and Single-Step TGV mitigated the dipole artifacts (indicated by the orange arrows) more successfully. Nevertheless, the artifact mitigation obtained from the proposed methods came at a cost of reduced contrast between white matter and gray matter (indicated by the green arrows). Supplementary Figure 3 shows the results of the additional comparison where we reconstructed the susceptibility maps using all the methods with the same number of SMV kernels (5 SMV kernels).
Figure 6.
3D-EPI. The reconstructed magnetic susceptibility maps obtained from the multistep (14 SMV kernels) and single-step (5 SMV kernels) methods. Single-Step TV and Single-Step TGV mitigated the dipole artifacts (indicated by the orange arrows) more successfully, however with reduced contrast between white matter and gray matter (indicated by the green arrows).
Multi-Echo Wave-CAIPI at 3T
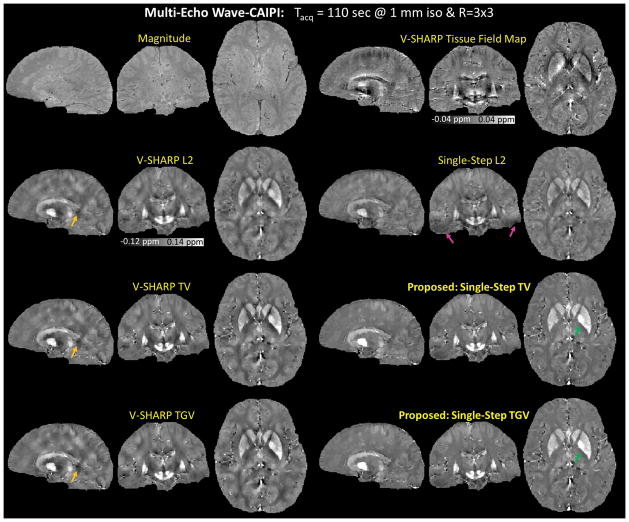
As shown in Figure 7, the reconstructed susceptibility map obtained using the proposed methods had the lowest level of dipole artifacts (indicated by the orange arrows), however with reduced contrast between white matter and gray matter (indicated by the green arrows). Compared to Single-Step L2, the proposed methods with the same SMV kernel sizes alleviated the B0 artifacts in the temporal lobes as indicated by the pink arrows in the Single-Step L2 reconstructed susceptibility map.
Figure 7.
Multi-Echo Wave-CAIPI. The reconstructed magnetic susceptibility maps obtained from six different QSM algorithms. The proposed methods had the lowest level of dipole artifacts (indicated by the orange arrows), however with reduced contrast between white matter and gray matter (indicated by the green arrows). Compared to Single-Step L2, the proposed methods with the same SMV kernel sizes alleviated the B0 artifacts in the temporal lobes in the Single-Step L2 reconstructed susceptibility map (pink arrows).
High-resolution Wave-CAIPI at 7T
Figure 8 shows the reconstructed magnetic susceptibility maps of the high-resolution in vivo Wave-CAIPI data at 7T. The proposed methods alleviated the artifacts that were apparent in the other four methods as indicated by the orange arrows. The susceptibility maps reconstructed using the multi-step methods and the single-step methods have different visual appearance. Compared to the multi-step methods, the proposed methods removed the artifacts while preserving small details such as edges. As indicated by the pink arrow in the V-SHARP tissue field map, the cortical regions became blurred after the dipole inversion in the multi-step methods. Compared to Single-Step L2, the proposed methods had fewer streaking artifacts.
DISCUSSION
In this work, the background phase was removed by exploiting the harmonic mean value property which involves the convolution of the total phase with SMV kernels (17). An SMV kernel with large radius is typically desirable because it provides a better approximation of the radially symmetric SMV kernel since it suffers less from discretization effects. Nevertheless, since the voxels close to the object boundary have contributions from the regions with no detectable MRI signal in the convolution process, the size of the trustable region becomes smaller when a larger SMV kernel is employed. Although a smaller SMV kernel could be used to enlarge the trustable region, the small SMV kernel would cause a large residual phase error amplification, which reduces the background phase removal accuracy within the trustable region (49). In order to take an advantage of larger SMV kernels without significantly shrinking the trustable region, SMV kernels with different radii can be employed (49). By using multiple SMV kernels with different radii, the trustable region is enlarged by the smaller SMV kernels, and the background phase removal accuracy within the trustable region is improved toward the center of the brain because larger SMV kernels are used near the center.
By incorporating the use of multiple SMV kernels into our models and estimating the underlying susceptibility distribution in a single step, potential error propagation from one step to the subsequent steps has been prevented. Furthermore, the proposed methods use TV and TGV regularizations, which provide more natural signal models than quadratic smoothing. In particular, TV promotes a piecewise-constant solution, and the second-order TGV promotes a piecewise-smooth solution. Consequently, the proposed methods successfully suppressed dipole artifacts while preserving the edges in the signal. Because the proposed methods benefit from the combination of multiple SMV kernels, single-step reconstruction, and TV/TGV regularization, they gave the reconstructed susceptibility maps that had the lowest level of dipole artifacts compared to the other methods evaluated in this work. As demonstrated using numerical and in vivo experiments, the proposed single-step methods mitigated dipole artifacts more successfully than the methods that involved sequential SMV filtering followed by dipole inversion. As shown in the in vivo Multi-Echo Wave-CAIPI result, the proposed methods also removed the background phase contamination more effectively, especially in regions with large B0 inhomogeneity, compared to the single-step QSM with quadratic smoothing regularization.
The optimization problems associated with the proposed methods were efficiently solved using ADMM with variable splitting to decompose the original problem into smaller ones that can be solved easily. We have applied variable splitting not only to the regularization terms, but also to the data consistency term (59) so that the sub-problems were further simplified. Moreover, by recognizing the special structures of the matrices in our problem, all the updates for the sub-problems were performed using the analytical formulas described in the Appendix.
This work also introduced Multi-Echo Wave-CAIPI, which is an efficient sequence that fully utilizes the TR for data sampling, hence boosting the SNR in the GRE phase and magnitude images. While Wave-CAIPI substantially mitigates the g-factor noise amplification penalty due to parallel imaging reconstruction, the -penalty due to the k-space subsampling intrinsically reduces the SNR of the acquired data. Multi-Echo Wave-CAIPI mitigates this intrinsic SNR penalty by continuously sampling the data during the entire acquisition window. The magnitude images are combined by taking the RMS over the echoes, providing SNR benefit that can be useful for Susceptibility Weighted Imaging (SWI) (60). Additionally, the frequency maps are computed by unwrapping the raw phase of each echo, normalizing by their TEs, and averaging to improve SNR.
Combination of the channels in an array coil is an important step for imaging phase and susceptibility contrast. The estimated coil sensitivities used in the combination should not include the phase of the imaged object, otherwise the combined phase will be severely underestimated. The sensitivity estimates also need to capture the fringe lines in order to prevent their propagation to the combined phase image. An effective way to address both of these issues is to acquire additional reference data with slowly varying phase in the birdcage mode or with the body coil (58). Alternatively, multi-echo reference images can be collected to estimate the phase offset of the sensitivities (31,61). In this work, we used a 4-sec, low-resolution, single-echo calibration acquisition with the array coil for calibration. As demonstrated in (38), the dominant singular vector of SVD coil compression can serve as a virtual body coil for phase reference. Since this is a linear combination of all channels, it will still contain the object phase, while being sufficiently smooth to exclude phase singularities at 3T. At ultra-high field where the coil sensitivity profiles become more complicated, the smooth assumption may no longer hold, and the virtual body coil may contain singularities. For automated estimation of sensitivities, we employ ESPIRiT (39), which uses the first channel as phase reference. As such, when the dominant singular vector of the SVD compression is arranged to be the first channel, it acts as a virtual body coil reference during ESPIRiT reconstruction. Processing the rapid calibration data with ESPIRiT and the SVD virtual coil concept thus allows phase-sensitive estimation of coil sensitivities.
Extensions and limitations
Although the combination of ADMM and variable splitting enables an efficient solver for the regularized optimization, more augmented Lagrangian parameters corresponding to the consensus constraints are introduced in the proposed algorithms. To simplify parameter selection, we chose the same value for all Lagrangian parameters of the proposed methods. For Single-Step TGV, we fixed the ratio between the regularization parameters α0:α1 to 2:1. Consequently, we were left with two parameters in the proposed methods, one for regularization and one for the consensus constraints that needed to be tuned. For the numerical simulations, these parameters were chosen to minimize the RMSE. For the in vivo experiments, all the augmented Lagrangian parameters of the proposed methods were set to 0.1, and the regularization parameter was chosen using the L-curve criterion.
As described in the Appendix, the proposed algorithm allows the parallel updates of the variables associated with each sub-problem. However, the current implementation uses the sequential updates for the z2,i’s, so the reconstruction time could be further reduced by using the parallel updates for all the subproblems. The improvement in the computation time could be used towards increasing the number of SMV kernels by including even larger filter diameters, which would lead to improved background phase removal. A further algorithmic advancement could be using an exponential signal model rather than a linear system in the single-step reconstruction, which had enabled high quality susceptibility mapping even when a crude brain mask was employed (34).
For Multi-Echo Wave-CAIPI acquisition, a model-based approach that jointly estimates magnitude and frequency components across the echoes could provide improved reconstruction. This would entail a signal model comprising the product of a complex amplitude and a complex exponential per voxel. These two unknowns could then be estimated from subsampled k-t space using model-based reconstruction similar to (62). As the number of echoes acquired increases, the accuracy of the model fit would improve, since it would be easier to estimate two unknowns from several data points. This could potentially improve parallel imaging quality and could enable alternative sampling schemes where each echo samples a different k-space location.
CONCLUSION
In this work, we proposed novel QSM methods that unify SMV filtering with multiple kernels and TV/TGV regularization within a single step. Using ADMM with variable splitting and exploiting special structures of the matrices in the models, we developed efficient algorithms that involve analytical solutions for all of the optimization steps. As demonstrated using the numerical phantoms and in vivo data sets, the proposed methods better mitigated the dipole artifacts compared to other QSM methods evaluated. We also introduced an automated sensitivity estimation scheme that relies on a rapid 4-sec acquisition for phase-sensitive coil combination. This permitted high quality parallel imaging with Wave-CAIPI, which was extended to acquire multiple echoes for improved SNR efficiency. Combination of Multi-Echo Wave-CAIPI and single-step QSM with TV/TGV regularization thus enabled high-quality susceptibility mapping with efficient acquisition and reconstruction.
Supplementary Material
Acknowledgments
Grant Support: NIH R01EB017219, P41EB015896, 1U01MH093765, R24MH106096, 1R01EB017337-01
The authors thank Susie Y. Huang, Michael Khalil, Salil Soman, and Jeffrey Stout for helpful discussions. Grant Support: NIH R01EB017219, P41EB015896, 1U01MH093765, R24MH106096, and 1R01EB017337-01.
APPENDIX
Closed-form iterations for TGV-regularized single-step QSM
Using the discrete version of the second order total generalized variation (TGV) regularizer, recovering the underlying magnetic susceptibility distribution involves solving the following optimization problem
| (A.1) |
where G is the 3-dimensional gradient operator, ℰ is a symmetrized derivative as defined in (26), and α0 and α1 are regularization parameters. By introducing the additional variables z0, z1, and z2 with the consensus constraints, Eq. (A.1) becomes
| (A.2) |
To efficiently solve Eq. (A.2), we adopt the alternating direction method of multipliers (ADMM) (40–48) to decompose the original problem into smaller sub-problems that are easy to solve.
The sub-problem for the (χ, v) pair is
| (A.3) |
where s0, s1, and s2 are the scaled dual variables; μ0, μ1, and μ2 are the augmented Lagrangian parameters. Taking the gradients with respect to both χ and v of Eq. (A.3) and setting them to zero yields the system of linear equations with circulant blocks. Diagonalizing each block by the discrete Fourier transform and then reordering the resulting diagonal-block matrix, we obtain the following system
| (A.4) |
where the An’s are 4×4 Hermitian positive definite matrices that represent the system associating with voxel n, un = (Fχ, Fvx, Fvy, Fvz)T at voxel n, and N is the number of voxels. We can update each un independently because the systems associated with the voxels are decoupled. Moreover, since the An’s have small dimensions of 4×4, we can easily update μn using many techniques such as the factor-solve method, Cramer’s rule, and even a direct inversion (63,64).
The z0- and z1-updates can be performed using the voxel-wise soft-thresholding operations
| (A.5) |
| (A.6) |
where ○ denotes the Hadamard product, and the subscript in parenthesis is the voxel label.
The sub-problem for z2 is
| (A.7) |
The systems associated with the z2,i’s are decoupled, so we can update each z2,i independently. By taking the gradient of Eq. (A.7) with respect to z2,i and setting it to zero, we obtain the following analytical solution
| (A.8) |
We can precompute and . It is trivial to compute the inverse of because it is a diagonal matrix. As a result, we only need only two FFT operations and a few matrix multiplications and matrix additions for each z2,i update.
Finally, we can update the scaled dual variables as follow
| (A.9) |
| (A.10) |
| (A.11) |
In summary, the TGV-regularized single-step QSM is solved by iterating Eqs. (A.4–A.6) and Eqs. (A.8–A.11) until convergence as implemented in the accompanying MATLAB code. The TV-regularized single-step QSM implementation can be derived using the same approach. Please see the accompanying MATLAB code for the implementation.
References
- 1.Duyn J, van Gelderen P, Tie-Qiang L, de Zwart JA, Koretsky AP, Fukunaga M. High-field MRI of brain cortical substructure based on signal phase. Proc Natl Acad Sci. 2007;104:11796–11801. doi: 10.1073/pnas.0610821104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Liu C, Li W, Tong KA, Yeom KW, Kuzminski S. Susceptibility-weighted imaging and quantitative susceptibility mapping in the brain. J Magn Reson Imaging. 2015;42:23–41. doi: 10.1002/jmri.24768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang Y, Liu T. Quantitative susceptibility mapping (QSM): decoding MRI data for a tissue magnetic biomarker. Magn Reson Med. 2015;73:82–101. doi: 10.1002/mrm.25358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Marques JP, Bowtell R. Application of a Fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts Magn Reson Part B Magn Reson Eng. 2005;25B:65–78. [Google Scholar]
- 5.Deistung A, Schäfer A, Schweser F, Biedermann U, Turner R, Reichenbach JR. Toward in vivo histology_: A comparison of quantitative susceptibility mapping ( QSM ) with magnitude-, phase-, and R2*-imaging at ultra-high magnetic field strength. Neuroimage. 2013;65:299–314. doi: 10.1016/j.neuroimage.2012.09.055. [DOI] [PubMed] [Google Scholar]
- 6.Argyridis I, Li W, Johnson GA, Liu C. Quantitative magnetic susceptibility of the developing mouse brain reveals microstructural changes in the white matter. Neuroimage. 2014;88:134–142. doi: 10.1016/j.neuroimage.2013.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Li W, Wu B, Batrachenko A, Bancroft-Wu V, Morey RA, Shashi V, Langkammer C, De Bellis MD, Ropele S, Song AW, Liu C. Differential developmental trajectories of magnetic susceptibility in human brain gray and white matter over the lifespan. Hum Brain Mapp. 2014;35:2698–713. doi: 10.1002/hbm.22360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bilgic B, Pfefferbaum A, Rohlfing T, Sullivan EV, Adalsteinsson E. MRI estimates of brain iron concentration in normal aging using quantitative susceptibility mapping. Neuroimage. 2012;59:2625–35. doi: 10.1016/j.neuroimage.2011.08.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Acosta-Cabronero J, Williams G, Cardenas-Blanco A, Arnold RJ, Lupson V, Nestor PJ. In Vivo Quantitative Susceptibility Mapping (QSM) in Alzheimer’s Disease. PLoS One. 2013;8:e81093. doi: 10.1371/journal.pone.0081093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Langkammer C, Liu T, Khalil M, Enzinger C, Jehna M, Fuchs S, Fazekas F, Wang Y, Ropele S. Quantitative susceptibility mapping in multiple sclerosis. Radiology. 2013;267:551–9. doi: 10.1148/radiol.12120707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wisnieff C, Ramanan S, Olesik J, Gauthier S, Wang Y, Pitt D. Quantitative susceptibility mapping (QSM) of white matter multiple sclerosis lesions: Interpreting positive susceptibility and the presence of iron. Magn Reson Med. 2015;74:564–70. doi: 10.1002/mrm.25420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fan AP, Benner T, Bolar DS, Rosen BR, Adalsteinsson E. Phase-based regional oxygen metabolism (PROM) using MRI. Magn Reson Med. 2012;67:669–78. doi: 10.1002/mrm.23050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fan AP, Evans KC, Stout JN, Rosen BR, Adalsteinsson E. Regional quantification of cerebral venous oxygenation from MRI susceptibility during hypercapnia. Neuroimage. 2015;104:146–55. doi: 10.1016/j.neuroimage.2014.09.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fan AP, Bilgic B, Gagnon L, Witzel T, Bhat H, Rosen BR, Adalsteinsson E. Quantitative oxygenation venography from MRI phase. Magn Reson Med. 2013;72:149–59. doi: 10.1002/mrm.24918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. Neuroimage. 2011;55:1645–1656. doi: 10.1016/j.neuroimage.2010.11.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Witoszynskyj S, Rauscher A, Barth M. Phase unwrapping of MR images using ΦUN–A fast and robust region growing algorithm. Med Image Anal. 2009;13:257–268. doi: 10.1016/j.media.2008.10.004. [DOI] [PubMed] [Google Scholar]
- 17.Schweser F, Deistung A, Lehr BW, Reichenbach JR. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: An approach to in vivo brain iron metabolism? Neuroimage. 2011;54:2789–2807. doi: 10.1016/j.neuroimage.2010.10.070. [DOI] [PubMed] [Google Scholar]
- 18.Liu T, Khalidov I, de Rochefort L, Spincemaille P, Liu J, Tsiouris aJ, Wang Y. A novel background field removal method for MRI using projection onto dipole fields (PDF) NMR Biomed. 2011;24:1129–1136. doi: 10.1002/nbm.1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.De Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wu J, Wang Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magn Reson Med. 2010;63:194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
- 20.Bilgic B, Chatnuntawech I, Fan A, Setsompop K, Cauley S, Wald L, Adalsteinsson E. Fast image reconstruction with L2-regularization. J Magn Reson Imaging. 2014;40:181–191. doi: 10.1002/jmri.24365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Liu T, Xu W, Spincemaille P, Avestimehr AS, Wang Y. Accuracy of the morphology enabled dipole inversion (MEDI) algorithm for quantitative susceptibility mapping in MRI. Med Imaging, IEEE Trans. 2012;31:816–824. doi: 10.1109/TMI.2011.2182523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu T, Liu J, de Rochefort L, Spincemaille P, Khalidov I, Ledoux JR, Wang Y. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: comparison with COSMOS in human brain imaging. Magn Reson Med. 2011;66:777–83. doi: 10.1002/mrm.22816. [DOI] [PubMed] [Google Scholar]
- 23.Liu J, Liu T, de Rochefort L, Ledoux J, Khalidov I, Chen W, Tsiouris AJ, Wisnieff C, Spincemaille P, Prince MR, Wang Y. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map. Neuroimage. 2012;59:2560–8. doi: 10.1016/j.neuroimage.2011.08.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bilgic B, Fan AP, Polimeni JR, Cauley SF, Bianciardi M, Adalsteinsson E, Wald LL, Setsompop K. Fast quantitative susceptibility mapping with L1-regularization and automatic parameter selection. Magn Reson Med. 2014;72:1444–59. doi: 10.1002/mrm.25029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schweser F, Sommer K, Deistung A, Reichenbach JR. Quantitative susceptibility mapping for investigating subtle susceptibility variations in the human brain. Neuroimage. 2012;62:2083–100. doi: 10.1016/j.neuroimage.2012.05.067. [DOI] [PubMed] [Google Scholar]
- 26.Bredies K, Kunisch K, Pock T. Total Generalized Variation. SIAM J Imaging Sci. 2010;3:492–526. [Google Scholar]
- 27.Bredies K, Ropele S, Poser Ba, Barth M, Langkammer C. Single-Step Quantitative Susceptibility Mapping using Total Generalized Variation and 3D EPI. Proceedings of the 22nd Annual Meeting of ISMRM; Milan, Italy. 2014. p. 604. [Google Scholar]
- 28.Langkammer C, Bredies K, Poser BA, Barth M, Reishofer G, Fan AP, Bilgic B, Fazekas F, Mainero C, Ropele S. Fast quantitative susceptibility mapping using 3D EPI and total generalized variation. Neuroimage. 2015;111:622–30. doi: 10.1016/j.neuroimage.2015.02.041. [DOI] [PubMed] [Google Scholar]
- 29.Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med. 2009;61:196–204. doi: 10.1002/mrm.21828. [DOI] [PubMed] [Google Scholar]
- 30.Bilgic B, Xie L, Dibb R, Langkammer C, Mutluay A, Ye H, Polimeni JR, Augustinack J, Liu C, Wald LL, Setsompop K. Rapid Multi-Orientation Quantitative Susceptibility Mapping. Neuroimage. 2015 doi: 10.1016/j.neuroimage.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Khabipova D, Wiaux Y, Gruetter R, Marques JP. A modulated closed form solution for quantitative susceptibility mapping--a thorough evaluation and comparison to iterative methods based on edge prior knowledge. Neuroimage. 2015;107:163–74. doi: 10.1016/j.neuroimage.2014.11.038. [DOI] [PubMed] [Google Scholar]
- 32.Wharton S, Bowtell R. Whole-brain susceptibility mapping at high field: a comparison of multiple- and single-orientation methods. Neuroimage. 2010;53:515–525. doi: 10.1016/j.neuroimage.2010.06.070. [DOI] [PubMed] [Google Scholar]
- 33.Sharma S, Hernando D, Horng D, Reeder S. A joint background field removal and dipole deconvolution approach for quantitative susceptibility mapping in the liver. Proceedings of the 22nd Annual Meeting of ISMRM; Milan, Italy. 2014. p. 606. [Google Scholar]
- 34.Liu T, Zhou D, Spincemaille P, Yi W. Differential approach to quantitative susceptibility mapping without background field removal. Proceedings of the 22nd Annual Meeting of ISMRM; Milan, Italy. 2014. p. 597. [Google Scholar]
- 35.Bilgic B, Langkammer C, Wald LL, Setsompop K. Single-Step QSM with Fast Reconstruction. Third International Workshop on MRI Phase Contrast & Quantitative Susceptibility Mapping; Durham, NC, USA. 2014. [Google Scholar]
- 36.Chambolle A, Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging. J Math Imaging Vis. 2011;40:120–145. [Google Scholar]
- 37.Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magn Reson Med. 2015;73:2152–2162. doi: 10.1002/mrm.25347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Buehrer M, Boesiger P, Kozerke S. Virtual Body Coil Calibration for Phased-Array Imaging. Proceedings of the 17th Annual Meeting of ISMRM; Honolulu, Hawaii, USA. 2009. p. 760. [Google Scholar]
- 39.Uecker M, Lai P, Murphy M, Virtue P, Elad M, Pauly JM, Vasanawala S, Lustig M. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71:990–1001. doi: 10.1002/mrm.24751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Glowinski R, Marroco A. Sur l’approximation, par éléments finis d'ordre un, et la résolution, par pénalisation-dualité d'une classe de problèmes de Dirichlet non linéaires. Rev Fran¸caise d’Automatique, Informatique, Rech Op′erationelle. 1975;9:41–76. [Google Scholar]
- 41.Gabay D, Mercier B. A dual algorithm for the solution of nonlinear variational problems via finite element approximation. Comput Math with Appl. 1976;2:17–40. [Google Scholar]
- 42.Fortin M, Glowinski R. Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary-Value Problems. Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary-Value Problems. 1983 [Google Scholar]
- 43.Bertsekas DP, Tsitsiklis JN. Parallel and Distributed Computation: Numerical Methods. 1989 [Google Scholar]
- 44.Eckstein J, Bertsekas DP. On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math Program. 1992;55:293–318. [Google Scholar]
- 45.Fukushima M. Application of the Alternating Direction Method of Multipliers to Separable Convex Programming Problems. Comput Optim Appl. 1992;1:93–111. [Google Scholar]
- 46.Eckstein J, Fukushima M. Some reformulations and applications of the alternating direction method of multipliers. Large Scale Optim State Art. 1993:119–138. [Google Scholar]
- 47.Chen G, Teboulle M. A proximal-based decomposition method for convex minimization problems. Math Program. 1994;64:81–101. [Google Scholar]
- 48.Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found Trends® Mach Learn. 2010;3:1–122. doi: 10.1561/2200000016. [DOI] [Google Scholar]
- 49.Wu B, Li W, Guidon A, Liu C. Whole brain susceptibility mapping using compressed sensing. Magn Reson Med. 2012;67:137–47. doi: 10.1002/mrm.23000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Li W, Avram AV, Wu B, Xiao X, Liu C. Integrated Laplacian-based phase unwrapping and background phase removal for quantitative susceptibility mapping. NMR Biomed. 2014;27:219–227. doi: 10.1002/nbm.3056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn Reson Med. 2011;65:480–491. doi: 10.1002/mrm.22595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Schofield MA, Zhu Y. Fast phase unwrapping algorithm for interferometric applications. Opt Lett. 2003;28:1194. doi: 10.1364/OL.28.001194. [DOI] [PubMed] [Google Scholar]
- 53.Hansen PC. The L-Curve and its Use in the Numerical Treatment of Inverse Problems. WIT Press; Southampton: 2000. [Google Scholar]
- 54.Christ A, Kainz W, Hahn E. The Virtual Famil--development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol. 2010;55:N23. doi: 10.1088/0031-9155/55/2/N01. [DOI] [PubMed] [Google Scholar]
- 55.Wisnieff C, Liu T, Spincemaille P, Wang S, Zhou D, Wang Y. Magnetic susceptibility anisotropy: cylindrical symmetry from macroscopically ordered anisotropic molecules and accuracy of MRI measurements using few orientations. Neuroimage. 2013;70:363–76. doi: 10.1016/j.neuroimage.2012.12.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Poser Ba, Koopmans PJ, Witzel T, Wald LL, Barth M. Three dimensional echo-planar imaging at 7 Tesla. Neuroimage. 2010;51:261–266. doi: 10.1016/j.neuroimage.2010.01.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gagoski B, Bilgic B, Eichner C. RARE/turbo spin echo imaging with simultaneous multislice Wave-CAIPI. Magn Reson Med. 2015;73:929–938. doi: 10.1002/mrm.25615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Pruessmann K, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42(5):952–962. [PubMed] [Google Scholar]
- 59.Ramani S, Fessler JA. Parallel MR Image Reconstruction Using Augmented Lagrangian Methods. IEEE Trans Med Imaging. 2011;30:694–706. doi: 10.1109/TMI.2010.2093536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Haacke E, Xu Y, Cheng YCN, Reichenbach JR. Susceptibility weighted imaging (SWI) Magn Reson Med. 2004;52:612–618. doi: 10.1002/mrm.20198. [DOI] [PubMed] [Google Scholar]
- 61.Robinson S, Grabner G, Witoszynskyj S, Trattnig S. Combining phase images from multi-channel RF coils using 3D phase offset maps derived from a dual-echo scan. Magn Reson Med. 2011;65:1638–1648. doi: 10.1002/mrm.22753. [DOI] [PubMed] [Google Scholar]
- 62.Sumpf T, Uecker M. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J Magn Reson Imaging. 2011;34:420–428. doi: 10.1002/jmri.22634. [DOI] [PubMed] [Google Scholar]
- 63.Weller DS, Ramani S, Fessler JA. Augmented lagrangian with variable splitting for faster non-cartesian L1-SPIRiT MR image reconstruction. IEEE Trans Med Imaging. 2014;33:351–361. doi: 10.1109/TMI.2013.2285046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Guo W, Qin J, Yin W. A New Detail-Preserving Regularization Scheme. SIAM J Imaging Sci. 2014;7:1309–1334. doi: 10.1137/120904263. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.