Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Dec 23;6:38492. doi: 10.1038/srep38492

Collisional cross-section of water molecules in vapour studied by means of 1H relaxation in NMR

Daniele Mammoli 1,a, Estel Canet 1,2,3, Roberto Buratto 1, Pascal Miéville 1, Lothar Helm 1, Geoffrey Bodenhausen 2,3
PMCID: PMC5180102  PMID: 28008913

Abstract

In gas phase, collisions that affect the rotational angular momentum lead to the return of the magnetization to its equilibrium (relaxation) in Nuclear Magnetic Resonance (NMR). To the best of our knowledge, the longitudinal relaxation rates R1 = 1/T1 of protons in H2O and HDO have never been measured in gas phase. We report R1 in gas phase in a field of 18.8 T, i.e., at a proton Larmor frequency ν0 = 800 MHz, at temperatures between 353 and 373 K and pressures between 9 and 101 kPa. By assuming that spin rotation is the dominant relaxation mechanism, we estimated the effective cross-section σJ for the transfer of angular momentum due to H2O-H2O and HDO-D2O collisions. Our results allow one to test theoretical predictions of the intermolecular potential of water in gas phase.

Water is the most extensively studied molecule on Earth. A precise determination of its intermolecular potential would allow accurate predictions of its properties in gas, liquid and solid phase. However, despite huge theoretical efforts1,2, a full agreement with experiments3,4,5,6 has not yet been achieved. Nuclear magnetic resonance (NMR) of molecules in gas phase7 has some unique features. The coupling between nuclear spins and magnetic moments induced by molecular rotation implies that collisions between molecules lead to a relaxation, i.e. to the return of the longitudinal magnetization Mz to its equilibrium after a perturbation, through a mechanism known as spin-rotation. If spin-rotation is the dominant mechanism, cross-sections for the transfer of angular momentum can be obtained from NMR relaxation rates in gas phase. Such relaxation rates have been measured over a wide range of pressures and temperatures8,9,10. Experimentally determined cross-sections can be used to refine intermolecular potentials11,12,13. In methane, isotopic substitution14,15,16 affects relaxation rates associated with the different isotopomers such as CH4, CH3D, CH2D2, and CHD3. In supercritical water17,18,19, spin-rotation significantly contributes to NMR relaxation despite the high density. In the context of our attempts to prepare para-water20,21,22,23,24,25,26 and related spin states in other molecules27,28,29,30,31,32, we have measured longitudinal relaxation rates R1 = 1/T1 of gaseous H2O and HDO at different temperatures and pressures. To the best of our knowledge, this is the first time that such observations are reported. Our measurements are useful to refine intermolecular potentials for water vapour. These may be compared with water confined in matrices33,34 or in fullerene cages21,35 where a gas-phase like behaviour can be observed.

Theory

Collisions between molecules can induce transitions between rotational quantum states. As a result, spin-dependent interactions vary as a function of time and, if the fluctuations occur at frequencies in the vicinity of the nuclear Larmor frequency ω0, longitudinal NMR relaxation takes place. Comprehensive theoretical treatments of NMR relaxation can be found elsewhere36,37,38,39,40,41,42,43,44. In this article, we shall only mention some aspects of spin-rotation and dipole-dipole relaxation mechanisms that are relevant to longitudinal relaxation in gas phase.

Spin-rotation (SR) relaxation is due to collisions that modulate local fields induced at the sites of the nuclei by the rotation of the surrounding electronic cloud.

Relaxation induced by spin-rotation can be described by ref. 45:

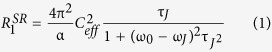graphic file with name srep38492-m1.jpg

where:

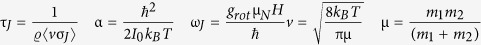graphic file with name srep38492-m2.jpg

τJ is the spin-rotation correlation time, Ceff (in Hz) the spin-rotation constant, ωJ the rotational frequency (in rad/s)46, Inline graphic is the number density of molecules, v is the average thermal velocity, σJ is the collisional cross-section for the transfer of angular momentum, I0 is the moment of inertia, grot is the g-factor, μN is the nuclear magneton, H is the magnetic field and μ is the reduced mass of the two colliding particles. The correlation time τJ is related to the lifetime of the rotational quantum states. The relaxation process can be described by characterizing the cross-section for the transfer of angular momentum. Intermolecular potentials used to model the interaction mostly consist of an isotropic part, usually a radial function, depending only on the distance between particles (e.g., Lennard-Jones potential) and an anisotropic part, depending also on the orientation of the molecules with respect to each other. The intermolecular potential of a molecule can be written by considering its axial symmetry47 and can be linked to relaxation rates via the Bloom – Oppenheim theory48.

Dipole-dipole (DD) relaxation is due to fluctuations of the interaction between magnetic dipoles, which are induced by physical rotation. The DD interactions are described by a correlation time τC that is related to the mean time needed for the molecule to undergo a rotation through one radiant. DD relaxation can occur between spins in the same molecule (intramolecular DD) or between spins in different molecules (intermolecular DD). Relaxation by the intramolecular DD interaction between the two protons of water is described by ref. 36:

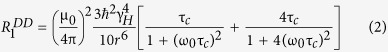graphic file with name srep38492-m4.jpg

where r is the distance between the protons, γH is the gyromagnetic ratio of protons and μ0 is the magnetic permeability in vacuum.

In liquid phase, the rotational correlation time τC is linked to τJ by the Hubbard relation49 τC/τJ = 1/6. For dilute gases (τJ → ∞), the ratio of correlation times τC/τJ varies from 5/4 (Ivanov model) to 1/4 (extended diffusion model) or 1/24.4 (Langevin model)14,15.

Results

We measured longitudinal relaxation rates R1 by the conventional inversion-recovery method. Experiments were carried out at temperatures T = 353, 363, and 373 K and pressures 9 < p < 101 kPa. The translational diffusion of water molecules does not affect our measurements of longitudinal relaxation rates R1 (see Methods), although it might interfere with measurements of transverse relaxation rates R2. The rates R1 observed in neat water (samples 1–4, H2O-H2O collisions) and in a mixture of HDO and D2O (sample 5, HDO-D2O collisions) are reported in Table 1.

Table 1. Longitudinal relaxation rates R 1 for gaseous H2O (samples 1 to 4) and gaseous HDO (sample 5) at 800 MHz and at different temperatures and pressures.

Samples H2O in H2O
 HDO in D2O
1
 2
 3
 4
 5
T (K) p (kPa) R1 (s−1) p (kPa) R1 (s−1) p (kPa) R1 (s−1) p (kPa) R1 (s−1) p (kPa) R1 (s−1)
353 9 73 ± 9 15 79 ± 9 34 57 ± 5 47 54 ± 7 47 57 ± 8
363 10 72 ± 9 18 80 ± 7 42 52 ± 6 69 43 ± 6 69 42 ± 5
373 11 79 ± 9 21 80 ± 7 60 40 ± 6 101 36 ± 7 101 31 ± 3
Open in a new tab

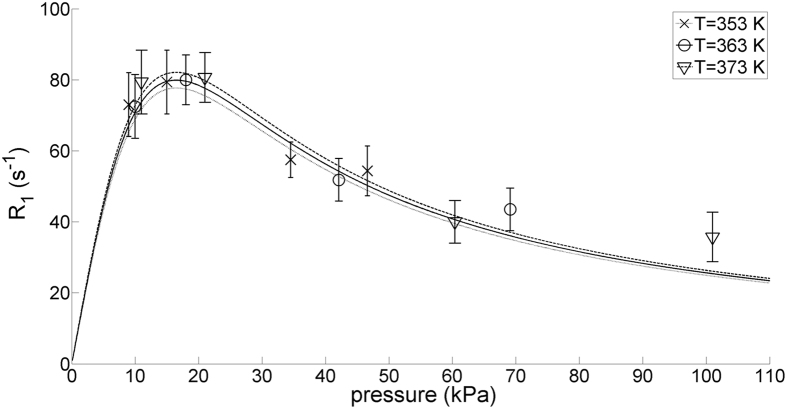
We shall initially consider spin-rotation to be the dominant relaxation mechanism, neglecting dipole-dipole relaxation. Under our experimental conditions, water vapour is mainly monomeric50,51,52 and the extreme narrowing regime 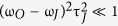Inline graphic is not fulfilled: R1 shows a maximum at a pressure pmax where τJ = 1/(ωO − ωJ) (see Fig. 1).

Figure 1. (Points) Experimental rates R1 of gaseous H2O at 800 MHz and at pressures 9 < p < 101 kPa.

Figure 1

Open in a new tab

(Lines) Estimates of R1 arising from spin-rotation, using Eq. 1 with the parameters in Table 2.

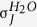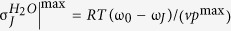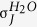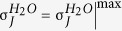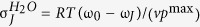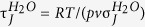The number density Inline graphic at pressure p can be estimated via the ideal gas law (see Methods) yielding τJ = RT/(pvσJ). Hence, it is possible to calculate the cross-section Inline graphic for H2O:H2O collisions at pmax as Inline graphic. If we assume Inline graphic to be independent of p (i.e. 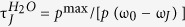Inline graphic) at the low pressures used in our experiments, we can substitute Inline graphic in Inline graphic to find Inline graphic. This last relationship can be used to predict the dependence of R1 on p, at a given T, by using Eq. 1 and the parameters in Table 2. All three curves result from fitting a single parameter (pmax), all the other parameters being fixed to the values given in Table 2. The fitted value pmax = (17 ± 3) kPa provides a fair agreement between experimental relaxation rates (points) and predicted rates (lines) (Fig. 1). The spin-rotation tensor depends on the symmetry of the molecule: in our approximation we take into account only the isotropic constant Ceff35,53,54 which we consider to be independent of both pressure and temperature. The fitted value of pmax is constant while Ceff is fixed to values comprised in its confidence range.

Table 2. Parameters used to calculate cross-sections via Eq. 1.

  Ceff (kHz) ω0(rad/s) ωJ (rad/s) μ (kg) I0 (kg·m2)
HDO 42.8 ± 0.1(a) 5 · 109 6 · 108(b) 1.64 · 10−26 2.91 · 10−47
H2O 32.2 ± 0.5(a) 5 · 109 6 · 108(b) 1.51 · 10−26 1.94 · 10−47
Open in a new tab

(a)Ref. 53

(b)Ref. 66.

In a more refined analysis we included contributions 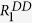Inline graphic due to the intramolecular dipole-dipole interaction (Eq. 2). We fixed τC to values predicted by the Ivanov model (τC = 5/4τJ), extended diffusion model (τC = 1/4τJ) or Langevin model (τC = 1/24.4τJ)14,15. Our experimental data are compatible with a negligible dipole-dipole contribution or with the Langevin model (τC ≪ τJ), according to which significant contributions of 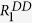Inline graphic only occur at low pressures p < 10 kPa.

For HDO-D2O mixtures, experimental relaxation rates R1 (sample 5) are reported in Table 1. In this case, we can safely neglect DD contributions. The experimental rates R1 in Table 1 and the parameters in Table 2 are substituted into Eq. 1 to calculate the collision cross-sections.

Cross sections and correlation times for the transfer of the angular momentum in H2O:H2O and HDO:D2O collisions are reported in Table 3.

Table 3. Correlation times τ J and cross-sections σ J for the angular momentum transfer in H2O:H2O and HDO:D2O collisions, calculated with Eq. 1 and parameters in Table 2.

T (K) Cross-section σJ (Å2)
 Correlation time τJ(ps)
H2O:H2O collisions HDO:D2O collisions H2O:H2O collisions HDO:D2O collisions
353 K 140 ± 26 378 ± 49 82 ± 15 32 ± 5
363 K 142 ± 26 367 ± 42 56 ± 10 22 ± 3
373 K 144 ± 27 354 ± 31 38 ± 7 16 ± 2
Open in a new tab

Discussion

Our analysis provides information about H2O-H2O and HDO-D2O collisions at pressures below 101 kPa and temperatures between 353 and 373 K. The ratio of cross-sections 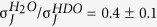Inline graphic differs from the ratio of the moments of inertia 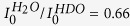Inline graphic. This discrepancy suggests that there must be appreciable differences between the intermolecular potentials for HDO:D2O and H2O:H2O collisions. This hypothesis is compatible with the fact that H2O and D2O have almost equal electric dipole moments55 while the electric dipole moment of HDO differs in intensity and orientation from those of H2O and D2O55. NMR relaxation studies on the influence of hydrogen/deuterium isotopic substitution on collisional cross-sections have been reported for methane15,16. However, by isotopic substitution on methane only the moment of inertia is markedly altered. A direct comparison with isotopic substitution on the highly polar H2O is therefore not possible.

The collisional cross-sections calculated from our NMR data can be used to refine the anisotropic part of the intermolecular potentials for collisions in gas phase56,57,58 via the Bloom – Oppenheim theory59. However, such calculations are beyond the scope of this work.

Our findings may be relevant for Dissolution Dynamic Nuclear Polarization (D-DNP)60 where a frozen sample is rapidly heated by injecting a burst of superheated D2O (T > 373 K) into the cryostat, and the liquid HDO ‘bolus’, usually containing a hyperpolarized solute, is pushed by pressurized helium gas (typically at 1 MPa) through a polyethylene tube with a 1 mm inner diameter running through a “magnetic tunnel”61, with a length of ca. 4 m between the polarizer and the NMR or MRI system. Attempts to monitor the speed of the bolus moving through the tube by optical means have shown that it tends to break up into small droplets during the transfer. This increases the surface area where water molecules can exchange between the liquid and gaseous phases. If the liquid/gas exchange is fast, the averaged longitudinal relaxation rates are likely to be much shorter than those in liquid water. The shortening of T1 would lead to a rapid loss of hyperpolarization during the transfer between the polarizer and the NMR magnet. Note that the viscosity and surface tension of the transferred liquid are difficult to control, since it consists of an aqueous solution containing analytes, polarizing agents like TEMPOL and glass-forming agents such as glycerol.

To summarize, we reported NMR relaxation rates due to binary H2O:H2O and HDO:D2O collisions in the gas phase and evaluated the cross-sections for the transfer of the angular momentum which can be used to refine the intermolecular potentials.

Methods

Our experimental setup consisted of a pair of coaxial glass tubes (Fig. 2).

Figure 2. Schematic view of the coaxial tubes: outer tube (10 mm outer diameter) filled with toluene-d8 and inner tube (5 mm outer diameter, held by Teflon spacers) containing water vapour sealed under vacuum.

Figure 2

Open in a new tab

The inner tube with 5 mm outer diameter was held in the center of a 10 mm tube by holders made of PTFE (Teflon). The outer tube contained about 2 mL of deuterated toluene-d8 (boiling point Tbp = 384 K). Its deuterium signal allows one to lock the static field and to shim its homogeneity. The inner tube contained water that was frozen and flame-sealed under vacuum (p = 1 kPa). Four tubes of 3.5 to 4 cm length, labeled as samples 1, 2, 3 and 4, were filled with ca 0.1, 0.2, 0.3 and 4.5 mg H2O, determined with a precision balance (±0.1 mg, max. tara 31 g). A fifth tube (sample 5) was filled with 2 mg of 98% D2O and 2% H2O (v:v), hence containing ca. 2% HDO. The inner tube was completely immersed in the solvent contained in the outer tube (Fig. 2) in order to have a homogeneous temperature and to avoid condensation of water on the walls of the inner tube in regions outside the area where the temperature is accurately controlled. Before and after inserting the samples into the spectrometer, the temperature in the probe was determined with a platinum PT-100 resistance thermometer (“iTRON 08” by JUMO)62 using a similar set of two concentric tubes with toluene-d8 in the outer tube. After each experiment the maximum temperature variations were ±1 K. Two typical 1H NMR spectra are shown in Fig. 3: the peak near 3.2 ppm (w.r.t. TMS) is due to water in the gas phase at T = 363 K.

Figure 3. Proton NMR spectra of samples described in Fig. 2 at 800 MHz and at 300 K (top) or 363 K (bottom).

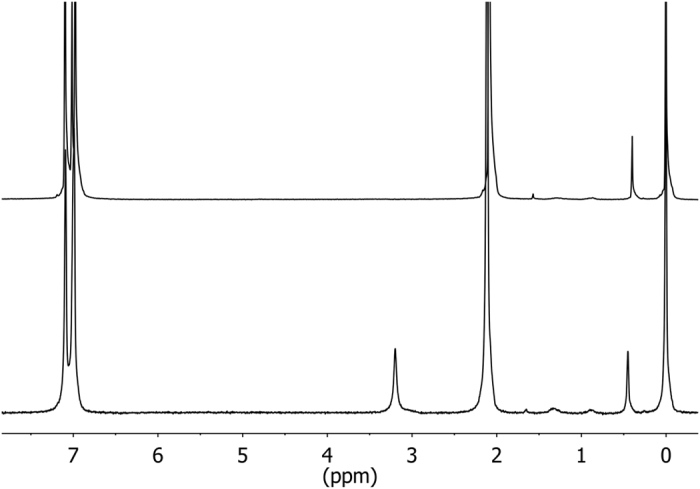
Figure 3

Open in a new tab

The signals at 2.1 and 7 ppm are attributed to residual protons in incompletely deuterated toluene-d8. The signal at 3.2 stems from water in gas phase. Small peaks between 0.3 and 2 ppm are due to impurities in toluene-d8. We diluted TMS in toluene-d8 to use its resonance at 0 ppm as chemical shift reference.

NMR instrumentation

All NMR experiments have been performed on a Bruker Avance-II 800 MHz spectrometer equipped with a 10 mm BBO probe.

Evaluation of pressure and density

To determine the pressure p and the number density Inline graphic of the water in samples 1 to 5 we measured the mass of water and estimated the volume of the inner tubes. Samples 4 and 5 contain saturated vapour (p = psat). In that case the pressure psat can be calculated using Antoine’s equation63:

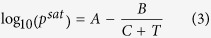graphic file with name srep38492-m19.jpg

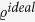where T is the temperature and A, B and C are sample-specific constants. When expressing the pressure in bar and the temperature in K, we assumed64 A = 5.08354, B = 1663.125 and C = −45.622 for both H2O and D2O, since their vapour pressures are similar within 1% over our range of temperatures65. The number density Inline graphic at a pressure p can be estimated provided that the equation of state of the gas is known a priori. We have compared Inline graphic predicted by the ideal gas law with 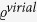Inline graphic obtained from a second-order virial expansion. The deviation 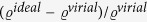Inline graphic is always below 2% in the range of pressures and temperatures under investigation, so that the use of the ideal gas law is legitimate.

The quantity of water vapour in samples 1 to 3 has been determined by integration of the relevant signals in the NMR spectra. As a reference for integration we added 1,1,2,2-tetrachloroethane (C2H2Cl4, 0.2% v:v) to the toluene-d8 in the outer sample tube. We calibrated the integral of the C2H2Cl4 reference peak (near ~ 6 ppm) with respect to the number density of sample 4 (saturated vapour). The pressures in samples 1 to 3 are then determined by scaling the peak intensities of the vapour peak with respect to sample 4. The error on the pressures is assumed to be ±10%. The active volume of the 5 mm inner tube has been estimated from documentation by the manufacturer (Wilmad) to be 0.4 cm3.

Translational diffusion and convection

Translational diffusion of water molecules in gas phase is very fast. Translational motion of water molecules between the active volume of the 1H NMR coil and the space outside the coil can affect inversion-recovery measurements of T1 relaxation. Indeed, molecules that carry inverted magnetization −Mz = −Mzeq within the active volume may be contaminated with molecules than come from areas outside the rf coil that carry magnetization in equilibrium Mzeq that has not been inverted. To ascertain the relevance of these effects on the time scale of the T1 measurement (max. 5 · T1 = 140 ms) we performed the following test. The inner tubes were only a few mm longer than the active region of the 1H coil of the 10 mm probe which is about 3 cm long. We measured R1 at the highest temperature T = 373 K (where the effects of diffusion are most pronounced) in two arrangements. First, we centered the inner tube with respect to the active region of the 1H coil. In this configuration, molecules can diffuse to and from the volumes above and below the active region. Secondly, we moved the inner tube up so that its bottom end was aligned with the lower end of the active region of the coil. In this manner, only molecules that cross the limit of the active region of the rf coil from above can influence the NMR signal. Any difference in R1 observed with these two configurations should be due to diffusion or convection. We found the R1 values to be identical within their errors, suggesting that contributions from diffusion can be neglected. Since we immersed the inner tube completely in a liquid with a controlled temperature, we assumed that there was no significant temperature gradient, so that convection due to differences in density should be negligible. Nevertheless, the experimental errors of the relaxation rates were doubled to take into account uncertainties stemming from diffusion and convection.

Additional Information

How to cite this article: Mammoli, D. et al. Collisional cross-section of water molecules in vapour studied by means of 1H relaxation in NMR. Sci. Rep. 6, 38492; doi: 10.1038/srep38492 (2016).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Acknowledgments

We are indebted to the Swiss National Science Foundation (FNRS), the École polytechnique fédérale de Lausanne (EPFL), the French Centre national de la recherche scientifique (CNRS) and the European Research Council (ERC) for providing financial support.

Footnotes

Author Contributions D.M., E.C. and R.B. designed and performed the experiment. P.M., L.H., G.B. conceived the experiment. D.M. analysed the data and wrote the paper.

References

  1. Bukowski R., Szalewicz K., Groenenboom G. C. & van der Avoird A. Predictions of the Properties of Water from First Principles. Science 315, 1249–1252 (2007). [DOI] [PubMed] [Google Scholar]
  2. Nilsson A. & Pettersson L. G. M. The structural origin of anomalous properties of liquid water. Nat. Commun. 6, 8998 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Astrath N. G. C., Malacarne L. C., Baesso M. L., Lukasievicz G. V. B. & Bialkowski S. E. Unravelling the effects of radiation forces in water. Nat. Commun. 5, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Russo J. & Tanaka H. Understanding water’s anomalies with locally favoured structures. Nat. Commun. 5, (2014). [DOI] [PubMed] [Google Scholar]
  5. Elgabarty H., Khaliullin R. Z. & Kühne T. D. Covalency of hydrogen bonds in liquid water can be probed by proton nuclear magnetic resonance experiments. Nat. Commun. 6, 8318 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ramasesha K., De Marco L., Mandal A. & Tokmakoff A. Water vibrations have strongly mixed intra- and intermolecular character. Nat. Chem. 5, 935–940 (2013). [DOI] [PubMed] [Google Scholar]
  7. Jameson C. J. Gas-phase NMR spectroscopy. Chem. Rev. 91, 1375–1395 (1991). [Google Scholar]
  8. Armstrong R. L., Kisman K. E. & Kalechstein W. Longitudinal Relaxation Time Measurements in Hydrogen Gas Mixtures at Low Densities. Can. J. Phys. 53, 1–4 (1975). [Google Scholar]
  9. Jameson C. J., Jameson A. K., Smith N. C. & Jackowski K. Cross sections for transfer of rotational angular momentum in CO2 from 13C spin relaxation studies in the gas phase. J. Chem. Phys. 86, 2717 (1987). [Google Scholar]
  10. Jameson C. J. & Jameson A. K. Effective collision cross sections for SF6 from nuclear magnetic relaxation. J. Chem. Phys. 88, 7448 (1988). [Google Scholar]
  11. Riehl J. W. Spin-lattice relaxation and the anisotropic part of the H[sub 2][Single Bond]He and H[sub 2][Single Bond]Ne intermolecular potential. J. Chem. Phys. 58, 4571 (1973). [Google Scholar]
  12. Zarur G. Effective potential formulation of molecule-molecule collisions with application to H2[Single Bond]H2. J. Chem. Phys. 60, 2057 (1974). [Google Scholar]
  13. Jameson C. J. In New Developments in NMR - Chapter 1. Fundamental Intramolecular and Intermolecular Information from NMR in the Gas Phase (eds. Jackowski K. & Jaszunski M.) 1–51 (Royal Society of Chemistry, 2016). [Google Scholar]
  14. Jameson C. J., Jameson A. K., Smith N. C., Hwang J. K. & Zia T. Carbon-13 and proton spin relaxation in methane in the gas phase. J. Phys. Chem. 95, 1092–1098 (1991). [Google Scholar]
  15. ter Horst M. A., Jameson C. J. & Jameson A. K. Molecular reorientation of CD4 in gas-phase mixtures. Magn. Reson. Chem. 44, 241–248 (2006). [DOI] [PubMed] [Google Scholar]
  16. Bloom M., Bridges F. & Hardy W. N. Nuclear spin relaxation in gaseous methane and its deuterated modifications. Can. J. Phys. 45, 3533–3554 (1967). [Google Scholar]
  17. Lamb W. J. NMR study of compressed supercritical water. J. Chem. Phys. 74, 913 (1981). [Google Scholar]
  18. Jonas J., DeFries T. & Lamb W. J. NMR proton relaxation in compressed supercritical water. J. Chem. Phys. 68, 2988 (1978). [Google Scholar]
  19. Lamb W. J. Self-diffusion in compressed supercritical water. J. Chem. Phys. 74, 6875 (1981). [Google Scholar]
  20. Mammoli D. et al. Challenges in preparing, preserving and detecting para-water in bulk: overcoming proton exchange and other hurdles. Phys Chem Chem Phys (2015). [DOI] [PubMed] [Google Scholar]
  21. Beduz C. et al. Quantum rotation of ortho and para-water encapsulated in a fullerene cage. Proc. Natl. Acad. Sci. 109, 12894–12898 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Mamone S. et al. Nuclear spin conversion of water inside fullerene cages detected by low-temperature nuclear magnetic resonance. J. Chem. Phys. 140, 194306 (2014). [DOI] [PubMed] [Google Scholar]
  23. Horke D. A., Chang Y.-P., Długołęcki K. & Küpper J. Separating Para and Ortho Water. Angew. Chem. Int. Ed. 53, 11965–11968 (2014). [DOI] [PubMed] [Google Scholar]
  24. Kravchuk T. et al. A Magnetically Focused Molecular Beam of Ortho-Water. Science 331, 319–321 (2011). [DOI] [PubMed] [Google Scholar]
  25. Tikhonov V. I. Separation of Water into Its Ortho and Para Isomers. Science 296, 2363–2363 (2002). [DOI] [PubMed] [Google Scholar]
  26. Meier B. et al. Electrical detection of ortho–para conversion in fullerene-encapsulated water. Nat. Commun. 6, 8112 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Mammoli D. et al. Hyperpolarized para -Ethanol. J. Phys. Chem. B 119, 4048–4052 (2015). [DOI] [PubMed] [Google Scholar]
  28. Bornet A. et al. Long-Lived States of Magnetically Equivalent Spins Populated by Dissolution-DNP and Revealed by Enzymatic Reactions. Chem. - Eur. J 20, 17113–17118 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Zhang Y., Soon P. C., Jerschow A. & Canary J. W. Long-Lived 1 H Nuclear Spin Singlet in Dimethyl Maleate Revealed by Addition of Thiols. Angew. Chem. Int. Ed. 53, 3396–3399 (2014). [DOI] [PubMed] [Google Scholar]
  30. Tayler M. C. D. et al. Direct Enhancement of Nuclear Singlet Order by Dynamic Nuclear Polarization. J. Am. Chem. Soc. 134, 7668–7671 (2012). [DOI] [PubMed] [Google Scholar]
  31. Stevanato G. et al. A Nuclear Singlet Lifetime of More than One Hour in Room-Temperature Solution. Angew. Chem. Int. Ed. 54, 3740–3743 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kovtunov K. V. et al. Long-Lived Spin States for Low-Field Hyperpolarized Gas MRI. Chem. - Eur. J 20, 14629–14632 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Fajardo M. E., Tam S. & DeRose M. E. Matrix isolation spectroscopy of H2O, D2O, and HDO in solid parahydrogen. J. Mol. Struct. 695–696, 111–127 (2004). [Google Scholar]
  34. Redington R. L. & Milligan D. E. Infrared Spectroscopic Evidence for the Rotation of the Water Molecule in Solid Argon. J. Chem. Phys. 37, 2162 (1962). [Google Scholar]
  35. Li Y. et al. Comparison of Nuclear Spin Relaxation of H2O@C60 and H2 @C60 and Their Nitroxide Derivatives. J. Phys. Chem. Lett. 3, 1165–1168 (2012). [DOI] [PubMed] [Google Scholar]
  36. Kowalewski J. & Mäler L. Nuclear spin relaxation in liquids: theory, experiments, and applications (Taylor & Francis, 2006). [Google Scholar]
  37. Abragam A. The principles of nuclear magnetism (Oxford Univ. Press, 2006). [Google Scholar]
  38. Bransden B. H. & Joachain C. J. Physics of atoms and molecules (Prentice Hall, 2003). [Google Scholar]
  39. Callaghan P. T. Principles of nuclear magnetic resonance microscopy (Clarendon Press, 2007). [Google Scholar]
  40. Protein NMR spectroscopy: principles and practice (Academic Press, 2007). [Google Scholar]
  41. Keeler J. Understanding NMR spectroscopy (John Wiley and Sons, 2010). [Google Scholar]
  42. Levitt M. H. Spin dynamics: basics of nuclear magnetic resonance (John Wiley & Sons, 2008). [Google Scholar]
  43. Ernst R. R., Bodenhausen G. & Wokaun A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions (Clarendon Press, Oxford, 1987). [Google Scholar]
  44. Slichter C. P. Principles of magnetic resonance (Springer-Verlag, 1992). [Google Scholar]
  45. Courtney J. A. & Armstrong R. L. A Nuclear Spin Relaxation Study of the Spin–Rotation Interaction in Spherical Top Molecules. Can. J. Phys. 50, 1252–1261 (1972). [Google Scholar]
  46. Anderson C. H. & Ramsey N. F. Magnetic Resonance Molecular-Beam Spectra of Methane. Phys. Rev. 149, 14–24 (1966). [Google Scholar]
  47. Gray C. G. On the theory of multipole interactions. Can. J. Phys 46, 135–139 (1967). [Google Scholar]
  48. Bloom M. & Oppenheim I. In Advances in Chemical Physics (ed. Hirschfelder J. O.) 12, 549–599 (John Wiley & Sons, Inc., 1967). [Google Scholar]
  49. Hubbard P. S. Theory of Nuclear Magnetic Relaxation by Spin-Rotational Interactions in Liquids. Phys. Rev. 131, 1155–1165 (1963). [Google Scholar]
  50. Slanina Z. Computational studies of water clusters: temperature, pressure, and saturation effects on cluster fractions within the RRHO MCY-B/EPEN steam. J. Mol. Struct. 237, 81–92 (1990). [Google Scholar]
  51. Mhin B. J., Lee S. J. & Kim K. S. Water-cluster distribution with respect to pressure and temperature in the gas phase. Phys. Rev. A 48, 3764–3770 (1993). [DOI] [PubMed] [Google Scholar]
  52. Johansson E., Bolton K. & Ahlström P. Simulations of vapor water clusters at vapor–liquid equilibrium. J. Chem. Phys. 123, 24504 (2005). [DOI] [PubMed] [Google Scholar]
  53. Bluyssen H., Dymanus A., Reuss J. & Verhoeven J. Spin-rotation constants in H2O, HDO and D2O. Phys. Lett. A 25, 584–585 (1967). [Google Scholar]
  54. Puzzarini C., Cazzoli G., Harding M. E., Vázquez J. & Gauss J. The hyperfine structure in the rotational spectra of D217O and HD17O: Confirmation of the absolute nuclear magnetic shielding scale for oxygen. J. Chem. Phys. 142, 124308 (2015). [DOI] [PubMed] [Google Scholar]
  55. Clough S. A. Dipole moment of water from Stark measurements of H2O, HDO, and D2O. J. Chem. Phys. 59, 2254 (1973). [Google Scholar]
  56. Rajan S., Lalita K. & Babu S. V. Intermolecular potentials from nmr data. 1. CH4-N2 AND CH4-CO2. Can. J. Phys. 53, 1624–1630 (1975). [Google Scholar]
  57. Pandey L., Reddy C. P. K. & Sarkar K. L. Intermolecular potentials from nmr data - H2-N2O AND H2-CO2. Can. J. Phys. 61, 664–670 (1983). [Google Scholar]
  58. Coroiu I., Demco D. E. & Bogdan N. Anisotropic intermolecular potential from nuclear spin-lattice relaxation in hexafluoride gases. Appl. Magn. Reson. 14, 9–17 (1998). [Google Scholar]
  59. Bloom M. & Oppenheim I. In Advances in Chemical Physics 12, 549–599 (Hirschfelder J.O.). [Google Scholar]
  60. Ardenkjaer-Larsen J. H. et al. Increase in signal-to-noise ratio of >10,000 times in liquid-state NMR. Proc. Natl. Acad. Sci. USA 100, 10158–10163 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Milani J. et al. A magnetic tunnel to shelter hyperpolarized fluids. Rev. Sci. Instrum. 86, 24101 (2015). [DOI] [PubMed] [Google Scholar]
  62. Ammann C., Meier P. & Merbach A. A simple multinuclear NMR thermometer. J. Magn. Reson. 1969 46, 319–321 (1982). [Google Scholar]
  63. Antoine C. ‘Tensions des vapeurs; nouvelle relation entre les tensions et les températures’ [Vapor Pressure: a new relationship between pressure and temperature]. Comptes Rendus des Séances de l’Académie des Sciences (in French) 107, 681–684, 778–780, 836–837 (1888). [Google Scholar]
  64. NIST database. http://webbook.nist.gov/cgi/cbook.cgi?ID=C7732185&Mask=4&Type=ANTOINE&Plot=on.
  65. Jones W. M. Vapor Pressures of Tritium Oxide and Deuterium Oxide. Interpretation of the Isotope Effects. J. Chem. Phys. 48, 207 (1968). [Google Scholar]
  66. Schwenke D. W. Beyond the Potential Energy Surface: Ab initio Corrections to the Born−Oppenheimer Approximation for H2O†. J. Phys. Chem. A 105, 2352–2360 (2001). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES