Abstract
Objective
The goal of this study was to explore the relationship between global brain activity, changes in whole-brain connectivity, and changes in brain states across subjects using resting-state functional magnetic resonance imaging.
Methods
We extended current methods that use a sparse set of co-activation patterns to extract critical time points in global brain activity. Critical activity time points were defined as points where the global signal is greater than one standard deviation above or below the average global signal. Four categories of critical points were defined along dimensions of global signal intensity and trajectory. Voxel-based methods were used to interrogate differences in connectivity between these critical points.
Results
Several differences in connectivity were found in functional resting-state networks (RSNs) as a function of global activity. RSNs associated with cognitive functions in frontal, parietal, and sub-cortical regions exhibited greater whole-brain connectivity during lower global activity states. Meanwhile, RSNs associated with sensory functions exhibited greater whole-brain connectivity during the higher global activity states. Moreover, we present evidence that these results depend in part upon the standard deviation threshold used to define the critical points, suggesting critical points at different thresholds represent unique brain states.
Conclusion
Overall, the findings support the hypothesis that the brain oscillates through different states over the course of a resting-state study reflecting differences in RSN connectivity associated with global brain activity.
Significance
Increased understanding of brain dynamics may help elucidate individual differences in behavior and dysfunction.
Keywords: dynamic connectivity, brain states, co-activation patterns, resting-state, connectivity
I. Introduction
Resting-state functional magnetic resonance image (rs-fMRI) enables the investigation of spatial and temporal patterns of brain activity without the need for an explicit behavioral task. These patterns of brain activity have been used to cluster distinct brain regions to form resting-state networks (RSN) [1, 2]. RSNs divide the brain along known anatomical and functional boundaries [3], are highly reliable across populations [4, 5], and are present under anesthesia [6, 7] and during sleep [8]. Canonical RSNs include the default mode network (DMN), sensory/motor network, visual networks, salience network, and several networks related to attention and cognitive control [2, 9, 10]. These networks have been correlated with many cognitive functions [11, 12] and dysregulation of RSNs may play a key role in clinical disorders [13, 14]. However, these RSNs often represent “average” patterns defined over relatively long, continuous periods of time [15, 16] which may not permit a complete characterization of the temporal dynamics of these RSNs [16].
To investigate these dynamics, recent studies have begun exploring the contribution of co-activation patterns from a sparse set of critical points in time (defined as when a particular key node of a network enters periods of high activity) in establishing RSNs [17-20]. For example, the DMN can be established using only ~20 critical points when the posterior cingulate cortex (PCC; a key node in the DMN) is entering periods of activity one standard deviation above its mean activity [17-20]. These results suggest that RSNs arise from brief, dynamic interactions rather than average correlated activity over sustained periods.
However, studies to date have focused on critical points identified from the activity of single regions of interest (ROIs) and have not explored critical points defined in the context of whole-brain activity. Although this global brain signal is traditionally removed during analysis of rs-fMRI data [21], emerging evidence suggests that key information is embedded within this signal [22-24]. As such, critical points defined based the global signal, instead of single ROIs, may help elucidate the dynamics of whole-brain connectivity in RSNs.
We hypothesized that whole-brain connectivity in RSNs would vary with the level of global activity, as reflected by the blood oxygenation level dependent (BOLD) signal averaged across the grey matter. We analyzed 100 subjects with 48 minutes of rs-fMRI data and extracted critical time points from the fMRI timecourse, defined as points where the grey matter BOLD signal was entering or exiting periods of high or low activity [17, 18]. Our acquisition protocol collected 40 minutes of rs-fMRI data for each subject allowing a sparse temporal parcellation of critical time points (less than 20% of the data) while still retaining sufficient data to reliably estimate voxel-based connectivity. The intrinsic connectivity distribution (ICD) [31], a voxel-based connectivity method, was used to assess differences in whole-brain connectivity between these global activity levels.
II. EXPERIMENTAL DESIGN AND SETUP
A. Motivation
The goal of this work was to investigate the relationship between the global activity of the brain (i.e. the global signal) and functional connectivity between well-known RSNs. We hypothesized that RSNs would strengthen and weaken as the global signal, g(t), changed over time, t. We model specific points in the trajectory of g(t) where the signal enters and exits periods of higher and lower activity. If networks vary in their strength as a function of g(t), then more extreme values of the global signal (i.e high or low global activity) should offer more power to detect these differences. Additionally, by selecting only points with the same magnitude of g(t) relative to the standard deviation, we ensure that data for all subjects are equally scaled and can therefore be combined. Finally, it is likely that entering and exiting periods of high/low activity represents different biological processes involving different RSNs. As such, we propose to separate these points based on the derivative of g(t), g′(t). In this work we focus only on the sign of g′(t) and do not incorporate the magnitude of g′(t). Given the slow and narrow frequencies used for rs-fMRI (~0.01-0.1 Hz), variations in the magnitude of g′(t) are expected to be small.
B. Participants and Imaging Protocols
One hundred healthy right-handed adults between the ages of 18 and 65 participated in the study. Participants were recruited (using posters and word of mouth) from the local area. Subjects were screened using self-reports, and had no history of psychiatric or neurological illness. All participants provided written informed consent in accordance with a protocol approved by the Human Research Protection Program of Yale University. The analyses included 50 females (age=33.6±12.4) and 50 males (age=34.9±10.1); all subjects were part of a previous study [25].
Participants were scanned on two identically configured Siemens 3T Tim Trio scanners at the Yale Magnetic Resonance Research Center and were instructed to rest with their eyes open, to not think of anything in particular, and to not fall asleep. The first 59 participants were scanned using a 12-channel head coil. The remaining 41 participants were scanned using a 32-channel head coil. There were no significant differences in the distribution of males and females or ages scanned between the two head coils (see [26] for further details).
Each session began with a localizing scan, followed by a low-resolution sagittal scan for slice alignment, and then the collection of 25 axial-oblique T1-weighted slices aligned with the AC-PC such that the top slice was at the superior brain. Resting-state functional data were collected at the same slice locations as the T1-weighted anatomical data, using a T2*-sensitive gradient-recalled single shot echo-planar pulse sequence (TR = 1550 ms, TE = 30 ms, flip angle = 80 degrees, FOV = 220×220 mm2, 64×64 matrix, resolution = 3.435 × 3.425 × 6 mm). Eight functional runs were used, each containing 240 volumes (approximately 6 minutes, for a total of approximately 48 minutes of resting-state data). The first six volumes of the functional runs were discarded to allow the signal to reach a steady state. Finally, a high-resolution anatomical image was collected using an MPRAGE sequence (TR = 2530 ms, TE = 2.77 ms, TI = 1100 ms, flip angle = 7°, resolution = 1 mm3).
C. Preprocessing
Images were slice-time and motion corrected using SPM5 and were iteratively smoothed until the smoothness for any image had a full width half maximum of approximately 6 mm [27, 28]. All further analysis was performed using BioImage Suite [29] unless otherwise specified. Several covariates were regressed from the data including linear and quadratic drift, a 24-parameter model of motion [30], mean cerebral-spinal fluid (CSF) signal, and mean white matter signal. Finally, the data were temporally smoothed with a zero mean unit variance Gaussian filter (cutoff frequency=0.12 Hz). A gray matter mask was applied to the data so that only voxels in the gray matter were used in the calculation.
D. Definition of critical points
Critical points were defined using a modified point-process method [17, 18]. After preprocessing, the average gray matter timecourse was extracted for each run and each participant. As a result of the bandpass filtering, this global signal has a mean of zero. This timecourse was then normalized by dividing by the standard deviation across all time points. This z-score-like normalization does not change the underlying patterns of activity in the gray matter but allows for the timecourse for each participant to be comparably scaled. Critical points of activity were defined as points where the normalized signal crosses time points either one standard deviation above or below the average signal. A threshold of one standard deviation is consistent with previous work [17, 18]. If networks vary in their strength as a function of global activity, then extreme values should offer more power to detect these differences.
Positive critical points (PCPs) were defined as time points where the global signal crossed the threshold marking one standard deviation above the mean signal. Likewise, negative critical points (NCPs) were defined as time points where the global signal crossed the threshold marking one standard deviation below the mean signal (Fig. 1). The PCPs and NCPs were further delineated based on the trajectory of the global signal at the critical point (i.e., the sign of the derivative of the signal). This slope distinguishes whether the signal was entering or exiting periods of high or low activity (i.e., PCPs with a positive slope are points where the signal is increasing to values greater than one standard deviation above the mean, see Fig. 1). We define a positive trajectory of the global signal as moving away from the mean signal. Thus, for PCPs, a positive trajectory indicates a positive slope while, for NCPs, a positive trajectory indicates a negative slope. For this initial study, we only include the sign, and not magnitude, of the trajectory in the critical point definition. Faster or slower crossings may represent meaningful differences. However, given the slow nature of the blood oxygenation changes that the rs-fMRI signal measures, faster crossings may represent some level of artifact likely from motion or other physiological noise.
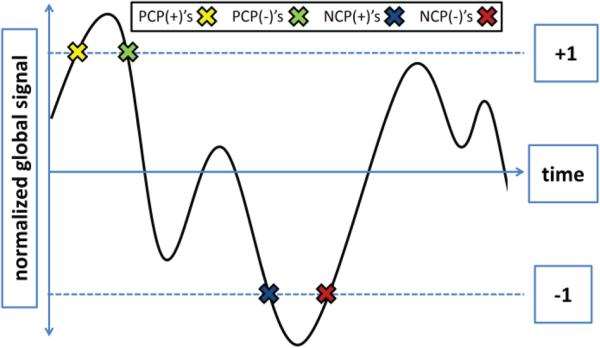
Fig. 1.
Definition of critical points. The average gray matter signal was normalized by dividing by the standard deviation across all timepoints. Critical points of activity were defined as points where the normalized signal was either one standard deviation above or below the average signal. PCP(+)'s are defined as points where the trajectory of the signal is moving away from the mean and crosses the threshold marking one standard deviation above the mean (yellow X). PCP(−)'s are defined as points where the trajectory of the signal is moving towards from the mean and crosses the threshold marking one standard deviation above the mean (green X). NCP(+)'s are defined as points where the trajectory of the signal is the moving away from the mean and crosses the threshold marking one standard deviation below the mean (blue X). NCP(−)'s are defined as points where the signal is trajectory of the moving towards from the mean and crosses the threshold marking one standard deviation below the mean (red X).
Altogether, we defined four sets of critical points (Fig. 1). PCP(+)'s are points where the trajectory of the signal is moving away from the mean and crosses one standard deviation above the mean. PCP(−)'s are points where the trajectory of the signal is moving towards from the mean and crosses one standard deviation above the mean. NCP(+)'s are points where the trajectory of the signal is the moving away from the mean and crosses one standard deviation below the mean. NCP(−)'s are points where the trajectory of the signal is moving towards from the mean and crosses one standard deviation below the mean.
These critical points were identified using the following algorithm. First, the global grey matter signal was z-score normalized. Second, time points within one standard deviation of the mean were set to zero and time points beyond one standard deviation from the mean were set to 1. Third, the derivative of this binary timecourse was estimated with a backwards difference operator. Critical points were identified as time points associated with a derivative of 1 or −1. Fourth, these critical points were categorized as PCP(+)'s, PCP(−)'s, NCP(+)'s, or NCP(−)'s based on their signal trajectory and normalized signal intensity as described above. This algorithm was performed independently for each run and each subject.
E. Whole-brain connectivity
For each participant, frames identified as critical points of each type were concatenated for further analysis, resulting in four sets of data for each participant. Next, to investigate differences between these four sets of data, voxel-wise whole-brain functional connectivity was calculated independently for each of the four types of critical points and for each individual participant as described previously [31]. This voxel-wise whole-brain functional connectivity can be measured by the intrinsic connectivity distribution (ICD) efficiently. Voxel-based functional connectivity measures involve correlating the timecourse for any voxel with the timecourse of every other voxel in the grey matter. Traditionally, these correlations are summarized using a network theory metric, such as degree or strength. Such metrics can be calculated from the distribution of correlations for any voxel x. First, f(x,r) is defined as the distribution of the correlations (r) for the timecourse at voxel x to the timecourse at every other voxel in the brain and can be estimated by computing the histogram of these correlations. Degree (d), based on a binary graph, can be estimated as the integral of this distribution from any threshold τ to 1, . Strength (s) can be estimated as the mean of this distribution or a distribution of transformed correlations, , where w(r) is generally the correlation coefficients or the Fisher transform of the correlation coefficients. In contrast, ICD models the entire survival function corresponding with f(x,r). Each point on the survival function is simply degree, based on a binary graph, evaluated at that particular threshold, τ. The ICD approach is to parameterize the change in a voxel's degree as the threshold defining whether voxels are connected (i.e., correlation threshold) is increased. Previously [31], we showed that a stretched exponential decay with unknown variance parameter (α) and shape parameter (β) was sufficient to model this survival function. Modeling the survival function with a stretched exponential is equivalent to modeling the underlying distribution as a Weibull distribution: , where x is the spatial location of a voxel, r is a correlation between two timecourses, α is the variance parameter, and β is the shape parameter. Thus, ICD models the distribution of correlations between a voxel and every other voxel in the brain, with α as the parameter of interest. No thresholds are needed to estimate the variance or model the distribution. This algorithm was performed for all voxels in the gray matter resulting in a parametric image of the alpha parameter for each participant.
To interrogate relative differences in connectivity, each participant's alpha map was normalized by subtracting the mean alpha value across all voxels and dividing by the standard deviation across all voxels. This z-score-like normalization does not affect the underlying connectivity pattern but does permit the investigation of relative differences in connectivity in the presence of large global differences in connectivity [32]. This normalization also has been shown to reduce the effects of confounds related to motion [33].
F. Common space registration
To facilitate comparisons of imaging data, all single-participant ICD results were warped to a common template space through the concatenation of a series of linear and non-linear registrations. The functional series were linearly registered to the T1 axial-oblique (2D anatomical) images. The 2D anatomical images were linearly registered to the MPRAGE (3D anatomical) images. Finally, the 3D anatomical images were non-linearly registered to the template brain. All transformation pairs were calculated independently and combined into a single transform that warps the single participant results into common space. This single transformation allows the individual participant images to be transformed to common space with only one transformation, reducing interpolation error. All transformations were estimated using the registration algorithms in BioImage Suite.
G. Motion Analysis
As group differences in motion have been shown to confound functional connectivity results [34], the frame-to-frame displacement was calculated for each critical point. No significant differences (p>0.8, for all comparison) in motion were found between the PCP(+)'s, the PCP(−)'s, the NCP(+)'s, and the NCP(−)'s. Additionally, we employed regression of a 24 parameter motion model, z-score-like normalization, and an iterative smoothing algorithm. All have been shown to minimize motion confounds associated with rs-fMRI [28, 33].
H. Statistical analysis
ICD maps were analyzed using voxel-wise paired t-test to examine the differences between the PCP(+)'s, the PCP(−)'s, the NCP(+)'s, and the NCP(−)'s. Imaging results are shown at a cluster-level threshold of p<0.05 using family-wise error (FWE) correction as determined by AFNI's 3dClustSim program. Anatomical locations were localized using the Yale Brodmann Atlas.
III. RESULTS
The Results section is organized in the following manner. First, we describe characteristics of the global signal and of the critical points. Second, we compare critical points with different trajectories but with the same signal value such that PCP(+)'s are compared with PCP(−)'s and NCP(+)'s are compared with NCP(−)'s. Third, we compare critical points with different signal values but the same trajectory (PCP(+)'s vs NCP(+)'s and PCP(−)'s vs NCP(−)'s). Next, we compare critical points that differ both in signal value and trajectory (PCP(+)'s vs NCP(−)'s and PCP(−)'s vs NCP(+)'s). We then quantify how connectivity in canonical RSNs changes at each of these critical points, derived from mean connectivity from ICD estimates of whole-brain connectivity. Finally, we present qualitative results examining the effect of different standard deviation thresholds used to define critical points.
A. Characterizing the global signal and critical points
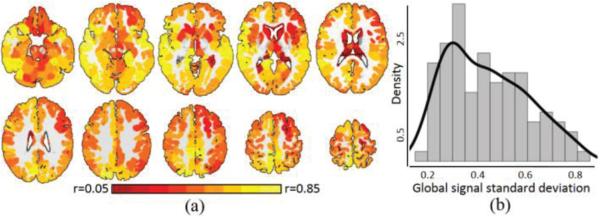
To characterize which regions contribute to the global signal, the timecourse for each region in the Shen 268 functional atlas [10, 35] was correlated with the global signal and these correlations were averaged across participants. As shown in Fig. 2A, 265 out of the 268 (>98%) regions showed significant correlation (p<0.05) with the global signal, exhibiting an average correlation of 0.43±0.14. The three regions that did not contribute to the global signal were located in the brainstem. Fig. 2B shows the distribution of the standard deviation of the global signal across participants.
Fig. 2.
Characteristics of the global signal. A) Greater than 98% of the grey matter showed significant correlations with the global signal, with an average correlation of r=0.43±0.14. Warmer colors represent greater correlation with the global signal. B) The distribution of the standard deviation of the global signal showed a heavy tail. The black line represents a kernel density estimate of the distribution.
There was a similar number of instances of each of the four categories of critical points (PCP(+)'s=83.1±9.7, PCP(−)'s =82.3±9.7, NCP(+)'s=83.1±9.8, NCP(−)'s=82.2±9.7). On average, instances of each category of these critical points occurred less than 5% of the total time; when combined, instances of all critical points occurred less than 20% of the total time. There were no significant main effects of scanner or head coil for any category of critical point (p>0.2, all pairwise comparisons). Women had a greater number of critical points (Table 1). The number of critical points was not correlated with age (p>0.15 for all correlations). There was no difference in the number of critical points between the eight resting-states runs (p>0.2 for all types). No temporal clustering of critical points was observed and the amount of time between adjacent critical points appears follow a lognormal distribution.
TABLE I.
THE NUMBER OF CRITICAL POINTS FOR MEN AND WOMEN
| Type | Men | Women | p-value |
|---|---|---|---|
| PCP(+) | 80.56±0.19 | 85.56±0.12 | 0.009 |
| PCP(−) | 80.58±0.14 | 83.72±0.05 | 0.110 |
| NCP(+) | 80.48±0.18 | 85.78±0.10 | 0.006 |
| NCP(−) | 80.60±0.15 | 83.94±0.09 | 0.085 |
B. Comparison between critical points with the same intensity but different signal trajectories
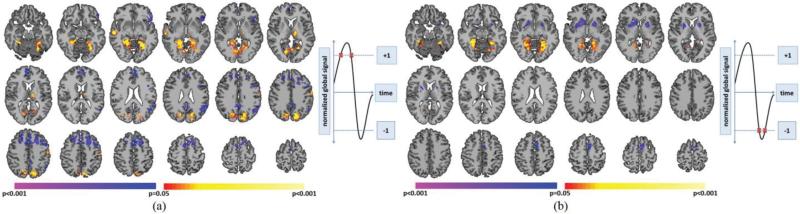
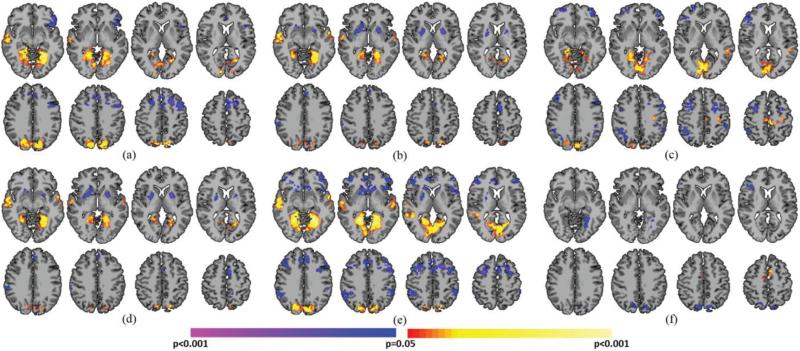
PCP(+)'s demonstrated significantly greater whole-brain connectivity in visual areas (BA7, fusiform), right BA22, left motor cortex, and left thalamus when compared to PCP(−)'s (Fig. 3A). PCP(−)'s exhibited significantly greater whole-brain connectivity in medial and lateral prefrontal cortex (PFC), left inferior frontal gyrus (IFG), left BA39, and posterior cingulate cortex (PCC) when compared to PCP(+)'s (Fig. 3A). NCP(+)'s demonstrated significantly greater whole-brain connectivity in bilateral fusiform and BA19 compared to NCP(−)'s (Fig. 3B). NCP(−)'s demonstrated significantly greater whole-brain connectivity in the medial frontal cortex and striatum when compared to NCP(+)'s (Fig. 3B).
Fig. 3.
Comparison between critical points with the same intensity but different signal trajectories. A) PCP(+)'s compared to PCP(−)'s. Warmer colors indicate regions with greater whole-brain connectivity during PCP(+)'s. Cooler colors indicate regions with greater whole-brain connectivity during PCP(−)'s. B) NCP(+)'s compared to NCP(−)'s. Warmer colors indicate regions with greater whole-brain connectivity during NCP(+)'s. Cooler colors indicate regions with greater whole-brain connectivity during NCP(−)'s. All results shown for p<0.05 corrected for multiple comparisons. Graphs on the right indicate which critical points are being compared.
C. Comparison between critical points with different intensities but the same signal trajectory
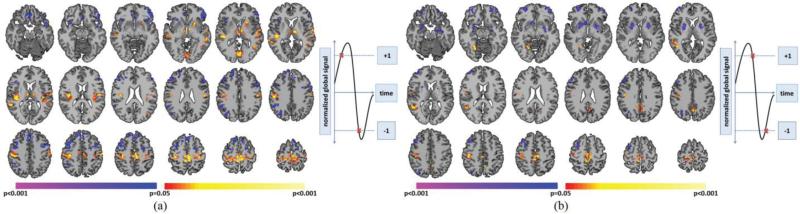
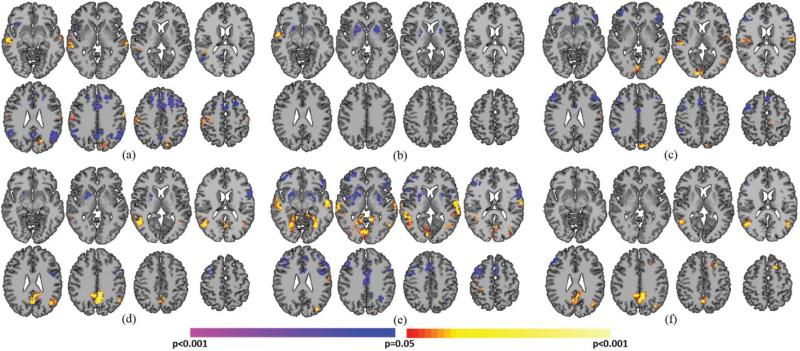
PCP(+)'s demonstrated significantly greater whole-brain connectivity in bilateral sensorimotor cortex (SMC), bilateral auditory cortex, bilateral thalamus, bilateral BA22, and the left putamen when compared to NCP(+)'s (Fig. 4A). NCP(+)'s demonstrated significantly greater whole-brain connectivity in lateral PFC, medial PFC, and right lateral parietal lobe when compared to PCP(+)'s (Fig. 4A). PCP(−)'s demonstrated significantly greater whole-brain connectivity in the SMC and right BA22 when compared to NCP(−)'s (Fig. 4B). NCP(−)'s demonstrated significantly greater whole-brain connectivity in lateral PFC, right lateral parietal lobe, and striatum when compared to PCP(−)'s (Fig. 4B).
Fig. 4.
Comparison between critical points with the same intensity but different signal trajectories. A) PCP(+)'s compared to PCP(−)'s. Warmer colors indicate regions with greater whole-brain connectivity during PCP(+)'s. Cooler colors indicate regions with greater whole-brain connectivity during PCP(−)'s. B) NCP(+)'s compared to NCP(−)'s. Warmer colors indicate regions with greater whole-brain connectivity during NCP(+)'s. Cooler colors indicate regions with greater whole-brain connectivity during NCP(−)'s. All results shown for p<0.05 corrected for multiple comparisons. Graphs on the right indicate which critical points are being compared.
D. Comparison between critical points with different intensities and different signal trajectories
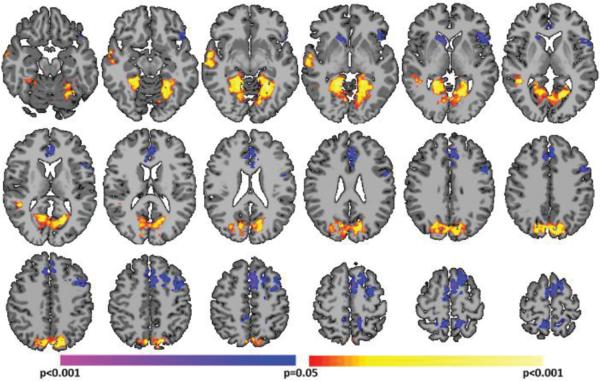
PCP(+)'s demonstrated significantly greater whole-brain connectivity in bilateral SMC, visual cortex (including the fusiform), and bilateral BA22, when compared to NCP(−)'s (Fig. 5A). NCP(−)'s demonstrated significantly greater whole-brain connectivity in the PFC, caudate, and bilateral lateral parietal lobe when compared to PCP(+)'s (Fig. 5A). PCP(−)'s demonstrated significantly greater whole-brain connectivity in right auditory cortex, PCC, medial SMC, and left lateral PFC when compared to NCP(+)'s (Fig. 5B). NCP(+)'s demonstrated significantly greater whole-brain connectivity in the inferior frontal lobe compared to PCP(−)'s (Fig. 5B).
Fig. 5.
Comparison between critical points with different intensities and signal trajectories. A) PCP(+)'s compared to NCP(−)'s. Warmer colors indicate regions with greater whole-brain connectivity during PCP(+)'s. Cooler colors indicate regions with greater whole-brain connectivity during NCP(−)'s. B) PCP(−)'s compared to NCP(+)'s. Warmer colors indicate regions with greater whole-brain connectivity during PCP(−)'s. Cooler colors indicate regions with greater whole-brain connectivity during NCP(+)'s. All results shown for p<0.05 corrected. Graphs on the right indicate which critical points are being compared.
E. Split half analysis
As our results are dependent on subsampling a large amount of data per participant, we performed an exploratory analysis to investigate whether less data would produce similar results. For each participant, we split the data into halves (the first 4 runs and the last 4 runs) and repeated the main analysis, resulting in two sets of the six contrasts between different types of critical points defined above. Using the Shen 268 functional atlas [10, 35], we calculated the average contrast for each of the 268 ROIs in the atlas, creating a 268-entry vector for each contrast from each half of the data. For each contrast, the correlation between vectors from both halves of the data was computed to assess similarity. As shown in Table 2, given the same contrasts, the two halves were significantly correlated, suggesting that similar network differences are detected within each half of the data.
TABLE 2.
SIMILARITY OF CONTRASTS USING THE 1ST AND 2ND HALVES OF THE DATA
| Contrast | Correlation | Contrast | Correlation |
|---|---|---|---|
| PCP(+)-PCP(−) | 0.69 | PCP(−)-NCP(−) | 0.51 |
| NCP(+)-NCP(−) | 0.82 | PCP(+)-NCP(−) | 0.50 |
| PCP(+)-NCP(+) | 0.73 | PCP(−)-NCP(+) | 0.31 |
F. Association between canonical RSNs and critical points
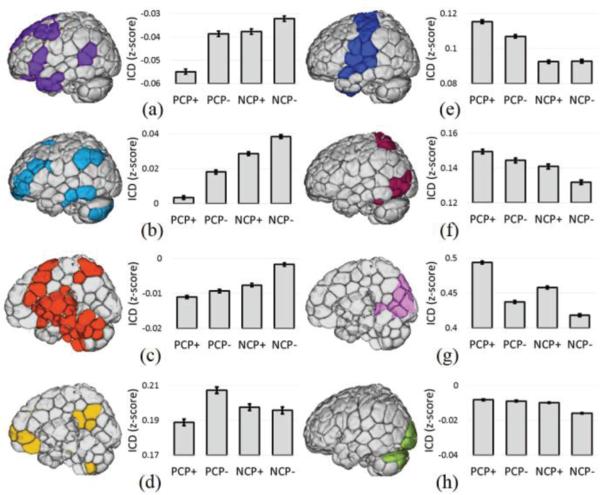
The previous analyses of voxelwise whole-brain connectivity suggested that specific networks are particularly associated with each category of critical points perhaps reflecting particular brain states. For example, sensory networks tended to exhibit the greatest connectivity during PCP(+)'s. We quantified this using eight canonical RSNs defined in Finn et al. [10] by calculating the average whole-brain connectivity within each RSN for each type of critical point. As shown in Fig. 6, each network (with the exception of the inferior visual network, Fig. 6H) exhibited significantly (p<0.01) greater connectivity during one specific category of critical point than during the other critical points. For cognitive networks (medial frontal (MF), frontoparietal (FPN), and sub-cortical/salience networks), whole-brain connectivity was greatest during NCP(−)'s. For the PCC-PFC , whole-brain connectivity was greatest during PCP(−)'s (Fig. 6D). For sensory networks (motor, visual association and visual networks), whole-brain connectivity was the greatest during PCP(+)'s (Fig. 6E-G). The inferior visual network was the one network to exhibit similar whole-brain connectivity across several different critical points (Fig. 6H).
Fig. 6.
RSN analysis of critical points. Whole-brain connectivity averaged across eight canonical RSNs revealed that specific networks exhibit the greatest connectivity during specific critical points. A) The medial frontal (MF) network, B) the frontoparietal (FPN) network, and C) the sub-cortical/salience network showed the greatest whole-brain connectivity during NCP(−)'s. D) The PCC-PFC network showed the greatest whole-brain connectivity during PCP(−)'s. E) The motor network, F) visual association network, and G) visual network showed the greatest whole-brain connectivity during PCP(+)'s. H) The inferior visual network was no associated with any critical point in particular.
G. Critical points for other thresholds
As our definition of critical points relies on a threshold, we repeated our main analysis using three additional standard deviation thresholds (SD threshold=0.5, 1.5, and 2) to explore threshold-related effects. Unsurprisingly, using a standard deviation threshold of 0.5 resulted in a 1.5-fold increase in the number of critical points identified (PCP(+)'s=122.6±12.8, PCP(−)'s=122.7±13.4, NCP(+)'s=122.7±13.3, NCP(−)'s =122.5±13.4). Qualitatively, similar associations between the critical points and whole-brain connectivity were found using a threshold of 0.5 (Fig. 7) compared with a threshold of 1 (Figs. 3, 4, and 5). Notably, however, certain associations between the motor network and the critical points were observed at a threshold of 1 (Figs. 3A, 3B, 4A, and 4B) but not at the lower threshold of 0.5 (Figs. 6C-F). When using a standard deviation threshold of 1.5, the number of critical points decreased (PCP(+)'s=44.0±5.9, PCP(−)'s=44.1±6.1, NCP(+)'s=43.3±6.0, NCP(−)'s=43.0±6.1). Qualitatively, similar associations between the critical points and whole-brain connectivity were found using a threshold of 2 (Fig. 8) compared with a threshold of 1 (Figs. 3, 4, and 5). Notable differences between results using a threshold of 0.5 vs. 1 were observed in the fusiform and the DMN. Differences in the fusiform were less prominent at the higher threshold; whereas, differences in the DMN were more prominent at the higher thresholds. When using a standard deviation threshold of 2, the number of critical points decreased (PCP(+)'s=18.1±3.3, PCP(−)'s=18.3±3.3, NCP(+)'s=18.1.7±3.6, NCP(−)'s =17.9±3.7). Comparison between the different types of critical points is not presented as the number of points available at this threshold may not be enough to reliably estimate voxel-based functional connectivity or detect meaningful differences.
Fig. 7.
Critical point analysis using a standard deviation threshold of 0.5. Pairwise comparisons of A) PCP(+)'s and PCP(−)'s, B) NCP(+)'s and NCP(−)'s, C) PCP(+)'s and NCP(+)'s, D) PCP(−)'s and NCP(−)'s, E) PCP(+)'s and NCP(−)'s, and F) PCP(−)'s and PCP(+)'s revealed similar differences as in the main analysis. All results shown for p<0.05 corrected for multiple comparisons.
Fig. 8.
Critical point analysis using a standard deviation threshold of 1.5. Pairwise comparisons of A) PCP(+)'s and PCP(−)'s, B) NCP(+)'s and NCP(−)'s, C) PCP(+)'s and NCP(+)'s, D) PCP(−)'s and NCP(−)'s, E) PCP(+)'s and NCP(−)'s, and F) PCP(−)'s and PCP(+)'s revealed similar differences as in the main analysis. Notably, regions in the DMN are more prominent whereas the fusiform is less prominent at the higher threshold of 1.5 compared to the lower threshold of 0.5 in Fig. 7. All results shown for p<0.05 corrected for multiple comparisons.
Finally, we repeated this analysis using a standard deviation threshold of 0, which represents the lowest possible threshold. At this threshold, only the sign of derivative of the global signal is used to define critical points as positive and negative critical points do not exist at this threshold. The average number of positive slope critical points, CP(+), was 140.2±15.2 and the average number of negative slope critical points, CP(−), was 140.0±15.5. As shown in Fig. 9, the comparison of CP(+)'s vs. CP(−)'s was strikingly similar to the PCP(+)'s vs. PCP(−)'s comparison (Fig. 3A). Together, these results further suggest the stability of many of the observed differences across critical point definitions.
Fig. 9.
Critical point analysis using a standard deviation threshold of 0. At this threshold, only the sign of derivative of the global signal is used to define critical points as no distinction between above or below the mean is made. This comparison of CP(+)'s to CP(−)'s was strikingly similar to the PCP(+)'s vs PCP(−)'s comparison (Fig. 3A). All results shown for p<0.05 corrected for multiple comparisons.
IV. DISCUSSION
Employing a temporal parcellation scheme driven by global brain activity and a voxel-based measure of functional brain organization, these data suggest that connectivity in well-established resting-state networks varies with global brain activity. We defined four brain states—or “critical points”—where the brain was entering or exiting periods of activity more than one standard deviation above or below the mean. When comparing these critical points, regions associated with cognitive functions in the frontal and parietal lobes and sub-cortical regions displayed greater whole-brain connectivity during the low activity states. Conversely, regions of the brain associated with sensory functions displayed greater whole-brain connectivity during the high activity states. Finally, we demonstrated that these results depend on the standard deviation threshold used to define the critical points.
In accordance with these results, previous studies have shown that a large portion of typical RSN patterns can be captured using only a small number of critical points in the BOLD timecourse where a region of interest enters periods of high activity [17-20]. An interpretation of the current and previous results is that RSNs arise from dynamic interactions between regions [8] occurring only at a few specific and discrete time points, rather than a continuous and sustained interaction. This work builds upon these recent studies by extending the critical point methodology to incorporate whole-brain connectivity, the global signal, negative critical points, and differences in signal trajectory. Our whole-brain connectivity results suggest that RSNs dynamically change within and between network connections in accordance with previous reports [16, 36, 37]. Additionally, these connectivity results suggest that, for many of these RSNs, a single state is associated with the greatest level of whole-brain connectivity. Our results suggest that NCPs and critical points with trajectories towards the mean hold unique and possible biologically-relevant information. Contrasting these different critical points revealed additional dynamics that may be missed by other methods. These results agree with other studies that include NCPs [20].
When comparing the average whole-brain connectivity in each of the 8 RSNs, a trend emerged suggesting that cognitive networks displayed the greatest connectivity during the NCPs and sensory networks displayed the greatest connectivity during the PCPs. This result also emerges from pairwise comparisons as the motor/somatosensory network consistently demonstrated greater connectivity during the PCPs compared to the NCPs (Figs. 3A, 3B, 4A, and 4B) and the FPN consistently demonstrated greater connectivity during the NCPs compared to the PCPs (Figs. 3A, 3B, and 4A). Of interest, the striatum, which supports both motor and cognitive functions, has higher connectivity during the NCP(−)'s, as also occurs for the cognitive networks (Figs. 2B, 3B, 4A). A similar relationship between sensory and cognitive networks has been observed in a previous study [20] where co-activation patterns for sensory networks occurred at the opposite sign of global activity as cognitive and attention networks. In addition, it has been shown that the FPN dynamically alters its connectivity to sensory networks in order to exert cognitive control during tasks [36, 38]. This interaction between connectivity and global activity may be explained by a model in which the brain collects sensory information during periods of higher activity and subsequently directs attention to this collected information for further processing during periods of lower activity.
While the number of critical points did not vary with scanner, head coil, or age, we did observe an effect of sex. Across all four types of critical points, women displayed a greater number of critical points either at significance or trend levels compared to men. Sexual dimorphism is observed in a number of neuroimaging and brain studies [39], including rs-fMRI [5, 26, 40-42]. Previously observed sex-related differences in RSNs may be related to the different number of critical points as a greater number of critical points could lead to stronger network and better network statistics. These results also suggest a greater amount of “state” changes in women compared to men. These differences in critical points between men and women should be considered preliminary and future studies should aim to more carefully characterize these effects.
Our main results were generated using a standard deviation threshold of 1, which is consistent with previous studies using critical point methods [17-20]. We qualitatively investigated the impact of varying this threshold by repeating our analysis using thresholds of 0.5 and 1.5. Using these two thresholds produced results qualitatively similar to the main analysis. However, potentially interesting differences emerged between thresholds. For example, differences in the DMN were more pronounced at higher thresholds, while differences in the fusiform were more pronounced at lower thresholds. There may be, however, pragmatic reasons to avoid higher thresholds than 1.5; a threshold of 2 produced only 18 critical points, which may not be enough to reliably estimate voxel-based functional connectivity or detect meaningful differences. Overall, these small differences across thresholds may indicate that the some portion of relationship between the global signal and the connectivity is threshold-dependent; that is, critical points at different thresholds may represent unique brain states.
A unique aspect of this study is the large amount of data available per subject. Nearly 50 minutes of data was acquired for each subject. The large amount of data enabled the use of a novel temporal parcellation scheme which produced a sparse set time points (less than 20% of the total data for each set) that still matched the amount of time points in a typical rs-fMRI experiment. Split-half analysis of the data suggests that similar results are detected using less data. However, more data may be required for each subject to fully capture individual differences using rs-fMRI [10, 37].
Several limitations of this study exist. One limitation is the lack of behavioral measures to relate to PCPs and NCPs. It remains unclear if or how these dynamic changes in connectivity and brain state are associated with behavior. Additionally, while the repetition time (TR) used is this study (1.55 seconds) is relatively short compared with standard fMRI sequences, the TR may still be too long to completely uncouple the relationship between RSNs and global activity. More rapid interactions may therefore be missed but it should be noted that given the typical temporal response of the blood oxygenation signal there are unlikely to be high frequency changes that can be measured with this mechanism. For this reason, we expect results consistent with the ones present in this work when shorter TR's are used.
Future work includes the use of higher temporal resolution multiband sequences to estimate finer grain dynamics, incorporating the magnitude of the derivative of the global signal into the estimation of critical points, and modeling all points in the global signal instead of just the extreme values.
V. Conclusion
As the study of RSNs progresses, our ability to understand and characterize the interactions between distinct RSNs will continue to increase in importance. We demonstrated that global brain activity moderates the interactions between RSNs in the frontal lobe, SMC, and visual cortex. Future studies of global brain activity, interactions between RSNs, and the relationship between these networks and dynamic oscillations between brain states are promising avenues for elucidating individual differences in behavior and dysfunction.
Acknowledgments
This work was supported by the National Institutes of Health under Grants R01 EB00966 and T32 DA022975.
REFERENCES
- 1.Greicius MD, et al. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci U S A. 2003 Jan;100(1):253–8. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Damoiseaux JS, et al. Consistent resting-state networks across healthy subjects. Proc Natl Acad Sci U S A. 2006 Sep;103(37):13848–53. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Smith SM, et al. Correspondence of the brain's functional architecture during activation and rest. Proc Natl Acad Sci U S A. 2009 Aug;106(31):13040–5. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shehzad Z, Kelly AM, Reiss PT, Gee DG, Gotimer K, Uddin LQ, Lee SH, Margulies DS, Roy AK, Biswal BB, Petkova E, Castellanos FX, Milham MP. The resting brain: unconstrained yet reliable. Cereb Cortex. 2009 Oct;19(10):2209–29. doi: 10.1093/cercor/bhn256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Biswal BB, et al. Toward discovery science of human brain function. Proc Natl Acad Sci U S A. 2010 Mar;107(10):4734–9. doi: 10.1073/pnas.0911855107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Martuzzi R, et al. Functional connectivity and alterations in baseline brain state in humans. NeuroImage. 2010;49(1):823–834. doi: 10.1016/j.neuroimage.2009.07.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Vincent JL, et al. Intrinsic functional architecture in the anaesthetized monkey brain. Nature. 2007;447(7140):83–86. doi: 10.1038/nature05758. [DOI] [PubMed] [Google Scholar]
- 8.Tagliazucchi E, Behrens M, Laufs H. Sleep neuroimaging and models of consciousness. Front Psychol. 2013;4:256. doi: 10.3389/fpsyg.2013.00256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Power JD, et al. Functional network organization of the human brain. Neuron. 2011 Nov;72(4):665–78. doi: 10.1016/j.neuron.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Finn ES, et al. Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nat Neurosci. 2015 Oct; doi: 10.1038/nn.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hampson M, et al. Connectivity-behavior analysis reveals that functional connectivity between left BA39 and Broca's area varies with reading ability. NeuroImage. 2006;31(2):513–519. doi: 10.1016/j.neuroimage.2005.12.040. [DOI] [PubMed] [Google Scholar]
- 12.Cole MW, et al. Global connectivity of prefrontal cortex predicts cognitive control and intelligence. J Neurosci. 2012 Jun;32(26):8988–99. doi: 10.1523/JNEUROSCI.0536-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cole MW, et al. Variable Global Dysconnectivity and Individual Differences in Schizophrenia. Biological psychiatry. 2011;70(1):43–50. doi: 10.1016/j.biopsych.2011.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Finn ES, et al. Disruption of Functional Networks in Dyslexia: A Whole-Brain, Data-Driven Analysis of Connectivity. Biol Psychiatry. 2013 Oct; doi: 10.1016/j.biopsych.2013.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Smith SM, et al. Temporally-independent functional modes of spontaneous brain activity. Proc Natl Acad Sci U S A. 2012 Feb;109(8):3131–6. doi: 10.1073/pnas.1121329109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hutchison RM, et al. Dynamic functional connectivity: promise, issues, and interpretations. Neuroimage. 2013 Oct;80:360–78. doi: 10.1016/j.neuroimage.2013.05.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu X, Duyn JH. Time-varying functional network information extracted from brief instances of spontaneous brain activity. Proc Natl Acad Sci U S A. 2013 Mar;110(11):4392–7. doi: 10.1073/pnas.1216856110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tagliazucchi E, et al. Criticality in large-scale brain FMRI dynamics unveiled by a novel point process analysis. Front Physiol. 2012;3:15. doi: 10.3389/fphys.2012.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu X, Chang C, Duyn JH. Decomposition of spontaneous brain activity into distinct fMRI co-activation patterns. Front Syst Neurosci. 2013;7:101. doi: 10.3389/fnsys.2013.00101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Karahanoğlu FI, Van De Ville D. Transient brain activity disentangles fMRI resting-state dynamics in terms of spatially and temporally overlapping networks. Nat Commun. 2015;6:7751. doi: 10.1038/ncomms8751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fox MD, et al. The global signal and observed anticorrelated resting state brain networks. J Neurophysiol. 2009 Jun;101(6):3270–83. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yang GJ, et al. Altered global brain signal in schizophrenia. Proc Natl Acad Sci U S A. 2014 May;111(20):7438–43. doi: 10.1073/pnas.1405289111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.McAvoy M, et al. Unmasking Language Lateralization in Human Brain Intrinsic Activity. Cereb Cortex. 2015 Jan; doi: 10.1093/cercor/bhv007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wong CW, et al. The amplitude of the resting-state fMRI global signal is related to EEG vigilance measures. Neuroimage. 2013 Dec;83:983–90. doi: 10.1016/j.neuroimage.2013.07.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Garrison KA, et al. The (in)stability of functional brain network measures across thresholds. Neuroimage. 2015 May; doi: 10.1016/j.neuroimage.2015.05.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Scheinost D, et al. Sex differences in normal age trajectories of functional brain networks. Hum Brain Mapp. 2014 Dec; doi: 10.1002/hbm.22720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Friedman L, et al. Reducing inter-scanner variability of activation in a multicenter fMRI study: role of smoothness equalization. Neuroimage. 2006 Oct;32(4):1656–68. doi: 10.1016/j.neuroimage.2006.03.062. [DOI] [PubMed] [Google Scholar]
- 28.Scheinost D, Papademetris X, Constable RT. The impact of image smoothness on intrinsic functional connectivity and head motion confounds. Neuroimage. 2014 Jul;95:13–21. doi: 10.1016/j.neuroimage.2014.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Joshi A, et al. Unified framework for development, deployment and robust testing of neuroimaging algorithms. Neuroinformatics. 2011 Mar;9(1):69–84. doi: 10.1007/s12021-010-9092-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Satterthwaite TD, et al. An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data. Neuroimage. 2013 Jan;64:240–56. doi: 10.1016/j.neuroimage.2012.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Scheinost D, et al. The intrinsic connectivity distribution: a novel contrast measure reflecting voxel level functional connectivity. Neuroimage. 2012 Sep;62(3):1510–9. doi: 10.1016/j.neuroimage.2012.05.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mitchell MR, et al. A preliminary investigation of Stroop-related intrinsic connectivity in cocaine dependence: associations with treatment outcomes. Am J Drug Alcohol Abuse. 2013 Nov;39(6):392–402. doi: 10.3109/00952990.2013.841711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yan CG, et al. A comprehensive assessment of regional variation in the impact of head micromovements on functional connectomics. Neuroimage. 2013 Aug;76:183–201. doi: 10.1016/j.neuroimage.2013.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Van Dijk KR, Sabuncu MR, Buckner RL. The influence of head motion on intrinsic functional connectivity MRI. Neuroimage. 2012 Jan;59(1):431–8. doi: 10.1016/j.neuroimage.2011.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shen X, et al. Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. Neuroimage. 2013 Nov;82:403–15. doi: 10.1016/j.neuroimage.2013.05.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cole MW, et al. Multi-task connectivity reveals flexible hubs for adaptive task control. Nat Neurosci. 2013 Sep;16(9):1348–55. doi: 10.1038/nn.3470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Laumann TO, et al. Functional System and Areal Organization of a Highly Sampled Individual Human Brain. Neuron. 2015 Aug;87(3):657–70. doi: 10.1016/j.neuron.2015.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Seeley WW, et al. Dissociable intrinsic connectivity networks for salience processing and executive control. J Neurosci. 2007 Feb;27(9):2349–56. doi: 10.1523/JNEUROSCI.5587-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cosgrove KP, Mazure CM, Staley JK. Evolving knowledge of sex differences in brain structure, function, and chemistry. Biol Psychiatry. 2007 Oct;62(8):847–55. doi: 10.1016/j.biopsych.2007.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tomasi D, Volkow ND. Gender differences in brain functional connectivity density. Hum Brain Mapp. 2012 Apr;33(4):849–60. doi: 10.1002/hbm.21252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Allen EA, et al. A baseline for the multivariate comparison of resting-state networks. Front Syst Neurosci. 2011;5:2. doi: 10.3389/fnsys.2011.00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Satterthwaite TD, et al. Linked Sex Differences in Cognition and Functional Connectivity in Youth. Cereb Cortex. 2015 Sep;25(9):2383–94. doi: 10.1093/cercor/bhu036. [DOI] [PMC free article] [PubMed] [Google Scholar]