Perturb-seq: Dissecting molecular circuits with scalable single cell RNA profiling of pooled genetic screens

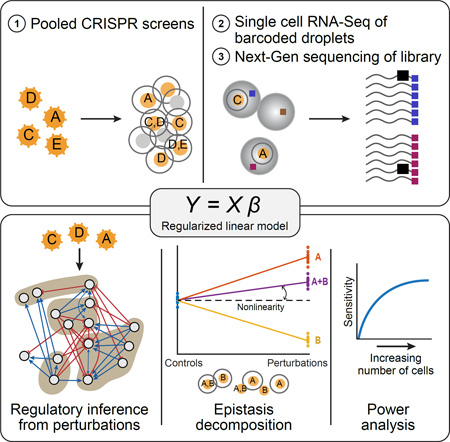
SUMMARY

Genetic screens help infer gene function in mammalian cells, but it has remained difficult to assay complex phenotypes – such as transcriptional profiles – at scale. Here, we develop Perturb-seq, combining single cell RNA-seq and CRISPR based perturbations to perform many such assays in a pool. We demonstrate Perturb-seq by analyzing 200,000 cells in immune cells and cell lines, focusing on transcription factors regulating the response of dendritic cells to lipopolysaccharide (LPS). Perturb-seq accurately identifies individual gene targets, gene signatures, and cell states affected by individual perturbations and their genetic interactions. We posit new functions for regulators of differentiation, the anti-viral response, and mitochondrial function during immune activation. By decomposing many high content measurements into the effects of perturbations, their interactions, and diverse cell metadata, Perturb-seq dramatically increases the scope of pooled genomic assays.

Graphical Abstract

INTRODUCTION

Genetic screens systematically analyze gene function in mammalian cells. Such screens are designed in either: (1) an individual (“arrayed”) format, where each perturbation is delivered and assessed separately; or (2) a pooled format, performed en masse. Pooled readouts measure cell autonomous phenotypes, such as growth, drug resistance, or marker expression. Pooled screens are more efficient and scalable, but have been limited to low-content readouts. Distinguishing between different molecular mechanisms that yield similar phenotypes requires time and labor intensive follow-up.

Bridging the gap between rich profiles and pooled screens has been challenging. In mammalian cells, a few studies transcriptionally profiled hundreds of individual perturbations (Berger et al., 2016; Parnas et al., 2015). In yeast (Hughes et al., 2000), up to ~1,500 knock out (KO) strains have been assessed (Kemmeren et al., 2014). Even signature screens were only performed in centralized efforts (Lamb et al., 2006).

Profiling may particularly help interpret the combined nonlinear effects of multiple factors. Comprehensive analysis of genetic interactions in growth phenotype between pairs of genes has been performed in yeast (Costanzo et al., 2016). In mammals, only small sets of pre-selected pairs have been assessed for cell viability (Bassik et al., 2013) or morphology (Laufer et al., 2013). One yeast study determined the combined effects of regulators on expression profiles in a circuit of 3–5 genes (Capaldi et al., 2008). Very few studies have examined higher order interactions (Elena and Lenski, 1997; Haber et al., 2013), and none have coupled those with a high content scalable readout.

To address this challenge, we develop Perturb-seq, combining the modularity of CRISPR/Cas9 to perform multi-locus gene perturbation (Cong et al., 2013; Qi et al., 2013) with the scale of massively parallel single cell RNA-seq (scRNA-seq) (Klein et al., 2015; Macosko et al., 2015) as a rich genomic readout. We demonstrate Perturb-seq in primary post-mitotic immune cells and in proliferating cell lines. We develop a computational framework, MIMOSCA, to decipher the effect of individual perturbations and the marginal contributions of genetic interactions on the level of each transcript, program, and cell state. Our framework can be extended to other high dimensional molecular phenotypes or diverse cell metadata.

RESULTS

Perturb-seq: pooled, combinatorial CRISPR screens with scRNA-seq readout

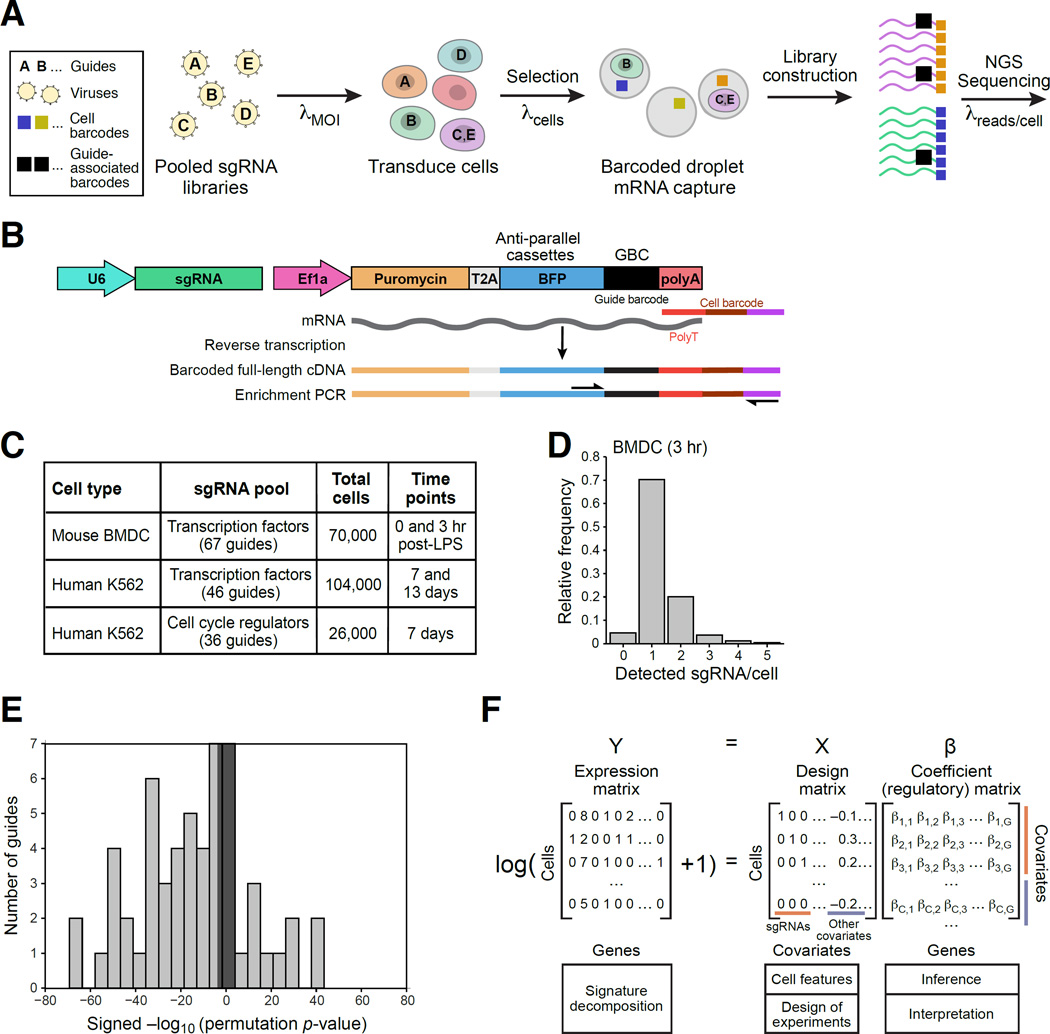
We developed Perturb-Seq to combine a pooled CRISPR screen with scRNA-seq by encoding the identity of the perturbation on an expressed guide barcode (GBC) (Figure 1 and S1). We first infect cells with a pool of lentiviral constructs that encode sgRNAs (Figure 1A). Here and in a companion study (Adamson et al., 2016), we designed and used a CRISPR lentiviral vector that both delivers an sgRNA to a cell and reports on the identity of the sgRNA by an expressed GBC (Figure 1B). By varying the multiplicity of infection (MOI), we tune the screen to study single gene or epistatic effects. Cells are grown, differentiated, and/or stimulated, followed by scRNA-seq (Figure 1A). scRNA-seq, performed in a single pool, tags each cell’s mRNA, including the GBC, with a unique cell barcode (CBC) and a unique molecular identifier (UMI) (Figure 1A). The CBC associates the cell’s transcriptional profile with the delivered genetic perturbation(s), encoded by the GBC. Here, we use CRISPR/Cas9 in the KO context. In a companion study (Adamson et al., 2016), Perturb-seq is used with CRISPRi.

Figure 1. Perturb-seq: pooled screening of transcriptional profiles of perturbations.

(A) Overview. (B) Perturb-seq vector. (C) Perturb-seq screens in this study. (D) Distribution of number of guides detected per cell in stimulated BMDCs. (E) Distribution of the significance (−log₁₀(P-value)) of the effect of each guide on its target (gray shaded rectangle corresponds to p<0.05 threshold). (F) Modeling framework. We fit coefficients of a (regulatory) matrix (β) to the observed expression profiles of each cell (matrix Y) given the sgRNA and other covariates in the design matrix (X). See also Figure S1.

We performed six Peturb-seq experiments, analyzing 200,000 cells (Figure 1C). In bone-marrow derived dendritic cells (BMDCs), we targeted 24 transcription factors (TFs) (Table S1) (Amit et al., 2009a; Garber et al., 2012), and measured the effects pre-stimulation (0h) and at 3h post-LPS. In K562 cells, we targeted 14 TFs and 10 cell cycle regulators, in separate pooled experiments (Table S1). For K562 TFs, we performed experiments using lower and higher MOI, and at two time points. We collected reference scRNA-seq data from unperturbed cells separately (Table S1).

Perturb-seq detection of GBCs and on-target knockdown

We developed an optimized enrichment protocol to detect the GBCs (Methods and Resources). We associated each sgRNA with its corresponding GBC by sequencing, and converted the plasmids into lentivirus for pooled transduction. The plasmid construct included an ORF encoding a BFP-T2A-Puromycin (Figure 1B), allowing us to select for transduced cells by FACS sorting or by antibiotics. Finally, we designed a PCR protocol to enrich for the GBC following WTA (Figure 1B). In some cases, we observed more than one GBC in a cell. To distinguish between those arising from multiple infections and those due to PCR chimeras or ambient RNA, we filter low-abundance contaminants by normalizing the observed GBCs within each CBC (Figure S1D,E), and retain cells with more than one GBC for epistasis analysis (Figure 1D). Most of these are not doublets, given their higher frequency than expected by our cell yield, and their comparable number of genes vs. single GBC cells (Figure S1F).

We estimated the probability of GBC detection and MOI by assuming a zero-truncated Poisson distribution (due to BFP⁺ selection), convolved with a binomial process (for the probability of detection) (Methods and Resources). The predicted fit was indistinguishable from the observed frequencies of number of guides per cell (Figure S1A–C, KS-test). We had a 94% (92–96%) detection probability with an initial MOI of ~0.63 in the K562 TF pool, a 98% probability with an MOI of ~0.35 in the cell cycle pool, and a 60% detection probability with an MOI of ~1.4 in BMDCs at 3h. The lower detection in BMDCs is due to the lower complexity of these smaller cells’ profiles (Table S1), and increases (to 70%) after filtering cells with the lowest complexity. Rather than apply an arbitrary filter, we address the detection rate in our analysis.

For most of the guides, there is a significant reduction in the expression of the targeted gene (Figure 1E and S1G–I, averaged over cells with a particular guide). The ability to determine a reduction is affected by the target’s expression level in WT cells (Figure S1I), the cell’s capture efficiency, and incomplete nonsense mediated decay of frameshifted transcripts.

A computational model to stratify transcriptional effects of single cell perturbations

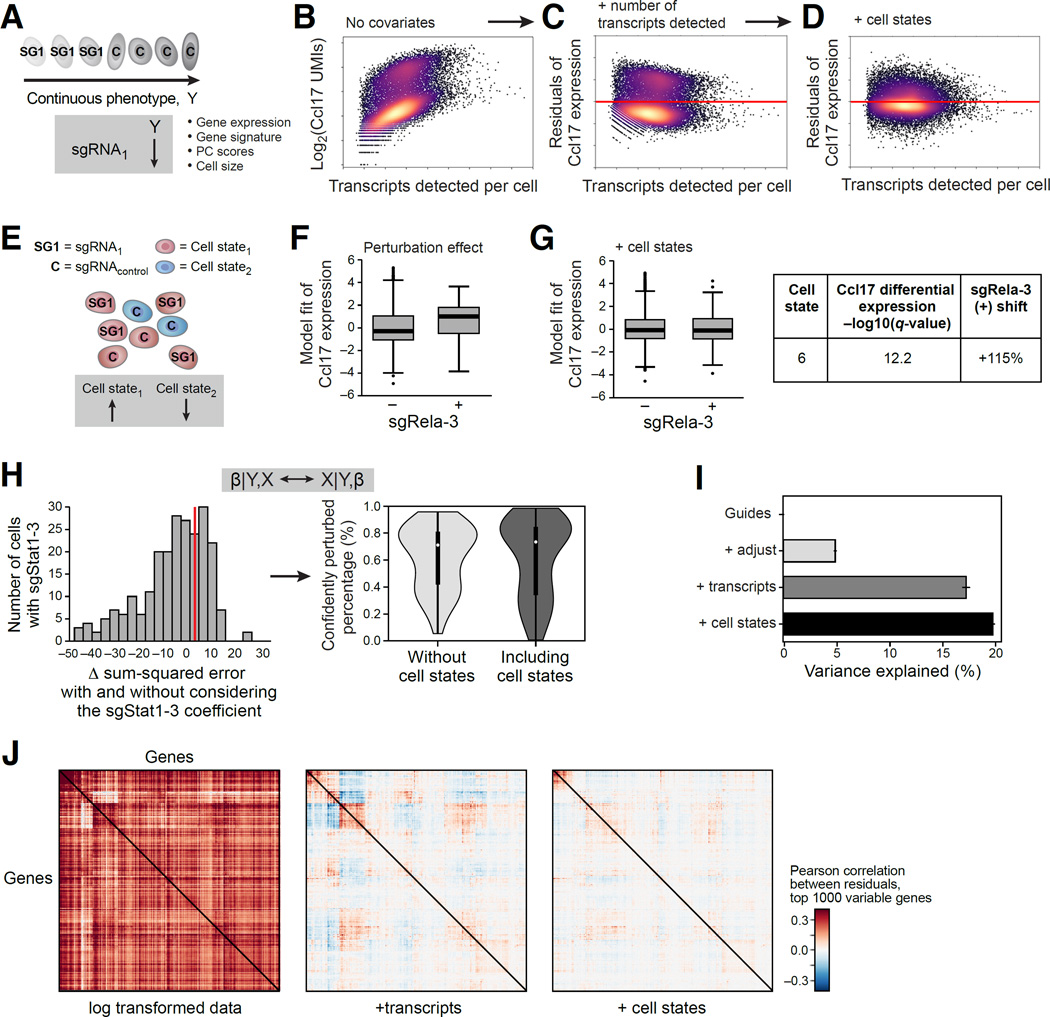
We devised a computational framework, MIMOSCA (Multi Input, Multi Output Single Cell Analysis) based on a regularized linear model, to estimate the impact of perturbations on gene expression (Figure 1F, 2 and S2, Methods and Resources). In simplest form, the model predicts each gene’s (log) expression level (expression matrix Y) as a linear combination of the effects of guides (design matrix X), yielding the regulatory effect of each guide on each gene (coefficient matrix β). We do not use information on which gene each guide targets or which guides target the same gene. We fit the coefficient matrix with elastic net regularization, to reduce the number of hypotheses tested, and to address correlated covariates and noisy data. We evaluate the significance of the each coefficient with a permutation-based test (Figure S2D–G).

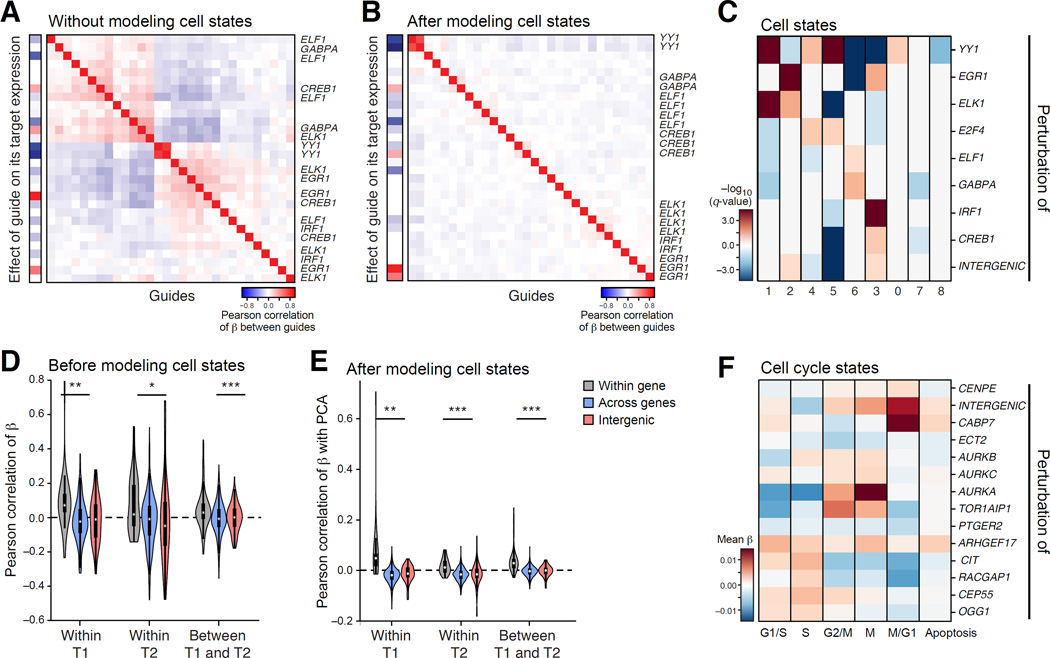
Figure 2. MIMOSCA: A scalable model for Perturb-seq.

(A) Model relates a continuous phenotype (arrow) to a covariate (here, guide identity). (B–D) Accounting for differences in cell quality and state. Scatter plots show for every cell (dot) the relation between the expression of Ccl17 (Y axis) or its residual after a model is fit and the number of transcripts in the cell (X axis; log (total transcripts detected)), in the original data (B), after including quality measures as covariates (C) and after also including cell state proportions (D). (E) Cell states. Cells are in either of two states (red, blue) and perturbation by sgRNA₁ increases the proportion of cells in one over the other. (F,G) Accounting for cell states. Effect on Ccl17 expression (Y axis) in cells with (+) and without (−) sgRela-3, in the original model (left) and when including cell state proportions (right). Table: high Ccl17 expression in cell state 6, whose proportion changes most due to sgRela-3. (H) Distinction of cells affected or unaffected by a perturbation. Left: Distribution of number of cells with sgStat1-3 that have a given fit (X axis) to the model of the effect of this perturbation. Right: distribution of percentage of cells confidently perturbed by each guide. (I) Contribution of each model component (Y axis) to the % variance explained (X axis) by R² values from cross-validation. (J) Correlation matrix between genes in the residuals of the model. See also Figure S2.

Next, we use the framework to account for technical covariates (Figure 2A–H). We account for the number of observed transcripts in a cell (cell quality) (Shalek et al., 2014), by including them as covariates in the model. We also address the probability that a perturbation successfully affected the cell, filtering cells that did not have a successful perturbation (Figure 2H and S2I, Methods and Resources), as often observed in CRISPR experiments. We use the initial regulatory matrix (β) fit by the model as a first assessment of the perturbations’ effects. We revisit each cell and evaluate the extent to which its profile was consistent with the assigned perturbation (Figure 2H, right). Finally, we re-estimate the model with a corrected perturbation-to-cell assignment. (This iteration is analogous to applying Expectation-Maximization to the linear model). Based on the estimated fit, over 66% of cells are affected by their delivered perturbation, on average (Figure 2H). While filtering significantly improves the model fit, we did observe consistent, albeit dampened, effects without this procedure.

We also consider biological covariates of distinct cell sub-types (e.g., in BMDCs (Helft et al., 2015; Shalek et al., 2014)) or states (e.g., the cell cycle in K562 cells) (Figure 2D,E,G) (Buettner et al., 2015; Zeisel et al., 2015). We classify profiles using the matched, genetically unperturbed, experiments (Methods and Resources), and incorporate the predicted classifications of each cell as covariates. We fit the model either with or without cell state covariates. Cell states explain a significant proportion of observed variation (Figure 2D), and some of the sgRNAs’ effects are accounted for (Figure 2F vs. G), suggesting that those perturbations may have primarily affected subtype proportions.

We can incorporate nonlinear interactions in our framework, by adding interaction terms between covariates (Figure 2H), such as genetic interactions between perturbations or interactions between perturbations and cell states (cell state specific gene expression changes). Here, we do this for genetic interactions.

The linear model is robust, reproducible and predictive

We determined the proportion of the variance in the data explained by each of the three components of the model (Figure 2I and S2A–C, Methods and Resources). For stimulated BMDCs, the perturbations explain 5% of the variance, 17% is explained when adding cell quality covariates, and up to 20% with added cell state covariates (Figure 2I). We obtain similar results with the other datasets (Figure S2A–C). Gene-gene correlations in the residuals were also significantly reduced as we added covariates (Figure 2J). We note that guides targeting genes have stronger and more consistent effects than a control guide (Figure S2I).

Perturb-seq dissects the transcriptional program in the BMDC response to LPS

To show how Perturb-Seq recovers the correct genes, processes and states regulated by TFs, we analyzed the effect of 24 TFs in BMDCs. ~2000 genes are induced in this response through the action of dozens of TFs (Amit et al., 2009b). The response is not fully synchronous (Shalek et al., 2013, 2014), and, moreover, cells may consist of at least two sub-types whose function is not fully elucidated (Helft et al., 2015).

We cultured precursors from the bone marrow of Cas9 transgenic mice in GM-CSF (Platt et al., 2014a), and, after two days, infected them with a lentiviral pool targeting 24 TFs (67 guides) and a non-targeting control. After another 7 days, we stimulated the cells with LPS, and collected cells for scRNA-seq at 0 and 3h (32,624 and 37,369 cells, respectively, Table S1). Perturbations did not strongly affect fitness (Figures S3E) or the number of transcripts/cell (Figure S3D). Pilot experiments validated our sensitivity (80%) and specificity (90%) to detect – with ~100 single cells/guide – the correct genes regulated by the perturbation compared to bulk RNA-seq following the same perturbation (Parnas et al., 2015) (Figure S3F and S7I).

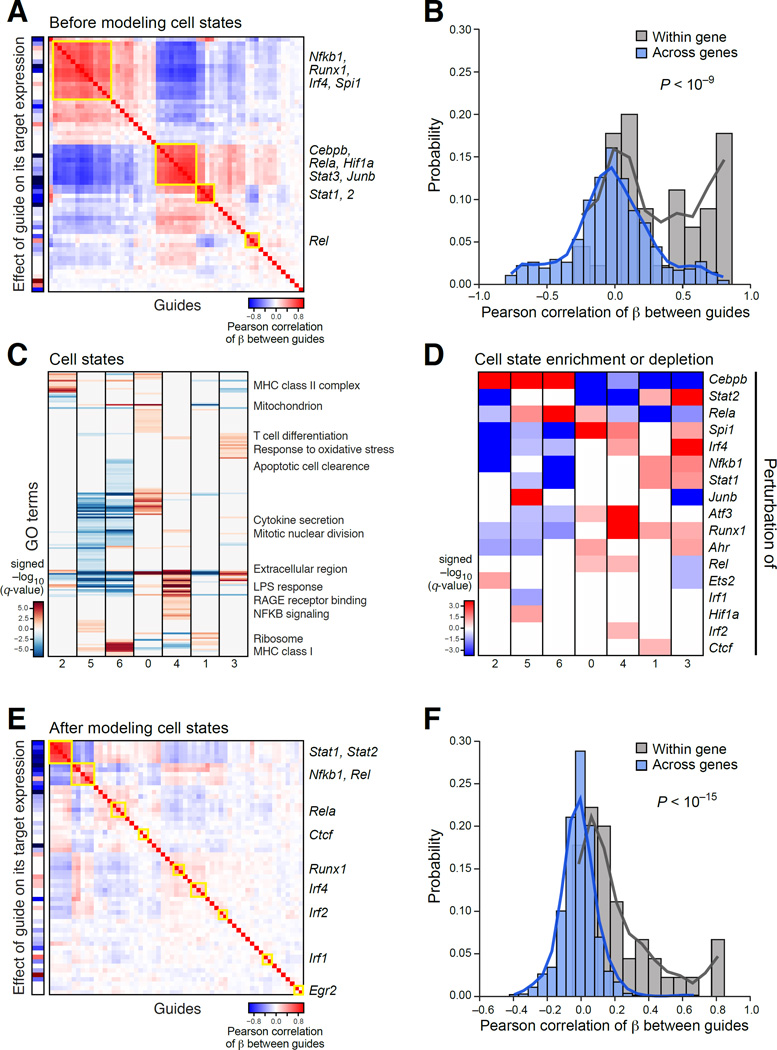
A simple model for stimulated BMDCs (Figures 3 and 4, Table S3, Methods and Resources) performed well by two basic measures: guides targeting the same gene had a similar impact (Figure 4A), with correlated regulatory coefficients profiles (Figure 3B, P<10⁻⁹, Wilcoxon signed-rank test), and guides typically repressed their direct target (Figure 3A, left column).

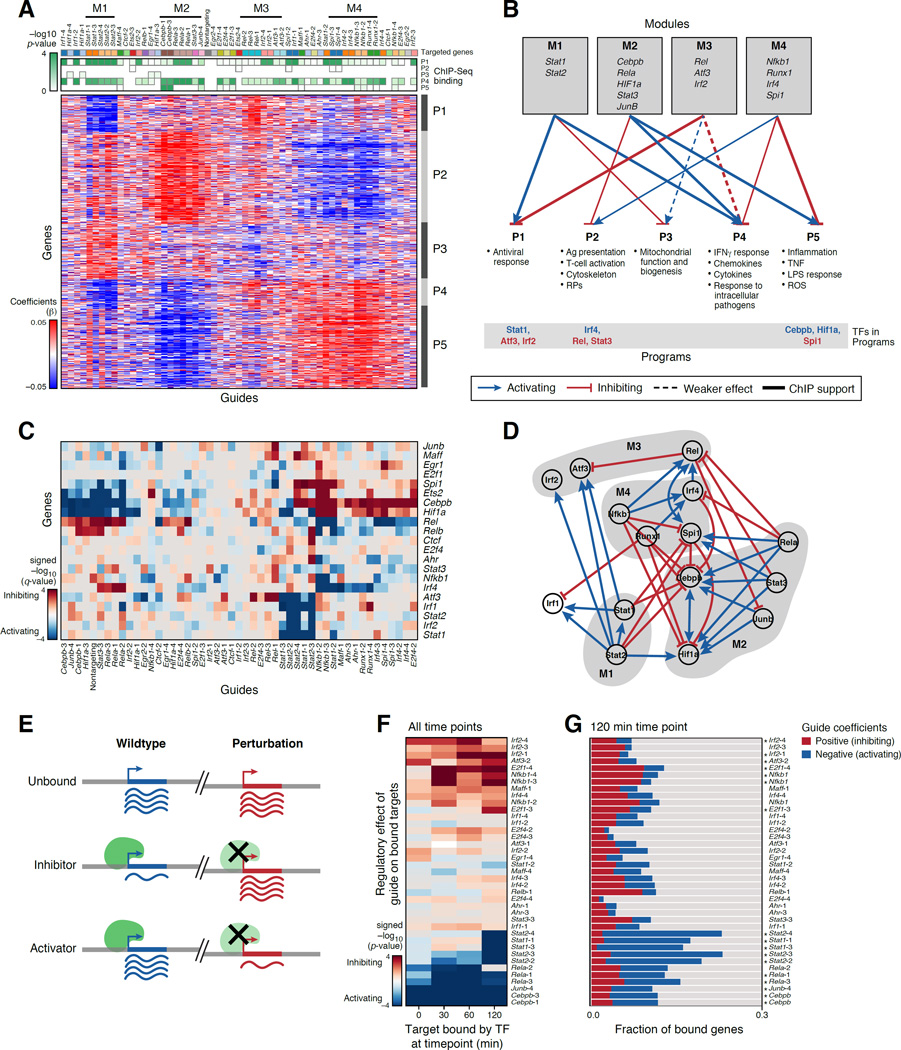
Figure 3. The role of 24 TFs in BMDCs stimulated with LPS.

(A) TF modules. Pearson correlation (color bar) between the regulatory coefficients of each pair of guides (rows, columns) in a model without cell state covariates. Yellow rectangles: TF modules. Leftmost column: on-target effect. (B) Agreement between guides targeting the same gene. Distribution of correlations between guides targeting the same gene (grey) or different genes (blue). (C) Cell states. Enrichment (−log₁₀(q-value)) of induced (red) and repressed (blue) genes with GO gene sets (rows) in each cell state (columns) defined for wild-type stimulated BMDC. (D) TF effects on cell state proportions. q-values for enrichment (red) or depletion (blue) of guides in cells in each state (columns; as in C). (E, F) TF-specific effects. Heatmap (E) as in (A) in a model with cell state covariates. Distribution of correlations (F) between guides targeting the same (grey) or different genes (blue). See also Figure S3.

Figure 4. A gene regulatory circuit for BMDCs balances states and responses.

(A,B) TF modules controlling transcriptional programs. (A) Regulatory coefficient (β) of each guide (columns, color coded) on each gene (rows) in a model without cell state covariates. Guides and genes are clustered. Green-white: enrichment of ChIP-bound targets of each TF (columns) in each program (rows). (B) Graph, based on (A), associating TF modules (top) to programs (bottom). Blue/red arrows: module TFs activate/inhibit program (opposite of regulatory coefficient). Bottom: module TFs that are members of program (blue/red: activator/repressor of program). (C,D) TF circuit. (C) Heatmap, as in (A), but only of genes (rows) that encode TFs targeted by guides (columns). (D) Schematic of the associations in (C). Nodes: TFs; Blue/red arrows: activation/inhibition; Modules: grey shading. (E–G) Agreement with ChIP-seq. (E) Expected effects of TF perturbation. (F) Average regulatory effect of each guide (rows) on the genes bound by its target at four time points (columns). (G) Proportion of bound targets at 120 min post-LPS for each TF (rows) that are repressed (blue), activated (red) or unaffected (grey) by the TF’s perturbation. Asterisks: significant (as in F, P < 0.05). See also Figure S4.

Next, we used the regulatory effects of each perturbed TF on each gene, to group TFs into modules by their similar regulatory effects and to group genes into programs by how they are affected by the perturbations. There were four TF modules (M1–M4) (Figure3A and 4A): (M1) the anti-viral TFs Stat1 and Stat2; (M2) the pioneer factor Cebpb, with JunB, Rela, Stat3 and Hif1; (M3) Rel, Irf2, and Atf3; and (M4) the pioneer factor Spi1/Pu.1, with Runx1, Irf4, and Nfkb1. There were five gene programs, each enriched for distinct processes (P1–5; Figure 4A and B, Table S6): (P1) an anti-viral response; (P2) antigen presentation, cytoskeleton and ribosomal proteins (RP); (P3) mitochondrial function and biogenesis; (P4) an interferon gamma response to intracellular pathogens; and (P5) an inflammatory TNF response.

The TF modules regulate programs consistent with known functions. For example, Stat1 and Stat2 (M1) are known activators of the anti-viral program (P1) (Gao et al., 2012). The predicted repression of the antiviral program by M2 (Rel, Irf2, Atf3) is supported by studies (Labzin et al., 2015) that Atf3 is a transcriptional repressor of interferon beta and the anti-viral response. Our prediction that Stat1 and 2 are repressors of mitochondrial biogenesis (P3) (Figure 4A,B) is supported by Stat1’s inhibition of mitochondrial biogenesis in mouse liver (Sisler et al., 2015) and Stat2 mutations in children with mitochondrial disorders (Shahni et al., 2015).

The model predicts the details of regulation of the anti-parasitic response genes Gbp2,2b,3,4,5 and 7. These are all positively regulated by Stat1 and 2, and negatively regulated by Rel and Irf2, consistent with studies on Stat1 (Ramsauer et al., 2007) and Rel (Wei et al., 2008). Our model also predicts that Stat2 activates Irf8 – a key TF that controls GBP expression (Tussiwand et al., 2012), suggesting that Stat2’s impact on GBPs may be mediated through Irf8. Conversely, Batf is induced by Stat2 perturbation, a possible compensation (Tussiwand et al., 2012).

Opposing programs of BMDC differentiation controlled by two modules wired by positive and negative feedback loops

Further analysis shows that Module M2 and M4 have opposite effects on the proportion of cells in two mutually exclusive cell states, reflected by programs P2 and P4/5. These correspond to alternative cell differentiation or maturity types. The opposing functions are wired through multiple positive and negative loops, such that perturbing the module controlling one subtype switches the cells to the other.

Modules M2 and M4 had opposite effects on P2 (repressed by M2 and induced by M4) and P4 and P5 (induced by M2 and repressed by M4) (Figure 4A,B). P4 and P5 reflect key aspects of the response to LPS and pathogens. P2 is enriched for genes for antigen presentation, cytoskeleton proteins, and RPs, and includes key genes associated with distinct cell identity, especially SerpinB6 (from “cluster disrupted cells”, a sub-population that expresses some maturation genes even prior to stimulation (Shalek et al., 2014)) and CD86 (DC maturation, (Cannoodt et al., 2016; Schlitzer et al., 2015)). Ribosomal, cytoskeletal and MHC II proteins are induced in pre-DCs, and several pre-DCs and late-pre-DC genes are members of P2 (e.g., lglas3, Itgax, Crip1, Cd74, H2-Ab1,H2-AA, H2-Eb1) (Cannoodt et al., 2016; Schlitzer et al., 2015), as are Il12, Id2, Irf8, and Cd24a (whereas Zeb2 and Sirpa are in P4). Thus, P2 may reflect a distinct cell state or type, either less differentiated or abortive ex vivo.

We hypothesized that the regulatory effects on P2 and P4/5 reflect the impact of the perturbed TFs on the distribution of cells across possible BMDC subtypes (Methods and Resources). To test this, we identified seven cell clusters in 1,310 wild type LPS stimulated cells (Figure 3C). The clusters are significantly associated with the induction of genes from the five programs (P2 in cluster 2, 5, 6; P3 in cluster 1; P4/5 in clusters 0, 1, 3, 4; Figure S4A). Thus, induction of P2 and P4/5 represent different BMDC states, present even absent perturbation. Testing the association of each guide or targeted gene with each state (Figure 3D), cells perturbed for M2 TFs (Cebpb, Rela, JunB) are enriched in clusters matching P2 and depleted in clusters matching P5, whereas those perturbed for M4 TFs (Spi1, Irf4, Nfkb1, Runx1) have the opposite effect (Figure 3D).

Thus, M2 and M4 – with their distinct pioneer factors Cebpb and Spi1, respectively – have mutually opposing effects: M2 may promote differentiation, leading to LPS-responsive programs (P4 and P5), whereas M4 promotes a mutually exclusive state that is either less differentiated, or less productive ex vivo (P2). Both states are present in different cells absent genetic perturbation; the perturbations shift their proportions. The two TF modules are present and have the same effect even prior to LPS stimulation (Figure S3A,B and S4B, P1 and P3, Table S6).

Our modules self-reinforce and mutually inhibit to balance the programs. First, P2 and P5 include as member genes their key positive and negative regulators (Figure 4B, bottom): Irf4 from M4 is a member of P2 (positive feedback), whereas Stat3 from M2, is also in P2 (negative feedback); Cebpb and Hif1a of M2 are members of P5 (positive feedback), but so is Spi1 of M4 (negative feedback). Similarly, in the antiviral program (P1), Stat1 of M1 is a member (positive feedback), but so are Irf2 and Atf3 of M3 (negative feedback). Moreover, based on the significant transcriptional effects of the perturbed TFs on each other (Figure 4C,D), most of the TF modules (Figure 4D, shaded areas) have internally reinforcing activation (e.g., Hif1a and Cebpb by each other and by JunB, Stat3, Rela (M2); Stat1 by Stat2 (M1); Irf4 by Nfkb1 and Runx1 (M4)), and repression between modules (e.g.. Cebpb and Hif1a in M2 repressed by Runx1 and Nfkb1 in M4; Rela in M4 repress Irf2 in M2; Stat3 and Rela in M4 repress Rel in M3).

The genetic circuit is supported by TF binding profiles

The targets our model predicted for most TFs are strongly supported by ChIP-seq data of the genes bound by these TFs in bulk populations (Garber et al., 2012) (Figure 4E–G, Methods and Resources). For example, targets bound in either unstimulated or stimulated cells by the constitutively bound, activating TFs Rela and Cebpb are downregulated when these TFs are perturbed. Targets bound at 2h post LPS by the dynamically bound activators Stat1 and Stat2 are downregulated in perturbed BMDCs post-stimulation.

The model also correctly predicted the targets and logic of repressors (Figure 4F,G), such as Irf2, Atf3, and Nfkb1. Perturbing Irf2 affects its bound targets both pre- and post-stimulation, consistent with its role as a repressor pre-bound pre-LPS (Garber et al., 2012) (Figure S4B). The targets bound by Atf3 and preferentially induced by its perturbation are enriched for anti-viral genes (P<10⁻⁵), supporting it as a repressor of the antiviral response. Nfkb1 (encoding p50) is predicted by the model to act as a repressor for its bound targets, suggesting that its perturbation affected a p50-p50 repressor homodimer (Elsharkawy et al., 2010), more than a p50-p65(Rela) activator heterodimer post LPS.

The TF binding patterns also support their direct regulation of P1, P4 and P5 (Figure 4A,B, green/white heatmap). Genes bound by M1 TFs are enriched in P1 and P4 (positively regulated by M1); genes bound by the repressors Atf3 and Irf2 (M3) are enriched in P1 (negatively regulated by M3); genes bound by Atf3 are also enriched in P4 (including IL-6 (Gilchrist et al., 2006)); Stat3- and Rela- (M2) bound genes are enriched in P4, and Cebpb bound genes are enriched in P5 (both positively regulated by M2). Bound targets of M4 TFs (Irf4, Runx1, Nfkb1) are enriched in P4, and Nfkb1 targets are also weakly enriched in its repressed target program P5. The remaining two programs do not show such enrichments for bound TF targets (Figure S4C), e.g., suggesting that Stat1 and 2 regulate P2 indirectly, perhaps through mitochondrial signaling (Meier and Larner, 2014).

TF-specific programs revealed once accounting for global effects

Global effects on cell states may mask other specific effects of a TF within cells in a given state. To recover those, we added the assignment of the perturbed cells into the seven states (Figure 3C, Table S2) as covariates. Following this, guides targeting the same TF grouped particularly tightly (Figure 3E–F compared to A–B). The model showed that MHCII genes are positively regulated by Runx1 and Ctcf, and negatively regulated by Rel (Figure S4D, Table S6), and a strong repression of the IFNγ response by Irf2. The two models are complementary: one emphasized global effects; the other uncovers TF specific effects.

Genetic interactions affect gene expression and global cell states

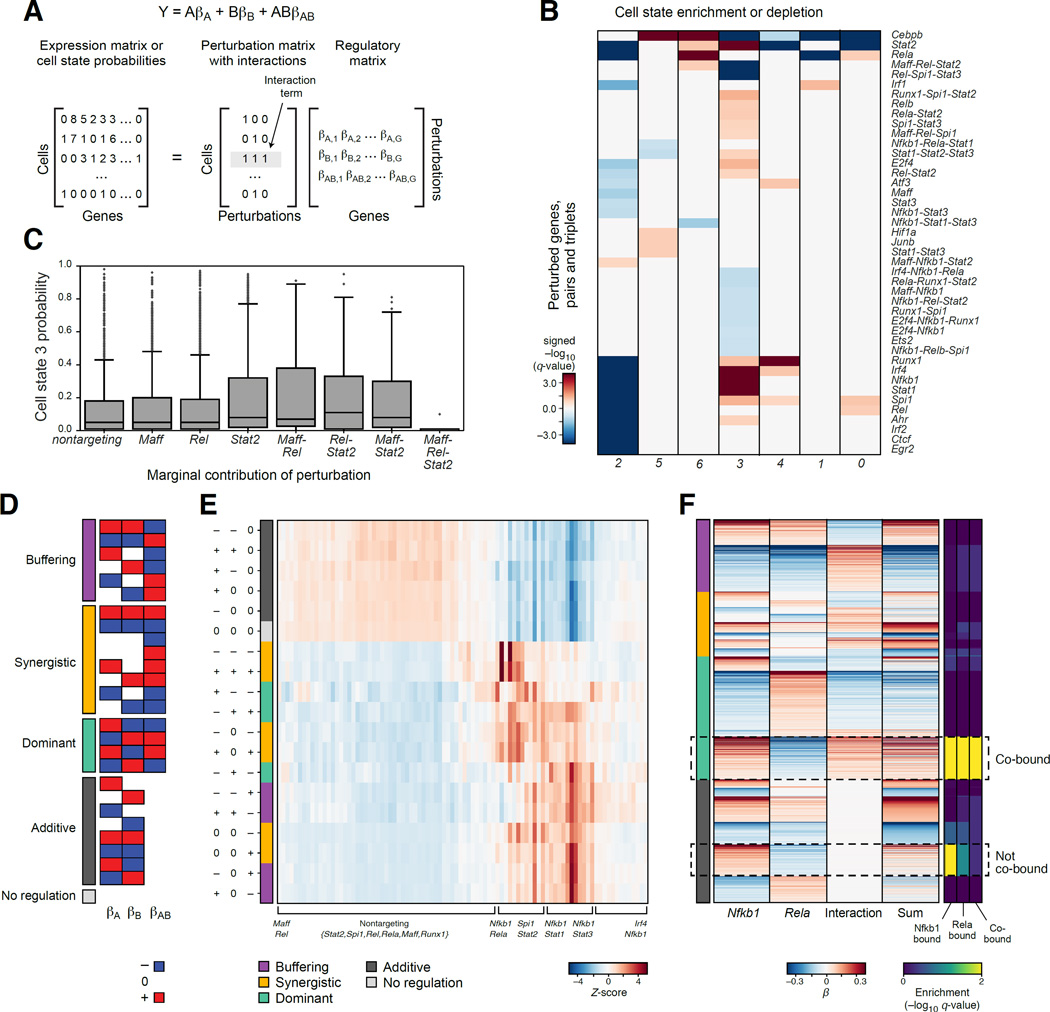
To dissect how the effects of multiple TFs combine, we analyzed cells containing more than one guide after strict filtering of GBCs (Figure 1D, S1E, and 5). First, in many cases pairs, and even triplets of TFs affected in a non-additive way the probability that a cell assumes one of the seven cell states (Figure 5B). For example, cells containing GBCs for all three of Maff, Rel, and Stat2 have a lower probability of being in cell state 3 than expected by their individual and pair-wise effects (Figure 5C).

Figure 5. Genetic interactions between TFs in BMDCs.

(A) Model with interactions. (B) TF interactions affecting cell states in stimulated BMDCs. Enrichment (red) or depletion (blue) of single, pair and triplets of guides (rows) in cells in each state (as in Figure 3C). (C) Three-way genetic interaction reduces probability of cell state 3. Probabilities of assignment to cell state 3 of the individual, pair-wise and three-way interactions. (D) 27 genetic interaction categories between two genes (A,B), with positive (red), negative (blue) or no (white) regulatory coefficients marginally associated with each individual guide or their combination. (E) Distribution of target genes in each of the 27 categories (rows) for every pair of perturbations assayed for interaction (columns). (F) Genetic interaction between Rela and Nfkb1 associated with co-binding. Marginal regulatory coefficients for Rela, Nfkb1 and their interaction term for each gene (rows) with at least one non-zero coefficient, sorted by key categories (color code, left). Right: ChIP-seq enrichment of individually bound and co-bound targets in each group.

Next, we assessed the effect of genetic interactions on the expression of each gene using our model with interaction terms (Figure 5A, Methods and Resources). For each pair of perturbed TFs, we assessed the relative proportion of target genes where their relation is additive (no interaction), synergistic, buffering (antagonistic), or dominant (when the two factors have opposing effects, and the interaction term enhances one of them) (Figure 5D,E). Most TF pairs involving one of Runx1, Irf1, Irf2, or Irf4 had mostly additive effects, whereas pairs with combinations of Stat1, Stat2, Stat3, Rela, Nfkb1 and Spi1 were enriched for interactions. Only those involving Nfkb1 (Stat1-Nfkb1, Stat3-Nfkb1, Rela-Nfkb1, Spi1-Nfkb1) were enriched for buffering interactions (Figure 5E).

Finally, we related the different categories of interactions to TF binding, illustrated for Nfkb1 and Rela (Figure 5F). Individually, Nfkb1 and Rela have opposing effects on the genes in P4 and P5: Nfkb1 as a repressor, and Rela as an activator. These target genes are partitioned in two by the model with genetic interaction (Figure 5F, hatched boxes): in one subset, the joint perturbation of Rela and Nfkb1 is additive (no interaction), whereas in the other there is a dominant interaction (of Nfkb1 over Rela). Both sets belong to the same programs (Figure 5F, hatched boxes), and both are enriched for ChIP targets of both Nfkb1 and Rela (Figure 5F, right), but only the set with the dominant interaction is enriched for co-binding (Figure 5F, right). Similar cases, where genetic interactions are present only when the two factors are co-bound, are found for additional pairs (e.g., Runx1-Rel, Irf4-Nfkb1).

Global transcriptional modules and specific TF effects in K562 cells

To test the generality of our approach, we performed Perturb-seq targeting 10 TFs in K562 cells, a rapidly proliferating cell line (Figure 6, S5 and S6, Table S4). Fitting a linear model without cell state covariates, the TFs partition into two modules (Figure 6A and S6B). Guides to the same gene were correlated in their effects, both within and across experiments of different durations (Figure 6E and S6B).

Figure 6. Perturb-seq of non-essential TFs and cell cycle regulators in K562 cells.

(A–E) TFs. (A,B) Modules. As in Figure 3A, for models either without (A) or with (B) cell state covariates. (C) TFs effects on cell state proportions. As in Figure 3D, for TFs (rows) in each state (shown in Figure S6G). (D,E) Agreement of guide effects across time points. Distribution of correlations between guides targeting the same gene (grey), different genes (blue) and a gene and an intergenic region (red) within and across time points (T1=7d, T2=14d), in either a model that does not (D) or does (E) include cell state covariates. (F) Cell cycle regulators. The effect (color bar, average regulatory coefficients) of guides targeting each gene (rows) on cell cycle phase signatures (columns). See also Figure S6.

We defined nine cell states by clustering of WT cells (Figure S6G), and found specific perturbations enriched in individual states (Figure 6C), consistent with known functions of the perturbed genes. For example, cells perturbed in EGR1 are depleted from cell state 6, which has an increased expression of hemoglobin biosynthesis genes, consistent with EGR1’s known role (Sripichai et al., 2009). Cells perturbed in YY1 are enriched in state 5 (induction of cholestrerol biosynthesis genes), consistent with its known role as a repressor of this process (Villagra et al., 2007).

Next, we fitted a model that accounted for cell states. Because these states are likely continuous (e.g., cell cycle phase) rather than discrete types, we performed PCA on WT K562 cells, scored the cells from the Perturb-seq experiment against those PC scores, and introduced the state PC scores as covariates. In the resulting model (Figure 6B), individual guides to the same gene are more consistent in their effects, especially across experiments and durations (Figure 6E), suggesting that TF-specific effects are reproducible even if cell state proportions change over time.

The model correctly predicts individual TF functions. For example, GABPA perturbation represses mitochondrial functions (P < 10⁻⁸, Figure S6C, Table S6), consistent with its known role (Yang et al., 2014). YY1 perturbation is correctly (Goffart and Wiesner, 2003) predicted to represses oxidative phosphorylation (P<10⁻¹⁰) and induce an innate immune response (P<10⁻¹⁰), and is enriched for its ChIP-seq targets (Guo and Gifford, 2015)).

Perturbations of cell cycle regulators reveal distinct profiles associated with similar fitness effects and mitotic arrest

Individual cells in a rapidly dividing cell line vary in their cell cycle state, readily observed by scRNA-seq (Buettner et al., 2015; Macosko et al., 2015). Cell cycle phenotypes can be screened by morphology or markers, but two genes with the same phenotypic effect may act through different mechanisms. To address this, we targeted in K562 cells 13 genes (33 guides) (Table S1) that were previously identified by a mitotic arrest phenotype in a genome-wide imaging screen in HeLa cells (Figure S6D, from (Neumann et al., 2010)).

Determining the fitness effects of each perturbation (Methods and Resources), we found a strong proliferative advantage conferred by perturbing PTGER2, CABP7 and CIT, and a disadvantage when perturbing AURKA, TOR1AIP1, and RACGAP1 (Figure S6H). (Among K562 TFs, perturbing EGR1 had a disadvantage; Figure S6A.) Furthermore, supervised analysis using signature gene sets for cell cycle phases (Macosko et al., 2015) showed that perturbations of AURKA and TOR1AIP1 (both decrease fitness) are associated with an increase in G2/M and M signatures (Figure 6F). Perturbation of CABP7 (increases fitness) has an opposite effect: decrease in G2/M and M signatures and increase in the M/G1 signature (Figure 6F). Perturbation of CIT increases G1/S and S states, a different cell cycle route manifested as increased fitness (Figure 6F).

Our model (Figure S6E, Table S5 and S6) shows that distinct processes are affected by factors with positive and negative fitness effects, but also highlights two different routes underlying increased fitness. Perturbation of CABP7 strongly induced a program of mitochondrial respiration and biogenesis (P < 10⁻¹⁰), NFkB signaling (P < 10⁻⁵), and mitotic division (P < 10⁻⁸), consistent with the fitness advantage. Perturbation of CIT and PTGER2 (also increased fitness) repressed these programs but induced the expression of other genes, especially 11 histone genes induced by CIT. The overall partitioning of factors by their regulatory effects (Figure S6E) mostly followed their groupings by morphology in HeLa cells (Figure S6D, (Neumann et al., 2010)): (1) CIT, PTGER2 and RACGAP1 (binuclear phenotype); (2) CENPE and ARHGEF17 (grape-like phenotype and mitotic delay); and (3) Aurora kinases A, B, and C (proliferation and migration defects). An exception is CABP7, which, despite a similar binuclear phenotype to that of CIT, PTGER2 and RACGAP1, has a distinct transcriptional phenotype (Figure S6E, above).

A guide to the miserly: effects on gene signatures are robust to downsampling of cells and reads

The regulatory coefficients associated with our perturbations are highly structured (Figure 3–6), with sets of targets similarly affected across sets of perturbations, consistent with modular gene regulation (Heimberg et al., 2016; Kemmeren et al., 2014). Thus, recovery of effects on gene signatures– e.g., guides that affect the antiviral response – should be achieved even with low numbers of cells and reads.

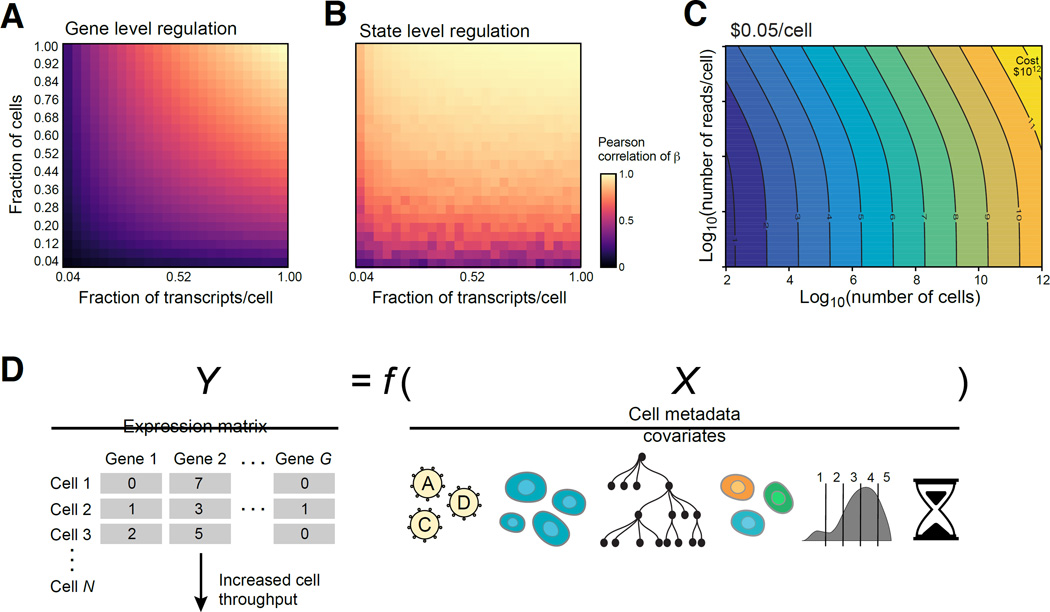
We quantified our ability to detect gene level regulation vs. signature or state level regulation (data-driven clusters or known gene sets), when we down-sample cells and reads/cell (Figure 7 and S7, Methods and Resources). The number of cells and reads required for signature level effects is lower than that needed to detect effects on individual genes (10’s vs. 100–200 cells/perturbation; 400 vs. 1,000 transcripts, Figure 7A,B and S7B–H, J–L). These estimates provide helpful guidelines for future Perturb-seq applications.

Figure 7. Prospects for Perturb-seq.

(A,B) Saturation analysis. Effect of the number of cells (Y axis) and reads (X axis) on recovery as measured by correlation (color bar) with either the per gene (A) or cell state signature (B) effects observed in the full data. The number of cells per perturbation (1.0) is a mean of 300 and a median of 155 and the number of transcripts per cell (1.0) is a median of 5,074. (C) Tradespace of number of cells (X axis) and measurements per cell (Y axis) required for scaling Perturb-seq. (D) Future extensions, by scaling the number of cells (left) or incorporating other cell covariates (right), such as lineage (tree), marker expression (binned distribution), or time course information (timer), and a more generalized modeling of the relationship between X and Y (Y=f(X)).

To support the feasibility of large Perturb-seq screens, we also demonstrated that all steps in Perturb-seq could be performed in a single pool (Figure S5). We synthesized an array of sgRNAs targeting 7 chromatin regulators and 5 intergenic controls, and performed pooled cloning, virus preparation, transduction, cell growth, scRNA-seq (14,000 cells), and model fitting. Guides to the same gene agreed well (P<10⁻³). Early pooling may cause recombination in lentivirus, but allows large screens with appropriate strategies (Adamson et al., 2016).

DISCUSSION

We developed Perturb-seq, a method to analyze the transcriptional effect associated with genetic manipulations on genes, processes, and states. Perturb-seq decreases the time and cost associated with assaying the complex effects of large numbers of perturbations, including combinations.

Future enhancements of precision and facility

An important advantage of using Perturb-seq is that higher order interactions can be assayed without further need to generate complex reagents. Due to the Poisson loading of perturbation per cell, the same experiment used for a single perturbation can also uncover the genetic interactions between the perturbed genes. Future work could leverage the ability of Cpf1 to autonomously process an entire array, and deliver several sgRNAs (or an unprocessed array) on one construct (Zetsche et al., 2016).

Current and future scale of Perturb-seq

At its current scale, Perturb-seq can be readily applied for targeted screens of a subset of genes of interest and their interactions (Figure 7C), as we have done here. In some systems, growth or marker-based screens may first be performed to identify this subset prior to Perturb-seq (as in (Adamson et al., 2016)). Perturb-seq will scale as both the cost of sequencing and of scRNA-seq decreases (Figure 7C).

By varying the number of surveyed cells and the sequencing depth, screens can be adjusted to focus on cell states and signatures or on effects on individual genes. Our analysis suggests that a broad survey of transcriptional phenotypes across thousands of perturbations can be performed with as few as 10 cells per perturbation (Figure 7B).

Genome-wide or large combinatorial screens will also require increased computational bandwidth. MIMOSCA (Figure S2H) is designed foreseeing screens with millions of cells, with fast, scalable, and parallelizable algorithms. It is publically available with worked examples (https://github.com/asncd/MIMOSCA).

Challenges and opportunities for understanding the vast space of possible genetic interactions

As we showed, Perturb-seq can in principle dissect higher order effects (Figure 5C), but systematic analysis of genetic interactions remains an ambitious goal. First, both the probability of detecting all perturbations and the probability of all perturbations resulting in an effect scale exponentially with the order of perturbations (Figure S7A). Our inference framework (Figure 2) and future improvements can help deconvolve mixtures of knockouts, and is potentially scalable to higher order interactions. However, while Perturb-seq significantly reduces time and cost, these still scale linearly with the number of perturbations assayed, whereas the size of combination space grows exponentially as the order of combinations grows.

We hypothesize that a plausible alternative strategy exists, combining substantial under-sampling of this vast space with appropriate analytics (Beerenwinkel et al., 2007; Du and Hwang, 2000; Weinberger, 1991) that make inference possible even when the number of possible combinations is much larger than the number of samples. We are motivated by two biological assumptions: (1) modularity(Costanzo et al., 2016; Ihmels et al., 2002), as we have shown for both the perturbations and the gene targets; and (2) sparsity, such that the majority of gene pairs (or higher order combinations) do not manifest genetic interactions (supported by fitness studies of genetic interactions in yeast (Costanzo et al., 2016)). If sparsity holds for expression phenotypes, a subset of experiments can be performed, in which most cells receive a relatively large number of perturbations (e.g., 5) and we infer both partially observed and even entirely unobserved interactions at a lower order effects (e.g., 2 or 3). Perturb-seq was designed with such future studies, which will leverage group structure in perturbations and their interactions, in mind.

A general framework to combine rich readout with cellular metadata

Other CRISPR-based perturbations are readily compatible with Perturb-seq, including CRISPRi as in our companion study (Adamson et al., 2016), CRISPRa, and alternative editors (e.g., Cpf1). Expressed barcodes can also be used to mark cells derived from a common ancestor for the purposes of lineage tracing (Figure 7D). Other measurement platforms, such as multiplex PCR (Fan et al., 2015) or multiplex protein measurements (Frei et al., 2016) can help focus on a subset of target transcripts or proteins, respectively. It should also be possible to apply Perturb-Seq in vivo, or in co-cultures of perturbed cells in droplets, merging them with scRNA-seq.

We hope that the experiments and analysis provided here and in (Adamson et al., 2016) will be starting points for future experiments that combine scRNA-seq and pooled screens. These will bridge the gap between genetic screening and molecular follow up experiments, and will facilitate causal studies of how specific genotypes lead to phenotypes.

METHODS AND RESOURCES

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to the Lead Contact: Aviv Regev, aregev@broadinstitute.org.

Experimental Model and Subject Details

Cas9 transgenic mouse

For all BMDC experiments, we derived cells (as described below) from six- to eight-week old constitutive Cas9-expressing female mice, from the transgenic mice we described previously (Platt et al., 2014b), and that are also available from the Jackson labs. All animal protocols were reviewed and approved by the MIT / Whitehead Institute / Broad Institute Committee on Animal Care (CAC protocol 0609-058-12) and all experiments conformed to the relevant regulatory standards.

Bone marrow derived dendritic cells

To obtain a sufficient number of cells, we implemented a modified version of the DCs isolation protocol as previously described (Amit et al., 2009b; Chevrier et al., 2011; Garber et al., 2012; Lutz et al., 1999; Rabani et al., 2011). RPMI medium (Invitrogen) supplemented with 10% heat inactivated FBS (Invitrogen), β-mercaptoethanol (50µM, Invitrogen), L-glutamine (2mM, VWR), penicillin/streptomycin (100U/ml, VWR), MEM non-essential amino acids (1X, VWR), HEPES (10mM, VWR), sodium pyruvate (1mM, VWR), and GM-CSF (20 ng/ml; Peprotech) was used throughout the study. At day 0, cells were collected from femora and tibiae and plated in 100mm non tissue culture treated plastic dishes using 10ml medium per plate at concentration of 2 × 10⁵/ml. At day 2, cells were fed with another 10ml of medium per dish. At day 5, 12ml of the medium were carefully removed (to avoid removal of cells) and 10ml of fresh medium were added back to the original dish. Cells were fed with another 5ml medium at day 7. At day 8, all non-adherent and loosely bound cells were collected and harvested by centrifugation. Cells were then re-suspended with medium, plated at a concentration of 10×10⁶ cells in 10ml medium per 100mm dish. At day 9, cells were stimulated with LPS (100ng/ml, rough, ultrapure E. coli K12 strain, Invitrogen) and harvested. Cells were always plated at concentration of 2 × 10⁵/ml at day 0. Cells were harvested post stimulation after 0hr or 3hr and cells from cultures that contained 10% BFP positive cells were sorted for BFP+ and GFP+ (contain CAS9).

K562 cell cultures

We used transgenic K562 cells constitutively expressing Cas9 (Wang et al., 2015). K562 cells were transduced using several titers of virus and cells where spin infected in 2,000 rpm for 30 min. For the low MOI experiment we used cultures that contained 10% BFP+ and for the high MOI 50% BFP+. Cells were grown in RPMI Medium 1640 + GlutaMAX (ThermoFisher) + 10% heat inactivated FBS (Invitrogen). Cells were grown to a confluence of 30–60% and spun down at 300× g for 5 min. The supernatant was removed, and cells were suspended in 5 mL of 1× PBS + 0.2% BSA (Sigma cat #A8806) for sorting: BFP+ and GFP+ (CAS9 expressing) cells were sorted. Cells were harvested for library preparation 7 days post transduction for most experiments and 13 days post transduction for the second time point of the TF pool experiment.

After sorting BFP+ GFP+ cells passed through a 40-micron cell strainer (Falcon, VWR cat #21008-949), wash twice and counted.

Method Details

Construction of lenti-vector and transduction

A lentivirus backbone was constructed containing: antiparallel cassettes of a mouse U6 promoter for sgRNA and EF1α promoter for expression of puromycin, BFP and a polyadenylated GBC cassette (same vector here and in Adamson et al., 2016). The vector was digested using BlpI and BstXI and annealed oligonucleotides, encoding sgRNAs, were ligated in an arrayed format. Association between GBCs and sgRNAs was determined using Sanger sequencing to generate a sgRNA/GBC dictionary. sgRNAs for BMDCs were designed using published methods for the BMDCs (Doench et al., 2014) and the K562 guides were deigned by a preexisting library’s design (Wang et al., 2015). Plasmids were pooled together prior to lentivirus preparation.

Cloning of array-synthesized guide pools

We also devised, for proof-of-concept experiments, a two-step cloning procedure to enable cloning to be performed in a pool followed by next generation sequencing to create the sgRNA/GBC dictionary, as in Figure S5A.

Vector backbone compatible with pooled cloning

We assembled sgPS, a lentiviral vector similar to the one described above (Figure 1B) containing antiparallel cassettes of a human U6 promoter for sgRNA expression and a high-diversity library of GBCs. However, in place of the EF1α-Puro-T2A-BFP cassette, we inserted a NotI site so the sgRNA and its GBC are close enough to be associated through next generation sequencing.

sgRNA library cloning

We synthesized an oligo pool corresponding to several sgRNA libraries with PCR tags (purchased from CustomArray, Bothell, WA):

GGCCAGTGAGCTCGACAAGTTTCAGtatcttgtggaaaggacgaaacaccGNNNNNNNNNNNNNNNNNNNNgtttaagagctatgctggaaacagcatagGGGTGGTTAGTGATTTGCCCGTCAC

(Ns denote guide RNA sequence, uppercase denotes subpool specific PCR handles, lowercase denotes PCR handles for GuidePool Fwd/Rev)

We enriched for the desired sub-pool of oligonucleotides by PCR using sub-pool-specific primers (SubpoolAmp Fwd/Rev) and purified the product using a 2× volume of AMPure XP SPRI beads (Beckman Coulter, Danvers, MA). We then added homology arms for Gibson assembly by performing PCR with primers GuidePool Fwd/Rev and purified the product with 1× SPRI beads.

We prepared the vector backbone by digesting sgPS with BsmBI (New England Biolabs (NEB), Ipswich, MA) followed by purification with 0.75× AMPure XP SPRI beads. We assembled 70 ng amplified library into 500 ng digested vector in a 50 µL Gibson reaction (NEB), cleaned it with 0.75× AMPure XP SPRI, eluted in 15 µL H₂O and electroporated the entire volume into Endura competent cells (Lucigen, Middleton, WI). We expanded the cells in liquid culture for 18 hours at 30°C.

Next generation sequencing to create sgRNA/GBC dictionary

We generated a paired-end Illumina sequencing library, where read1 corresponded to the sgRNA and read2 corresponded to the GBC by PCR amplifying the intermediate plasmid pool with custom primers containing Illumina sequencing adaptors and sequenced them to an average depth of >100 reads per GBC with an Illumina MiSeq.

Insertion of EF1α-Puro-T2A-BFP cassette

We amplified the EF1α-Puro-T2A-BFP cassette from the vector described above (Figure 1B) by PCR with primers to add Gibson arms compatible for cloning into the NotI-digested intermediate pool. We assembled 300 ng of the amplified cassette into 300 ng of a digested intermediate pool in a 20 µL Gibson reaction (NEB), cleaned it with 0.75× AMPure XP SPRI, eluted in 15 µL H₂O and electroporated the entire volume into Endura competent cells (Lucigen). We expanded the cells in liquid culture for 18 hours at 30°C and purified the pooled library plasmid with the Endotoxin-Free Plasmid Maxiprep Kit (Qiagen, Hilden, Germany).

Name	Sequence	Note
SubpoolAmp_Fwd	GGCCAGTGAGCTCGACAAGTTTCAG
SubpoolAmp_Rev	GTGACGGGCAAATCACTAACCACCC
GuidePoolAmp_Fwd	GGCTTTATATATCTTGTGGAAAGGACGAAACACCG
GuidePoolAmp_Rev	CTTATTTAAACTTGCTATGCTGTTTCCAGCATAGCTCTTAAAC
IlluminaPoolSeq_Fwd	AATGATACGGCGACCACCGAGATCTACA NNNN CGATTTCTTGGCTTTATATATCTTGTGG	Ns denote sequencing barcode
IlluminaPoolSeq_Rev	CAAGCAGAAGACGGCATACGAGAT NNNNNNNN ACAGTCGAGGCTGATCAGC	Ns denote sequencing barcode
CustomRead1 Primer	CAAGCAGAAGACGGCATACGAGAT NNNNNNNN ACAGTCGAGGCTGATCAGC
CustomRead3 Primer	CGATTTCTTGGCTTTATATATCTTGTGGAAAGGACGAAACACCG
CustomIndex Primer	GCTGATCAGCGGGTTTAAACGGGCCCTCTAGG
CassetteAmp_Fwd	CCCGTTTAAACCCGCTGATCAGCCTCGACTGT
CassetteAmp_Rev	TCGCCAGGGTTTTCCCAGTCACGACGCTTAATTAAGCTTGTGCCCCAGT

Lentivirus was made using 293T cells transfected with lentiGuide-Puro, psPAX2 (Addgene 12260), and pMD2.G (Addgene 12259) at a 10:10:1 ratio, using Lipofectamine LTX and additional reagents according to the manufacturer’s instructions.

Single cell library preparation

In our current implementation, we rely on a droplet method, which is now commercially available (Zheng et al., 2016), but our design is compatible with additional single-cell RNA-seq methods (Fan et al., 2015; Klein et al., 2015), and we have tested it successfully with Drop-Seq (Macosko et al., 2015) in both K562 cells and BMDCs, albeit with different gene targets than in the rest of this study (AD, OP, BL, and AR, unpublished data).

Prior to analysis, cells were diluted to the final concentration in 1× PBS + 200 µg/mL BSA (NEB, cat # B9000S). Sorted cells (BMDCs or K562 cells) were loaded on the 10× Chromium system (Zheng et al., 2016) (8,000 cells/channel) and single cell RNA-seq libraries were generated following the manufacturer’s instructions.

Following WTA, a fraction of the WTA was used to amplify GBCs using a dial-out PCR strategy with the primer sequences below (the full primer sequence is a concatenation of the columns). The template material was approximately 5ng of WTA libraries. 25 cycles of PCR were performed using one of the dial-out primers below with the P7 Illumina reverse primer.

Primer sequences:

P5	Barcode	R1	Primer (BFP location of pBA439)
AATGATACGGCGACCACCGAGATCTACAC	NNNNNNNN	TCGTCGGCAGCGTCAGATGTGTATAAGAGACAG	TAGCAAACTGGGGCACAAGC
AATGATACGGCGACCACCGAGATCTACAC	TCGCCTTA	TCGTCGGCAGCGTCAGATGTGTATAAGAGACAG	TAGCAAACTGGGGCACAAGC
AATGATACGGCGACCACCGAGATCTACAC	CTAGTACG	TCGTCGGCAGCGTCAGATGTGTATAAGAGACAG	TAGCAAACTGGGGCACAAGC
AATGATACGGCGACCACCGAGATCTACAC	TTCTGCCT	TCGTCGGCAGCGTCAGATGTGTATAAGAGACAG	TAGCAAACTGGGGCACAAGC
AATGATACGGCGACCACCGAGATCTACAC	GCTCAGGA	TCGTCGGCAGCGTCAGATGTGTATAAGAGACAG	TAGCAAACTGGGGCACAAGC
AATGATACGGCGACCACCGAGATCTACAC	CATGCCTA	TCGTCGGCAGCGTCAGATGTGTATAAGAGACAG	TAGCAAACTGGGGCACAAGC
AATGATACGGCGACCACCGAGATCTACAC	GTAGAGAG	TCGTCGGCAGCGTCAGATGTGTATAAGAGACAG	TAGCAAACTGGGGCACAAGC

P7 Ilumina Reverse Primer:

CAAGCAGAAGACGGCATACGAGAT

We used the following PCR protocol:

	1 rxn
Q5 2X master mix	25
P7 primer @10uM	1.25
pBA439_rev @ 10uM	1.25
Template (5ng total)	x
water (qs up to final rxn of 50ul)	y
Total	50

Temp	time
98 C	10s
98 C	2s	repeat 65 C 5s for 25 cycles
65 C	5s
72 C	10s
72 C	1 min

The resulting PCR product was run on a 2% Agarose gel, the appropriate band was extracted, and next-generation Illumina sequencing was performed using NextSeq.

Quantification and Statistical Analysis

Read alignment and generation of expression matrix

A digital expression matrix was obtained for each experiment using 10X’s CellRanger pipeline with default parameters. Their pipeline uses STAR for alignment. All subsequence analysis information is also available and maintained in current form in the following Git repository https://github.com/asncd/MIMOSCA.

Alignment of cell barcode / GBC libraries

To associate cell barcodes with guides, the sgRNA/GBC dictionary generated by either Sanger or NGS was used. Paired-end reads containing a cell barcode and UMIs on one side and GBC barcode on the other side were isolated and collapsed into unique molecules by first demultiplexing a sequencing run using bcl2fastq2 with the following options --create-fastq-for-index-reads --barcode-mismatches 1 --no-lane-splitting --mask-short-adapter- reads 5 --minimum-trimmed-read-length 5 using a sample-sheet containing one line with polyG tracts in the index read columns (see below). The resulting Undetermined fastq files were split using kentools into two folders called split1 and split2 containing chunked R1 and R2 reads respectively.

Sample _ID	Sample_Name	I7_Index_ID	index	I5_Index_ID	index2
1	placeholder	silly1	GGGGGGGGGGGGGG	silly2	GGGGGGGG

The reads were then concatenated and GBC reads isolated using the following constant sequence within the GBC transcript: GGCACAAGCTTAATTAAGAATT.

All split files containing a particular index barcode were finally concatenated and collapsed to unique molecules using the following command.

cat *${inputbc}.txt | sort | uniq −c | sort −k1,1g | awk '{print $1"\t"$2"\t"$3"–"$4}' the result file format looks as follows (grey highlighting for actual barcode portion of GBC read):

279	1:N:0:GGTGATACCTCATT+TCGCATAA	CGCAAACTGGGGCACAAGCTTAATTAAGAATTCGATCAACGCAGAGACGGCCTAG
282	1:N:0:TCGAGCCTTATGGC+TCGCATAA	CGCAAACTGGGGCACAAGCTTAATTAAGAATTGCTTGACTCGTTAGCGAGCCTAG
286	1:N:0:ACTCGAGAGTTCGA+TCGCATAA	CGCAAACTGGGGCACAAGCTTAATTAAGAATTCGATCAACGCAGAGACGGCCTAG
294	1:N:0:GCACGTCTACTAGC+TCGCATAA	CGCAAACTGGGGCACAAGCTTAATTAAGAATTCTAACTCAGCGACTGGAGCCTAG
297	1:N:0:ATAGATTGTCCGAA+TCGCATAA	CGCAAACTGGGGCACAAGCTTAATTAAGAATTGCTTGACTCGTTAGCGAGCCTAG
299	1:N:0:GAGCAGGAGCTATG+TCGCATAA	CGCAAACTGGGGCACAAGCTTAATTAAGAATTAAACCCTCACTGCCGACGCCTAG
333	1:N:0:GGAGGCCTGTTACG+TCGCATAA	CGCAAACTGGGGCACAAGCTTAATTAAGAATTAGGGCTTGCAGTGCACGGCCTAG
339	1:N:0:CGACTCACGTTCAG+TCGCATAA	CGCAAACTGGGGCACAAGCTTAATTAAGAATTCGATCAACGCAGAGACGGCCTAG

Counts 1:N:0:Cellbarcode+Index/SampleBarcode GBCread-UMI

The resulting file along with the preassociated GBC and sgRNA dictionary was parsed using a custom Python script to create a new table of probability estimates of which sgRNA are present in each cell. The probability estimate is thresholded to create a dictionary of which cell barcodes contain which sgRNAs (Figure S1F).

For strict filtering, chimeric reads were removed by thresholding molecules that, for a given unique combination of cell barcode and UMI, received less that 20% of the reads.

See https://github.com/asncd/MIMOSCA for more on filtering chimeric reads.

Fit of distribution of guides per cell

We simultaneously fit a generative model of the number of guides per cell and the detection probability of observing a guide if a cell contains it using a maximum likelihood approach.

To approximate our probability of GBC detection, we considered two factors: (1) the initial MOI and (2) the technical transcript capture efficiency of the library preparation protocol. A third factor, the fitness effects of each of the guides, was not considered. We reasoned that for both our BMDCs TFs and K562 TFs pools our guides generally did not have strong fitness effects since their final representation correlated strongly with their initial abundance (Figure S3E,F and S6A). While fitness effects due to having multiple guides can create a skewed distribution, we noted a consistent distribution between the two time points in our K562 TF pool (separated by seven days of cell culture, Figure 6E,F).

We reasoned that these should be described well by a generative model, where we assume a zero-truncated Poisson distribution for infection with a guide-carrying lentivirus (zeros are truncated by BFP+ selection), convolved with a binomial process (for the probability of detection). Specifically we determined the maximum of the log likelihood by varying the two parameters: α, the detection probability and λ, the estimate of the initial MOI. The log-likelihood is evaluated as:

$$LL(\alpha ,\lambda )=\sum _{k=0}^{10}\text{log}(O(k)\sum _{j=k}^{10}(\begin{array}{c}\hfill m\hfill \\ \hfill j\hfill \end{array}\left){\alpha }^j{(1-\alpha )}^{m-j}\right(\frac{{\lambda }^j}{j!(e^{\lambda }-1)}))$$

Where O(k) is the number of cells with k guides detected. A “birthday problem” correction could be applied to account for the probability the same guide was present more than once in a cell, but this did not appear to significantly change our MOI or detection probability estimates (while more problematic for higher MOIs and low complexity libraries, this will not be an issue for high complexity libraries).

Determination of on-target effect

To assess the extent to which our observed reduction in on-target expression was significant, we performed a one-sample t-test to determine if the mean of our observed data was significantly less than zero. We also permuted the assignments between GBCs and cells and obtained a distribution of permuted means and compared to our observed means from which we calculated a permutation p-value (as in Figure 1E).

Linear model

To fit the linear model we compiled our covariate matrix X and our expression matrix (or one of the continuous covariates; as done for some assignments of cell states; below) as our matrix Y. Using the elastic net regularization (Zou and Hastie, 2005) through the Python implementation with the following parameters, to fit our model.

• sklearn.linear_model.ElasticNet(l1_ratio=0.5,alpha=0.0005,max_iter=10000)

The two regularization parameters were determined through cross-validation.

Alternating descent fit of perturbation probability

An overview of the problem, proofs that bound error for related approaches under specific assumptions, and useful citations can be found in (Loh and Wainwright, 2012).

To account for the contribution of unperturbed cells in the population containing a particular sgRNA, we constructed an approach in which the presence of sgRNA in a given cell was converted into a probability measure of that sgRNA having a phenotypic effect on the cell, as follows:

We note that by Bayes’ rule, the probability of being in a particular class of a two class outcome can be written as:

$$P(X_j=1|Y)=\frac{P(Y|X_j=1)P(X_j=1)}{P(Y)}=\frac{P(Y|X_j=1)P(X_j=1)}{P(Y|X_j=0)P(X_j=0)+P(Y|X_j=1)P(X_j=1)}=\frac{1}{1+e^{-LL(Y)}}$$

The derived equation is effectively a logistic transform of the log likelihood.

For a single output (y) that could belong to one of two possible Gaussian distributed classes, the log likelihood can be written as follows:

$$LL(y)=\text{log}\left(\frac{\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{{(y-{\mu }_1)}^2}{2{\sigma }^2}}}{\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{{(y-{\mu }_0)}^2}{2{\sigma }^2}}}\right)=\frac{{(y-{\mu }_0)}^2-{(y-{\mu }_1)}^2}{2{\sigma }^2}$$

Based on the derivations above, we fit using the multivariate regression on Y=X with Ŷ = Xβ

Next, we evaluate the fit with the guide covariate set to 0, Xo

$$\mathrm{P}({\mathrm{X}}_{\mathrm{j}}=1)=\mathit{\text{logistic}}(\frac{{\mathrm{\Sigma }}_i[Y_{ij}-X_o{\beta }_i{]}^2-{[Y_{ij}-{Ŷ}_{ij}]}^2}{2{\sigma }^2});\text{ where}\mathit{\text{logistic}}(x)=\frac{1}{1+e^{-x}}$$

Finally, we use the new covariate matrix X_M whose entries consist of P(X_j = 1) = 1 to recompute β_M.

Significance testing for coefficients of linear model

We devised a permutation strategy to empirically obtain a null distribution of the coefficients associated with our sgRNA effects. Specifically, we randomized the guide assignments to cells (such that co-occurrence between guides was preserved) and the linear model was recomputed with all other covariates being held constant. We repeated this ten times. We noticed that three significant as-yet latent factors impacted the empirical null distribution of coefficients: (1) the mean expression level of a gene; (2) the variance in expression of a gene; and (3) the number of cells a particular sgRNA was present in.

To control for these factors when assessing significance, each empirical null coefficient’s value was assigned a point in 4-space: [Gene mean, gene variance, number of cells, value]. We then estimated the multivariate density using a binning approach (np.histogramdd in Python). True nonzero coefficients were evaluated for significance relative to a matched set of bins (to create an empirical conditional cumulative probability distribution) conditioned on the first three factors.

A less stringent null was generated by obtaining a permuted distribution of coefficients based on a permuted cell-to-guide assignment, but only calculating the significance on a per guide basis without consideration of the mean expression level or variance of the gene being considered.

In both cases, we used a Benjamini-Hochberg procedure to control for multiple hypothesis testing.

Residuals analysis

To determine the marginal effect of each covariate in explaining the observed gene expression variation, we estimated the model R² by cross-validated (trained on 80% of the data and tested against 20%) for the addition of each of the covariates.

To determine the extent to which our covariates explained the major axes of variation in our data, we decomposed the residuals using the same randomized PCA approach described in the Definition of Cell States section. Two major metrics were evaluated: (1) the eigenvalue distribution, and (2) the extent to which the top loadings were enriched for biological terms. This analysis is relevant for Figure 2J.

Cross validated R²

To estimate the generalizability of the model, we determined a cross-validated R² by training our model on 80% of our data and determining the fit on the remaining 20%. This analysis is relevant to Figure 2I, and S2A–C.

Definition of cell states

Cell states were defined using parallel experiments with cells that did not have sgRNAs introduced. Starting from an expression matrix Y, variable genes were selected based on fitting a nonparametric Loess regression (using a moving window of 25 percent of the data) to the relationship between the average expression of a gene and its respective coefficient of variation (after normalizing each cell for complexity). Genes with high residuals (i.e., more variable than genes at comparable expression levels) were selected (approximately 1,000 genes).

Next, the expression matrix was normalized per cell (the sum of the number of transcripts for each cell is renormalized to 10,000), log₂ transformed with a pseudocount of 1 and the genes were Z-transformed. Randomized PCA was performed on the Z transformed expression matrix using Facebook’s implementation through the python package fbpca retaining the top 50 components.

A combination of the elbow method looking at the eigenvalue gap of each component, GO enrichment of each component using jackstraw (Chung and Storey, 2015) and a PC robustness analysis (in which increasing amounts of random noise is added to the data and the stability of each principal component with respect to the original components is evaluated) was used to determine the number of principal components to retain (which in general was approximately 10).

Clustering was performed using Infomap (Rosvall and Bergstrom, 2008) with k refined so that slightly more clusters are created than one would expect. Clusters are subsequently merged in an iterative fashion such that no pairwise comparisons between clusters have fewer than 100 differentially expressed genes (Shekhar et al., 2016). Differential expression is evaluated using a Welch’s t-test (adjusted for unequal variance) on the Z-transformed values between each cluster and the rest of the cells. A Benjamini-Hochberg FDR procedure (Benjamini and Hochberg, 1995) was used to control for multiple hypothesis testing. The clusters are evaluated for GO enrichment using FDR corrected p-values (see Interpretation of Results).

Relation of perturbed cells to unperturbed states

To define the relationship between the cell states in the unperturbed cells and the perturbed cells, we projected the perturbed cells onto the same significant principal component vectors derived from the unperturbed cells. The projection onto these components was used as a covariate by itself, especially with K562 cells, where the major axes of variation, such as cell cycle, describe more continuous processes. For BMDCs, discrete cell types are readily discernable. There, we trained a random forest classifier using class labels obtained by the merged Infomap clusters with features consisting of PC scores.

$$\mathit{\text{from sklearn}}.\mathit{\text{ensemble import RandomForestClassifier}}clf=\mathit{\text{RandomForestClassifier}}\mathit{(}n\_\mathit{\text{estimators}}=100,n\_\mathit{\text{jobs}}=-1,oob\_\mathit{\text{score}}=\mathit{\text{True}},\mathit{\text{class}}\_\mathit{\text{weight}}=\text{'}\mathit{\text{balanced}}\text{'}\mathit{)}$$

We used the out-of-bag probability estimates to generate ROC curves to determine the sensitivity and specificity of classification per cluster. Finally, the random forest was applied to the projected PC scores of the perturbed cells to obtain class membership predictions.

Tests of sgRNA effect on outputs other than gene expression

To evaluate the effect of an sgRNA on an output such as number genes detected, transcripts detected, or cell state, our regression framework is modified to predict these outputs instead of gene expression. The major modification is that the L₁ sparsity-inducing penalty is removed, resulting in ridge regression.

Fitness effects of sgRNAs

To assess the fitness effects of sgRNAs we obtained estimates of the initial abundances of each sgRNA in the pool. The initial abundance of each plasmid in the pool was quantified using NGS of the GBC. The GBC / sgRNA dictionary was used to convert the readout into a relative abundance estimate of sgRNA in the initial pool. Then, we calculated the fold change of the observed abundance of cells containing a particular sgRNA compared to its respective abundance in the original pool. This analysis is relevant to Figure S3E, S6A, and S6H.

To quantify the significance of these fold changes we developed a Bayesian probabilistic model that computes the expected probability of each guide in the resulting cell population. The model is based on the null hypothesis that the fitness effects of gene targeting guides is equivalent to the fitness effects of non-targeting or intergenic guides. Let M, d, f_g, and d_g,c denote the MOI, the overall guide detection rate, the frequency of guide g in the initial library, and the event of detecting guide g in cell c, respectively. We model the infection with guide g as a Poisson(f_g · M). To avoid effects of genetic interactions we compute the expected probability of each guide given that the cell was infected only with one guide and survived BFP selection.

$$P(d_{g,c}=1|\sum _g{d}_{g,c}=1,BFP)=\frac{e^{f_{g}Md}-1}{{\sum }_g(e^{f_{g}Md}-1)}$$

We then examine if the observed frequency of each guide in the pertaining cell subpopulation deviates from the expected frequency, compute a binomial p-value, correct for multiple hypotheses via Bonferroni correction, and report the significant findings.

Analysis of perturbation effects on individual genes and gene modules

The most variable genes from all each Perturb-Seq experiment were filtered by using the jackstraw approach (Chung and Storey, 2015) to identify the most significant genes (q-value < 0.01) in the top 20 PCs of the coefficient matrix. The genes were then clustered using k-means clustering by their coefficients. Optimal k was chosen by visual inspection of clustering results. Gene ontology (GO) enrichment analysis was performed on each cluster using goatools (Tang et al., 2015) with FDR threshold of 0.05.

Comparison to ChIP-seq binding profiles

We analyzed assignments of TF binding in gene promoters in BMDCs following LPS stimulation across four time points (0, 30, 60, and 120 minutes) (Garber et al., 2012). To test for significant binding, two tests were used. First, the regulatory coefficients of bound genes were compared to those of unbound genes using a non-parametric Mann-Whitney test to identify significantly different means. Because of the possibility that this significance was driven by skewed covariates from unbound genes, we also tested whether the coefficients of bound genes significantly deviated from 0, using the non-parametric one-sample Wilcox test. Finally, because TFs could both activate and repress genes, we examined the number of bound genes significantly up- or down-regulated. To do this, we used the distribution of covariates of unbound genes to define thresholds at the 5^th percentile of lowest negative and highest positive coefficients. Any bound genes with coefficients that surpassed the thresholds were considered significant. Between the set of genes with significant positive and negative coefficients, we used the larger set to infer whether the transcription factor was activating or inhibiting gene expression. Only BMDC expressed genes were considered in all ChIP-Seq analysis.

Power analysis and experimental design considerations

Power analysis was performed to determine how many cells are required to observe a signal as a function of observed effect size and baseline expression of a gene.

As an estimate of required read depth, we downsampled at the UMI level. For example, for a vector of gene expression for a cell with the following values: [2,0,1,6] we convert it into the following vector [1,1,3,4,4,4,4,4,4] on which downsampling is performed with equal probability without replacement. It is reconstructed into the original probability space by binning the observed integer counts. We also downsampled cells are without replacement from our observed set.

We performed our regression analysis on the downsampled expression matrix for various amounts of downsampling and recomputed resulting regulatory matrix. For each level of downsampling, 10 instances are averaged. We compared between the original regulatory matrix and the matrix that results after downsampling using either a Pearson correlation. For the supplementary figures, we thresholded the original regulatory matrix at the specified effect size and then calculated the sensitivity and specificity relationship for each downsampled regulatory matrix. We report the maximum sensitivity achievable if the false positive rate is kept under 10%.

Supplementary Material

1. Figure S1, related to Figure 1. Performance of Perturb-Seq.

(A–C) GBC detection and MOI. Top: Log-likelihood functions as a function of detection probability (X axis) and MOI (Y axis) for a zero-truncated zero-inflated Poisson distribution for the indicated experiment (label on top). Bottom: Cumulative distributions for the observed distribution of guides per cell (blue) and the expectation from the maximum likelihood estimate (green). (D) Specificity of GBC detection. Scatter plot shows the percentage of reads for a GBC within a given cell (CBC: cell barcode) (Y axis) as a function of the log₂(reads) it received in that cell (X axis). Low level contaminants are below the red line. (E) Same as D, after filtering out chimeric reads. (F) Relationship between the number of GBCs detected (X axis) and the number of genes detected for a given CBC (Y axis). Cells with multiple GBCs are not associated with higher number of transcripts, suggesting they are not doublets. (G) Distribution of on-target effects in BMDC at 3h post-LPS. Shown is the distribution of on-target expression (X axis) in cells carrying the corresponding targeting guides (blue) and permuted results for a single permutation (grey). Rectangle is the 99% confidence interval for the permuted mean. Mean on-target effects of individual guides are in tick marks, including one outlier exceeding even the permuted data. (H) Effect on target. Cebpb transcript expression (Y axis) in cells carrying an sgRNA targeting Cebpb (sgCebpb-1, right) compared to all other cells (left). Box plots denote outliers and three quartiles. (I) Relationship between overall mean expression of the on-target gene (X axis) and the observed effect on its expression (Y axis) by the guides that target it, in BMDCs at 3h post-LPS. (J,K) Relationship between population expression measurements and a 10-cell average (top) and a 100-cell average for BMDCs (J) and K562 cells (K). (L) Relationship between transcript length (X axis) and the difference between population expression and single cell average expression (Y axis).

6. Figure S6, related to Figure 6. Additional analysis of the role TFs and cell cycle regulators in K562 cells.

(A) Fitness effects of TF perturbations in K562 cells. Shown are the fold changes of sgRNA abundance compared to their input abundance (X axis) for the guides (dots) targeting each gene (Y axis). (B,C) TF control of transcriptional programs in K562 cells. Shown is the regulatory coefficient of each guide (labeled columns) on each gene (rows) based on a model that either does not (B) or does (C) account for cell states as covariates. Guides and genes are clustered by k-means clustering. Target programs are marked in (C) with key enriched annotations as discussed in the text. Green-white heatmap in C shows the enrichment of bound targets of each TF in each program (rows), based on either a lenient, genome-wide background (top) or a strict background (bottom) restricted only to the expressed genes in each program. (D) Cell cycle genes in our screen. Shown is the biological classification of our genes (Figure reproduced from (Neumann et al., 2010)). (E) Effects of perturbing cell cycle genes on transcriptional programs in K562 cells. Plot as in (B, C) but for the cell cycle regulators. (F) Pearson correlation (color bar) between the regulatory coefficients of each pair of guides for the cell cycle screen (rows, columns) in a model without cell state covariates (leftmost column: on-target effect). (G) Cell states in K562. Shown are enrichments −log₁₀(q-value) for GO gene sets (rows) in induced (red) and repressed (blue) genes in each of nine cell states (columns) defined for genetically unperturbed K562. Key terms are marked on right. (H) Fitness effects of cell cycle perturbations in K562 cells. Shown are the fold changes of sgRNA abundance compared to their input abundance (X axis) for the guides (dots) targeting each gene (Y axis).

7. Figure S7, related to Figure 7: Saturation analysis for differential expression.

(A) Theoretical probability p^k of having a successful perturbation in every target as a function of the number of perturbations k, assuming independence at different probability of detection (colors). (B–H and J–L) Saturation analysis. Shown is the effect of the fraction of cells per perturbation (Y axis) and transcripts per cell (X axis) on the sensitivity (color bar) to recover either the PCA scores (B–D), gene signature effects (E–H) or per-gene transcriptional effects (J–L) based on the BMDC 3h stimulated screen data. Heatmaps, from left to right, are conditioned on increasing effect sizes. The number of cells per perturbation (1.0) is a mean of 300 and a median of 155 and the number of transcripts per cell (1.0) is a median of 5,074. PCA scores were obtained by projecting the expression matrix Y onto the top 11 PCs defined by variability of expression in the unperturbed BMDC at 3hr. Effect size units are arbitrary units (A.U). For gene signatures, effects sizes are in units of average log₂(UMI) across the antiviral, peak inflammatory, sustained inflammatory, and maturity signatures defined in (Shalek et al., 2014). For an individual gene level, effect sizes are in units of log₂(UMI). The false positive rate is controlled to be less than 10% for all estimates of sensitivity. (I) Sensitivity (blue) and false positives (1-specificity, green) associated with downsampling cells compared to population RNA-seq. Shaded areas correspond to 1 s.d. intervals about the mean for 20 repeated subsamples (see also Figure S3F).

8. Table S1, Related to Figure 1: Summary statistics for each pool and sgRNAs.

Tab 1: Summary Statistics for each pool

Tab 2: sgRNAs for K562 TFs

Tab 3: sgRNAs for Cell cycle regulators

Tab 4: sgRNAs for BMDCs

Tab 5: sgRNA for K562 pooled cloning experiment

9. Table S2, related to Figure 3. Unperturbed cell states.

Tab 1: GO enrichment per state BMDC 3hr

Tab 2: GO enrichment per state BMDC 0hr

Tab 3: GO enrichment per state K562

Tab 4: Percentages of cells in different states BMDC 3hr

Tab 5: Percentages of cells in different states BMDC 0hr

Tab 6: Percentages of cells in different states K562 TFs

10. Table S3, related to Figures 3 and 4: Regulatory matrices for BMDC.

Tab 1: without modeling cell states, BMDC 3hr

Tab 2: with cell state covariates, BMDC 3hr

Tab 3: without modeling cell states, BMDC 0hr

Tab 4: with cell state covariates, BMDC 0hr

11. Table S4, related to Figure 6: Regulatory matrices for TFs in K562 cells.

Tab 1: without modeling cell states

Tab 2: with cell state covariates

12. Table S5, related to Figure 6: Regulatory matrices for cell cycle regulators in K562 cells.

Tab 1: without modeling cell states

13. Table S6, related to Figures 4, S4, S6: GO enrichment by program for each screen.

Tab 1: BMDC 0hr no cell states

Tab 2: BMDC 3hr without modeling cell states

Tab 3: BMDC 3hr after modeling cell states

Tab 4: K562 Transcription Factors after modeling cell states

Tab 5: K562 Cell cycle regulators without modeling cell states

2. Figure S2, related to Figure 2. Performance of MIMOSCA framework.

(A–C) Contribution of each component in the model (Y axis) to the % variance explained (X axis) based on the R² values from cross-validation in each of three screens (labeled on top). (D–F) Significance of regulatory coefficients. Shown are the distributions of signed log₁₀(q-value) for each of three sgRNAs (marked on top). Values capped at 3; Zero coefficients (due to shrinkage by regularization) have no assigned FDR. (G) Relationship between the number of cells carrying a given sgRNA (X axis) and the number of significant genes for each sgRNA (Y axis). One outlier guide (sgStat1–2) is marked and – while included for completeness in all subsequent plots – was not considered in any biological analysis. (H) Computational flowchart for MIMOSCA. Raw input data (orange) is processed into intermediate data types that require less (purple) or more intensive (green) analysis. Output data (blue) is generated and interpreted biologically. (I) Examination of the extent to which expression effects are consistent across thousands of genes for a given cell. Scatter plots show conceptual (left) and real (middle and right) examples of the total support (sum of squared error) for genes fit better when including the guide as a covariate (Y axis) and the support for genes fit better without including the guide as a covariate (X axis). Each dot is a cell. Conceptually (left column), cells in a pure population of perturbed (top) or in a well separated population of perturbed and unperturbed cells (middle) should be far from the diagonal line, whereas a poor performing guide (or a nontargeting control) (bottom) would have many cells close to the diagonal. Indeed, a guide targeting Rela in BMDC (3h post-LPS) (top middle and top right) has a distinguishable effect compared to a non-targeting guide (below) in a model without cell state covariates (middle) and even when considering cell states (right). Bottom middle and right plots: The mean deviation of cells from the x=y line (i.e., more deviation means stronger and more consistent effects) for each guide (X axis). Red line: the non-targeting control.

3. Figure S3, related to Figure 3. Analysis of the role of 24 TFs in BMDCs.

(A) Cell states in BMDCs pre-stimulation. Shown are enrichments (−log₁₀(q-value) for GO gene sets (rows) with induced (red) and repressed (blue) genes in each of four cell states (columns) defined for genetically unperturbed BMDC at 0h (pre-stimulation). Key terms are marked on right. (B) TFs group by their effects on cell state proportions pre-stimulation. Shown are the q-value for enrichment (red) or depletion (blue) of guides in cells with each of four states (columns; as in A). (C) Relationship between effects pre- and post-stimulation. Box plots comparing the correlations of regulatory coefficients between guides targeting the same gene within the 3hr LPS stimulated cells (light blue), within unstimulated cells (white), as well as across the two conditions, either without (dark blue) or with (blue) modeling cell states. (D) Distribution of number of detected transcripts per cell (X axis) for cells harboring guides targeting each gene (Y axis). (E) Assessing potential fitness effects. Shown is the distribution of fold changes of sgRNA abundance compared to the input abundance (X axis) for the guides (dots) targeting each gene (Y axis). (F) Perturb-Seq reliably recovers effects as in individual perturbation experiments followed by bulk RNA-Seq. False positive (X axis) and true positive (Y axis) rates based on comparing scRNA-seq profiles of Dad1 perturbations to population RNA-seq of the same perturbation calculated separated for upregulated (black) and downregulated (blue) genes. True positives are defined as those determined to have a q-value less than 0.05 in the population RNA-seq. False positives are those considered significant in the scRNA-seq in the opposite direction to what was found in the population RNA-seq.

4. Figure S4, related to Figure 4. Additional aspects of the regulatory circuitry of BMDCs.

(A) Relation between cell states and regulatory programs. Shown is the significance (−log₁₀(P-value) of the hypergeometric test) of the overlap between the expressed genes in each of the programs P1–P5 (as in Figure 4A) and the genes induced in each of the seven cell states of genetically unperturbed DCs at 3h post-LPS (as in Figure 3C). (B) TF control of transcriptional programs in BMDCs pre-stimulation (0h). Shown is the regulatory coefficient of each guide (labeled columns) on each gene (rows) based on a model that does not account for cell states as covariates. Guides and genes are clustered by k-means clustering. Four target programs are marked (P1–4, distinct from the programs of Figure 4A). Green-white heatmap shows the enrichment of bound targets of each TF (Garber et al., 2012) in each program (rows) based on either a lenient, genome-wide background (top) or a strict background (bottom) restricted only to the genes in the four programs. (C) Enrichment in bound targets of each TF in each BMDC post-LPS (3h) expression program (rows, see Figure 4A) based on a lenient, genome-wide background. (D) Relation between TFs and transcriptional programs in BMDCs at 3h post-LPS after accounting for cell states. Shown is the regulatory coefficient of each guide (labeled columns) on each gene (rows) based on a model that accounts for cell states as covariates. Guides and genes are clustered by k-means clustering. Five target programs (P1–5) are marked (distinct from the programs of Figure 4A).

5. Figure S5, related to Figure 6. A pooled cloning strategy for Perturb-Seq.

(A) Overview. Pooled cloning can be performed by oligo synthesis of an array of sgRNA (top) followed by a two-stage cloning protocol (bottom) to insert the library, sequence with next generation sequencing, and to insert the intervening sequence. (B) Application in K562 cells. Left: Pearson correlation (color bar) between the regulatory coefficients of each pair of guides (rows, columns) in a set targeting seven chromatin regulators in a model without cell state covariates (leftmost column: on-target effect). Right: Correlation in the effects between guides targeting the same gene (left, light grey) and different genes (right, dark grey).

HIGHLIGHTS.

• Pooled CRISPR screen with scRNA-seq readout

• Integrated model of perturbations, single cell phenotypes, and epistatic interactions

• Effect of TFs on genes, programs, and states in LPS response in immune cells

• Downsampling assessment of feasibility of genome-wide or combinatorial screens

In brief.

A technology combining single-cell RNA sequencing with CRISPR-based perturbations termed pertub-seq makes analyzing complex phenotypes at a large scale possible