Abstract
Motivation: Copy number variants (CNVs) have been implicated in a variety of neurodevelopmental disorders, including autism spectrum disorders, intellectual disability and schizophrenia. Recent advances in high-throughput genomic technologies have enabled rapid discovery of many genetic variants including CNVs. As a result, there is increasing interest in studying the role of CNVs in the etiology of many complex diseases. Despite the availability of an unprecedented wealth of CNV data, methods for testing association between CNVs and disease-related traits are still under-developed due to the low prevalence and complicated multi-scale features of CNVs.
Results: We propose a novel CNV kernel association test (CKAT) in this paper. To address the low prevalence, CNVs are first grouped into CNV regions (CNVR). Then, taking into account the multi-scale features of CNVs, we first design a single-CNV kernel which summarizes the similarity between two CNVs, and next aggregate the single-CNV kernel to a CNVR kernel which summarizes the similarity between two CNVRs. Finally, association between CNVR and disease-related traits is assessed by comparing the kernel-based similarity with the similarity in the trait using a score test for variance components in a random effect model. We illustrate the proposed CKAT using simulations and show that CKAT is more powerful than existing methods, while always being able to control the type I error. We also apply CKAT to a real dataset examining the association between CNV and autism spectrum disorders, which demonstrates the potential usefulness of the proposed method.
Availability and Implementation: A R package to implement the proposed CKAT method is available at http://works.bepress.com/debashis_ghosh/.
Contacts: xzhan@fhcrc.org or debashis.ghosh@ucdenver.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
CNVs are deletions and duplications of DNA segments in the genome, ranging in size from one kilobase (Kb) to several megabases (Mb), which represent the most common form of structural genetic variation in human genome (Lupski, 2007; Sebat et al., 2004). The advent of high-throughput technologies such as comparative genomic hybridization (CGH) and single nucleotide polymorphisms (SNPs) microarrays has enabled rapid discovery of genetic variants including CNVs (Carter, 2007; Girirajan et al., 2011a). As more and more CNVs have been detected throughout the human genome, there is a growing appreciation for studying their potential role in the etiology of many conditions and diseases, including autism spectrum disorders (ASD), intellectual disability, schizophrenia and many other neurodevelopment disorders (Girirajan et al., 2011b, 2013; Marshall et al., 2008; Sanders et al., 2011; Sebat et al., 2007). Understanding the relationship between CNVs and these diseases can contribute important new insights into the underlying genetics etiology and may further lead to effective means in prevention and treatments. A useful means to study the complex relationship between CNVs and human health conditions is through genetic association studies (Ionita-Laza et al., 2009; McCarroll and Altshuler, 2007; McCarroll, 2008; McCarthy et al., 2008).
A powerful mode of genetic association analysis is collapsing methods, which study the association between a group of genetic variants and traits. Such methods have been widely used in SNPs association analysis (Wu et al., 2010) and rare variants association analysis (Lee et al., 2014; Wu et al., 2011). However, these collapsing methods cannot be directly applied to CNV association analysis due to its unique features. First, SNPs are probe-based in that different subjects have the same loci genotyped. On the other hand, CNVs are sample-based in that different CNVs can be detected in different subjects. It is very common that a particular rare CNV is detected in few subjects while is absent in the rest. In other words, a typical SNP data matrix is a regular matrix while a CNV data matrix is irregular in that different rows (samples) have different length of columns (CNVs). A SNPs collapsing method usually combines multiple columns together for analysis. However, it is not clear how CNVs should be grouped together in the irregular data matrix. Second, It is more complicated to model the effect of CNVs than that of SNPs. SNPs usually takes values 0, 1, 2 (in an additive model) representing the copy of minor alleles. On the other hand, CNVs has multi-scale features including a start position, an end position and a type (deletion or duplication). Phenotypic heterogeneity (a deletion CNV and a duplication CNV can have different effects) are often observed. Also, it has been hypothesized that both CNV size (length) and CNV type (deletion or duplication) may affect the disease risk. Due to all these reasons, it is not straightforward to extend most current SNP or rare variant collapsing methods (Wu et al., 2010, 2011) to CNV association analysis.
One way to fix those aforementioned difficulties is to break the multi-dimensional CNV information into pieces, and to apply some collapsing methods on a certain piece. For example, the recent CNV collapsing random effects test (CCRET) (Tzeng et al., 2015) treats the length of CNV as fix effect, and the CNV dosage (copy number) as random effect of interest. To test for association with traits, kernel-based collapsing methods (Wu et al., 2010, 2011) can be easily applied to the CNV dosage (Tzeng et al., 2015). Despite its feasibility, the interpretation of this method may be slightly different from classical CNV association analysis. It is no longer the CNV effect on the disease risk, but the CNV dosage effect on the disease risk, conditioned on the CNV length. Alternatively, instead of breaking the multi-scale CNV information into pieces, the presence/absence analysis is often used in case–control studies. Typically, a contingency table is created based on counting whether a CNV is detected in a subject, and then a statistical test such as Fisher’s exact test (Agresti and Kateri, 2011), is applied to evaluate the association. This kind of analysis only utilizes the presence/absence information of a CNV and ignores other information, such as CNV type and size. Thus, neither CCRET nor Fisher’s exact test exploits the full information in a CNV.
In this study, to utilize both type and size information in a CNV, we propose the CNV kernel association test (CKAT). We first design a single-CNV kernel which accounts for the multi-scale features of a CNV. Intuitively speaking, the kernel is used as a similarity measure between two CNVs. To overcome low prevalence of CNVs, we pool CNVs together to form CNV regions (CNVRs) and carefully aggregate the single-CNV kernel to a CNVR kernel which describes the similarity between two CNVRs. Compared with a single CNV, more samples are likely to have CNVs detected in a region which can makes the CNVR kernel more informative. Finally, association between CNVR and the trait is tested by comparing the similarity in CNVRs (captured by the CNVR kernel) to that in the trait. In particular, the trait we considered in this paper is disease status. If the CNVR similarity between two patients (or two healthy controls) is consistently higher than the CNVR similarity between one patient and one healthy control, then it may suggest existence of association between the CNVR and the disease risk. Statistically speaking, the similarity comparison is evaluated in a logistic random effect model and the P-value for the association test is also analytically calculated via a variance component score test in the logistic regression framework. Using extensive simulation studies, we demonstrate that the proposed CKAT always has correct type I error rate and high power in a wide range of settings. Finally, the CKAT is applied to a real ASD data example which provides new insights and formal testing results for previous observations.
2 Materials and methods
2.1 Autism spectrum disorders data
All the CNV calls used in this study were generated from individuals with autism and typically developing controls using NimbleGen microarrays and processed as described previously (Girirajan et al., 2011b). A Hidden Markov model (HMM)-based CNV caller bundles up sets of consecutive probes and calls CNV if the region is greater than 2 SD (standard deviation) above the mean intensity for the chromosome (Day et al., 2007). Then post hoc analysis is to just check individual hotspots for events, where the hotspot regions are between 500 kbp and 5 Mbp in length and have genes that are known to be associated with neurological development based on previous studies (Itsara et al., 2009). The hotspot array can accurately detect CNVs > 50 kbp in the 120 genomic hotspots and >300 kbp CNVs in the rest of the genome. Both CNV datasets from the cohort of ASD patients and healthy controls are publicly available (Girirajan et al., 2011b). Specifically, the ASD cohort contains 1285 CNVs on 310 individuals, while the control data contains 1074 CNVs on 278 individuals. All CNVs are segmented and each CNV is characterized by three factors: start and end chromosomal position in a certain chromosome and type. The type variable is identified by HMM as either a deletion (copy number < 2) or a duplication (copy number > 2).
2.2 Kernels for CNVs
Kernels have been widely used as a similarity measure to construct statistical tests in genetics association studies (Liu et al., 2007, 2008; Wu et al., 2010, 2011; Zhan et al., 2015a,b). A typical kernel association test proceeds in the following way. First, an appropriate positive semi-definite kernel function is used to summarize the similarities between two (multi-dimensional) genetic variants x1 and x2. Then, this similarity on genotypes (captured by the kernel) is compared to the similarity in phenotypes (usually captured by the correlation coefficient if the phenotype is continuous) to test whether there is any association between genotype and phenotype. A high correspondence between genotypic similarity and phenotypic similarity may suggest existence of association. In those studies, it has been shown that a kernel is able to pool the information across multiple genetic variants and hence amplify the association signal between genotype and phenotype, which further leads to powerful tests (Wu et al., 2010, 2011). Motivated by this kind of strategy, we first design meaningful kernels which can appropriately summarize the similarity between two CNVs.
2.2.1 Single-CNV kernel
Let denote a CNV, where is length/size of the CNV which equals to end position minus start position, and is the type information of the CNV, taking values 1 (deletion CNV) and 3 (duplication CNV). Considering two arbitrary CNVs X1 and X2, we define the kernel function between two CNVs as
| (1) |
As mentioned before, is used to describe the similarity between X1 and X2. As defined in (1), both size and type of CNV contribute to the kernel similarity measure. The first term is the contribution from CNV size, which is described by a Gaussian kernel function. The second term is the contribution from CNV type. It has value 1 when two CNVs are of the same type and 0.5 otherwise. It is possible to replace 1 and 0.5 by other values, say a and b respectively. In principle, we require a > b to have a proper similarity function. Also, we expect b > 0; otherwise the contribution of CNV length would vanish when two CNVs are of different type. The size of a CNV, , can be in the order of thousands of base pairs. Even the size difference () can take a wide range of values. Compared with the second term, the first term can be really small. That is, the contribution from CNV size vanishes under such a scenario. Simulations have been conducted to study the effect of ρ and the results are reported in Section 2.1 of the Supplementary materials available online. Based on the simulation results, a large shape parameter is preferred if the disease risk is truly associated with CNV size. As long as the shape parameter is selected to be large, then the test may be no longer sensitive to the shape parameter. In practice, we operationally standardize the CNVR to [0,1] and set the shape parameter ρ = 1. Then, the two terms in (1) are comparable and the corresponding test is powerful in detecting both CNV type effect and CNV size effect in our numerical studies. Last, to appropriately describe similarities for association testing purpose, we usually need the kernel function to be positive semi-definite (Wu et al., 2010, 2011). A proof of this is included in the Supplementary materials available online.
2.2.2 CNVR kernel
Kernel-based association analysis are often conducted in the variant-set level rather than single variant level (Lee et al., 2014; Wu et al., 2010, 2011). Hence, kernel-based CNV association analysis should focus on CNVRs with multiple CNVs instead of a single CNV (Tzeng et al., 2015). There are two reasons for performing kernel association analysis at the CNVR level. First, kernels can summarize the similarity between samples in terms of their CNVs. We emphasize that the pairwise similarity is taken on two samples, not two CNVs. Unlike SNP data, which is probe-based, CNV data is sample-based, which means that different samples can have totally different CNV profiles. One sample may have 5 CNVs and another sample may have only 1 CNV. Then it is not clear what is the similarity between the two samples in terms of CNVs, because 5 single-CNV kernels can be calculated. Alternatively, a kernel compares the whole CNV profiles (such as all CNVs in a region) is preferred. Second, most CNVs are rare, and some even only can be found in a unique sample. In such a scenario, using a kernel to describe similarities between samples in terms of the rare single-CNV can be less informative. Considering CNVRs can pool all CNVs information in that region together, which further lead to higher power in detecting an existing association. This phenomenon has been widely observed in rare variant association studies (Lee et al., 2014; Wu et al., 2011), where the testing unit of association analysis is usually a set of rare variants. Therefore, we propose a CNVR kernel which describes the sample pairwise similarity between all CNVs in a CNVR.
Suppose the CNVR is pre-fixed, and let be the CNV profiles of sample i in that region, where are CNVs sorted according to their positions and pi is the number of CNVs in sample i in the region. Similarly, we have a corresponding CNVs series for another sample j. Then the CNVR kernel function between sample i and j in this particular region is defined as
| (2) |
where is the single-CNV kernel defined in (1). This CNVR kernel measures the one-to-one correspondence in the CNV sequences of two subjects. The maximum operation in the definition of searches for the best CNV-to-CNV correspondence in the CNV profiles of sample i and j in the CNVR. Other means (e.g. by taking average) of aggregating the single-CNV kernel to the CNVR kernel is also possible. Due to space limitations, we leave the question to future investigation.
As will be seen in the kernel association analysis section 2.3, in order to build an association test, we need to guarantee positive semi-definiteness of this new kernel , or equivalently, positive semi-definiteness of the corresponding kernel matrix K, where . It is possible that such a CNVR kernel matrix K may not be positive semi-definite. To overcome such a potential issue, we modify the kernel similarity matrix by reweighting the self-similarities (diagonal of the kernel matrix) while preserving the similarities between distinct sample pairs. In particular, let λmin be the smallest eigenvalue of K. If , we replace the kernel matrix with , where I is the identity matrix. Otherwise, we keep the kernel matrix, that is, . It is easy to see that the modified kernel matrix is always positive semi-definite and hence valid to be used in the kernel-based association analysis described in the following section.
2.3 Kernel-based association analysis
In this section we propose the CKAT for evaluating the association between disease status and CNVs. Notationally, let yi be the disease status with yi = 1 denoting the disease group and yi = 0 denoting the control group, where are subjects. Let be the CNVs within the CNVR from subject i. The following logistic regression model is used to relate the disease risk to CNVs
| (3) |
where Z are covariates such as age, gender, and is a centered unknown function in the space spanned by the CNVR kernel . Based on (3), the hypothesis of no association between disease and CNVs can be tested as . To test , one way is to treat the CNV effect vector as a random effect vector which is distributed as , where and K is the n × n CNVR kernel matrix. It can be seen from here that K is treated as covariance matrix of the random effect, which needs to be positive semi-definite. It has been shown that testing is equivalent to testing in the logistic mixed effect model (Liu et al., 2008), Moreover, τ is a variance component parameter in the logistic mixed effect model, which can be tested using a restricted maximum likelihood (REML)-based score test (Liu et al., 2008; Wu et al., 2010, 2011). Skipping technical details, the score test statistic is , where is estimated under the null model . Its asymptotic exact distribution (Chen et al., 2016) is used to calculate the test P-value.
2.4 Forming CNVR
A key aspect of the proposed CKAT approach is formation of a CNVR so that the global association between the CNVR and the disease risk can be tested. We emphasize that the proposed CKAT is essentially testing whether a CNVR is associated with the disease risk. The CNVR-based analysis can pool information across multiple CNVs to overcome the low prevalence of CNVs. A similar approach has been widely adopted in the rare variants literature (Lee et al., 2014; Wu et al., 2011).
Currently, there is no clear consensus on how to form CNVRs in the literature. Some suggestions of forming CNVRs are available in literature (Jeng et al., 2015; Tzeng et al., 2015). They largely depend on the conditions or requirements of the underlying methodology. For example, each CNVR formed in CCRET in Tzeng et al. (2015) corresponds to each column of the input matrices. The CNVR can have at most 1 CNV for each subject, otherwise it is not clear how to calculate those input matrices in their current CCRET methodology framework (Tzeng et al., 2015). The scanning procedure in Jeng et al. (2015) requires the region to be neither too short nor too long. By contrast, the CKAT method is more robust to formation of CNVRs. The CNVR in CKAT can contain any number of CNVs, and our testing procedure is robust to the CNVR size since it is standardized as [0,1] and we can adjust the shape parameter ρ to offset the effect of CNVR size if necessary. In this paper, we used the similar strategy as suggested in Tzeng et al. (2015) to form the CNVR by merging overlapped CNVs. Any two CNVs/CVNRs overlapped with each other for any amount of base pairs are grouped together until the rest CNVs/CNVRs are all disjoint. Other schemes are also possible but not pursued in this paper due to the limit of space.
As can be seen from model (3), under the null hypothesis , Ri does not affect the disease risk. In other words, CKAT is valid (in the sense of protecting the nominal type I error rate) irrespective of how the CNVR is formed. A ‘well-formed’ CNVR can enhance the interpretation of association testing results. For example, forming a CNVR based on prior biological knowledge may lead to scientifically meaningful results. Also, it can improve the statistical power of the test if the CNVR is formed properly. For instance, for some rare CNVs which are only detected in very few samples, a relative large CNVR containing those rare CNVs may improve the power of the association test if these rare CNVs are causal. However, it may also dilute the association signal when the added CNVs are noise variables. One way to address this is through adaptive testing (Pan et al., 2015; Zhan et al., 2015a), which is of importance and warrants further investigation.
2.5 Simulation
We conducted extensive simulation studies (using R statistical software) to assess the performance of CKAT and to verify that it can correctly control type I error and have relatively high power in detecting an existing association. We focused on the scenario of testing the association between disease status and CNVs in a pre-fixed CNVR. When multiple CNVRs were involved, depending on the purpose, one could either apply CKAT to each CNVR separately and then adjust for multiple testings, or combine all CNVRs as a new and huge CNVR for testing in CKAT. Without loss of generality, we assumed the CNVR to be the interval [0,1] throughout this simulation.
Besides CKAT, two other methods, the Fisher’s exact test (Agresti and Kateri, 2011) and the CCRET (Tzeng et al., 2015), were also studied. Ignoring the gene–intersection effects (which are not present in the dataset we considered in this paper), the CCRET evaluates the association between disease risk and CNV through the following model:
| (4) |
where is the disease risk, ZLen is the length of the CNV, DS denotes the dosage of the CNV (1 = deletion, 2 = normal, 3 = duplication, 4 = triplication, etc.). The parameter hDS is the random effect distributed as , and KDS is the genetic similarity matrix (linear kernel is used in CCRET) in terms of CNV dosage. Then, the CCRET uses a score test to examine . Since the format of the input matrix CCRET requires that each CNVR can contain at most one CNV, we compared CKAT to Fisher’s exact test and CCRET in two separate simulations denoted as Simulation I and Simulation II respectively, which are described in the following.
To mimic a real ASD dataset analyzed later in this paper, a total of 600 subjects were simulated with 300 cases and 300 controls. For subject , we randomly generated mi CNVs. Under Simulation I (CKAT versus Fisher’s exact test), mi took values 0, 1, 2, 3 with probabilities 0.6, 0.2, 0.1, 0.1 respectively. Under Simulation II (CKAT versus CCRET), mi took values 0, 1 with probabilities 0.8, 0.2 respectively. For each CNV, we randomly simulated two endpoints in the CNVR and treated the smaller one as the start position and the larger one as the end position. When under Simulation I, to avoid the overlap of different CNVs, we simulated endpoints and sorted them from smallest to largest. The first two endpoints formed the position information of the first CNV, the next two formed the second CNV, and so on. Finally, we randomly simulated a Bernoulli variable with success probability 0.5 as the type of each CNV.
After the CNVs were simulated, we generated the 0/1 group label yi from the following logistic model
| (5) |
where implies a prevalence of roughly 0.018 for ASD, is the jth CNV of the ith subject, and are the log of the odd ratio (OR) of CNV j for deletion and duplication respectively. and shared the same absolute values but might have different signs. For simplicity, we called a CNV risk-associated (R) if the associated or , protective (P) if the corresponding β-coefficient is smaller than 0, or neutral (N) on ASD if the corresponding β-coefficient equals 0.
Two different types (denoted by A and B) of CNVRs were considered in our simulations. Type A CNVR is homogeneous, and without loss of generality we assumed all CNVs are deletions. Type B CNVRs is heterogeneous, which contains both deletions and duplications with even probability. Both types of CNVRs are widely observed in practical scenarios. For a type A CNVR, the deletion CNV can be either R or P under the alternative model. For a type B CNVR, the effects of deletions and duplications have 8 possible scenarios (Del, Dup)= (R,R), (R,N), (R,P), (N,R), (N,P), (P,R), (P,N), (P,P). For ease of presentation, we only report powers under 4 scenarios (Del, Dup) = (R,R), (R,N), (R,P), (P,R). Results under other scenarios were similar and hence not reported.
Depending on comparisons between different methods and types of CNVRs, there are in total four different simulation scenarios: I-A, I-B, II-A and II-B. For each scenario, we assumed the effect size , where when it was a causal CNV (R or P) under the alternative model, and f = 0 when the CNV was neutral (N) under the null model. After the data was simulated, we compared CKAT with Fisher’s exact test under Simulation I-A and Simulation I-B, and compared CKAT with CCRET under Simulation II-A and Simulation II-B. For each simulation scenario, we simulated 105 datasets under the null model, and 103 datasets under the alternative model. Then type I error rate and power were calculated as the proportion of datasets with P-values smaller than the nominal significance level.
3 Results
3.1 Simulation I: CKAT versus fisher’s exact test
The QQ-plots of null P-values of CKAT and Fisher’s exact test under Simulation I-A are presented Figure 1. Those under Simulation I-B are almost identical and hence not reported. The type of CNVR does not make any difference under the null model, since both types of regions have zero effects. Based on the QQ-plot, CKAT is on top of the 45 degree line, which indicates that CKAT can always have the correct type I error rate under different nominal significance levels even as low as . On the other hand, Fisher’s exact test is a little conservative when the significance level is α is small. The fact that CKAT is able to have very small P-values with an appropriate probability is very desirable in genome-wide association studies (GWAS), which often requires very small P-values to achieve the whole-genome significance due to the heavy multiple testing adjustment burden.
Fig. 1.
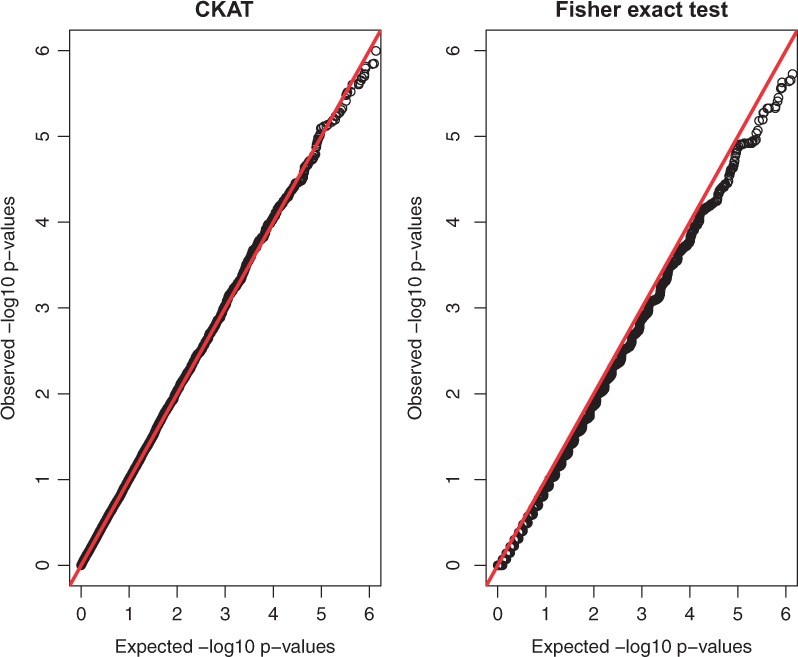
P-value based QQ plots of CKAT and Fisher’s exact test under Simulation I-A. The x axis represents expected P-values and the y axis represents observed P-values
The empirical powers of CKAT and Fisher’s exact test under two CNVR scenarios are presented in Figures 2 and 3 respectively. For ease of presenting, only was used as the nominal significance level. When the CNVR is homogeneous (Simulation I-A), CKAT has similar powers as Fisher’s exact test with both risk-associated CNVs or protected CNVs (Fig. 2). This is because every CNV is a deletion under Simulation I-A, and the type information does not affect disease risk based on (5) since the second term simply reduces to . The size information of CNVR is equivalent to the presence/absence information in that CNV size > 0 is equivalent to presence of the CNV. In this sense, both CKAT and Fisher’s exact test utilize the similar information which determines the disease risk πi, and hence have similar powers. When the CNVR is heterogeneous (Simulation I-B), the power patterns of two methods can be different. If two types of CNV have the same direction of effect, then CKAT still has similar powers as the Fisher’s exact test, as observed at the top left panel in Figure 3. Due to our simulation design, if they have the same sign. Hence, in (5) reduces to or since . Then this is similar to Simulation I-A where the type information of CNV does not affect the disease risk, and CKAT and Fisher’s exact test again have similar powers. However, we can see that CKAT can be much more powerful than Fisher’s exact test when different types of CNVs have different signs. This is because, under such a scenario, the type information of the CNV makes a difference in disease risk. Failing to account for this information leads to power loss in the Fisher’s exact test.
Fig. 2.
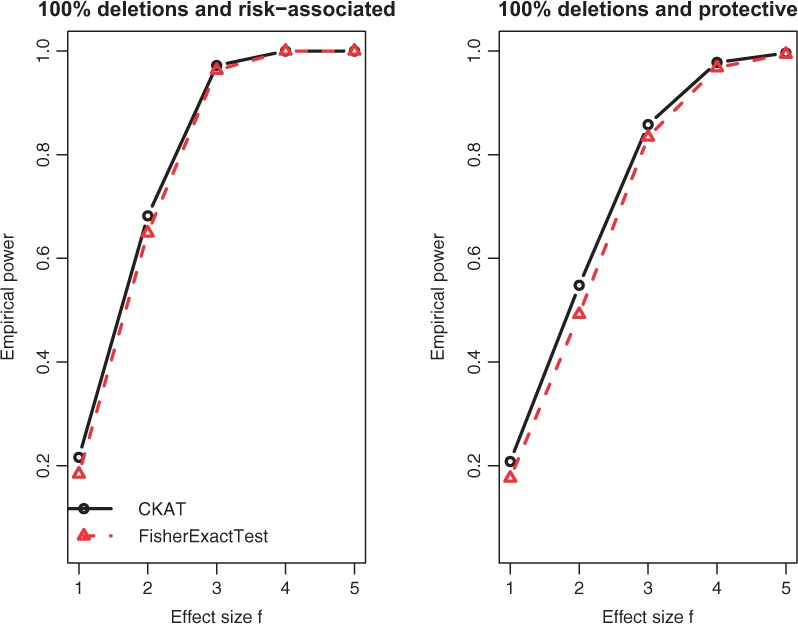
Empirical power of CKAT and Fisher’s exact test under Simulation I-A. The solid line is for CKAT and the dotted line is for Fisher’s exact test
Fig. 3.
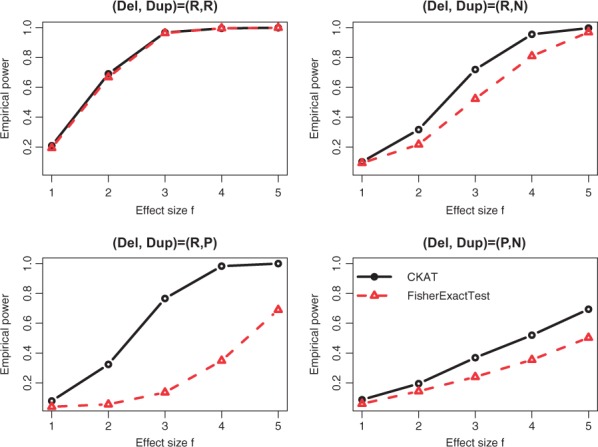
Empirical power of CKAT and Fisher’s exact test under Simulation I-B. The solid line is for CKAT and the dotted line is for Fisher’s exact test
3.2 Simulation II: CKAT versus CCRET
The QQ-plots of null P-values of CKAT and CCRET under Simulation II-A are presented Figure 4. Those under Simulation II-B are almost identical and hence not reported. As shown in the figure, both CKAT and CCRET can protect the correct type I error rate at different nominal significance levels.
Fig. 4.
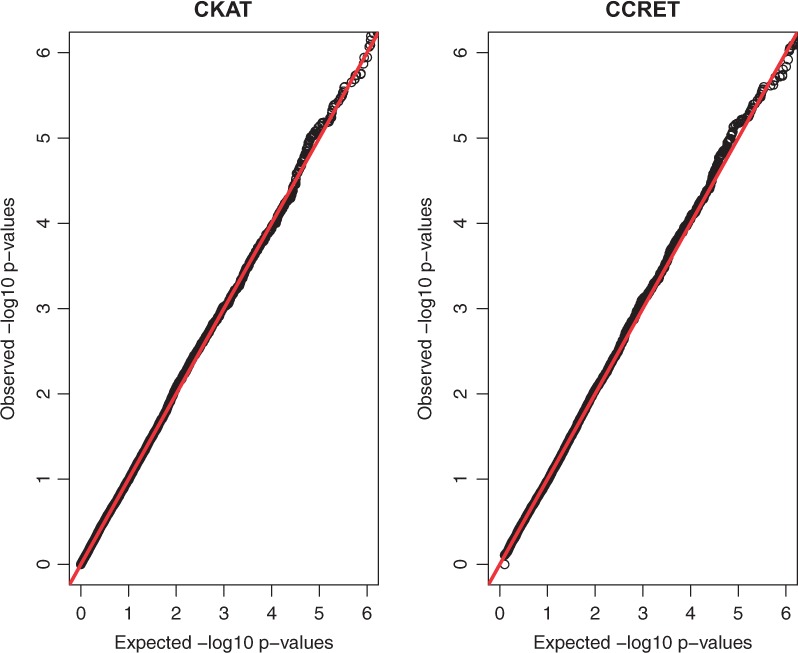
P-value based QQ plots of CKAT and CCRET under Simulation II-A. The x axis represents expected P-values and the y axis represents observed P-values
The empirical powers of CKAT and CCRET under two CNVR scenarios are presented in Figures 5 and 6 respectively. Under the homogeneous CNVR scenario, model (5) reduces to . The dosage/type variable has no effect on disease risk πi at all. Hence, the CCRET model has no testing power for under Simulation II-A. On the other hand, CKAT assumes a different model as , and it is robust to detect either CNV type effect or CNV size effect. A similar argument can explain the same phenomenon observed under the Simulation II-B (R,R) scenario. Under other scenarios of Simulation II-B, can affect πi. Hence CCRET starts to gain power, and seems to be comparable with CKAT depending on whether the main effect (of type and size) or the interaction effect dominates. From all power comparisons in Figures 5 and 6, we can see that CKAT is more robust to the underlying CNV-effect pattern compared with CCRET in that it can always have good powers under each scenario. Finally, one can observe that powers under Simulation I are much higher than those under Simulation II. This is because there are more CNVs in the CNVR in Simulation I than Simulation II. Under such a scenario, CKAT can be more powerful since more information can be pooled and further leads to amplification of the association signal.
Fig. 5.
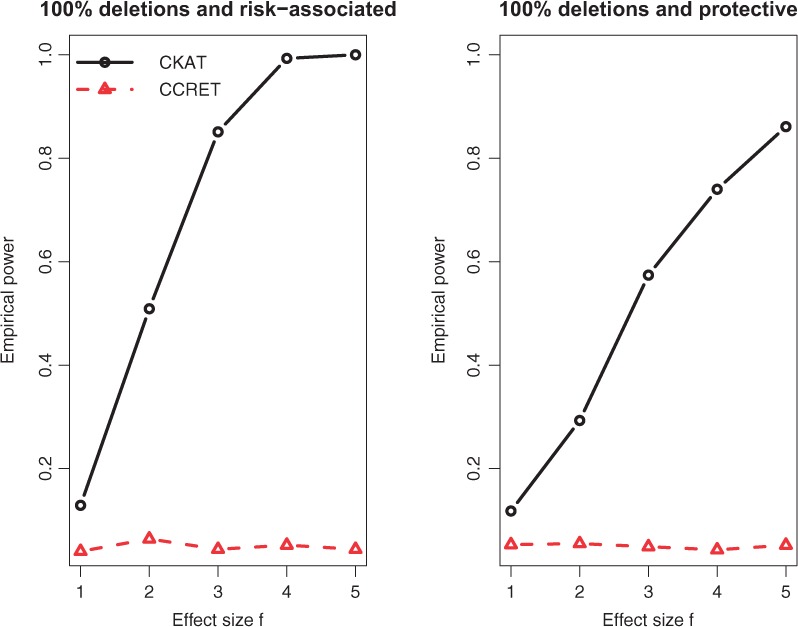
Empirical power of CKAT and CCRET under Simulation II-A. The solid line is for CKAT and the dotted line is for CCRET
Fig. 6.
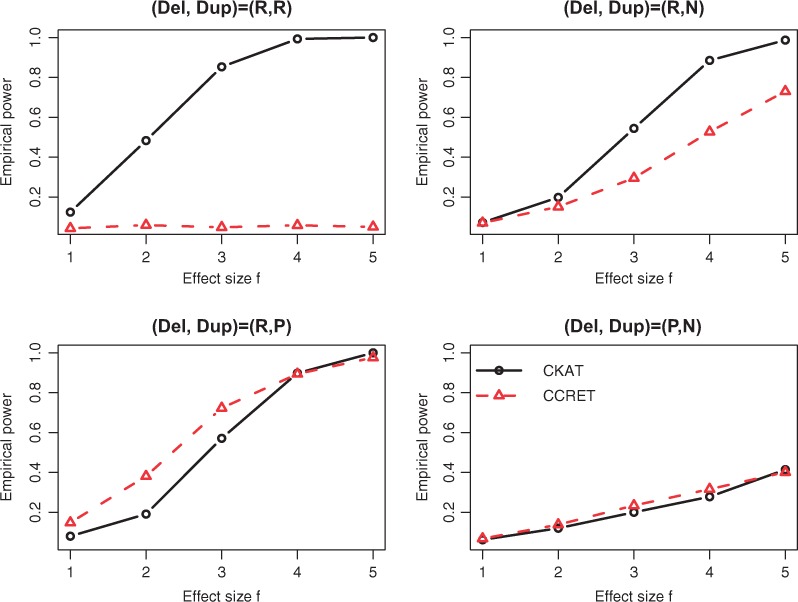
Empirical power of CKAT and CCRET under Simulation II-B. The solid line is for CKAT and the dotted line is for CCRET
3.3 Real data analysis
A total of 2359 CNVs was detected in both ASD samples and healthy controls in the original study (Girirajan et al., 2011b). Most of those CNVs were large (>50 kbp in hotspot and >300 kbp in the rest of genome) and rare (frequency < 1%). Hence, it is important to perform the CKAT analysis in a proper CNVR to pool information of rare CNVs together in order to gain statistical power to detect true association signals. We first treat each chromosome as a CNVR. Next, we picked one chromosome as an illustratory example and further partitioned it into multiple smaller CNVRs by merging overlapped CNVs. Other schemes of forming CNVR (e.g. prior biological knowledge) is also possible but not explored here. Finally, we conducted the proposed CKAT analysis on each CNVR to test the association between CNVs in the CNVR and ASD. The P-values of CKAT, Fisher’s exact test and CCRET are reported in Table 1. Bonferroni correction is used for multiple testing adjustment to control the family-wise error rate (FWER) of . Hence, the P-value threshold for a whole-genome (i.e. across all chromosomes) significance is , where 23 is the total number of CNVRs being tested (no CNVs were detected on Chromosome 21 in this ASD data, and hence were not tested).
Table 1.
Testing P-values of association between ASD and CNVs in each chromosome
| Chromosome | #CNVs | CKAT | Fisher’s exact | CCRET |
|---|---|---|---|---|
| chr1 | 175 | 8.2e-2 | 3.1e-1 | 3.5e-2 |
| chr2 | 45 | 1.7e-4 (*) | 4.3e-4 (*) | 2.4e-2 |
| chr3 | 49 | 0 (*) | 1.8e-14 (*) | 1 |
| chr4 | 112 | 8.2e-1 | 8.3e-1 | 8.6e-1 |
| chr5 | 242 | 2.3e-2 | 2.3e-2 | 9.4e-2 |
| chr6 | 17 | 1.2e-4 (*) | 3.4e-5 (*) | 1 |
| chr7 | 25 | 1.2e-4 (*) | 1.4e-4 (*) | 3.1e-2 |
| chr8 | 3 | 0.1e-1 | 2.5e-1 | 1 |
| chr9 | 13 | 7.7e-1 | 7.8e-1 | 2.1e-1 |
| chr10 | 130 | 4.7e-1 | 3.3e-1 | 4.2e-1 |
| chr11 | 257 | 8.8e-1 | 8.0e-1 | 5.6e-1 |
| chr12 | 3 | 2.7e-1 | 6.1e-1 | 1.1e-1 |
| chr13 | 5 | 7.4e-1 | 1 | 3.2e-1 |
| chr14 | 2 | 1.8e-1 | 5.0e-1 | 1 |
| chr15 | 919 | 5.4e-1 | 2.6e-1 | 1 |
| chr16 | 140 | 3.7e-1 | 8.4e-1 | 6.0e-2 |
| chr17 | 27 | 2.3e-3 | 4.5e-3 | 2.4e-1 |
| chr18 | 6 | 1 | 1 | 1 |
| chr19 | 17 | 3.2e-2 | 8.0e-2 | 3.5e-2 |
| chr20 | 3 | 1.3e-1 | 2.5e-1 | 3.0e-1 |
| chr21 | 0 | NA | NA | NA |
| chr22 | 166 | 0 (*) | 1.3e-21 (*) | 3.0e-1 |
| chrX | 2 | 1.4e-2 | 2.2e-1 | 1 |
| chrY | 1 | 2.9e-1 | 4.7e-1 | 1 |
# denotes the number of CNVs on that chromosome, 1.0e-2 stands for , and (*) denotes significance after Bonferroni adjustment at family-wise error rate (FWER) of 0.05.
As one can see from Table 1, CCRET is less powerful and cannot detect any significant regions in this data example. This is because information pooling in CCRET is performed across different CNVRs, and it requires dense CNV genotyping arrays to guarantee a high power. In this dataset, because large and rare CNVs were studied (Girirajan et al., 2011b), we tested each chromosome as a CNVR. Hence, CCRET is less powerful. On the other hand, CKAT is more robust with respect to the CNVRs in that it can pool information across multiple CNVs in an arbitrarily region. It can also been seen from Table 1 that both CKAT and Fisher’s exact test detect five significant CNVRs after multiple testing. The performance of CKAT and Fisher’s exact test are close in this ASD data. This is because CNVs in the ASD data are relatively large and rare (Girirajan et al., 2011b) and previous studies indicated that large CNVs tends to be more homogeneous in the effect of disease risk as more causal genes might be impacted (Tzeng et al., 2015). As shown in the left top panel of Figure 3, when the effects of deletions and duplications are homogeneous, both CKAT and Fisher’s exact test are very powerful. It also partially explains why CCRET has low power according to the left top panel of Figure 5 under the homogeneous effect scenario. Even though CKAT and Fisher’s exact test detect the same significant CNVRs at FWER = 0.05, the P-values of CKAT tend to be smaller than those of Fisher’s exact test, which is consistent with the observation we have made in Figure 1. This could be a potential advantage of CKAT. Also, as shown in Figure 3, for other types of datasets where deletions and duplications have different directions of effect on the disease-risk, CKAT is expected to be much more powerful than Fisher’s exact test.
Of the five significant chromosomes in Table 1, Chromosome 22 was picked for further association analysis. That is, we partitioned Chromosome 22 into smaller CNVRs to further study the association between those CNVRs and autism. The reason of choosing Chromosome 22 is because that it has the most CNVs among those most significant chromosomes. We formed new smaller CNVRs in Chromosome 22 by merging overlapped CNVs. Any two CNVs overlapping with each other were clustered together as a CNVR, and we expanded this CNVR until no more CNVs were overlapped with it. Under this scheme, five mutually disjoint CNVRs were formed (see column 1 in Table 2). For each CNVR, CKAT was applied to test for association with autism. Based on the results reported in Table 2, two regions were detected as significantly associated with autism at FWER = 0.05 level. One significant region (chr22:17258338-19800553) is within the chromosome band 22q11.21 (chr22:16300001-20500000), which has been widely identified as associated with autism (Girirajan et al., 2011b; Glessner et al., 2009). The other significant region (chr22:20645784-23362762) has not been widely linked to ASD. However, the ADORA2A gene (chr22:23153530-23168325) within this region may increase the risk of ASD (Freitag et al., 2010).
Table 2.
CKAT testing results of CNV regions in chromosome 22
| Region | # of CNVs | CKAT P-value |
|---|---|---|
| chr22:16146386-16261271 | 1 | 3.4e-1 |
| chr22:17258338-19800553 | 23 | 5.3e-5 (*) |
| chr22:20645784-23362762 | 138 | 0 (*) |
| chr22:26924167-27361980 | 3 | 1.0e-1 |
| chr22:38790464-39138992 | 1 | 3.4e-1 |
# denotes the number of CNVs in that region and (*) denotes significance after Bonferroni adjustment at family-wise error rate (FWER) of 0.05.
To summarize, the proposed CKAT can evaluate the global association between all CNVs within a pre-specified regions and the disease-risk. In previous studies, disease associated CNVs are usually identified based on qualitative observations (Girirajan et al., 2011b). That it, putative CNVs or regions are picked as enrichments in disease patients compared to healthy controls. On the other hand, the proposed CKAT can provide a flexible and formal statistical testing for the data, which can bring new insights for previous studies. Although the sample size and the number of CNVs in the ASD dataset is modest, the application of CKAT to larger datasets and other disease-related traits has the potential to detect putative genes or regions which are associated with the traits.
4 Discussion
We have proposed the CKAT to evaluate the association between CNVs and disease-related traits. The kernel implemented in CKAT is elaborately designed so that it can capture special features of CNVs, such as multi-dimensionality (type and size) and heterogeneity effects. The kernel (1) is defined in a rather ad hoc fashion. Extra evaluations of the kernel and also comparisons with other similar kernels are available in Section 2.2 of the online Supplementary materials. However, we do not pursue an optimal CNV kernel choice in this paper. After the kernel is designed, we then apply the kernel strategy in the literature (Wu et al., 2010, 2011) to test the association between CNVR and disease-related outcomes. Simulation studies show that CKAT can always protect the type I error and have higher power than existing methods under a wide range of scenarios. Finally, CKAT is illustrated with a real data examining the association between CNV and autism. Many CNV regions are detected as significantly associated with ASD. Taking Chromosome 22 as an example, two regions are detected by CKAT. One has a well-established association with ASD in previous studies. The other contains a putative genes, ADORA2A, which might be functionally related to ASD. Further work is needed to understand the biological and genetic mechanisms of the region on ASD.
The proposed CKAT calculates the P-value of the association test analytically, which is computationally efficient and flexible for CNV association analysis, as demonstrated in our numerical studies. Compared with existing methods, it always has adequate power for detecting an existing association. Moreover, CKAT also has good performance when the nominal significance level of the test is extreme, which makes it a desirable tool in genome-wide association analysis where multiple testing burden is usually very high. Besides serving as a useful tool in CNV association analysis, the way of incorporating both CNV length information and CNV type information in the CNV kernels can be also extended to pooling information from different data types. For example, gene-intersection (GI) is often considered as an important feature of CNV (Tzeng et al., 2015). One can incorporate GI into the CNV kernel by using an appropriate kernel for GI and multiple it to existing single-CNV kernel in (1). Given the increasing availability of genome-wide information from different data sources, this mode of analysis can shed light on integrative genomics across multiple platforms in the foreseeable near future.
Supplementary Material
Acknowledgements
We thank three reviewers for helpful comments.
Funding
This work has been supported by NIH grants R01HG007508, U10CA180819 and the Hope Foundation (for MCW), NIH Grants R01GM117946 (for DG).
Conflict of Interest: none declared.
References
- Agresti A., Kateri M. (2011). Categorical Data Analysis. Springer, Berlin Heidelberg. [Google Scholar]
- Carter N.P. (2007) Methods and strategies for analyzing copy number variation using DNA microarrays. Nat. Genet., 39, S16–S21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J. et al. (2016) Small sample kernel association tests for human genetic and microbiome association studies. Genet. Epidemiol., 40, 5–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day N. et al. (2007) Unsupervised segmentation of continuous genomic data. Bioinformatics, 23, 1424–1426. [DOI] [PubMed] [Google Scholar]
- Freitag C.M. et al. (2010) Adenosine A2A receptor gene (ADORA2A) variants may increase autistic symptoms and anxiety in autism spectrum disorder. Eur. Child Adolesc. Psychiatry, 19, 67–74. [DOI] [PubMed] [Google Scholar]
- Girirajan S. et al. (2011a) Human copy number variation and complex genetic disease. Annu. Rev. Genet., 45, 203–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girirajan S. et al. (2011b) Relative burden of large CNVs on a range of neurodevelopmental phenotypes. PLoS Genet., 7, e1002334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girirajan S. et al. (2013) Refinement and discovery of new hotspots of copy-number variation associated with autism spectrum disorder. Am. J. Hum. Genet., 92, 221–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glessner J.T. et al. (2009) Autism genome-wide copy number variation reveals ubiquitin and neuronal genes. Nature, 459, 569–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ionita-Laza I. et al. (2009) Genetic association analysis of copy-number variation (CNV) in human disease pathogenesis. Genomics, 93, 22–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itsara A. et al. (2009) Population analysis of large copy number variants and hotspots of human genetic disease. Am. J. Hum. Genet., 84, 148–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeng J. et al. (2015) A statistical method for identifying trait-associated copy number variants. Hum. Hered., 79, 147–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S. et al. (2014) Rare-variant association analysis: study designs and statistical tests. Am. J. Hum. Genet., 95, 5–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D. et al. (2007) Semiparametric regression of multidimensional genetic pathway data: least-squares kernel machines and linear mixed models. Biometrics, 63, 1079–1088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D. et al. (2008) Estimation and testing for the effect of a genetic pathway on a disease outcome using logistic kernel machine regression via logistic mixed models. BMC Bioinformatics, 9, 292.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lupski J.R. (2007) Genomic rearrangements and sporadic disease. Nat. Genet., 39, S43–S47. [DOI] [PubMed] [Google Scholar]
- Marshall C.R. et al. (2008) Structural variation of chromosomes in autism spectrum disorder. Am. J. Hum. Genet., 82, 477–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarroll S.A., Altshuler D.M. (2007) Copy-number variation and association studies of human disease. Nat. Genet., 39, S37–S42. [DOI] [PubMed] [Google Scholar]
- McCarroll S.A. (2008) Extending genome-wide association studies to copy-number variation. Hum. Mol. Genet., 17, R135–R142. [DOI] [PubMed] [Google Scholar]
- McCarthy M.I. et al. (2008) Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat. Rev. Genet., 9, 356–369. [DOI] [PubMed] [Google Scholar]
- Pan W. et al. (2015) A powerful pathway-based adaptive test for genetic association with common or rare variants. Am. J. Hum. Genet., 97, 86–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders S.J. et al. (2011) Multiple recurrent de novo CNVs, including duplications of the 7q11. 23 Williams syndrome region, are strongly associated with autism. Neuron, 70, 863–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebat J. et al. (2004) Large-scale copy number polymorphism in the human genome. Science, 305, 525–528. [DOI] [PubMed] [Google Scholar]
- Sebat J. et al. (2007) Strong association of de novo copy number mutations with autism. Science, 316, 445–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzeng J.Y. et al. Swedish Schizophrenia Consortium. (2015) A new method for detecting associations with rare copy-number variants. PLoS Genet., 11, e1005403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu M.C. et al. (2010) Powerful SNP-set analysis for case–control genome-wide association studies. Am. J. Hum. Genet., 86, 929–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu M.C. et al. (2011) Rare-variant association testing for sequencing data with the sequence kernel association test. Am. J. Hum. Genet., 89, 82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan X. et al. (2015a) An adaptive genetic association test using double kernel machines. Stat. Biosci., 7, 262–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan X. et al. (2015b) Kernel approaches for differential expression analysis of mass spectrometry-based metabolomics data. BMC Bioinformatics, 16, 77.. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


