Joint sparse canonical correlation analysis for detecting differential imaging genetics modules

Abstract

Motivation: Imaging genetics combines brain imaging and genetic information to identify the relationships between genetic variants and brain activities. When the data samples belong to different classes (e.g. disease status), the relationships may exhibit class-specific patterns that can be used to facilitate the understanding of a disease. Conventional approaches often perform separate analysis on each class and report the differences, but ignore important shared patterns.

Results: In this paper, we develop a multivariate method to analyze the differential dependency across multiple classes. We propose a joint sparse canonical correlation analysis method, which uses a generalized fused lasso penalty to jointly estimate multiple pairs of canonical vectors with both shared and class-specific patterns. Using a data fusion approach, the method is able to detect differentially correlated modules effectively and efficiently. The results from simulation studies demonstrate its higher accuracy in discovering both common and differential canonical correlations compared to conventional sparse CCA. Using a schizophrenia dataset with 92 cases and 116 controls including a single nucleotide polymorphism (SNP) array and functional magnetic resonance imaging data, the proposed method reveals a set of distinct SNP-voxel interaction modules for the schizophrenia patients, which are verified to be both statistically and biologically significant.

Availability and Implementation: The Matlab code is available at https://sites.google.com/site/jianfang86/JSCCA.

Contact: wyp@tulane.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Imaging genetics is an emerging field of study in brain research (Hariri et al., 2006; Meyer-Lindenberg, 2012). It aims to discover genetic variants that explain brain activities, providing more comprehensive information that can hopefully inform the diagnosis and treatment of mental disorders (e.g. schizophrenia). To date, imaging and genomic data are collected and both modalities include a large number of variables. However, how to combine the large amount of multi-modal data remains a challenging problem.

Canonical correlation analysis (CCA) (Hotelling, 1936) and partial least squares (PLS) (Wold, 1985) are common multivariate approaches to integrate two or more data types. The basic idea is to maximize the correlation (or covariances in PLS) between linear combinations of variables from different data types to find the components that are associated with each other. Kernel CCA (Lai and Fyfe, 2000; Larson et al., 2014) and deep CCA (Andrew et al., 2013) are extensions to extract nonlinear correlation between two datasets. However, in genomic and brain imaging studies, the dimension of the data is usually much higher than the sample size. As a result, severe overfitting can occur when conventional CCA methods are applied. To address this problem, penalized CCA and related methods were introduced by employing sparse penalties to select a small number of features. Examples include sparse CCA (Parkhomenko et al., 2009; Witten and Tibshirani, 2009), sparse PLS (Chun and Keleş, 2010) and sparse reduced rank regression (Vounou et al., 2010), which have been demonstrated to be effective in detecting multivariate genomic and brain imaging associations (Grellmann et al., 2015; Liu and Calhoun, 2014). To incorporate biological prior knowledge and data structures to guide the search of associations, group SCCA (Lin et al., 2014) and network-guided sparse reduced rank regression (Wang et al., 2014) were proposed, which can further improve variable selection.

In all the above methods, a common assumption is that the data are collected from the same distributions. However, in real imaging genetic studies, the data are collected from subjects corresponding to different disease statuses (e.g. the schizophrenia patients and healthy controls). A separate estimation will suffer a lack of power due to the limited size of each individual class, but a simple combination of the data may miss the identification of the heterogeneity of the interactions. Therefore, it is desirable to discover both the common and class-specific interactions simultaneously by joint analysis of multi-class data. In (Chen et al., 2013), a statistical method was proposed to jointly study miRNA-gene interactions from multiple cancers. However, this method is restricted to univariate inference that is not able to detect complex multivariate correlations. A challenge was also recognized in (Chen et al., 2013) that the direct application of sparse multivariate methods may choose different sets of interaction pairs for each class. Especially for sparse CCA, similar patterns may appear in different orders, leading to the problem of mismatch during joint analysis across classes.

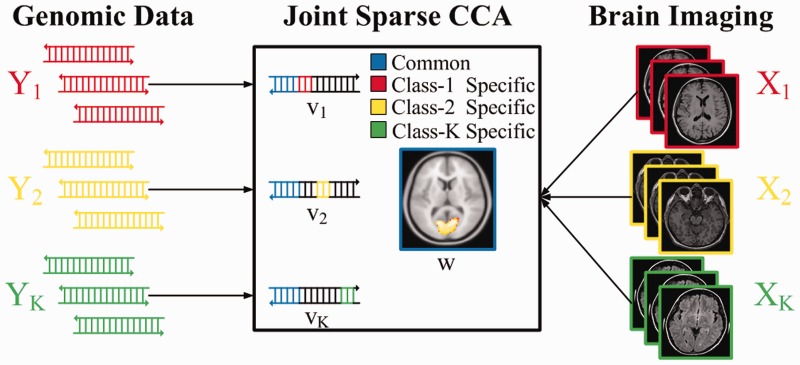
In this paper, we propose a novel sparse CCA method to jointly estimate multiple CCA models corresponding to different classes. As illustrated in Figure 1 with two types of data from K classes, the main idea is to find a common sparse linear combination of the variables from one type of data (for example the imaging data) and K joint sparse linear combinations from the other type (e.g. the genomic data) to maximize the summed correlation. In this way, the method can obtain the brain regions that are important for all classes and discover their differential interactions with the genetic variants. Specifically, by restricting the imaging canonical variables to be common across classes, the method overcomes the problem of mismatch that can make full combination of the data from multiple classes (see Fig. 1). We also apply a fused lasso penalty on the K canonical vectors for genetic data to encourage them to share a similar (but not the same) structure. The fused lasso penalty is chosen because it has been successfully applied to jointly estimate multiple graphical models to find differential dependency networks (Danaher et al., 2014; Tian et al., 2014; Yang et al., 2015). Inspired by the optimization framework for penalized CCA in (Witten et al., 2009), we design an efficient algorithm based on block coordinate descent for solving JSCCA. The JSCCA is featured as a multivariate method for joint interactions analysis, promising to detect complicated abnormal interaction modules between genomic variants and brain activities. We first apply the proposed method to the simulation data containing three classes. Through a comprehensive comparison, we demonstrate the effectiveness of JSCCA in discovering both shared and class-specific correlations. Next, we apply the JSCCA method to a schizophrenia dataset with 92 cases and 116 controls. The data include functional magnetic resonance imaging (fMRI) and single-nucleotide polymorphism (SNP) data, collected by The Mind Clinical Imaging Consortium (Gollub et al., 2013). We found a number of SNP-voxel modules with significantly increased correlation for schizophrenia patients.

Fig. 1.

An illustration of the JSCCA method for detecting differential imaging genetics modules. The method finds a common sparse set of voxels and K joint sparse set of SNPs to maximize the summed correlation. The SNP is selected in the kth class only if it is highly correlated with the voxels. Therefore, the class specific SNPs have potentially higher interactions with the detected voxels (Color version of this figure is available at Bioinformatics online.)

The rest of the paper is organized as follows. Section 2 introduces the joint sparse CCA method. The performance of the proposed method is evaluated through both simulations and real data analysis in Section 3, followed by some discussions and concluding remarks in the last section.

2 Methods

2.1 Sparse CCA

The CCA is a method that determines the associations between two datasets. More specifically, given datasets $X\in {\mathcal{R}}^{n\times p},Y\in {\mathcal{R}}^{n\times q}$ with n samples, where X has p features and Y has q features, the CCA method aims to find linear combinations of variables in X and Y to maximize the correlation:

$$\underset{w,v}{\max }{w}^T{X}^{T}Yv\text{\hspace{0.5em}\hspace{0.5em}s}.\text{t}.w^T{X}^{T}Xw=v^T{Y}^{T}Yv=1,$$ (1)

where we assume that the columns of X and Y are standardized to have zero mean and unit variance, and w, v are the corresponding canonical vectors.

However, in genomic and bio-imaging applications, the dimension of the data is much higher than the sample size. The (1) model tends to overfit and does not yield desirable results. To circumvent this problem, sparse CCA has been proposed in recent years. By imposing sparse regularization on the canonical vectors, sparse CCA can achieve better model fitting with variable selection. In this paper, we adopt the formulation in (Witten and Tibshirani, 2009) with L₁ regularization as follows:

$$\underset{w,v}{\min }-w^T{X}^{T}Yv+\lambda w\left|\right|w|{|}_1^1+\lambda v|\left|v\right|{|}_1^1\text{\hspace{0.5em}s}.\text{t}.\left|\right|w\left|\right|2=\left|\right|v\left|\right|2=1,$$ (2)

where λ_w and λ_v are the regularization parameters. In (2), the variance matrix of X and Y is treated as diagonal matrix, which has shown to be effective and efficient for high-dimensional data (Grellmann et al., 2015; Witten and Tibshirani, 2009).

2.2 Joint sparse CCA (JSCCA)

In this paper, we consider how to perform multivariate association analysis of K classes of normalized data, $Xk\in {\mathcal{R}}^{nk\times p},Yk\in {\mathcal{R}}^{nk\times q},k=1,\dots ,K$, where n_k is the number of observations in the kth class. As described in the introduction and Figure 1, the main idea is to jointly estimate CCA models belonging to multiple classes with one common canonical vector for X and K related sparse canonical vectors for Y. More formally, the joint sparse CCA model is given by:

$$\begin{array}{cc}{\displaystyle \underset{w,v}{\min }}& -{\displaystyle \sum _{k=1}^K\frac{1}{nk}}{w}^T{X}_k^{T}Ykvk+\lambda w\left|\right|w|{|}_1^1\\ & +{\displaystyle \sum _{k=1}^K\lambda v}\left|\right|vk|{|}_1^1+{\displaystyle \sum _{k<k\prime }\tau }||vk-vk\prime |{|}_1^1\\ & \text{s}.\text{t}.\left|\right|w|{|}_2^2=|\left|V\right|{|}_F^2=1\end{array}$$ (3)

where w and $V=[v1,\dots ,vK]$ are the canonical vectors of X_k and Y_k respectively, $\left|\right|V|{|}_F^2=\sum _k||vk|{|}_2^2,\lambda w,\lambda v,\tau$ are regularization parameters. In (3), we apply the general fused lasso penalty (Danaher et al., 2014; Hoefling, 2010) on V. The L₁-penalty on each v_k, controlled by λ_v, encourages the sparsity over each individual canonical vector. The L₁-penalty on the differences between every two canonical vectors from different classes encourages them to share a similar structure. In this way, all of the components v_k from Y are correlated with the common component w from X; hence their shared and class-specific interactions can be determined. The parameter τ plays an important role to adjust the degree of fusion. Specifically, when τ = 0, there is no fusion across the canonical vectors. When τ = ∞, (3) is obtained only when all canonical vectors are identical to each other. Moreover, if we add the constraint $\left|\right|V|{|}_F^2=1$ as a whole instead of constraining each canonical vector, we realize a joint estimation. When K = 1, this reduces to regular sparse CCA.

2.3 Numerical algorithm

In this section, we introduce the algorithm to obtain w and V that can minimize (3). To begin with, we outline the key steps of the optimization. In JSCCA, the object function is convex with respect to w when V is fixed and vice versa. So the block coordinate descent, which is widely used in SCCA method, can be applied to solve this problem. Roughly speaking, the iteration procedures mainly contain two steps:

$$\begin{array}{l}{\displaystyle \underset{\left|\right|w\left|\right|2=1}{\min }}-{\displaystyle \sum _{k=1}^K\frac{1}{nk}}{(X_k^{T}Ykvk)}^{T}w+\lambda w\left|\right|w|{|}_1^1,\\ {\displaystyle \underset{\left|\right|V\left|\right|F=1}{\min }}-{\displaystyle \sum _{k=1}^K\frac{1}{nk}}{w}_k^T{X}_k^{T}Ykvk+\lambda v\left|\right|vk|{|}_1^1+{\displaystyle \sum _{k<k\prime }\tau }||vk-vk\prime |{|}_1^1\end{array}$$

According to (Witten et al., 2009), the solution of the first problem is given by $w=\frac{\widehat{w}}{\left|\right|\widehat{w}\left|\right|2}$, where

$$\widehat{w}=H({\displaystyle \sum _{k=1}^K\frac{1}{nk}}{X}_k^{T}Ykvk,\lambda w),$$

and H is the soft-thresholding operator defined by $H(x,\lambda )=\text{sgn}(x)\text{max}(|x|-\lambda ,0)$.

To obtain V when w is fixed, we follow the results from Section 2.3 in (Witten et al., 2009) and can easily get (the proof is omitted):

Proposition 1 —

The solution of

$$\underset{\left|\right|V\left|\right|F=1}{\min }{\displaystyle \sum _{k=1}^K-}{z}_k^{T}vk+\lambda v\left|\right|vk|{|}_1^1+{\displaystyle \sum _{k<k\prime }\tau }||vk-vk\prime |{|}_1^1,$$

where $zk={(\frac{1}{nk}{Y}_k^{T}Xkwk)}^T$, is given by $\widehat{V}/\left|\right|\widehat{V}\left|\right|F$, where $\widehat{V}$ is the optimum of

$$\underset{V}{\min }{\displaystyle \sum _{k=1}^K|}|vk-zk|{|}_2^2+\lambda v\left|\right|vk|{|}_1^1+{\displaystyle \sum _{k<k\prime }\tau }||vk-vk\prime |{|}_1^1$$ (4)

The problem of (4) is a special case of the fused lasso signal approximation (Hoefling, 2010). A very efficient algorithm for the solution is available (Danaher et al., 2014; Hocking et al., 2011). Specifically, (4) can be solved in successively three steps: a fusion step, a sparsification step and a normalization step. In the fusion step, a $\overline{V}$ is obtained by setting λ_v = 0, which fuses the variables that do not have significant difference (dependent on τ). Here, we say that the variable i in Y is fused between the kth and $k\prime$th classes if $\overline{v}ki=\overline{v}k\prime i$. In the sparsification step, $\widehat{V}$ is derived through soft-thresholding on $\overline{V}$, that is, $\widehat{v}k=H(\overline{v}k,\lambda v)$. Finally, in the normalization step, $V=\frac{\widehat{V}}{\left|\right|\widehat{V}\left|\right|F}$ leads to the solution.

Since $n<<q$, a very sparse solution is required to ensure the reliability. This highly increases the sensitivity of the selection of λ_w and λ_v (Parkhomenko et al., 2009), hence increasing the difficulty in parameter selection. To mitigate this problem, we adopt the sparsity level of the solution to guide the selection of the tuning parameters (Duan et al., 2014; Zongben et al., 2012). Then the selection can be searched around the sample size n, yielding a much less sensitive searching process. In particular, we set the λ_w based on κ_w, which is the number of non-zeros in w. There is a correspondence between λ_w and κ_w by setting λ_w in each iteration to satisfy

$$\lambda w\in \left[\left|w\right|\kappa w+1,\left|w\right|\kappa w\right],$$

where $\left|w\right|\kappa w$ is the κ_wth largest absolute magnitude of w. Meanwhile, it was found in both simulations and real applications that using the same λ_v for different classes will result in unstable solutions (see Fig. S1 in supplementary data). To overcome this problem, we instead keep the sparsity κ_v the same for each class. We set the λ_vk based on the same sparsity κ_v, where the corresponding relationship can be obtained accordingly. This procedure will result in different thresholds, which makes it overestimate the number of changes among v_k. Nevertheless, the difference of the thresholds was found to be small in practice and we can still detect the changes by comparing $\overline{v}k$ after the fusion step.

Finally, we describe how to obtain multiple canonical vectors. Suppose we have derived the first K pairs of canonical vectors using the iterations described above, we calculate the remaining matrix $Xk=Xk-Xkw{w}^T,Yk=Yk-\frac{Ykvk{v}_k^T}{\left|\right|vk|{|}_2^2}$, from which we can obtain the second K pairs of canonical vectors. The subsequent canonical vectors can be obtained by repeating the above procedures.

We summarize the JSCCA algorithm in Algorithm 1.

Algorithm 1 Algorithm for joint sparse CCA

Require: Normalized data $Xk\in {\mathcal{R}}^{nk\times p},Yk\in {\mathcal{R}}^{nk\times q}$, parameters $\kappa w,\kappa v,\tau$.

Ensure: Canonical vectors w and V.

1: Initialize w as the first left-singular vector of $\sum _k\frac{1}{nk}{X}_k^{T}Yk$,

2: repeat

3:   $\overline{V}=\text{arg}\underset{V}{\min }\sum _{k=1}^K||vk-\frac{1}{nk}{Y}_k^{T}Xkw||+\sum _{k<k\prime }\tau ||vk-vk\prime |{|}_1^1$;

4:   for k = 1 to K do

5:     $\lambda vk=\left|\overline{v}k\right|\kappa v+1$;

6:     $\widehat{v}k=H(|\overline{v}k|,\lambda vk)$;

7:   end for

8:   $V=\widehat{V}/\left|\right|\widehat{V}\left|\right|F$;

9:   $\overline{w}=\sum _{k=1}^K\frac{1}{nk}{X}_k^{T}Ykvk$;

10:     $\lambda w=\left|\overline{w}\right|\kappa w+1$;

11:     $\widehat{w}=H(\overline{w},\lambda w)$;

12:     $w=\widehat{w}/\left|\right|\widehat{w}\left|\right|2$;

13: until Convergence

14: Calculate $Xk=Xk-Xkw{w}^T,Yk=Yk-\frac{Ykvk{v}_k^T}{\left|\right|vk|{|}_2^2}$; return to Step 2 to get the next L pairs of canonical vectors.

2.4 Parameter selection

There are mainly three tuning parameters κ_w, κ_v, τ in the JSCCA model. The first two control the number of selected features and the third one determines how similar the derived genomic features are. However, conventional parameter selection methods, such as the cross validation, is not well suited. On one hand, limited by the samples size, the optimized parameters selected from cross validation could still yield many irrelevant features (Wang et al., 2014). On the other hand, since the imaging and genetic correlation is quite low (Grellmann et al., 2015) the selected parameters vary a lot during repeated trials. As an alternative, we apply a hybrid of Monte Carlo validation and stability selection (Meinshausen and Bühlmann, 2010) to select the parameter τ and correlated features.

Specifically, we perform random sampling from the original dataset without replacement for B times with the same portion of observations, leading to training samples $Xbk,Ybk,b=\mathrm{1\dots },B$ and testing samples $X_{bk}^C,Y_{bk}^C$. For each subsample, the JSCCA is fitted with fixed κ_w, κ_v and a candidate set of τ, and the canonical vectors $w_{\tau }^b,v_{k\tau }^b$ are obtained. First, the τ* that maximizes the averaged test correlation on the test subsamples $\sum _b\sum _k\text{c}\text{orr}(X_{bk}^{C}wb\tau ,Y_{bk}^C{v}_{k\tau }^b)$ is selected, where corr(x, y) calculates the Pearson correlation between vectors x and y. Second, the canonical vectors $w^b,v_k^b$ corresponding to the selected τ* are collected. For the imaging canonical vectors, we measure the importance of a voxel by the empirical selection probability

$$pwi=\frac{1}{B}{\displaystyle \sum _{b}I}(|w_i^b|>0),$$ (5)

where I is the indicator function. Based on which a set of important voxels is selected with a cut-off as $Sw=\{i:pwi>\pi w\}$.

For the genomic canonical vectors, we focus on the differences in the selected SNPs across multiple classes. We compare the canonical weights in a pairwise way. In particular, for every two class $k,k\prime$, we measure the degree of specificity from k to $k\prime$ by the following probability

$$p_{vi}^{kk\prime }=\frac{1}{B}{\displaystyle \sum _{b}I}(|v_{ki}^b|>|v_{k\prime i}^b|,|{\overline{v}}_{ki}^b|\ne |{\overline{v}}_{k\prime i}^b|),$$ (6)

where the first condition requires that there exists difference. Since stability selection needs multiple runs on the resampled data and each run will result in either weaker or stronger |v_ki| than $\left|vk\prime i\right|$, we only count the cases that $\left|v_{ki}^b\right|>\left|v_{k\prime i}^b\right|$ in $p_{vi}^{kk\prime }$ to make subsequent analysis more informative (the case of stronger $vk\prime i$ is considered in $p_{vi}^{k\prime k}$). The second condition requires the difference to be large enough, determined by whether the canonical weights are fused during the fusion step in Algorithm 1. The high-rank SNPs, determined by a cut-off π_v, are then picked as the candidate set of differential SNPs $S_v^{kk\prime }=\{i:p_{vi}^{kk\prime }>\pi v\}$. In this way, we expect to find class-k specific (as compared to class $k\prime$) SNPs, that frequently have stronger correlations with the imaging features than in class-$k\prime$.

2.5 Differential correlated modules detection

The high-ranked voxels and differential SNPs are more likely to be differentially correlated, and we propose to detect the differential correlated modules by selecting cut-offs that properly control the module FDR (mFDR) of pairwise differential correlation between elements in S_w and $S_v^{kk\prime }$. Specifically, the difference of the Pearson correlation of each pair of selected voxel and SNP in S_w and $S_v^{kk\prime }$ is calculated

$$\Delta {\rho }_{ij}^{k,k\prime }=|\text{corr}(Xki,Ykj)|-|\text{corr}(Xk\prime i,Yk\prime j)|.$$ (7)

and the corresponding significance p_ij is estimated by the permutation test. More specifically, to get p_ij, the null hypothesis of no different correlation between a SNP i and voxel j in class k and $k\prime$ can be formulated as $H0:\Delta {\rho }_{ij}^{k,k\prime }=0$ versus the alternative hypothesis, $H1:\Delta {\rho }_{ij}^{k,k\prime }\ne 0$. To test the hypothesis, we first calculate $\Delta {\rho }_{ij}^{k,k\prime }$. By comparing the observed statistic with the null statistics $\Delta {\rho }_{ijb}^{k,k\prime },b=1,\dots ,T$, i.e. with T times permutation of the class label of the samples, we can evaluate the significance of the correlation by

$$pij={\displaystyle \sum _{b=1}^{T}I}(\Delta {\rho }_{ijb}^{k,k\prime }\ge \Delta {\rho }_{ij}^{k,k\prime })/T$$

Then the mFDR is calculated by

$$\frac{{\displaystyle \sum _{i\in Sw}{\displaystyle \sum _{j\in S_v^{kk\prime }}I}}(pij>0.05)}{\left|Sw\right|\left|S_v^{kk\prime }\right|}.$$ (8)

Finally, the π_w and π_v are selected by maximizing the module size (for example $\left|Sw\right|\left|S{v}^{kk\prime }\right|$) that satisfies mFDR$\le \pi f$. In this paper, we set $\pi f=0.1$ by considering the weak voxel-SNP correlation and some possible missing edges in the modules.

3 Results and discussions

3.1 Simulations

In a series of simulations, we aim at evaluating the potential power of JSCCA in detecting imaging genetics associations. We first compared SCCA and JSCCA with varied tuning parameters. Then we investigated the influence of noise level on the performance of detection.

3.1.1 Simulation setup

In all simulations, we consider the data belonging to three classes. Each class consists of n samples of fMRI data and SNP data.

To simulate the correlation between fMRI and SNPs, a latent variable model similar to (Lin et al., 2014; Parkhomenko et al., 2009) was used. We first generated one imaging canonical vector α with l non-zero entries and three genomic canonical vectors β_k with m non-zero entries. Among the m canonical variables, m_s of them had the same value while m_c of them were only present in one class (e.g. having zero entries in the other two, see Fig. 1). Each non-zero variable in α and β_k was drawn independently from a uniform distribution with support on $[-1,-0.5]\cup [0.5,1]$.

Given a pair of canonical vectors α and $\beta k(k=1,2,3)$, we generated a latent variable h with normal distribution $N(0,\sigma h)$ for each sample, where σ_h is the signal to noise level (e.g. a noise variance of 1). For the imaging data, the voxels were simulated using a Gaussian distribution $N(\alpha h,Il)$ for correlated voxels and $N(0,Ip-l)$ for uncorrelated ones. For the genomic data, the SNP was coded by 0 (no minor allele), 1 (one minor allele) and 2 (two minor allele) and the minor allele frequency η was uniformly drawn from U [0.2, 0.4]. The ith SNP was simulated from a binomial distribution $B(2,{\text{logit}}^{-1}(-\beta kih+\text{logit}(\eta i)))$ if it is a correlated variable and B(2,η_i) otherwise. Here $\text{logit}(p)=\text{log}(\frac{p}{1-p})$ is the logit function.

We used the true positive rate (TPR), false positive rate (FPR) and precision to evaluate the performance of the model. Specifically, we applied stability selection to JSCCA and SCCA and compared their ability in identifying the canonical voxels and the differential canonical SNPs. For JSCCA, we calculated the selection probability as in (5) and (6), and determined the positives according to a given cut-off threshold. When applied to multi-group problems, the TPR and FPR for differential canonical SNPs were calculated based on the summation of the number of FPs and TPs between every two groups. For SCCA, we estimate the canonical vectors individually on each class, and calculated the selection probability on the voxels using (5) separately but on the differential SNPs using (6) jointly. Two methods were compared to identify voxels for SCCA. One used the selection probability from a single class, which is denoted as SCCA (single). The other refers to SCCA (combined), which identified voxels when the selection probabilities for all the three classes exceeded the cut-off threshold. For the SNPs, we followed the same procedures for JSCCA. In each simulation, the statistics were averaged over 100 replications.

3.1.2 Simulation results

First, we evaluated the JSCCA with varied parameter τ. We generated 100 samples for each class (totally 300 samples) with 1000 voxels and 1000 SNPs. We set l = 100, m_s = 100, m_c = 50, σ_h = 0.2. The receiver operating characteristics (ROC) curve was adopted for the comparisons in identifying the canonical voxels and the differential canonical SNPs with different τ. Specifically, for each τ, we set κ_w = 200, κ_v = 200 and draw the curves by varying the cut-off probabilities. The SCCA was also included in the comparisons.

Figure 2(a), (b) displays the TPR against FPR on the selected voxels. We can see that the SCCA with single class data and combined threshold performs much worse than the JSCCA. The combined threshold performs even worse than single class case. Moreover, as the parameter τ increases, the area under curve does not change too much. Figure 2(c), (d) evaluates the success in detecting differential canonical SNPs. The figure implies that JSCCA in all setting performs no worse than the SCCA. In addition, for JSCCA, as the parameter τ increases from 0 to 0.2, the TPR increases constantly, especially given a low FPR. But when τ = 0.4, the performance decreases. All these results indicate that the parameter τ plays an important role in combining the power of each individual class to reduce the false detections in both SNPs and the related voxels. But excessive fusion will hinder the power in the detection for the differential canonical SNPs. Hence, a proper balance is required to yield a desirable solution. To study the proposed method in different scenarios, a set of simulations were conducted to evaluate the effect of l, m_s, m_c on the performance, which are available in supplementary data.

Fig. 2.

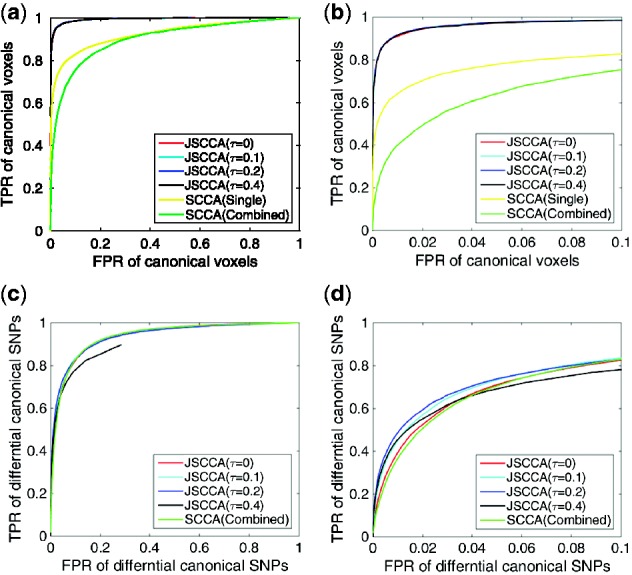
A comparison of SCCA and JSCCA in identifying the differential interactions. (a) TPR versus FPR on the detection of canonical voxels. (b) The detailed comparison on the detection of canonical voxels. (c) TPR versus FPR on the detection of differential canonical SNPs. (d) The detailed comparison on the detection of differential canonical SNPs (Color version of this figure is available at Bioinformatics online.)

We then varied the noise level σ_e from 0.05 to 0.5 to see its effects on the performance. Figure 3 draws the precision for the detection of the canonical voxels and differential canonical SNPs. In particular, we selected the top ranked 100 voxels and 100 differential SNPs for each method to calculate the precision. Obviously, as the signal to noise level σ_h increases, the precision increases for all methods in the two cases. The JSCCA performs better than SCCA for both the canonical voxels and differential canonical SNPs. In addition, as the tuning parameter τ increases, the precision increases for JSCCA, but the improvement is quite small for the detection of canonical voxels. We also studied the performance with top ranked 50 and 200 features (see Figs S8 and S9 in supplementary data), which show that less selected features provide more reliable results. All these results indicate that the JSCCA with proper fusion could yield the best combination of multi-class data to increase the detection accuracy.

Fig. 3.

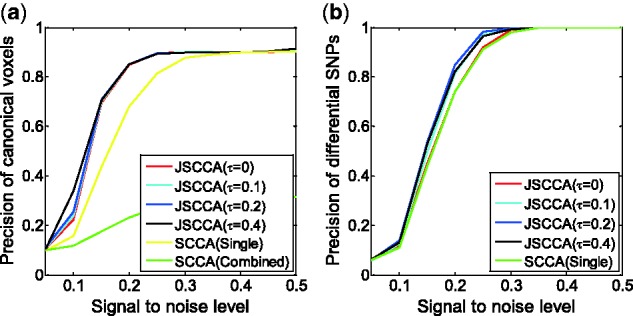
A comparison of the precision under different signal to noise levels. (a) precision for the detection of canonical voxels. (b) precision for the detection of differential canonical SNPs (Color version of this figure is available at Bioinformatics online.)

3.2 Application to a schizophrenia dataset

Schizophrenia is a complex mental disorder often characterized by abnormal thinking, speech and behavior of a patient. It is considered to be related to a number of genetic factors and the study of the associations between genetic factors and brain activities will facilitate our understanding of the biological mechanisms underlying the disease. Comparing the difference in the association of imaging and genetics between cases and controls could yield disease-specific features.

We applied the method to SNP and fMRI data collected by The Mind Clinical Imaging Consortium (MCIC). The data were from 208 subjects, among them 92 are schizophrenia patients (age: 34 ±11, 22 females) and 116 healthy controls (age: 32 ±11, 44 females). We follow the same preprocessing procedures as in Lin et al. (2014), resulting in 41, 236 voxels and 777, 635 SNPs. Then, the voxels with the mean response less than 0.3 were removed while the SNPs included by the Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway were selected (Kanehisa and Goto, 2000), resulting in finally a dataset with 8, 891 voxels and 129, 145 SNPs.

3.2.1 Experimental results

We applied the algorithm in Section 2 to the data provided. The data were normalized according to samples from each class. The κ_w and κ_v were set to be 200. We found that κ_w and κ_v did not affect too much on the results if they were small enough, e.g. at the same order as the sample size. We randomly sampled 120 subjects without replacement for 1000 times, and performed JSCCA on each sub dataset to find the optimum parameter τ. Given the selected τ, we then applied stability selection and picked important voxels by the probability p_w and the degree of specificity of SNPs for cases and controls by the probability $p_v^{10}$(0 for control and 1 for case) as described in Section 2. The differential correlated modules were selected as described in Section 2.5. The analysis of the first two modules were presented.

We first show the module components. The selected voxels were plotted in Figure 4. As shown in the figure, for the first group, 95 voxels were selected, which are mainly from the bilateral putamen. For the second group, 159 voxels were selected, which are mainly from the right inferior frontal gyrus and right insula. The selected SNPs were summarized in Table 1. There were 7 SNPs from 6 genes and 10 SNPs from 8 genes selected by the first and second module, respectively.

Fig. 4.

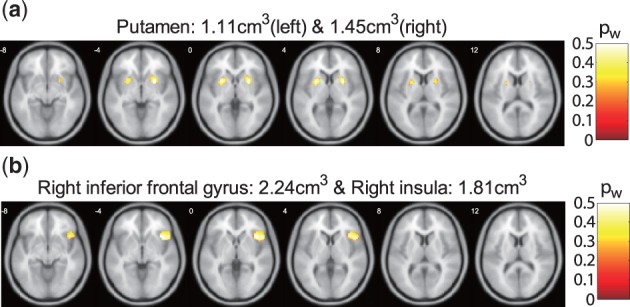
Maps showing the brain regions related to the SNPs. The magnitudes are the corresponding selection probability. (a) The first module, (b) the second module (Color version of this figure is available at Bioinformatics online.)

Table 1.

The susceptibility schizophrenia-specific canonical SNPs related to the brain region

SNP ID	Gene	Chr	SNP ID	Gene	Chr
The first module
rs163907	AGXT2	5	rs6121460	CDH4	20
rs16955972	CES7	16	rs7186424	CES7	16
rs1059611	LPLa	8	rs12512830	SLIT2	4
rs132946	PLA2G6a	22
The second module
rs10183370	B3GNT2a	2	rs12211663	EPHA7	6
rs10251347	CNTNAP2a	7	rs7691506	HADH	4
rs12427675	CSNK1A1L	13	rs3796992	HADH	4
rs1555639	CSNK1A1L	13	rs10513805	MASP1	3
rs7033245	NOTCH1	9	rs17160670	PDE1C	7

^aGenes reported to have potential relationship with schizophrenia.

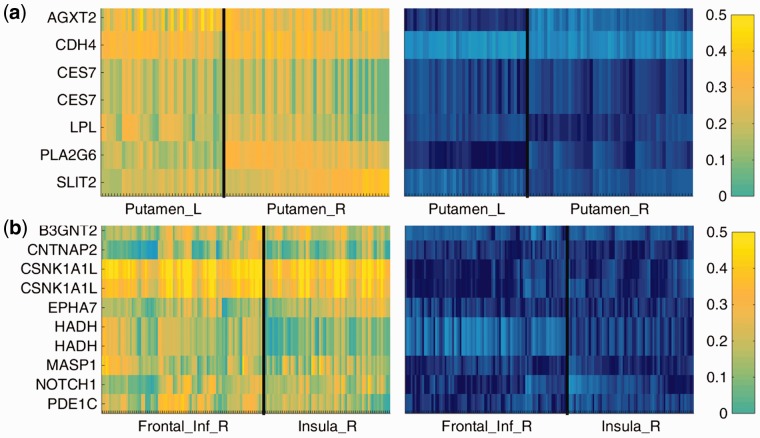
Moreover, we plotted the detailed SNP-voxel correlations between the selected SNPs and voxels in Figure 5. For both the first and second module, the correlations are high in case group but are constantly low in control group. Specifically, the mean difference of the SNP-Voxel correlation between cases and controls is 0.2917 (P < 1e–6) for the first module and 0.2872 (P < 1e–6) for the second module (the p value was estimated by permutation test), which further proves that these case–specific SNPs have significantly increased correlations with the detected brain regions.

Fig. 5.

Heatmaps showing the pair-wise absolute Pearson correlation between the selected voxels and SNPs given the common colormap on the right, where the left is for cases while the right is for controls. (a) The first module, (b) the second module (Color version of this figure is available at Bioinformatics online.)

We tested the selected SNPs for gene set over-representation analysis using ConsensusPathDB (Kamburov et al., 2013). The Gene ontology (GO) terms related to neural activity enriched with p-value less than 0.01 are summarized in Table 2. There are mainly three GO terms enriched for the first module, by genes CDH4 and SLIT2. There are mainly eight GO terms enriched for the second module, primarily by genes EPHA7, NOTCH1, B3GNT2 and CNTNAP2.

Table 2.

The enriched gene ontology terms that are related to the neural activity

GO term	Gene	P-value
Neuron projection extension		3.5e–4
Neuron projection guidance	CDH4, SLIT2	4.5e–3
Positive regulation of nervous system Development		4.7e–3
Neuron projection development		3.2e–4
Neuron development		5.6e–4
Neuron differentiation	EPHA7, NOTCH1, B3GNT2, CNTNAP2	1.2e–3
Neurogenesis		2.1e–3
Nervous system development		8.9e–3
Brain development		2.2e–3
Head development	EPHA7, NOTCH1, CNTNAP2	2.6e–3
Central nervous system development		5.1e–3

3.3 Discussions

In the realm of imaging genetics, CCA is regarded as an efficient algorithm for multivariate analysis of correlations with low computational complexity, which has been used in our previous studies (Lin et al., 2014). Our main results in this paper presented an extension of sparse CCA to discover differential association modules from different disease statuses. Inspired by the idea of a joint sparse model (Baron et al., 2005) and fused graphical lasso (Danaher et al., 2014; Yang et al., 2015), we proposed an JSCCA method and verified its performance in a schizophrenia dataset. The dataset consists of fMRI data and SNP data with 116 healthy controls and 92 schizophrenia patients. We designed to explore abnormal brain-genomic associations in schizophrenia patients. We first applied JSCCA to find a common brain component and two genetic components (for cases and controls respectively) to maximize their summed correlations. Then the stability selection method was used to pick up a candidate set of SNPs that are differentially associated with the target brain components. Finally, modules are detected by controlling the mFDR of the pair-wise differential correlation. Overall, the differences of group-size associations can infer specific genomic functions in brain activities for schizophrenia patients.

3.3.1 Comparison with sparse CCA

In simulation studies, we have shown the advantages of JSCCA over SCCA in identifying the differential correlated components when there is only one pair of canonical vectors. The problem would be more complicated in real applications. For example, when applying SCCA separately to cases and controls, we found the voxels selected by SCCA in the 3rd and 4th component in cases, in the 1st and 10th component in controls, are most relevant to the voxels in the two modules detected by JSCCA. Therefore, a matching procedure is usually required before the comparison among the results given by SCCA. However, unlike the case in the simulation, the components cannot always be ideally matched, which may further degrade the performance. In contrast, as shown in Figure 1, the JSCCA provides a joint model which naturally pairs the components so that the joint analysis becomes more reliable. An alternative approach for matching high dimensional imaging genetics data has been proposed within an independent component analysis framework (Liu et al., 2008; Pearlson et al., 2015). It would be interesting to do a direct comparison of these different approaches, which we plan to do in future work.

3.3.2 Biological implications

Two brain components were recognized by JSCCA. In particular, the first brain component includes the region of bilateral putamen. The putamen is one of the basal ganglia nuclei and part of the striatum, and is associated with the motor skills. Dopamine is concentrated within the putamen (Meador-Woodruff et al., 1996) and dopamine synthesis capacity has been found related to schizophrenia and symptom severity (Howes et al., 2013). In addition, decreased volume and total neuron number were found in putamen in schizophrenia patients (Kreczmanski et al., 2007). The second brain component includes the region of right inferior frontal gyrus and right insula. The right inferior frontal gyrus is a component of the prefrontal lobe, which is involved in inhibition and attention control (Hampshire et al., 2010). Decreased neural activation was found in the right inferior frontal gyrus for schizophrenia patients (Zandbelt et al., 2011; Zhang et al., 2016). The insula is related to emotional processing and motor function, and plays an important role in schizophrenia. The pathological function of the insula in schizophrenia was summarized in (Wylie and Tregellas, 2010), which primarily includes the emotional facial processing, auditory affect processing, self versus non-self, etc. Moreover, a network connectivity study has shown aberrant functional connectivity between the right insula and inferior frontal gyrus (Voegler et al., 2016).

There were two groups (modules) of SNPs identified in this paper. In the first module, we have discovered seven SNPs from six genes. Among them, the LPL, PLA2G6 were reported to have potential relationship with the risk of schizophrenia. The LPL gene is expressed in the brain regions with functionally relevant cognitive functions, and was found to be related to schizophrenia (Le-Niculescu et al., 2007; Xie et al., 2011). PLA2G6 (Phospholipase A2 group 6) gene is important for normal brain development and synaptic functioning. The role of PLA2G6 in schizophrenia was reviewed in (Law et al., 2006), which indicated their potential relationship. In the second module, we have discovered 10 SNPs from 8 genes. The B3GNT2 and CNTNAP2 were reported to have potential relationship with the risk of schizophrenia. The B3GNT2 is an immune-related gene and was implicated to be tied to schizophrenia (Sanders et al., 2013). The CNTNAP2 gene is among the top schizophrenia genes and has been reported with increased susceptibility (Friedman et al., 2008; O’Dushlaine et al., 2011; Wang et al., 2010). In addition, several GO terms related to the neuron projection, neuron and brain development were enriched by CDH4, SLIT2, EHHA7, NOTCH1, B3GNT2 and CNTNAP2. All these findings further demonstrate the biological significance or implications of the selected modules.

Finally, we are interested in how their interactions affect and distinguish schizophrenia. One study in (Ross et al., 1999) suggested decreased PLA2 activity in putamen for schizophrenia patients. It was also shown in (Whalley et al., 2011) that the association between CNTNAP2 gene and brain activity exists in the right inferior frontal gyrus in healthy individuals during a language task, which may indicate the potential risk to mental illness.

3.3.3 Potential limitations

In JSCCA, the assumption on a completely common imaging feature is too strict in practice, although this assumption provides a fair way for comparison between classes. To overcome this problem, we are working on some postprocessing methods (e.g. partial correlation network) to further eliminate unrelated and indirectly related connections.

The parameter selection method for penalized CCA is still an open problem. Especially when the correlation is weak between genetic variant and brain activity, it is more important to detect reliable associations while reducing the FDR (Grellmann et al., 2015). Stability selection is a recently proposed strategy that can better control Type-1 error rate (Meinshausen and Bühlmann, 2010; Wang et al., 2014), hence it is adopted in our proposed method. The simulations in the supplementary data also demonstrate that the stability selection can yield better results than cross validation. However, the selection of the cut-off probability for stability selection remains a challenging issue, especially for high dimensional data. Although the proposed module detection method worked effectively, it is still far from optimal. We will continue to work on this problem.

In this paper, the method was evaluated on a case–control study. We proposed a method to detect the differential correlated modules. However, the method introduced in Section 2.5 cannot be directly applied to detect common modules. This is because the calculation of mFDR is based on the permutation test, where the null hypothesis is built for detecting differences but not for detecting similarities. More robust and appropriate statistical methods will be studied in the future to enable the detection of both common and differential correlations simultaneously. Moreover, the proposed model could be more powerful for analyzing data from more than two classes or from multiple conditions. For example, we can easily extend the study to imaging genomic data collected from a combination of different research groups and different mental disorders. This would be a very interesting topic.

4 Conclusion

The main contributions of the present paper can be summarized as follows. First, we propose a JSCCA method, which can discover relationship among data from observations corresponding to distinct classes to infer their common and different association patterns. Second, we present an efficient algorithm to solve the model. Third, we study the numerical performance of JSCCA via a series of simulations. Our results show that an appropriate fusion of multiple data can improve the detection accuracy of both common and differential associations. Finally, we applied the proposed method to the analysis of schizophrenia data. We discovered some novel abnormal interactions between a group of SNPs with some interesting brain regions. The differential interaction can infer some important information on how the dysfunction of genes-brain interactions can imply the risk of schizophrenia. The interpretation of these interactions should be further confirmed via replications and additional biological evidences, which needs further research.

Funding

The authors wish to thank the National Institutes of Health (R01GM109068, R01MH104680, R01MH107354, P20GM103472) and National Science Foundation (#1539067) for their partial support.

Conflict of Interest: none declared.