A feasibility study of nonlinear spectroscopic measurement of magnetic nanoparticles targeted to cancer cells

Abstract

Objective

Magnetic nanoparticles (MNPs) are an emerging platform for targeted diagnostics in cancer. An important component needed for translation of MNPs is the detection and quantification of targeted MNPs bound to tumor cells.

Method

This study explores the feasibility of a multi-frequency nonlinear magnetic spectroscopic method that uses excitation and pick-up coils and is capable of discriminating between quantities of bound and unbound MNPs in 0.5 ml samples of KB and Igrov human cancer cell lines. The method is tested over a range of five concentrations of MNPs from 0 to 80 μg /ml and five concentrations of cells from 50 to 400 thousand count per ml.

Results

A linear model applied to the magnetic spectroscopy data was able to simultaneously measure bound and unbound MNPs with agreement between the model-fit and lab assay measurements (p<0.001). The detectable iron of the presented method to bound and unbound MNPs was < 2 μg in a 0.5 ml sample. The linear model parameters used to determine the quantities of bound and unbound nanoparticles in KB cells were also used to measure the bound and unbound MNP in the Igrov cell line and vice versa.

Conclusion

Nonlinear spectroscopic measurement of magnetic nanoparticles may be a useful method for studying targeted MNPs in oncology.

Significance

Determining the quantity of bound and unbound MNP in an unknown sample using a linear model represents an exciting opportunity to translate multi-frequency nonlinear spectroscopy methods to in vivo applications where MNPs could be targeted to cancer cells.

I. Introduction

Magnetic nanoparticles (MNPs) have a long history in biomedical research with many practical applications [1-3]. The magnetic properties of these nanomaterials are also being controlled and exploited in increasingly sophisticated ways. The diverse applications of MNPs include testing for bacterial contamination [4-6], cancer diagnostics [7, 8], cell tagging [9, 10], drug targeting [11], DNA detection [12], assay measurement [13-18], multi-MNP tracer systems [19, 20], health monitoring [21], temperature measurement [22-24], stem cell tracking [25, 26], and detection of plant viruses [27]. Remote detection of MNPs via magnetic field measurements is particularly attractive for in vivo applications because these technologies can be noninvasive, highly sensitive, and can readily differentiate MNPs from background tissue. Beyond simple MNP localization and quantification, measurements that leverage nonlinear magnetic properties can provide more detailed contextual insights. For example, distinguishing free MNPs from those that are bound to cells. Strategies for probing the local environmental status of MNPs (e.g., bound vs. unbound) include detection of even, odd, and intermodulation frequencies [28-32], the use of ratios between harmonics[21, 33], rotational drift non-linearity [34] and magnetic particle spectroscopy (MPS) [35, 36]. MPS is a technique that uses a large applied field in order to measure a number of harmonic frequencies to determine a spectroscopic difference in the MNP response when MNPs are in a bound state. Researchers have also proposed the idea of using two frequency bands to distinguish between Brownian and Néel relaxation behavior in bound and unbound MNP states in Magnetic Particle Imaging (MPI) [37]. These methods have shown good promise in measuring targeted MNPs. For instance, magnetic spectroscopy of nanoparticle Brownian motion (MSB) has been shown to measure 100 ng of MNPs bound to single-stranded DNA [21] and changes in signal as MNPs are bound to cancer cells over time [33]. In a staphylococcal toxin measurement, an intermodulation measurement method was able to measure as little as 3 ng of MNPs [5]. Another method has been shown to measure less than 10 ng/ml of MNPs targeted to plant viruses [27]. Another method using magnetorelaxometry (MRX) has also been used to study binding behavior [38] and has the ability to image samples of bound and unbound MNPs using linear models [11, 39]. One difference between MRX and the other methods described is the use of Super Conducting Quantum Interface Devices (SQUIDs) to measure MNP relaxation when exposed to magnetic fields. To date nonlinear magnetic spectroscopy methods have not attempted to separate bound and unbound MNPs within a sample with a linear model. Generally samples are either washed to clear unbound MNPs or a difference is measured between a known MNP sample and a sample with targeted binding. This is a reasonable approach for in situ measurements but makes in vivo measurement more challenging.

This study introduces a three frequency spectroscopic method that shows promise for determining the bound and unbound MNP concentrations within a sample with a linear separation model. Using a calibration data set, the model is able to predict unknown MNP samples using a single excitation coil and gradiometer pickup coil. This method could one day be extended to allow for imaging of tumors with targeted MNPs and shows early promise for quantifying bound and unbound MNPs even when the cell-MNP interactions are not fully characterized.

II. Materials and Methods

In this study we test a three frequency, third harmonic magnetic method to measure MNPs targeted to KB and Igrov cancer cell lines. We prepared 25 samples of each cell type with five concentrations of cells and five concentrations of MNPs to create a 5 × 5 measurement grid. Using these two cell lines we use a simple linear model to evaluate if this nonlinear spectroscopic method is capable of separating the bound and unbound MNPs. We then evaluate whether the model parameters computed for each cell type are able to quantify the bound and unbound MNPs in the other cell type.

A. Cells and nanoparticle preparation

KB cells were derived from a human squamous cell carcinoma of the oral cavity and were obtained as a gift from Dr. Philip S. Low at Purdue University (West Lafayette, IN). IGROV-1 cells were obtained as a gift from Dr. Mary Jo Turk at the Geisel School of Medicine (Hanover, NH). These cells were found to produce disseminated peritoneal tumors that are representative of advanced ovarian cancer in humans. Cells were maintained as a monolayer in folate-free RPMI 1640 medium (Gibco, Life Technologies, Grand Island, NY) supplemented with 100 U/ml penicillin, 100 μg/mL streptomycin and 10% fetal bovine serum (FBS) at 37 °C in a humidified atmosphere consisting of 5% CO₂ and 95% air. Cells were harvested with 0.25% trypsin, suspended, and spun down at 1200 RPM prior to re-suspension and use in the following assay measurement experiments.

Samples of 110 – 120 nm hydrodynamic diameter MNPs with embedded carboxymethyl dextran (CMD) in their core structure were synthesized by the Dartmouth nanoparticle core facility using previously described methods and size distributions [40, 41]. Briefly, commercially available ferric chloride (FeCl₃·6H₂O), ferrous sulfate (FeSO₄·7H₂O), 25 wt. % ammonium hydroxide solution, NaNO₃ and NaOH were purchased from VWR (Radnor, PA). Carboxymethyl-dextran 40 kDa was purchased from TdB Consultancy AB (Uppsala, Sweden). All reactants were used as received without further purification. Ten percent solutions of Fe(II) and Fe(III) salts were precipitated by ammonia solution in the presence of excess of polysaccharide. The mixture was placed on a sand bath and heated to 70 °C. Then NaOH and NaNO₃ were added to oxidize Fe(II) and maintain alkali media (pH > 10). The temperature was raised to 100 °C at a speed of 10 °C/h. The resulting solution was spun at 5000 rpm for 15 min to remove large aggregates. The remaining MNPs were purified using Macs separation LS columns (Miltenyi Biotec, Auburn, CA) and eluted with sterile water. Nanoparticles were maleimide functionalized by adding N-(2-Aminoethyl) maleimide (Sigma-Aldrich, St. Louis, MO) and EDC (Sigma-Aldrich, St. Louis, MO) in 100-fold molar excess and incubating for 2 hours at room temperature in 100 mM MES pH 6.3. The excess N-(2-Aminoethyl) maleimide and EDC were removed by buffer exchange with 30 mM MES pH 6.5 using Macs separation LS columns.

Farletuzumab Fab antibody fragment (Ffab) was purified and characterized as described earlier [42]. Cysteine-reduced Ffab was added to the maleimide-functionalized CMD at a 1:10 (w/w) ratio and incubated at room temperature for 16 hours at 4 °C on a shaker set at 125 rpm. This ratio was empirically determined to yield high-binding MNP conjugates and reproducible conjugation results. The unbound protein was then removed using Macs separation LS columns and a magnetic field. All processes were performed in a sterile environment using sterile and endotoxin free buffers. Micro BCA assay (Thermo Scientific, Rockford, IL) was used to determine the amount of Ffab covalently bound to MNP, as described previously [42].

B. Analog and Digital Systems

The experimental setup had three coils as depicted in Fig 1. The coils (Jantzen-1257, 0.3 mm diameter wire, 7 mH, 11.8 Ω at DC, 15 mm inner diameter × 15 mm height × 26 mm outer diameter, Jantzen, Praestoe, Denmark) were arranged in a vertical stack with one excitation coil and a gradiometer pickup arrangement. The excitation coil was positioned between the two pickup coils to provide an AC magnetic field in the sensing zone. The pickup coils were balanced in order to reduce coupling from the excitation coil. To increase the magnetic field and reduce noise, the excitation coil was part of a resonant circuit with a center frequency of 1050 Hz. The sample was placed such that it sat in the top pickup coil and partially in the excitation coil. The resulting magnetization of the sample induced a signal that was predominantly coupled into the top pickup coil and only slightly coupled into the bottom pickup coil. The electric current had an approximate amplitude of 600 mA and produced magnetic fields of approximately 10 mT in the center of the excitation coil. Due to the proximity to the excitation coil, the induced magnetization of the sample contained measurable nonlinear harmonics. The current was swept through five AC frequencies corresponding to 900, 1000, 1050, 1100 and 1200 Hz. Measurements of the current and magnetic response were made at 300 kSamples/s (NI-DAQ USB 6289, National Instruments, Austin, TX). In addition to an AC magnetic field, 13 neodymium permanent magnets were positioned at the base of the testing apparatus to create a DC magnetic field gradient across the sensing zone. A digital lock-in amplifier was used to measure the third harmonic of the magnetic susceptibility response. After subtracting the background field measurement, the in-phase and out-of-phase measurements were used to compute the model parameters used to estimate bound and unbound quantities of MNPs.

Fig 1.

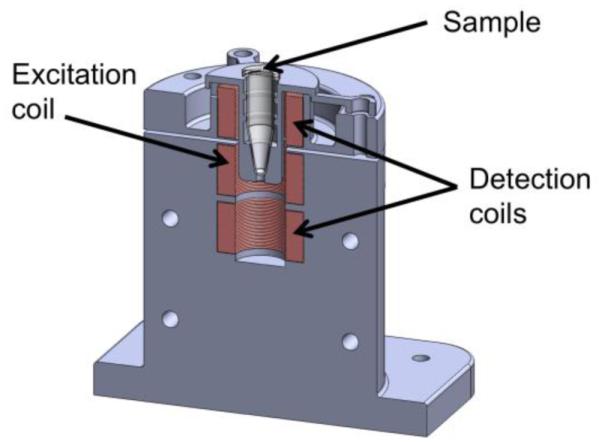
CAD rendering of the MNP spectroscopy device. Shown is a rendering that cuts the device down the middle so that the sample and the coils can be seen.

C. Experimental Procedure

1) Magnetic Measurements

The dynamic magnetic susceptibility of an MNP sample is a combination of two magnetic phenomena termed Néel relaxation and Brownian relaxation. Néel relaxation is a form of magnetic behavior where the crystals within the MNP core align with an applied magnetic field without rotating the MNP, whereas Brownian relaxation involves the MNP rotating to align with the applied magnetic field. Additionally, cellular binding may change MNP interparticle distances and alter the dipolar interactions thereby affecting the relaxation times. In order to simultaneously measure MNPs in bound and unbound states with AC magnetic spectroscopy, it is essential that: 1) the MNPs exhibit some form of relaxation behavior, 2) bound and unbound MNPs have simultaneously measurable signals, 3) a spectroscopic difference exists between the magnetic susceptibility of these two states at the operating frequencies, and 4) the measurements are a linear superposition of signals from the two binding states.

To test this idea, we measured the magnetic susceptibility response of each sample at each of the five test frequencies. In a previous study we confirmed that our experimental apparatus is able to distinguish between different sized MNPs through spectroscopic measurement [43]. Spectroscopic measurement was accomplished by placing each sample in the test holder (Fig 1) and multiplexing through each frequency for 5 s. Prior to the measurement of a sample, a background measurement was also taken. Using a 5 s buffer for placing and removing the sample, each of these measurements took 30 s to complete.

2) Estimate of Iron Content with Assay Measurements

For unbound CMD-Fab nanoparticles determination, different amounts of IGROV-1 and KB cells (400 000, 200 000, 100 000 and 50 000 cells/well) were seeded in a 48-well plate (Corning, Tewksbury, MA) and challenged with different concentration of functionalized Ffab-CMD nanoparticles (10, 20, 40 and 80 μg/ml) in a total volume of 500 μl of folate-free RPMI 1640 growing medium. Cells were incubated at 37 °C, 5% CO₂ with gentle shaking (125 rpm) for 4 hours. Antibody targeted CMD MNPs have been shown previously to be stable for more than 8 hours under these conditions [42]. Cells were centrifuged at 1200 rpm for 10 minutes and the supernatant containing the unbound Ffab-CMD nanoparticles was collected for a ferrozine assay as described earlier [42]. Briefly, 300 μl of HCl 1.4 M was added to 20 μl supernatant in a 48-well plate (Corning, Tewksbury, MA) and incubated at 70 °C for 2 hours. After incubation, 300 μl of ferrozine reagent (6.5 mM ferrozine, 13 mM neocuproine, 2M ascorbic acid diluted in 5M ammonium acetate) was added to each well and shaken for 5 minutes. Plates were read at 562 nm on a plate reader (Spectramax 190, Molecular Devices, Sunnyvale, CA) and the amount of iron per well calculated using a standard curve of iron (FeCl₃) which was identically processed as the samples. Since measurements were made on 20 μl aliquots of supernant, the iron calculation needed to be scaled by a factor of 25 to represent the content of the full 500 μl sample.

D. Separation Model

1) Calculating bound MNP Fe from lab assay data

Known total MNP Fe quantities (10 to 80 μg/ml) were added to each sample and the unbound MNP content was measured by lab assays as explained earlier. The bound MNP content was then calculated by subtraction

$${\mathbf{Fe}}_{B,KB}={\mathbf{Fe}}_{T,KB}-{\mathbf{Fe}}_{U,KB}$$ (1)

and

$${\mathbf{Fe}}_{B,Igrov}={\mathbf{Fe}}_{T,Igrov}-{\mathbf{Fe}}_{U,Igrov}$$ (2)

where Fe represents the iron content and subscripts B the bound, U the unbound and T the total iron in that state. The cell line is represented at KB and Igrov.

2) Determining the relation between iron content and magnetic spectroscopy data

After an initial examination of the data, three of the five frequency measurements were selected for further analysis. Since this was a pilot study to determine if nonlinear spectroscopy could be used to determine bound and unbound MNPs, it was not known in advance how many frequencies would be needed in the analysis. During data processing, it was found that the data from 1000 and 1100 Hz provided redundant information with the 1050 Hz resonant center frequency. Therefore the set of frequencies included in analysis was reduced to 900, 1050 and 1200 Hz.

The magnetics data was organized into composite matrices with data sets of 25 samples by 3 frequencies for the KB cell line. This results in a 25 ? 6 matrix of experimental data when divided into in-phase and out-of-phase data.

$${\mathbf{M}}_{KB}=\left[{\mathbf{M}}_{KB,f}^{\prime }{\mathbf{M}}_{KB,f}^{\prime \prime }\right]$$ (3)

and the Igrov cell line

$${\mathbf{M}}_{Igrov}=\left[{\mathbf{M}}_{Igrov,f}^{\prime }{\mathbf{M}}_{Igrov,f}^{″}\right],$$ (4)

where M′ and M″ are the in-phase and out-of-phase magnetics responses respectively. To estimate the relation between bound and unbound MNPs and the magnetic spectroscopy data we set up a forward model for the magnetic spectroscopy data using a linear relation with the unbound and bound Fe in the KB cell samples

$$\begin{array}{cc}\hfill {\mathbf{Fe}}_{U,KB}& ={\mathbf{M}}_{KB}{\mathbf{a}}_U+noise\hfill \\ \hfill ,{\mathbf{Fe}}_{B,KB}& ={\mathbf{M}}_{KB}{\mathbf{a}}_B+noise\hfill \end{array}$$ (5)

where a_KB is the coefficient vector that relates the magnetic spectroscopy measurement to the iron content of bound and unbound MNPs through

$${\mathbf{a}}_{U,KB}=\left[\begin{array}{c}\hfill a_{U,KB,f_1}^{\prime }\hfill \\ \hfill a_{U,KB,f_2}^{\prime }\hfill \\ \hfill a_{U,KB,f_3}^{\prime }\hfill \\ \hfill a_{U,KB,f_1}^{″}\hfill \\ \hfill a_{U,KB,f_2}^{″}\hfill \\ \hfill a_{U,KB,f_3}^{″}\hfill \end{array}\right],{\mathbf{a}}_{B,KB}=\left[\begin{array}{c}\hfill a_{B,KB,f_1}^{\prime }\hfill \\ \hfill a_{B,KB,f_2}^{\prime }\hfill \\ \hfill a_{B,KB,f_3}^{\prime }\hfill \\ \hfill a_{B,KB,f_1}^{″}\hfill \\ \hfill a_{B,KB,f_2}^{″}\hfill \\ \hfill a_{B,KB,f_3}^{″}\hfill \end{array}\right].$$ (6)

This coefficient array contains one parameter per frequency and has one coefficient for in-phase data and one coefficient for out-of-phase data, for a total of six coefficients for bound MNPs and six coefficients for unbound MNPs.

Using the experimental data and three estimates of iron in a sample, the coefficients of the model a were then estimated by least squares

$$\begin{array}{cc}\hfill {\widehat{\mathbf{a}}}_{U,KB}& ={\left({{\mathbf{M}}_{KB}}^T{\mathbf{M}}_{KB}\right)}^{-1}{{\mathbf{M}}_{KB}}^T{\mathbf{Fe}}_{U,KB}\hfill \\ \hfill {\widehat{\mathbf{a}}}_{B,KB}& ={\left({{\mathbf{M}}_{KB}}^T{\mathbf{M}}_{KB}\right)}^{-1}{{\mathbf{M}}_{KB}}^T{\mathbf{Fe}}_{B,KB},\hfill \end{array}$$ (7)

where superscript T indicates matrix transpose. These twelve coefficients estimate the bound and unbound MNP quantities in the 150 magnetic spectroscopy measurements with triplicate measurements of the iron content for a total of 450 data points. The same procedure was used to estimate the model coefficients for the Igrov cells a_Igrov.

3) Testing the fit between iron content and magnetic spectroscopy data

When testing the magnetic spectroscopy model the forward model was applied to estimate the bound and unbound iron content from new magnetic measurement data

$$\begin{array}{cc}\hfill {\mathbf{Fe}}_{U,KB}& =\mathbf{S}{\widehat{\mathbf{a}}}_{U,KB},\hfill \\ \hfill {\mathbf{Fe}}_{B,KB}& =\mathbf{S}{\widehat{\mathbf{a}}}_{B,KB},\hfill \end{array}$$ (8)

where S is the measured magnetic spectroscopy data. The estimates for bound and unbound Igrov cells were made in the same way using a model found from the Igrov spectroscopic and lab assay data.

To check if the model can translate across cell lines, the measured magnetic spectroscopy signal S, of (8) is taken from the Igrov cell line testing instead of from the KB cell line testing.

4) Estimation of detectable iron

To estimate the detectable bound and unbound iron we used the standard deviation of the residual of the correlation between iron estimates from the lab assay and magnetic spectroscopy measurements.

III. Results

Cell targeting through MNP functionalization allows for preferential cancer cell association. In this study 110 – 120 nm (20-40 nm iron core) MNPs were functionalized with a Fab fragment of the Farletuzumab antibody (Ffab), which specifically binds to the alpha folate receptor cell surface marker (αFR). These Ffab-MNP conjugates have previously been shown to selectively bind to cancer cells that overexpress αFR, whereas negative control MNP targeted to botulinum toxin fail to exhibit any cellular association under the same conditions [42]. In Fig 2, we show the measured quantities of bound and unbound MNPs in the KB and Igrov human cancer cell lines. The functionalized MNPs were found to bind to both cell lines in a dose-dependent fashion, exhibiting greater proportional binding with increasing cell concentration. KB cells showed higher MNP binding than Igrov cells, though the cellular and MNP concentration dependence were similar for both cell types, and differences were consistent with the known αFR expression levels of the cells [42].

Fig 2.

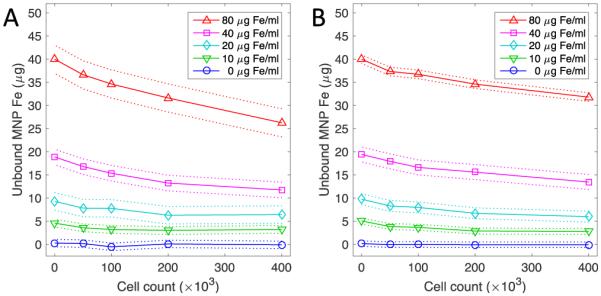
Experimental determination of unbound MNP following incubation with cancer cells. (A) KB and (B) Igrov cancer cells in 0.5 ml sample volumes were incubated with antibody-functionalized MNPs. Unbound MNPs in the cell supernatant were quantified using a colorimetric ferrozine assay. Points indicate the mean of triplicate measurements, 95% confidence intervals are shown as dotted lines, and the solid line is provided as a visual guide.

Magnetic spectroscopic data was collected by measuring the third harmonic of the magnetic signal at three frequencies (Fig 3). The magnitude of the magnetic signal is related to the iron content as well as to the cell concentration. This relationship arises because the magnetic signal is proportional to the concentration of iron. Additionally, unbound MNPs have a higher magnetic moment than bound MNPs giving rise to a larger magnetic signal. At higher cell concentrations, it is expected that the proportion of bound MNPs will increase (Fig 2). In addition, each frequency exhibits a different magnitude indicating its relative position to the resonance frequency and also a small magnetic susceptibility difference across frequencies. The phase measurement is noisy and not shown but at higher MNP concentrations, it is possible to notice small frequency related differences in the phase. The magnetic susceptibility related differences in the amplitude and phase are essential for the separation model.

Fig 3.

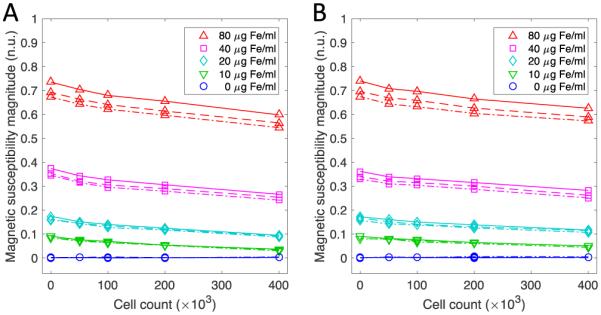
Magnetic spectroscopy data from the 0.5 ml samples containing KB cells (A) and Igrov cells (B) during application of an AC field at each of the 3 frequencies (repeated line types). The magnitude data shows signal separation with respect to frequency. The frequencies shown in the figure are 900 Hz (dot dash line), 1050 Hz (solid line) and 1200 (dashed line).

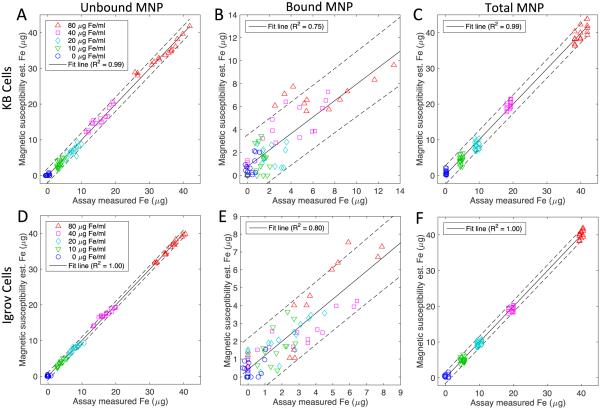
Using the forward model, estimates of the bound, unbound, and total MNPs were estimated for each of the 25 samples per cell line. To estimate an overall 95% confidence bound on all of the data, a single correlation was performed between estimated magnetic susceptibility and assay values (Fig 4). Since assay measurements were repeated three times, there were a total of 75 data points per cell line in the correlation calculations. The estimates of unbound MNPs for both cell lines fall within the 95% confidence bounds and reflect values less than 2 μg from the expected means. These estimates are of high quality since the measurement data directly reflects the quantity of unbound MNPs (Figure 2) with the Igrov cell line correlations being slightly higher than the KB cell correlations. The estimate of MNPs bound to the Igrov cell line has a 95% confidence bound of 1.9 μg whereas the KB cell line has a confidence bound of 3 μg. In both cell lines, the quantity of bound MNP is less than 10 μg, which is only present for samples that started with 80 μg Fe/ml. In lower concentration samples, the bound quantity drops to less than 5 μg. Given the confidence of the measurements and the quantity of bound MNP, the correlations for bound MNPs are not expected to be as high as those for the unbound MNPs but nevertheless remain reasonable given the difficulty in estimating the bound fraction. The estimates of the total MNPs reflect the sum of the bound and unbound quantities in the sample and overall the method captures the binding trends and in each of these six cases the slope of the regression line is highly statistically significant (p<0.001). Using the standard deviation of the residual from the correlation we estimated the detection limits for the KB cell line to be 0.9 μg and for the Igrov cell line 0.5 μg.

Fig 4.

Correspondence of magnetic spectroscopy estimates and lab assay measurements of the unbound (A, D), bound (B, E) and total (C, F) MNP Fe content in 0.5 ml samples containing KB cells (A, B, C) and Igrov cells (D, E, F). The correlation incorporates triplicate assay measurements at 25 combinations of MNP concentration and cell count (N=75). The solid line represents a linear regression between the two data sets. The dashed lines are the 95 % confidence interval for the linear regression of data from 900, 1050 and 1200 Hz. In each case the line is significant (p< 0.001).

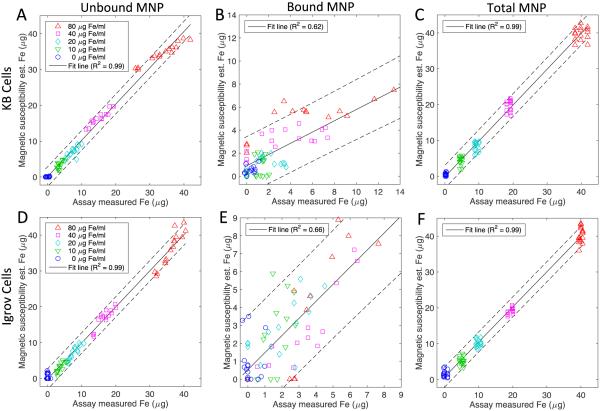
To measure the quality of the separation model, a cross validation was also performed and shown in Fig 5. In this figure, the separation model is the same as shown in Fig 4 but the magnetic spectroscopy data is from the opposite cell line. This cross validation is intended to determine if the model is capable of estimating the bound and unbound MNPs of an unknown data set and to test the idea that the cell line has minimal impact on the magnetic measurements. The quality of the unbound MNP estimations remains similar to Fig 4 but the quality of the bound estimations is lower. The 95% confidence bounds on the KB is now 2.8 μg while the confidence on the Igrov cell line increased to 3.2 μg. Given the two conditions that are being tested in this cross validation, the loss in the quality of the correlation is expected and in each of the six cases the linear regression remains highly significant (p<0.001). Using the standard deviation of the residual from the correlation we estimated the detection limits for the KB cell line to be 1.6 μg and for the Igrov cell line 0.9 μg.

Fig 5.

To determine the generalizability of the models, cross-tests of the correspondences between magnetic spectroscopy estimates using mismatched estimation models and cell types compared to lab assay measurements of unbound (A, D), bound (B, E) and total (C, F) MNP. Models from KB cell data are tested using Igrov cell data (A, B, C) and models from Igrov data are tested using KB cell data (D, E, F). The solid line represents a linear regression between the two data sets. The dashed lines are the 95% confidence interval for the linear regression of data from 900, 1050 and 1200 Hz. In each case the line is significant (p< 0.001).

IV. Discussion

With the success of this feasibility study, we believe that it will be possible to optimize the method to achieve higher sensitivity. A host of factors like MNP size, molecular structure, composition, coating, shape, and iron content each affect AC magnetic susceptibility measurements. The focus of the present study was to demonstrate the principle of simultaneously measuring bound and unbound MNPs. Evaluating the full range of covariates requires a large-scale systematic analysis. In future work, we plan to characterize specific MNPs over a range of frequencies and AC and DC magnetic field amplitudes. This will enable our method to be tuned to the specific frequencies and field strengths that optimize the differences between the bound and unbound MNPs with a particular set of physical properties. The magnetic susceptibility of unbound MNPs relies on a combination of the Brownian and Néel relaxation mechanisms. However, it is important that Brownian relaxation be present since Néel relaxation is not affected by the binding state [44]. In the bound state, MNPs exhibit a reduced Brownian relaxation and therefore it can be advantageous to have a strong Néel relaxation to ensure that the bound MNPs can be measured. The MNPs used in this study are built to deliver a high specific absorption rate (SAR) for use in magnetic hyperthermia [40, 41]. Due to this optimization, the core sizes of these MNPs are not ideal for Néel relaxation measurements. In future studies, we plan to optimize the MNPs, AC and DC field strengths and frequency range to make the method suitable for targeted nonlinear spectroscopy applications.

In this study we estimate that we can detect less than 2 μg of bound MNPs. This value is somewhat larger than other values reported in the literature. However, it should be noted that 2 μg refers not only to acquiring a signal from a given input quantity of MNP, but more importantly to the ability to separate bound and unbound MNPs in a sample. A recent preclinical study by our group showed that up to 3% of targeted MNPs accumulated in mouse tumors after 24 hours [45]. The quantity of MNP in the tumor was roughly doubled from untargeted MNPs and was at a concentration of 230 μg Fe/g tissue. Even with the current limits of detectability, this method could be useful for some in vivo preclinical studies.

One of the key challenges in this experiment is that the quantity of unbound MNPs is an order of magnitude greater than the bound MNPs. This creates a problem for measuring these two quantities and also for validating that the measurement model is capable of successfully estimating these parameters. A particular concern is that the measurement noise of the lab assay data is on the order of the quantity of bound MNPs for many of the samples. Additionally, we did not use an optimized set of measurement frequencies, creating limited separation of the magnetic susceptibility properties. Without a low noise estimate of the bound MNPs, training of the model is prone to estimation errors. This is observed in the estimates of the bound MNPs for both KB and Igrov cell lines. In most cases, the estimates computed by the model fall within the 95% confidence bounds of the lab assay measurement. While this nonlinear magnetic spectroscopy method shows promise, future work will require more calibration measurements to help reduce noise and improve model accuracy.

The use of a single model to predict the bound and unbound MNPs for different cell lines is particularly useful for in vivo experimentation where a cell line might not be entirely characterized. In this study we showed that there was correlation between a model built by one cell line and applied to the data of the other cell line. This correlation was weaker than applying a model trained for a particular cell line to itself. We believe the main reason the correlation is lower is that another source of noise was introduced by correlating across cell lines. It is possible that the cell line introduces some distortion in the magnetic spectroscopy measurement that remains unaccounted for in the model. However, we believe the cell line has a weak effect on the magnetic measurement; with better lab assay data, the cross-correlation results would be much improved.

Although many of the methods reported in the literature have not attempted to separate bound and unbound MNPs within a sample, some of these methods could possibly reproduce these results. In order to separate bound and unbound quantities it is necessary to make multiple measurements of a sample to form some type of discriminatory data set. The advantage of multi-frequency nonlinear spectroscopy is that measurement data is acquired at the third harmonic. This means measurement data is exclusive to the MNPs and the signal to noise ratio (SNR) is high. SNR is high with this method because the signal from harmonic measurement decreases exponentially as the harmonic number increases. A distinguishing feature of our nonlinear spectroscopy system and method is that it can be configured to take one-sided measurements for translation to clinical work where an “open” hardware configuration is required.

V. Conclusion

This study tested the feasibility of a nonlinear three frequency magnetic spectroscopic method for quantitative measurement of MNPs targeted to KB and Igrov cancer cell lines and determination of MNP binding state with a linear model. After model calibration we show that it is possible to determine the content of an unknown sample. Experimentally, we prepared 25 samples of each cell type with five concentrations of cells and five concentrations of MNPs to create a 5 × 5 measurement grid and we measured the 3^rd harmonic at three input frequencies. Using these two cell lines we showed that the method is capable of successfully separating down to 2 μg of bound and unbound MNPs. This study is particularly important for the translation of this method into in vivo measurement where the quantity of MNP in both the bound and unbound states would be unknown. Based on these preliminary results and available methods for optimization of the system, we believe that quantitative imaging of targeted MNPs that are specifically bound to cancer cells will be possible in the future. Being able to successfully measure the quantity of bound MNPs is needed to support the translation of MNP-based targeted cancer diagnostics and molecular therapies.