Single toxin dose-response models revisited

Abstract

The goal of this paper is to offer a rigorous analysis of the sigmoid shape single toxin dose-response relationship. The toxin efficacy function is introduced and four special points, including maximum toxin efficacy and inflection points, on the dose-response curve are defined. The special points define three phases of the toxin effect on mortality: (1) toxin concentrations smaller than the first inflection point or (2) larger then the second inflection point imply low mortality rate, and (3) concentrations between the first and the second inflection points imply high mortality rate. Probabilistic interpretation and mathematical analysis for each of four models, Hill, logit, probit, and Weibull is provided. Two general model extensions are introduced: (1) the multi-target hit model that accounts for the existence of several vital receptors affected by the toxin, and (2) model with a nonzero mortality at zero concentration to account for natural mortality. Special attention is given to statistical estimation in the framework of the generalized linear model with the binomial dependent variable as the mortality count in each experiment, contrary to the widespread nonlinear regression treating the mortality rate as continuous variable. The models are illustrated using standard EPA Daphnia acute (48 hours) toxicity tests with mortality as a function of NiCl or CuSO₄ toxin.

1 Introduction

Modeling of the dose-response relationship and involved methodological issues has a long history, Fisher (1935), Berkson (1944, 1951), Finney (1947, 1971), to name a few. Four types of models have been developed over the years to characterize mortality rates as a function of toxin concentration: Hill, logit, probit, and Weibull. By dose-response relationship we understand the mortality probability, m among organisms exposed to a toxin with concentration, x, during a constant short period of time, typically referred to as sigmoid function. For example, in standard acute tests the number of responded (dead) organisms k_i in a beaker with toxin concentration x_i initially having n_i (typically, n_i = const) organisms alive is counted after 48 hours of the exposure where i = 1, 2, ‥, N is the number of beakers/experiments, USEPA (2002). The dose-response relationship, or in our case the mortality function, specifies the probability that an organism dies within 48 hours,

$$\text{Pr}(\text{individual dies within }48\text{ hours }|x)=m(x;\mathit{\theta }),$$

where θ is a vector of parameters to be estimated from the mortality data. The number of death counts k_i among n_i individuals in the beaker with toxin concentration x_i follows a binomial distribution with probability m(x_i; θ). This fact gives rise to estimation of parameters θ using the method of maximum likelihood.

Although there exists a rich literature on the dose-response relationship it is scattered across the disciplines of epidemiology, toxicology and pharmacology. It is no wonder that the terminology and emphasis varies among these disciplines sometimes leading to confusion. The goal of this paper is to systematically describe classic models for dose-response relationships using mathematical definitions and introduce some new general concepts to help discriminate between models and identify the appropriate fields of application. Although much of the focus in the current literature is on multiple toxins, we feel that the success in these fields has been obstructed due to the lack of solid and rigorous establishment of the dose-response theory for single toxins.

This paper offers a rigorous study of the sigmoid mortality functions with a single toxin and provides concrete formulas for computing special points on the mortality curve. Special attention is given to the appropriate methods of estimation using the method of maximum likelihood (ML). We show how mortality data can be analyzed with the statistical package R using the simple a built-in function glm or a ML user-contributed R code for more complicated mortality functions.

The bulk of the work in toxicology concerns computation and analysis of LC₅₀ (or in another notation EC₅₀), like in a recent paper by Jiang and Kopp-Schneider (2015). The impetus of the present paper is our belief that more insights into the mechanism of toxicity can be gained by considering other points on the mortality curve such as where the effect of the toxin concentration changes form weak to strong or reverse, referred to as inflection points.

2 Classic dose-response relationships

Since the dose-response relationship is understood as the probability m(x) dying within short test period of time due to toxin exposure with concentration x, it must satisfy certain conditions, assuming that function m is continuous and differentiable.

The properties of the mortality function:

1. m(0) = 0 meaning that no animals die within the short test period in the absence of the toxin;

2. function m(x) is an increasing function, i.e. higher toxin concentration lead to increased mortality rate;

3. lim_x→∞ m(x) = 1 meaning that all organisms die when the toxin concentration becomes indefinitely high.

All mortality functions discussed below satisfy these properties. These three conditions imply that mortality probability is bound within 0 and 1, or 0 ≤ m(x) ≤ 1. This means that any probability cumulative distribution function (cdf) of a nonnegative random variable may serve as a mortality function. For example, the cumulative distribution function of the gamma-distribution as a mortality function was suggested by Altshuler (1981).

An important characteristic of a toxin is the ability to cause mortality. Following the rules of basic calculus, we consider the instantaneous increase of mortality, Δm, due to increase of toxin concentration from x to x+Δx. It is important to take into account the concentration level, x itself. Indeed, if x = 1 and Δx = 1 we are looking at the increase in mortality when concentration doubles. When x = 10 and Δx = 1 the concentration increases by 10% and therefore the implied rate cannot be compared with the rate at x = 1. When mortality is studied on the relative scale the following definition is justified.

Definition 1

The efficacy function, E, at the level concentration x is defined as

$$E=\underset{\mathrm{\Delta }x\to 0}{\text{lim}}\frac{\mathrm{\Delta }m}{\mathrm{\Delta }x/x}=\frac{dm}{d(\text{ln }x)}.$$ (1)

Following this definition we compute the instantaneous mortality change due to the relative change of the concentration, Δx/x. Since the change of the toxin concentration should be computed on the relative scale the log transformation seems natural. Toxin efficacy defined by equation (1) allows the comparison of toxin concentrations within the mortality curve as well as across the curves. If the mortality function is viewed as cdf expressed in ln x then the efficacy function is the density function, the milestone concept of the probability theory. Geometrically, the efficacy function is the slope of the tangent line at the mortality curve plotted versus toxin concentration on the log scale.

This definition justifies expressing and plotting the mortality function and E on the log scale as m(ln x) and consequently E(ln x). The fact that it is better to plot mortality data on a log scale is well known: our definition of the efficacy just provides a theoretical justification. Since m(0) = 0 and m(∞) = 1 elementary calculus confirms that lim_x→0 E(ln x) = lim_x→∞ E(ln x) = 0, so that E reaches its maximum at some point (see below).

2.1 Four special points of the dose-response curve

First, we discuss four special points on the general sigmoid mortality curve and then illustrate them with four popular dose-response curves.

The median lethal concentration, LC₅₀ (sometimes denoted as ED₅₀ or EC₅₀) is the toxin concentration x that leads to 50% of the population death, or in mathematical terms the solution of the equation m(x) = 0.5. This point on the mortality curve is a popular way to express the killing strength of the toxin. Dose-response relationships are often symmetric around LC₅₀ on the log scale; the formal definition follows.

Definition 2

The mortality function on the log scale, m = m(ln x), is symmetric around ln LC₅₀ if

$$m(\text{ln }x-\text{ln }L{C}_{50})=1-m(\text{ln }L{C}_{50}-\text{ln }x).$$ (2)

This definition is similar to the definition of the symmetry of distribution of random variable expressed via cumulative distribution function, in our case m given by Evans et. al (2004). We will illustrate this in more detail later.

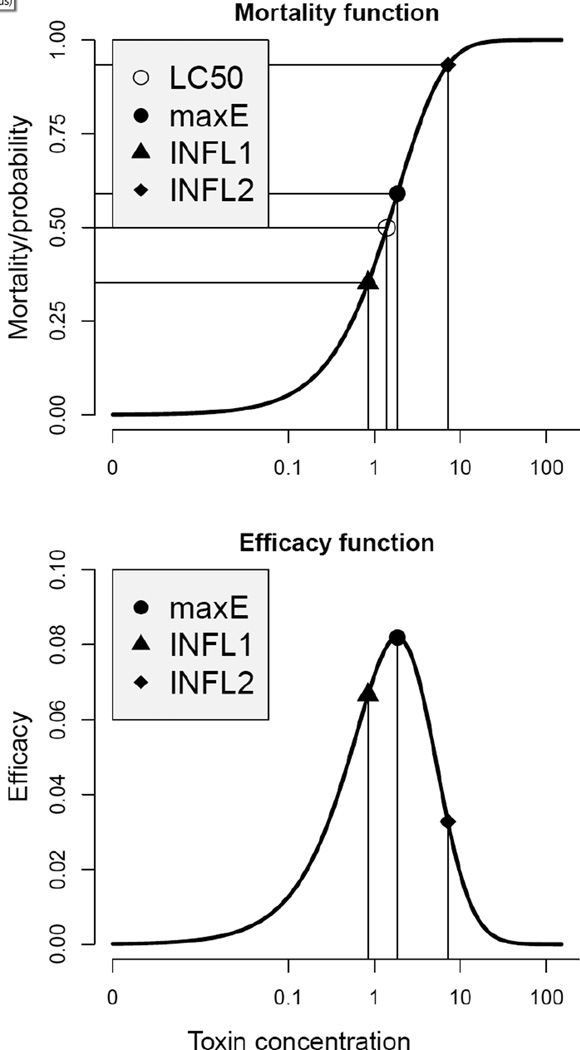
Below we introduce three other special points in terms of the toxin efficacy using the E curve as described above; see Figure 1 for the illustration.

Figure 1.

Four special points on generic dose-response curve (top) and the respective efficacy function (bottom). Points INFL1 and INFL2 depict the toxin concentration where convexity turns to concavity.

Definition 3

The first inflection point on the E curve is where convexity changes to concavity, or in mathematical terms, this point is the least solution of the equation

$$\frac{d^{2}E(\text{ln }x)}{d\text{ ln }{x}^2}=0.$$ (3)

The point of the maximum efficacy is the solution of the equation

$$\frac{dE(\text{ln }x)}{d\text{ ln }x}=0.$$ (4)

The second inflection point is where concavity changes to convexity, and mathematically is the greatest solution of equation (3).

Inflection point equation (3) has two solutions: the smaller solution corresponds to the first inflection point, where the efficacy curve has maximum slope, and the larger solution corresponds to the second inflection point, where the efficacy curve has minimum slope. Equation (4) merely tells how to find the maximum point on the E curve: take the derivative and set it to zero (the first-order condition for maximum). If the efficacy function is viewed as the density function of the normal distribution with mean μ and standard deviation σ (probit dose-response, see below) inflection points are μ ± σ, where the slope of the density is maximum in absolute value.

The efficacy function may be viewed as a rigorous definition of the visual perception of a sigmoid curve on the log scale: the maximum efficacy point is where the mortality function has the steepest slope; the first inflection point is where the slow mortality growth turns into a rapid growth and the second inflection point is where the growth slows down.

For mortality functions symmetric around LC₅₀, the maximum efficacy occurs at LC₅₀ and the first and second inflection points are symmetric around LC₅₀. This means that four special points reduce to three because maximum efficacy occurs at LC₅₀. To prove this statement we show that the efficacy function is symmetric around LC₅₀. Indeed, differentiating equation (2) with respect to ln x we have

$$\frac{dm(\text{ln }x-\text{ln }L{C}_{50})}{d\text{ ln }x}=\frac{dm(\text{ln }L{C}_{50}-\text{ln }x)}{d\text{ ln }x}$$

that implies E(ln x − ln LC₅₀) = E(ln LC₅₀ − ln x), function E is symmetric around ln LC₅₀.

Before the first inflection point (INFL1) the rate of mortality is slow; it is highest in the interval of concentration levels [INFL1,INFL2] and after INFL2 slows down reaching maximum at maxE; see Figure 1. These points are derived from the efficacy function: point INFL1 is where convexity turns into concavity and points INFL2 where concavity turns back into convexity, and therefore may be referred to as the turning points. Loosely speaking, toxin concentrations smaller than INFL1 and larger than INFL2 may be referred to as small mortality rate concentration and within INFL1 and INFL2 may be referred to as high mortality rate concentration.

Although many authors refer to the slope of the dose-response relationship no rigorous definition is given. The following concept defines the slope as the relative rate of mortality change with respect to relative change of the toxin concentration (Glaholr et al., 2012). As we argued above, it is appropriate to measure the change of concentration on the relative change as Δx/x. By the same reasoning we need to take into account the mortality value where the change occurs. For example, as in Figure 1 a change from 0.2 to 0.2+0.1 constitutes 50% increase in mortality. On the other hand when the change is from 0.6 to 0.6+0.1 it constitutes only 17%. Thus to adequately characterize the mortality change it is more appropriate to use the relative change, Δm/m In addition, this relative change should be computed on the proportion survived because the toxin acts on living organisms which finally leads to Δm/m(m(1 − m)). These considerations give rise to the following definition.

Definition 4

The instantaneous relative mortality rate (IRMR) is defined as

$$\underset{\mathrm{\Delta }x\to 0}{\text{lim}}\frac{\frac{\mathrm{\Delta }m}{m(1-m)}}{\frac{\mathrm{\Delta }x}{x}}=\frac{1}{m(1-m)}\frac{dm}{d\text{ ln }x}=\frac{1}{1-m}\frac{d\text{ ln }m}{d\text{ ln }x}.$$ (5)

We interpret IRMR as the percent change of mortality with respect to survival proportion upon 1% change of the toxin concentration. In the general case, IRMR depends on where on the mortality curve it is computed but for the logit response dose-response it is constant, as we will see later.

The IRMR serves the same purpose as the interpretation of regression coefficients to quantify how a small change in the predictor (or explanatory variable) changes the dependent variable. For example, in linear relationship we have y = a+bx and coefficient b reflects change of y upon change of x, or in mathematical language, b = dy/dx. For a power relationship, y = Ax^b, we measure the relative change of y with respect to the relative change of x taking the derivative on the log scale, or in mathematical language, b = d ln y/d ln x, similarly to definition (5) with the only difference being that this change is on the scale of survival.

The special points introduced in this section are illustrated below on four popular dose-response models: Hill, logit, probit, and Weibull.

2.2 Hill dose-response

The most popular dose-response relationship with a single concentration is borrowed from biochemistry and expressed via the “Hill” equation

$$m_{\text{Hill}}(x)=\frac{{(x/s)}^b}{1+{(x/s)}^b},$$ (6)

where s and b are positive parameters, sometimes loosely referred to as scale and slope parameters. This function is widely used in pharmacokinetics as a part of a compartment model (Holford et al., 1981). It is easy to see that this function holds the properties of the mortality function (a–c) listed in the previous section. Also, since (x/s)^b = 1 when x = s we infer that LC₅₀ = s. The toxin efficacy is

$$E(x)=x{m}_{\text{Hill}}^{\prime }(x)=b\frac{{(x/s)}^b}{{[1+{(x/s)}^b]}^2}.$$

To find its maximum we let z = (x/s)^b and maximize function g(z) = z/(1+z)². Taking the derivative of this function and setting it to zero we obtain that maximum of g = b/4 occurs at z = 1, i.e. maximum toxin efficacy attains at x_E = s. This means that the maximum toxicity slope on the semilog scale is equal to E_max = b/4 and occurs when mortality = 1/2, i.e. when x = s = LC₅₀.

2.3 Logit dose-response

Logit dose-response is one of the oldest models used to mathematically describe the relationship between toxin concentration and implied mortality. This function is frequently used in epidemiology and known as logistic regression in statistics. It is also widely used in toxicology when it comes to parameter estimation, due in part to ample software availability. Originally the logit mortality function was used on the original scale of toxin expressed in the form e^a+bx/(1 + e^a+bx), originally studied by Berkson (1944, 1951). However, this function does not comply with condition (a) from the previous section which is why later it was used on the log scale

$$m_{\text{logit}}(\text{ln }x)=\frac{e^{a+b\text{ ln }x}}{1+e^{a+b\text{ ln }x}}.$$ (7)

Hereafter we will refer to mortality function (7) as logit on the log scale. Obviously, all three conditions (a)–(c) hold for this function. Logit mortality function on the log scale (7) is equivalent to the Hill mortality function (6) with s = e^−a/b. Note that both functions have the same slope (b) but different intercepts/scale. Consequently, we can express

$$L{C}_{50}=e^{-a/b}.$$

so that (7) turns into (6) letting a = −b ln LC₅₀.

The mortality functions discussed in this paper depend on the linear function of the log toxin concentration hereafter referred to as log-linear scale. Many properties of these functions are easier to express on the log-linear scale as well. Therefore letting

$$L=a+b\text{ ln }x,$$ (8)

we represent (7) simply as e^L/(1+e^L) with the LC₅₀ = 0 on the L scale; Scholze et al. (2001) used notation η for our L. Hereafter transformation (8) will be referred to as the log-linear transformation on the x-axis. It is simpler to define the special points of the dose-response relationship in terms of mortality—then we talk about m scale; see Table 1.

Table 1.

Five single toxin models and their four special points, D = (5p + 1) (p + 1).

		logit/Hill	probit	Weibull	1HMT logit	AHMT logit
1	Mortality function formula	$\frac{e^{a+b\text{ ln }x}}{1+e^{a+b\text{ ln }x}}$	Φ(a + b ln x)	1 − e−ea+b ln x	$1-\frac{1}{{(1+e^{a+b\text{ ln }x})}^p}$	$\frac{{(e^{a+b\text{ ln }x})}^p}{{(1+e^{a+b\text{ ln }x})}^p}$
2	Inverse mortality function	$\text{ln}\frac{m}{1-m}$	Φ−1(m)	ln(− ln(1 − m))	$\text{ln }(\frac{1}{{(1-m)}^{1/p}}-1)$	$\text{ln}\frac{m^{1/p}}{1-m^{1/p}}$
3	LC50 on the L = a + b ln x scale	0	0	ln ln 2	ln(21/p − 1)	− ln(21/p − 1)
4	IRMR on the L scale	b	$b\frac{\varphi (L)}{\mathrm{\Phi }(L)(1-\mathrm{\Phi }(L))}$	$b\frac{e^L}{1-e^{-e^L}}$	$b\frac{p(1+e^L)}{1-{(1+e^L)}^{-p}}$	$b\frac{p{(1+e^L)}^{p-1}}{{(1+e^L)}^P-e^{p^L}}$
5	Efficacy function on L scale	$\frac{b{e}^L}{{(1+e^L)}^2}$	bϕ(L)	beL−eL	$\frac{bp{e}^L}{{(1+e^L)}^{p+1}}$	$\frac{pb{e}^{pL}}{{(1+e^L)}^{p+1}}$
6	Efficacy function on m scale	bm(1 − m)	bϕ(Φ−1(m))	−b(1 − m) ln(1 − m)	$bp(1-m)(1-{(1-m)}^{\frac{1}{p}})$	$pbm(1-m^{\frac{1}{p}})$
7	Maximum efficacy on L scale	0	0	0	− ln p	0
8	Maximum efficacy value	b/4	$b/\sqrt{2\pi }$	b/e	$\frac{b{p}^{p+1}}{{(p+1)}^{p+1}}$	$\frac{bp}{2^{p+1}}$
9	Maximum efficacy on m scale	1/2	1/2	(e − 1)/e ≃ 0.632	$1-\frac{p^p}{{(1+p)}^p}$	$\frac{p^p}{{(1+p)}^p}$
10	1st inflection point on L scale	$\text{ln}(2-\sqrt{3})\simeq -1.32$	−1	$\text{ln}\frac{3-\sqrt{5}}{2}\simeq -0.962$	$\text{ln }\left(\frac{3p+1-\sqrt{D}}{2p^2}\right)$	$\text{ln }\left(\frac{3p+1-\sqrt{D}}{2}\right)$
11	1st inflection point on m scale	$\frac{2-\sqrt{3}}{3-\sqrt{3}}\simeq 0.211$	Φ(−1) ≃ 0.159	$e^{-(3+\sqrt{5})/2}\simeq 0.073$	$1-{\left(\frac{2p^2}{2p^2+3p+1-\sqrt{D}}\right)}^p$	${\left(\frac{3p+1-\sqrt{D}}{3+3p-\sqrt{D}}\right)}^p$
12	2nd inflection point on L scale	$\text{ln}(2+\sqrt{3})\simeq 1.32$	1	$\text{ln}\frac{3+\sqrt{5}}{2}\simeq 0.962$	$\text{ln }\left(\frac{3p+1+\sqrt{D}}{2p^2}\right)$	$\text{ln }\left(\frac{3p+1+\sqrt{D}}{2}\right)$
13	2nd inflection point on m scale	$\frac{2+\sqrt{3}}{3+\sqrt{3}}\simeq 0.789$	Φ(1) ≃ 0.841	$e^{-(3-\sqrt{5})/2}\simeq 0.683$	$1-{\left(\frac{2p^2}{2p^2+3p+1+\sqrt{D}}\right)}^p$	${\left(\frac{3p+1+\sqrt{D}}{3+3p+\sqrt{D}}\right)}^p$

Now we find the three special points of the logit mortality curve on the log scale using the efficacy function by taking dm_logit/d(ln x),

$$E_{\text{logit}}(\text{ln }x)=b\frac{e^{a+b\text{ ln }x}}{{(1+e^{a+b\text{ ln }x})}^2}.$$

It is easier to find max E_logit on the log-linear scale in terms of L defined in (8). Then E(L) = e^L(1 + e^L)⁻² with the derivative

$$\frac{d{E}_{\text{logit}}}{dL}=b{e}^L\frac{1-e^L}{{(1+e^L)}^3}.$$

Equating this equation to zero we obtain that the maximum of the efficacy function occurs when L = 0, i.e. at x = LC₅₀ (m = 1/2). Therefore, the maximum efficacy of a toxin occurs when the mortality is 50%. To find the first and second inflection point we need to take the second derivative of function E(L) and equate it to zero. Since

$$\frac{d^2{E}_{\text{logit}}}{d{L}^2}=b{e}^L\frac{e^{2L}-4e^L+1}{{(1+e^L)}^4}$$

and letting u = e^L, the inflection points satisfy the quadratic equation u² − 4u + 1 = 0 with two solutions $u_{1,2}=2\pm \sqrt{3}$. Furthermore, since the logit mortality function can be expressed as m(u) = u/(1 + u), we obtain that the first and second inflection points occur when mortality is

$$m_1=\frac{2-\sqrt{3}}{3-\sqrt{3}}\simeq 0.211,\hspace{1em}{m}_2=\frac{2+\sqrt{3}}{3+\sqrt{3}}\simeq 0.789.$$ (9)

The fact that the two mortalities add to 1 is not surprising due to symmetry. Finally, we can describe how the toxin affects organisms in terms of their mortality rate: 1) the toxin weakly affects organisms until mortality reaches 0.211; 2) after 0.211 the mortality accelerates and reaches its maximum when 50% of organisms are dead; 3) mortality rate remains high until it reaches 0.789 after which it begins to slow down.

The logit mortality curve is special because using elementary calculus one can show that IRMR=const= b. Thus, it can be rigorously proven that only for the logit mortality function IRMR=const. This property makes the logit mortality on the log scale very attractive because of ease of interpretation. For example, an increase of concentration by 1% leads to the relative increase of mortality by b%. It is worth noting that unlike previous literature where parameter b was vaguely referred to as the slope we rigorously define b in terms of IRMR.

2.4 Probit dose-response

Probit link was advocated by Finney (1971) to study the probability of mortality as a function of toxin concentration. As in the logit case, early authors considered probit on the original scale; later it was suggested to use the log scale so that the mortality function takes the form

$$m_{\text{probit}}(\text{ln }x)=\mathrm{\Phi }(a+b\text{ ln }x),$$ (10)

where Φ is the cumulative distribution function of the standard normal distribution,

$$\mathrm{\Phi }(L)={\int }_{-\mathrm{\infty }}^L{e}^{-u^2/2}du,$$

and a and b are parameters subject to estimation. Note that a and b in the logit and probit models are different; we simply use the same symbols not to overwhelm ourselves with the notation. It is well known that logit and probit functions are close upon rescaling (Amemiya, 1981; Demidenko, 2013), namely,

$$\frac{e^L}{1+e^L}\simeq \mathrm{\Phi }\left(\frac{L}{\sqrt{8/\pi }}\right).$$

Since $\sqrt{8/\pi }\simeq 1.6$ parameters of the logit (7) and probit (10) are approximately related through the coefficient 1.6.

Probit mortality function emerges via threshold in a simple linear model with a latent normally distributed variable (Mittelhammer et al., 2000). More specifically, let us assume that y represents the damage of a vital organ due to toxin x related as linear regression on the log scale, y = a_* + b_* ln x + ε, where ε is an unobservable normally distributed random variable with zero mean and variance σ². The damage variable is latent and unobservable but if it exceeds a threshold t the organisms dies. Therefore the mortality probability turns into the probit mortality function,

$$\text{Pr}(a_{*}+b_{*}\text{ ln }x+\epsilon >t)=\mathrm{\Phi }(-\frac{t-a_{*}-b_{*}\text{ ln }x}{\sigma })=\mathrm{\Phi }(a+b\text{ ln }x)$$

upon a reparametrization., a = (a_* − t)/σ and b = b_*/σ.

Now we find four special points for the probit mortality function. 50% mortality of the population occurs when L = a + b ln x = 0, i.e. LC₅₀ = e^−a/b. Since 1 − Φ(z) = Φ(−z), the condition (2) holds and probit is a symmetric mortality function. This means that (a) maximum toxin efficacy occurs at LC₅₀, and (b) the first and second inflection points are symmetric around LC₅₀. The efficacy function takes the form

$$E_{\text{probit}}(\text{ln }x)=b\varphi (a+b\text{ ln }x)$$

with maximum $b/\sqrt{2\pi }$ and a + b ln x = 0, i.e. when x = LC₅₀, where ϕ is the probability density function of the standard normal distribution. To find the inflection points we express E_probit(L) = hϕ(L) and solve the equation $E_{\text{probit}}^{″}(L)=0$. Since $E_{\text{probit}}^{″}(L)=h\varphi (L)(L^2-1)$ we conclude that the second and first efficacy points are at L = ±1, respectively. In the case of mortality values they are

$$m_1=\mathrm{\Phi }(-1)\simeq 0.159,\hspace{1em}{m}_2=\mathrm{\Phi }(1)\simeq 0.841.$$

Compared to logit values (9), we deduce that the toxic effect takes off at lower concentration and persists to higher concentration in probit compared to logit mortality function.

2.5 Weibull dose-response

The Weibull (sometimes referred to as Gumbel) dose-response relationship is another popular toxicity model (Carlborg, 1981; Christensen, 1984, 1985). This model emerges in connection to Poisson distribution (Demidenko, 2013). In this model, we assume that there are many vital organs affected by the toxin and k denotes the number of organs lethally damaged. This number is modeled via Poisson distribution conditional on the toxin concentration x as

$$\text{Pr}(k\text{ organs are damaged }|x)=\frac{1}{k!}{e}^{kL-e^L},\hspace{1em}k=0,1,\dots ,$$

where it is denoted L = a + b ln x to simplify the exposition and k = 0 indicates that no organs are affected (again, these a and b are not the same as in the logit and probit models). The whole organism dies if at least one organ is lethally damaged. Since the probability that no organs will be damaged is Pr(k = 0) = e^−eL the mortality function takes the form

$$m_{\text{Weibull}}(\text{ln }x)=1-e^{-e^{a+b\text{ ln }x}}.$$ (11)

This probability function has the link log(− log(1 − m_Weibull)) in the language of generalized linear model (GLM) and that is why it is called a complementary log-log dose-response relationship. Also, 1−e^−eL is the cumulative distribution function of the Weibull distribution that explains the name. Since this mortality function belongs to the family of GLMs the software is readily available.

It is easy to see that all three properties (a)–(c) hold for the Weibull mortality function. However, the Weibull function is asymmetric unlike logit or probit.

Now we identify the four special points on the Weibull curve. Solving 1 − e^{−ea+b ln x} = 0.5 leads to

$$\text{ln }L{C}_{50}=\frac{\text{ln ln }2-a}{b}\simeq -\frac{0.367+a}{b}.$$

The efficacy function takes the form

$$E_{\text{Weibull}}(\text{ln }x)=b{e}^{a+b\text{ ln }x-e^{a+b\text{ ln }x}}$$

with maximum w/e attained at a + b ln x = 0 or when mortality = (e − 1)/e = 0.632. Note that the maximum of the efficacy function occurs not at LC₅₀ where mortality is 0.5 as for logit and probit but later. To find the first and second inflection point we solve the equation e^3L−eL − 3e^2L−eL + e^L−eL = 0 or equivalently υ² − 3υ + 1 = 0 where υ = e^L. This equation has two positive solutions with ${\upsilon }_{1,2}=(3\pm \sqrt{5})/2$ corresponding to mortality values

$$m_1=e^{-\frac{3+\sqrt{5}}{2}}\simeq 0.073\hspace{1em}{m}_2=e^{-\frac{3-\sqrt{5}}{2}}\simeq 0.683.$$

Note that compared with logit and probit, Weibull function implies that the toxic effect is smaller at lower concentrations. As before, we interpret m₁ and m₂ as the range within which the mortality efficacy is maximum.

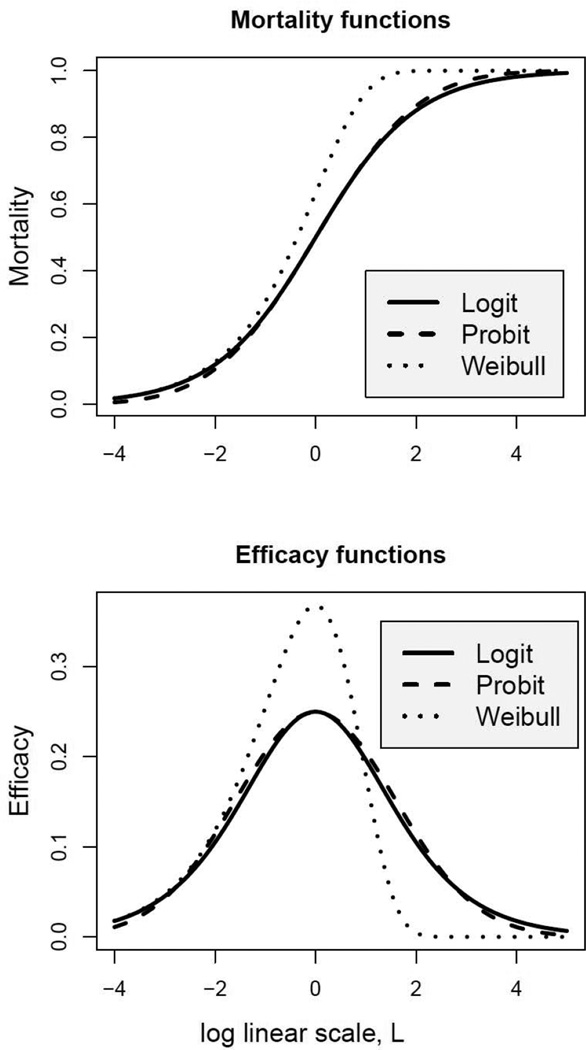
3 Comparison of three mortality functions

Three mortality curves with respective efficacy functions are plotted with L on the x-axis and the maximum toxin efficacy at zero (Hill equation is not considered here because it can be expressed through logit), see Figure 2. Probit and logit are very close after linear transformation: the maximum absolute difference < 0.01 as reported in Demidenko (2013, p. 336) and as shown in Figure 2. The Weibull mortality curve is asymmetric and resembles behavior of logit for lower toxin concentration. This statement is supported by the following calculus argument: when x is small L = a + b ln x is large and negative (−4 on the x-axis in the figure), so that y = e^L ≃ 0. Now using a well known approximation e^y ≃ 1+y for small y and letting y = e^L we obtain

$$m_{\text{Weibull}}=1-\frac{1}{e^{e^L}}=1-\frac{1}{e^y}\simeq 1-\frac{1}{1+y}=1-\frac{1}{1+e^L}=\frac{e^L}{1+e^L}=m_{\text{logit}}.$$

The Weibull mortality function is steeper then logit and probit resulting in a higher efficacy of the toxin at L = 0. Once it reaches the maximum it drops to zero fast; see the bottom plot in Figure 2. This suggests that Weibull function is adequate to model toxic effects when organisms experience a tipping point in their tolerance when exposed to high toxin concentration

Figure 2.

Three popular mortality curves (top) and their efficacy functions (bottom).

4 Extensions of classic dose-response relationships

Two types of extensions are offered in this section to address complexities common among acute toxicity test data sets. The first extension reflects the fact that organisms, especially complex organisms, can repair the damage leading to a multi-target model. The second extension reflects the fact that during toxin exposure organisms can die due to natural reasons meaning that mortality occurs even when toxin concentration is zero. The extended versions increase the number of parameters from two to three. Unlike logit, probit, and Weibull, these functions require special software to estimate the parameters by method of maximum likelihood (see below).

4.1 Multi-target models

The concept of the multi-target model is borrowed from the cell survival models as described in Casarett (1968), Hall (2000), and Hanin et al. (1993). It is assumed that the toxin affects p receptors of the organism (p ≥ 1). Two types of the multi-target model are suggested.

In the first type, it is assumed that the whole organism dies if at least one of p receptors gets hit with concentration x. Assuming that the toxin individually affects each receptor with mortality function m(ln x) and hits are independent, the probability that at least one receptor is destroyed (i.e. organism dies) is

$$m_{1\mathrm{H}\mathrm{M}\mathrm{T}}(\text{ln }x)=1-{(1-m(\text{ln }x))}^p,$$

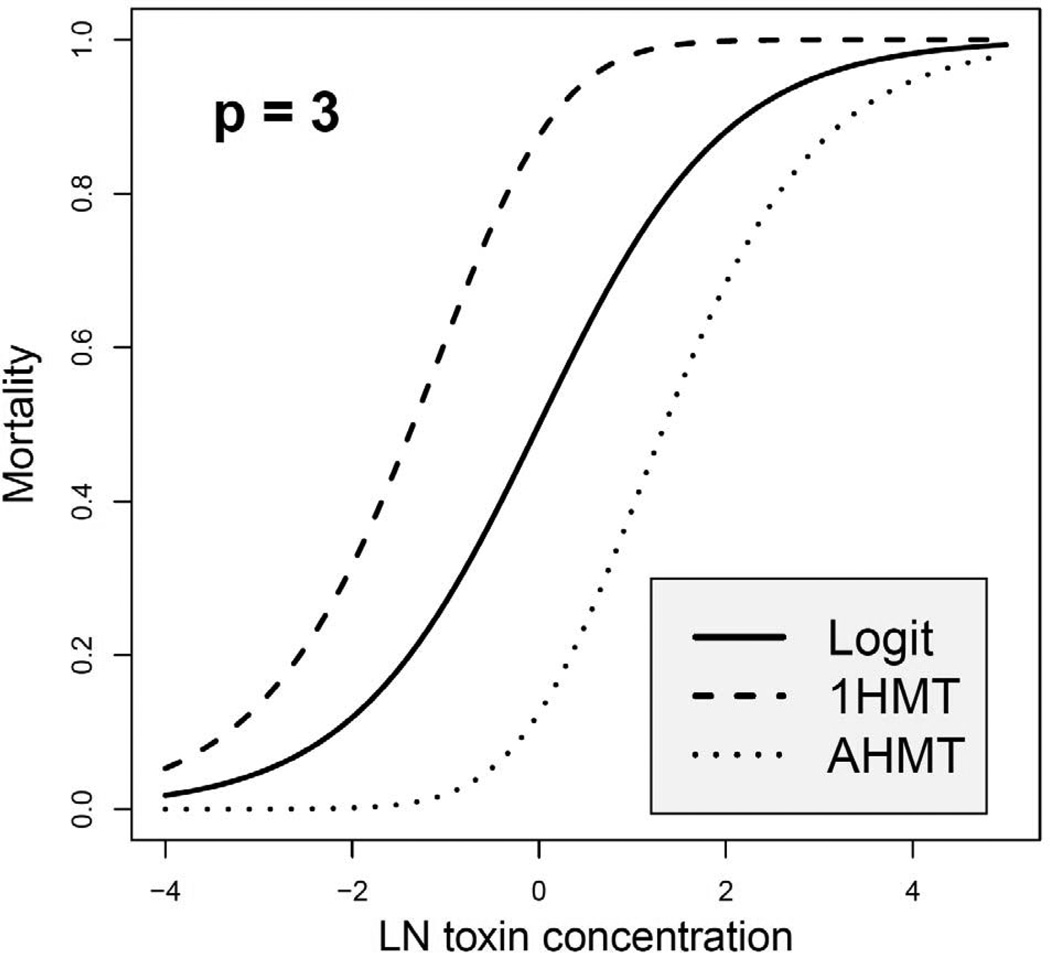
where 1HMT stands for one-hit-multi-target (Demidenko, 2013, p. 543). This model has several attractive properties: (1) when p = 1 (one receptor) the 1HMT model reduces to an individual mortality function, (2) mortality is zero when concentration is zero, (3) m_1HMT(ln x) is an increasing function of concentration x and approaches 1 if x → ∞, (4) m_1HMT(ln x) > m(ln x) for p > 1 reflecting the fact that each receptor is vital and therefore for more complex organisms survival rate declines. See Figure 3 for an illustration.

Figure 3.

Multi-target mortality functions based on the logit on the log scale with p = 3.

In the second type, it is assumed that the organism dies only if all p receptors get hit. Then the mortality function takes the form

$$m_{\mathrm{A}\mathrm{H}\mathrm{M}\mathrm{T}}(\text{ln }x)=m^p(\text{ln }x),$$

where AHMT stands for all-hit-multi-target. This model has the same three properties listed above but has a better survival meaning that m_AHMT(ln x) < m(ln x) for p > 1 reflecting the possibility of repair and healing when not all receptors get destroyed.

Any mortality function m discussed above can be used to create a multi-target mortality function.

4.2 Multi-target logit models

In this section, we illustrate the multi-target models using the logit mortality function on the log scale (7).

The one-hit-multi-target logit model takes the form

$$m_{1\mathrm{H}\mathrm{M}\mathrm{T}\text{ logit}}(\text{ln }x)=1-\frac{1}{{(1+e^{a+b\text{ ln }x})}^p},\hspace{1em}p\ge 1.$$

Scholze et al. (2001) refers to this function as Generalized Logit II. According to our interpretation, parameter p reflects the multiplicity of receptors’ damaged and unlike standard logit, it is not symmetric. Importantly, parameter p can be estimated along with a and b using dose-response data. Now we find the four special points of this curve. Solving equation m_{1HMT logit}(ln x) = 0.5 we determine that LC₅₀ on the L scale is ln(2^1/p − 1). The efficacy function of the log scale takes the form

$$E_{1\mathrm{H}\mathrm{M}\mathrm{T}\text{ logit}}(\text{ln }x)=\frac{bp{e}^{a+b\text{ ln }x}}{{(1+e^{a+b\text{ ln }x})}^{p+1}}.$$

Letting L = a + b ln x the maximum of this function reduces to the maximum of e^L(1 + e^L)^−(p+1). Differentiating this function with respect to L we find that maximum toxin efficacy occurs at e^L = 1/p, i.e. when mortality is 1−p^p(1+p)^−p. To find the first and second inflection point we differentiate the efficacy function twice and arrive at two solutions

$$L_1=\text{ln }\left(\frac{3p+1-\sqrt{D}}{2p^2}\right),\hspace{1em}{L}_2=\text{ln }\left(\frac{3p+1+\sqrt{D}}{2p^2}\right).$$

where D = (5p + 1) (p + 1) is the discriminant, corresponding to the mortality values

$$m_1=1-{\left(\frac{2p^2}{2p^2+3p+1-\sqrt{D}}\right)}^p,\hspace{1em}{m}_2=1-{\left(\frac{2p^2}{2p^2+3p+1+\sqrt{D}}\right)}^p.$$

It is possible to check that when p → 1 these values approach the mortality values given by (9).

The all-hit-multi-target logit model (Generalize Logit I in terminology of Scholze) takes the form

$$m_{\mathrm{A}\mathrm{H}\mathrm{M}\mathrm{T}\text{ logit}}(\text{ln }x)=\frac{{(e^{a+b\text{ ln }x})}^p}{{(1+e^{a+b\text{ ln }x})}^p},\hspace{1em}p\ge 1.$$

The four special points (LC₅₀, maximum toxin efficacy, 1st and 2nd inflection points) for multi-target logit models are presented in Table 1 in the last column.

4.3 Nonzero mortality models

Real experiments show that some organisms die of natural causes even during short experiments (e.g. 48 hour), when the toxin concentration is zero. The EPA acute toxicity test methods require less than 10% mortality in the controls for an experiment to be considered a quality test and therefore included in further analysis, USEPA (2002), Shaw et al. (2006). However, no account of this natural mortality is taken into consideration in the analysis. To address this problem we modify the models adding a new parameter r that reflects the rate of natural death over a constant period of time (e.g. 48 hours), that leads to a nonzero mortality model,

$$m_{\mathrm{N}\mathrm{D}}(\text{ln }x)=r+(1-r)m(\text{ln }x).$$

This modification is not new, e.g. Altshuler (1981) refers to this modification as the Abbot’s correction. The basis for the nonzero mortality model is the fact that the proportion of dead organisms is the sum of those who died naturally plus those affected by the toxin. The latter term is the proportion of natural survivors 1 − r times the mortality m caused by the toxin, i.e. (1 − r)m.

4.4 Five single toxin models: summary table

Table 1 presents formulas for the five single toxin models and the respective IRMR and efficacy functions along with the four special points on the log-linear scale (L) and mortality (m) scale: LC₅₀, maximum toxin efficacy, and two inflection points. For the latter three points, we present formulas on two scales: the log-linear scale, L = a + b ln x (the x-axis) and the mortality rate, m (the y-axis). The advantage of the log-linear scale is that it is parameter-independent and therefore, once parameters a and b are estimated, the respective toxin concentration can be simply derived as x = e^(L−a)/b. According to our approach, the response to toxin splits into three intervals: (1) weak response, from 0 to the 1st inflection point, (2) strong response, from the 1st to the 2nd inflection point with the maximum efficacy in between, and (3) finally, returning to weak response after the 2nd inflection point. For the majority of single toxin models maximum toxin efficacy (Table 1, line 9) attains at LC₅₀, due to symmetry. In the logit model, for example, organisms react slowly to the toxin to the point at which mortality reaches 21%; between 21% and 79% toxin efficacy is high, peaking at 50% mortality; after mortality reaches 79% the differential effect of the toxin slows down. Line 4 presents formulas for instantaneous relative mortality rate (IRMR). For the logit model, this rate is constant across all concentration values and equals b. As mentioned above, this is a characteristic and unique property of the logit model.

5 Estimation

Recovering (estimating) parameters of dose-response relationship from the data is an important task for scientists and regulators. Since mortality functions have a sigmoid shape the linear least squares does not apply. Here we critic the widespread approach for estimating parameters using the nonlinear regression because the variation of the mortality rate is not constant across the dose-response curve, e.g. the variation is close to zero when m(x) is close to 0 or 1. Instead, we advocate the maximum likelihood (ML) method for estimation by referring to the number of dead (counts) which follow the binomial distribution, not the proportion of dead and using the normal distribution as in nonlinear regression.

5.1 Link plot

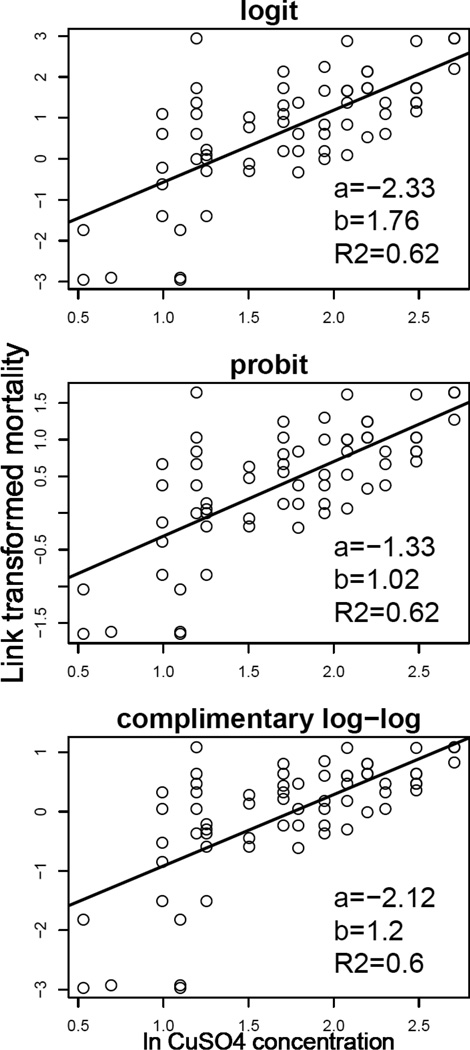
An advantage of the logit, probit and Weibull mortality functions is that they belong to the GLM family and therefore can be specified by a link function, or in other words, by a transformation from the mortality proportion to the log-linear scale, L = c + b ln x. For example, using the logit mortality function the link is $\text{ln}\frac{m}{1-m}$. The other two links are presented in Table 1, line 2. Not all mortality functions belong to the GLM family and therefore the linearizing transformation may not exist, such as for multi-target or nonzero mortality functions.

The GLM links can be used for a simple visualization by transforming the observed mortality rate m_i using the link function and plotting them against the log toxin concentration; hereafter such plots will be referred to as link plots. The better the fit by a linear function the better the dose-response explains mortality proportion. Simply put, if the transformed mortality rates fall around a straight line the mortality function is correct.

An example of the utility of a link plot is shown in Figure 4 using Daphnia acute toxicity tests with toxin CuSO₄. The y-axis of each point is the transformed mortality rate as the proportion number of dead animals to the total number of animals in the ith experimental unit (e.g. beaker) and the x-axis is ln x_i. The intercept and slope of the straight line are approximations of the respective parameters in the models specified by equations (7), (10), and (11). The coefficient of determination R² (squared correlation coefficient) characterizes the quality of the straight line fit. For example, R² = 0.62 means that 62% of the variation in the transformed mortality rate is explained by the toxin. As follows from this plot, the variation is fairly high with logit and probit having very similar configuration of points and coefficient of determination. The complementary log-log link has a slightly worse fit with R² = 0.6.

Figure 4.

Three link plots for Daphnia mortality data with CuSO₄ toxin.

5.2 Nonlinear regression versus GLM

Typically, the nonlinear least squares is used for estimation of dose-response relationships assuming that the model takes the form of the nonlinear regression

$$y_i=m(x_i;\mathit{\theta })+{\epsilon }_i,\hspace{1em}i=1,2,\dots ,n,$$ (12)

where y_i is the response variable and ε_i is the error term with zero mean and constant variance, σ². The errors are assumed normally distributed and the maximum likelihood turns into minimization of the residual sum of squares as used in Bates and Watts (1988), Seber and Wild (1989), Tallarida (2000), Manzo et al. (2013), Trögl et al. (2013), and more recently Gadagkar and Call (2015). The nonlinear regression model (12) is based on the assumption that the response variable is continuous and unbound. However, this assumption is not valid for fitting sigmoid curves with mortality data as the proportion of dead for which 0 ≤ y_i ≤ 1 due to the additive error term ε_i. Moreover, the errors cannot be symmetric. Indeed, if the error term ε_i has a symmetric distribution, according to model (12), the proportion of dead for zero concentration (ln x = −∞) is Pr(ε > 0) = 0.5, which contradicts biological expectation. Another troubling feature of the nonlinear regression approach is that the confidence intervals for mortality may be outside (0, 1) and contain values, such as −10% or 110%. Although some authors, including Ritz (2010), hint at the possibility of using the weighted nonlinear least squares to correct the situation, it is unclear how to determine the weights. Unfortunately, the method of nonlinear regression became very popular for estimation of sigmoid curves when values of the response variable belong to the unit interval as described by Scholze et al. (2001). A disturbing fact is that there is a statistical package drc for R based on the nonlinear least squares for dose-response models estimation, contributing to a wide usage of the model (12).

We advocate the generalized linear model (GLM) approach using the binomial distribution assumption to estimate the mortality function as the probability of an individual organism to die from the toxin concentration x_i. Disadvantages on nonlinear regression and the appropriateness of GLM for estimation of the mortality function using the binomial distribution of the number of dead was discussed previously by Kerr and Meador (1996) and more recently Iwasaki and Brinkman (2015). Here we criticize model (1) on statistical grounds.

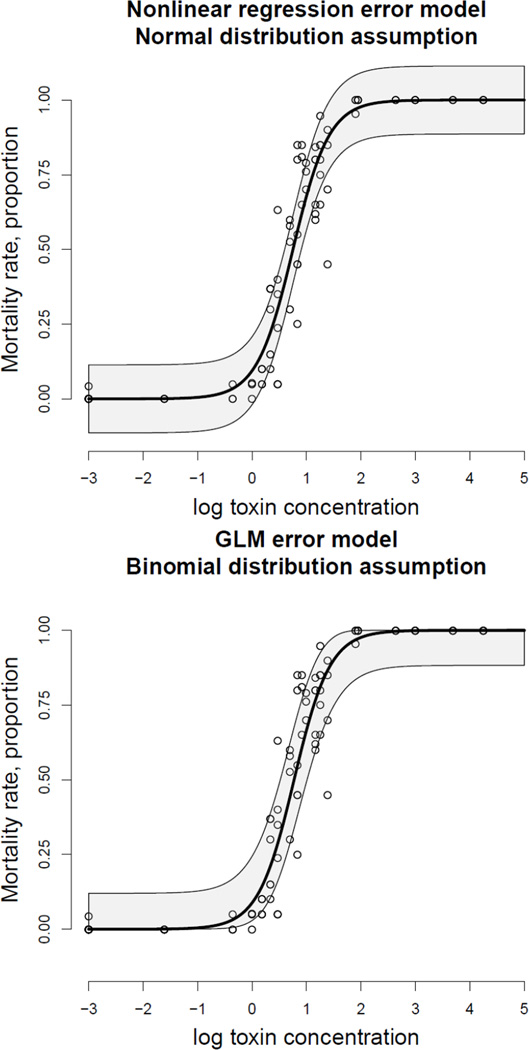
Denote n_i and k_i the number of animals before toxin exposure and the number of dead animals after exposure in the ith experimental unit. Since m(x; θ) defines the mortality probability, k_i follows the binomial distribution for each toxin concentration, x. The respective statistical model belongs to the family of GLM specified by the link listed in Table 1. We illustrate two approaches for estimation of dose-response relationships using two assumptions on the distribution of the response mortality rate in Figure 5. We use actual mortality data fitted with the logit dose-response using two statistical models and corresponding confidence region (shaded) with an approximate 65% coverage probability to emphasize the effect of the error model; the exact confidence region for binomial proportion is computed based on the classic method (Clopper and Pearson, 1934, Fleiss et al., 2003). The traditional normal distribution and the respective nonlinear regression are inadequate statistical models for mortality data because they imply that the proportion of dead is negative or greater than 1 with probability around 0.5 for small or high toxin concentration, respectively. In contrast, the binomial distribution assumption and the respective GLM are adequate for mortality data and comply with the fact that y_i ∈ [0, 1]. Although the parameter estimates from the two models may be close, their standard errors and respective significance testing results may be quite different. In short, estimation of mortality function using nonlinear regression does not reflect the probabilistic nature of the mortality event and is statistically inefficient.

Figure 5.

Two distribution assumptions and respective statistical models for estimation of the mortality dose-response curve. The nonlinear regression is an inappropriate model because errors around the curve cannot be symmetric without violating the assumption that the mortality rate belongs to the interval [0, 1]. To the contrary, the GLM model complies with the requirement that mortality is within [0, 1].

5.3 Maximum likelihood estimation for a general mortality function

Classic mortality functions (logit, probit and Weibull) can be estimated by method of maximum likelihood based on the GLM (Simpson et al. 1996) using the existing software CatReg as a component of BMDS developed at US Environmental Protection Agency (USEPA) with free download at https://www.epa.gov/bmds/catreg or PROAST developed at European Food Safety Authority (EFSA) with free download at http://www.rivm.nl/en/Documents_and_publications/Scientific/Models/PROAST. Alternatively, we suggest to use statistical package R (2014) or the maximum likelihood algorithm described below to estimate non-standard multi-target or nonzero mortality functions presented above (the R code is found online as a part of Supplementary material). Both agencies issued guidance documents on the Benchmark dose (BMD) approach (Budtz-Jørgensen et. al, 2001), that clarify modeling of dose-response relationships and their use for risk assessment and can be found at https://archive.epa.gov/raf/web/html/benchmarkdose.html and http://www.efsa.europa.eu/en/supporting/pub/113e.

As was indicated above, the binomial distribution for the count of dead adequately reflects the probabilistic nature of mortality of an individual due to toxin. This section describes how to estimate the parameters of the dose-response relationship by the method of maximum likelihood in the framework of GLM [28].

If m(z_i; θ) is the probability of dying from a toxin with concentration z_i = ln x_i the number of dead organisms, k_i among n_i individuals follows the binomial distribution with the log-likelihood

$$l(\mathit{\theta })=\sum _{i=1}^N[(n_i-k_i)\text{ ln }(1-m(z_i;\mathit{\theta }))+k_i\text{ ln }m(z_i;\mathit{\theta })].$$ (13)

Maximization of this function yields maximum likelihood estimate for θ, the vector of unknown parameters. This function is maximized iteratively using the Fisher scoring algorithm

$${\mathit{\theta }}_{s+1}={\mathit{\theta }}_s+{\mathbf{H}}_s^{-1}{\mathbf{g}}_s,\hspace{1em}s=0,1,\dots ,$$ (14)

where g_k and H_k are the gradient of the log-likelihood function and the information matrix (expected Hessian) evaluated at the sth iteration which are as follows:

$$\mathbf{g}=\frac{\partial l}{\partial \mathit{\theta }}=\sum _{i=1}^N\frac{k_i-m_i(\mathit{\theta })n_i}{m_i(\mathit{\theta })(1-m_i(\mathit{\theta }))}{ṁ}_i(\mathit{\theta }),$$

$$\mathbf{H}=\sum _{i=1}^N\frac{n_i}{m_i(\mathit{\theta })(1-m_i(\mathit{\theta }))}{\mathbf{ṁ}}_i(\mathit{\theta }){\mathbf{ṁ}}_i^{\prime }(\mathit{\theta }),$$

where ṁ_i is the vector derivative of m_i with respect to unknown parameters. For example, for standard logit and 1HMT logit the vectors of the derivatives with respect to unknown parameters are:

$${\mathbf{ṁ}}_i(a,b)=\left[\begin{array}{c}\hfill \frac{e_i}{{(1+e_i)}^2}\hfill \\ \hfill \frac{e_i{z}_i}{{(1+e_i)}^2}\hfill \end{array}\right],\hspace{1em}{\mathbf{ṁ}}_i(a,b,p)=\left[\begin{array}{c}\hfill \frac{p{e}_i}{{(1+e_i)}^{p+1}}\hfill \\ \hfill \frac{p{e}_i{z}_i}{{(1+e_i)}^{p+1}}\hfill \\ \hfill \frac{\text{ln}(1+e_i)}{{(1+e_i)}^p}\hfill \end{array}\right],$$

respectively, where e_i = exp(a + b ln x_i). For hypothesis testing, e.g. p = 1 in the 1HMT or r = 0 in the nonzero mortality models, we need standard errors which are estimated using the inverse of the information matrix H evaluated at the final iteration. Logit, probit and Weibull mortality functions are special cases of GLM with built-in MLE routines in many statistical packages including R. For other mortality functions the iterations (14) are required to get the MLE for parameter vector θ. To illustrate the utility of this method the following example is provided.

5.4 Daphnia mortality acute tests

In this section we discuss how to estimate the mortality functions in R using data from the originally conducted Daphnia toxicity tests, following slightly modified EPA standard acute testing methods (Shaw et al., 2006).

Mortality functions logit, probit and complementary log-log (Weibull) are built-in link functions and estimated in R as members of the binomial GLM. The initial number of animals per experimental unit (n), the number of (dead) animals responding to treatment (k), and the log toxin concentration (ln x) are the only data needed as shown in the data frame da.mort. For example, the data may look like this:

> da.mort

    n k lnx

1 20 4 −1.234

2 21 12 3.942

3 20 1 −2.670

4 20 19 5.487

…

To estimate the logit/Hill mortality function the following command is issued:

out.glm=glm(cbind(k,n−k)˜lnx,data=da.mort,family=binomial("logit"))

The result of the run is saved in variable out.glm. To see the summary output one issues summary(out.glm). For our Daphnia data set example the summary is as follows:

Call:

glm(formula=cbind(k,n−k)˜lnx,family=binomial("logit"),data=da.mort)

Deviance Residuals:

 Min 1Q Median 3Q Max

−2.52302 −0.85369 0.05411 0.59702 2.97333

Coefficients:

           Estimate Std.  Error z value Pr(>|z|)

(Intercept) −3.9961 0.2624 −15.23   <2e-16 ***

lnx          2.5515  0.1446   17.65  <2e-16 ***

---

Signif. codes:   0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

 Null deviance:  1447.76 on 93 degrees of freedom

Residual deviance:  150.92 on 92 degrees of freedom

AIC: 308.77

Number of Fisher Scoring iterations:  6

As follows from this run, the ML estimates for a and b are −3.9961 and 2.5515 in the notation (7), respectively. To run probit and Weibull functions we use "probit" and "cloglog" in the binomial argument instead.

Five mortality functions were fit to the Daphnia acute tests data using binomial distribution; see Figure 6. All five curves give similar fits. The maximum of the log-likelihood function (13) is a well established criterion by which we judge what model is better (the larger l the better the model). A convenient property of 1HMT and AHMT models is that they are reduced to logit when p = 1 (such statistical models are called nested models). According to the classical likelihood-ratio test −2 × (loglik_logit−loglik_1HMT) has the chi-square distribution with one degree of freedom, [22]. Since the value of the test statistic = −2×(−769.3+768.8) = 1.0, we obtain the p-value = 0.317 and therefore the null hypothesis that 1HMT coincides with logit cannot be rejected. Simply put, for this particular example, the logit model would be the right choice and models 1HMT and AHMT are statistically indifferent.

Figure 6.

Five toxin models for NiCl in Daphnia tests.

Four special points with five dose-response mortality and NiCl as the toxin are presented in Table 2. The NiCl LC₅₀ concentrations, as well as concentrations where the rate of mortality reaches its maximum (Max rate) are close in all five curves. However, the 1st and 2nd inflection points differ significantly despite the fact that curves are similar, as follows from Figure 6. Interestingly, logit yields a wide interval for the high rate mortality (from 0.56 to 7.7 mg/L). Much tighter range is generated by 1HMT and AHMT curves. Among classic dose-responses the probit mortality function is closest to 1HMT and AHMT.

Table 2.

Four special points on the NiCl (mg/L) scale for five dose-response models.

	Dose-response NiCl toxin model
Special point	logit/Hill	probit	Weibull	1HMT logit	AHMT logit
LC50	2.08	2.07	2.24	2.12	2.11
Max rate	2.08	2.07	2.68	2.20	2.38
1st inflection	0.56	0.77	1.66	1.41	1.46
2nd inflection	7.77	5.66	4.32	3.42	3.31
log-likelihood	−769.3	−791.9	−774.1	−768.8	−768.4

6 Discussion and summary points

This work offers a rigorous study of dose-response relationships and the associated calculus-defined curve’s features and special points of interest. Specifically, our major contributions are summarized as follows:

1. In previous studies, the coefficient at the log toxin concentration was loosely referred to as slope coefficient. We provide a rigorous interpretation of the coefficient via the definition of the instantaneous relative mortality rate (IRMR). For the logit model this coefficient is constant across all values of the toxin concentration.

2. The efficacy function of the toxin is introduced as the lethal ability on a relative scale. Three points with respective toxic effects are distinguished: 1) for toxin concentrations smaller than the first inflection point organisms react slowly to toxin, 2) from the first to the second inflection point the differential effect of the toxin is high reaching the maximum somewhere in the middle, and 3) for toxin concentrations higher than the second inflection point the toxic effect declines.

3. New interpretation of parameter p in 1HMT and AHMT is provided as the number of receptors affected by the toxin. For 1HMT, the organism dies if at least one receptor is destroyed and for AHMT the organism dies only after all receptors are destroyed.

4. A unified statistical methodology for estimation of mortality rate as a function of dose using binomial regression model is proposed. It indicates that the widespread approach to estimate the mortality rate function using the nonlinear regression technique is not efficient.

5. The mathematical analysis of five toxin models and the respective special points is summarized in Table 1. These models have been applied to Daphnia acute test data and compared using the likelihood-ratio test along with four special points presented in Table 2.

Traditionally, the dose-response curves are characterized by the toxin concentration that kills 50% of organisms, LC₅₀. This work is built on the recognition of other important points on sigmoid curves that characterize the toxicity effect and as such can be used in various disciplines. For example, the 1st inflection point can be used in epidemiology and environmental science as the maximum admissible threshold for a pollutant concentration. The range of concentration from the 1st to the 2nd inflection point has maximum killing efficacy and may be considered as can be used as the minimal dose of a pesticide to kill a pest. The traditional LC₅₀ to characterize the dose response curve does not match the scope of epidemiology and pharmacology: the domain of these sciences at the tails of the dose-response relationship, respectively, not in the middle. We believe that inflection points are more informative to characterize the strength of pollutant or drug or the entire range of the toxin concentrations.

The present work uses mortality as the endpoint of the toxicity outcome. As noted by one of the reviewers, our developments can be applied to dose-response curves with other endpoints, such as histopathology lesions, malformations, cancer, or disease incidence if the response to toxin follows a sigmoid shape.

A common feature of toxicity tests is the substantial variation of mortality especially in the vacinity of LC₅₀ which makes the choice of the model challenging, see Figure 6. It is a matter of future research to determine whether this variation is intrinsically individual and as such irreducable or partly explained by variation among experiments/beakers. To address the latter variability the generalized linear mixed model (GLMM), which recognizes two sources of variation of response to toxin, individual and variation across beakers, can be employed (Demidenko, 2013).