Saturation-Inversion-Recovery: a Method for T₁ Measurement

Abstract

Spin-lattice relaxation (T₁) has always been measured by inversion-recovery (IR), saturation-recovery (SR), or related methods. These existing methods share a common behavior in that the function describing T₁ sensitivity is the exponential, e.g., exp(-τ/T₁), where is the recovery time. In this paper, we describe a saturation-inversion-recovery (SIR) sequence for T₁ measurement with considerably sharper T₁-dependence than those of the IR and SR sequences, and demonstrate it experimentally. The SIR method could be useful in improving the contrast between regions of differing T₁ in T₁-weighted MRI.

Graphical abstract

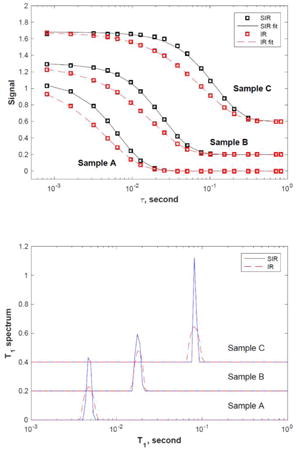
The inversion results show that both the IR and SIR methods yield the same T₁ value of 4.5 ms (sample A)，17 ms (sample B) and 79 ms (sample C), respectively. The SIR spectra are very similar to the IR ones but are noticably sharper.

1. Introduction

For many years, spin-lattice relaxation has always been measured by inversion-recovery (IR), saturation-recovery (SR), or related methods [1-3]. However, it is known that the resolution in T₁ is limited in such measurements [4-6]; it can be challenging to reliably discriminate between T₁ values less than half an order of magnitude apart. Better signal-to-noise ratio (SNR) may improve the discrimination between T₁ values with the downside of longer acquisition times [7-10].

The primary reason for such lack of T₁ resolution is that the magnetic resonance (MR) signal dependence on the relevant recovery time (recycle delay or inversion time) is smooth, not sharp [5-6]. For the saturation-recovery experiment, the signal K_SR at a recovery time τ is:

$$K_{\text{SR}}(\tau ,{\mathrm{T}}_1)=1-exp(-\frac{\tau }{{\mathrm{T}}_1})$$ (1)

This function describes the dependence of the signal on the experimental (τ) and material parameters (T₁) for a single T₁ value; we call this function the kernel of the experiment. For example, for τ = 1 s, the MR signal intensities corresponding to T₁s of 1 sec and 1.1 sec are very close: within 6% of each other. If a mixed sample contains materials with multiple T₁ values, the signal will be the sum of all components S_SR(τ) = Σ_if_i[1 – exp(−τ/T_1i)], where T_1i is the T₁ value of the i-th component and f_i is the weight of the component.

An experiment with a sharper kernel could improve the discrimination among different T₁ components [5,6]. For example, if an experiment can be performed with the following kernel:

$$K(\tau ,{\mathrm{T}}_1)={[1-exp(-\tau /{\mathrm{T}}_1)]}^2=K_2,$$ (2)

then the signal difference between T₁ = 1 and 1.1 s is increased to 12%, thus better discriminating between the different T₁s. In fact, higher exponents, such as K₅(τ, T₁) = [1 – exp(−τ/T₁)]⁵, shown in Fig. 1, will make the kernel even sharper and further improve the discrimination between different T₁ values.

Figure 1.

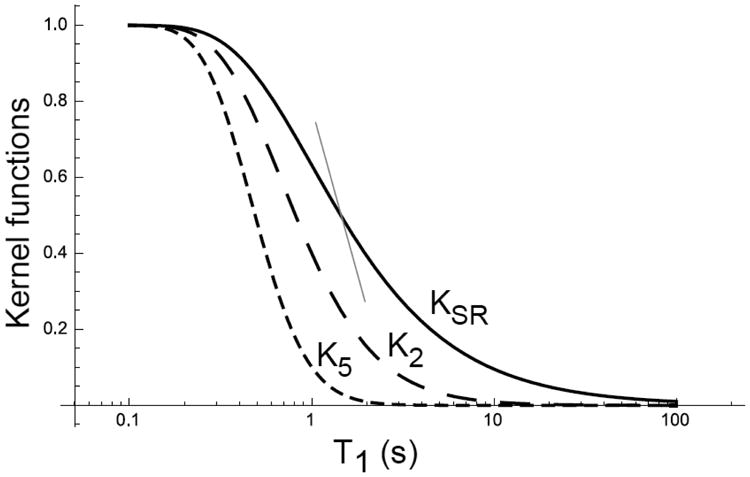
Plots of the kernel K_n for SR and other potential kernel functions at τ = 1 s. The solid curve for K_SR exhibits a gentle decay slope. The dashed and dotted curves represent K₂ and K₅, respectively, and exhibit progressively steeper slopes. The thin red line shows the slope of K₅ at K₅ = 0.5, displaced horizontally to intersect the curve for K_SR in order to highlight the difference between the two kernels.

In this paper, we describe an experimental implementation of the K₂ kernel. We designed a pulse sequence which can perform the kernel K₂ and demonstrated it experimentally on a high field spectrometer.

2. Description of the pulse sequence and experiment

2.1 Saturation-inversion-recovery (SIR) sequence

The SIR sequence is the 3-pulse sequence: 90° - τ - 180° - τ - 90° - acquisition. It can be viewed as an additional 90° pulse added in front of the IR sequence or a 180° pulse inserted in the middle of the SR sequence. The SIR sequence combines saturation and inversion processes, hence the name saturation-inversion-recovery sequence (SIR).

2.2 SIR kernel

For the SR sequence, immediately after each 90° saturation pulse, the longitudinal magnetization is zero (assuming transverse magnetization has dephased completely). Then the magnetization after the delay time τ follows Eq. 1, 1 – A, where A = exp(−τ/T₁). Thus measurement using a series of τ values generates the T₁ relaxation curve with signal recovery from zero to the thermal equilibrium value as shown in Figs. 2a and 2b. We define the thermal equilibrium normalized longitudinal magnetization equal to unity. For the IR experiment, after the 180° pulse, the magnetization is inverted and this magnetization decays from −A to zero. The recovery magnetization grows as 1 – A as τ increases; thus the total signal is 1 – 2A as shown in Figs. 2c and 2d. Such decay/recovery analysis is based on the coherent pathway formulism [11].

Figure 2.

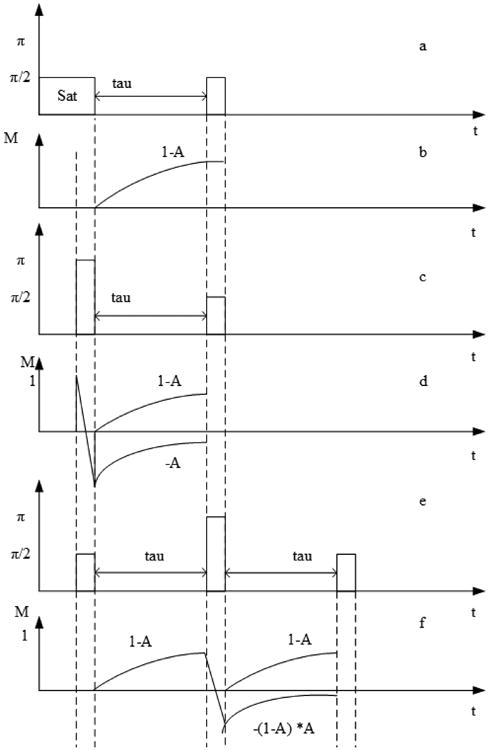
The magnetization recovery pathways of the several T₁ sequences. (a) SR sequence diagram; (b) evolution of longitudinal magnetization in SR; (c) IR sequence diagram; (d) evolution of longitudinal magnetization in IR; (e) SIR sequence diagram; (f) evolution of longitudinal magnetization in SIR.

The SIR sequence adds a 90° pulse before the IR sequence as shown in Fig. 2e, with the corresponding magnetization evolution shown in Fig. 2f. After the first 90° pulse, the longitudinal magnetization grows as 1 – A. The 180° pulse inverts it to −(1 – A) which then decays during the second τ period as −(1 – A)A. During this second τ, a recovery magnetization grows as 1 – A. Thus the total signal is the sum of the two pathways:

$$K_{\text{SIR}}=1-\mathrm{A}-(1-\mathrm{A})\mathrm{A}=1-2\mathrm{A}+{\mathrm{A}}^2={(1-\mathrm{A})}^2.$$ (3)

2.3 Signal shape and coherence pathway phase cycling

Application of several RF pulses can create many coherence pathways and thus signals (some are echoes, e.g., for diffusion measurements) [5, 12-16]. With the 3-pulse sequence, 90°-180°-90°, 9 signals (5 echoes and 4 FIDs) should be created with 9 different coherence pathways. We denote the coherence pathway as [q₀-q₁-q₂-q₃]. q₀ is the state before first 90° pulse, so q₀ is the prepared state and therefore q₀ = 0. q₁, q₂, q₃ is the state after each of the 3 pulses, with q₃ referring to the acquisition; by convention q₃ = −1. There are 9 possible coherence pathways [17] listed in Table 1.

Table 1. Coherence pathways of SIR.

Pathway	q0	q1	q2	q3
1	0	-1	-1	-1
2	0	-1	0	-1
3	0	-1	1	-1
4	0	0	-1	-1
5	0	0	0	-1
6	0	0	1	-1
7	0	1	-1	-1
8	0	1	0	-1
9	0	1	1	-1

For SIR, only the 5th signal [0, 0, 0, −1] is to be detected. We designed a phase cycling scheme to remove the unwanted signals: ph₁ = [0° 90° 180° 270° 180° 270° 90° 0°], ph₂ = [270° 180° 90° 0°], ph₃ = ph_rec = [180° 270° 0° 90°]. Using this phase cycling, we observe a consistent signal phase for all τ values from very short (τ = 0.8 ms) through very long (τ = 2048 ms), demonstrating the selection of the single coherence pathway.

2.4 RF pulse error correction

For the SIR sequence, RF pulse inaccuracy and off-resonance effects are considered here. Fig. 3 a illustrates the pulse sequence with imperfect pulses and Fig. 3b shows the resulting signals with the 90° pulses replaced with α₁ degree pulses, and the 180° pulse replaced by an α₂ degree pulse. Transverse magnetization and residual longitudinal magnetization from the previous repetition of the pulse sequence are neglected in this analysis. Immediately following the α₁ pulse a residual normalized longitudinal magnetization cosα₁ remains, and it will decay as S″ = A cosα₁ in the delay time τ where A = exp(−τ/T₁). At the same time, another longitude magnetization will appear as S′ = (1 – A). Immediately following the α₂ pulse, S′ and S″ are transferred to the inverse Z direction and then decay as S₂ = S′Acosα₂ and S₃ = S″Acosα₂ separately. Meanwhile, there will appear another longitudinal magnetization S₁ = 1 – A. Thus after the last acquired RF pulse, the amplitude of the signal should be the sum of S₁, S₂ and S₃, that is

Figure 3.

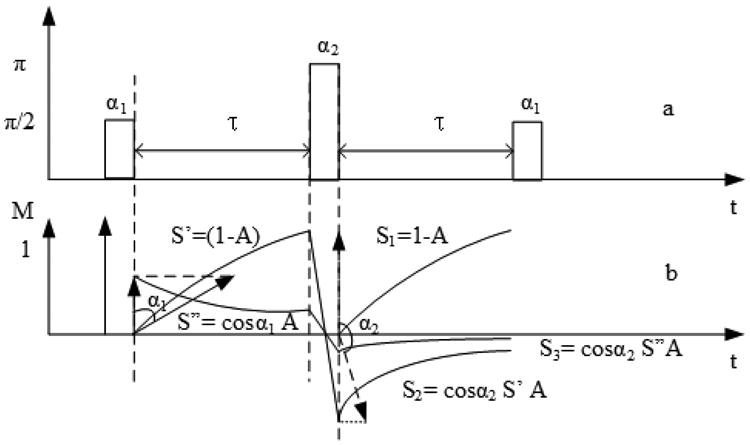
Analysis of SIR sequence with imperfect RF pulses. (a) Sequence diagram; (b) Evolution of the longitudinal magnetization.

$$\mathrm{S}=1-(1-cos{\alpha }_2)\mathrm{A}-cos{\alpha }_2(1-cos{\alpha }_1){\mathrm{A}}^2.$$ (4)

To explore the consequences of inaccurate RF pulse lengths we define C₁ = (1 – cosα₂) and C₂ = −cosα₂(1 – cosα₂) such that the SIR signal may be expressed as

$${\mathrm{S}}_{\text{SIR}}=1-{\mathrm{C}}_1\mathrm{A}+{\mathrm{C}}_2{\mathrm{A}}^2$$ (5)

If α₁ = 90° and α₂ = 180°, then S_SIR = (1 – A)² as given in Eq. 3. The T₁ relaxation curve should begin (at τ = 0) with an amplitude of 0 if the pulses are perfect, and with an amplitude 1 – C₁ + C₂ if they are not. The variation of the terms C₁ and C₂ as well as the initial value of the relaxation curve are plotted in Fig. 4.

Figure 4.

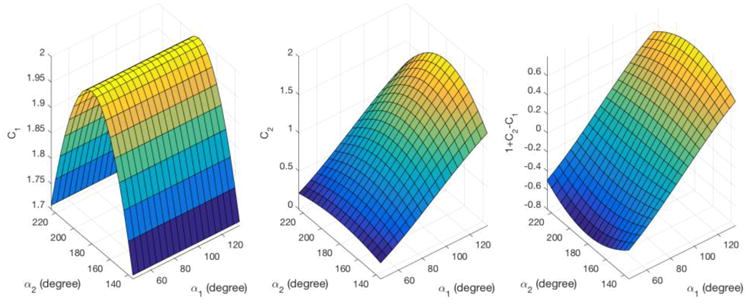
The dependence of C₁, C₂ and the initial value of the SIR T₁ relaxation curve 1 – C₁ + C₂ on the flip angles α₁ and α₂. Left: C₁ is strongly dependent on α₂ and independent of α₁. Center: C₂ is strongly dependent on α₁ and modestly on α₂. Right: the initial value of the T₁ curve exhibits a strong dependence on α₁ and a much weaker dependence on α₂.

Fig. 5 shows the simulated SIR relaxation curves for several α₁ and α₂ values around 90° and 180°, respectively. The simulations clearly demonstrate that small errors in the initial 90° pulse result in changes in the T₁ relaxation curve while the effect due to the 180° pulse error is much smaller. This suggests that the use of a saturation pulse train for the initial pulse instead of a single 90° pulse could be advantageous.

Figure 5.

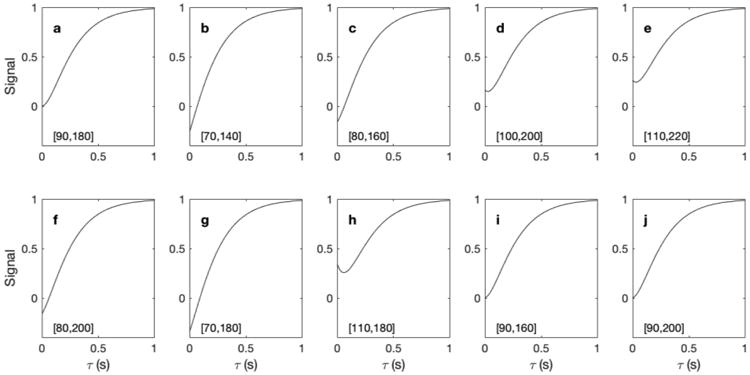
Simulated T₁ recovery curve for different tipping angles of α₁ and α₂. (a-h) The [α₁, α₂] values (in degrees) are displayed in each panel. The T₁ value in this simulation is 200 ms.

3. Experimental Results and Discussion

In order to test the SIR sequence, we prepared water solutions of CuSO₄·5H₂O yielding different T₁ values. The concentrations of samples A, B, and C were 7.13%, 1.78% and 0.36% by weight, respectively. The experiments were performed on a Bruker BioSpin (Billerica, MA, USA) Avance II spectrometer interfaced to a Magnex 14T (600 MHz) 89 mm vertical bore magnet using a Bruker 5-mm solution probe. For measurements on mixed fluid samples, a Wilmad-LabGlass (Vineland, NJ, USA) 4.14-mm outside diameter spherical microcell insert was used to contain fluid 1, and the 5-mm NMR tube with 0.36 mm wall thickness to contain fluid 2. The outer and inner diameters of the microcell are 4.14 mm and 3.25 mm, respectively. Thus the sample volume inside the microcell was about 10% of total fluid for a coil length of 15 mm. For each sample, we carried out T₁ measurements with the IR and SIR sequences using 22 recovery time values ranging from 0.8 to 2048 ms. The results are shown in Fig. 6 for the single fluid samples and Fig. 7 for the mixed fluid samples. The lengths of the pulses were adjusted to 90° and 180° (about 10 and 20 μs) for each sample.

Figure 6.

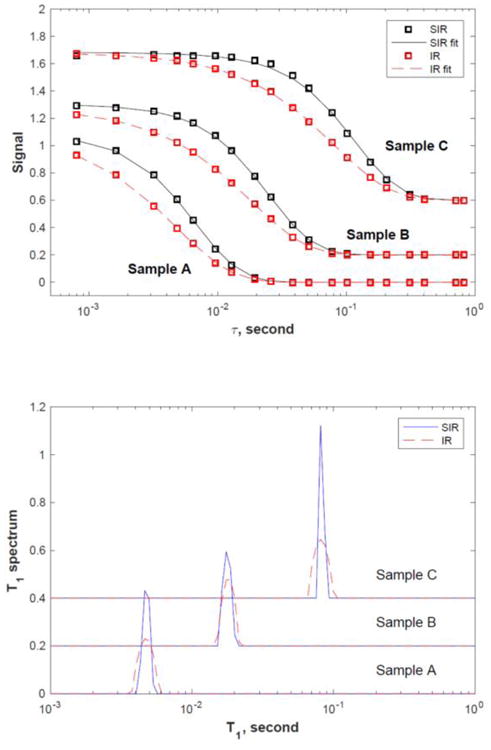
Decay signal curves, S(τ = ∞) – S(τ), (top panel, SIR: black circles, IR: red squares) and the corresponding T₁ spectra (bottom panel, SIR: solid line, IR: dotted line) for samples A (4.5 ms), B (17 ms), and C (79 ms). The lines in the top panel are fitting results from the Laplace inversion. The data for sample B and C in both panels are shifted upward for clarity.

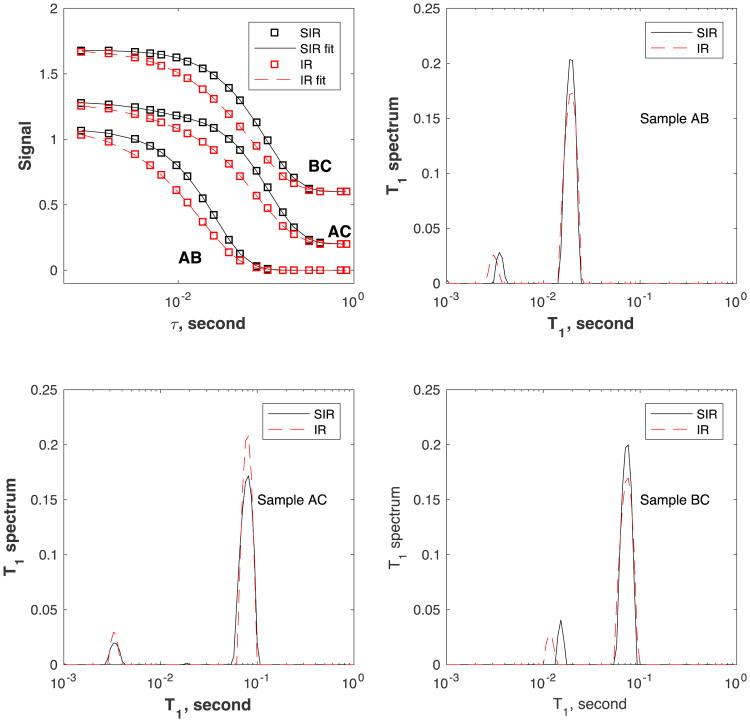
Figure 7.

Signal decay curves S(τ = ∞) – S(τ) (top-left panel, SIR: black circles, IR: red squares) and corresponding T₁ spectra (right and bottom panels, SIR: solid line, IR: dotted line) for the mixed samples AB, AC, and BC. The lines in the top-left panel are fitting results using the Fast Laplace inversion algorithm [18]. The data for samples AC and BC in the top-left panel are shifted upward for clarity.

The top panel of Fig. 6 shows the signal amplitude (S(τ = ∞) – S(τ)) as a function of the recovery time τ, for samples A, B and C, respectively. S(τ = ∞) is chosen to be the signal at the longest τ = 2048 ms for each sample. The IR data (red squares) is scaled by 1.8 in order to match the SIR data (black circles) for easy comparison. It is clear that the SIR decay is noticeably sharper than the corresponding IR decay for all samples. The lower panel shows the corresponding T₁ spectra obtained using the Fast Laplace Inversion (FLI) algorithm [18] with the regularization parameter chosen to be 0.0001 for all measurements. The inversion kernel for SIR is shown in Eq. 6 and the values of C₁ and C₂ are calibrated using the experimental data of sample A (α₁ = 84.6° and α₂ = 180°) and used for all other samples.

The inversion results show that both the IR and SIR methods yield the same T₁ value of 4.5 ms (sample A), 17 ms (sample B) and 79 ms (sample C), respectively. The SIR spectra are very similar to the IR spectra but are noticably sharper.

We also performed measurements on samples of mixed T₁, such as A+B, A+C, and B+C, and the results are shown in Fig. 7. Similar to the data for the single-fluid samples, the SIR decay curves are much sharper than that for the IR experiment reflecting the different kernel. The SIR and IR spectra are shown in the same plot for each sample to allow easy comparison. All spectra show two peaks corresponding to the two fluids present in each sample. The large peak is due to fluid 2 in the 5-mm NMR tube while the smaller one is from the fluid in the microcell. The signal ratio of the small-to-large peaks is found to be 8.0%, 7.6%, 9.1% from SIR, and 8.5, 8.3%, 8.2% from IR, for the three samples (AB, AC, and BC), respectively. It appears that the variation of the smaller peak signal is less in the IR measurement. Both IR and SIR are able to isolate the different peaks and the linewidths of the individual peaks are similar for the SIR and IR measurements.

The position of the large peak is very consistent between the two measurements (SIR and IR). On the other hand, the smaller peaks are slightly different for the SIR and IR measurements. For example, for sample AB, the T₁ value of the smaller peak is 3.1 ms for IR, and 3.5 ms for SIR. For sample AC, these values are 3.3 and 3.3 ms, and for sample BC, 11 and 15 ms, respectively. Comparing to the T₁ values obtained from the single fluid samples, the T₁ value of the smaller peak is less accurate in both SIR and IR measurements (SIR is slightly better). Such behavior (inaccuracy of the smaller amplitude signal in Laplace inversion) is expected [5].

Using theoretical analysis and experimentation, we demonstrate that the SIR approach for T₁ measurement exhibits a kernel very different from that of conventional IR and SR measurements and their variants. This difference is most highlighted in the time-domain signals where the SIR sequence provides a significantly sharper τ or T₁ dependence for both single-fluid samples and mixed-fluid samples. Such enhanced constrast could be used in measurements to better identify or detect sample constituents based on their T₁ values, for example in T₁-weighted MRI. In this scenario, enhanced T₁ contrast might be achieved by inserting an SIR magnetization preparation module into the imaging pulse sequence to impose differential saturation among tissues. To better illustrate this hypothetical example, Fig. 8 plots the signal ratio of brain white matter (taking T₁ ∼ 0.65 s) and grey matter (T₁ ∼ 1 s), demonstrating a clear superiority of SIR contrast (defined as normalized signal ratio less unity) compared to conventional SR.

Figure 8.

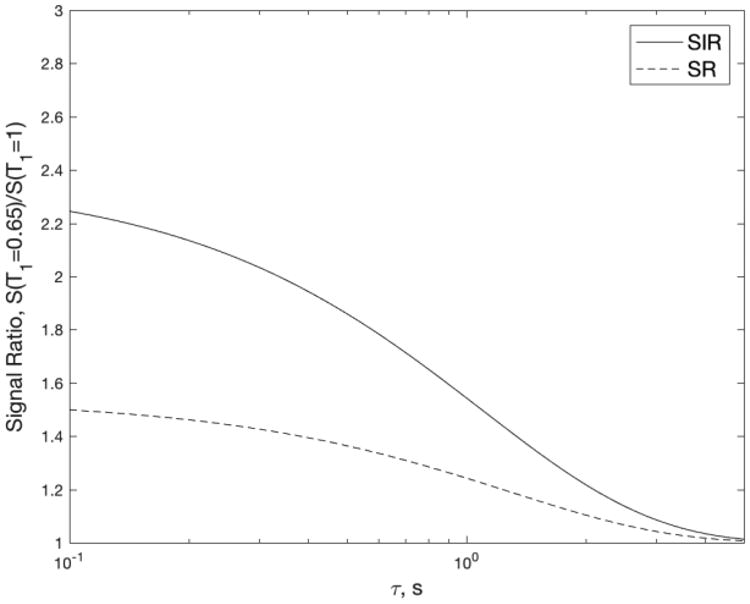
Ratio of signals with T₁ = 0.65 s and 1 s as a function of the recovery time τ for SIR (solid line) and SR (dashed line) sequences. The higher value for SIR shows an improved contrast between the different T₁ values. For example, at τ = 0.65 s, SIR achieves more than twice the contrast (defined as normalized signal ratio less unity) of SR.

When using Laplace inversion to obtain the T₁ spectrum, we observed a significant improvement of T₁ resolution in the single-fluid samples (single peak spectra). For the mixed 2-fluids samples where the difference of the T₁ values is large, both SIR and IR methods are able to separate the two peaks. Application of the SIR method to broad T₁ distributions (such as porous and biological samples) is ongoing.

As shown in Fig. 1, other functional forms, such as K₅, may provide even an sharper kernel than K₂ (K_SIR). The question is whether a pulse sequence can be constructed to obtain such kernels. One option is to extend SIR to apply more 180° pulses with the same spacing τ between them. For convenience, we name these sequences SIRN where N is the number of 180° pulses. The kernel for such an SIR sequence family can be written as:

$$K_{\mathit{\text{SIR}}}^N(\tau ,T_1)={\sum }_{i=0}^N{(-1)}^i(1-A)A^i.$$ (6)

For example, when N = 0, the sequence corresponds to saturation recovery; when N = 1, to SIR. For N = 2,

$$K_{\mathit{\text{SIR}}}^2(\tau ,T_1)=1-2A+2A^2-A^3.$$ (7)

Fig. 9 (left panel) plots the first few kernels in this family with N = 0, 1 and 2. Interestingly, sequences with higher N do not become sharper; in fact, they fall between SR and SIR.

Figure 9.

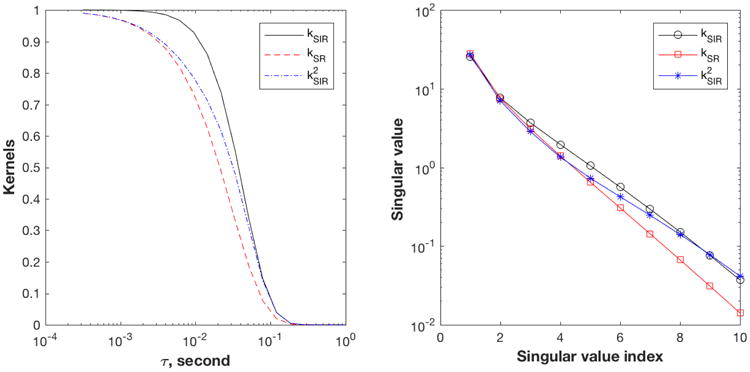
Comparison of kernels of SIR family sequences. SIR (solid line), SR (red dashed line) and SIR2 (blue dash-dotted line). Left: Signal decay curves for T₁ = 0.03 s for the three sequences. Right: Plot of the singular values of the three kernels. The kernel matrices are evaluated as K(τ, T₁) with 20 τ values from 0.3-1000 ms, and 100 T₁ values from 1-1000 ms. SVD is calculated using MATLAB (Mathworks, Natick MA).

Singular value decomposition (SVD) is a useful approach to determine the quality of the kernels [5,6]. If a kernel is smooth, the singular values decay rapidly, indicating that the inversion is more ill-conditioned. Fig. 9 (right) plots the singular values of the three kernels showing that the decay of the singular values is slowest for SIR and fastest for SR, and therefore that the SIR kernel is less ill-conditioned than that of SR. The SIR2 singular values fall between SR and SIR, consistent with the picture from the τ dependence (Fig. 9 left).

4. Conclusion

This work reports the theory and experimental results of a T₁ measurement scheme that combines at least two different T₁ relaxation periods in the pulse sequence. This is quite different from traditional inversion-recovery and saturation-recovery. The traditional methods incorporate only one decay period, and thus the decay function is exponential. The SIR method changes the basic functional form of the relaxation decay and results in a noticeably sharper kernel, which can enhance discrimination between similar T₁ values. It is possible to further improve it by incorporating relaxation intervals with different durations. In addition to benefiting NMR studies of porous media and other materials with wide T1 dispersion, this method could provide a significant improvement in T₁-weighted MRI to yield higher contrast among tissues.

Highlights.

• An improvement over conventional inversion-recovery (IR) or saturation-recovery (SR) spin-lattice relaxation time measurement is proposed.

• The new method, saturation-inversion-recovery (SIR), combines saturation and inversion to achieve better discrimination between closely spaced T₁ values.

• Experimental demonstration of SIR method showing the sharper signal decay for single and multi-components samples indicative of improved differentiation of T₁s.

• An analysis of flip angle errors in SIR measurement is provided.