Multi-template analysis of human perirhinal cortex in brain MRI: Explicitly accounting for anatomical variability

Abstract

Rational

The human perirhinal cortex (PRC) plays critical roles in episodic and semantic memory and visual perception. The PRC consists of Brodmann areas 35 and 36 (BA35, BA36). In Alzheimer's disease (AD), BA35 is the first cortical site affected by neurofibrillary tangle pathology, which is closely linked to neural injury in AD. Large anatomical variability, manifested in the form of different cortical folding and branching patterns, makes it difficult to segment the PRC in MRI scans. Pathology studies have found that in ~97% of specimens, the PRC falls into one of three discrete anatomical variants. However, current methods for PRC segmentation and morphometry in MRI are based on single-template approaches, which may not be able to accurately model these discrete variants

Methods

A multi-template analysis pipeline that explicitly accounts for anatomical variability is used to automatically label the PRC and measure its thickness in T2-weighted MRI scans. The pipeline uses multi-atlas segmentation to automatically label medial temporal lobe cortices including entorhinal cortex, PRC and the parahippocampal cortex. Pairwise registration between label maps and clustering based on residual dissimilarity after registration are used to construct separate templates for the anatomical variants of the PRC. An optimal path of deformations linking these templates is used to establish correspondences between all the subjects. Experimental evaluation focuses on the ability of single-template and multi-template analyses to detect differences in the thickness of medial temporal lobe cortices between patients with amnestic mild cognitive impairment (aMCI, n=41) and age-matched controls (n=44).

Results

The proposed technique is able to generate templates that recover the three dominant discrete variants of PRC and establish more meaningful correspondences between subjects than a single-template approach. The largest reduction in thickness associated with aMCI, in absolute terms, was found in left BA35 using both regional and summary thickness measures. Further, statistical maps of regional thickness difference between aMCI and controls revealed different patterns for the three anatomical variants.

1. Introduction

The human perirhinal cortex (PRC) is a cortical region in the anterior medial temporal lobe (MTL) encompassing Brodmann areas 35 and 36 (BA35 and BA36) (Ding and Van Hoesen, 2010; Suzuki and Amaral, 1994a, 1994b). The PRC receives input from the sensory association cortices (Jones and Powell, 1970). Its output is to the entorhinal cortex (ERC) and hippocampal subfields subiculum (SUB) and cornu ammonis 1 (CA1) (Van Hoesen and Pandya, 1975a, 1975b; Van Hoesen, 1982; Van Hoesen et al., 1972, 1975). Serving as a conduit between sensory inputs and MTL substructures associated with memory, the PRC plays an essential role in episodic memory, semantic memory (Murray and Richmond, 2001) and visual perceptual processing systems (Meunier et al., 1993; Murray and Richmond, 2001; Murray et al., 2005; Zola-Morgan et al., 1989).

The PRC is also an important region for observing effects of early Alzheimer's disease (AD) on the brain. The hallmark molecular pathologies of AD are extracellular amyloid plaques and intracellular neurofibrillary tangles (NFT). The latter are more directly linked to neurodegeneration in AD (Bennett et al., 2004; Gómez-Isla et al., 1997). The PRC is the first site in the cortex to be affected by NFT pathology, which appears first in the BA35 (also referred to as the “transentorhinal” region), then spreads out to the ERC, the hippocampus and, eventually, to the rest of the brain (Braak and Braak, 1995). Accurate quantification of the volume and thickness of the PRC (and BA35 in particular) from in vivo MRI has the potential to improve early AD diagnosis and disease progression monitoring in early stages, as well as to enhance brain-behavior studies of the MTL.

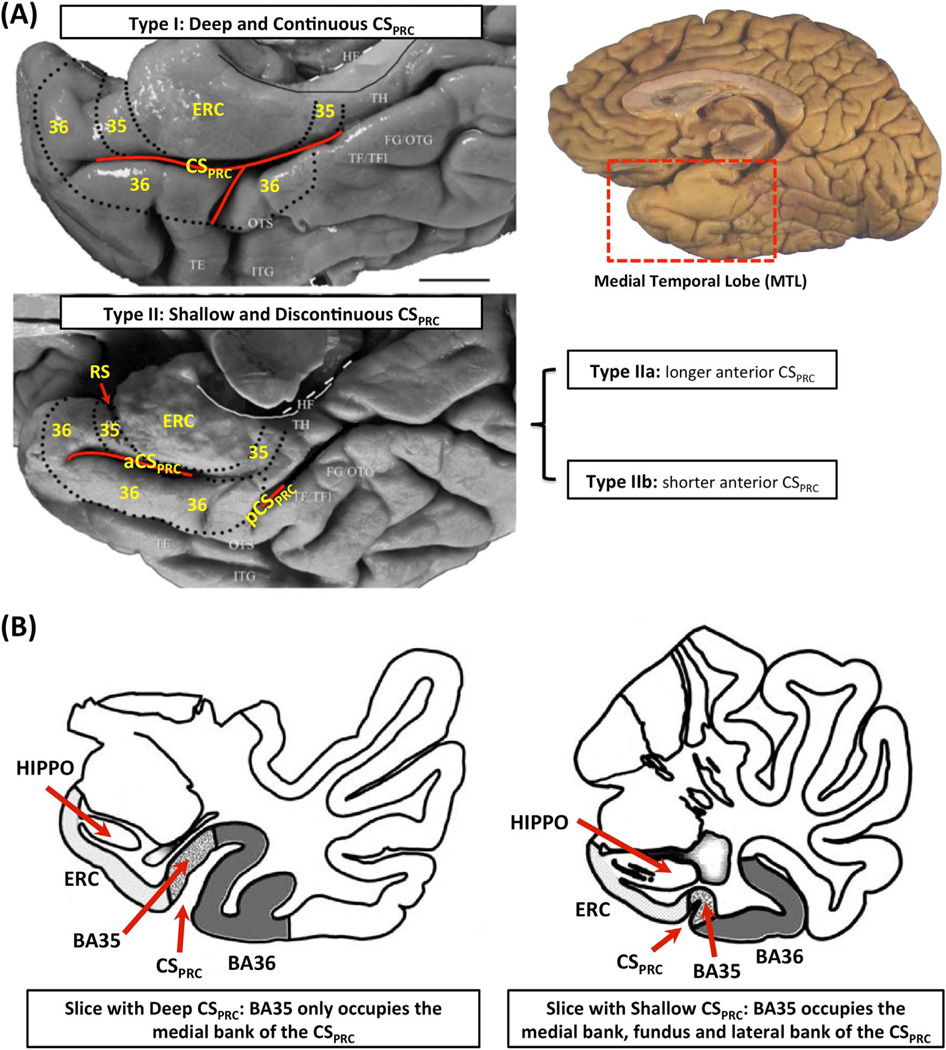
Despite its critical importance in AD and memory models, the PRC is surprisingly overlooked in the biomedical image analysis literature. This is likely due to challenges in accurately identifying its borders in MRI scans. The PRC and the adjacent MTL regions exhibit a large degree of anatomical variability, i.e. different cortical folding and branching patterns (Insausti et al., 1998), which affects the lateral borders of the PRC, making it difficult to perform accurate segmentation and morphometric analysis. Recently, Ding and Van Hoesen (2010) examined a large number of ex vivo human PRC specimens and described three discrete anatomical variants, defined by the depth and the branching pattern of the anterior portion of the collateral sulcus (CS) adjacent to the PRC (named CS_PRC, whereas the portion of the CS adjacent to parahippocampal cortex (PHC) is referred to as CS_PHC). These three variants accounted for 97% of all cases examined by Ding and Van Hoesen (2010). They are shown in Fig. 1A. Variant 1 has continuous CS_PRC; Variant 2 has discontinuous CS_PRC with the anterior branch of the CS_PRC shorter than the posterior branch; Variant 3 has discontinuous CS_PRC with the anterior CS_PRC branch longer than the posterior branch. According to Ding and Van Hoesen (2010) and Kivisaari et al. (2013), the borders and extent of BA35 and BA36 depend highly on the depth of CS_PRC. Where CS_PRC is deep (depth > 1.5 cm), the BA35 occupies a part of the medial bank (the example on the left in Fig. 1B), while for shallow portions of CS_PRC, the BA35 encompasses the whole medial bank, the fundus and even the lateral bank of CS_PRC (the example on the right in Fig. 1B). Difference in lateral boundaries of BA36 is even larger (Ding and Van Hoesen, 2010; Kivisaari et al., 2013). Since different variants have different depth patterns of CS_PRC along the anterior-posterior axis, the definition of the PRC borders differs substantially between them. Failure to account for this variability during segmentation can degrade the accuracy of subsequent morphometric analysis and reduce the utility of the PRC quantitative measures as an imaging biomarker.

Fig. 1.

(A) Three anatomical variants of the PRC defined by the folding and branching patterns of the collateral sulcus. (B) Two examples in Ding and Van Hoesen (2010) showing that the borders and extent of BA35 and BA36 depend on the depth of CS_PRC. Figure adapted from Ding and Van Hoesen (2010). Abbreviations: ERC=entorhinal cortex; 35, 36=Brodmann areas 35 and 36; BA35, BA36=Brodmann areas 35 and 36; PRC=perirhinal cortex; CS=collateral sulcus; CS_PRC=the portion of CS adjacent to PRC; aCS_PRC/pCS_PRC=anterior/posterior CS_PRC; HF=hippocampal fissure; RS=rhinal sulcus; FG=fusiform gyrus; HIPPO=Hippocampus; OTG=occipito-temporal gyrus; OTS=occipito-temporal sulcus; ITG=inferior temporal gyrus; TE, TH, TF=temporal areas TE, TH, TF defined in (Von Economo, 1929); TFl=lateral subdivisions of area TF.

Several manual protocols for labeling MTL cortical subregions (PRC, ERC, PHC) in MRI scans have been developed. They target different MRI acquisitions, including approximately 1.0×1.0×1.0 mm³ T1-weighted (T1w) 1.5 T and 3 T MRI (Insausti et al., 1998; Kivisaari et al., 2013); as well as oblique coronal T2-weighted (T2w) MRI with high in-plane resolution (0.5×0.5 mm² or smaller, usually obtained at the cost of increasing slice thickness and partial brain coverage) at 3 T (Duncan et al., 2014; Ekstrom et al., 2009; Libby et al., 2012; Olsen et al., 2009, 2013; Preston et al., 2010; Yushkevich et al., 2015b; Zeineh et al., 2001) and 7 T (Zeineh et al., 2012). Expert human raters can generate segmentations of the PRC that account for anatomical variability. However, labor intensive and time consuming manual segmentation is impractical for large-scale studies. Large neuroimaging studies of memory and dementia can benefit from accurate automatic segmentation of the MTL cortices. To our knowledge, only two automatic analysis pipelines for the PRC have been published so far (Augustinack et al., 2013; Yushkevich et al., 2015b). These methods rely on a single template to model the anatomical variation among the population. Augustinack et al. (2013) use high-resolution postmortem MRI from multiple specimens to build a single probabilistic template of the location of BA35, which is then used for segmentation and thickness measurement in in vivo T1w whole brain MRI within the FreeSurfer framework (Fischl, 2012). In our prior work (Yushkevich et al., 2010; Yushkevich et al., 2015b), multi-atlas segmentation with 29 expert-labeled in vivo T2w MRI scans is used to label the MTL cortical regions, including BA35 and BA36. A single template is subsequently constructed from the multi-atlas segmentation results and used to establish inter-subject correspondences and analyze regional thickness.

Directly using a single template to model anatomical variability of the PRC, either in the segmentation step (Augustinack et al., 2013) or in the thickness measurement step (Yushkevich et al., 2015b), may introduce errors in the analysis because the borders and extent of BA35 and BA36 depend on the pattern of CS_PRC. The goal of the current study is to develop a multi-template thickness analysis approach for the PRC that explicitly accounts for the existence of discrete anatomical variants. This paper extends work presented at the 17th international conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) (Xie et al., 2014). That paper showed that by automatically clustering subjects into three groups based on the pairwise similarity in PRC shape and building separate templates to model the variation within each group, increased the sensitivity of the PRC thickness measures over the single-template approach in a cross-sectional comparison of amnestic mild cognitive impairment (aMCI) to normal aging. However, the lack of pointwise correspondences between templates limited the thickness analysis in Xie et al. (2014) to global summary measures. The current study addresses this limitation and performs regional (pointwise) thickness analysis in the multi-template context by establishing pointwise correspondences between multiple templates. Inter-template correspondences are computed, and a unified template linking the three templates of the PRC variants is derived using a graph-based approach that builds on the ideas from recent work on group-wise image registration using manifold learning (Hamm et al., 2010; Wolz et al., 2010; Wu et al., 2011). Additionally, the current study extends (Xie et al., 2014) by incorporating the superresolution technique in Manjón et al. (2010a) into the automatic segmentation pipeline, which reduces step artifacts caused by large slice thickness of the T2w MRI scans used for high-resolution MTL imaging.

The proposed multi-template thickness analysis pipeline is evaluated in this paper in the context of aMCI, a group commonly conceptualized as enriched in patients at prodromal stage of AD (Petersen et al., 2009). First, the discriminative ability of the PRC summary thickness measures derived from the current pipeline is compared with volumetric measurements, thickness measures derived from the single-template approach (Yushkevich et al., 2015b) and FreeSurfer (Fischl, 2012). Second, we compare the localized effects of aMCI on the PRC using maps of regional thickness derived from the multi-template and single-template approaches. Third, statistical maps of regional thickness difference between aMCI and controls with templates of the three variants are computed separately and compared.

2. Materials and methods

2.1. Participants

Ninety-two participants, 45 aMCI and 47 cognitively normal controls (NC), were recruited from the Penn Memory Center / Alzheimer's Disease Center (PMC/ADC) at the University of Pennsylvania. This is the same dataset that was used by Yushkevich et al. (2015b). Diagnosis of aMCI was made following the criteria established by Peterson and others (Petersen, 2004; Petersen et al., 2009; Winblad et al., 2004). Informed consent was provided by all subjects. This study was approved by the Institutional Review Board of the University of Pennsylvania. Demographic and psychometric data for the aMCI and NC groups are shown in Table 1.

Table 1.

Demographic and cognitive testing results of the full cohort.

	aMCI (n=45)	NC (n=47)
Age	72.1 (6.9)	70.7 (9.6)
Education (Years)	16.4 (2.7)	16.6 (2.8)
Sex (Female/Male)	21/24	27/20
MMSE	27.3** (1.8)	29.4 (0.9)
10-item Word List Immediate Recall	17.0** (4.6)	23.8 (3.6)
10-item Word List Delayed Recall	3.7** (2.3)	8.3 (1.6)
Category Fluency (Animals)	16.4** (5.0)	22.9 (5.2)
Boston Naming Test Total	26.3** (3.2)	28.4 (1.8)

Note: Standard deviations are in parentheses.

^*: p < 0.05,

^**: p < 0.01, two-tailed, compared to the NC, tested by contingency χ² test (sex) or two-sample t-test (the other items).

Abbreviations: aMCI = amnestic mild cognitive impairment; NC = normal control; MMSE: mini–mental state examination.

2.2. MRI acquisition and preprocessing

2.2.1. Imaging protocol and quality control

MRI scans were acquired on a 3 T Siemens Trio MRI scanner (Erlangen, Germany) at the University of Pennsylvania over the course of 3.5 years. Scans from 77 subjects (37 aMCI and 40 NC) were acquired using an 8-channel array coil. Due to a change of protocol, a 32-channel array coil was used for the final 15 subjects (8 aMCI, 7 NC). Both imaging protocols include (1) a whole brain T1w (Magnetization Prepared Rapid Acquisition Gradient Echo, MPRAGE) MRI scan; (2) a T2w (Turbo Spin Echo, TSE) MRI scan with partial brain coverage and oblique coronal slice positioned orthogonally to the main axis of the hippocampus (Thomas et al., 2004; De Vita et al., 2003). The parameters for T2w MRI scans obtained with an 8-channel coil are as follows: {TR/TE=5310/68 ms, 18.3 ms echo spacing, 15 echo train length, 150° flip angle, 0% phase oversampling, 0.4×0.4 mm² in-plane resolution, 2.0 mm slice thickness, 30 interleaved slices with 0.6 mm gap, 7:12 min acquisition time} and for T1w MRI scans {TR/TE/TI=1600/3.87/950 ms, 15° flip angle, 1.0×1.0×1.0 mm³ isotropic resolution, 5:13 min acquisition time}. The parameters for T2w scans obtained with the 32-channel coil are: {TR/TE=7200/76 ms, 15 echo train length, 150 degree flip angle, 15.2 ms echo spacing, 75% phase oversampling, 0.4×0.4 mm² in-plane resolution, 2.0 mm slice thickness, 30 interleaved slices with no gap, 6:29 min acquisition time} and for T1w MRI scans {TR/TE/TI=1900/2.89/900 ms, 9° flip angle, 1.0×1.0×1.0 mm³ isotropic resolution, 4:26 min acquisition time}.

The quality of the T2w MRI scans was visually assessed, as described in Yushkevich et al. (2015b). Five scans that suffered from moderate to severe motion artifacts and one scan that failed to cover the full anterior-to-posterior extent of the hippocampus were excluded from the study. Overall, data from 86 subjects (42 aMCI, 44 NC) remained for the subsequent analyses.

2.2.2. T2w MRI preprocessing using a patch-based super-resolution technique

The T2w MRI protocol yields high in-plane resolution scans that are preferred for MTL subregion segmentation, particularly in the manual segmentation literature (Yushkevich et al., 2015a). However, one challenge of T2w MRI is the 2.0 mm (32-channel coil) or 2.6 mm (8-channel coil) slice thickness, which results in highly anisotropic MRI voxels with a 5 to 1 or 6.5 to 1 aspect ratio, making it difficult to resolve the shape of the hippocampus and adjacent cortices in the slice direction. Isotropic T1w MRI, on the other hand, has higher resolution (1.0 mm) along the long axis of hippocampus, but lacks the in-plane resolution to distinguish subfields visually. In order to take advantage of the information provided by the T1w MRI, a multimodal patch-based super-resolution (SR) technique (Manjón et al., 2010a) was used to upsample the T2w MRI scans from 0.4×0.4×2.0 mm³ to 0.4×0.4×1.0 mm³ (data acquired using 32-channel coil) or from 0.4×0.4×2.6 mm³ to 0.4×0.4×1.3 mm³ (data acquired using 8-channel coil) as a preprocessing step. We refer to the upsampled T2w MRI as SR-T2w MRI. Different from conventional trilinear or tricubic interpolation, patch-based SR techniques aim to recover high frequency information and generate biologically plausible results by taking advantage of the redundant information contained in the image patches centered on each voxel. It was shown in (Coupé et al., 2013; Manjón et al., 2010a, 2010b) that patch-based SR techniques generate upsampled images with higher signal to noise ratio than conventional interpolation methods. The SR technique used in this paper is based on an iterative reconstruction-correction scheme. In the reconstruction step, the intensity of each voxel J in the upsampled image is updated by taking the weighted average of neighborhood patches, where the weight of each patch is assigned based on its similarity to the patch centered on voxel J. If a high-resolution image of another modality from the same subject is available, such as the T1w MRI in our application, it can be used as a prior and image patches from that modality are also used to estimate the weights in a similar manner. In the mean correction step, the reconstructed image at the current iteration is adjusted so that its downsampled version matches the original low-resolution image, thereby constraining the solution to be biologically plausible. Appendix A provides additional details on the patch-based SR implementation in this paper.

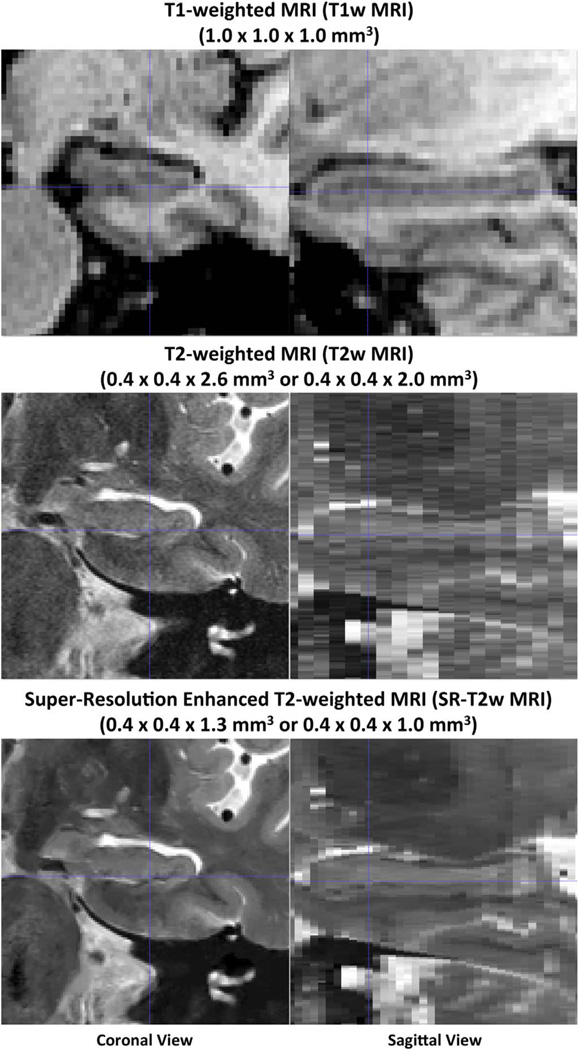
As shown in Fig. 2, the SR-T2w MRI reveals the curved shape of the hippocampus and adjacent cortices in the sagittal plane (which is visible in the T1w MRI, but not in the native T2w MRI), while preserving the details of MTL anatomy in T2w MRI slice plane.

Fig. 2.

Examples of the T1-weighted MRI (T1w MRI), native resolution T2-weighted MRI (T2w MRI) and super-resolution enhanced T2w MRI (SR-T2w MRI) used in this study. The scans are from the same subject and shown in the same space.

2.3. Automatic segmentation of hippocampal subfields and MTL cortices

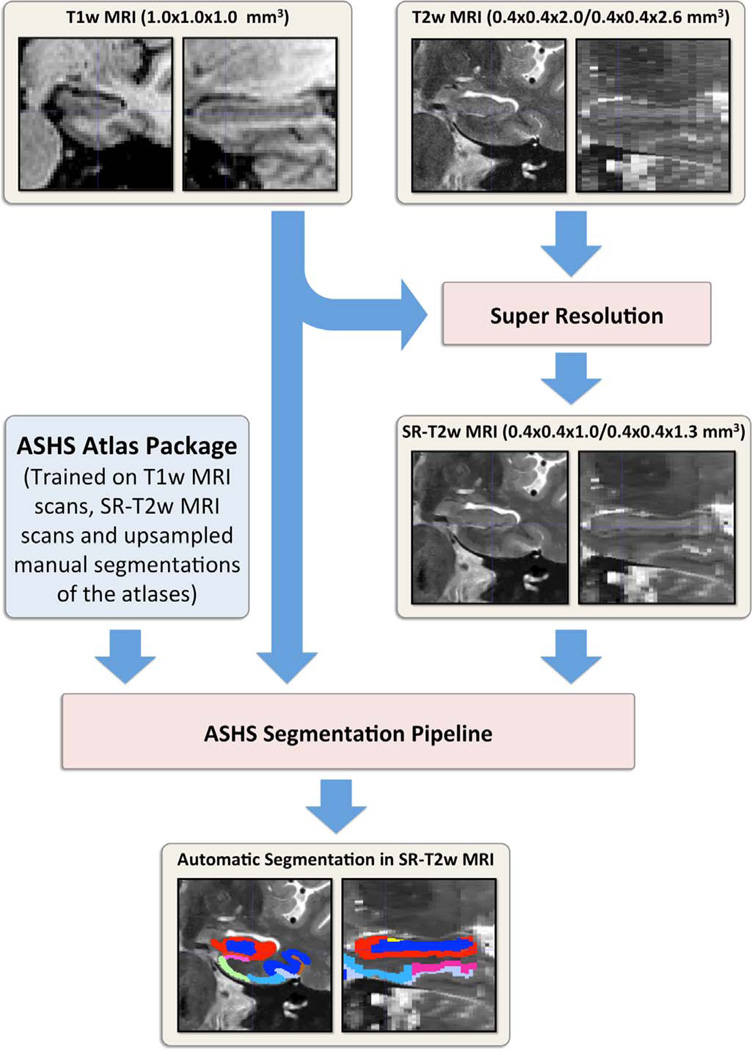
Segmentations of MTL cortical regions and hippocampal subfields were obtained using the multi-atlas segmentation pipeline ASHS (short for “Automatic Segmentation of Hippocampal Subfields”) which is described and evaluated in Yushkevich et al. (2015b) and briefly summarized in Appendix B. As illustrated in Fig. 3, in the current paper, ASHS was trained on T1w MRI, SR-T2w MRI and upsampled manual segmentations of the atlases and generated automatic segmentations in the SR-T2w MRI space of a new subject. By contrast, in Yushkevich et al. (2015b), ASHS was applied to native-resolution T2w MRI. Retraining ASHS using SR-T2w MRI scans required the additional step of upsampling the manual segmentations of the atlas images into the SR-T2w space. This step is described in Appendix A.

Fig. 3.

Automatic segmentation flow chart in this study. T2w MRI is first upsampled to generate SR-T2w MRI using the patch-based SR technique (Manjón et al., 2010a). Then, taking T1w MRI and the SR-T2w MRI as input, ASHS segmentation pipeline (Yushkevich et al., 2015b) is applied to generate the segmentation of hippocampal subfields and medial temporal lobe substructures in SR-T2w MRI space. Abbreviations: ASHS =Automatic Segmentation of Hippocampal Subfields package; T1w MRI=T1-weighted MRI; T2w MRI=T2-weighted MRI; SR-T2w MRI=super-resolution enhanced T2w MRI; SR=super-resolution.

The ASHS atlas set for this study consists of 29 subjects (14 aMCI and 15 NC) who are part of the overall 86-subject cohort. For the purposes of this study, automatic segmentations were generated for these subjects in a leave one out manner by using the remaining 28 subjects’ data as atlases. The remaining 57 subjects were segmented using the whole atlas set. ASHS failed in one aMCI subject, whose data was excluded from the current study.

The manual segmentations of the atlas images were expanded from the published ASHS algorithm (Yushkevich et al., 2015b) to include the posterior portion of the parahippocampal cortex (PHC) and the occipito-temporal sulcus (OTS). These changes to the segmentation protocol are described in Appendix C and the Supplementary material. As a result, 11 labels, including cornu ammonis fields 1–3 (CA1–3), dentate gyrus (DG), SUB, ERC, BA35, BA36, PHC, CS and OTS, were generated for the bilateral MTL of each atlas in the space of the original T2w MRI, upsampled to the space of SR-T2w MRI, and used for multi-atlas segmentation.

Once the automatic segmentation is generated, the label CS is automatically divided into portions that are adjacent to PRC (CS_PRC) and PHC (CS_PHC) for the purpose of measuring PRC similarity between subjects in the multi-template thickness analysis pipeline (Section 2.4). Since only the portion of CS that is adjacent to PRC is highly variable, as discussed in Section 1, it is the CS_PRC, rather than the whole CS, that is used for PRC similarity measurement. CS_PRC is defined as the CS that is anterior to the most anterior slice where the number of PHC voxels is larger than that of PRC. The rest of the CS is labeled as CS_PHC.

Label maps generated by ASHS (i.e., images in the space of SR-T2w MRI in which each voxel is assigned a unique anatomical label) serve as the input to the methods in the subsequent sections. Since the focus of this paper is on MTL cortical regions, and not hippocampus, only labels ERC, BA35, BA36, PHC, CS_PRC and CS_PHC are considered below. Each hemisphere is treated independently throughout the analysis.

2.4. Multi-template thickness analysis pipeline

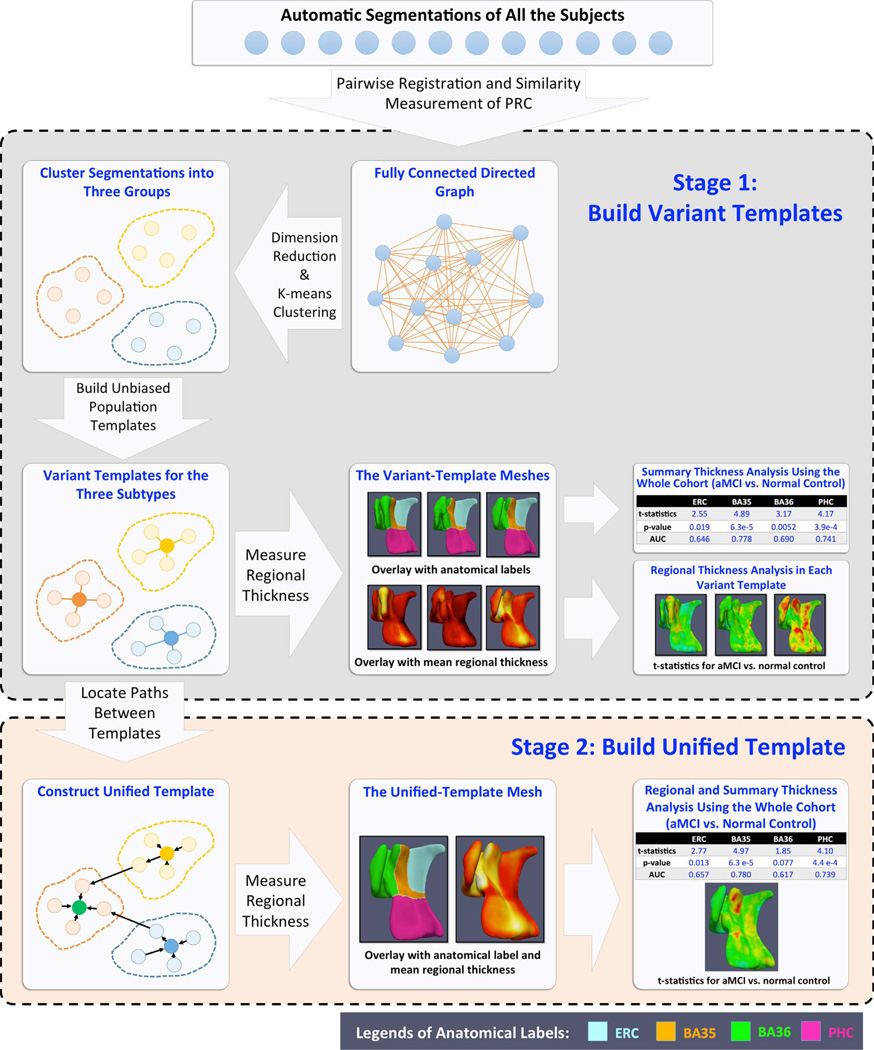
As reported in Yushkevich et al. (2015b), ASHS yielded moderate to high accuracy in segmenting hippocampal subfields and MTL cortices. For most subregions, ASHS accuracy was in line with the reported inter-rater reliability of manual segmentation. However, the automatic segmentations may not be smooth at the edges and have step edge discontinuities in the MRI slice direction, even with the use of SR methods, making them unsuitable for the direct computation of MTL cortical thickness. Furthermore, multi-atlas segmentation does not directly provide a way to match corresponding points across the segmentations of different subjects. To make group-wise analysis of cortical thickness possible, it is necessary (1) to approximate the “blocky” ASHS output with a smooth surface mesh representation from which a regional thickness map can be extracted reliably and that is topologically consistent across all subjects sharing the same PRC anatomical subtype; and (2) to establish meaningful pointwise correspondences between all subjects, allowing pointwise statistical analysis of thickness to be performed. We propose a multi-template thickness analysis pipeline to achieve these goals. This pipeline consists of two stages shown in Fig. 4: (1) building separate templates (termed variant templates (VT)) for the three discrete anatomical variants of the PRC described by Ding and Van Hoesen (2010) and (2) constructing a single unified template (UT) that captures meaningful correspondences between the VTs and, by extension, between all subjects. The details of the two stages are described in Sections 2.4.1 and 2.4.2.

Fig. 4.

Schematic flowchart of the proposed multi-template thickness analysis pipeline. The proposed pipeline takes label maps from ASHS as inputs. At the first stage (top block), subjects are automatically clustered into three groups. A separate “variant template” is generated for each group. At this stage, regional thickness analysis can only be performed within subjects sharing the same anatomical variant, while summary thickness analysis can be performed using the whole cohort. At the second stage (bottom block), by locating the intermediate subjects linking the variant templates, pointwise correspondences are established between them, and a unified template is generated. This allows both regional and summary thickness analyses using all the subjects.

2.4.1. Anatomical variant template generation

2.4.1.1. Automatic clustering of anatomical subtypes

VTs are generated by clustering subjects into groups with similar PRC anatomy. First, a pairwise similarity matrix S ∈ ℝ^n×n, where n is number of subjects, is computed, as in Xie et al. (2014). Label maps generated by ASHS are transformed into the space of the ASHS whole-brain T1w MRI template (Yushkevich et al., 2015b) for initial alignment, and then all pairs of label maps are registered using affine and high-dimensional deformable algorithms in ANTs (Avants et al., 2008, 2011). Only coarse deformable registration is performed.¹ The registration minimizes the sum of mean square intensity difference metrics computed separately for each label. Generalized Dice similarity coefficient (GDSC) (Crum et al., 2006) is computed for labels BA35, BA36 and CS_PRC after registration, referred to as s_ij for the pair of subjects i, j. The underlying assumption is that coarse deformable registration can only account for small differences in shape, and thus the residual disagreement between label maps after coarse registration is indicative of anatomical dissimilarity. By contrast, dense deformable registration has the potential to match very different shapes closely in some cases, but not in others, e.g., due to differences in the topology of the labels or due to convergence to a local minimum. Thus neither the residual disagreement after dense registration, nor the measure of the amount of deformation, are likely to serve as good surrogate measures of anatomical similarity, although a combination of the two may indeed provide a good metric (Aljabar et al., 2011). The added benefit of using coarse registration is that it reduces the computational time for the pairwise similarity measurements.

To assign the label maps into discrete anatomical variants we first project the pairwise similarity matrix S into a lower-dimensional space X ∈ ℝ^q×n, where q < n, using probabilistic principal component analysis (PPCA) (Tipping and Bishop, 1999), and then perform k-means clustering (MacQueen, 1967) in that space.

PPCA is a generalized probability formulation of principal component analysis (Jolliffe, 2002) that has practical advantages outlined in Tipping and Bishop (1999). In detail, dimension reduction using PPCA is done by solving a latent variable model (Everitt, 1984). For each n-dimensional observation s⃗_․j, j = 1,2,…,n, PPCA finds a q-dimensional vector of latent variables x⃗_․j that satisfy the following linear relationship:

$${\overrightarrow{\mathit{s}}}_{․\mathit{j}}={\overrightarrow{\mathit{W}\mathit{x}}}_{.j}+\overrightarrow{\mathit{\mu }}+\overrightarrow{\mathit{\epsilon }}$$

where W is a n × q matrix that relates the two sets of variables, μ⃗ is the mean of all the columns of S, ε⃗ ~ 𝒩 (0, σ² 1⃗) is the isotropic Gaussian noise term with standard deviation σ. Given all the columns in S, the matrix W and σ can be estimated using the E–M algorithm as described in Tipping and Bishop (1999). The matrix X, consisting of the columns x⃗_.j, is a low dimension representation of the matrix S.

k-means clustering (MacQueen, 1967) is applied in ℝ^q×n to divide the subjects into k groups. We set the number of clusters k equal to three based on the number of dominant variants described by Ding and Van Hoesen (2010). Similarity computation, dimensionality reduction, and clustering are performed separately in the left and right hemispheres, yielding a total of six groups. Since both PPCA and the k-means algorithm are initialized randomly and may yield different partitions, we repeated the analysis 50 times and chose the partition that yields the greatest difference between mean in-group and out-of-group similarity to be the final partition. PPCA was chosen over other dimension reduction algorithms empirically, as it gave the best in-group vs. out-of-group mean similarity difference in the current dataset. The number of PPCA modes (q) was set to 3 based on the same criterion. One possible reason why PPCA, a linear approach, is better than a non-linear one, i.e. spectral clustering used in our prior work (Xie et al., 2014), is that the distributions of the three clusters may be compact or have convex boundaries. Linear mapping from high-dimensional space to low-dimensional space is sufficient for the three clusters to be separated by hyperplanes in the low-dimensional space.

2.4.1.2. Unbiased population averaging and surface mesh generation

Within each group, the VT is constructed by applying the unbiased population template algorithm (Joshi et al., 2004) with shape averaging (Avants et al., 2008) to the label maps. This iterative approach alternates between deformable registration from input label maps to the current estimate of the unbiased template, and updating the template from warped label maps. Within each group, we choose the segmentation that is most similar to the others in its group (based on the pairwise similarity matrix) as the initial estimate of the template. In the first three iterations of the algorithm, affine registrations are performed between the subject label maps and the template; in the subsequent iterations, dense deformable registrations are performed. The subject-to-template registrations use the same similarity metric as the pairwise registrations above. At each iteration, the template estimate is updated by simple majority voting among the warped label maps. The method effectively converges after five iterations of dense deformable registration.

2.4.1.3. Regional thickness measurement

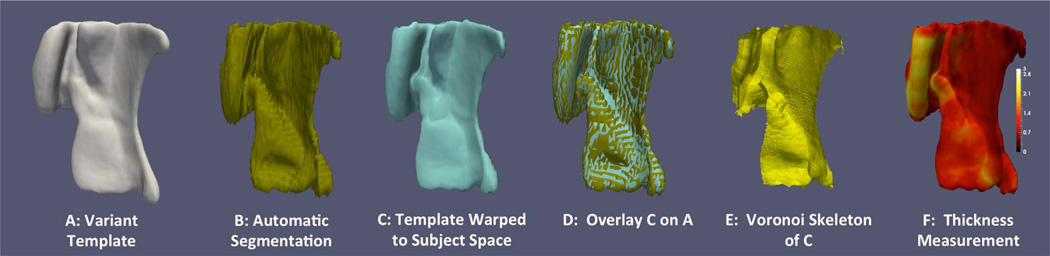
After the VT is computed for each group, a combined surface mesh is generated for all the gray matter labels (ERC, BA35, BA36 and PHC). These surfaces (Fig. 5A) are much smoother than the “blocky” surfaces of the input ASHS label maps (Fig. 5B). VT surface meshes are then transformed back into each subject's native SR-T2w space using the deformation field computed in the course of building the VT. This gives a smooth surface approximation of the previously blocky ASHS segmentation (Fig. 5C/D). This smooth template-based approximation of the subject's cortical surface is better suited for quantifying regional thickness.

Fig. 5.

Steps of computing thickness from automatic segmentation generated by ASHS. Figure adapted from Yushkevich et al. (2015b).

To estimate thickness, we compute the pruned Voronoi skeleton (Ogniewicz and Kübler, 1995) of the warped VT surface in each subject's native space (Fig. 5E). The thickness at each point of this surface is defined as the distance to its corresponding point on the skeleton (Fig. 5F). While this approach ensures that thickness measures are symmetric and unambiguous, the measures are unstable, as the topology of the skeleton is sensitive to small perturbations of the surface. While we account for this by pruning the skeleton (Ogniewicz and Kübler, 1995), it is possible that alternative thickness measures (Jones et al., 2000; Kim et al., 2005; Yezzi and Prince, 2003; Yushkevich, 2009; Yushkevich et al., 2006) may yield more robust statistics due to reduced variance.

2.4.2. Unified template (UT) generation

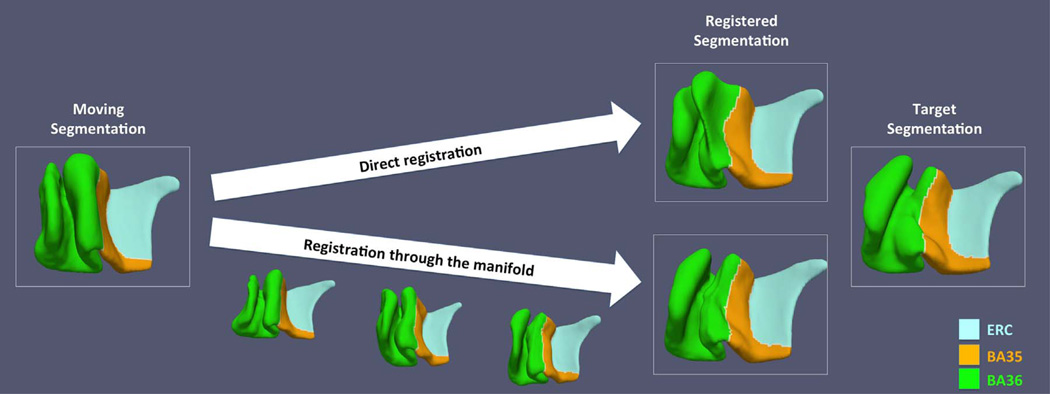
The VTs encode pointwise correspondences between subjects in each anatomical variant group. However, lack of pointwise correspondence across all subjects limits the ability to perform statistical analysis of thickness to summary measures (mean thickness of particular anatomical structure) or to per-variant regional thickness difference maps. To make regional analysis of thickness possible across all subjects, we use an approach inspired by manifold² learning (Hamm et al., 2010; Wolz et al., 2010; Wu et al., 2011) to construct a common UT that establishes meaningful correspondences across the VTs.

The UT is generated by inserting the VTs into the graph described by the similarity matrix S and then searching for the path between the VTs in this graph. This yields a sequence of diffeomorphic transformations that take each VT to the others through the intermediate anatomical configurations found in the cohort of subjects.

2.4.2.1. Inserting VTs into the manifold

The matrix S describes a complete graph in which subjects are vertices and elements of S are edge weights. Each VT is inserted as a new vertex into this graph, with edges connecting it to the vertices in its corresponding group. The weights of these edges are computed the same way as in Section 2.4.1.1, by registering each VT to and from the subjects in its group using coarse registration approach and setting the weights equal to the GDSC of BA35, BA36 and CS_PRC after registration. Note that the deformable registrations computed in Section 2.4.1.2 between each VT and the subjects in its group are dense ones, and thus separate coarse registrations are performed. By doing this, a graph with all the subjects and the VTs is constructed for each hemisphere.

2.4.2.2. Locating paths between VTs

Prim's minimum spanning tree (MST) algorithm (Dijkstra, 1959; Prim, 1957) is applied to locate the paths between all pairs of VTs in the graph (Algorithm 1). This greedy algorithm starts from the source VT as the root of the spanning tree, and grows the tree one edge at a time by considering all edges in the graph that connect nodes in the tree to the nodes not in the tree, and appending the edge with the largest weight. The tree is grown until the target VT enters the tree. The deformation field between VTs is obtained by composing the sequence of deformations along the unique path between them in the MST.

The rationale for using the MST algorithm to find a path between pairs of VTs is that this path, while potentially long, is composed of smooth deformations that are individually as small as possible. Choosing deformations that are as small as possible helps ensure the preservation of topology between the two VTs because small smooth deformations are more likely to preserve topology. Also, the composition of any number of topology-preserving deformations would generate topology-preserving deformation. However, this strategy is premised on the assumption that edge weights are indicative of the amount of deformation between nodes. Our approach does not guarantee this, but only performing coarse registration between subjects (as described in Section 2.4.1.1) helps ensure that GDSC after registration is a good surrogate measure of anatomical similarity. Additionally, it is possible that even the path provided by MST will include deformations that are not topology-preserving, e.g., if the nodes are clustered into two or more disjoint groups with distinct topologies. However, in the case of the MTL anatomy, it appears that there is more of a continuum of anatomical configurations that makes linking the VTs via the MST algorithm feasible.

Algorithm 1.

Pseudo code of the proposed path search algorithm.

Input: the graph with all the subjects and the three variant tem-     plates

Output: path from variant template i to variant template j

Initialization: Spanning tree T = variant template i

While variant template j is not in T.

1. Find the connection C with the highest weight between the nodes     in T and the nodes that are not in T.

2. Grow T with C.

End

Trace the path from the root (variant template i) to variant template   j in spanning tree T.

2.4.2.3. UT generation

Once we have the deformations between VTs, each VT can be warped to the space of the other two VTs. The VT whose label map is most similar to the warped label maps of the other two VTs (measured by the GDSC of ERC, BA35, BA36 and PHC) is chosen to be the reference template and all the subjects’ segmentations are transformed to it. This is done by composing the deformations from each subject to its VT and from this VT to the reference VT, if the latter is different. The UT is then constructed using the same approaches in Section 2.4.1.2 with the warped segmentations. Since the warped segmentations are well aligned, a smaller number of iterations is performed in the UT constriction (two iterations of affine registration and four iterations of dense deformable registration). Similarly, regional thickness measurement is conducted again using the mesh generated in the UT space similar to Section 2.4.1.3. Now, instead of correspondences within each VT, we obtain pointwise correspondences between all subjects, which makes regional thickness analysis possible. In this study, VT 3 was chosen as the reference template to construct the UT at both hemispheres using the criterion discussed above.

2.5. Additional measurements

2.5.1. Intracranial volume (ICV)

As in Yushkevich et al. (2015b), intracranial volume was estimated from the whole brain mask generated from ASHS. For each subject, the mask was obtained by warping the brain mask in the ASHS T1w template space to the subject's T1w MRI space. The brain mask in the template space was generated by applying FSL BET (Smith, 2002) to the ASHS T1 template. ICV was used as a covariate in the statistical analyses.

2.5.2. Summary thickness measurements

The summary thickness of each MTL cortical label (ERC, BA35, BA36 and PHC) at each hemisphere was computed for each subject by integrating thickness over all vertices on the surface mesh that belong to that label. For comparison, summary thickness measures were derived using both VT and UT meshes warped to subject space (as described in Sections 2.4.1.3 and 2.4.2.3).

2.5.3. Single-template SR-T2w thickness measurements

For comparison with Yushkevich et al. (2015b), summary and regional thickness measures were computed using a single-template (ST) approach. The ST was computed in the same way as the VTs, but using all subjects as inputs (no grouping by subtype).

2.5.4. Thickness measures of ERC and BA35 using FreeSurfer

In order to compare thickness measures of MTL cortices extracted from the proposed pipeline using T2w MRI to that from the leading alternative T1w-based methods for ERC (Fischl et al., 2009) and BA35 (Augustinack et al., 2013) thickness estimation, FreeSurfer 6.0 (Fischl, 2012) was used to process the T1w MRI scans. Average ERC and PRC thickness were extracted from the “lh.BA_exvivo.thresh.stats” and “rh.BA_exvivo.thresh.stats” files.

3. Experiments and results

All the experiments were based on the label maps generated by ASHS in the SR-T2w MRI space. The accuracy of ASHS with SR-T2w MRI scans is reported in Appendix D, and is comparable to previously published native resolution results (Yushkevich et al., 2015b).

To investigate whether ASHS implicitly accounts for the existence of anatomical variants in the PRC, we compared the label fusion weights in the PRC in cases where the atlas and the target subject had the same anatomical subtype and in cases where the anatomical subtypes between the atlas and target were different. We hypothesized that atlases that share a common subtype with the target subject would contribute more to the multi-atlas label fusion. In both hemispheres, there are significant differences in the PRC averaged label fusion weights (tested by paired t-tests, left: t₈₄=17.5, p < 0.00001; right: t₈₄=12.9, p < 0.00001) between atlases with the same subtype (left: 0.051 ± 0.009; right: 0.046 ± 0.009) and atlases with different subtypes (left: 0.025 ± 0.007; right: 0.029 ± 0.005), confirming this hypothesis.

To evaluate the proposed multi-template thickness analysis pipeline, we first inspected the quality of the fitted smooth VT surface in subject space qualitatively and quantitatively. We then used the extracted summary and regional MTL cortical thickness measures to discriminate aMCI from NC. For comparison, we also extracted regional and summary thickness measures from SR-T2w MRI using the ST approach (Section 2.5.3); as well as summary thickness measures of ERC and PRC from FreeSurfer 6.0 (Fischl, 2012) (Section 2.5.4).

3.1. Templates generated by the proposed approach

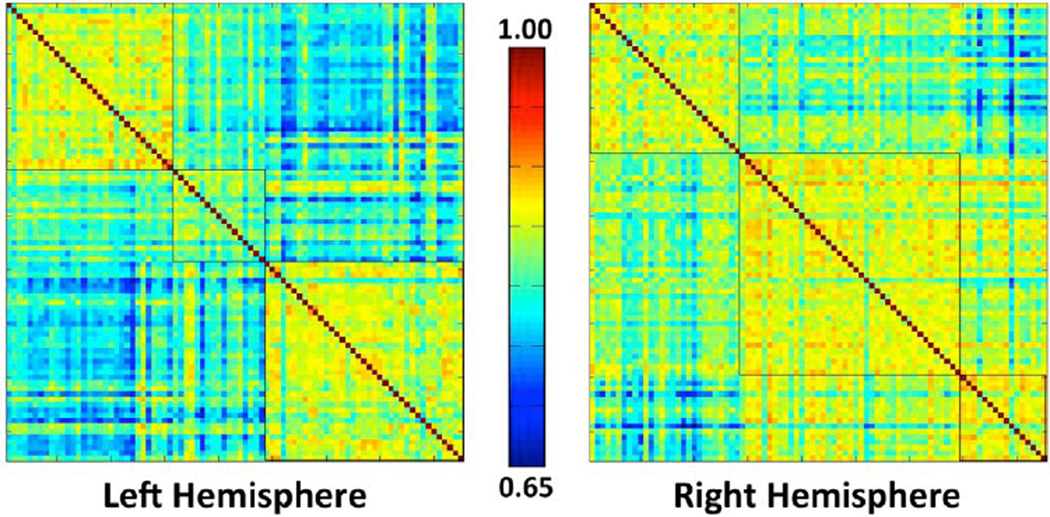
The number of subjects assigned to each cluster/VT in each hemisphere is shown in Table 2. Contingency χ² tests show that the proportions of variants between NC and aMCI subjects in the whole dataset (left: χ²=3.0, p > 0.1; right: χ²=2.1, p > 0.1) and in the atlas set (left: χ²=0.6, p > 0.1 right: χ²=1.4, p > 0.1) are not significantly different. Fig. 6 shows the pairwise similarity matrices in both hemispheres, reordered so that the subjects belonging to the same cluster are placed together. The clustering of the data is visually apparent. In addition, among the 50 random trials performed in Section 2.4.1.1, the variations of the in-group vs. out-of-group average similarity differences are small in both hemispheres. Their means and the standard deviations are 0.14 ± 0.02 (standard deviation is 14% of the mean) on the left side and 0.10 ± 0.01 (standard deviation is 10% of the mean) on the right side.

Table 2.

The repartition of the 3 variants within the whole dataset and the atlas set in both hemispheres.

	Whole Dataset			ASHS Atlas Set
	All	aMCI	NC	All	aMCI	NC
Total	85	41	44	29	14	15
Left Hemisphere
Variant Template 1	31	12	19	12	6	6
Variant Template 2	17	11	6	3	2	1
Variant Template 3	37	18	19	14	6	8
Right Hemisphere
Variant Template 1	28	12	16	12	7	5
Variant Template 2	41	23	18	13	6	7
Variant Template 3	16	6	10	4	1	3

Fig. 6.

The pairwise PRC similarity matrices of both hemispheres. The subjects are reorganized so that those belong to the same cluster are put together. Black contours outline the three clusters generated using probabilistic principal component analysis (PPCA) and k-means algorithm. The number of subjects at each cluster is summarized in Table 2.

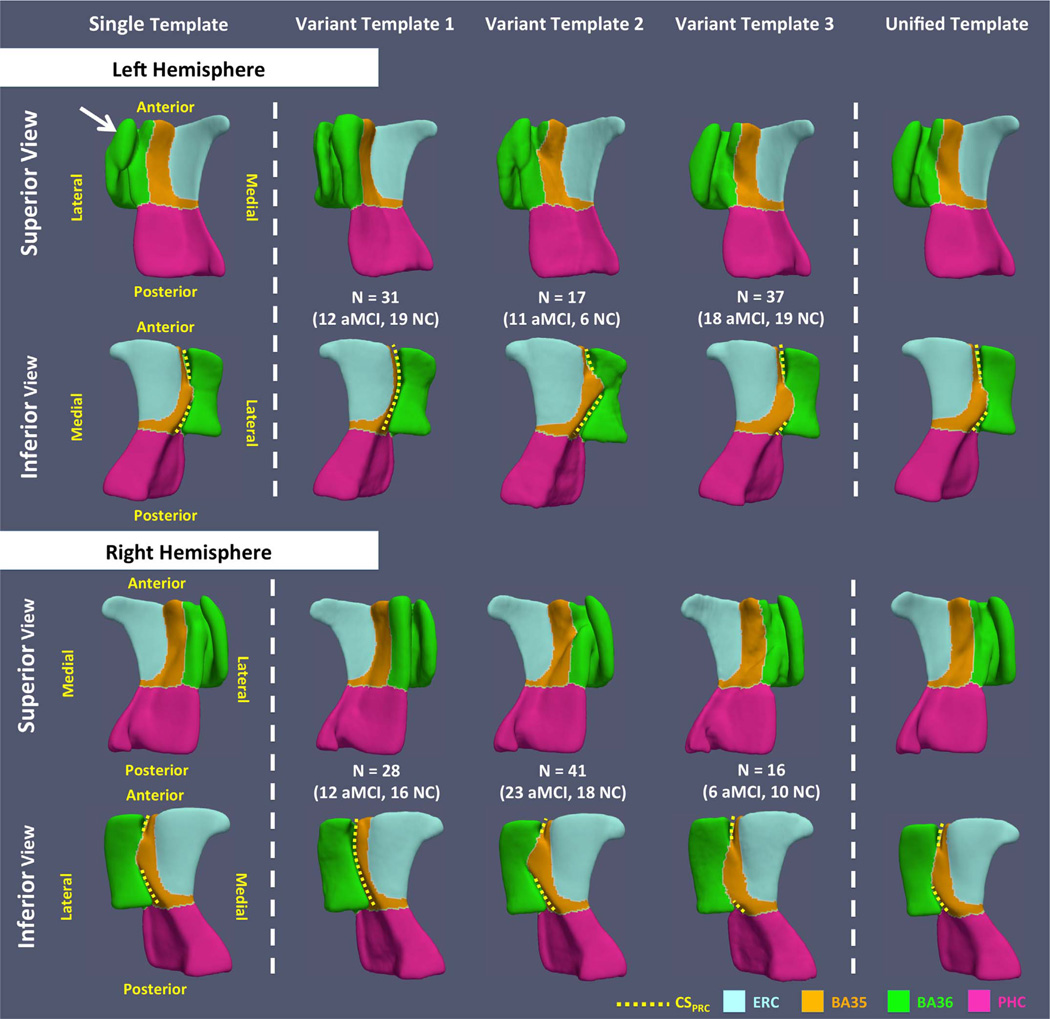
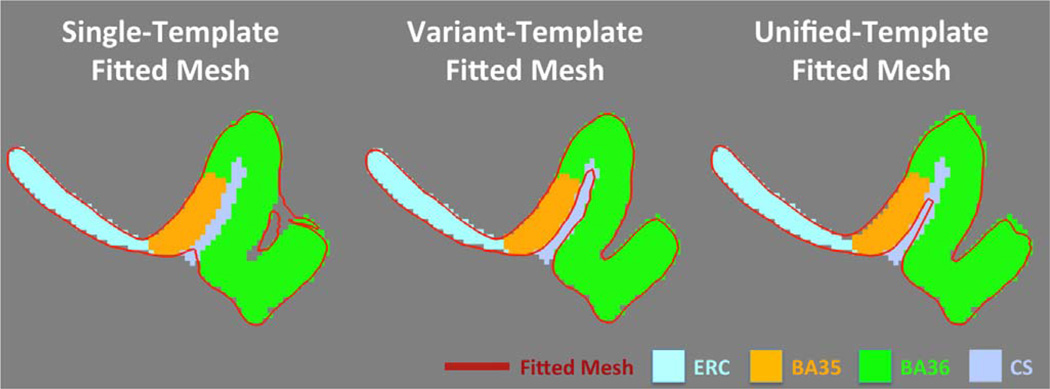
Fig. 7 shows the smooth meshes of all the six VTs (three per hemisphere). The VTs appear to be consistent with the three anatomical subtypes defined in the anatomy literature (Ding and Van Hoesen, 2010). VT 1 resembles the continuous CS_PRC variant. VTs 2 and 3 reflect discontinuous CS_PRC differing, as expected, by the relative length of the anterior and posterior CS_PRC (i.e. anterior CS_PRC is shorter in VT 2 while it is longer in VT 3). The templates constructed using the ST approach (Yushkevich et al., 2015b) look like a blend of the three VT meshes of the corresponding hemisphere. The odd shape of BA36 in the left ST (indicated by the white arrow in Fig. 7), with an anatomically implausible connection between the medial and lateral borders of BA36, is likely the result of failure to account for multiple anatomical variants. When warping the ST back to the native space of each subject, this implausible structure maps to the medial border of BA36 in some subjects and the lateral border in others (Fig. 8), which results in incorrect correspondences that are discussed further in Section 3.2.

Fig. 7.

Template meshes obtained using the single-template (ST), variant-template (VT) and unified-template (UT) approaches for both hemispheres. The white arrow points to the structure that connects the medial and lateral borders of BA36 generated by the ST approach, which is anatomically implausible. Yellow dashed curves mark CS_PRC in all templates. VT 1 resembles the continuous CS_PRC variant. Discontinuous CS_PRC is observed in VT 2 and VT 3, and these VTs differ, as expected, by the relative length of the anterior and posterior CS_PRC (i.e. anterior CS_PRC is shorter in VT 2 while it is longer in VT 3). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 8.

Comparisons of fitted smooth meshes from single-template, variant-template and unified-template approaches for subjects with deep (top) and shallow (bottom) CS_PRC. The yellow dashed circles highlight the incorrect correspondences between subjects established by the single-template approach: the biological implausible structure in left single template (white arrow in Fig. 7) maps to the medial border of BA36 of one subject (top) and the lateral border of BA36 of the other subject (bottom). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The UTs of both hemispheres are shown in the last column in Fig. 7. Since VT 3 is the reference template for initialization, the UT is similar to it in both hemispheres. However, the anterior CS_PRC is deeper in the UT. This could be the result of additional inclusion of subjects with relatively deep anterior portion of CS_PRC (variant 1 and variant 2 subjects) when building the UT. To demonstrate that the intertemplate registration established meaningful correspondences, the intermediate steps of the registration between the left VT 1 and VT 3 are shown in Fig. 9. Compared to registering these templates to each other directly, which may generate a biologically implausible result, the registration through the manifold generates a more meaningful deformation. Notably, the registration between left VT 1 and VT 3 is the most difficult of all the VT pairwise registrations because of the very deep CS_PRC in the left VT 1. The manifold-based registrations between all VTs to the corresponding VT 3 on each side generated anatomically plausible results.

Fig. 9.

Comparison of direct and manifold-based registrations between variant templates. Result generated from manifold-based registration matches the target shape much better than that produced by direct registration.

3.2. Quality of the fitted smooth meshes

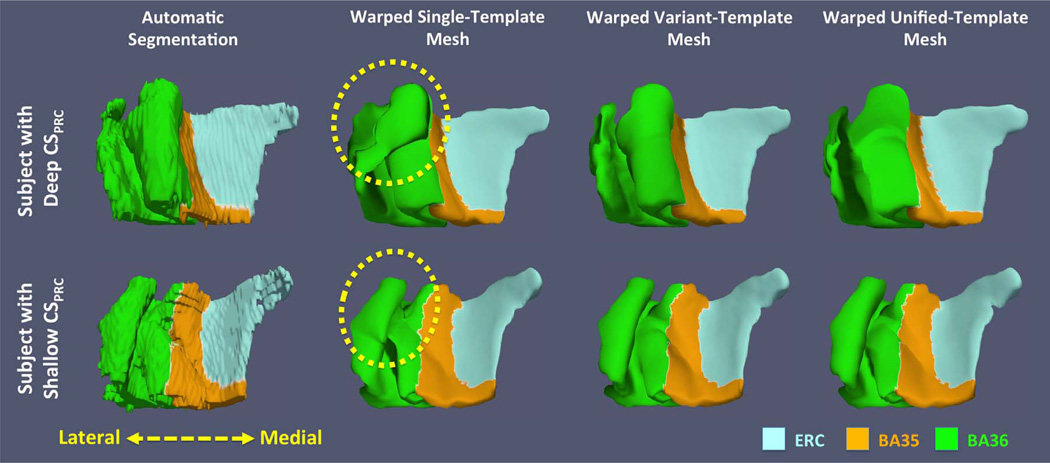
The purpose of building VTs is to generate smooth surface meshes that better fit the blocky ASHS label maps, which are necessary for extracting meaningful thickness measures. To visualize the difference between meshes generated by the ST, VT and UT approaches, Fig. 8 shows two examples of the fitted meshes and the blocky label maps. The first example has deep and continuous CS_PRC while the second one has shallow and discontinuous CS_PRC. The smooth meshes from VT approach fit the segmentations the best, whereas the ST approach generated topologically mismatched fitted meshes. Interestingly, as discussed at Section 3.1, the anatomically implausible structure at the lateral BA36 region in the left ST highlighted by the white arrow in Fig. 7 corresponds to medial BA36 in the first example and to lateral BA36 in the second example (highlighted by the yellow dashed circles in Fig. 8), which demonstrates the incorrect correspondences established by the ST approach. Lastly, the UT approach generates similar meshes to the VT with some minor distortion, likely caused by the registering though multiple intermediate label maps.

In addition to incorrect correspondences, the surface mesh generated by the ST approach has limited capacity in fitting the ASHS label maps accurately. As shown in Fig. 10, the fitted ST mesh has difficulty deep inside the CS and includes CS as part of the PRC. The fitted VT mesh better corresponds to the CS and ASHS label map. Fitted mesh generated by UT has intermediate performance.

Fig. 10.

The fitted meshes generated by the variant-template and unified-template approaches approximate the ASHS label map better than that generated by the single-template approach.

To evaluate the quality of fit quantitatively, we warp the template segmentation back to each subject and compute the average Dice similarity coefficient (DSC) and average Hausdorff distance for ERC, BA35, BA36, CS_PRC, CS_PHC and PHC between the warped template label map and the subject's ASHS label map in the native SR-T2w space of each subject. The higher the average DSC and the lower the average Hausdorff distance, the better the fit. The results, as shown in Table 3, are consistent with the qualitative assessment above. For the structures that have large variability, i.e., BA35, BA36 and CS_PRC, the VTs have the highest quality of fit among almost all the labels (except right BA35). The UT yields intermediate quality, while the ST approach performs the worst. This is especially true for CS_PRC, the label that has the most variability. Another important observation is that the quality is nearly the same across methods for the ERC, PHC and CS_PHC, which demonstrates that the proposed pipeline does not degrade the quality of the fitted surfaces for relatively consistent adjacent structures.

Table 3.

Quantitative evaluation of the quality of fit between warped template label maps and blocky ASHS label maps in subject space. Average Dice similarity coefficient (top) and average Hausdorff distance (bottom) are reported (standard deviation in parentheses).

Approaches	Labels that are highly variable			Relatively consistent labels
	BA35	BA36	CSPRC	ERC	PHC	CSPHC
Average Dice Similarity Coefficient
Left Hemisphere
Single Template	0.952 (± 0.015)	0.957 (± 0.013)	0.799 (± 0.075)	0.982 (± 0.005)	0.977 (± 0.008)	0.927 (± 0.031)
Variant Template	0.960 (± 0.015)**	0.972 (± 0.011)**	0.865 (± 0.091)**	0.981 (± 0.005)**	0.978 (± 0.009)**	0.935 (± 0.029)**
Unified Template	0.948 (± 0.015)**	0.967 (± 0.011)**	0.856 (± 0.069)**	0.976 (± 0.005)**	0.972 (± 0.010)**	0.948 (± 0.025)**
Right Hemisphere
Single Template	0.952 (± 0.011)	0.971 (± 0.011)	0.774 (± 0.098)	0.981 (± 0.006)	0.981 (± 0.008)	0.946 (± 0.031)
Variant Template	0.961 (± 0.011)**	0.976 (± 0.008)**	0.850 (± 0.074)**	0.981 (± 0.007)*	0.981 (± 0.008)	0.947 (± 0.032)
Unified Template	0.958 (± 0.011)**	0.978 (± 0.008)**	0.825 (± 0.093)**	0.984 (± 0.005)**	0.983 (± 0.007)**	0.954 (± 0.027)**
Average Hausdorff Distance (mm)
Left Hemisphere
Single Template	0.117 (± 0.035)	0.180 (± 0.047)	0.637 (± 1.060)	0.066 (± 0.020)	0.084 (± 0.022)	0.202 (± 0.237)
Variant Template	0.104 (± 0.046)**	0.119 (± 0.050)**	0.431 (± 0.864)**	0.070 (± 0.028)**	0.080 (± 0.021)**	0.177 (± 0.201)**
Unified Template	0.126 (± 0.029)**	0.134 (± 0.043)*	0.467 (± 0.907)**	0.081 (± 0.015)**	0.100 (± 0.017)**	0.163 (± 0.185)**
Right Hemisphere
Single Template	0.113 (± 0.028)	0.122 (± 0.065)	0.492 (± 0.686)	0.067 (± 0.017)	0.081 (± 0.045)	0.127 (± 0.141)
Variant Template	0.096 (± 0.021)**	0.101 (± 0.051)**	0.311 (± 0.466)**	0.066 (± 0.008)	0.077(± 0.033)**	0.121 (± 0.112)
Unified Template	0.114 (± 0.028)	0.103 (± 0.039)**	0.372 (± 0.544)**	0.067 (± 0.016)	0.082 (± 0.041)	0.120 (± 0.106)

Note:

^*p < 0.05;

^**p < 0.01. Compared with single-template approach, tested by two-tailed paired t-tests.

For the 29 subjects in the ASHS atlas set, manual segmentations were available. We hypothesized that smoothing the ASHS label maps via VT and UT fitting would not reduce their accuracy relative to manual segmentation, while smoothing via ST fitting would reduce accuracy. A paired t-test was used to compare DSC between ST, VT and UT smoothed leave-one-out segmentations of the atlas subjects and the manual segmentations to the DSC between the “blocky” ASHS label maps and manual segmentations. The results in Table 4 mostly fit our hypothesis. For VT-based smoothing the accuracy is greater or the same as ASHS for all labels except the CS. For UT-based smoothing the accuracy is lower than ASHS for bilateral CS and slightly lower for the left BA35. For ST-based smoothing, the accuracy is lowest overall. These results demonstrate that the additional processing introduced in this paper to compute thickness generally does not degrade the accuracy of cortical labels (ERC, BA35, BA36 and PHC) compared to the initial ASHS segmentation and even improves it slightly in some cases. The decrease of CS accuracy with template-based smoothing is likely due to the thinness of this structure, which is difficult for the templates to fit well even after accounting for anatomical variants.

Table 4.

Comparisons of the accuracy of ASHS automatic segmentations and the warped segmentations of the single-template, variant-template and unified-template approaches. Accuracy is measured by the Dice similarity coefficient (DSC) between each label of the warped template segmentation and that of the manual segmentation. Each label's mean DSC and its standard deviation (in parenthesis) at each hemisphere are reported in the table.

Label	Single Template vs. Manual	Variant Template vs. Manual	Unified Template vs. Manual	ASHS vs. Manual
Left Hemisphere
ERC	0.7800 (0.0493)**	0.7802 (0.0492)**	0.7799 (0.0483)	0.7785 (0.0491)
BA35	0.6847 (0.0837)	0.6870 (0.0819)	0.6878 (0.0777)*	0.6843 (0.0809)
BA36	0.7613 (0.0540)**	0.7679 (0.0563)	0.7670 (0.0556)	0.7683 (0.0558)
PHC	0.7689 (0.0510)*	0.7692 (0.0507)**	0.7689 (0.0511)**	0.7665 (0.0516)
CS	0.5639 (0.0918)**	0.5826 (0.0991)**	0.5795 (0.0939)**	0.6040 (0.0970)
Right Hemisphere
ERC	0.7606 (0.0662)*	0.7608 (0.0659)**	0.7603 (0.0660)*	0.7591 (0.0652)
BA35	0.6733 (0.0742)**	0.6772 (0.0760)	0.6742 (0.0744)*	0.6777 (0.0752)
BA36	0.7596 (0.0611)*	0.7617 (0.0612)	0.7615 (0.0607)	0.7618 (0.0604)
PHC	0.7785 (0.0458)	0.7786 (0.0456)	0.7784 (0.0457)	0.7783 (0.0457)
CS	0.5915 (0.0704)**	0.6125 (0.0748)**	0.6007 (0.0704)**	0.6339 (0.0785)

Note:

^*: p < 0.05;

^**: p < 0.01.

Red/blue stars denote significant increase/decrease of performance compared with the DSC of ASHS automatic segmentations vs. manual segmentations, tested by two-tailed paired t-tests.

3.3. Evaluation in the context of aMCI group analysis

Sections 3.1 and 3.2 indicate that the proposed multi-template thickness analysis pipeline can generate a faithful smooth approximation of the ASHS label maps, with pointwise correspondences within anatomical variants (for the VTs) and across all subjects (for the UT). This enables robust computation and statistical analysis of summary and regional measures of thickness (the latter requiring the UT for population-level analyses). In this section, we evaluate the proposed pipeline in the context of group difference analysis between aMCI and NC using summary and regional thickness measures. The performance of the proposed pipeline is compared to the ST approach (Yushkevich et al., 2015b), as well as volumetric measures derived by ASHS and T1w MRI cortical thickness measures generated by FreeSurfer 6.0 (Augustinack et al., 2013; Fischl, 2012; Fischl et al., 2009).

3.3.1. Summary thickness analysis

Summary thickness measures of MTL cortices, i.e. ERC, BA35, BA36 and PHC, were generated using VT, UT and ST approaches. For comparison, we computed the volumes of these same regions from ASHS label maps, as well as the thickness of the ERC and PRC from FreeSurfer (Section 2.5.4).

Additionally, we separately computed the summary thickness of the anterior BA35. In our segmentation protocol, following Ding and Van Hoesen (2010), the most posterior slice of BA35 extends farther medially than in the more anterior slices, and a small strip of BA35 is located between the ERC and PHC. Due to the large slice thickness of the T2w MRI, this posterior portion of the BA35 is associated with more frequent ASHS segmentation errors than the anterior BA35. These errors were hypothesized to contribute additional noise to the BA35 summary thickness measurements. To test this, summary thickness measures were obtained for the anterior portion of BA35, which was defined geometrically by taking the anterior half of the slices in which BA35 was labeled by ASHS.

For each summary measure, we fitted a general linear model (GLM) with group membership as the factor of interest, and age, and ICV as covariates, and obtained the t-statistics for the NC-aMCI contrast. The p-values of all the measurements were corrected for multiple comparisons using false discovery rate (FDR) approach (Benjamini and Yekutieli, 2001). We also performed receiver operating curve (ROC) analysis for each summary measure, after residualizing it by age and ICV, and report area under the curve (AUC) for the discrimination between aMCI and NC groups. The results of this statistical analysis are reported in Table 5. Furthermore, an optimal threshold was chosen for each measurement by maximizing its corresponding Youden's index (specificity+sensitivity−1) (Youden, 1950). Using this threshold, each measurement's sensitivity, specificity, accuracy as well as balanced accuracy was calculated and reported in Table 6. The results can be summarized as follows:

• Among all the measurements, the thickness of left BA35 generated by the UT (t=4.97, AUC=0.780) and VTs (t=4.89, AUC=0.778) methods best discriminate aMCI from NC, and limiting measures only to the anterior portion (left anterior BA35) further increases the statistical power (t=5.39, AUC=0.786 and t=5.12, AUC=0.782 for UT and VTs, respectively). The discriminative power of the left CA subfield, ERC and hippocampus, the latter two commonly used AD biomarkers, are strong but not as high, in absolute terms, as for left BA35 thickness.

• The t-statistics of thickness measurements from the proposed multi-template approach (UT and VTs) in discriminating aMCI from NC is overall larger than those generated by the ST approach and ASHS volumetry.

• Compared to the proposed pipeline, thickness measurements generated by FreeSurfer show stronger effect in left ERC (FreeSurfer thickness of ERC: t = 3.53, AUC = 0.708; UT thickness of ERC: t = 2.77, AUC= 0.657) and weaker effect in left BA35 (FreeSurfer thickness of BA35: t=3.21, AUC=0.681; UT thickness of anterior BA35: t=5.39, AUC=0.786). The DeLong test (DeLong et al., 1998) was performed to compare the discriminative power of ROC curves. The stronger effect in left ERC of FreeSurfer does not reach significance (z = 0.759, p = 0.776) while the proposed pipeline generates a statistically significant stronger effect in left anterior BA35 (z = 1.79, p = 0.037). Direct comparison between the best measurements of FreeSurfer and the proposed pipeline, i.e. left ERC thickness of FreeSurfer and left anterior BA35 thickness of the proposed pipeline respectively, does not reach significance (z = 1.16, p = 0.123). On the right side, the effects of the two approaches are similar and are much weaker than that of the left side. Interestingly, the mean thickness from FreeSurfer for both ERC and BA35 is about 1 mm greater and more variable than that from the T2w MRI.

Table 5.

Statistical analysis results of summary measurements. Units for thickness and volumetric measures are mm and mm³. The three measurements with the best statistical power in discriminating aMCI from NC at each hemisphere are highlighted in bold.

Label	Measurements	NC Mean (SD)	aMCI Mean (SD)	t-stat	Corrected p-value	Cohen's d ES	AUC	AUC 95% C.I. radius
Left Hemisphere
CA	Volume	1254 (158)	1101 (200)	4.45	2.3e-4	0.85	0.775	0.101
DG	Volume	733 (94)	654 (143)	3.54	0.0020	0.65	0.719	0.114
SUB	Volume	425 (56)	402 (76)	1.79	0.087	0.34	0.583	0.124
HIPPO	Volume	2413 (278)	2157 (397)	4.00	5.8e-4	0.75	0.743	0.108
ERC	Volume	468 (70)	423 (97)	2.95	0.0093	0.53	0.700	0.115
	ST Thickness	1.81 (0.14)	1.72 (0.19)	2.55	0.019	0.54	0.643	0.119
	VT Thickness	1.82 (0.15)	1.73 (0.19)	2.55	0.019	0.53	0.646	0.118
	UT Thickness	1.81 (0.14)	1.72 (0.20)	2.77	0.013	0.52	0.657	0.118
	FS Thickness	3.01 (0.43)	2.64 (0.54)	3.53	0.0020	0.76	0.708	0.111
BA35	Volume	476 (84)	408 (106)	4.19	3.9e-4	0.71	0.756	0.106
	ST Thickness	2.05 (0.15)	1.88 (0.24)	4.17	3.9e-4	0.85	0.742	0.110
	VT Thickness	2.16 (0.16)	1.96 (0.25)	4.89	6.3 e-5	0.95	0.778	0.101
	UT Thickness	2.00 (0.15)	1.80 (0.23)	4.97	6.3 e-5	1.03	0.780	0.100
	FS Thickness	3.31 (0.38)	3.00 (0.54)	3.21	0.0050	0.66	0.681	0.115
Anterior BA35	ST Thickness	2.19 (0.15)	1.95 (0.31)	4.75	9.0 e-5	0.99	0.753	0.110
	VT Thickness	2.23 (0.16)	1.97 (0.31)	5.12	5.0 e-5	1.05	0.782	0.099
	UT Thickness	2.23 (0.20)	1.91 (0.34)	5.39	5.0 e-5	1.15	0.786	0.098
BA36	Volume	1747 (327)	1571 (349)	2.71	0.014	0.52	0.642	0.118
	ST Thickness	2.17 (0.13)	2.09 (0.18)	2.74	0.013	0.51	0.647	0.118
	VT Thickness	2.39 (0.16)	2.27 (0.21)	3.17	0.0052	0.64	0.690	0.114
	UT Thickness	2.22 (0.21)	2.14 (0.20)	1.85	0.077	0.39	0.617	0.121
PHC	Volume	955 (155)	832 (172)	3.93	6.8 e-4	0.75	0.737	0.107
	ST Thickness	2.14 (0.17)	2.00 (0.18)	4.20	3.9 e-4	0.80	0.740	0.106
	VT Thickness	2.15 (0.16)	2.00 (0.18)	4.17	3.9 e-4	0.88	0.741	0.106
	UT Thickness	2.10 (0.16)	1.96 (0.18)	4.10	4.4 e-4	0.82	0.739	0.106
Right Hemisphere
CA	Volume	1297 (184)	1147 (213)	3.91	6.9 e-4	0.75	0.728	0.108
DG	Volume	748 (114)	674 (125)	3.20	0.0050	0.62	0.684	0.114
SUB	Volume	414 (58)	400 (75)	1.07	0.30	0.21	0.566	0.126
HIPPO	Volume	2459 (320)	2221 (385)	3.55	0.0020	0.67	0.695	0.114
ERC	Volume	454 (83)	425 (84)	1.87	0.013	0.35	0.610	0.123
	ST Thickness	1.83 (0.19)	1.76 (0.18)	1.91	0.077	0.38	0.644	0.119
	VT Thickness	1.84 (0.19)	1.76 (0.18)	2.01	0.062	0.43	0.646	0.119
	UT Thickness	1.80 (0.18)	1.73 (0.17)	2.07	0.055	0.40	0.661	0.118
	FS Thickness	3.09 (0.49)	2.86 (0.58)	1.93	0.071	0.43	0.620	0.122
BA35	Volume	479 (96)	427 (92)	2.78	0.013	0.55	0.672	0.116
	ST Thickness	2.16 (0.24)	2.07 (0.20)	1.87	0.077	0.41	0.646	0.119
	VT Thickness	2.21 (0.23)	2.10 (0.22)	2.30	0.034	0.49	0.651	0.119
	UT Thickness	2.04 (0.21)	1.94 (0.18)	2.66	0.015	0.51	0.692	0.114
	FS Thickness	3.45 (0.35)	3.14 (0.49)	3.36	0.0033	0.73	0.698	0.115
Anterior BA35	ST Thickness	2.22 (0.28)	2.09 (0.28)	2.15	0.047	0.46	0.639	0.118
	VT Thickness	2.19 (0.25)	2.07 (0.28)	2.13	0.049	0.45	0.640	0.119
	UT Thickness	2.08 (0.26)	1.92 (0.28)	2.69	0.014	0.59	0.671	0.117
BA36	Volume	1572 (329)	1559 (362)	0.25	0.81	0.04	0.507	0.125
	ST Thickness	2.30 (0.20)	2.27 (0.20)	0.71	0.49	0.15	0.557	0.124
	VT Thickness	2.37 (0.19)	2.31 (0.18)	1.55	0.13	0.32	0.610	0.122
	UT Thickness	2.28 (0.19)	2.24 (0.20)	1.12	0.28	0.21	0.574	0.124
PHC	Volume	950 (145)	890 (171)	1.90	0.073	0.38	0.576	0.124
	ST Thickness	2.20 (0.15)	2.10 (0.20)	2.89	0.011	0.57	0.647	0.121
	VT Thickness	2.21 (0.15)	2.10 (0.20)	2.86	0.011	0.62	0.645	0.121
	UT Thickness	2.14 (0.15)	2.04 (0.19)	2.76	0.013	0.58	0.626	0.122

Abbreviations: ST=single template; VT=variant template; UT=unified template; FS=FreeSurfer; ES=effect size; HIPPO=hippocampus; SD=standard deviation.

Table 6.

Sensitivity, specificity, accuracy and balanced accuracy of summary measurements. The optimal threshold of each measurement was obtained by maximizing its Youden index (Youden, 1950).

Label	Measurements	Sensitivity	Specificity	Accuracy	Balanced Accuracy
Left Hemisphere
CA	Volume	0.707	0.795	0.753	0.751
DG	Volume	0.537	0.909	0.729	0.723
SUB	Volume	0.488	0.705	0.600	0.596
HIPPO	Volume	0.561	0.864	0.718	0.712
ERC	Volume	0.488	0.909	0.706	0.698
	ST Thickness	0.293	0.977	0.647	0.635
	VT Thickness	0.341	0.909	0.635	0.625
	UT Thickness	0.512	0.750	0.635	0.631
	FS Thickness	0.488	0.864	0.682	0.676
BA35	Volume	0.610	0.818	0.718	0.714
	ST Thickness	0.732	0.750	0.741	0.741
	VT Thickness	0.732	0.773	0.753	0.752
	UT Thickness	0.707	0.773	0.741	0.740
	FS Thickness	0.561	0.818	0.694	0.690
Anterior BA35	ST Thickness	0.756	0.750	0.753	0.753
	VT Thickness	0.659	0.818	0.741	0.738
	UT Thickness	0.585	0.886	0.741	0.736
BA36	Volume	0.854	0.432	0.635	0.643
	ST Thickness	0.463	0.773	0.624	0.618
	VT Thickness	0.732	0.591	0.659	0.661
	UT Thickness	0.683	0.591	0.635	0.637
PHC	Volume	0.634	0.795	0.718	0.715
	ST Thickness	0.537	0.864	0.706	0.700
	VT Thickness	0.732	0.682	0.706	0.707
	UT Thickness	0.683	0.705	0.694	0.694
Right Hemisphere
CA	Volume	0.659	0.705	0.682	0.682
DG	Volume	0.512	0.818	0.671	0.665
SUB	Volume	0.390	0.841	0.624	0.616
HIPPO	Volume	0.415	0.955	0.694	0.685
ERC	Volume	0.561	0.705	0.635	0.633
	ST Thickness	0.488	0.795	0.647	0.642
	VT Thickness	0.610	0.682	0.647	0.646
	UT Thickness	0.610	0.705	0.659	0.657
	FS Thickness	0.366	0.864	0.624	0.615
BA35	Volume	0.732	0.591	0.659	0.661
	ST Thickness	0.732	0.614	0.671	0.673
	VT Thickness	0.463	0.864	0.671	0.664
	UT Thickness	0.610	0.750	0.682	0.680
	FS Thickness	0.707	0.659	0.682	0.683
Anterior BA35	ST Thickness	0.585	0.659	0.624	0.622
	VT Thickness	0.756	0.545	0.647	0.651
	UT Thickness	0.537	0.864	0.706	0.700
BA36	Volume	0.171	0.909	0.553	0.540
	ST Thickness	0.610	0.545	0.576	0.578
	VT Thickness	0.683	0.591	0.635	0.637
	UT Thickness	0.659	0.545	0.600	0.602
PHC	Volume	0.293	0.932	0.624	0.612
	ST Thickness	0.390	0.932	0.671	0.661
	VT Thickness	0.415	0.886	0.659	0.650
	UT Thickness	0.415	0.864	0.647	0.639

Abbreviations: ST=single template; VT=variant template; UT=unified template; FS=FreeSurfer; HIPPO=hippocampus.

3.3.2. Regional thickness analyses on the whole cohort

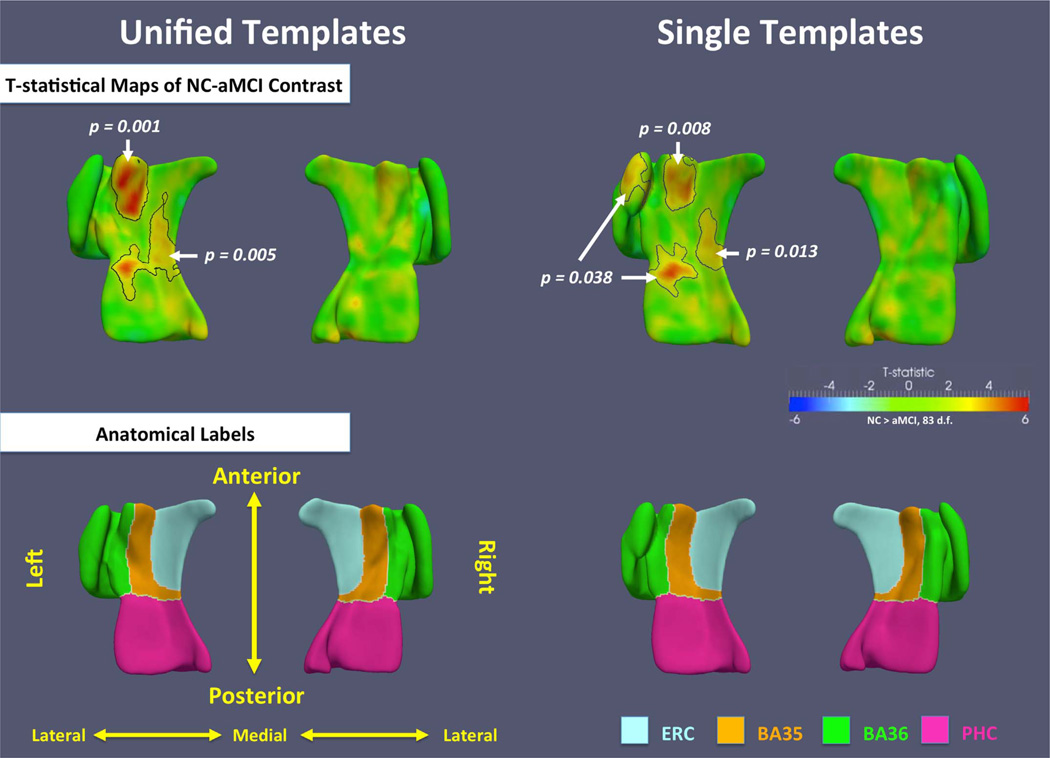
Statistical analysis of regional thickness maps was performed in the UT space using data from the whole cohort. Pointwise thickness measurements derived in subject space were brought back into the UT space and at each vertex on the UT surface, a GLM model was fitted at each vertex with thickness as the dependent variable, group membership as the factor of interest, and age and ICV as covariates. To account for multiple statistical comparisons, cluster-level family-wise error rate (FWER) correction was used (Nichols and Hayasaka, 2003). Specifically, clusters were obtained by thresholding the t-maps at t = 2.64(p = 0.01). Permutation testing with 1000 permutations (with clusters pooled between the left and right hemispheres) was used to assign a corrected p-value to each cluster. For comparison, the same analysis was repeated for the ST approach.

Fig. 11 shows the t-statistic maps for the NC-aMCI contrast, outlines the statistically significant clusters, and gives their corrected p-values. Several significant clusters are found in the left MTL using both the UT and ST analyses. The clusters in the anterior BA35, the anterior PHC and the posterior ERC largely overlap between the UT and ST analyses, with the UT clusters having smaller p-values. A cluster in the left BA36 in the ST analysis has no counterpart in the UT analysis. This cluster is likely the consequence of the incorrect correspondences established by the ST approach, as illustrated in Fig. 8. By contrast, the stronger effect in the anterior BA35 in UT approach is likely due to the more meaningful correspondences established by the proposed pipeline. On the right side, the effects are much weaker than on the left, which is consistent with the summary thickness analyses.

Fig. 11.

T-statistical maps of NC-aMCI contrast in the unified templates and the single templates using data from all subjects. Black contours outline significant clusters after cluster-level family-wise error rate (FWER) correction. The corrected p-value of each cluster is indicated by the white arrow and text. Anatomical labels are shown in the bottom row.

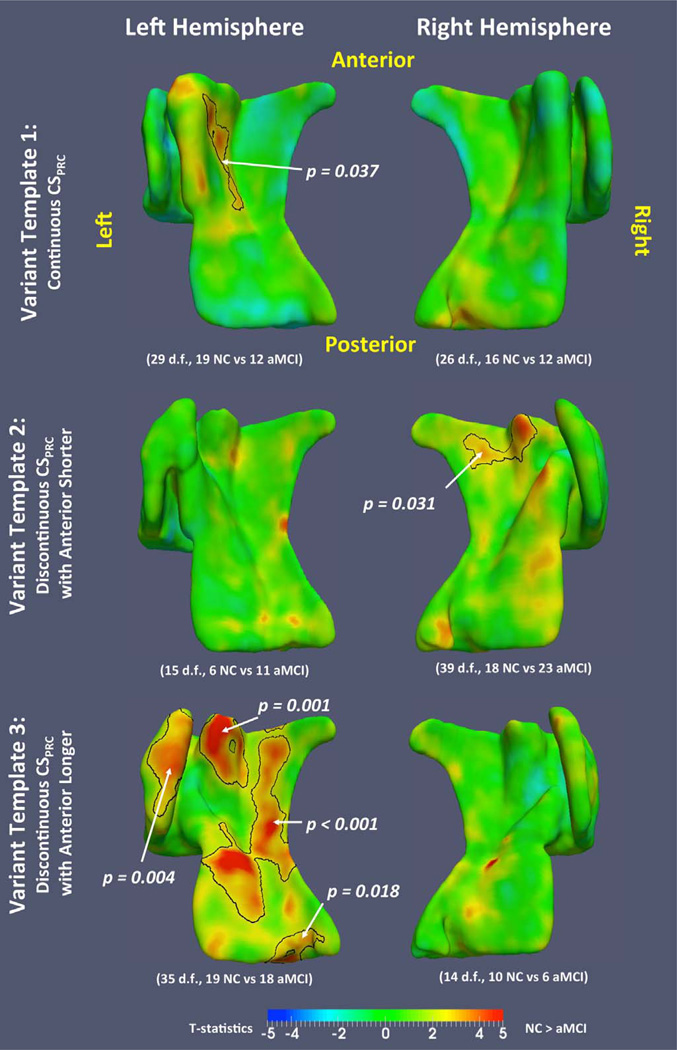
3.3.3. Regional thickness analyses of the three anatomical variants of PRC

Similar regional thickness analyses were also performed in each of the VTs to investigate whether the MTL atrophy associated with aMCI is different between the three anatomical variants. As in Section 3.3.2, cluster-level FWER correction was performed in each VT (Nichols and Holmes, 2002), with the same empirically chosen cluster threshold (t=2.40). Fig. 12 plots the t-statistics for the NC-aMCI contrast for the three VTs in both hemispheres, with significant clusters outlined. On the left side, VT 3 shows strong effects throughout the MTL cortices, while the effects in VT 1 are localized to the medial portion of the PRC. Also, the effects in VT 1 (deep and continuous CS_PRC) spread throughout the anterior and posterior extent of the medial portion of the PRC, and for VT 3 (shallow and discontinuous CS_PRC), the effects are located at anterior medial and lateral PRC. The number of subjects in VT 2 is too small (6 NC and 11 aMCI) to show any meaningful effects. On the right side, only VT 2 has significant clusters. Overall, the patterns of effects are different in the three VTs.

Fig. 12.

T-statistical maps of NC-aMCI contrast in the variant templates. Black contours outline significant clusters after cluster-level family-wise error rate (FWER) correction. The corrected p-value of each cluster is indicated by the white arrow and text.

Interestingly, some of the clusters in the left VT 3 have p-values that are as low or lower than the most significant clusters in the UT analysis, even though the number of subjects in VT 3 is much smaller. This suggests that the differences associated with aMCI may be more consistent within variants than across variants.

4. Discussion

The dataset analyzed in this study was previously analyzed in Xie et al. (2014), Yushkevich et al. (2015b), and the overall findings concerning the correlates of aMCI in the MTL are consistent. The largest correlates of aMCI are found in the left BA35 as in these prior analyses, and on the whole, the regional maps of thickness reveal similar patterns. However, the introduction of the UT space in the current paper yielded thickness maps that are more consistent with the known AD pathology compared to the analysis in ST space reported previously in Yushkevich et al. (2015b): stronger effects at left BA35 and no group differences in BA36. Additionally, the current paper for the first time examined thinning patterns associated with aMCI separately in different anatomical variants of the MTL. Further, these previous papers did not examine PHC thinning, and the current paper detected aMCI correlates in the PHC.

4.1. The multi-template approach is well-suited for analyzing structures with discrete anatomical variants

The main novel aspect of this study and the prior study in Xie et al. (2014) was to explicitly account for discrete anatomical variants of the PRC when analyzing summary and regional thickness of MTL subregions. The proposed multi-template approach yields smooth label maps that are accurate representations of the input ASHS label maps, as well as pointwise correspondences between subjects that appear to be more anatomically meaningful than the correspondences obtained by a ST approach. By improving within-variant and between-variant correspondence, the multi-template approach enhanced the ability to discriminate aMCI from NC, yielding the highest statistics, in absolute terms, than the other approaches tested in this study (Augustinack et al., 2013; Fischl, 2012; Yushkevich et al., 2015b).

The multi-template approach is implemented as a post-processing step applied after multi-atlas segmentation of MTL subregions using ASHS (Yushkevich et al., 2015b). In theory, multi-atlas segmentation is better adapted to anatomical heterogeneity than single-atlas or single-template based approaches due to the availability of multiple atlases with different exemplars of anatomy. We verified this, in part, by finding that ASHS atlases that shared a common PRC variant with the target subject were assigned greater label fusion weights than the atlases whose variant differed from the target (Section 3.0). This suggests that ASHS is implicitly accounting for the existence of different anatomical variants.

The multi-template approach for computing thickness from ASHS label maps consistently demonstrated better inter-subject correspondences than the ST approach in Yushkevich et al. (2015b). The ST approach fails to match anatomically corresponding locations between subjects and produces implausible anatomical configurations in template space (Figs. 7 and 9). The proposed VT and UT approaches provide a closer fit to the initial ASHS label maps (Table 3) as well as to the underlying manual segmentations (Table 4) than the ST approach. The templates themselves are more anatomically plausible (Fig. 7). Since the high quality of the fitted surface mesh and correct correspondences between subjects are important for accurate thickness measurement and regional thickness analysis, the proposed multi-template pipeline is more suitable for analyzing PRC thickness. The larger t-statistics in discriminating aMCI from NC and the more biologically plausible pattern of statistically significant clusters found in the regional analysis further support the conclusion that the multi-template approach is more suitable than ST approaches for PRC thickness analysis.

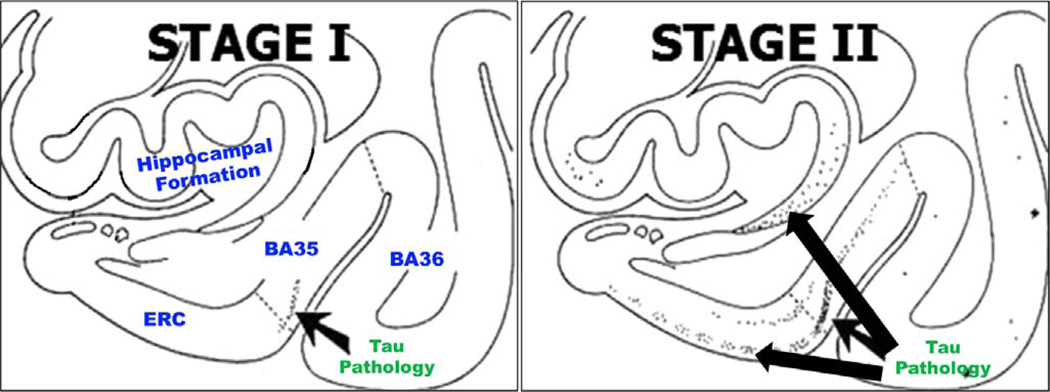
Direct comparisons between the UT/VT thickness measures and those produced by FreeSurfer (Augustinack et al., 2013; Fischl, 2012; Fischl et al., 2009) is infeasible due to differences in the MRI modality, the segmentation protocol, and the methods used to extract thickness. Instead, an indirect comparison of these approaches with regard to statistical power in discriminating aMCI from NC groups was carried out. FreeSurfer yielded stronger discriminative power in the ERC, while the VT/UT approach yielded a stronger group difference in BA35. The effect in left BA35 with the VT/UT approach was stronger than that yielded by FreeSurfer in either BA35 (statistically significant) or ERC (only in absolute terms). A stronger effect in BA35, rather than ERC, is consistent with the known spread of NFT pathology from this region (Braak and Braak, 1995). As shown in Fig. 13, BA35 is the first site in the MTL affected by NFT pathology in early Braak stages I/II, during which most subjects do not have symptoms of cognitive impairment. While the aMCI patients analyzed in this study are likely to have more advanced NFT pathology (Braak stages III or later, affecting ERC, CA1 and other parts of the MTL), the strong morphological differences detected in BA35 between aMCI patients and controls are consistent with there being a delay between the formation of NFTs in a given region and a detectable macroscopic change in gray matter thickness.

Fig. 13.

The progression of tau neurofibrillary tangle (NFT) pathology in the MTL in Braak stages I and II (Braak and Braak, 1995). NFT pathology in BA35 precedes its spread to the ERC and the hippocampus. Braak stages III–VI are not shown. Figure adapted from Braak and Braak (1995).

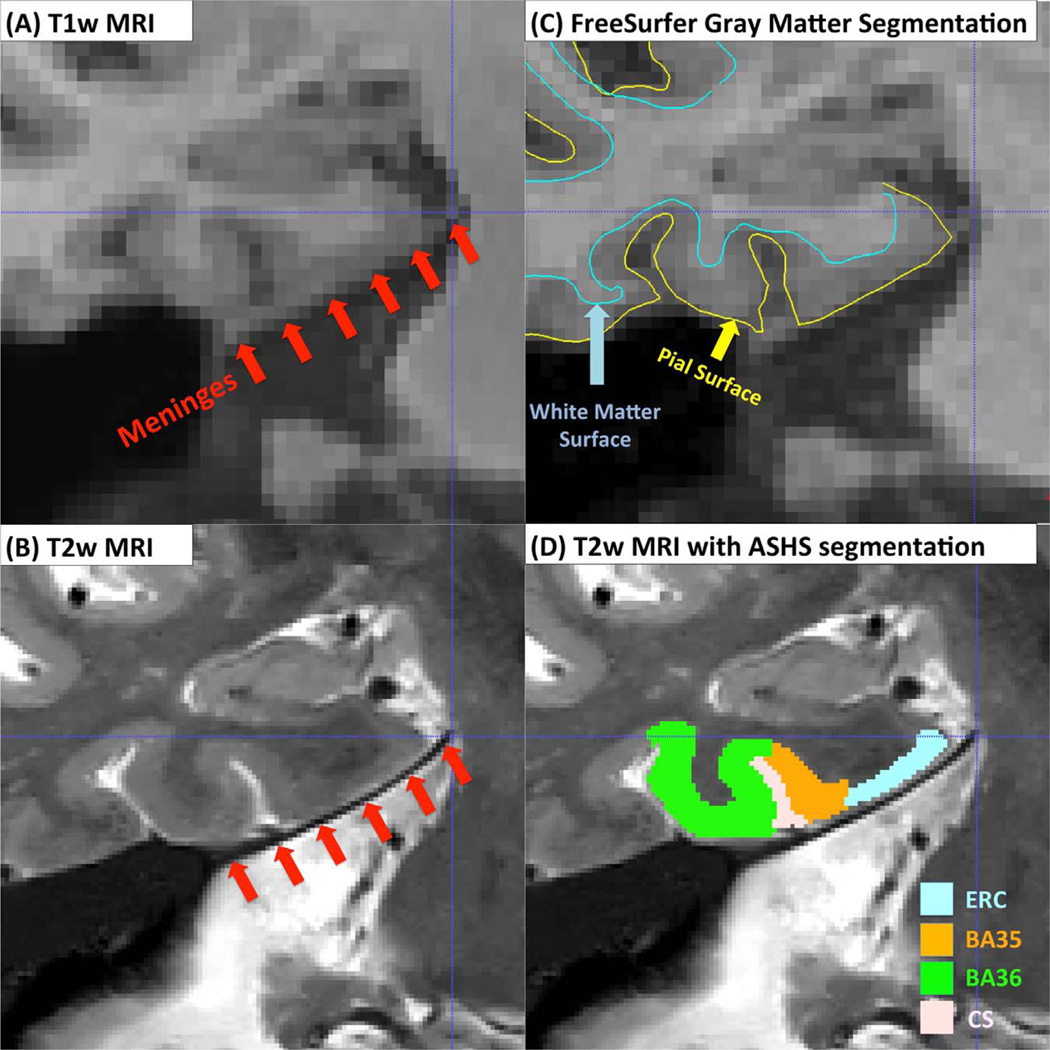
Smaller effects in the NC-aMCI comparisons for FreeSurfer may be due to its use of a single template to model the PRC. However, another potential source of noise in FreeSurfer PRC measurements is due to the meninges, three layers of membranes (dura mater, arachnoid mater and pia mater) that cover the brain and spinal cord. The dura, a thick outer layer, has similar intensity to the gray matter in T1w MRI (Fig. 14A) and parts of the ERC and PRC appear merged with parts of the meninges. This can cause FreeSurfer to sometimes include the meninges in its estimation of ERC and PRC thickness (Fig. 14C). In T2w MRI, meninges have low intensity, and the contrast between the dura and gray matter is very high (Fig. 14B). Thus ASHS segmentations of PRC and ERC are not confounded in this manner (Fig. 14D). This is likely the reason why the mean thickness of ERC and BA35 in FreeSurfer is about 1 mm greater than the corresponding measures obtained using the proposed pipeline (Table 5). It is likely that the meningeal layer adds noise to the ERC and PRC thickness measurements derived from T1w MRI.

Fig. 14.

The possible confound of meninges when deriving MTL cortical thickness measures from T1w MRI. The layer of meninges (red arrows) appears dark in T2w MRI (B) but has similar intensity to the MTL gray matter in T1w MRI (A). This may cause over-segmentation of the ERC and PRC in T1w MRI (C), reducing the accuracy of thickness measurements. Over-segmentation is unlikely in T2w MRI because of the strong contrast between the meninges and MTL gray matter (D). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4.2. Spatial distributions of disease effects

Since the cortex is organized like a sheet, it is reasonable to expect that the location of the earliest NFT pathology within the PRC would be variable across different anatomical subtypes. If this were true, failure to account for this variability would likely reduce the sensitivity of MRI-derived measures of the PRC for detection of early AD pathology. Modeling this anatomy-pathology relationship would likely further improve our ability to use MRI as an early AD biomarker. T-statistical maps in Fig. 12 reveal different patterns of cortical thinning among anatomical subtypes in this study. If we focus on left BA35, the region where the strongest effect is detected in the UT space, pathology emerges on the medial bank of the CS in people with a deep CS_PRC (VT 1) while in people with shallow sulcus (VT 3), it emerges more laterally. Although the small sample size and different numbers of aMCI/NC subjects in each VT prevent us from drawing any firm conclusions, the different patterns found in different VTs indicate possible differential effects of early AD pathology among anatomical variants. A larger dataset would be needed to test this hypothesis. By quantifying the relationship between PRC anatomical variants and the spatial distribution of early AD pathology, it would be possible to infer for each individual subject where in the MTL AD-related changes are most likely to occur in that subject, potentially leading to individualized biomarkers for disease progression monitoring.

In the ERC, the significant cortical thinning associated with aMCI, (left UT, Fig. 11; left VT 3 and right VT 2, Fig. 12) is not unexpected because the ERC is also a site of early NFT pathology according to the Braak and Braak staging system shown in Fig. 13 (Braak and Braak, 1995). More surprisingly, we observe significant thinning in the PHC in aMCI patients (left UT and left VT 3). Although the PHC has not been identified as an early Braak stage region, its adjacency to the PRC makes it possible for pathology to spill over by the aMCI phase of the disease.

4.3. Computational cost

The construction of the templates in our pipeline is moderately computationally expensive, requiring n (n + 1) coarse deformable registrations and 9n dense deformable registrations to build 3 VTs and 1 UT (each hemisphere) using n subjects. In the case of the PRC, each coarse registration required 2.6 min and each dense registration required 8.2 min, on average, on a single modern CPU core (Xeon^® CPU E5-2660, 2.2 GHz). Other parts of the pipeline required negligible computational time. The algorithm is highly parallelizable. Using 40 cores, the whole training pipeline with 85 subjects requires about 13 h for each hemisphere.

Mapping a new subject to the templates is efficient, requiring only 3 coarse deformable registrations and 1 dense registration for each hemisphere (total of 20 min on a single core). It includes the following steps: (1) Register the automatic segmentation of the new subject to the three VTs using the same coarse deformable registration approach in Section 2.4.1.1; (2) measure the similarity of the registered segmentation of the new subject with the three VTs in the same way as that in Section 2.4.1.1 and select the VT with highest similarity; (3) Perform dense deformable registration, the same as that in Section 2.4.1.2, between the selected VT and the automatic segmentation of the new subject; (4) The mesh of the UT is first warped to the selected VT space (using existing deformation field constructed in Section 2.4.2.2) and then to the new subject's space. Thickness is then extracted from the warped UT mesh similar to Section 2.4.1.3.

4.4. The multi-template approach may be applicable to other brain regions

The proposed pipeline is almost completely automated (except for deciding the number of clusters), and can be generalized and applied to other brain regions where discrete anatomical variants exist, such as the medial frontal cortex (Fornito et al., 2008). Indeed, it is possible to envision the proposed method used as part of a “divide and conquer” strategy to handle anatomical variability. Each human brain is unique in terms of its folding pattern and the distribution of underlying cytoarchitecture. Characterizing anatomical variability of the brain “on the whole” may not be feasible given the almost infinite number of anatomical configurations. However, when focusing on specific local cortical regions, the regional anatomical variability can often be described by discrete variants, such as the three variants of PRC in the MTL. A future strategy for characterizing brain variability may involve creating multiple templates for different anatomical regions.

4.5. Limitations and opportunity for improvement

A limitation of the proposed pipeline is that it only models anatomical variation associated with CS_PRC branching and depth. The rhinal sulcus, which varies from not existing, to shallow and deep, is also an important sulcus in the MTL that affects the definition of PRC boundaries (Ding and Van Hoesen, 2010), although to a lesser extent than CS_PRC. Further, the posterior MTL, not a focus of the current work, also exhibits some degree of variability. Extending the current pipeline to model the variation of two or more sulci would yield more accurate measurements but will likely require more subjects to account for the increase in the number of variants.

The estimation of ICV based on registration to a whole-brain template in which the brain was extracted using BET (Smith, 2002) is a limitation because this approach does not include exterior CSF in the ICV estimate. However, the proposed pipeline can be used with any ICV estimation approach, e.g. approaches in Malone et al. (2015) and Manjón et al. (2014).

Another limitation lies in the separation of the automatic segmentation and thickness analysis pipelines. Currently, the thickness measurement and inter-template registration highly depend on the accuracy of automatic segmentation. Developing a unified pipeline where segmentation and correspondence-finding are performed concurrently is desirable.

5. Conclusions

In this study, a novel multi-template framework for analyzing the thickness of the MTL cortical regions was developed and evaluated. The framework explicitly models the existence of discrete anatomical variants of the PRC previously defined in the neuroanatomy literature. Both qualitative and quantitative evaluations demonstrate that the proposed pipeline generated better correspondences between subjects’ anatomies and allowed more accurate estimation of regional thickness than the conventional single-template approach, which does not explicitly account for the existence of multiple anatomical variants. Further, when applied to a dataset of patients with aMCI and NC, the multi-template approach yielded larger t-statistics in discriminating the two groups compared to the single-template approach, volumetric measurements based on multi-atlas segmentation, and thickness measures extracted from T1w MRI by FreeSurfer. This method may have important utility in the diagnosis and monitoring of early AD, as well as for providing accurate measurements to enhance brain-behavior studies in the MTL.

Abbreviations

AD

Alzheimer's disease

ASHS

automatic segmentation of hippocampal subfields

AUC

area under the curve

aMCI

amnestic mild cognitive impairment

BA35 and BA36

Brodmann area 35 and 36

CA

cornu ammonis

CS

collateral sulcus

DG

dentate gyrus

DSC

Dice similarity coefficient

ERC

entorhinal cortex

FDR

false discovery rate

FWER

family-wise error rate

GDSC

generalized Dice similarity coefficient

GLM

general linear model

HD

Hausdorff distance

ICV

intracranial volume

MST

minimum spanning tree

MTL

medial temporal lobe

NC

normal control

NFT

neurofibrillary tangle

OTS

occipito-temporal sulcus

PHC

parahippocampal cortex

PPCA

probabilistic principal component analysis

PRC

perirhinal cortex

ROC

receiver operating curve

ST

single template

SUB

subiculum

SR

super-resolution

T1w

T1-weighted

T2w

T2-weighted

UT

unified template

VT

variant template

Appendix A. T2w MRI preprocessing and manual segmentation upsampling

Preprocessing using the patch-based SR technique

The SR technique includes the following steps: (1) T1w and T2w MRI scans are denoised using a non-local image denoising algorithm (Coupé et al., 2008; Manjón et al., 2010c); (2) The T1w MRI scan is upsampled to 0.5×0.5×1.0 mm³ using a non-local SR scheme (Coupé et al., 2013; Manjón et al., 2010b); (3) the T2w MRI is registered to T1w MRI using both FLIRT (Smith et al., 2004) and ANTS (Avants et al., 2008) rigid registration algorithm (6 degrees of freedom) with normalized mutual information (NMI) as similarity metric. The result that yields higher NMI will be used; (4) The T2w MRI scan is upsampled to 0.4×0.4×1.0 mm³ (16-channel coil) or 0.4×0.4×1.3 mm³ (8-channel coil) using self-similarity and the registered upsampled T1w image as image prior (Manjón et al., 2010a) and is referred to as SR-T2w MRI.

Upsampling manual segmentations to the space of SR-T2w MRI

Manual segmentation upsampling is different from that for T2w MRI because there is no redundant information in local neighborhood patches. One option is to upsample the manual segmentation using conventional interpolation techniques and then perform manual correction. However, this would be impractical because the manual correction could take as much time as manually segmenting the whole structure. Since the preprocessing step can be viewed as inserting one slice between every two coronal slices in the T2w MRI, we can take advantage of the neighboring coronal slices to generate labels for the newly inserted slice. We propose an application-specific technique with the following steps: (1) the original T2w MRI and the corresponding manual segmentation are upsampled to the space of the SR-T2w MRI using nearest neighbor interpolation, referred to as NN-T2w MRI and NN-Seg; (2) 2D multi-atlas segmentation is performed to label each coronal slices of the SR-T2w MRI using the corresponding slice and its 4 neighboring coronal slices of the NN-T2w MRI and NN-Seg as atlases (corresponding to the corresponding slice and its 2 immediate neighbor coronal slices in the original T2w MRI).

Appendix B. An abbreviated explanation of ASHS algorithm/package

ASHS is a multi-atlas label fusion algorithm that propagates anatomical labels from a set of manually-labeled MRI scans called “atlases” to new unlabeled “target” MRI scans. It includes the following steps: (1) ASHS uses symmetric greedy diffeomorphic registration in the ANTs software (Avants et al., 2008) to warp each atlas to the target MRI; (2) the joint label fusion algorithm to combine the anatomical labels from the warped atlases into a single consensus segmentation in a way that assigns spatially varying weights to each atlas based on patch-level similarity to the target image while accounting for possible redundancy among the atlases (Wang et al., 2012); (3) the corrective learning algorithm to correct for systematic segmentation biases using classifiers learned from leave-one-out segmentation of the atlas images (Wang et al., 2011); (4) bootstrapping, i.e., using the results of multiatlas segmentation to initialize deformable registration to improve atlas-target matching. The accuracy of ASHS relative to manual segmentation was evaluated in Yushkevich et al. (2010) and Yushkevich et al. (2015b) using cross-validation, and shown to be comparable to the inter-rater accuracy of manual segmentation of MTL subregions.

Table 7.

ASHS automatic segmentation accuracy in SR-T2w MRI relative to manual segmentations, measured by Dice similarity coefficient (DSC) using leave-one-out cross validation. Mean and standard deviation (in parentheses) are reported in the table.

	All (n=29)	aMCI (n=14)	NC (n=15)
CA1	0.770 (0.031)	0.761 (0.032)*	0.778 (0.027)
CA2	0.515 (0.122)	0.477 (0.121)*	0.551 (0.113)
CA3	0.473 (0.112)	0.464 (0.097)	0.481 (0.126)
CAb	0.765 (0.031)	0.756 (0.032)*	0.773 (0.029)
DG	0.801 (0.032)	0.795 (0.032)	0.807 (0.031)
SUB	0.723 (0.047)	0.723 (0.045)	0.723 (0.050)
HIPPOb	0.874 (0.020)	0.872 (0.021)	0.876 (0.019)
ERC	0.769 (0.058)	0.760 (0.066)	0.777 (0.049)
BA35	0.681 (0.077)	0.677 (0.094)	0.685 (0.059)
BA36	0.765 (0.058)	0.763 (0.070)	0.767 (0.045)
PRCb	0.780 (0.052)	0.773 (0.065)	0.787 (0.037)
PHC	0.772 (0.049)	0.769 (0.054)	0.776 (0.044)

Note:

^*p < 0.05, comparing with NC group, tested by two-tailed two-sample t-test.

^bDSCs for the compound labels (in italics) are measured using the merged label of corresponding sub-labels (CA: CA1–3; HIPPO: CA1–3, DG, SUB; PRC: BA35, BA36).

Appendix C. Updated manual segmentation protocol

As in our prior work (Yushkevich et al., 2015b), manual segmentation was performed by author JP. Author JP's intra-rater reliability of segmenting MTL substructures using T2w MRI has been evaluated in Yushkevich et al. (2015b) and the DSCs were above 0.818 for all extra-hippocampal regions. The current segmentation protocol was expanded from the published ASHS algorithm (Yushkevich et al., 2015b). All the changes are related to MTL cortices and the protocol for segmenting hippocampal subfields remains the same. In brief, the following changes were made: (1) the posterior bounds of BA35 and BA36 are extended one slice posteriorly and BA35 occupies the whole medial bank of collateral sulcus; (2) the PHC label is added for posterior parahippocampal gyrus; (3) label CS is extended posteriorly to the most posterior slice of PHC; (4) a label OTS for occipitotemporal sulcus is added. Please refer to Supplementary material for a detailed description of the segmentation protocol.

Appendix D. ASHS segmentation accuracy for SR-T2w MRI

ASHS segmentation accuracy was evaluated in T2w-MRI scans in Yushkevich et al. (2015b). Here we repeat this evaluation for SR-T2w MRI to ensure that upsampling does not degrade segmentation accuracy. A leave-one-out cross validation scheme is used to compare ASHS segmentations to the corresponding manual segmentations. The average DSC between the automatic and manual segmentation of each ASHS atlas subject is reported for each anatomical label in Table 7. Average DSC is also reported separately for the aMCI and NC groups. The segmentation accuracy in SR-T2w MRI space is comparable to that in the original T2w-MRI space, as reported in Yushkevich et al. (2015b). The slightly poorer performance in SR-T2w may be due to the error caused by upsampling manual segmentations to SR-T2w MRI space.

Appendix E. Supplementary material

Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.neuroimage.2016.09.070.