Rapid Measurement of Brain Macromolecular Proton Fraction with Transient Saturation Transfer MRI

Abstract

Purpose

To develop an efficient MRI approach to estimate the non-water proton fraction (f) in human brain.

Methods

We implement a brief, efficient MT pulse that selectively saturates the magnetization of the (semi-) solid protons, and monitor the transfer of this saturation to the water protons as a function of delay after saturation.

Results

Analysis of the transient MT effect with two-pool model allowed robust extraction of f at both 3 T and 7 T. This required estimating the longitudinal relaxation rate constant (R_1,MP and R_1,WP) for both proton pools, which was achieved with the assumption of uniform R_1,MP and R_1,WP across brain tissues. Resulting values of f were approximately 50% higher than reported previously, which is partly attributed to MP pulse efficiency and R_1,MP being higher than assumed previously.

Conclusion

Experiments performed on human brain in-vivo at 3 T and 7 T demonstrate the ability of the method to robustly determine f in a scan time of about 5 minutes.

INTRODUCTION

Although MRI almost exclusively measures the signal of water hydrogen protons (WPs), a substantial fraction (‘f’) of tissue hydrogen protons resides in molecules other than water, predominantly protein and lipid (here, for simplicity, these are categorically indicated by “macromolecular hydrogen protons” or MPs). While MPs are generally not directly visible because of their rapid transverse relaxation owing to restricted mobility, they can dramatically affect the MRI signal and the apparent longitudinal and transverse relaxation time constants (T₁ and T₂ respectively) through interaction with WPs.

In human brain, a relatively high fraction of MP (f ~0.2–0.3) is found in white matter (WM)(1–5), primarily because of its high content of myelin. Myelin, which is important for nerve conduction, is rich in proteins and lipids, and may contain up to 60% of MPs in white matter (6–8). Study of the effect of MPs on WP T₁ and T₂ relaxation therefore provides an opportunity to indirectly detect myelin loss (9).

One way to study myelin loss is through T₂ relaxation. In WM, T₂ relaxation has been shown to be multi-exponential, with the most rapid relaxation (shortest T₂) attributed to a pool of water trapped between the myelin layers, and strongly interacting with MPs in these layers (9,10). The size of this pool has been shown to correlate with brain myelin content (11). Similarly, the MPs in myelin are a strong contributor to T₁ relaxation (12), and in fact it has been argued that outside the iron rich subcortical grey matter, f is the main determinant of T₁ (4,13–15). Thus, changes in f related to myelin loss may be sensitively detected by T₁-weighted techniques. Nevertheless, it should be realized that NMR relaxation processes are generally complex and that both changes in T₁ relaxation and T₂ relaxation may not be specific to changes in f. A further complication is a potential bias resulting from inter-compartmental exchange, which may lead to and underestimation of tissue myelin content (10).

Another approach to investigate variations or changes in brain myelination is by determining f through the classical MT experiment (16) in which radiofrequency (RF) irradiation is used to selectively reduce (saturate) the longitudinal magnetization of MPs and monitor the effect on the WP signal. This selectivity is based on the short T₂ of MPs, which has been found to be generally below 100 μs for proteins and lipids based on super-Lorentzian lineshapes (6).

To maximize the effect on WP saturation, most modern MT methods used for studying pathological changes in f in human brain use the so called “steady state approach”, in which the MT effect is measured after long (relative to the T₁ of WP) continuous or repeated pulsed irradiation. However, while steady state approaches allow large saturation effects and provide good sensitivity, the loss of information about transient aspects of the MT process complicates interpretation and quantitative measurement of f, as the MT effects become strongly dependent of various parameters, including irradiation specifics, T₂ of the MP pool, and T₁ of both WP and MP pools. Mitigation of these issues is possible using so-called quantitative MT (qMT) techniques (17–22), which have shown promise in detecting myelin loss in multiple sclerosis and other neurological diseases (22–24). While rapid approaches may be possible (22), accurate qMT techniques are generally time-consuming and require collection of several reference datasets to mitigate confounds, such as variations in T₁ and RF amplitude.

An alternative to the steady-state approach, and a potentially faster way to measure f is to use of a “transient” MT approach which uses a single, brief irradiation pulse to differentially affect the longitudinal magnetization (M_z) of MPs and WPs (e.g. saturation of MP and inversion of WP magnetization) and monitors the equilibration process as a function of delay after the MT pulse. This approach was initially implemented on NMR spectrometers to study MT in tissue samples, and relied on direct measurement of signal from both the short T₂ MP pool and the longer T₂ WP pool (25–29). Combining this approach with a 2-pool model to fit to the MP and WP signal evolution allowed quantification of f as well as MT exchange rates. Subsequently, a number of studies has explored ways to use the transient MT approach to extract f without the need to detect the MP signal, which would make the method amendable for use on clinical MRI scanners (20,30–33).

One of the outstanding issues with measurement of f using transient MT approaches is the difficulty in estimating MP T₁ (in the following referred to as R_1,MP, equal to the inverse of MP T₁), a parameter in the 2-pool model whose value significantly affects f. This is also an issue (possibly to a lesser extent) for steady state MT approaches, which typically assume R_1,MP to be similar to R_1,WP (around 1 s⁻¹ in white matter). It has been pointed out however that actual values for R_1,MP may be much higher, and that this would lead to an underestimation of f (34). To address this for the transient MT approach, we jointly analyzed MT and inversion recovery (IR) data from human brain using a 2-pool model of exchange and explored the validity of a number of simplifying assumptions. Based on this, we arrived at realistic estimates for R_1,MP in human brain at 3 T and 7 T, allowing us to properly quantifying f from a transient MT experiment with a measurement time as short as 5 minutes.

METHODS

Our method for quantifying f is based on the notion that in most brain regions outside the iron-rich sub-cortical grey matter (e.g. globus pallidus, caudate and red nuclei, and substantia nigra), longitudinal WP relaxation has a dominant contribution from MT with MP and that tissue contrast primarily results from variations in f (13). Thus, rather than assuming R_1,MP and R_1,WP to be equal, as has generally been done in the analysis of MT experiments, we allowed them to differ but assumed them to constant across the brain. We then performed pulsed, transient MT using a highly efficient MP saturation pulse, as well as inversion recovery (IR) to facilitate estimation of R_1,MP and R_1,WP. For this purpose MT and IR data were jointly analyzed with a 2-pool model of exchange, during which R_1,MP and R_1,WP values were determined that led to realistic values of MP saturation and allowed estimation of f. Additionally, we evaluated the feasibility of estimating f from MT data only by introducing additional constraints.

MRI Scanning

Experiments were performed on 3 T and 7 T Siemens MRI scanners (Erlangen, Germany; Skyra and Magnetom platforms respectively). Eleven subjects (6 female, ages 19–60, average 30) were scanned at both field strengths under an IRB-approved protocol to investigate the robustness in determining f. On 5 subjects at the 3 T only, a second scan was performed to assess test-retest reproducibility.

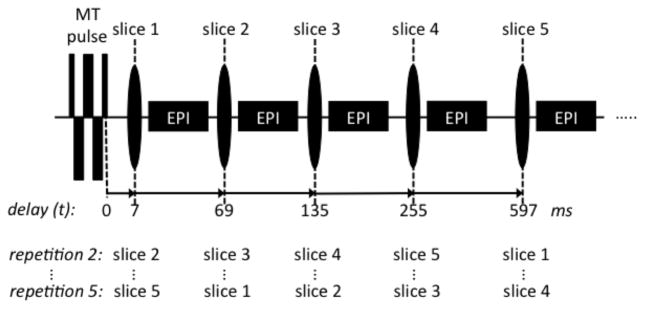
Our transient MT experiment (Fig. 1) used a brief, T₂-selective composite RF saturation pulse (33,35,36) to saturate MP, after which multiple image slices at variable delay t were acquired with EPI. We first determined the appropriate RF pulse (in the following called “MT pulse”) parameters to achieve optimal saturation characteristics, and then studied the feasibility to robustly extract f using a two-pool model of exchange.

Figure 1.

Image acquisition for the pulsed transient MT experiment. Five image slices are acquired at incrementally increasing delay times t after an MT pulse. By shifting the order of the slices in subsequent repetitions, all five delay times are sampled for each slice location.

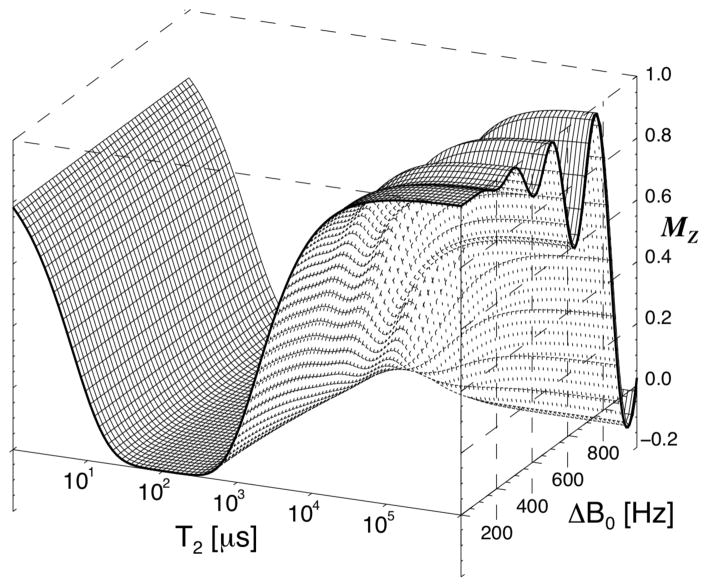
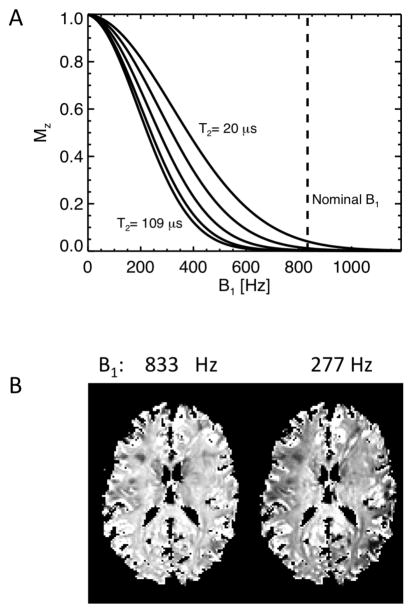
The composite, phase modulated MT pulse had a constant B₁ amplitude of 19.6 μT and consisted of 16 sub-pulses of with nominal flip angles of 60°, −120°,120°,−120°….. 120°,−60°. Its duration of 6 ms was sufficient to achieve a near optimal (about 90% of maximum, see below) saturation of MP, as judged from the delayed effect on the WP signal. This was based on initial experiments (n=6) that measured dependence of the saturation effect on increasing the MT pulse duration from 6 up to 11 ms (by adding −120°,120° pulse segments). Numerical simulation of the effects of the 6 ms pulse (based on the Bloch equations), shown in Fig. 2, confirmed the efficient saturation of MPs assuming a Lorentzian lineshape with T₂ in the range of 20–400 μs. This range roughly covers the range of values reported in literature (6,7,37). A Lorentzian line shape was used in order to allow simulations using the time domain Bloch equations. In terms of the saturation effect of our MT pulse, the applied Lorentzian T₂ range is roughly equivalent to the T₂ range of 5–20 μs reported for super-Lorentzian MP lineshapes (17,18,38–42). At the same time, the pulse had an only minor (<10%) effect on T₂ species > 20 ms (WPs), as long as it was applied close enough (<500Hz) to resonance (Fig. 2). A simulation of the MP saturation as function of B₁ amplitude for a range of T₂ values in shown in Fig. 3a, demonstrating that MP saturation is nearly complete for the expected range of T₂ and B₁ values. At high B₁ amplitude, only minimal sensitivity of the saturation level to variations in B₁ amplitude is observed. This is further illustrated with the experimental data shown in Fig. 3b, confirming uniform MP saturation at high B₁.

Figure 2.

M_z after a 6 ms composite MT pulse, as function of T₂ and frequency offset (B₀), based on simulation of the Bloch equations. The MT pulse effectively saturates spins with a T₂ in the range from 20 to 400 μs at all offset frequencies (for a Lorentzian lineshape). Long T₂ spins suffer only a small perturbation on resonance (< 5% for T₂ > 36 ms), with a larger effect for frequencies > 500 Hz.

Figure 3.

Robustness of transient MT approach to variations in B₁. A) Simulated MP saturation levels (FS_MP(0)) after a 6 ms MT pulse for (Lorentzian) MP T₂ values of 20, 32, 48, 72 and 109 μs. The curves for T₂’s up to 400 μs fall between the 32 and 109 μs lines. The dashed line represents the nominal (brain-averaged) B₁ of 833 Hz used in the experiments. The plots show that MP magnetization is effectively saturated for a range of B₁ and T₂ values, reducing the sensitivity of the experiments to variations in B₁ amplitude. B) Experimental (7 T) demonstration of B₁ dependence of MP saturation. FS_MP(0) was calculated with approach 1 from data at actual (833 Hz) B₁ and a strongly reduced (277 Hz) B₁. Incomplete MP saturation is only seen at strongly reduced B₁, in particular towards the edges of the brain where B₁ is lowest. The images were normalized to level in the SCC.

The order of the five EPI slices acquired sequentially after each repetition of the MT pulse (Fig. 1) was cycled to allow time-efficient collection of the five delay times (43). Delay (t) values of 7, 69, 135, 255 and 597 ms were chosen to cover most of the saturation dynamics. EPI scan parameters were: echo spacing 0.77 ms, bandwidth 250 kHz, 45% ramp-sampling, matrix size 144×108, FOV 240×180 mm², SENSE rate 2, 2 mm slice thickness, 5.4 mm slice spacing (center to center), TE 30 ms (3 T) and 24 ms (7 T), TR = 3 s. The slice spacing was chosen relatively large to reduce potential MT effects of the excitation pulses, see supplementary material (Fig. S1). Artifacts from scalp lipids were suppressed by acquiring every other repetition with a shifted EPI echo train (1.15 ms and 0.48 ms at 3 T and 7 T respectively), which resulted in a phase-inverted lipid signal. Addition of the two repetitions allowed elimination of this lipid signal, assuming the T₂ is small compared to the applied shift in echo time. Twenty scan repetitions were performed at each slice location, taking a total scan time of 5 minutes. Four of the 20 repetitions were acquired without MT pulse to serve as reference signal.

IR scans were performed by replacing the MT pulse with a hyperbolic-secant inversion pulse (5.12 ms, 19.6 μT maximum B₁ amplitude, 830 Hz maximum frequency modulation, β = 1400 s⁻¹ (44) with an adjustment of the amplitude to start at zero B₁). Delay times t (also called inversion times (TIs)) of 6, 69, 135, 282 and 1197 ms were used. The TR for these scans was 4 s, the number of repetitions was 18 for 3 T and 22 for 7 T. Again, four of the repetitions were acquired without inversion pulse to serve as reference signal to calculate the fractional saturation resulting from the MT (or IR) pulse.

Estimation of model parameters

The extraction of f and other model parameters was based on fitting the delay-dependent signal to a two-pool model of MT (26,29,45,46). The same model was used for both preparation pulses (MT and IR pulses) albeit with different initial magnetization levels for the MP and WP pools. The calculations were based on the fractional saturation FS derived from the MT weighted signal S measured at delay t and reference signal S_ref: ${FS}_{\text{WP}}(t)=\frac{s_{\text{ref}}-s(t)}{s_{\text{ref}}}$. For both WP and MP, FS(t) can be written as the sum of 2 exponentials (29):

$${FS}_{\text{WP}}(t)=a{e}^{-{\lambda }_{1}t}+b{e}^{-{\lambda }_{2}t}$$ [1]

$${FS}_{\text{MP}}(t)=a\left(1-\frac{({\lambda }_1-{\mathrm{R}}_{1,\text{WP}})}{k_{\text{MW}}}\frac{1-f}{f}\right)e^{-{\lambda }_{1}t}+b(1-\frac{({\lambda }_2-{\mathrm{R}}_{1,\text{WP}})}{k_{\text{MW}}}\frac{1-f}{f})e^{-{\lambda }_{2}t}$$ [2]

with:

$$\begin{array}{l}2{\lambda }_{1,2}\\ ={\mathrm{R}}_{1,\text{WP}}+{\mathrm{R}}_{1,\text{MP}}+k_{\text{MW}}/(1-f)\\ \pm \sqrt{{({\mathrm{R}}_{1,\text{MP}}-{\mathrm{R}}_{1,\text{WP}})}^2+2({\mathrm{R}}_{1,\text{MP}}-{\mathrm{R}}_{1,\text{WP}})k_{\text{MW}}(1-2f)/(1-f)+k_{\text{MW}}^2/{(1-f)}^2}\end{array}$$ [3]

In these equations, R_1,MP, R_1,WP are the longitudinal relaxation rates of both pools in the absence of exchange; k_MW and k_WM refer to the rates of change in FS_MP and FS_WP due to MT. These rates are the volume-fraction normalized equivalent of the often used cross-relaxation rate constant k, i.e. k_MW = k/f, and k_WM = k/(1-f) (see e.g ref. (47)).

Both MT and IR data can be analyzed by this model, and Eq. [1] will fit with the same exponential rate constants (λ₁ and λ₂) but with different coefficients (a and b). After determining a, b, λ₁ and λ₂ from fitting of Eq. [1] to the experimental data, one can proceed with solving for k_MW, f, R_1,MP and R_1,WP using [3], and the initial saturation levels FS_WP(0) and FS_MP(0) from Eqs. [1] and [2]. This requires two additional pieces of information, as we have only four equations for 6 unknowns.

To solve this problem, and to investigate the possibility of omitting some of the data from the analysis in order to shorten the measurement protocol, four analysis approaches with different simplifying assumptions were evaluated. Briefly, four different combinations of parameters were fixed to (field specific) values common to all brain voxels: 1) R_1,MP and R_1,WP; 2) R_1,MP and FS_MP(0); 3) R_1,MP, R_1,WP and FS_MP(0); 4) R_1,MP, R_1,WP, FS_MP(0) and FS_WP(0). The extracted values for k_MW and f were then compared between the four approaches, as well as their consistency across field strengths.

Global, fixed values for R_1,MP and R_1,WP under approach 1 were estimated from joint analysis of MT and IR data. Fixing R_1,MP and R_1,WP was motivated by a previously proposed model of T₁ relaxation, in which MT between WP and MP is the dominant source of T₁ contrast (4,13–15). This model has been shown to accurately describe T₁ relaxation in most brain regions, perhaps with exception of iron rich grey matter areas (e.g. globus pallidus, caudate and red nuclei, substantia nigra) (13). To estimate R_1,MP and R_1,WP, first the MT and IR data were fitted jointly in every voxel with Eq. [1], resulting in one set of rate constants (λ₁ and λ₂) and two sets of amplitudes (a and b) for every voxel. Then R_1,MP and R_1,WP were varied to obtain reasonable values FS_MP(0) values for both the MT and IR data. That is, for each combination of R_1,MP and R_1,WP values (within a realistic range), FS_MP(0) for both the MT and IR experiments were calculated (together with corresponding values k_MW and f ) in each voxel and the number of voxels with permissible values was used as a criterion to select R_1,MP and R_1,WP that best described the data. The permissible range was set as follows: FS_MP(0) for both IR and MT experiments could not exceed 1.0 (i.e. complete saturation), while the value for IR data should be between 0.7 and 1.0 times that for MT (that is, the MP saturation after the inversion pulse is somewhere between 70 and 100% of the saturation after the MT pulse). The data from all subjects was combined for this analysis, resulting in one global R_1,MP and one global R_1,WP value for each field strength.

Under approach 2, we used the fixed value for R_1,MP found with approach 1, and as well as a fixed value for the FS_MP(0) for the MT experiment. Again, as in approach 1, one set of rate constants (λ₁ and λ₂) and two sets of amplitudes (a and b) extracted from the MT and IR data were used. The motivation of this approach was to evaluate the variation in R_1,WP, based on the notion that variation in FS_MP(0) for the MT experiment was constrained within a rather restricted range (between about 0.8 and 1.0, judged from simulations (see above) and experiments (see RESULTS, first paragraph).

Under approach 3, fixing both R_1,MP and R_1,WP, as well as FS_MP(0) allowed omission of the IR data from the analysis. Now, only the MT data was fitted with Eq. 1, which represented only three degrees of freedom due to the dependence introduced between a, b, λ₁ and λ₂ by fixing the three parameters.

Finally, under approach 4, fixing a fourth parameter (FS_WP(0)) obviated the need for measuring S_ref and reduced the 4 parameter model represented in Eq. 1 to a 3 parameter model:

$$S(t)=S_0(1-(a{e}^{-{\lambda }_{1}t}+b{e}^{-{\lambda }_{2}t})),$$ [4]

where S₀ is a scaling factor for the signal level, λ₁ and λ₂ are defined as above, and two amplitudes a and b are now constants derived from the fixed average saturation levels of the two pools at t = 0 (FS_WP(0) and FS_MP(0)). From the fitted parameters S₀, λ₁ and λ₂, both f and k_MW can be derived when applying Eq. [3] with fixed values for R_1,MP and R_1,WP.

All fitting was performed on both a pixel-by-pixel basis and on the average signal in four region of interest (ROI): in white matter of the splenium of the corpus callosum (SCC), in grey matter in the globus pallidus (GP), the putamen (Put) and the head of the caudate nucleus (NC). The ROIs were manually selected directly on the EPI images using both the implicit T₂^* contrast and the T₁ contrast from the IR data. The SCC-ROI encompassed 33–86 voxels (average 61), the GP-ROI size was 18–110 (67), the Put-ROI 86–245 (150) and the NC-ROI 73–143 (103). Fitting was based on a simple and robust iterative grid search and refinement of the non-linear parameters to be optimized, in combination with linear least squares (LLS) optimization for the linear parameters (either a,b or S₀)(48). That is, for each choice of non-linear parameters, the linear parameters (amplitude factors) were estimated using LLS, and the residual was calculated. For each iteration, all combinations of parameters were tested in a search grid centered on the initial values. After selection of the best set (the one with the lowest residual), the step size was reduced to refine the search grid and next iteration was started using the current best fit as initial values. During joint fitting of MT and IR data, a single set of decay rates was used (λ₁ and λ₂) while the amplitudes (a,b) were allowed to be different to accommodate for the different saturation levels resulting from the MT and IR pulse. For both field strengths, average and standard deviation (SD) of the resulting parameter values was calculated. Results obtained from the ROI analysis were reported as averages and standard deviation over subjects. To investigate a potential bias related to magnetic field strength, differences of the results on the same subjects at the two field strengths were calculated for the SCC. The averages of the differences show a potential field related bias, while the SD of the differences reflects variability excluding inter subject variations. Approach 1 was only used to analyze data from white matter, as the grey matter ROIs are known to be high in iron and as a result have an R_1,WP substantially different from the global average. For the fixed R_1,WP needed for approaches 3 and 4, the average over subjects of the values fitted in approach 2 were used instead.

To estimate the precision (reproducibility) of the fitted parameters under influence of noise in the input data, simulated noise was incrementally added to 3 T and 7 T model curves, based on the average parameters found for the SCC. The resulting simulated data were fitted for each noise realization and the SD of the extracted f and k_MW values were determined. The sensitivity of the fitted parameters to the variations in R_1,MP and FS_MP(0) is shown in the supplementary material. The plots were derived by recalculating the fitted parameters for a range of values for R_1,MP and FS_MP(0).

Image reconstruction and pre-processing

All image analysis was performed off-line using in-house IDL (Harris Geospatial Solutions, Boulder, CO, USA) based software and C code. The SENSE unfolding matrix, required for image reconstruction, was calculated from (multi–echo) GRE reference data acquired at the same slice position and resolution as the EPI data. This reference data were also used to derive field maps to calculate the geometric distortion corrections for the EPI. All resulting images in each scan session were spatially registered to the first volume to correct for in-plane motion. Through-plane motion was not corrected, as this proved difficult with the limited number of slices and large inter-slice gaps. Image registration included a fixed contrast adjustment to allow registration between reference, IR and MT data.

The addition of TE-shifted and non-shifted images for scalp lipid suppression was performed after calculating signal magnitude from the complex valued data; this proved sufficient and reduced problems with phase instabilities occasionally encountered at 7 T. However, for the IR scans, images acquired at the longest delay t required complex addition, due to the sign inversion of the longitudinal magnetization in some tissues. In this case, occasional manual phase adjustment was necessary. For earlier TIs, data were combined in magnitude mode and inverted (to reflect the negative polarity of the magnetization).

For both MT and reference data, signals were averaged over repetitions. In addition, for the reference signal (i.e. signal without inversion or MT), further averaging was performed over the acquisition with the different delay times to further improve image signal-to-noise ratio (SNR). Prior to multi-parametric fitting, voxels with a reference signal below 5% were eliminated, and signal intensities (S(t)) were converted to fractional saturation levels according to ${FS}_{\text{WP}}(t)=\frac{S_{\text{ref}}-S(t)}{S_{\text{ref}}}$. With this normalization, MT and IR signals decay from 1 to 0 and 2 to 0 with increasing delay t respectively.

RESULTS

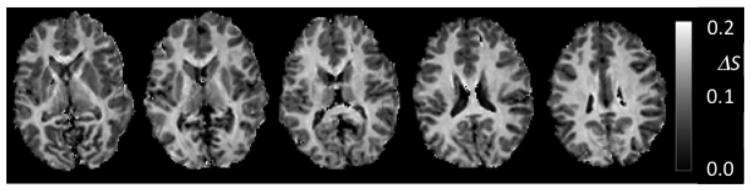
At both 3 T and 7 T, saturation of MP with a single, 6 ms MT pulse led to a delay dependent reduction in WP signal. As expected, this reduction was strongest in white matter and reached a maximum of around 15–20% at a delay between 150 and 250 ms (see Figs. 4, 5). Fig. 4 shows the averages and SD of FS_WP(t) obtained for SCC at the two field strengths. The plots show high reproducibility over subjects, and furthermore indicate that the MT effect is more pronounced at 7 T. This is attributed to the slower T₁-relaxation at high field. Fig. 5 shows the difference in saturation level between t = 7 ms and t = 255 ms, providing a model-free measure indicative of the MP fraction in human brain. Comparison of the fractional saturation levels (FS_WP(0) in equations above) at t = 255 ms between the 6 ms and the 11 ms MT pulse (n=6) suggested effective saturation of macromolecular protons for the 6 ms pulse (FS_MP(0) = 0.88 ±0.03 and 0.93 ±0.02 at 3 T and 7 T respectively, this assumed FS_MP(0) = 1.0 for the 11 ms pulse). These values were subsequently used for the extraction of k_MW and f with fitting approaches 2–4 (see METHODS).

Figure 4.

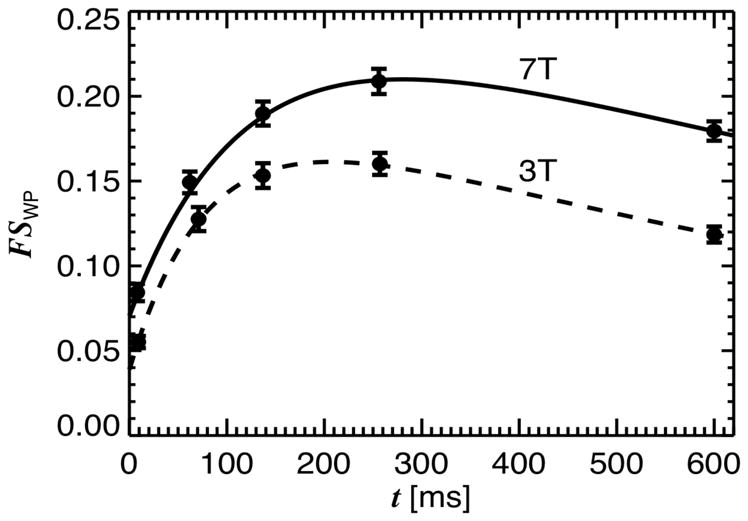
Fractional saturation of water protons (FS_WP) at delay time t after MT pulse, for both 3 T and 7 T experiments. FS_WP was averaged over ROI’s in the splenium of the corpus callosum; error bars reflect the SD over subjects (n=11). Solid lines represent 2-pool model fit with subject-averaged parameters.

Figure 5.

Fractional MT-related signal change ΔS (at 7 T) calculated from signal difference between images acquired at t = 7 ms and $t=258\text{ms}(\mathrm{\Delta }S=\frac{S(t=7\text{ms})-S(t=258\text{ms})}{S(t=7\text{ms})})$.

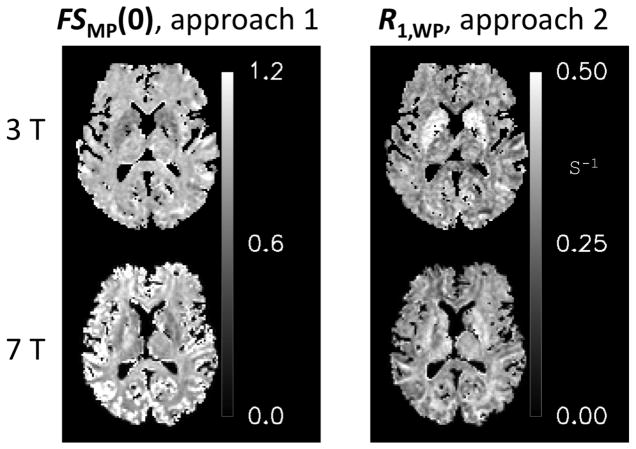
Conjoint fitting of the IR and MT data using fitting approach 1 and 2 consistently produced maps of the four fitted parameters a, b, λ₁ and λ₂ as exemplified in Fig. 6. Estimation of appropriate R_1,MP and R_1,WP values common to all brain voxels with approach 1 resulted in estimates of 4.0 s⁻¹ and 2.05 s⁻¹ for R_1,MP 3 T and 7 T, and 0.40 s⁻¹ and 0.35 s⁻¹ for R_1,WP at 3 T and 7 T. These were the values used for approaches 3 and 4. At these values, the brain distribution of FS_WP(0) derived from approach 1 (Fig. 7) showed minimal variation at both field strengths, with values ranging between 0.8 and 1.0, confirming the validity of fixing this parameter in approaches 3 and 4. Similarly, R_1,WP (derived from approach 2) was rather uniform across the brain (Fig. 7), with exception of the subcortical grey matter regions.

Figure 6.

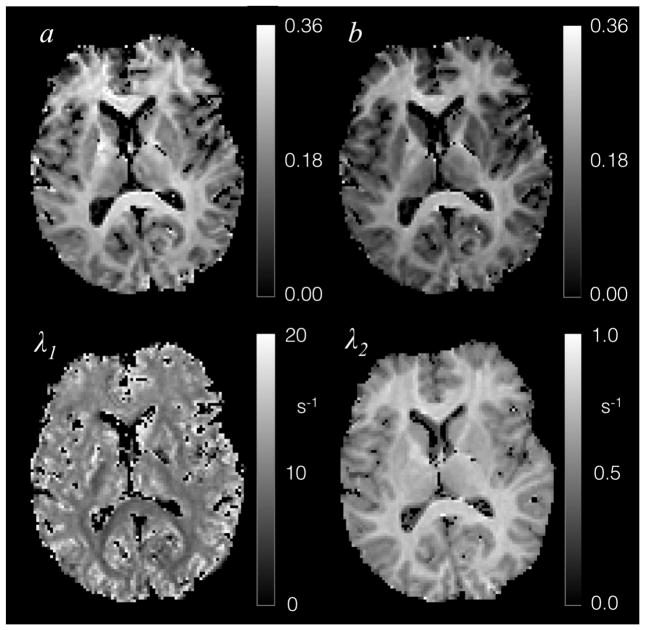
Single slice example of fitted parameters of the 2-pool model (Eq. [1]) for 7 T data.

Figure 7.

Variation in FS_MP(0) and R_1,WP over the brain, deduced with analysis approaches 1 and 2 respectively.

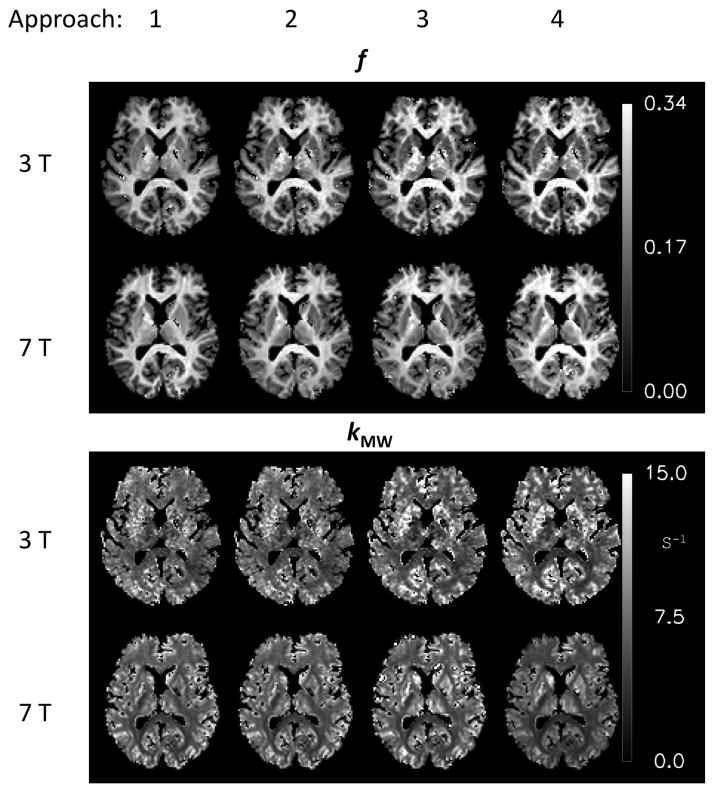
All approaches allowed reliable extraction of f and k_MW in most brain regions (Fig. 8, Table 1). Values for f were in the range of 5–30% across the brain, and in the range of 20–30% in white matter. Exchange rate constant k_MW varied in the range of 4–12 s⁻¹. Similar values for f were found between 3 T and 7 T, whereas values for k_MW were somewhat (5–20%) lower at 7 T (Table 1). Fit residuals (Table 1) indicate a somewhat more robust fit at 7 T; this is attributed to the lower R_1,MP and consequently a larger available MT signal at the higher field strength. The average values for the WP exchange rate k_WM were 2.3 s⁻¹ (3 T) and 1.9 s⁻¹ (7 T). The SDs of the differences were similar to SDs of the data acquired at each field, suggesting the inter-subject variability is small compared to the measurement induced SD and so these SDs are dominated by the reproducibility of the experiments. The observed differences between field strengths are not significant given the SDs of the data, with exception of the values for f and k_MW in approach 1. Analysis results of the grey matter ROIs are reported in Table 2. The R_1,WP values for these regions resulting from analysis approach 2 are given in Table 3. Slice coverage in one subject did not allow creation of a GP ROI and this data was therefore not included in this part of the study. The average k_MW values in grey matter were higher than the value found in SCC white matter. However, it should be realized that the SD of the grey matter k_MW values was relatively high (up to 20%), and k_MW values themselves were not consistent between field strengths, suggesting they should be interpreted with caution.

Figure 8.

MP fraction f and exchange rate constant k_MW extracted with the four analysis approaches for 3 T and 7 T.

Table 1.

Comparison of the four fitting approaches based on the 2-pool model, progressively fixing more parameters. Averages (Av) and SD (n=11) are shown for f and k_MW for the SCC ROI, together with fit residue. The SD of the differences the 3 and 7 T data (diff) is an indication of the intra-subject reproducibility, the residue is reflects the fitting of the 2-pool model, which is the same for approaches 1 and 2 (both contain only 2 assumptions and therefore the same free fit of Eq. 1 to the data).

		Approach 1: Fixed R1,MP, R1,WP		Approach 2: Fixed R1,MP, FSMP(0)		Approach 3: + fixed R1,WP		Approach 4: + fixed FSWP(0)
		Av	SD	Av	SD	Av	SD	Av	SD
f	3 T	0.262	0.012	0.274	0.014	0.287	0.021	0.282	0.022
	7 T	0.293	0.010	0.273	0.012	0.267	0.013	0.266	0.013
	diff	−0.031	0.008	0.002	0.015	0.020	0.022	0.016	0.023
kMW [s−1]	3 T	6.11	0.56	6.04	0.54	5.41	0.57	5.55	0.63
	7 T	5.01	0.29	5.13	0.32	5.30	0.45	5.30	0.46
	diff	1.09	0.66	0.91	0.68	0.12	0.75	0.25	0.81
Residue	3 T	1.7E-5				2.0E-5		1.8E-5
	7 T	0.6E-5				0.5E-5		0.5E-5

Table 2.

Results of three grey matter ROIs: Globus Pallidus (GP), Putamen (Put) and Head of the Caudate Nucleus (NC), shown as the average and SD over 10 subjects. The R_1,WP used in approaches 3 and 4 was taken from the result of approach 2, as use of the global value for R_1,WP is not suitable for these iron rich regions.

	B0	ROI	Approach 2: Fixed R1,MP, FSMP(0)		Approach 3: + fixed R1,WP		Approach 4: + fixed FSWP(0)
			Av	SD	Av	SD	Av	SD
f	3	GP	0.172	0.010	0.176	0.012	0.172	0.013
		Put	0.124	0.009	0.125	0.010	0.122	0.010
		NC	0.113	0.005	0.113	0.006	0.111	0.008
	7	GP	0.181	0.013	0.185	0.015	0.182	0.015
		Put	0.122	0.014	0.126	0.017	0.124	0.016
		NC	0.114	0.011	0.116	0.015	0.114	0.013
kMW [s−1]	3	GP	9.3	1.9	8.3	1.7	8.6	1.2
		Put	10.2	1.3	9.8	1.3	9.9	1.2
		NC	10.4	1.6	9.8	1.6	9.9	0.7
	7	GP	7.1	1.3	6.3	1.3	6.4	1.2
		Put	8.9	1.3	7.6	1.5	7.7	1.6
		NC	8.4	1.3	7.8	1.7	7.9	1.7

Table 3.

The average and SD over ten subjects of the R_1,WP values for the 3 grey matter ROIs following from approach 2 as used in approaches 3 and 4.

B0	ROI	R1,WP [s−1]
		Av	SD
3	GP	0.505	0.035
	Put	0.466	0.018
	NC	0.449	0.016
7	GP	0.448	0.032
	Put	0.444	0.018
	NC	0.426	0.021

The test-retest results (repeated scans at 3 T, n=5) indicated a 0.5% error for the ROI average f values in SCC, and a 5% error for the corresponding k_MW values at 3 T. Voxel-by-voxel test-retest analysis showed the error in f and k_MW in white matter to be around 0.015 and 1.1 s⁻¹ respectively equivalent to 6% and 18% errors. The signal to noise ratio (SNR) in the (baseline) images was in the range of 200–400 at 7 T and 100–250 for 3 T. The image stability, based on the average variance in the SCC ROI over the repetitions within one scan series, was 2.9 (±0.4)% at 3 T and 1.7 (±0.4)% at 7 T. Omission of the IR data from approaches 1 and 2 strongly affected the fitting procedure, resulting in poor convergence and widely varying values for f and k_MW. This was not the case for approaches 3 and 4, in which the fixing of additional parameters improved fitting stability, and which led to similar results as approaches 1 and 2 (Fig. 8 and Table 1). This indicates that IR data can be omitted from the analysis when fixing R_1,WP and FS_MP(0) to values common to all brain pixels.

The estimated precision (the variability due to measurement noise) of the various fitting results is shown in Table 4 for an input SNR (i.e. input to the fitting program) of 500. This estimate was derived from the stability of the SCC-ROI averaged signals over repetitions, in combination with the effects of averaging over time and dividing by the reference data. It was found that fitting errors simply scale (inversely) with SNR. The test-retest errors for f and k_MW were consistent with the numbers shown in the Table 4. The simulation shows that in spite of the high input SNR, the precision of k_MW is limited, and the results need to be interpreted with some care.

Table 4.

Estimated precision for f and k_MW for an (ROI-) SNR of 500 (for both saturation and reference scans), based on fitting of model data with simulated noise; the model data was based on average values found for f and k_MW in the SCC (Table 1). The relative precision is given in parenthesis.

		Approach 1,2: Fixed R1,MP, FSMP(0)	Approach 3: + fixed R1,WP	Approach 4: + fixed FSWP(0)
f	3T	0.0081 (3%)	0.011 (4%)	0.0084 (3%)
	7T	0.0054 (2%)	0.0064 (2.5%)	0.0054 (2%)
kMP [s−1]	3T	0.32 (6%)	0.39 (7%)	0.25(5%)
	7T	0.22 (4%)	0.26 (5%)	0.17 (3%)

DISCUSSION

The experiments described in this work indicate the feasibility to measure the macromolecular proton (MP) fraction in human brain in scan times as short as 5 minutes. The measurement approach is based in instantaneous MP saturation, and analyzing the transfer of this saturation to WP as function of delay after the MT pulse using a 2-pool model of magnetization exchange. The feasibility of this approach relies on the high (~90%) saturation efficiency of the composite MT pulse, as well as several simplifying assumptions, including the notion that R₁ relaxivity in human brain white matter is linearly dependent on MP fraction.

Strongly saturating MP while minimally (~10%) saturating WP is difficult to achieve with conventional MT approaches that use continuous off-resonance RF irradiation. A major advantage of the strong MP saturation achieved here is an excellent sensitivity in extracting f, owing to the large MT effect. In addition, strongly saturating MP reduces sensitivity to B₁ inhomogeneities as confirmed with simulations and experiments (Fig. 3). This property enabled reliable extraction of f, even at 7 T where B₁ inhomogeneity is substantial. In contrast, poorly designed MT pulses may show reduced saturation in areas with low B₁, which, if not accounted for, will cause f to be underestimated.

Another advantage of the type of MT pulse used here is its minimal affect on WP, by virtue of their long T₂ WP, even in the presence of off-resonance effects due to B₀ inhomogeneities. Sensitivity to the latter can be adjusted by changing the number of sub-pulses, while keeping pulse duration constant. The overall pulse energy (time integral of B₁ amplitude squared) determines the T₂ value below which MPs are fully saturated, while the combination of B₁ amplitude and number of sub-pulses determines the T₂ values above which WP magnetization is left untouched. Within the limits of the scanner hardware and allowable tissue heating, this gives sufficient flexibility to efficiently implement the pulsed MT approach at both 3 T and 7 T.

Quantifying f and k_MW with the 2-pool model fitting approach required simplifying assumptions which, in this study, involved fixing two or more parameters to values common to all brain voxels and all subjects (n=11). These parameters included R_1,MP, R_1,WP and the saturation levels of MP and WP resulting for the direct effect of the MT pulse. Similar values for f and k_MW were obtained for different sets of parameter combinations, and the similarity of the results between 3 T and 7 T supported the validity of this approach. Importantly, fixing 3 or more parameters (approaches 3 and 4, see METHODS) obviated the need for inclusion of IR data in the fitting process, reducing the measurement time to only 5 minutes. The use of four fixed parameters (approach 4) allows further scan time reduction as it removes the necessity of acquiring a reference scan without MT pulse.

The excellent precision of the MP-pool fraction estimate, as determined from simulations and the test-retest results, demonstrates the sensitivity of the proposed transient MT approach. This is further supported by the small SD over subjects of the difference of the measurements at 7 T and 3 T. The short, 5-minute scan time compares favorably to the more traditional steady-state qMT methods, which generally require longer scan times and may be difficult to perform at high field (7 T and above) due to the significant RF power deposition associated by conventional saturation approaches. In addition, in contrast to steady-state MT approaches, the transient MT approach proposed here is minimally sensitive to variations in R_1,WP, therefore obviating the need for additional IR experiments. This is because of the assumed relationship between f and λ₂, and the relative low saturation level of WP resulting from the pulsed saturation. Although resulting in a less direct measurement of f, the proposed method may be more practical than approaches based on direct detection of MP signal at very short TE (6,7,49,50), which suffer from limited sensitivity and are technically challenging.

The white matter MP fractions reported here (f~15–25%) are substantially larger than the range of 9–16% found previously with quantitative MT methods (18,19,22,23,38,51). This may in part relate to methodological differences, for example the efficiency of the MT pulses used to saturate MP between the different methods. Nevertheless, our values seem reasonable considering the water content of white matter, which has been reported to be around 70% (1–5). Since the proton density of the 30% non-water fraction is at least similar to that of water (e.g. proton density of myelin is 35% higher than that of water (7), while in proteins it may be somewhat lower than in water), one would expect that the MP fraction in white matter to not be far below 30%. This of course assumes that all of the saturated MPs participate in the MT process. As in white matter, the grey matter MP fractions found here are somewhat higher than estimates from qMT measurements: 8–9% for GP, 7% for Put, and 5.3–6.7 % for NC (18,19,52). On the other hand, the k_WM are similar to literature values (1.4–2 s⁻¹) (19). Compared to estimates based on the non-water content of tissue (23–26% for GP, 18–21% for Put and 17–19% for NC (1–5)), our MT-based estimates are somewhat low but not entirely unreasonable given the uncertainty in grey matter ¹H content.

In addition to differences in MP saturation levels, a reason for the relatively high values of f reported here as compared to much of the MT literature may be differences in assumed values for R_1,MP. Previous MT studies have generally assumed R₁ to be similar between MP and WP (e.g. around 1 s⁻¹ at 1.5 T), and it has been pointed out that this value may be too low and lead to under-estimation of f (34). In the current work much higher values of 3.8 s⁻¹ and 2 s⁻¹ were estimated for R_1,MP at 3 T and 7 T respectively, based on fitting of the 2-pool model to the MT and IR data. Since much of the R₁ relaxivity of WM is thought to originate from exchange with MP (12,13,15), such high values for R_1,MP are not unexpected. A further indication that R_1,MP may previously have been underestimated comes from the observation that fixing R_1,MP to 1 s⁻¹ during the fitting procedure indeed led to lower values of f: reductions of about 20% and 10% were estimated at 3 T and 7 T respectively (see supplementary material, Fig. S2). However, under this condition, the fits led to inconsistent values for k and f between the two field strengths.

The finding of R_1,MP being substantially higher than R_1,WP is consistent with earlier analysis of the relationship between apparent R₁ and f based on of large collection of MRI brain data (13). Further support for a relatively high R_1,MP comes from measurements on membrane lipids in model systems, which have found values ranging from 1.6 s⁻¹ to 4.6 s⁻¹ for R_1,MP at fields ranging from 8 to 1.4 T (53–55). Nevertheless, it should be realized that R_1,MP is difficult to measure directly and dependent on experimental conditions (e.g. temperature). Thus, the precise value of R_1,MP remains uncertain and likely is not uniform across and within molecular species: for example it may vary substantially between different lipids.

In order to be able to estimate k_MW and f without the use of IR data, we assumed R_1,WP to be constant over the brain. This was motivated by the notion that much of T₁ relaxation in brain tissue is mediated by MT between MP and WP. Nevertheless, there are other contributions to T₁ relaxation, most notably those from paramagnetic substances such as iron. In fact, in regions richest in iron such as the basal ganglia (concentration up to 0.2 mg/g (56)), R_1,WP may increase by as much as 0.15 s⁻¹ at 7 T (13). This was also observed in the results of analysis approach 2, in which R_1,WP was allowed to vary (Figure 6). Failure to take this into account will affect the values of k_MW and f: simulations indicate that it will bias their estimates by about 15% (data not shown). Thus, accurate determination of k_MW and f throughout all of the brain may require collection of additional data (e.g. T₂^*-weighted MRI (57)) from which the local concentration of iron can be inferred, and then used to adjust R_1,WP. Alternatively, R_1,WP can be estimated using joint analysis of IR and MT data, as was done here with analysis approach 2. The resulting R_1,WP values were indeed higher than the global values, consistent with the effect of iron on R₁ relaxivity (13).

The values for exchange rates k_MW and k_WM found here are somewhat lower than those reported in literature. For example, the value of ~2 s⁻¹ for here for k_WM found here is somewhat below the range of 2.5–3.9 from previous studies (19,51,58). Again (as with f), a potential source for this discrepancy is the value used for R_1,MP which we estimated higher than assumed previously. It is also interesting to compare the exchange rates found here with those from fitting of transient MT data to a 4-pool model in a previous study (32). This study reported on cross-relaxation time constants T_CR, a measure of exchange rates defined by T_CR= k_MW ⁻¹ + k_WM ⁻¹. In SCC, T_CR representing exchange between MP in myelin to WP outside the myelin sheath (i.e. the water visible in our study) was reported to be at least 1280 ms and limited by exchange between water compartments within and outside the myelin sheath (32). A similar calculation based on a 3-pool exchange model for rat optic nerve data yields a T_CR of 890 ms (10). These values compare to a value of about 600 ms calculated from Table 1. Thus, while our exchange rates appear somewhat slower than reported in previous MT studies, they are higher than those suggested by cross-relaxation studies that take into account a myelin water compartment. Due to the short T₂^* of myelin water, our measurements were dominated by signal from axonal and interstitial water, and therefore could not account for the effect of inter-compartmental water exchange on k_WM.

Although the fitting results suggest that both k_MW and f can be robustly estimated with the proposed method, there are several factors that can affect the accuracy of the estimated values. We will discuss a few of them, realizing that our list may be incomplete.

First, it is possible that a sizeable fraction of MP is incompletely saturated, which would lead to a commensurate underestimation of f. If not properly taken into account, this can bias f and therefore also k_MW. From experiments with varying MT pulse durations, in particular the comparison of the 6 ms saturation to the 11 ms pulse, it is apparent that the longer pulse is only 10% more effective, suggesting these pulses saturate the MP-pool nearly completely (if not, dependence on pulse duration should be stronger). This notion of nearly complete saturation with the 6 ms pulse is only valid for MP with T₂ < 400 μs, i.e. those that are relatively immobile; protons on freely rotating end-groups of larger molecules are not included in the measured MP-fraction as they are not efficiently saturated by the MT pulse. Fortunately, such mobile protons form only a small fraction of the total MP pool, and will therefore not substantially affect the estimate of f.

Secondly, a small error is introduced due of the incomplete signal recovery associated with the finite TR in our experiments. The TR of 3 s for the MT experiment was substantially longer than the effective T₁ in tissue, but not sufficiently long to ignore incomplete signal recovery: ideally this should be incorporated in the analysis model. Fortunately, because this issue affects both the MT and the reference data, simulations indicated that associated errors were small, i.e. lower than 2% for f and 7% for k_WM and k_MW,. Nevertheless, when using the proposed method with a shorter TR to increase time efficiency, it may become necessary to account for incomplete signal recovery effects in the model equations.

Third, the precision of the exchange rates k_MW and k_WM estimate depends on the available signal differences and therefore on the size of the MP-pool. If the MP-pool fraction f is low, the precisions of k_MW and k_WM will be low too. This effect and possibly partial volume effects with CSF explain the brighter pixels towards the edge of the brain slices shown in Fig. 8, especially for the (lower SNR) 3 T images.

Fourth, the two-pool model applied here is a gross simplification and may cause significant systematic errors in the estimates of f and the exchange rates. For example, accurately representing magnetization transfer through multiple myelin layers and between white matter water compartments (e.g. intra-axonal versus interstitial) may require a many-pool model, or the modeling of a diffusion process. This problem may be exacerbated when the actual MP and WP R₁ strongly deviate from their assumed average values, or have a distribution that is not accurately represented by an average. The values of k_MW and f also depend somewhat on the measurement approach, and the extent to which TE and TR affect the visibility of the different water pools. For example, about 15% of WP in WM may be situated between the myelin layers (10,11,59) and only marginally visible at the long TEs used in our experiments. This biases f, because of an underestimation of WP volume. Similarly, limited visibility of WP between the myelin layers biases k_MW, as its determination, in our experiments, depends on mixing of the magnetization between the various WP pools.

Fifth, as indicated above, the assumption of single value of R_1,WP and R_1,MP for all brain tissues may not be valid, and lead to inaccuracies in k_MW and f. For example, in disease, R_1,WP and R_1,MP could change due to iron accumulation or changes in tissue molecular structure respectively; also, it is possible that pathological conditions could render k_MW too low to cause WP saturation levels sufficient for accurate quantification of f. It remains to be seen to what extent these issue arise in practice.

Our approach compares favorably with previous methods proposed for rapid measurement of f. An interesting comparison is with IR-based methods (29) which have the potential in providing improved sensitivity (compared to out MT approach) owing to a potentially 2-fold increase in initial saturation difference between MP and WP. However, this improvement may not be realized in practice due to the difficulty in inverting WP without substantial saturation of MP. In addition this MP saturation will be dependent on B₁ power, rendering the quantification of f sensitive to B₁ inhomogeneities. Alternatively, rapid measurement of f can be performed with a transient MT method based on a stimulated echo preparation (30): this approach however suffers from a 2-fold sensitivity reduction associated with stimulated echoes, and furthermore has substantial sensitivity to B₁ inhomogeneities.

In the presented experiments, only few slices were acquired, the number of which was tied to the number of delay times. One way to extend slice coverage is to move the selected set of slices with successive repetitions of the MT pulse, while shortening the MT repetition time. When keeping the slice repetition time (i.e. time between successive excitations of the same slice) constant, this should only minimally affect the sensitivity of the experiment, as the WP saturation caused by the MT pulse is a small fraction of the total magnetization. Alternatively, or additionally one can perform simultaneous multi-slice acquisitions, or acquire data in 3D fashion, where the excitation is performed over the entire brain and phase encoding is performed over the through-plane direction (perpendicular to the plane encoded by EPI). This would allow large brain coverage in clinically feasible scan times, in particular when reducing the number of delay times to three (or even two) by fixing an increasing number of model parameters. The practical benefits of these approaches are currently being investigated in our laboratory.

CONCLUSION

We implemented a rapid, transient MT approach to measure the fraction of macromolecular protons f. Because of its insensitivity to B₁ inhomogeneities, and its minimal RF power deposition, the approach can be readily applied at high field, where its sensitivity benefits substantially from the slower T₁ relaxation of macromolecular protons. Values of f in white matter, obtained by fitting the MT data to a 2-pool model, and assuming a dominant contribution of MT to longitudinal relaxation, were found to be about 50% higher than previous estimates. This is partly attributed to discrepancies in the estimates of R₁ of macromolecular protons, which was much higher here than reported previously.