Impact of transcytolemmal water exchange on estimates of tissue microstructural properties derived from diffusion MRI

Abstract

Purpose

To investigate the influence of transcytolemmal water exchange on estimates of tissue microstructural parameters derived from diffusion MRI using conventional PGSE and IMPULSED methods.

Methods

Computer simulations were performed to incorporate a broad range of intracellular water life times τ_in (50 – ∞ ms), cell diameters d (5 – 15 μm), and intrinsic diffusion coefficient D_in (0.6 – 2 μm²/ms) for different values of signal to noise ratio (10 to 50). For experiments, murine erythroleukemia (MEL) cancer cells were cultured and treated with saponin to selectively change cell membrane permeability. All fitted microstructural parameters from simulations and experiments in vitro were compared with ground-truth values.

Results

Simulations showed that, for both PGSE and IMPULSED methods, cell diameter d can be reliably fit with sufficient SNR (≥ 50), while intracellular volume fraction f_in is intrinsically underestimated due to transcytolemmal water exchange. D_in can be reliably fit only with sufficient SNR and using the IMPULSED method with short diffusion times. These results were confirmed with those obtained in the cell culture experiments in vitro.

Conclusion

For the sequences and models considered in this study, transcytolemmal water exchange has minor impacts on fittings of d and D_in with physiologically relevant membrane permeabilities if SNR is sufficient (> 50), but f_in is intrinsically underestimated.

Introduction

Diffusion-weighted MRI provides a non-invasive means to probe biological tissue microstructure, and has been widely used for the diagnosis of neurodegenerative diseases and cancer (1). Apparent diffusion coefficients (ADC) obtained from conventional diffusion MRI measurements report the overall averaged diffusion properties of biological tissues. ADC has been found to be sensitive to variations of a variety of tissue properties, including but not limited to cell size (2), cell membrane permeability (3), intra- and extracellular diffusion coefficients (4), and intracellular volume fraction (5). When diffusion times are short enough (such as those obtained using oscillating gradient spin echo (OGSE) sequences at moderately high gradient frequencies(6)), ADC can be sensitive to intracellular microstructural variations such as the sizes of nuclei (7) and organelles (8). Therefore, ADC provides a powerful approach to probe a variety of tissue features from sub- to supra-cellular scales if appropriate diffusion times are used. However, specific microstructural changes usually cannot be directly determined from ADC measurements alone. In many cases, the detection of specific microstructural parameters such as cell size and intracellular volume fraction may provide additional and sometimes more useful diagnostic information (9). Hence, there is a need to develop quantitative diffusion MRI methods to derive more specific microstructural changes from experimental measurements.

To date, there are various diffusion MRI methods developed for quantitative characterization of tissue microstructure. Q-space imaging provides a means to measure apparent compartment sizes (2), but tends to bias cell size because of the inability of distinguishing contributions from intra- and extracellular spaces (10) and the violation of the short gradient pulse condition (11). If the transcytolemmal water exchange between intra- and extracellular spaces is slow enough to be ignored, the overall diffusion signals can be assumed to represent simply the sum of signals from each space. This provides an opportunity to decouple intra- and extracellular signals, and thereby to measure specific microstructural parameters. The AxCaliber method, based on the CHARMED model that assumes cylindrical compartments with hindered diffusion in the extracellular space (with a constant diffusion coefficient), has been implemented to measure axon size distributions in animals in vitro (12) and in vivo (13), and humans in vivo (14). The ActiveAx method was developed to measure indices of mean axon diameter instead of a diameter distribution for better clinical feasibility (15,16). In addition to these conventional pulse gradient spin echo (PGSE) based methods, double-PGSE (17) and OGSE (18) sequences have also been developed for quantitative characterization of cell size and intracellular volume fraction. Recently, a temporal diffusion spectroscopy (TDS) based approach (19) has been developed to combine PGSE (long diffusion times) and OGSE (short diffusion times) acquisitions to cover a broader range of effective diffusion times for better quantitative characterization of microstructure at different length scales simultaneously, i.e. from intracellular diffusion effects up to the impact of cell size and spacing. We term this new experimental approach as the Imaging Microstructural Parameters Using Limited Spectrally Edited Diffusion (IMPULSED) method.

All the models used to interpret data from these quantitative diffusion methods assume that transcytolemmal water exchange between intra- and extracellular spaces can be ignored. This assumption is usually believed true in neural tissues because the typical diffusion time t_D in PGSE measurements is < 100 ms, smaller than the intracellular water lifetime τ_in of brain tissues in vivo reported as 622±29 ms (20) or ∼ 550 ms (21). However, some studies have suggested that the “slow” water exchange still significantly affects MRI measurements of nerves in vitro (22) and in vivo (23). Our recent study indicates that the influence of transcytolemmal water exchange on ADC measurements can be ignored only when t_D is at least one order of magnitude smaller than τ_in (24). More complicatedly, transcytolemmal water exchange typically increases significantly in e.g. lesions caused by Parkinson's (25) and Alzheimer diseases (26), and tumors (27) especially in apoptotic regions (28). This raises concerns if the estimates of microstructural parameters are biased by transcytolemmal water exchange. Previous computer simulations have suggested that the estimated intracellular volume fraction may be underestimated in case of short exchange times (29,30). However, comprehensive studies have not been reported up to date to investigate the influence of transcytolemmal water exchange on the accuracy of fitted microstructural parameters obtained using quantitative diffusion MRI methods.

The present work aims to address the concerns mentioned above. Diffusion MRI sequences using different diffusion times were investigated. Computer simulations and cell culture studies in vitro were performed, and the cell membrane permeability was selectively changed without affecting other cellular microstructure in order to evaluate the precise impact of transcytolemmal water exchange on fitted microstructural parameters. In addition, the influences of signal-to-noise (SNR) and the choices of pre-assigned D_in used in the fittings were also studied to evaluate their impacts on fitted parameters.

Methods

Theory

Diffusion MRI signals were modeled as the sum of signals from intra- and extracellular spaces without water exchange between them, namely,

$$S=f_{\mathit{\text{in}}}\cdot S_{\mathit{\text{in}}}+(1-f_{\mathit{\text{in}}})\cdot S_{\mathit{\text{ex}}}$$ [1]

where f_in is the water fraction of intracellular space, S_in and S_ex are the signal magnitudes from intra- and extracellular spaces, respectively. Note that T₂ relaxation is not considered here. For simplicity, tissues were modeled as tightly-packed spherical cells with an effect mean cell diameter d. The analytical expressions to predict diffusion signals of intracellular water restricted by spheres have been reported previously (31). The expression for extracellular water depends on the effective diffusion time, as detailed below. Note that Eq.[1] is widely-used for various diffusion methods (15,18,32). After the diffusion signals were obtained from simulations or experiments, all diffusion MRI signals were fit to Eq.[1]. By comparing fitted values and ground truth, the impact of transcytolemmal water exchange on quantitative characterization of tissue microstructure can be evaluated. Three diffusion methods PGSE_I, PGSE_II and IMPULSED, were investigated.

PGSE_I and PGSE_II methods

The analytical expression for S_in using PGSE acquisitions based on the Gaussian phase approximation is given by

$$S_{\mathit{\text{in}}}(\text{PGSE})=S_{0,\mathit{\text{in}}}\cdot exp\{-\sum _k\frac{2B_k{\gamma }^2{g}^2}{{\lambda }_k^2{D}_{\mathit{\text{in}}}^2}\times \{{\lambda }_k{D}_{\mathit{\text{in}}}\delta -1+exp(-{\lambda }_k{D}_{\mathit{\text{in}}}\delta )+exp(-{\lambda }_k{D}_{\mathit{\text{in}}}\mathrm{\Delta })(1-cosh({\lambda }_k{D}_{\mathit{\text{in}}}\delta ))\}\}$$ [2]

Where S_0,in is T₂-weighted intracellular signal, γ is the gyromagnetic ratio, δ is the gradient duration, Δ is the gradient separation, g is the gradient strength, D_in is the intracellular free diffusion coefficient, λ_k are B_k are cell diameter d dependent parameters (19,31).

Previous analyses of PGSE data (12–16) usually assume the extracellular diffusion is hindered, i.e. extracellular diffusion coefficient is a constant independent of diffusion time, and hence

$$S_{\mathit{\text{ex}}}(\text{PGSE})=S_{0,\mathit{\text{ex}}}\cdot exp(-b\cdot D_{\mathit{\text{ex}}}).$$ [3]

Note that the accuracy of this approximation has been previously questioned (33,34). Nevertheless, Eq.[3] was used to describe extracellular diffusion to follow the current widely-used approaches.

Altogether, four independent parameters may be fit using this method: d, f_in, D_in, and D_ex. We term this combination of measurement and analysis as the PGSE_I method. It has been reported that PGSE acquisitions with relatively long diffusion times have low sensitivity to intracellular features (6,7), and hence previous studies have assigned D_in to an empirical constant value in fittings to reduce the number of free parameters (9,13,15,16). In this case, three free parameters may be fit: d, f_in, and D_ex, and we term this as the PGSE_II method. Note that the influence of different choices of D_in has not been fully investigated before, so we studied this influence on fitted microstructural parameters in the simulations in the present work.

IMPULSED method

We previously proposed a new experimental IMPULSED method. In this method, PGSE acquisitions are used to obtain data with a long diffusion time t_D (e.g. 52 ms) and acquisitions using oscillating gradients with two or more frequencies are used to sample other regions of the diffusion spectrum with shorter diffusion times (where the oscillating frequency f is related to the effective diffusion time as t_D = 1/(4f) for cosine-modulated waveforms). By such as means, it covers a broader range of diffusion times and therefore provides a more comprehensive sensitivity to different length scales (19). The analytic expressions for intracellular cosine-modulated OGSE signals have been derived (31) and validated with phantoms (35) previously as

$$S_{\mathit{\text{in}}}(\text{OGSE})=S_{0,\mathit{\text{in}}}\cdot exp\{-2{\gamma }^2{g}^2\sum _k\frac{B_k{\lambda }_k^2{D}_{\mathit{\text{in}}}^2}{{({\lambda }_k^2{D}_{\mathit{\text{in}}}^2+4{\pi }^2{f}^2)}^2}\times [\frac{\delta ({\lambda }_k^2{D}_{\mathit{\text{in}}}^2+4{\pi }^2{f}^2)}{2{\lambda }_k{D}_{\mathit{\text{in}}}}-1+exp(-{\lambda }_k{D}_{\mathit{\text{in}}}\delta )+exp(-{\lambda }_k{D}_{\mathit{\text{in}}}\mathrm{\Delta })(1-cosh({\lambda }_k{D}_{\mathit{\text{in}}}\delta )\left]\right\},$$ [4]

where f is diffusion gradient frequency.

When the experimental diffusion times are relatively short, the extracellular diffusion usually cannot be assumed as a t_D–independent constant. Due to the complexity of extracellular structure, it is challenging to derive a general analytical equation to describe the diffusion spectra arising from the extracellular space. An empirical model for extracellular diffusion has been recently proposed to describe packed cylindrical axons (36). However, previous studies have found that if only a narrow range of relatively low gradient frequencies is used (such as 0, 40 and 80 Hz used in the current work), the extracellular diffusion coefficient can be approximated as a linear function of gradient frequency (18,33,34,37). Therefore, extracellular diffusion signals can be simplified as

$$S_{\mathit{\text{ex}}}=S_{0,\mathit{\text{ex}}}\cdot exp[-b\cdot (D_{\mathit{\text{ex}}0}+{\beta }_{\mathit{\text{ex}}}\cdot f)]$$ [5]

where D_ex0 is the apparent diffusion coefficient of extra-cellular space measured at very long diffusion times (f → 0) and β_ex is the slope of D_ex with respect to gradient frequency f. D_ex0 is mainly determined by the extracellular tortuosity and β_ex indirectly reflects microstructural information (38). PGSE measurements with a single long diffusion time are used in IMPULSED method and treated as 0 frequency. Note that this only affects the modeling of extracellular diffusion, while intracellular diffusion of PGSE measurements is diffusion time dependent determined by Eq. [2]. Therefore, five independent parameters are fit using the IMPULSED method: d, f_in, D_in, β_ex and D_ex0. The IMPULSED method has been successfully implemented to measure mean axon diameter (18) and cell size (19), both with validations using light microscopy.

Computer simulations

A finite difference method was used to simulate diffusion signals obtained using different sequences as shown in (19). The tissue was modeled as tightly-packed spherical cells on a face-centered-cubic lattice (Figure 2 in ref. (31)) with f_in = 61.8%, D_in = 1 μm²/ms, D_ex = 2 μm²/ms, and homogenous relaxation times everywhere for simplicity. 11 different values of cell diameter d evenly distributed from 5 to 20 μm were simulated to emulate typical cancer cell sizes, and each d incorporated 16 different intracellular water lifetimes τ_in's: 50, 60, 70, 80, 90, 100, 125, 150, 200, 250, 300, 350, 400, 500, and ∞ ms. Note that τ_in of rat brain in vivo has been reported as ∼ 550 ms (21). The transmembrane water apparent exchange rate has been reported as 2.9 ± 0.8 s^-1 (τ_in ∼ 500 ms) for viable human brain tumor (27) and tumor cell exchange rate is expected to increase during treatment-induced apoptosis (28). The finite difference simulations actually incorporated cell membrane permeability P_m instead of τ_in as described previously (39), where P_m is related to τ_in as (40)

$$\frac{1}{P_m}=\frac{6{\tau }_{\mathit{\text{in}}}}{d}-\frac{d}{10D_{\mathit{\text{in}}}}.$$ [6]

All the other pulse sequence parameters in the simulations were the same as those used in the MR experiments (see below). All simulations (176 combinations of 11 cell diameters and 16 intracellular water lifetimes) took ∼18.2 hours using Matlab R2015a running on a 64bit Linux machine with a Xeon 3.30 GHz CPU.

Three studies were performed based on simulation-generated datasets:

• [Study I] To compare the accuracy of fitted d, f_in, and D_in using IMPULSED, PGSE_I, and PGSE_II methods. Note the PGSE_II method does not provide fitted D_in. The percentage differences of fitted and ground truth values were evaluated with a broad range of τ_in 50 - ∞ ms and d 5 – 15 μm.

• [Study II] To investigate the different choices of pre-defined D_in on the accuracy of fitted d and f_in using the PGSE_II method. Only cells with d = 10 μm were simulated here. Five D_in values were investigated: 0.6, 0.8, 1.0 (true value), 1.5, and 2.0 μm²/ms. Fitted results with different choices of D_in were compared with ground truth values.

• [Study III] To investigate the influence of SNR on the contrast and stability of the fitted parameters obtained using the PGSE_II and IMPULSED methods. Three SNR's were investigated: 10, 20, and 50, and each with four τ_in's: 50, 100, 250, and 500 ms. Random noise with targeted SNR's based on the non-diffusion-weighted signals were added to simulated noise-free signals according to the approach described in (41), and then microstructural parameters were fit based on signals with noise. This process was repeated 100 times for each of the 12 combinations of SNR and τ_in, and the mean of the 100 fitted values of each microstructural parameter (d, or f_in, or D_in) was calculated and compared with the ground truth values.

Cell sample preparation

Murine erythroleukemia (MEL) cancer cells purchased from American Type Culture Collection (Manassas, Virginia, USA) grew under standard culture conditions described previously (24). Large scale of MEL cells were cultured in multiples 150 mm dishes, after spun down and washed with PBS, the cells were fixed with 4% paraformaldehyde in PBS for about 2 hours. After fixation, cells were washed and divided into four groups at a cell density 4.2×10⁷ cell/ml, each treated with 0%, 0.01%, 0.025% and 0.05% (w/v) -saponin at room temperature for 30 minutes to induce various degree of cell membrane permeability. Note that saponin does not cross cell membranes at low concentration, so that it is unlikely to change other cell microstructure e.g. nuclear envelope. For each concentration of saponin treatment, cells were divided approximately evenly into six 0.65ml microtubes (each tube contains about 120 million cells). After centrifuge at 6000g for 2 minutes, top fluid was carefully removed and the cell pellet samples were then used for MR experiments. Small aliquoted sample was spotted on glass slides and imaged directly under phase contrast microscopy for cell diameter estimation.

MR measurements

All MR diffusion measurements were performed on a Varian 4.7T MRI spectrometer. The sample temperature was maintained at ∼ 17°C using a cooling water circulation system. The acquisition time was ∼7 min for measurements of τ_in, and 9 min for PGSE and IMPULSED experiments.

Measurements of τ_in

The intracellular exchange lifetime τ_in was estimated using constant gradient (CG) experiments (20,40). With a stimulated echo (STEAM) sequence, diffusion weighting was achieved by keeping δ = 10 ms and varying the gradient separation Δ in 30 increments. The minimum Δ was 20 ms and the maximum Δ was 426, 426, 223, 121.5 ms for cell samples with saponin concentrations of 0, 0.01%, 0.025% and 0.05%, respectively. Diffusion gradients were applied simultaneously on three axes with gradient strength g = 5 G/cm. The experiment was repeated with a lower gradient strength g = 0.5 G/cm to normalize the higher gradient dataset in order to correct for T₁ relaxation effect during the mixing time. The ADC of the slowly decaying component (D_B) was determined by linear regression using the last 10 b-value points. The τ_in was then estimated as (20,40,42)

$${\tau }_{\mathit{\text{in}}}=\frac{1}{{\gamma }^2{g}^2{\delta }^2{D}_B}.$$ [7]

Note that Eq. [7] is derived from Karger model based on several assumptions and its validity is supported by computer simulations (40).

PGSE experiments

Diffusion signals were measured with PGSE sequences at four different diffusion times (δ = 4 ms, and Δ = 10, 25, 35, 50 ms). Diffusion gradients were applied simultaneously on three axes with 11 gradient strengths varying linearly from 0 to 20 G/cm. Other parameters included: repetition time TR = 3.5 sec; number of excitation = 2; number of dummy scans = 2; receiver bandwidth = 50 kHz; spectral resolution = 390.625 Hz; echo time TE = 60 ms.

IMPULSED experiments

The IMPULSED measurements used both PGSE and OGSE sequences. For the PGSE measurements, δ = 4 ms, and Δ = 52 ms. For OGSE experiments, cosine-modulated waveforms were applied with δ/Δ = 25/30 ms at two oscillation frequencies (f = 40 and 80 Hz). TR = 3.5 sec and TE = 60 ms for both PGSE and OGSE measurements. Nine b values evenly distributed between 0 and 2 ms/μm² were used in both measurements. The maximum gradient strength used in this study was 30 G/cm, which is achievable on e.g. the cutting-the-edge human brain gradient coil (43).

Data analysis

Diffusion signals obtained in PGSE acquisitions were fit to Eqs.[1-3], and those from IMPULSED experiments were fit to Eqs.[1], [2], and [4-5]. Four parameters were fit using the PGSE_I method: d, f_in, D_in, and D_ex, three using PGSE_II by assuming D_in = 1 μm²/ms: d, f_in, and D_ex, and five using the IMPULSED method: d, f_in, D_in, β_ex, and D_ex0. The lsqcurvefit function in Matlab was used in the optimization with constraints of parameters limited to biophysically meaningful values: 0 ≤ d ≤ 30 μm, 0 ≤ f_in ≤ 1, 0.1 ≤ D_in ≤ 3 μm²/ms, 0.1 ≤ D_ex, D_ex0 ≤ 3 μm²/ms, and 0 ≤ β_ex ≤ 30 μm². To avoid local minima, each fitting was repeated 100 times with randomly-generated initial conditions, and the analyses corresponding to the smallest fitting residuals were chosen as the final results.

Results

Simulated influence of fitted parameters on τ_in and d

Figure 1 shows the simulated fitting errors of fitted parameters compared with ground truth values dependent on d and τ_in for all three methods. Both IMPULSED and PGSE_II provide accurate estimates of d with error < 5% for τ_in > 150 ms and d > 7 μm, while the PGSE_I can provide ≤ 5% errors only when τ_in > 350 ms and d was between 10 and 16 μm. Consistent with previous computer simulation results (29,30), all three methods significantly underestimated f_in, except for IMPULSED and PGSE_II methods when τ_in is infinitely large. All fitted f_in decreases rapidly with smaller τ_in, indicating transcytolemmal water exchange has a strong influence on fitted f_in. The IMPULSED method provides reasonable fits of D_in with errors ≤ 10% for most τ_in and d values, although the fits with errors ≤ 5% occurred only when d was between 7 – 13 μm. The PGSE_I could provide fits of D_in with errors < 10% only when d is large (≥ 12 μm) and τ_in is long (≥ 400 ms), and those with ≤ 5% errors only occur at a few combinations of τ_in and d. We need to reemphasize that D_in was empirically pre-defined in the PGSE_II method, so it cannot be obtained in the fittings. Note that some plots in Figure 1 appear to be noisy, the main reason is that some fitted parameters reached the boundaries of loose fitting constraints.

Figure 1.

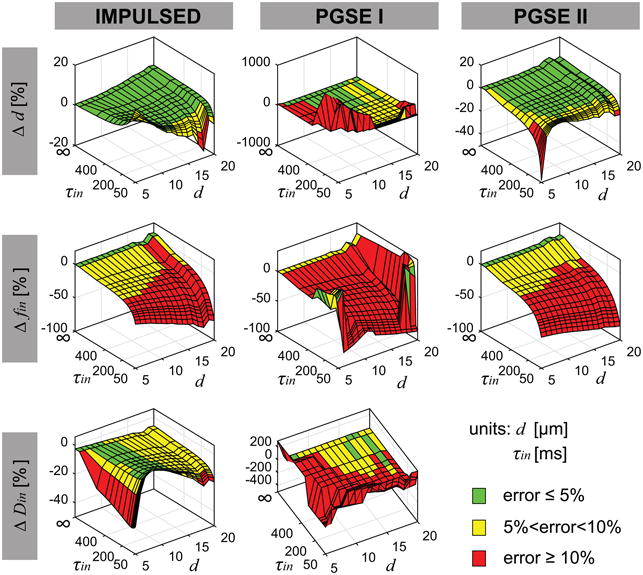
Simulated dependence of the fitting errors compared with ground truth values of fitted parameters on d and τ_in for all three methods.

Simulated influence of pre-defined D_in on PGSE_II fitting

Figure 2 shows the simulated dependence of the fitted PGSE_II parameters on the choice of pre-defined D_in used in the fittings. Note that only d = 10 μm was simulated here. Except for fast transcytolemmal water exchange (τ_in < 100 ms), the choices of D_in had minor effects on the fittings of PGSE_II. For example, the fitted d were all within 5% difference when the pre-defined D_in was in the range of 0.6 – 2.0 μm²/ms when τ_in > 100 ms, indicating the accuracy of fitted d is not influenced by the choice of D_in used in the fittings. f_in is consistently underestimated across all τ_in values, while the discrepancy decreases with longer τ_in. The ground truth extracellular diffusion coefficient is provided in Figure 2, which is much higher than fitted D_ex which is the extracellular diffusion coefficient at very long diffusion times, i.e., mainly determined by the extracellular tortuosity. Note that both the fitted f_in and D_ex had small dependences on pre-defined D_in: < 10% changes occur when D_in changes from 0.6 to 2.0 μm²/ms. These results are encouraging. In most cases, D_in is unknown. If the influence of D_in on the fitted parameters of the PGSE_II method is minor, an empirical value of D_in can be implemented and the fitting accuracy is preserved.

Figure 2.

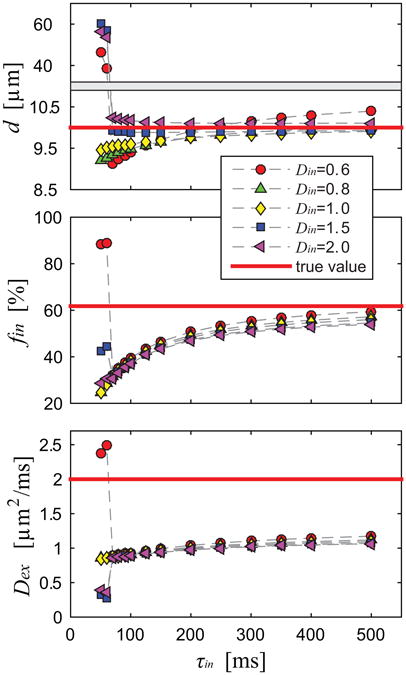
Simulated parameters obtained using the PGSE_II method dependent on different choices of pre-defined D_in used in the fittings.

Simulated influence of SNR

The influence of SNR on fitted d using the IMPULSED and PGSE_II methods is shown in Figure 3. For each real d value, the fittings were repeated 100 times and each with different noises at the same SNR. Hence, 100 fitted d values were obtained (green +) for each real d, and the mean of the repetitions (black ×) are also shown in Figure 3 to indicate the fitting accuracy. For both IMPULSED and PGSE_II methods at low SNR = 20, there was a broad range of fitted d values for each real d, indicating the precision was significantly reduced by noise. By contrast, at SNR = 50, d could be reliably fit using the IMPULSED or PGSE_II methods despite different τ_in. The mean values of all fitted results indicate the accuracy of fittings. At SNR = 20, the PGSE_II method provided relatively more accurate fittings compared with the IMPULSED method, while the latter overestimated d for all ground-truth d and τ_in values. Note that this is at least partially due to the less data points (28 b values) acquired using the IMPULSED method compared with the 45 b values used in the PGSE_II method. By contrast, both diffusion methods provided more reliable fittings at SNR = 50. The IMPULSED method provided more accurate and precise fittings compared with the PGSE_II method especially for d 5 – 10 μm. The fitted results showed slightly less variations with higher τ_in and SNR = 50, indicating transcytolemmal water exchange has a minor influence on the fittings of d when SNR is sufficient. For SNR = 20, the influence of τ_in on d fittings was more significant, especially for the IMPULSED method. Based on these findings, we can conclude that when SNR is low (e.g. 20 in the current simulation), the transcytolemmal water exchange does affect fitted d, and higher τ_in (slower water exchange) and higher SNR would lead to more accurate estimates of d.

Figure 3.

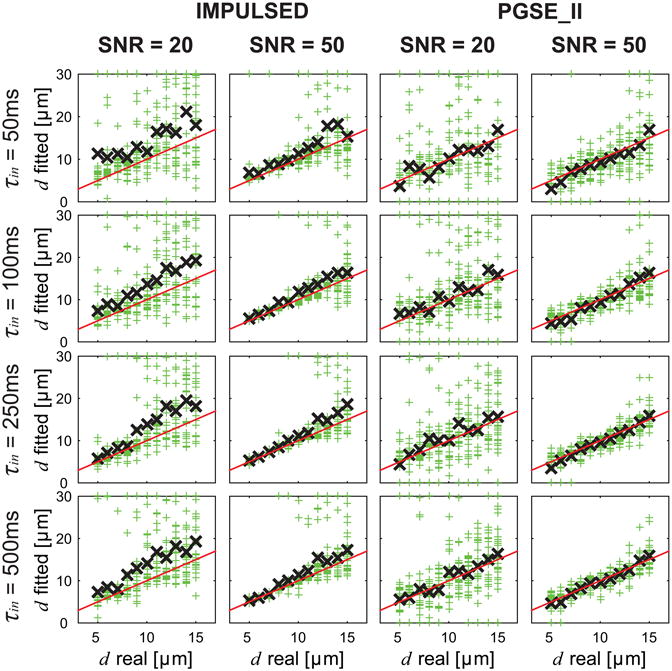
Simulated influence of SNR on fitted d using the IMPULSED and PGSE_II methods. For each real d, the fittings were repeated 100 times (green +) each with different noises but at the same SNR level, and the mean of the repetitions (black ×) are also shown. The red lines represent the identity lines.

Figure 4 shows the simulated influence of SNR and τ_in on fitted D_in values using the IMPULSED method. SNR significantly affects the accuracy of fitted D_in values. For SNR = ∞, D_in can be fit well with < 10% errors except when d ≤ 6 μm. This is consistent with previous findings that D_in cannot be reliably fit when the restriction dimension is too small and the highest gradient frequency used is limited (35). For SNR = 10, D_in tends to be overestimated with large variations. For SNR = 20, better estimates of D_in were achieved when τ_in > 250 ms and real d ≥ 10 μm. For SNR = 50, it seems D_in were all fit reasonably well with most errors < 20% except for τ_in = 50 ms. This suggests that the accuracy and precision of D_in fitting using the IMPULSED approach were mainly limited by SNR when transcytolemmal water exchange is not too fast (e.g. τ_in > 100 ms). Recall that the PGSE_II method is incapable of providing any D_in information, while the PGSE_I method estimates D_in poorly even with the noise-free signals (see Figure 1). This suggests an advantage of using the IMPULSED method to quantitatively characterize tissues in practice.

Figure 4.

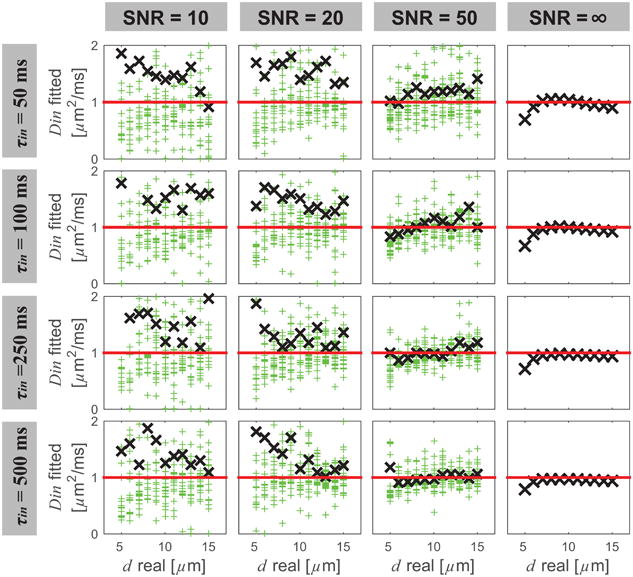
Simulated influence of SNR and τ_in on fitted D_in values using the IMPULSED method. Meanings of symbols and lines are the same as in Figure 3.

Experimental results of in vitro studies

Cell size and τ_in

Based on the light microscopy experiments and the analysis approach described previously (19), the MEL cell diameter was measured as 11.34±1.68 μm, consistent with previous reported 11.74±1.30 μm (19). The volume weighted cell diameter d was then calculated as 12.11 μm used as ground truth value in Figure 5. The CG-experiments provided τ_in values of 161.8±9.4, 157.8±8.9, 106.6±4.3, and 59.4±3.7 ms for 0, 0.01, 0.025, and 0.05% concentration of saponin, respectively.

Figure 5.

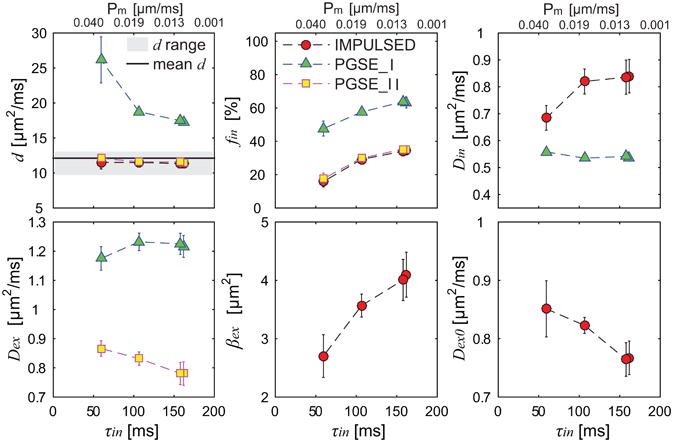
Summary of fitted microstructural parameters vs τ_in using three diffusion methods. Error bars in each sub-figure denote across-sample STD. d range means histology-derived mean cell diameter ± STD of all cells, and mean d is volume-weighted cell diameter.

Microstructural parameters of cell samples

Figure 5 summarizes all fitted microstructural parameters of cultured MEL cells with four different cell membrane permeabilities. The IMPULSED and PGSE_II methods provide accurate fittings of d independent of permeability over a broad range of τ_in (59.40 – 161.80 ms), while fitted f_in decreased rapidly with τ_in. This is consistent with simulated results shown in Figure 1 and Figure 3 that, if SNR is not too low (e.g. > 50) and τ_in is not too small (e.g. > 50 ms), transcytolemmal water exchange has minor influence on the estimations of d over a broad range of τ_in values, while estimations of f_in could be significantly biased by fast transcytolemmal water exchange i.e. higher τ_in values. D_in estimated by the IMPULSED method showed approximately no dependence over the τ_in range of 106.58 to 161.80 ms, but decreased to 0.69 μm²/ms when τ_in decreased to 59.40 ms. This suggests that although D_in is slightly more susceptible to transcytolemmal water exchange compared with d, D_in still can be reliably estimated if τ_in is not too small (e.g. > 100 ms). D_in fitted from the PGSE method were approximately constant over the τ_in range of 106.58 to 161.80 ms. However, as suggested by the simulations shown in Figure 1, the PGSE method intrinsically underestimates D_in even with noise-free signals, and hence D_in obtained using the PGSE method may not be reliable. All other fitted parameters, D_ex from the PGSE_I and PGSE_II methods, k_ex and D_ex0 from the IMPULSED method, showed dependence on τ_in.

Discussion

The present work investigated the influence of transcytolemmal water exchange on quantitative characterization of tissue microstructure using diffusion MRI methods. Despite the significant variations of τ_in present in simulations and in vitro experiments, all diffusion signal data sets were fit to currently widely-used models that assume no water exchange between intra- and extracellular spaces. The results suggest that fitted d is relatively insensitive to τ_in with reasonable SNR in both PGSE_II and IMPULSED experiments, while f_in is significantly underestimated for all diffusion methods tested. D_in can be reliably fit only using IMPULSED experiments when SNR is sufficient (e.g. 50). These findings may assist better interpretation of quantitative characterization of tissue microstructure in tumors, in which the transcytolemmal water exchange is often much faster than normal tissue and cannot be ignored (27,28). For example, a previous study using the IMPULSED method provided d and f_in maps of an MDA-MBA-231 triple-negative breast cancer xenograft in vivo (44). Although d was fit reasonably well and confirmed with histology, f_in was significantly underestimated (< 50%) in most regions. Based on the findings of the present work, the fitting accuracy of these in vivo findings can be explained by the enhanced transcytolemmal water exchange in tumors. To prove this, the transcytolemmal water exchange needs to be mapped using a method such as filter exchange imaging (FEXI) (27,45) in addition to quantitative diffusion MRI measurements.

It is possible to incorporate transcytolemmal water exchange into quantitative diffusion models, and hence fit all microstructural parameters including τ_in simultaneously. The two-exchanging-component-system describing diffusion measurements has been thoroughly investigated by Karger et al. by assuming two freely-diffusing components (46), and was later improved to include restrictions (i.e. d and D_in) on the intracellular water component (40,42,47). However, this method requires very high b values e.g. 580 ms/μm², as was used in rat brain in vivo (20). Stanisz et al. performed comprehensive fittings to measure cell size, volume fraction, membrane permeability simultaneously in bovine optic nerves ex vivo (48). However, high b values ≈ 40 ms/μm², high gradient strength 140 G/cm and rise time ∼ 500 μs were used, which are not achievable in practical imaging. Therefore, one major disadvantage of combining transcytolemmal water exchange in quantitative diffusion models is that these methods would become complicated and demand very high SNR and long scanning time. This will significantly limit the feasibility of translating these methods into clinical practice. Diffusion MRI usually suffers low SNR and long scanning time in practice and hence it is desirable to keep quantitative models simple with fewer free parameters. Partially due to this reason, the PGSE_II method was able to provide more accurate fits of d compared with the PGSE_I method because PGSE_II has less free parameters.

The minor influence of pre-defined D_in on the fitting accuracy of the PGSE_II method is encouraging. D_in is usually unknown in practice. Previous studies assigned D_in empirical values in the fittings (9,13,15,16), but the exact influence of different choices of empirical D_in values on fitted results has not been fully investigated. The current study suggests that the influence of D_in can be ignored if assigned D_in is in a reasonable range (between -40% and +100% difference in the present work) when τ_in is not too short (> 100 ms shown in Figure 2). Since this influence is minor on fitted results, it is recommended to use the PGSE_II method other than the PGSE_I method due to its better accuracy and stability (see Figure 1). Note that neither PGSE_I nor PGSE_II methods used in the present work can reliably fit D_in, presumably because of the relatively long diffusion times used. By incorporating PGSE acquisitions with a long diffusion time (Δ = 50 ms) and OGSE acquisitions with short diffusion times (40 and 80 Hz, corresponding to t_D 6.25 and 3.125 ms), the IMPULSED method is capable of providing a more comprehensive means to fit both intracellular D_in and cellular dimension d simultaneously. Note that the IMPULSED method used in the current work incorporates three different t_D values, and fits five parameters, while the PGSE_II method incorporates four t_D values and fits three parameters. The fitted d using the IMPULSED method with less data points is more prone to noise than the PGSE_II method shown in Figure 3. We need to emphasize that it is possible to include more acquisitions with additional diffusion times in the IMPULSED method to enhance the sensitivity to d, but this in turn will increase the total scanning time. Therefore, it is desirable to optimize the IMPULSED method for specific applications in vivo.

Two relatively low frequencies (40 and 80 Hz) were used in the current work. The two low frequencies correspond to t_D 6.25 and 3.125 ms, and root-mean-square displacements of 3.5 and 2.5 μm if diffusion coefficient is 1 μm²/ms. This is already much smaller than typical cancer cell size (e.g. 11.34 μm in the present work), which enables the feasibility to probe D_in. Note that the fitted D_in represents an averaged intracellular diffusion properties, and even smaller intracellular microstructure such as nuclear size and organelles may not be probed by the frequencies used in the present work (8). To be sensitive to smaller sizes (∼ 2 μm), much higher frequencies (∼ 250 Hz) would be required (18,38).

To ensure translatability of our results, maximum gradient strengths were limited < 30 G/cm which is achievable on the cutting-the-edge human gradient coils (43). Note that even with typical maximum gradient strength 8 G/cm, OGSE has been implemented on human scanners and shows promising potential to probe microstructure of human brain in vivo (49,50) and may assist interpret ADC data in stroke patients (51). However, the lowest frequency achievable is limited by echo time, so OGSE acquisitions have reduced sensitivity to larger scale dimensions. Combined with PGSE acquisitions with long diffusion times, sensitivity to both intra- and supracellular scales can be achieved. In return, both d and D_in can be fit which provides more microstructural information than d alone as provided by the PGSE_II method. Note that higher gradient performance can improve the estimates of the fitting results (52). This is particular true for the IMPULSED method which uses OGSE acquisitions (53).

Conclusions

Both computer simulations and in vitro cell studies suggest that: for PGSE methods with relatively long diffusion times, empirically assigning D_in as a constant in fittings significantly increases the accuracy of other fit parameters. Both IMPULSED and PGSE_II methods provide accurate fits of mean cell diameter d independent of transcytolemmal water exchange with sufficient SNR (e.g. 50), while intracellular volume fraction f_in was intrinsically underestimated in both methods and decreased rapidly with shorter τ_in. The IMPULSED method is capable of estimating intracellular diffusion coefficient D_in when appropriate ranges of d (7 – 15 μm), τ_in > 100 ms and sufficient SNR e.g. 50 were satisfied, while D_in cannot be reliably estimated using the PGSE methods even for noise-free data. These results can assist better interpreting diffusion data for quantitative characterization of e.g. tumors, where transcytolemmal water exchange cannot be ignored.