Evaluation of interpolation methods for TG-43 dosimetric parameters based on comparison with Monte Carlo data for high-energy brachytherapy sources

Abstract

Purpose

The aim of this work was to determine dose distributions for high-energy brachytherapy sources at spatial locations not included in the radial dose function g_L(r) and 2D anisotropy function F(r,θ) table entries for radial distance r and polar angle θ. The objectives of this study are as follows: 1) to evaluate interpolation methods in order to accurately derive g_L(r) and F(r,θ) from the reported data; 2) to determine the minimum number of entries in g_L(r) and F(r,θ) that allow reproduction of dose distributions with sufficient accuracy.

Material and methods

Four high-energy photon-emitting brachytherapy sources were studied: ⁶⁰Co model Co0.A86, ¹³⁷Cs model CSM-3, ¹⁹²Ir model Ir2.A85-2, and ¹⁶⁹Yb hypothetical model. The mesh used for r was: 0.25, 0.5, 0.75, 1, 1.5, 2–8 (integer steps) and 10 cm. Four different angular steps were evaluated for F(r,θ): 1°, 2°, 5° and 10°. Linear-linear and logarithmic-linear interpolation was evaluated for g_L(r). Linear-linear interpolation was used to obtain F(r,θ) with resolution of 0.05 cm and 1°. Results were compared with values obtained from the Monte Carlo (MC) calculations for the four sources with the same grid.

Results

Linear interpolation of g _L(r) provided differences ≤ 0.5% compared to MC for all four sources. Bilinear interpolation of F(r,θ) using 1° and 2° angular steps resulted in agreement ≤ 0.5% with MC for ⁶⁰Co, ¹⁹²Ir, and ¹⁶⁹Yb, while ¹³⁷Cs agreement was ≤ 1.5% for θ < 15°.

Conclusions

The radial mesh studied was adequate for interpolating g_L(r) for high-energy brachytherapy sources, and was similar to commonly found examples in the published literature. For F(r,θ) close to the source longitudinal-axis, polar angle step sizes of 1°-2° were sufficient to provide 2% accuracy for all sources.

Purpose

Treatment planning systems (TPS) used in brachytherapy, employ the American Association of Physicists in Medicine (AAPM) Task Group No. 43 Report (TG-43) formalism [1, 2] in which the radial dose function g_L(r) and 2D anisotropy function F(r,θ) are introduced in the form of single and double entry tables, respectively, using a specific mesh for each parameter. Current TPS require dose calculation in a clinical implant using higher spatial resolution of radial distance r and polar angle θ than the entered parameter data, i.e., g_L(r) and F(r,θ). Therefore, TPS must interpolate g_L(r) and F(r,θ) values from data tables.

A review of the published data for various brachytherapy sources indicated that different authors used a variety of spatial and angular increments and ranges in their reporting. Therefore, a standardized methodology for interpolation from the published data may be required to determine the dose rate distributions at spatial locations not explicitly included in the published data. The AAPM TG-43U1 [2] report provided guidelines for interpolation from 2D and 1D dosimetry parameters for the case of low energy sources of ¹²⁵I and ¹⁰³Pd. The supplement to 2004 TG-43 report (i.e., TG-43U1S1) [3] included further clarification and modifications of the interpolation techniques in order to assemble these procedures as more accurate and user-friendly.

The TG-43U1 and TG-43U1S1 reports recommended log-linear interpolation for g_L(r) and linear-linear interpolation for F(r,θ). An accuracy of ± 2% was required for establishing r and θ resolution, interpolation techniques and fitting procedures. The TG-43U1S1 indicated that these interpolation techniques may be extended to other brachytherapy sources in general. Polynomial fits are usually included, although tri-exponential fits and other fitting functions recently have been explored with very good agreement for all sources [4–9].

The TG-43 formalism has also been extended for high-energy sources of ⁶⁰Co, ¹³⁷Cs, ¹⁹²Ir and ¹⁶⁹Yb [10]. However, given the contradictory behaviour of g_L(r) and F(r,θ) between low-energy and high-energy brachytherapy sources due to photon interactions, it is quite interesting to determine whether the TG-43U1 and TG-43U1S1 recommendations on interpolation and extrapolation for low-energy sources are applicable to high-energy sources [11, 12]. Therefore, the objectives of this study are: 1) to check what interpolation method allows accurate acquisition of g_L(r) and F(r,θ) from the published data; 2) to determine the minimum number of entries in g_L(r) and F(r,θ) that allow reproduction of dose distributions with sufficient accuracy.

Material and methods

Four high-energy photon-emitting brachytherapy sources were studied in the present work: (1) ⁶⁰Co source from BEBIG (model Co0.A86) [13]; (2) ¹³⁷Cs source from BEBIG (model CSM-3) [14]; (3) ¹⁹²Ir source from BEBIG (model Ir2.A85-2) [15]; and (4) a hypothetical ¹⁶⁹Yb source having the same design as ¹⁹²Ir Flexisource from Isodose Control [16], but with central core composed of ¹⁶⁹Yb. These sources represents the typical high-energy sources in shape and material composition. All four sources had active lengths L = 0.35 cm with the exception of ¹³⁷Cs source that had an equivalent active length (number of seeds times separation between sources) of L = 1.8 cm [17].

For these sources, we used the Monte Carlo (MC) raw data, $\stackrel{.}{D}$(r,θ), in a mesh of 0.5 mm from 0 to 10 cm in θ = 1° steps obtained in previous publications [13–15], and performed equivalent simulations for ¹⁶⁹Yb theoretical source. The g_L(r) and F(r,θ) brachytherapy dosimetry parameters were derived using this dense mesh. Detailed description of the MC study of ⁶⁰Co, ¹³⁷Cs and ¹⁹²Ir sources can be found in respective publications. The study for ¹⁶⁹Yb source has been performed with the same methodology as for the other. A summary of methodology employed is presented below:

1. Geant4 toolkit was used [18].

2. Cross-section libraries based on EPDL97 [19].

3. Radiation spectra was adopted from the National Nuclear Data Center (NNDC) [20].

4. Water- and air-kerma per photon history were scored using linear track-length estimator of energy deposition.

5. Each source was placed at the centre of a spherical water phantom with radius R = 40 cm, except for ⁶⁰Co where the radius used was 50 cm. Kerma estimation in water used spherical voxels that were arranged every 0.05 cm in 1° steps.

6. Source materials considered were assumed from the corresponding publication of each source.

7. Water and air composition and conditions were recommended by the TG-43U1.

8. Photons were generated uniformly and distributed within the active source core.

9. The quantity of simulated photon histories was sufficient enough to assure good statistical uncertainties (see each publication for additional details).

Published g_L(r) and F(r,θ) tables for high-energy sources used a radial mesh for r that typically includes a combination of 0.25, 0.5, 0.75, 1, 1.5, 2-8 (integer steps) and 10 cm. Some authors may add supplementary data points for r < 10 cm [21, 22] or at larger distances such as r = 12 cm or r = 15 cm [13–16]. In case of F(r,θ), the typical spatial resolution for θ is 0°-5° (in 1° steps), 5°-10° (in 2° steps), 10°-30° (in 5° steps), 30°-90° (in 10° steps) with the same possibility of supplementary angles. In some studies of high-energy sources, lower angular resolutions were used such as 10° near the source longitudinal-axis [21, 22]. For the four sources examined, the published g_L(r) and F(r,θ) tables used the typical mesh as previously indicated. The TG-43U1 and TG-43U1S1 interpolation recommendations were examined in this context. Furthermore, linear-linear interpolation of g_L(r) was examined. Results were compared with the values obtained from the MC calculations for the aforementioned sources with the same grid.

Results

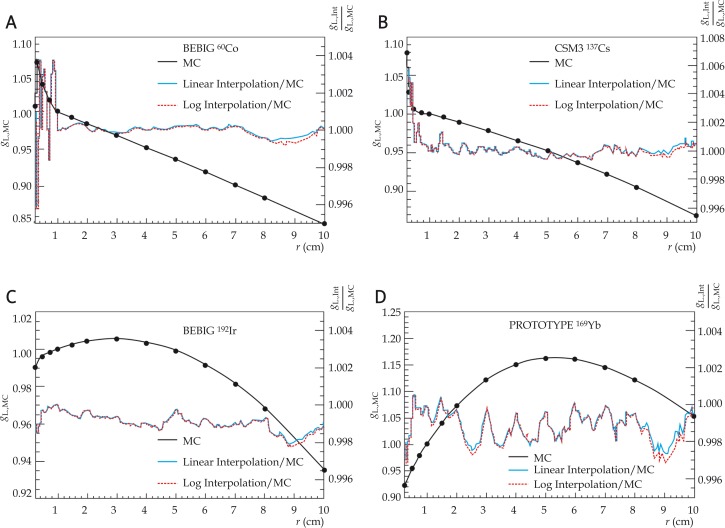
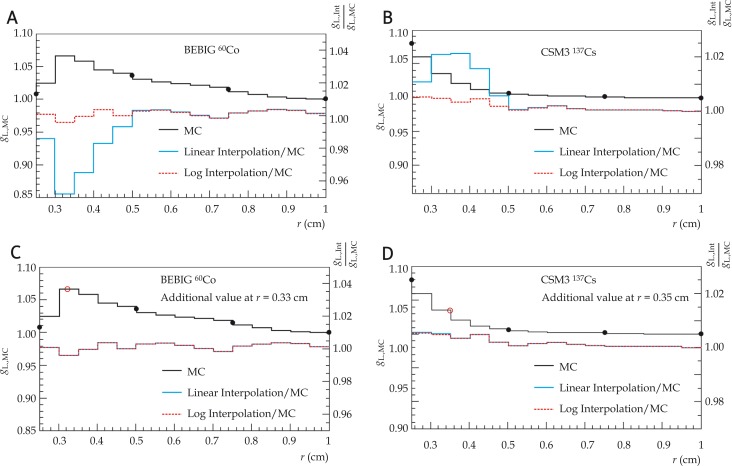
Results for linear-linear interpolation and logarithmic-linear interpolation did not differ significantly for g_L(r) as shown in Fig. 1. For ¹⁹²Ir and ¹⁶²Yb sources, interpolation differences were ≤ 0.5% compared with MC results over the entire radial range 0.25 ≤ r ≤ 10 cm. For ⁶⁰Co and ¹³⁷Cs sources, differences between MC and interpolation results were > 2% for 0.25 < r < 0.5 cm and ≤ 0.5% elsewhere. Dissimilarities between MC and interpolation results reduced to ≤ 0.5% upon addition of g_L(r = 0.33 cm) and g_L(r = 0.35 cm) for ⁶⁰Co and ¹³⁷Cs, respectively, to account for g_L(r) maximum in the case of ⁶⁰Co, and the high g_L(r) gradient in the case of ¹³⁷Cs (Fig. 2). Due to small (< 0.5%) rounding errors in the published data, the g_L,Int.(r)/g_L,MC(r) ratio is not equal to unity at radii corresponding to the tabulated data points. There were no substantial differences between the linear-linear and log-linear interpolations for the four sources examined.

Fig. 1.

Radial dose function gL(r) for the four sources studied (left scale) and ratio of interpolated gL(r) to MC raw data (right scale). Full black lines represent MC results in a mesh of 0.5 mm from 0 to 10 cm. Closed circles represent the same MC results but for the radial mesh typically used in published tables. The mesh points used for interpolation are shown as closed circles

Fig. 2.

Radial dose fuction gL(r) for the two sources studied in the radial range up to 1 cm (left) and with two additional points (right)

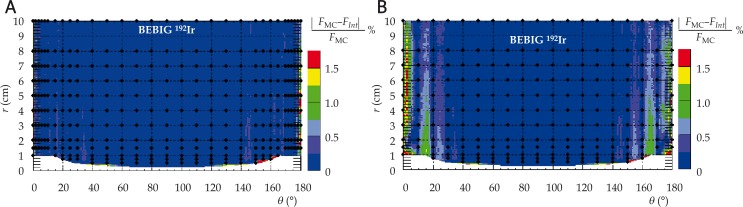
The results for F(r,θ) are shown in Table 1, with graphical representation for ¹⁹²Ir source shown in Fig. 3. For the four sources and four approximations in case of F(r,θ), differences with MC were ≤ 0.5% in the radial range up to 10 cm when using 1° and 2° polar angle steps, with the exception of ¹³⁷Cs where differences were ≤ 1.5% for θ < 15°. With 5° polar angle steps, differences for ⁶⁰Co, ¹³⁷Cs, ¹⁹²Ir, and ¹⁶⁹Yb sources were ≤ 0.5%, ≤ 1.5% for θ < 15°, ≤ 0.5%, and ≤ 2% for θ < 5°, respectively. With 10° polar angle steps, dissimilarities for ⁶⁰Co, ¹³⁷Cs, ¹⁹²Ir, and ¹⁶⁹Yb sources were ≤ 1.5% for θ < 5°, ≤ 2% for θ < 10°, ≤ 1.5% for θ < 25°, ≤ 2% for θ < 10°.

Table 1.

Differences of linear-linear interpolated F(r,θ) values compared to MC results

θ step	60Co	137Cs	192Ir	169Yb
1°-2°	≤ 0.5%	≤ 1.5% (θ < 15°) ≤ 0.5% (θ > 15°)	≤ 0.5%	≤ 0.5%
5°	≤ 0.5%	≤1.5% (θ < 15°) ≤ 0.5% (θ > 15°)	≤ 0.5%	≤ 2 % (θ < 5°) ≤ 0.5% (θ > 5°)
10°	≤ 1.5% (θ < 5°) ≤ 0.5% (θ> 5°)	≤ 2% (θ< 10°) ≤ 0.5% (θ > 10°)	≤ 1.5% (θ < 25°) ≤ 0.5% (θ > 25°)	≤ 2% (θ < 10°) ≤ 0.5% (θ > 10°)

Fig. 3.

Comparison between interpolated (Fint) and MC (FMC) 2D anisotropy function results for the BEBIG 192Ir source for two different angular resolutions: a) 2° increments and b) 10° increments. The mesh points (closed circles) used for interpolation are shown. The region inside the source capsule is shown in white near r = 0 and is not clinically relevant

Discussion

If dosimetric information is required (i.e., desire to evaluate organ-at-risk dose) for r > 10 cm, physicists should refer to the original MC publications. However, radiation scatter conditions and the water equivalence of tissues may need to be considered for accurate dose estimation [23].

In contrast with dosimetry parameter interpolation for low-energy brachytherapy sources, extrapolation to r ≤ r_rmin for high-energy sources is complicated by the lack of electronic equilibrium and the assumption that collisional kerma is equal to absorbed dose over the entire radial range. Significant issues that are generally not included in most publications on high-energy brachytherapy source dosimetry are the presence of electronic disequilibrium near the source and the contributions from emitted electrons [24]. Consequently, no extrapolation method can predict the behaviour of data without obtaining the physical basis in order to understanding the effect.

Conclusions

In contrast to the established standards (TG-43U1S1) for low-energy sources which recommends log-linear interpolation for g_L(r), linear-linear or log-linear interpolation methods, produced nearly the same results for high-energy sources. For g_L(r) and for sources analysed in this study, the typical mesh used in the literature was adequate for linear-linear or log-linear interpolations of ¹⁹²Ir and ¹⁶⁹Yb sources. For ⁶⁰Co and ¹³⁷Cs, the mesh was also adequate for g_L(r), however an additional g_L(r) point for 0.25 < r < 0.5 cm was included to keep minimize interpolation errors to < 0.5%. For F(r,θ) close to longitudinal axis source (i.e., θ < 15°), 1°-2° polar angle steps were adequate for all 4 sources examined.