Abstract
Purpose
Spatio-temporal encoding (SPEN) can deliver single-scan MR images without folding complications and with increased robustness to chemical shift and susceptibility artifacts. Yet it does so at the expense of relatively high Specific Absorption Rates (SAR), owing to its reliance on frequency-swept pulses. This study describes SPEN implementations aimed at full 3D multi-slice imaging, possessing reduced SAR thanks to an implementation based on new 2D RF pulses.
Methods
Fully refocused spin- and stimulated-echo SPEN sequences incorporating 2D spatial/spatial swept RF pulses were implemented at 3T, and compared to EPI. The use of effective 90° slice-selective excitation pulses enabled the scanning of 3D volumes with a low SAR.
Results
Experiments validating the theoretical expectations were carried out on phantoms and on human volunteers, including zooming and diffusion measurements. The chosen sequences showed much smaller SARs than EPI, while delivering similar sensitivities when targeting human brain and fewer distortions when targeting human breast.
Conclusion
2D RF pulses can exploit SPEN’s advantages while fulfilling the SAR and multi-slice coverage demands required for clinical imaging.
Keywords: MRI, SPEN, SAR, multidimensional RF pulses, single-scan MRI
Introduction
Spatiotemporal encoding (SPEN) presents an alternative approach to k-space encoding, enabling the acquisition of multi-dimensional MR spectra, images, or combinations of thereof, in a single scan (1–5). SPEN targets spins throughout the region of interest (ROI) progressively, sequentially exciting or inverting them as a linear function of time. This causes a quadratic dephasing of the spin-packets throughout the object of interest (6–8); proper pulses and suitable gradients subsequently refocus spin-packets positioned throughout the targeted ROI at different instants throughout the acquisition, leading to an emitted signal whose magnitude is proportional to the spin magnetization at uniformly spaced locations. This rasterized acquisition provides an image while obviating the need for a Fourier Transform (FT), enabling the use of stronger gradients than k-space counterparts like Echo Planar Imaging (EPI). Such stronger gradients are well suited for monitoring the low-bandwidth dimension of single-scan MRI scans –particularly at high fields or in challenging areas of the body (9–11). Thus, these experiments are usually carried out in a so-called “hybrid” mode where the SPEN is used to image what is usually EPI’s phase-encoded dimension, while the orthogonal, read-out (RO) direction is scanned in a usual k-space fashion. Additional image faithfulness may arise by executing hybrid SPEN under “fully refocused” conditions, whereby contributions to the final image arise devoid from T2* effects (11,12).
Despite these positive features, SPEN’s initial implementations faced substantial challenges. One of these concerned the sensitivity losses that as a non-FT method, SPEN suffered due to its lack of multiplexing. This effect was overcome with the development of super-resolution (SR) and other processing algorithms (3,5,11,13–15), which helped reinstate an EPI-like sensitivity. Another complication arose from SPEN’s initial use of chirped 90° excitation pulses for its encoding, an approach that limited experiments to single-slice 2D acquisitions or long 3D imaging times based on phase encoding the third dimension. Genuine multi-slice sequences where subsequently introduced where the initial chirp excitation was replaced by swept inversion pulses (16); by relying on dual flips of the non-imaged spins at each repetition, this provided SPEN with slice-selection (SS) capabilities. Still, this approach’s reliance on two 180° pulses –one of which is applied while in the presence of a dispersing gradient– leads to relatively high Specific Absorption Rate (SAR) values, exceeding by ca. 10x its EPI counterparts. This in turn limits multi-slice SPEN investigations in humans to a relatively low number of slices (usually ≤16), or to relatively long TRs. A SPEN-customized 2D RF pulse, imparting a slice-selective 90° nutation along one spatial dimension while imposing SPEN’s 1D quadratic spatial phase along an orthogonal axis, was proposed to deal with this limitation (17). Although successfully demonstrated in 3D multi-slice phantom images, this k-based pulse design lacked the robustness needed for in vivo acquisitions. A different approach for implementing 2D RF pulses based on discretized SPEN concepts and displaying an enhanced robustness vis-à-vis inhomogeneities, has been recently devised (18). This work explores the use of such discrete, SPEN-based 2D RF pulses, in the execution of in vivo multi-slice 2D SPEN MRI scans. Two slab-based pulse sequences are thus proposed based on these pulses, resulting in multi-slice images endowed with low SAR despite the use of conventional TRs. The enhanced robustness of these sequences to B0 inhomogeneity and to chemical shift effects are here demonstrated on phantom and human scans, the latter in combination with diffusion-weighted imaging.
Methods
RF pulse design
While the properties of SPEN-based 2D RF pulses were described in (18), we briefly depict their basis and modifications that were here taken. SPEN-based 2D pulses are, like their k-based counterparts (19–21), composed of discrete RF sub-pulses played out while in the presence of a bipolar oscillating gradient. In the present study these were chosen as sinc RF pulses, which collectively excited a rectangular slice or slab. In between these oscillating gradients, an orthogonal gradient was blipped in order to simulate the constant gradient effects present during SPEN’s 90° excitation; furthermore, to each RF sub-pulse, a suitable, quadratically-incremented phase was added, which mimicked the corresponding effects that would be imparted by a chirped pulse. In order to aim for the lowest possible SAR this blipped gradient was relatively weak; this placed the excitation sidebands that these discretized 2D pulses will originate (18), outside the targeted region of interest (ROI). This moving-out of the excitation sidelobes also requires setting a sufficiently large number of sub-pulses; in the experiments here presented these were ≥80, applied on both positive and negative lobes of the oscillating gradient defining the slice-selective excitation. Although this allowed us to shorten the overall excitation time, the fact that the rise-up and fall-down times within the oscillating gradient train amounted to up to 70% of the total pulse time, placed undue demands on the overall excitation length. This was handled by shaping the sinc’s timing within the oscillating gradients as per the VERSE approach (22), which allows one to pulse within the ramps of the gradients. This enabled us to reduce the overall duration of the excitation –which was set in turn equal to the acquisition time to fulfill the demands of fully-refocused operation (16)– thereby attenuating T2-related losses. It also helped to yield thinner excitation slabs, which were otherwise limited by the maximum achievable gradient amplitude and longest affordable period of the bipolar oscillating gradient blocks. Even with all these provisions, the strength of these slice-selective gradient amplitudes could not be increased to the point of allowing our clinical scanner to excite sufficiently narrow individual slices. The manner in which this was dealt with, is further detailed below.
Sequence variants
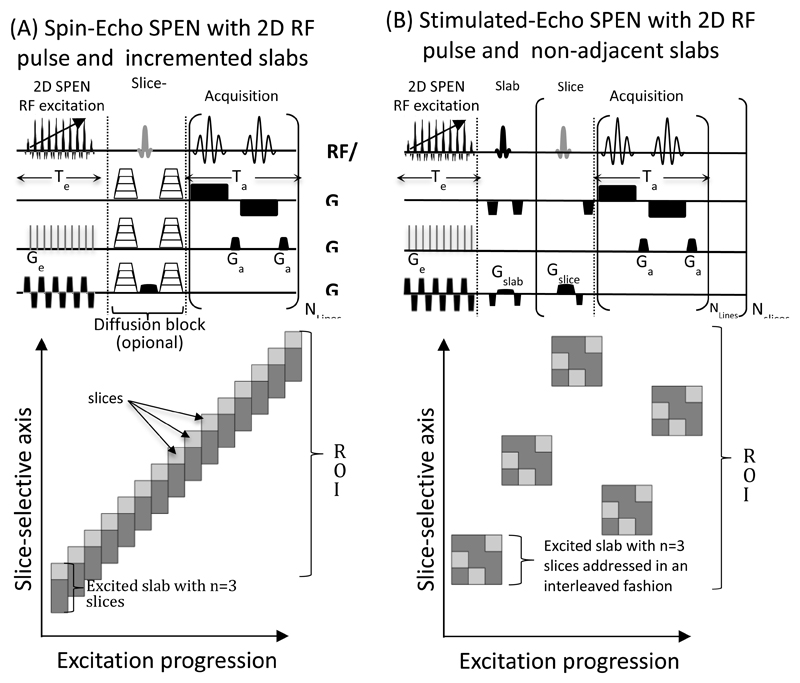
Numerous versions of fully-refocused SPEN have been described in the literature (2,16,23), involving either excitation- or refocusing-based encodings. Out of the five variants introduced in Ref. (11) we focused on two that involved solely swept excitations; this was done for the sake of minimizing SAR, as all the other variants involve higher-powered inversion pulses. These two sequences are illustrated in Figure 1; in them, the sequences’ original 90° swept pulses are replaced by swept variants based on the 2D spatially-selective pulses. These sequences include a fully-refocused spin-echo (SE) hybrid experiment (Fig. 1A), and a stimulated-echo (STE) SPEN version (Fig. 1B). Due to the gradient limitations mentioned above, none of the 2D RF pulses in these sequences aimed at exciting a single slice; rather they were assigned the excitation of a “slab”, that would eventually be composed of several (≈2-5) slices. In the simple SE variant (Fig. 1A) this restriction was dealt with by locating the center of the first excited slab underneath the first targeted ROI, and tuning the 180° slice-selection echoing pulse so as to refocus only the latter. Then, as indicated in the cartoon shown underneath the sequence, ascending the encoded slab together with the refocusing pulse by an offset equating to a slice’s width, allowed us to acquire solely images of the targeted ROIs in a multi-slice fashion –with no saturation or contamination effects. We henceforth refer to as “slab factor” to the number of slices that each slab contained in these experiments. In the STE variant a different approach was adopted: here the 2D pulse was designed so as to encode a slab containing multiple slices of interest; following a suitable storage, these slices were then read out in an individual, consecutive fashion by bringing them out of storage one-by-one. Operating with these combined slab / slice manipulations, allowed us to reduce the required slice-selective gradient amplitudes without lengthening the associated encoding pulses. These sequences, including the pulse-generating algorithms, are available upon request
Figure 1.
Pulse sequences utilized in this study, incorporating the encoding of single slabs (in dark grey) by 2D spatial/spatial SPEN pulses, and subsequent single-shot acquisitions on single slices (lighter grey, illustrated for a case where n=3 slices fit per slab). (A) Spin-echo version, incorporating (optional) stepped gradients for diffusion-encoding. (B) Stimulated-echo version. This slab/slice operation was adopted in (A) owing to the scanner’s inability to excite sufficiently narrow slices; the targeted slice is thus selected by the 180˚ spin-echoing pulse. Notice that the incremented positions arrangements allows one to operate without saturation and/or interslab excitation delays; for these cases, the number of slabs excited equals the number of slices observed. The interleaved spatial disposition strategy adopted in (B) is meant to minimize “leakage” effects between consecutive excitations; in this case n slices are observed per excited slab.
Experimental Details
Experiments were performed using a 3T Siemens whole-body scanner (Siemens Healthcare, Erlangen, Germany). Phantom experiments were run on an ACR cylindrical phantom (20 cm in diameter). Breast imaging scans were run on two healthy volunteers (26 and 29 years old) using a 4-channel breast coil. This protocol included the acquisition of T2 weighted images, of multislice SPEN scans and of EPI scans –the latter two with similar ROIs, number of slices and resolution. One of the volunteers was scanned by Diffusion Weighted Imaging (DWI) (24) using a scanner-supplied twice-refocused SE-EPI sequence and the SE-SPEN sequence illustrated in Figure 1A; nominal b-values of 50, 150, 300 and 400 were applied in these experiments along three orthogonal directions. A healthy volunteer (female, 26 years old) was also subject to brain imaging using a head-only 12-channel transceive coil, in a protocol that included T2 weighted anatomical images, multi-slice SPEN and EPI. These studies were approved by the Institutional Review Board of the Wolfson Medical Center (Holon, Israel), and signed informed consents were obtained from all of the participants.
Data processing
SPEN images were reconstructed using an in-house super-resolution algorithm (11) written on Matlab® (Mathworks, Natick, MA); all other images were processed on the actual scanner. Signal-to-Noise ratios (SNRs) for the various images were calculated by taking the ratio of medians for foreground and background regions. These regions were obtained by thresholding the images with suitable values, chosen to produce a clear separation. Brain images were repetitively scanned, and SNR was calculated as the median, over a thresholded foreground map, of voxel-wise SNR values defined as the ratio between the mean and the standard deviation of the voxel’s signal over time. Apparent Diffusion Coefficient (ADC) were also calculated voxel-wise by fitting two parameters (signal magnitude at b0 and ADC), to data measured for a b0 = 50 s/mm2 image and for three b = 400 s/mm2 images involving orthogonal diffusion-weighting gradients. This least-squares fit was done using QR decomposition with column pivoting (25). The low imaging gradient amplitudes used in these measurements led to constant b-values across the images, rendering the consideration of imaging/diffusion gradient cross-terms (10) unnecessary.
Results
Mutli-slice SPEN images
Both sequences in Figure 1 were successfully applied to breast imaging. The in-plane resolution was set to 2x2 mm2, and the slice thickness to 2.5 mm. For the spin-echo variant, 21 slices/slabs, with anywhere between n = 2-6 slices fitted in each slab, were acquired in 3.3 sec. For the stimulated echo sequence –which can provide a higher number of slices per TR– 30, 36 and 35 slices were acquired using either 10/15, 9 or 7 slabs, respectively. This means that 2/3, 4 or 5 slices were fitted in each slab for these experiments, all of which were conducted in 3.4 sec. Figure 2 presents images acquired using these sequences, and compares them with SE-EPI results and with multi-scan T2-weighted images used as references. The SE- and STE-SPEN images shown in Fig. 2A were collected with two slices per slab. SNR appeared constant across the various slices; notice as well the weaker distortions evidenced by SPEN close to the air/tissue interfaces (e.g., at the nipples) when compared to SE-EPI counterparts. The SNR of the SPEN images was also good –even if for some hitherto unclear reason, the SE-SPEN images showed a smaller SNR than either its SE-EPI or STE-EPI counterparts (Fig. 2A). Upon increasing the number of slices per slab, artifacts in the form of stripes became noticeable in the SE-SPEN images (Fig. 2B), probably as a result of ripples associated to an increased reliance on the edge of the sinc-excited profiles. These were absent in the STE-SPEN images, yet decreasing intensities as a result of longitudinal relaxation losses (augmented perhaps by diffusion effects) were evidenced as the slices per slab increased (Fig. 2B). Most important, the objective of reducing SPEN’s SAR was amply achieved by these sequences: in comparison to a SAR value of 32% reported by the scanner for SE-EPI, all SPEN variants assayed achieved a much reduced SAR value of 2% (while the SAR values for the various SPEN variants surely were not identical they were all reported identical by the system, which conveys them in full percent units of the maximum allowable deposited power per kg).
Figure 2.
Multi-slice breast scans collected under various conditions. (A) Rows of T2, SE-EPI, SE-SPEN (with a slab factor n = 2) and STE-SPEN (n = 2 slices per slab) images. Columns in these figures show representative slices, with every other scanned slice being shown. (B) Single-slice T2 and EPI images (top), compared against SE-SPEN and STE-SPEN images collected with different slab thicknesses (bottom). For SE-SPEN a signal reduction is visible as the slab factor increases, along with increased stripe-shaped distortions. For the STE-SPEN a SNR reduction – but no artifact– is visible as the slices per slab increase. For all single-shot experiments: resolution = 2x2x2.5 mm3 with no gap; in-plane ROI = 24x12.6cm2; see text for the number of slices.
Diffusion-weighted SPEN tests
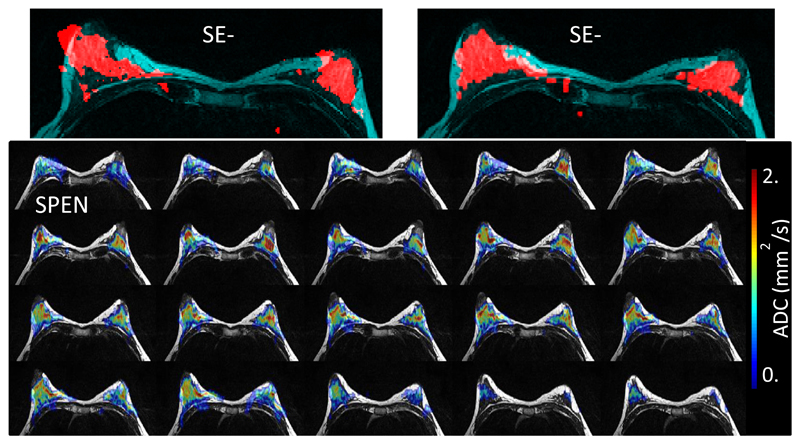
SE-SPEN was applied to mapping ADC coefficients using the pulsed field gradient approach illustrated in Fig. 1A. The top row of Figure 3 compares thresholded breast SE-EPI and SE-SPEN magnitude images arising from these DWI measurements, superimposed on T2–weighted anatomical images. Notice SPEN’s reduced distortions in regions close to fibroglandular (water)/fat and tissue/air interfaces vis-à-vis SE-EPI, thanks to the former’s increased robustness to B0 inhomogeneity effects. Notice as well SPEN’s much lower SAR: ~5% vs EPI’s 38% for similar TRs. The bottom panels in Figure 3 show multislice breast ADC maps obtained using SPEN from the same volunteer, also overlaid on anatomical images. These maps evidence minimal spatial distortions throughout the full breast, and yield mean values that quantitatively match those obtained from analogous EPI-based DWI scans.
Figure 3.
Top row: SE-EPI and SE-SPEN thresholded magnitude images collected using fat suppression (red), overlaid on T2-weighted multiscan images acting as reference (cyan). Brighter signals in the latter denote fatty tissue. Bottom row: ADC maps obtained using the SE-SPEN sequence in Fig. 1A, overlaid on bilateral T2-weighted anatomical images. Resolution = 2x2x2.5 mm3, ROI = 24x12.6cm2; 40 slices (n = 2); no gap.
Zoomed-in and interleaved SPEN acquisitions
Additional desirable features that have been demonstrated for SPEN include an ability to “zoom-in” along the low-bandwidth dimension without suffering from folding artifacts, and an ability to increase an image’s spatial resolution by utilizing interleaved acquisitions liable to joint processing without requiring ancillary navigator scans (11,26). These abilities were re-tested in sequences incorporating the new 2D RF pulsing modes introduced in Figure 1. Figure 4 evidences SE-SPEN’s ability to zoom-in without folding artifacts, using a simple phantom as test example. Different kinds of zoomed-in images were obtained in 25 sec TR with four interleaved segments, resulting in all cases in a sub-mm resolution along all spatial axes. The sequence’s ability to deliver these benefits in vivo is further illustrated in Figure 5, with images acquired on a volunteer’s occipital brain region. Zoomed-in two-scan interleaved SE-SPEN data collected with a slab factor n = 6, provided images with an in-plane resolution of 1.1x1.1 mm2 and a slice thickness of 2 mm; 26 slices covering an ROI of 150x103 mm2 were thus completed in 6.6 sec (i.e., with a pseudo-temporal resolution of 3.3 sec) with a SAR <5%. Figure 5 compares these data with corresponding multi-slice images arising from a standard 3 mm isotropic EPI acquisition with a similar ROI coverage (the number of slices in the EPI are thicker slices and thus their overall number is lower). The SPEN images provide a higher anatomical detail, while retaining their robustness to tissue/air interface distortions. The sequence allows repeated measurements, and the average SNR calculated from these measurements was ~8.1.
Figure 4.
Top: T2-weighted reference multi-scan image (single-slice illustrated) collected on a manufacturer-supplied ACR phantom. Bottom: Multi-slice mages of the zoomed regions indicated by the blue and red rectangles (identical except for a 90˚ rotation), collected using the SE-SPEN sequence with four interleaves. Resolution = 0.67x0.7x0.8 mm3, ROI = 21.6x11.4 cm2, 20 slices (n = 2, no gap), 25 sec total TR. SAR for zoom #1, #2: <5%.
Figure 5.
Demonstrating SPEN’s ability to zoom-in into a limited ROI while keeping low SAR thanks to the use of 2D RF pulses. Notice that while the entire acquisition for the two-scan-interleaved 3D image took 6.6 seconds, a functional scheme relying on reconstruction from the interleaved segments could provide an image every 3.3 seconds.
Discussion
This study introduced a new approach to multi-slice 2D SPEN acquisitions designed to deal with one of these experiment’s main obstacles: excessive SAR when assayed over dense, multi-sliced clinical acquisitions. Full-volume excitation limitations associated with the use of broad-band 90° chirped pulses had so far been dealt in such cases, by the use of 180° inversion/refocusing pulses. This alternative, which requires the use of a slice-excitation and two subsequent inversions, works very well in preclinical settings but has a heavy SAR tax when implemented on humans at short TRs. In an effort to alleviate this we had tried in the past to implement 90°-like encodings based on spatial/spatial 2D RF pulses designed on the basis of k-space algorithms; although acceptable in phantoms, we found these pulses insufficiently robust when attempting actual in vivo applications in either preclinical or clinical settings (17). The recent development of 2D RF pulses that also operate on the basis of spatio-temporal principles (18,27) prompted us to revisit this problem; this study discussed some of the resulting sequences for ultrafast, fully-refocused multi-slice SPEN imaging. These sequences were found versatile and capable of retaining previous SPEN-related features including robustness to inhomogeneities, zooming-in abilities and interleaved operation without requiring ancillary reference scans; at the same time they did indeed deliver very low (2-5%) SAR values –even lower than those of standard EPI– while achieving good multi-slice volume coverage. This could make these sequences useful in a variety of diffusion, functional and other kinds of dynamic imaging needs.
Despite these capabilities, a number of improvements remain to be made on this excitation mode. A main obstacle arose from the limited gradient slew rates and values found in our 3T machine. As 2D SPEN pulses operate on the basis of an oscillating gradient train over whose constant-amplitude periods the slice selection is to be defined, these two factors become crucial in determining the minimal slice thickness that can be encoded. They also define the total excitation time –which in fully-refocused SPEN is also related to the overall acquisition time, and hence to image SNR. For the hardware used in this study, over 30% of the overall encoding time was dedicated to ramping up and down the slice-selection gradient, meaning that only a fraction of the gradient train was available for defining the slices’ thicknesses. Slabs in the order of a few millimeters were thus the thinnest that could be achieved; this, even when relying on a VERSE-like approach whereby pulses also played out over the course of the ramps, and even though utilizing a carefully calibrated gradient train that enabled pulsing on both the positive and negative lobes of the gradient’s oscillation. As a result of this, trade-offs had to be made for the sake of decreasing the slice width; in this study, these were done by slab-segmentation approaches. In the spin-echo version of the experiments, a “slab factor” was adopted whereby an integer number of slices could be fit into the encoded slab. By progressing the encoded slabs monotonically from one end of the ROI to another in slice-wide steps, it was possible to narrow the effective responses. Alternatively, a stimulated echo approach whereby a full slab containing multiple slices was encoded but its constituting slices were recalled one-by-one, delivered a similar resolution enhancement. Unfortunately none of these approaches that “look inside the slab”, were free from penalties: in the spin-echo case these manifested themselves as stripped artifacts appearing at high slab factors; the stimulated-echo images were free from artifacts but showed a decreased SNR as the number of constituting slices per slab increased. Further improvement of these issues, including among other optimization of the 2D pulse performance and parallel transmission approaches, are under investigation.
Acknowledgments
We are grateful to Dr. Rita Schmidt for assistance during the initial stages of this work, and to Dr. Sagit Shushan (Wolfson Medical Center) and the Weizmann MRI team (Edna Furman-Haran, Fanny Attar and Nachum Stern) for assistance in the human scans. Financial support from the Israel Science Foundation grant 795/13, the EU through ERC-2014-PoC grant # 633888, the Kimmel Institute for Magnetic Resonance and the generosity of the Perlman Family Foundation, are also acknowledged.
Abbreviations
- ADC
Apparent Diffusion Coefficients
- DWI
Diffusion-Weighted Imaging
- EPI
Echo-Planar Imaging
- FID
Free Induction Decay
- FT
Fourier Transform
- MRI
Magnetic Resonance Imaging
- PE
Phase-Encode
- SAR
Specific Absorption Rate
- RF
Radio frequency
- RO
Read-Out
- ROI
Region of Interest
- SE
Spin-Echo
- STE
Stimulated Echo
- SNR
Signal-to-Noise Ratio
- SPEN
Spatiotemporal Encoding
- SR
Super-Resolution
- SS
Slice Selection
- TE
Echo Time
- TR
Repetition Time
References
- 1.Shrot Y, Frydman L. Spatially encoded NMR and the acquisition of 2D magnetic resonance images within a single scan. Journal of Magnetic Resonance. 2005;172(2):179–190. doi: 10.1016/j.jmr.2004.09.024. [DOI] [PubMed] [Google Scholar]
- 2.Chamberlain R, Park JY, Corum C, Yacoub E, Ugurbil K, Jack CR, Garwood M. RASER: a new ultrafast magnetic resonance imaging method. Magnetic Resonance in Medicine. 2007;58(4):794–799. doi: 10.1002/mrm.21396. [DOI] [PubMed] [Google Scholar]
- 3.Ben-Eliezer N, Irani M, Frydman L. Super-resolved spatially encoded single-scan 2D MRI. Magnetic Resonance in Medicine. 2010;63(6):1594–1600. doi: 10.1002/mrm.22377. [DOI] [PubMed] [Google Scholar]
- 4.Tal A, Frydman L. Single-scan multidimensional magnetic resonance. Progress in nuclear magnetic resonance spectroscopy. 2010;57(3):241–292. doi: 10.1016/j.pnmrs.2010.04.001. [DOI] [PubMed] [Google Scholar]
- 5.Chen Y, Li J, Qu X, Chen L, Cai C, Cai S, Zhong J, Chen Z. Partial Fourier transform reconstruction for single-shot MRI with linear frequency-swept excitation. Magnetic Resonance in Medicine. 2013;69(5):1326–1336. doi: 10.1002/mrm.24366. [DOI] [PubMed] [Google Scholar]
- 6.Kunz D. Use of frequency-modulated radiofrequency pulses in MR imaging experiments. Magnetic resonance in medicine. 1986;3(3):377–384. doi: 10.1002/mrm.1910030303. [DOI] [PubMed] [Google Scholar]
- 7.Pipe JG. Spatial encoding and reconstruction in MRI with quadratic phase profiles. Magnetic resonance in medicine. 1995;33(1):24–33. doi: 10.1002/mrm.1910330105. [DOI] [PubMed] [Google Scholar]
- 8.Pipe JG. Analysis of localized quadratic encoding and reconstruction. Magnetic resonance in medicine. 1996;36(1):137–146. doi: 10.1002/mrm.1910360122. [DOI] [PubMed] [Google Scholar]
- 9.Goerke U, Garwood M, Ugurbil K. Functional magnetic resonance imaging using RASER. Neuroimage. 2011;54(1):350–360. doi: 10.1016/j.neuroimage.2010.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Solomon E, Shemesh N, Frydman L. Diffusion weighted MRI by spatiotemporal encoding: analytical description and in vivo validations. Journal of Magnetic Resonance. 2013;232:76–86. doi: 10.1016/j.jmr.2013.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Seginer A, Schmidt R, Leftin A, Solomon E, Frydman L. Referenceless reconstruction of spatiotemporally encoded imaging data: Principles and applications to real-time MRI. Magnetic Resonance in Medicine. 2014;72(6):1687–1695. doi: 10.1002/mrm.25084. [DOI] [PubMed] [Google Scholar]
- 12.Ben-Eliezer N, Solomon E, Harel E, Nevo N, Frydman L. Fully refocused multi-shot spatiotemporally encoded MRI: robust imaging in the presence of metallic implants. Magnetic Resonance Materials in Physics, Biology and Medicine. 2012;25(6):433–442. doi: 10.1007/s10334-012-0318-7. [DOI] [PubMed] [Google Scholar]
- 13.Chen L, Li J, Zhang M, Cai S, Zhang T, Cai C, Chen Z. Super-resolved enhancing and edge deghosting (SEED) for spatiotemporally encoded single-shot MRI. Medical image analysis. 2015;23(1):1–14. doi: 10.1016/j.media.2015.03.004. [DOI] [PubMed] [Google Scholar]
- 14.Chen L, Bao L, Li J, Cai S, Cai C, Chen Z. An aliasing artifacts reducing approach with random undersampling for spatiotemporally encoded single-shot MRI. Journal of Magnetic Resonance. 2013;237:115–124. doi: 10.1016/j.jmr.2013.10.005. [DOI] [PubMed] [Google Scholar]
- 15.Cai C, Dong J, Cai S, Li J, Chen Y, Bao L, Chen Z. An efficient de-convolution reconstruction method for spatiotemporal-encoding single-scan 2D MRI. Journal of Magnetic Resonance. 2013;228:136–147. doi: 10.1016/j.jmr.2012.12.020. [DOI] [PubMed] [Google Scholar]
- 16.Schmidt R, Frydman L. New spatiotemporal approaches for fully refocused, multislice ultrafast 2D MRI. Magnetic Resonance in Medicine. 2014;71(2):711–722. doi: 10.1002/mrm.24714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ben-Eliezer N, Frydman L. Spatiotemporal encoding as a robust basis for fast three-dimensional in vivo MRI. NMR in Biomedicine. 2011;24(10):1191–1201. doi: 10.1002/nbm.1673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dumez J-N, Frydman L. Multidimensional excitation pulses based on spatiotemporal encoding concepts. Journal of Magnetic Resonance. 2013;226:22–34. doi: 10.1016/j.jmr.2012.10.010. [DOI] [PubMed] [Google Scholar]
- 19.Meyer CH, Pauly JM, Macovski A, Nishimura DG. Simultaneous spatial and spectral selective excitation. Magnetic Resonance in Medicine. 1990;15(2):287–304. doi: 10.1002/mrm.1910150211. [DOI] [PubMed] [Google Scholar]
- 20.Conolly S, Pauly J, Nishimura D, Macovski A. Two-dimensional selective adiabatic pulses. Magnetic resonance in medicine. 1992;24(2):302–313. doi: 10.1002/mrm.1910240211. [DOI] [PubMed] [Google Scholar]
- 21.Pauly J, Nishimura D, Macovski A. A k-space analysis of small-tip-angle excitation. Journal of Magnetic Resonance. 1989;81(1):43–56. doi: 10.1016/j.jmr.2011.09.023. [DOI] [PubMed] [Google Scholar]
- 22.Hargreaves BA, Cunningham CH, Nishimura DG, Conolly SM. Variable-rate selective excitation for rapid MRI sequences. Magnetic resonance in medicine. 2004;52(3):590–597. doi: 10.1002/mrm.20168. [DOI] [PubMed] [Google Scholar]
- 23.Ben-Eliezer N, Shrot Y, Frydman L. High-definition, single-scan 2D MRI in inhomogeneous fields using spatial encoding methods. Magnetic resonance imaging. 2010;28(1):77–86. doi: 10.1016/j.mri.2009.05.026. [DOI] [PubMed] [Google Scholar]
- 24.Bammer R. Basic principles of diffusion-weighted imaging. European journal of radiology. 2003;45(3):169–184. doi: 10.1016/s0720-048x(02)00303-0. [DOI] [PubMed] [Google Scholar]
- 25.Gu M, Eisenstat SC. Efficient algorithms for computing a strong rank-revealing QR factorization. SIAM Journal on Scientific Computing. 1996;17(4):848–869. [Google Scholar]
- 26.Solomon E, Avni R, Hadas R, Raz T, Garbow JR, Bendel P, Frydman L, Neeman M. Major mouse placental compartments revealed by diffusion-weighted MRI, contrast-enhanced MRI, and fluorescence imaging. Proceedings of the National Academy of Sciences. 2014;111(28):10353–10358. doi: 10.1073/pnas.1401695111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Snyder AL, Corum CA, Moeller S, Powell NJ, Garwood M. MRI by steering resonance through space. Magnetic Resonance in Medicine. 2014;72(1):49–58. doi: 10.1002/mrm.24888. [DOI] [PMC free article] [PubMed] [Google Scholar]