A Brief Review of Computational Gene Prediction Methods

Abstract

With the development of genome sequencing for many organisms, more and more raw sequences need to be annotated. Gene prediction by computational methods for finding the location of protein coding regions is one of the essential issues in bioinformatics. Two classes of methods are generally adopted: similarity based searches and ab initio prediction. Here, we review the development of gene prediction methods, summarize the measures for evaluating predictor quality, highlight open problems in this area, and discuss future research directions.

Introduction

Since the beginning of the Human Genome Program (HGP) in 1990, databases of human and model organism DNA sequences have been increasing quickly. Computational gene prediction is becoming more and more essential for the automatic analysis and annotation of large uncharacterized genomic sequences. In the past two decades, many gene prediction programs have been developed. Most of them are referenced at the website maintained by Wentian Li (http://www.nslij-genetics.org/gene/).

Gene discovery in prokaryotic genomes is less difficult, due to the higher gene density typical of prokaryotes and the absence of introns in their protein coding regions. DNA sequences that encode proteins are transcribed into mRNA, and the mRNA is usually translated into proteins without significant modification. The longest ORFs (open reading frames) running from the first available start codon on the mRNA to the next stop codon in the same reading frame generally provide a good, but not assured prediction of the protein coding regions. Several methods have been devised that use different types of Markov models in order to capture the compositional differences among coding regions, “shadow” coding regions (coding on the opposite DNA strand), and noncoding DNA. Such methods, including ECOPARSE, the widely used GENMARK, and Glimmer program, appear to be able to identify most protein coding genes with good performance (1).

In eukaryotic organisms, it is a quite different problem from that encountered in prokaryotes. Transcription of protein coding regions initiated at specific promoter sequences is followed by removal of noncoding sequences (introns) from pre-mRNA by a splicing mechanism, leaving the protein-encoding exons. Once the introns have been removed and certain other modifications to the mature RNA have been made, the resulting mature mRNA can be translated in the 5ʹ to 3ʹ direction, usually from the first start codon to the first stop codon. As a result of the presence of intron sequences in the genomic DNA sequences of eukaryotes, the ORF corresponding to an encoded gene will be interrupted by the presence of introns that usually generate stop codons (2). This review mainly focuses on the more complex problem of gene prediction in eukaryotic sequences.

Gene Prediction Methods

There are two basic problems in gene prediction: prediction of protein coding regions and prediction of the functional sites of genes. A large number of researches working on this subject have accumulated, which can be classified into four generations in summary. The first generation of programs was designed to identify approximate locations of coding regions in genomic DNA. The most widely known programs were probably TestCode (3) and GRAIL (4). But they could not accurately predict precise exon locations. The second generation, such as SORFIND (5) and Xpound (6), combined splice signal and coding region identification to predict potential exons, but did not attempt to assemble predicted exons into complete genes. The next generation of programs attempted the more difficult task of predicting complete gene structures. A variety of programs have been developed, including GeneID (7), GeneParser 8., 9., GenLang (10), and FGENEH (11). However, the performance of those programs remained rather poor. Moreover, those programs were all based on the assumption that the input sequence contains exactly one complete gene, which is not often the case. To solve this problem and improve accuracy and applicability further, GENSCAN (12) and AUGUSTUS (13) were developed, which could be classified into the fourth generation.

There are mainly two classes of methods for computational gene prediction. One is based on sequence similarity searches, while the other is gene structure and signal-based searches, which is also referred to as ab initio gene finding.

Sequence similarity searches

Sequence similarity search is a conceptually simple approach that is based on finding similarity in gene sequences between ESTs (expressed sequence tags), proteins, or other genomes to the input genome. This approach is based on the assumption that functional regions (exons) are more conserved evolutionarily than nonfunctional regions (intergenic or intronic regions). Once there is similarity between a certain genomic region and an EST, DNA, or protein, the similarity information can be used to infer gene structure or function of that region. EST-based sequence similarity usually has drawbacks in that ESTs only correspond to small portions of the gene sequence, which means that it is often difficult to predict the complete gene structure of a given region.

Local alignment and global alignment are two methods based on similarity searches. The most common local alignment tool is the BLAST family of programs, which detects sequence similarity to known genes, proteins, or ESTs. Two more types of software, PROCRUSTES (14) and GeneWise (15), use global alignment of a homologous protein to translated ORFs in a genomic sequence for gene prediction. A new heuristic method based on pairwise genome comparison has been implemented in the software called CSTfinder (16). The biggest limitation to this type of approaches is that only about half of the genes being discovered have significant homology to genes in the databases.

Ab initio gene prediction methods

The second class of methods for the computational identification of genes is to use gene structure as a template to detect genes, which is also called ab initio prediction. Ab initio gene predictions rely on two types of sequence information: signal sensors and content sensors. Signal sensors refer to short sequence motifs, such as splice sites, branch points, polypyrimidine tracts, start codons and stop codons. Exon detection must rely on the content sensors, which refer to the patterns of codon usage that are unique to a species, and allow coding sequences to be distinguished from the surrounding non-coding sequences by statistical detection algorithms.

Many algorithms are applied for modeling gene structure, such as Dynamic Programming, linear discriminant analysis, Linguist methods, Hidden Markov Model and Neural Network. Based on these models, a great number of ab initio gene prediction programs have been developed. Some of the frequently used ones are shown in Table 1, among which the programs GeneParser, Genie and GRAIL combine similarity searches.

Table 1.

Ab initio Gene Prediction Programs (Possibly with Homology Integration)

Program	Organism	Algorithm*	Website	Homology
GeneID	Vertebrates, plants	DP	http://www1.imim.es/geneid.html
FGENESH	Human, mouse, Drosophila, rice	HMM	http://www.softberry.com/berry.phtml?topic=fgenesh&group=programs&subgroup=gfind
GeneParser	Vertebrates	NN	http://beagle.colorado.edu/~eesnyder/GeneParser.html	EST
Genie	Drosophila, human, other	GHMM	http://www.fruitfly.org/seq_tools/genie.html	protein
GenLang	Vertebrates, Drosophila, dicots	Grammar rule	http://www.cbil.upenn.edu/genlang/genlang_home.html
GENSCAN	Vertebrates, Arabidopsis, maize	GHMM	http://genes.mit.edu/GENSCAN.html
GlimmerM	Small eukaryotes, Arabidopsis, rice	IMM	http://www.tigr.org/tdb/glimmerm/glmr_form.html
GRAIL	Human, mouse, Arabidopsis, Drosophila	NN, DP	http://compbio.ornl.gov/Grail-bin/EmptyGrailForm	EST, cDNA
HMMgene	Vertebrates, C. elegans	CHMM	http://www.cbs.dtu.dk/services/HMMgene/
AUGUSTUS	Human, Arabidopsis	IMM,WWAM	http://augustus.gobics.de/
MZEF	Human, mouse, Arabidopsis, Fission yeast	Quadratic discriminant analysis	http://rulai.cshl.org/tools/genefinder/

^*DP, dynamic programming; NN, neural network; MM, Markov model; HMM, Hidden Markov model; CHMM, class HMM; GHMM, generalized HMM; IMM, interpolated MM.

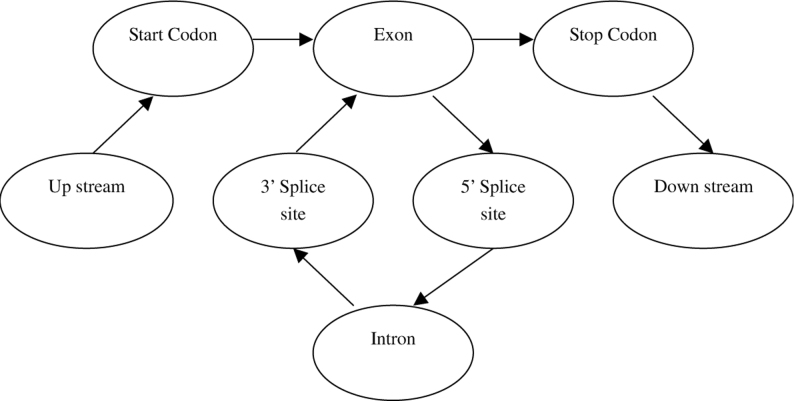
The most successful programs so far are based on Hidden Markov Model (HMM; ref. 17), which is mainly described here. Readers interested in other algorithms can learn from references. In Hidden Markov Model, transitions between sub-models corresponding to particular gene components are modeled as unobserved (“hidden”) Markov processes, which determine the probability of generating particular (observable) nucleotides. Since exon and intron lengths appear to be constrained by factors related to pre-mRNA splicing, and do not exhibit geometric distributions, a more general model is required to accurately account for the lengths of exons and introns in real genes. So a Generalized Hidden Markov Model (GHMM) is developed, in which subsequent states are generated according to a Markov chain but have arbitrary (instead of fixed unit) length distributions. Figure 1 illustrates the state transition in eukaryotic genomic sequences.

Fig. 1.

State transition of HMM modeling eukaryotic genes.

Suppose we are given a DNA sequence S of length L and a parse ϕ also of length L. The conditional probability of the parse ϕ, given that the sequence generated is S, can be computed using Bayes’ Rule as:

$$P\{\mathit{\varphi }|S\}=\frac{P\{\mathit{\varphi },S\}}{{\displaystyle \sum _{\psi \in \mathit{\varphi }L}}P\{\psi ,S\}}$$

Here, ϕL is the set of all parses of length L. Now, given a particular DNA sequence S, we can find a parse ϕL that maximizes the likelihood of generating. In other words, for a particular sequence, we can find the functional unit (for example, the promoter region) that the sequence is most likely to represent. Thus, the model can be used for automatic annotation of DNA sequences.

Other methods

The major limitation with HMM method is that we have a little knowledge of gene structures, especially for new sequencing genomes. Furthermore, current set of known genes is limited and certainly does not represent all potential gene features or their organizational themes. So recently some techniques in physics and signal processing have been applied to recognize genes.

It is well known that base sequences in the protein-coding regions of DNA molecules have a period-3 component because of the codon structure involved in the translation of base sequences into amino acids (18). Discrete Fourier Transform (DFT) is suitable for processing periodicity. For a DNA sequence of length N, assume u_A(n), u_T(n), u_C(n), and u_G(n), which represent the binary indicator function for the corresponding nucleotide. It takes the value 1 at index n if the corresponding nucleotide is present at that position, and takes the value 0 otherwise. Applying DFT to each of these sequences produces four spectral representations, represented as U_A(k), U_T(k), U_C(k), and U_G(k), respectively. The total frequency spectrum of the given DNA sequence is defined as:

$$S(k)=|U_A(k){|}^2+|U_T(k){|}^2+|U_C(k){|}^2+|U_G(k){|}^2$$

In coding regions of DNA, S(k) typically has a peak at the frequency k = N/3, whereas in noncoding regions, it generally does not have any significant peaks. By this property, gene predictor can be constructed. In 2003, a new measure for gene prediction in eukaryotes was presented by Kotlar and Lavner (19), which was based on DFT. The phase of the DFT at a frequency of 1/3 was distributed with a bell-shaped curve around a central value in coding regions, whereas in noncoding regions, the distribution was close to uniform. This regularity was used for discriminating between coding and noncoding regions in a given nonannotated genomic sequence (19).

The Z curve method (20) is another powerful tool in visualizing and analyzing DNA sequences. It has been applied to recognize coding sequences in the human genome (21), and to find genes in the genomes of yeast (22) and Vibrio cholerae (23). For predicting short coding sequence, it shows higher accuracy than GENSCAN, which is considered as one of the best ab initio gene prediction programs, while it is much simpler computationally than the latter.

In addition, with many genome sequencing projects currently under way, the comparative genome approach is becoming more promising in the field of gene prediction. In practice, its performance will depend on the evolutionary distance between the compared sequences. Initial results show that the relationship is not straightforward. Indeed, a greater evolutionary distance allows some algorithms to more accurately discriminate between coding and non-coding sequence conservation. Such comparative genome programs are often computer intensive and consequently much work remains to be done.

Evaluation of Gene Prediction Programs

The abundance of gene prediction program raises the problem of adequate evaluation of prediction program quality. Comparison of the accuracy and reliability must take into account the type of algorithms, for example, neural network, Hidden Markov Model, or others; the number of sequences used for training and testing; and the method used for evaluation. It is impossible to rank the predictors by only a single measure.

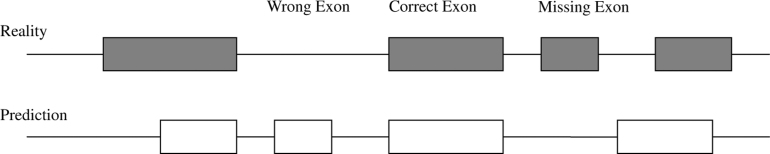
Sensitivity (Sn) and Specificity (Sp) are probably the two most widely used measures, which are explained by Burset and Guigó (24) in detail. The accuracy of the predictions can be measured at three different levels: coding nucleotide sequence, exonic structure, and protein product. The nucleotide level accuracy that measures Sn, Sp, CC (correlation coefficient) and AC (approximate coefficient) gives an overall sense of how closely the predicted and actual coding regions are in a sequence alignment, but does not accurately reflect the identification of precise exon boundaries. Evaluation at the exon level mainly provides how well the sequence signals (splice sites, start codon, and stop codon, etc.) are identified. The accuracy can be measured by comparing predicted and real exons along the test sequences (Figure 2).

Fig. 2.

Evaluation of gene prediction accuracy at the exon level.

Thus, sensitivity (Sn), specificity (Sp), miss rate (MR) and wrong rate (WR) are expressed as following:

$$\begin{array}{cc}Sn=\frac{CE}{AE}& Sp=\frac{CE}{PE}\\ MR=\frac{ME}{AE}& WR=\frac{WE}{PE}\end{array}$$

(AE, actural exons; PE, predicted exons; CE, correct exons; WE, wrong exons; ME, missing exons).

At the protein level, the accuracy is measured by comparing the protein product encoded by the actual gene in the test sequence with the protein product encoded by the predicted gene. In the gene prediction literatures, only Fields and Soderlund (25) provided an evaluation of the gm program at the final protein product level, which indicated that it is not widely used.

The prediction accuracy of some usual programs has been tested on Burset and Guigó’s sequence set (24), and the results at exon level are illustrated in Table 2 (12). It shows that GENSCAN based on GHMM is significantly more accurate than other programs.

Table 2.

Accuracy Comparisons of Gene Prediction Programs

Program	Sn	Sp	MR	WR
GENSCAN	0.78	0.81	0.09	0.05
FGENEH	0.61	0.64	0.15	0.12
GeneID	0.44	0.46	0.28	0.24
Genie	0.55	0.48	0.17	0.33
GenLang	0.51	0.52	0.21	0.22
GeneParser2	0.35	0.40	0.34	0.17
GRAIL2	0.36	0.43	0.25	0.11
SORFIND	0.42	0.47	0.24	0.14
Xpound	0.15	0.18	0.33	0.13

Future Directions in Gene Prediction

Since the early eighties of the twentieth century, there has been great progress in the development of computational gene prediction. However, some problems have not yet been solved. First, short exons are difficult to locate, because discriminative statistical characteristics are less likely to appear in short sequences. The more difficult cases are those where the length of a coding exon is a multiple of three (typically 3, 6 or 9 bp), because missing such exons will not cause a problem in the exon assembly as they do not introduce any changes in the frame. Lately, Gao and Zhang (26) compared the performance of various algorithms for recognizing short coding sequences and validated that the Z curve method is the best one.

Second, the problem of alternatively splicing has not yet been solved effectively, which in particular is an important regulatory mechanism in higher eukaryotes. Some gene prediction programs tried to handle this through the identification of sub-optimal exons (GENSCAN and MZEF). Nevertheless, a more relevant approach would consist of improving the identification of the intronic and exonic signals that dictate the choice of alternatively splicing sites (27).

In addition, the evaluation system of gene prediction programs is still in need of improvement. Some of the measures mentioned above often give results contradictory to each other, because many of them emphasize only a few or even only one of the several aspects of the prediction quality. So more reasonable and comprehensive criterions are needed for evaluation of gene prediction programs. Recently, Bajic introduced averaged score measure (ASM) and used it to assess the quality of programs for eukaryotic promoter prediction (28).

Further more, in order to compensate the insufficiency of any individual gene prediction program, the computational method to construct gene models by multiple evidences is becoming more promising. For the nonannotated genomic sequences, a diverse set of sources can be combined for annotation, including the locations of gene predictions from ab initio gene finders, protein sequence alignments, ESTs and cDNA alignments, promoter predictions, splice site predictions, and so on. Such integrative approach has been proved to consistently outperform even the best individual gene finder, and in some cases, can produce dramatic improvements in sensitivity and specificity (29).

Finally, it should be emphasized that for all gene prediction methods, the performances depend on the current biological knowledge to a large extent, especially knowledge at the molecular level of gene expression. So it requires great efforts by both experimental and computational biologists to make gene prediction more accurate, which can definitely speed up gene discovery and knowledge mining.

Acknowledgements

The authors would like to thank Dr. Qi Liu for reading the manuscript and for valuable discussions.