Abstract
In complex systems, a critical transition is a shift in a system’s dynamical regime from its current state to a strongly contrasting state as external conditions move beyond a tipping point. These transitions are often preceded by characteristic early warning signals such as increased system variability. However, early warning signals in complex, coupled human–environment systems (HESs) remain little studied. Here, we compare critical transitions and their early warning signals in a coupled HES model to an equivalent environment model uncoupled from the human system. We parameterize the HES model, using social and ecological data from old-growth forests in Oregon. We find that the coupled HES exhibits a richer variety of dynamics and regime shifts than the uncoupled environment system. Moreover, the early warning signals in the coupled HES can be ambiguous, heralding either an era of ecosystem conservationism or collapse of both forest ecosystems and conservationism. The presence of human feedback in the coupled HES can also mitigate the early warning signal, making it more difficult to detect the oncoming regime shift. We furthermore show how the coupled HES can be “doomed to criticality”: Strategic human interactions cause the system to remain perpetually in the vicinity of a collapse threshold, as humans become complacent when the resource seems protected but respond rapidly when it is under immediate threat. We conclude that the opportunities, benefits, and challenges of modeling regime shifts and early warning signals in coupled HESs merit further research.
Keywords: critical transitions, criticality, social–ecological systems, human-and-natural systems, early warning signal
In a coupled human–environment system (HES), a human system influences an environment system that in turn influences the human system (1). Other terms such as “coupled human-and-natural systems” and “socio-ecological systems” have been used to describe similar phenomena (2, 3). As the influence of humans on their environment continues to grow, so have the resulting impacts of the environment on humans, along with our awareness of those impacts and our efforts to mitigate them. Coupled HESs are therefore ubiquitous and occur in agriculture, water use, terrestrial and aquatic systems, the global climate system, and elsewhere (1, 4–10).
In forest systems, the relationship between public opinion and forest conservation often exemplifies coupled HES dynamics. Historically, significant declines in forest cover have often stimulated the perception of a resource crisis in the public, who have responded with public debate and pressure for governments to enact conservation measures, in turn resulting in increased forest cover. This has been noted through surveys, observational studies, and historical accounts in various countries over the past two centuries (11–16). Whereas the connection between public opinion and deforestation is complicated by other issues such as science communication, special-interest lobbies (17), and agro-economic drivers for forest transitions, the long history of forest conservation suggests a common trend by which declining forest cover can stimulate public demand for conservation and thereby reverse forest decline.
Regime Shifts in Coupled Human–Environment Systems.
Human and environment systems are often characterized by nonlinear interactions, even in isolation from one another (18). Coupling between and human and environment systems often introduces further nonlinearities. Thus, studying systems of differential equations where interactions between state variables are governed by nonlinear mechanisms is particularly well suited to describing coupled HESs (1). Nonlinear dynamical systems can exhibit regime shifts where the system is shifted from one stable equilibrium to another (19, 20). When the state of the system shifts abruptly to a qualitatively contrasting state in the neighborhood of a bifurcation point, it is called a critical transition and the corresponding bifurcation point is called a tipping point (19, 20).
Regime shifts have been studied in diverse natural systems such as lakes, epilepsy, and the global climate system ((21). The transition from healthy to collapsed forest can likewise be understood as a regime shift (22). Regime shifts in forest ecosystems have been identified as an important research priority in the climate change era (23, 24). A significant body of work also evaluates the collapse of human societies driven by regime shifts in natural systems, for instance the resilience of prehistoric human populations to regime shifts in the global climate (25). The environment influences human populations in this system, but it is not a fully coupled HES because the flow of influence from prehistoric humans back to the global climate was comparatively weak in the prehistoric era.
However, fully coupled HESs also appear to exhibit regime shifts in empirical study systems. Research has explored how interactions between land use and vegetation dynamics in Iceland caused regime shifts and hysteresis (26), how humans mitigate or prevent human-induced fisheries collapse (4), and how human-caused deforestation may have precipitated the collapse of the prehistoric Easter Island civilization (27). In infectious diseases, coupled HES dynamics are exemplified by the 2014–2015 Disneyland, California measles outbreak, where vaccine refusal caused the measles outbreak, which in turn stimulated a recovery of vaccine uptake (28).
Regime shifts in theoretical models of coupled HESs are also receiving growing attention (29). Hysteresis and critical transitions have been observed in coupled HESs on networks (30). Complex community structure in coupled HESs can create multiple small regime shifts instead of a single large one (31). Coupled behavior–disease dynamics can exhibit regime shifts too, where vaccine coverage suddenly plummets when a critical threshold in perceived vaccine risk is exceeded (32).
Human feedback in a coupled HES can be fundamental to shaping regime shifts in environmental systems. In particular, regime shifts corresponding to a breakdown in cooperation and collapse of a harvested resource may occur in a coupled HES, but not in the corresponding ecological system in the absence of human behavior (33). Because of nonlinear feedback, resource collapse can be caused by surprising and counterintuitive changes, such as an increase in the resource inflow rate (33). Thus, failing to account for human feedback can underestimate the potential for regime shifts in ecological systems (33).
The concept of resilience is inseparable from a discussion of coupled HESs (5, 34). A desirable resilient state for a coupled HES is one where both ecological function and human wellbeing are sustained. “Resilience” has been used in various ways in the HES literature (34, 35). For instance, with respect to regime shifts, a system can be described as resilient when it is far away from undesirable tipping points. Some previous research is concerned with interventions to help avoid undesirable regime shifts in coupled HESs, so that ecological collapse is avoided while also ensuring that humans can derive sustenance from the resource (36). Theoretical models have illustrated how sufficiently effective institutions can keep a coupled HES away from tipping points (37, 38). Furthermore, characteristics such as demographic stochasticity and spatial heterogeneity can make regime shifts smoother and thus easier to avoid or possibly even reverse, in the early stages of transition before the point of no return is reached (39, 40). A distinct but related definition of resilience is when small perturbations do not move the system far from its equilibrium state (2, 34). This corresponds closely with the concept of local stability of an equilibrium in a dynamical system (18) and is the sense in which we use resilience in this paper.
Early Warning Signals.
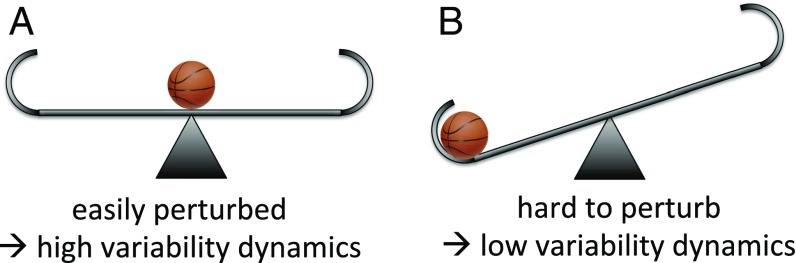
A coupled HES that is close to a tipping point is generally far less resilient to perturbations. As a tipping point is approached, the resilience of the system decreases: When the system is perturbed, it takes longer for the system to recover to its stable equilibrium (21). This property means that regime shifts often exhibit characteristic early warning signals (21). A physical model of a basketball on a seesaw is helpful for understanding early warning signals (Fig. 1). The tipping point is when the seesaw is in a perfectly horizontal position with the basketball on the vertex, because the basketball could easily roll left or right according to a tiny perturbation left or right (Fig. 1A). Close to the tipping point, the basketball is easy to perturb back and forth due to the relative flatness of the surface, so its dynamics are more variable (resilience is low). However, when the basketball is far away from the tipping point in a tight valley on the left- or right-hand side of the seesaw (Fig. 1B), it is relatively difficult to perturb and therefore the basketball’s motion is not highly variable (resilience is high).
Fig. 1.
Seesaw model for early warning signals. (A) At the tipping point the seesaw is horizontal so the basketball is easy to perturb, resulting in highly variable motion in the presence of noise. (B) In a stable state the basketball is hard to perturb so its motion is not highly variable in the presence of noise.
There are two ways the basketball can move to a different position on the seesaw. A very large push might move it past the vertex, causing the seesaw to tip toward the other side as the basketball shifts to the alternate position (this is like forcing a model’s state variable). In this case, the seesaw has two stable alternative stable states when the basketball is in one of the two valleys, and it also has an unstable state at the tipping point. Or someone can physically tilt the seesaw past the tipping point, causing the basketball to shift to the alternate side (this is like changing a model parameter).
Decreased resilience before a regime shift can manifest through effects such as critical slowing down—increasing variance and autocorrelation of a time series at lag 1 (21, 41, 42). Or the system may “flicker” between the basins of attraction of alternative stable states (43). Early warning signals have been widely studied in uncoupled systems such as lakes and climate systems, where their study goes hand in hand with study of regime shifts (21, 42). Early warning signals are also observed in natural systems subject to human stressors, such as in ecosystems service indicators in eastern China due to economic development (44).
Early warning signals are thought to be common to a broad range of dynamical systems because they depend on common features of dynamics (45). However, researchers are investigating how these signals may depart from the expected pattern or fail to manifest (46–48). Regime shifts can occur without warning in a broad class of ecological models (46), or variance may decrease instead of increasing near a regime shift (47). Thus, system-specific models still need to be studied (48).
In recent years, researchers have also begun to study early warning signals in coupled HES models. These often exhibit the same early warning signals as seen in many ecological systems, such as critical slowing down (31, 33, 49, 50) or transitional regimes (51). Early warning signals have been observed in coupled HES models of harvesting with resource dynamics (51), common pool dilemmas on complex networks (31), instabilities in socio-ecological networks (49), and common pool problems in populations with social ostracism directed against overharvesters (33, 50). Researchers have concluded that early warning signals may be useful for anticipating regime shifts in coupled HESs, although further study is required because many of the same caveats that limit their application to uncoupled systems also apply to coupled HESs (31, 33, 49–51).
Objective and Rationale.
Our objective is to study early warning signals for regime shifts in a simple coupled HES model. In Environment Dynamics Model we show how a simple ecological model representing harvesting through a fixed parameter tells a common story about regime shifts in ecological systems: Critical slowing down precedes a catastrophic regime shift where the system collapses. In Social Dynamics Model we present a model for human social dynamics including injunctive social norms and social learning in isolation from an environment subsystem.
In Coupled Human–Environment System Model we couple the two subsystems. We analyze its regime shifts, showing that the coupled HES has a wider variety of dynamical regimes than either human or environment subsystem in isolation from the other. We analyze its early warning signals. The coupled HES model shows that not only can the potential for regime shifts be underestimated if human feedback is not included (33), but also the qualitative nature of the regime shifts can be misread. The same early warning signal may equally well herald an impending environmental catastrophe or a shift to environmental sustainability, depending on the model parameters. We also show how human feedback partially mutes the early warning signal observed in either subsystem, making the regime shift harder to predict. Finally, we explore a variant of the HES model that makes the cost parameter of the coupled HES depend on the environmental state. The result is a system that can be doomed to linger perpetually in the neighborhood of the tipping point, due to adaptive human behavior. We conclude with a discussion.
Building on recent research in modeling coupled HESs (33, 50–53), we developed a relatively simple model because our goal was to gain intuition and illustrate concepts with clarity (54). Despite this, the model incorporates important features of the coupled dynamics of forests and conservation opinions such as social learning, injunctive social norms, economic costs, resource dynamics, and the inverse relationship between forest cover and public support for conservation noted earlier in the Introduction (11–15). In Discussion we address model limitations and speculate on the implications of relaxing our simplifying assumptions in future work.
Environment Dynamics Model
We model a stylized forest ecosystem where the proportion of forest cover grows logistically to its carrying capacity (rescaled to ) but is also harvested,
| [1] |
where is the net growth rate, is the harvesting efficiency, and controls the per capita demand for forestry products. This is a classic resource overharvesting model (55). The harvesting rate per unit area is , where the inverse dependence on arises because the per unit area demand for forestry products is assumed to increase as the supply declines. Human behavior is described by fixed parameters and , and therefore this is not a coupled HES. The three model equilibria correspond to no forest cover, stable forest cover, and unstable forest cover (SI Appendix, section S1).
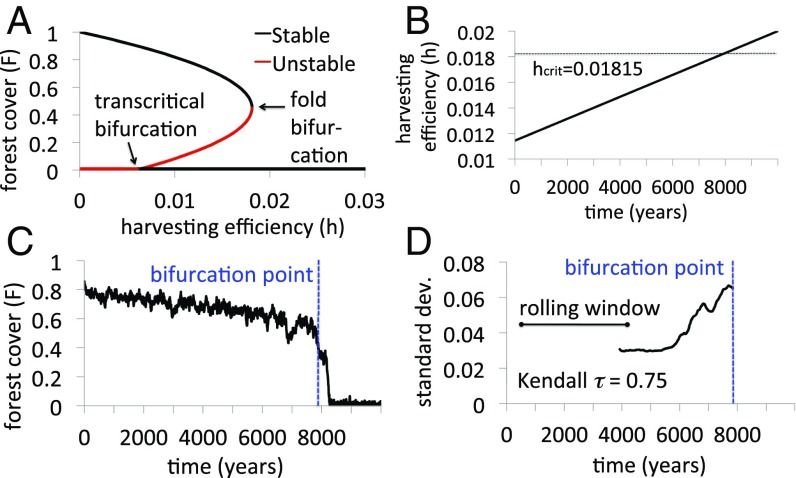
This model exhibits a regime shift typical of many ecological models. Regime shifts are best understood through bifurcation diagrams, which visualize a system’s equilibria and how their relationships change as a model parameter is varied (18). A bifurcation occurs when the stability of an equilibrium state changes, often due to “collision” with another equilibrium. In a bifurcation diagram of forest cover vs. harvesting efficiency , we observe that when is low, forest persists in a stable state (Fig. 2A). Now, we imagine that increases slowly over time, as might occur due to technological progress (Fig. 2B). When is large enough a tipping point is encountered at and a regime shift occurs: The stable state of high forest cover collides with the unstable state and only the stable state of forest collapse remains () (Fig. 2A and B). This type of tipping point is called a fold bifurcation, corresponding to the collision and annihilation of the stable and unstable equilibria at .
Fig. 2.
Forest collapse in the environment dynamics model. A–D show (A) a bifurcation diagram of forest cover vs. harvesting efficiency , (B) time series of increasing gradually and exceeding bifurcation point , (C) the resulting collapse of forest as the bifurcation point is exceeded, and (D) the increase in residual SD as the bifurcation point is approached. Other parameters are /y, . Methodology is shown in SI Appendix.
The forest collapse is visualized in a plot of forest cover vs. time , showing the gradual decline of forest as increases, followed by its sudden collapse as exceeds (Fig. 2C; see SI Appendix, section S3 regarding generation of stochastic dynamics). However, the system exhibits early warning signals before collapsing: The residual standard deviation—a measure of system variability—increases as the fold bifurcation is approached, in a pattern that is typical of early warning signals of regime shifts (Fig. 2D). The lag-1 autocorrelation also increases but the trend is weaker for these parameter settings and noise assumptions; therefore we use the residual SD throughout this paper.
Social Dynamics Model
To describe social dynamics we invoke the imitation dynamic of evolutionary game theory, capturing how humans tend to imitate successful strategies (32, 33, 56, 57). Each individual in the population adopts one of two opinions. Each opinion is associated with a “utility” that quantifies how strongly that opinion is preferred (58). Each individual samples other individuals in the population at a fixed rate. If the sampled person has the opposite position and is receiving a higher utility, the individual switches to the sampled person’s opinion with a probability proportional to the expected gain in utility.
Suppose that is the proportion of the population adopting opinion (e.g., “conservationists”), whereas a proportion adopts opinion (e.g., “nonconservationists”). can increase by individuals switching from to or decrease by individuals switching from to . A individual sampling at rate encounters individuals with frequency and finds the utility gain for switching positions is , where (respectively, ) is the utility associated with holding position (respectively, ). Because there are individuals in the population, the total rate at which individuals switch from to is . By similar reasoning, the total rate at which individuals switch from to is . Hence, the total rate of change in is given by
| [2] |
where . This simple system has two equilibria: Opinion dominates the population if , and dominates if . We note that Eq. 2 is formally identical to the replicator equation of evolutionary game theory (59).
Coupled Human–Environment System Model
In the study of early warning signals in uncoupled systems, parameters like the harvesting efficiency in Eq. 1 are treated as constantly and gradually increasing in time (Fig. 2B). In a coupled HES the harvesting rate is a function of a human state variable like , necessitating a change to the term in Eq. 1. Similarly, in an uncoupled human population, as in classical treatments of strategic interactions like the prisoner’s dilemma, is a fixed parameter, but in a coupled HES, depends on .
We combine Eqs. 1 and 2 to create a simple coupled-HES model. Socio-ecological feedbacks are known to slow down deforestation, and socio-economic factors can assist in reforestation (11–16). Therefore, we adopt a form for such that the utility for deforestation decreases when forest cover becomes too low, thereby causing more of the population to adopt a conservationist opinion. Similarly, we assume that the harvesting rate is lower when the proportion of the population adopting a conservationist opinion, , is higher,
| [3] |
| [4] |
Here, is the strength of injunctive social norms that tend to move individuals toward the opinion currently adopted by the majority of the population, is the cost of conservation (including both pecuniary costs and nonpecuniary costs such as time costs), is the harvesting efficiency, and (the “rarity valuation parameter”) controls how proportion of forest cover influences the utility of conserving forests. When is small, becomes large, thus incentivizing forest conservation. controls the steepness of this relationship, especially when is close to . Harvesting ceases completely at , as might occur for a critically endangered ecosystem in a protected area. We note that other assumptions could be made, such as harvesting continues at but is restricted to sustainable levels (33) or harvesting ceases as soon as to model majority voting in a democracy. Note that the harvesting rate is now instead of . This model has seven equilibria, in comparison with two for the human submodel and three for the environment submodel (see SI Appendix, section S2 for equilibria and stability analysis).
Similar models have been used in both coupled HESs (33, 50, 53, 60, 61) and human-epidemiological systems (32, 57, 62). Many previous models have been formulated at the level of the population doing the harvesting, where individuals have the choice to ostracize other harvesters who overharvest the shared resource (33, 50). In contrast, we interpret our model at the level of the general public removed from direct harvesting activity, so injunctive social norms represent processes whereby individuals tend to conform to a majority opinion, rather than being a penalty associated with overharvesting per se. At the timescale of interest for this model we are not accounting for preexisting institutions of social or environmental dynamics (except for injunctive social norms), but rather we consider institutions such as laws to be the outcomes of the social processes represented by the model.
We fitted the model to data on old growth forest cover in the Pacific Northwest United States (63) and longitudinal data on forest conservation opinions in Oregon (15) to demonstrate how the model can describe human–environment dynamics on relevant timescales (see Table 1 for best-fitting parameter values and SI Appendix, section S3 and Fig. S1 for fitting methodology and best-fitting model time series).
Table 1.
Baseline parameter values for coupled HES model
| Parameter | Definition | Baseline value |
| net growth rate/fecundity | 0.06/y | |
| supply and demand parameter | 0.8 | |
| harvesting efficiency | 0.075/y | |
| social learning rate | 0.17/y | |
| conservation costs | 0.35 | |
| rarity valuation parameter | 0.6 | |
| social norm strength | 0.5 |
Richer Dynamics.
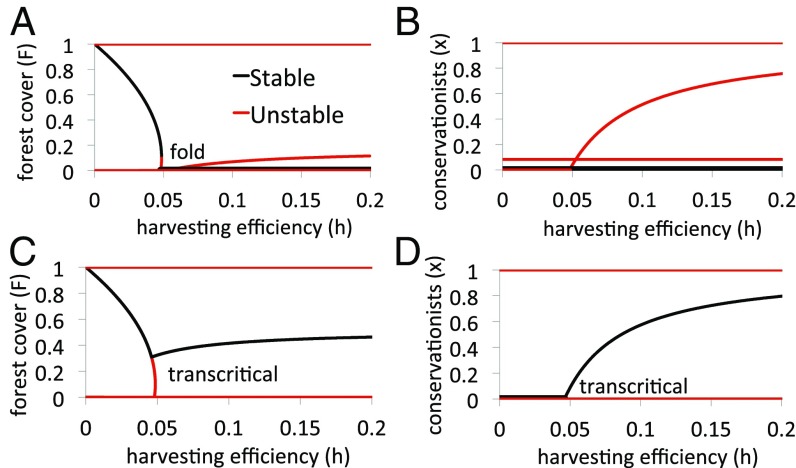
For certain parameter values, the coupled HES model exhibits outcomes similar to those of the uncoupled model. For instance, when the conservation cost is sufficiently high () and social norms are sufficiently strong (), the forest collapses as harvesting efficiency increases (Fig. 3A) because the cost of conservation is too high and injunctive social norms prevent conservationism from establishing itself in the population (, Fig. 3B).
Fig. 3.
Bifurcation diagrams illustrate the rich variety of regimes in the coupled HES model such as (A and B) collapse and (C and D) conservation scenarios. Shown are (A and C) forest cover and (B and D) conservationists , vs. harvesting efficiency for (A and B) , and (C and D) , . Other parameter values are in Table 1. See SI Appendix, section S3 for methodology.
However, this resemblance to the uncoupled model does not hold in general. Although harvesting is certainly the proximate cause of collapse, from the coupled HES perspective harvesting is simply the end result of larger social, economic, technological, and ecological factors. For instance, a very different outcome occurs if the conservation cost is smaller () and social norms are weaker (): As the harvesting efficiency increases beyond a tipping point, humans respond to declining forests by an increase in conservationism ( becomes stable, Fig. 3D). This in turn allows moderate forest cover to be maintained despite higher harvesting efficiency ( becomes stable, Fig. 3C). In contrast to the uncoupled system, the human population in the coupled system responds to the threat of forest collapse due to higher harvesting efficiency by limiting the harvesting rate, thus allowing forests to persist instead of collapse. Mathematically, the harvesting rate is given by and so when increases sufficiently quickly, harvesting can be limited despite high values of .
As this example illustrates, the coupled HES exhibits a richer variety of possible dynamics than the uncoupled system. Outcomes such as collapse can depend on complex interactions between model parameters. This rich variety can be appreciated through bifurcation diagrams involving other model parameters. For instance, as the conservation cost increases, the state of maximal forest cover and full conservationism, , can destabilize through a regime shift (SI Appendix, Fig. S2 A and B). Beyond this bifurcation point, the system enters a regime of stable oscillations in forest cover and public opinion. As decreases, public opinion shifts in favor of conservationism, which catalyzes a rebound in . This, in turn, causes a decline in conservationism and the cycle continues. The same bifurcation diagram entails a stable interior equilibrium where both and are nonzero and stable, but this equilibrium exists only for a limited range of and is easily lost through a Hopf or fold bifurcation.
These outcomes are reflected in local stability analysis: The equilibrium is locally asymptotically stable when , suggesting that sufficiently high conservation cost, weak social norms, or large values of the rarity valuation parameter can destabilize high forest cover and conservationism (SI Appendix, section S2). Interestingly, does not appear in this inequality. We note that the bifurcation diagrams for and mirror one another very closely at these parameter values. We also note that many other types of coupled systems that are not HESs also exhibit richer dynamics than their uncoupled counterparts (64).
Increasing the strength of injunctive social norms, , tends to push the population to the boundaries of no conservationism, , or full conservationism, , depending on initial conditions and environmental parameters. For instance, at parameters that favor conservationism, increasing the strength of social norms destabilizes the interior equilibrium through a fold bifurcation, causing a regime shift to a state of maximal forest cover and conservationism, (SI Appendix, Fig. S2 C and D). The corresponding catastrophic equilibrium is never stable at these parameter values. At higher values of , this fold bifurcation moves upward and disappears, being replaced by a transcritical bifurcation connecting the stable interior branch to the stable boundary branch (SI Appendix, Fig. S2 E and F). Hence, the population transitions smoothly to the desirable state as increases, rather than going through a critical transition. Other regions of parameter space with very high harvesting efficiency () show a severe critical transition from full conservationism to no conservationism as the conservation cost increases beyond .
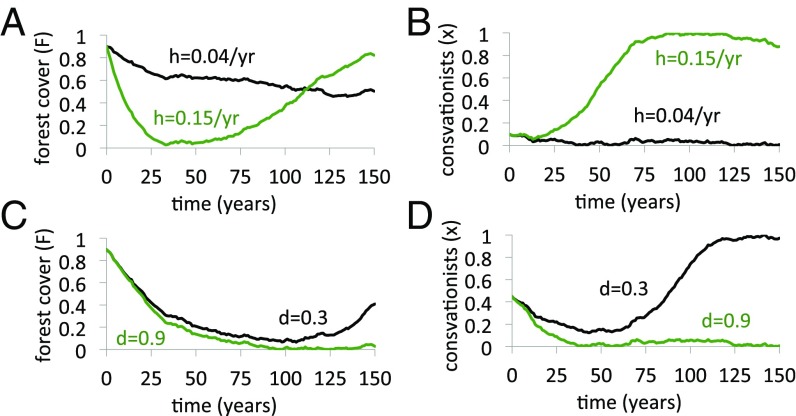
These rich dynamics are also illustrated in the system’s temporal evolution. We generated time series of and for initial conditions common to many coupled forest–human systems over the past few centuries: high initial forest cover and low initial prevalence of conservationists. We observe that low levels of harvesting efficiency (/y) only moderately impact forest cover () and thus fail to stimulate a social response to protect forests (, Fig. 4 A and B). However, higher levels of harvesting efficiency (/y) cause a dramatic decline in forest cover, which in turn stimulates a surge in conservationism that subsequently restores forest cover (Fig. 4 A and B). Paradoxically, the long-term forest cover is higher when the harvesting efficiency is larger (despite oscillations), due to the social response. This result is confirmed in a longer time series (SI Appendix, Fig. S3).
Fig. 4.
Outcomes differ widely for different social and harvesting parameters in the coupled HES model: high vs. low harvesting efficiency (A and B) and high vs. low social norm strength (C and D). /y, , and unless otherwise stated, with remaining parameters in Table 1. See SI Appendix, section S3 for methodology.
At other parameter values, the effect of social norms is again apparent. When the system starts from a state of high initial forest cover and low initial proportion of conservationists, the high initial forest cover permits a decline in conservationism, which causes a decline in forest (Fig. 4 C and D). When social norms are relatively weak (), it is possible for the population to evolve from a state of low conservationism to high conservationism, thereby conserving the forests. However, when social norms are stronger () and the initial prevalence of conservationists is not high enough (), the population becomes trapped in a state of suppressed conservationism in perpetuity after becomes small during the first few decades. As a result, forest cover also remains low over the long term. This is confirmed in a longer time series (SI Appendix, Fig. S3). We also note that if conservation initially starts off higher (), then high levels of conservationism can be sustained, again due to social norms.
Ambiguous and Muted Early Warning Signals.
The wider variety of possible outcomes for a coupled HES in comparison with the corresponding uncoupled system has implications for how we interpret early warning signals in the coupled HES. In particular, it makes it more difficult to interpret which regime the system will converge to after early warning signals are detected. This requires that we refine our early warning signal methodologies (50) and/or improve our understanding of the underlying dynamical model.
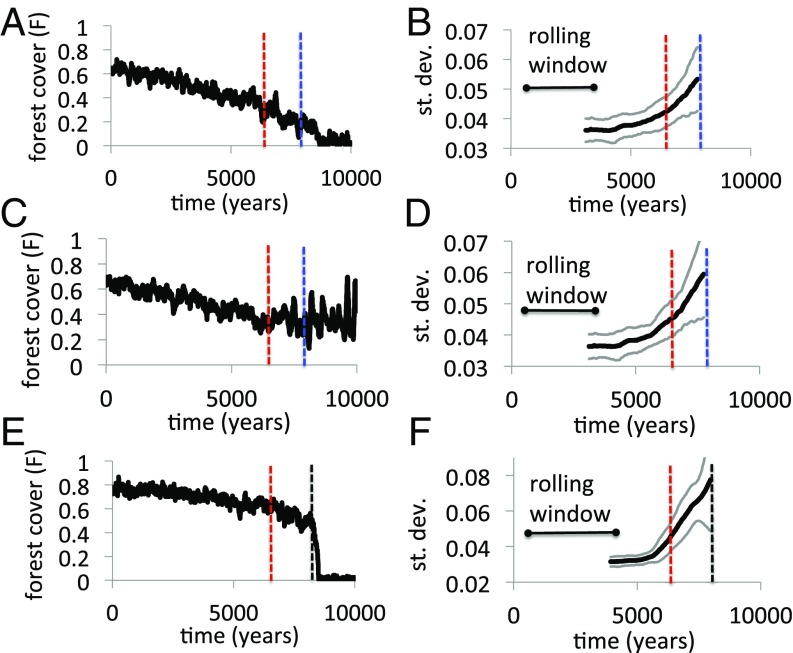
For instance, as the bifurcation point corresponding to forest collapse in the coupled HES model is approached (“collapse scenario,” Fig. 3 A and B), we observe the usual increase in the SD of the residual time series for , corresponding to an early warning signal (Fig. 5A and B; blue line shows bifurcation point for collapse scenario). However, if the bifurcation point corresponding to the blossoming of forest conservationism is approached instead (“conservation scenario,” Fig. 3 C and D), the increase in the SD of the residual time series is virtually the same—both qualitatively and quantitatively—to the collapse scenario, both leading up to and beyond the earlier bifurcation point of the conservation scenario (Fig. 5 C and D; red line shows bifurcation point for conservation scenario). Hence, an observer of the coupled HES in the years leading up to the point where the collapse and conservation scenarios diverge (the red line) would have no way of telling whether the early warning signal is heralding forest collapse or an era of forest conservation. Results are similar for ( SI Appendix, Fig. S4). This outcome is perhaps not surprising, because indicators are generic for typical local bifurcations (45). The problem becomes figuring out what regime shift the indicator is predicting. At the same time, these results do not rule out the possibility that other systems or other indicators might yield detectable differences between collapse and conservation scenarios (50).
Fig. 5.
Early warning signals are similar despite different outcomes. Shown are (A) collapse of forest in the coupled HES model for , and (B) early warning signal; (C) conservation of forest in the coupled HES model for , and (D) early warning signal; and (E) collapse of forest in uncoupled environment model and (F) early warning signal. Blue line is bifurcation point for system in A and B, red line is bifurcation point for system in C and D, and black line is bifurcation point for system in E and F. Other parameter values are in Table 1, except increases incrementally each year from /y to /y over a simulated time span. See SI Appendix for methodology.
In the uncoupled system a similar story unfolds but with an important difference (Fig. 5 E and F; black line shows bifurcation). The variability of the residual time series increases before collapse in a qualitatively similar way to that of the coupled model, which again makes it difficult to determine what kind of regime shift is coming. However, the SD increases much more as the bifurcation point is approached in the uncoupled system. We hypothesize that this difference occurs because of “muting”: Human behavioral feedback helps mitigate the variability in forest cover in the coupled system because dips in forest cover stimulate an increase in conservationist opinion and thus forest conservation (Eqs. 3 and 4). This results in a lower SD for . In contrast, the uncoupled system lacks this mitigating feedback and therefore the variability of close to the bifurcation point is higher.
To further explore muting we compared the eigenvalues of equilibria in the coupled and uncoupled models. If muting explains the observed differences, the eigenvalues in the coupled model should be larger and more negative than the eigenvalue of the corresponding equilibrium of the uncoupled model, leading to a more strongly attracting equilibrium in the coupled model and therefore a reduced variance of the stochastic trajectory near the equilibrium. In probabilistic sensitivity analysis of parameter values close to the bifurcation points in Fig. 5, as well as near (1,1) in the coupled system, we found this was indeed the case (SI Appendix, section S4).
In summary, human feedback in the coupled HES partially mutes the early warning signal, making the increase in variance before a regime shift smaller than it would be in the corresponding uncoupled system. Whereas this effect could make it harder to detect regime shifts in environmental systems under human influence, it may also help provide a way to distinguish early warning signals for collapse vs. conservation in coupled HESs, if the difference between muting in the two scenarios can be characterized.
Self-Evolved Criticality.
Our approach replaces a simple driver to represent human influence in the uncoupled system—the harvesting efficiency —by a more complex driver in the coupled HES—the realized harvesting rate . In research on early warning signals, it is often assumed that the system is moved past a tipping point by a simple driving factor. For Eq. 1 this was done by increasing every year according to , where is small (Fig. 2B). However, it can be argued that some parameters of the coupled HES model should not be fixed. For instance, the cost of conservation arguably should depend on , because it will cost more to conserve forests when they are abundant. Among other reasons, the opportunity cost of conservation should increase as increases, because land devoted to forest conservation cannot be used for other purposes like agriculture.
Similar to earlier research on modeling media influence in an epidemic model by making the transmission rate parameter depend on the prevalence of infection (65), we consider an extended model where the conservation cost changes with forest cover according to , where and are new parameters. We compare dynamics for this “extended model” with to our original “baseline model” Eqs. 3 and 4, where .
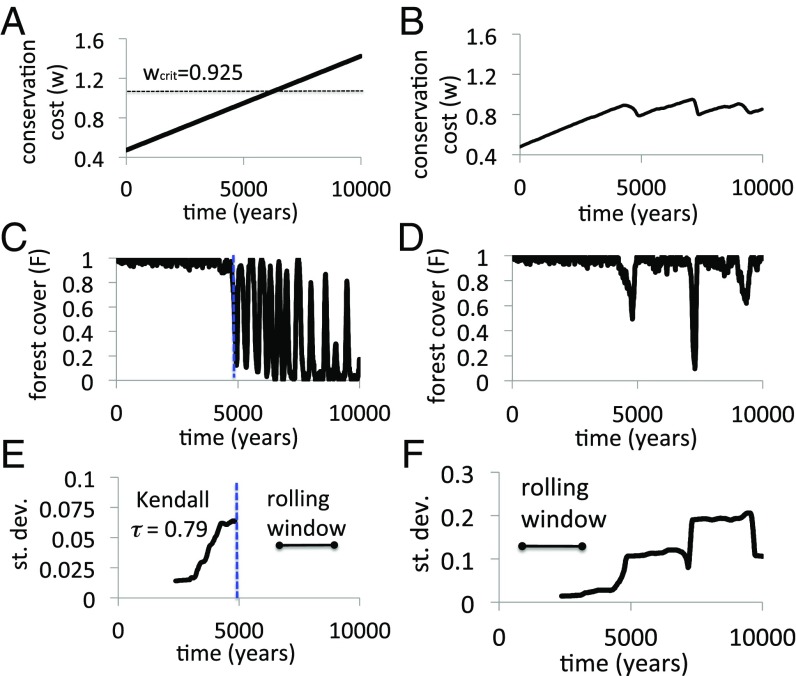
In a simulation experiment we initialize the population on the stable equilibrium of maximal forest cover and conservationism, . In the baseline model, the population is pushed past the critical point as usual (Fig. 6A). As a result, both forest cover and conservationism collapse due to higher conservation costs before recovering and entering a regime of long-term oscillations of extreme amplitude (Fig. 6C). The residual SD increases before the regime shift, providing an early warning signal (Fig. 6E).
Fig. 6.
Self-evolved criticality in the HES model. Shown are (A) fixed and (B) -dependent conservation costs resulting in (C) a regime shift in the fixed case vs. (D) self-evolved criticality in the -dependent case, with (E and F) corresponding early warning indicators. , . Methodological details are in SI Appendix.
In contrast, in the extended model, the conservation cost grows steadily as long as remains large. But as the system approaches the brink of collapse and fluctuations in increase, the conservation cost drops, causing the system to pull back from the bifurcation point (Fig. 6B). However, the feedback of upon is not sufficient to prevent deforestation for all time. Instead, the system exhibits sporadic outbreaks of deforestation and anticonservationism where forest cover drops to very low levels before feedback restores it (Fig. 6D). This result is caused by adaptive, strategic human behavior: When forest cover is too high, conservationism is not sufficiently attractive and humans become complacent, allowing forest cover to decline. When forests become threatened once again by overharvesting, conservationism becomes attractive again and recovers. In this way, the extended model is doomed to criticality such that the system lingers perpetually around the tipping point . The same behavior is observed in the variable (SI Appendix, Fig. S5).
These explosive outbreaks of deforestation resemble outbreaks of virulent pathogens that have been observed in spatially extended epidemiological models, where this dynamical behavior was called self-evolved criticality (SEC) (66). Moreover, the frequency distribution of deforestation outbreak sizes in the extended model obeys a power law, as observed in other systems exhibiting SEC (SI Appendix, Fig. S6). We speculate that SEC may be common in coupled HESs. Under some conditions, free riding should cause a coupled HES to move closer to the tipping point so that it perpetually flirts with resource collapse, despite the fact that such behavior is not socially (Pareto) optimal.
We note that dynamics will differ at other values of . For instance, ensures that always declines and thus generate stable forest cover. We also note that other parameters like and could be made to depend on and thus might also generate SEC. In the extended model we also observe an increase in the SD of the residual time series before the bifurcation, similar to that observed in the baseline model except that the increase does not correspond to a qualitatively different regime (Fig. 6F). Finally, we note that could instead depend on through a differential equation like . This might yield limit cycles in a 3D dynamical system, instead of explosive outbreaks of deforestation in the 2D system.
Discussion
In this paper we showed how a coupled HES can exhibit a richer variety of dynamical regimes than the corresponding uncoupled system. Thus, early warning signals can be ambiguous because they may herald either collapse or conservation. We also found that human feedback can partially mute the early warning signal of a regime shift or cause the system to evolve toward and perpetually remain close to a tipping point.
An argument in favor of using critical slowing down as an early warning signal is that it relies upon a common feature of many bifurcations: The eigenvalue of the linearized Jacobean at the equilibrium goes to zero, causing a loss of resilience (45). For coupled HESs, this universality is a double-edged sword because both collapse and conservation regimes may be indicated. This necessitates understanding the underlying dynamical model to properly interpret indicators (48).
The process of adding a model variable for human behavior and subsequently making conservation cost depend on forest cover raises the broader question of how many variables are necessary and what should be a state variable vs. what should be a fixed parameter. On longer timescales, many parameters of a coupled HES model could arguably be converted to state variables, because they will likely vary over time in response to other variables. Here, we illustrated how making the parameter depend on caused self-evolved criticality (66). Strategic, adaptive human behavior means the population supports just enough conservation to “get by,” causing the system to flirt repeatedly with an undesirable regime shift.
We made simplifying assumptions that could be relaxed in future work. Other processes can also influence the relationship between public opinion and forest cover. For instance, forest transitions can also be caused simply by rising crop yields requiring less clearing of forested areas (67). Our model does not explicitly capture the influence of institutions such as large organizations that can significantly influence dynamics in ways that merit mechanistic modeling (17).
Future research could also develop sophisticated methods for distinguishing whether an early warning signal heralds collapse or conservation or study the impact of social and spatial heterogeneity, both of which can alter dynamics in a wide variety of systems (68). Populations do not converge uniformly to perfect conservationism or anticonservationism, but rather form pockets of locally homogeneous opinions (69). This population structure has implications for how early warning signals are manifested. Turning to social media to obtain data on the human component of coupled HESs should also be valuable. Already, social media data are proving fruitful in the analysis of many social systems where natural dynamics are relevant (70–72).
In conclusion, more thought is required regarding the role of adaptive human feedback when we evaluate early warning signals for regime shifts in ecosystems, because the presence of human feedback can qualitatively change outcomes. Although the challenges in modeling coupled human–environment systems are considerable, the stakes are correspondingly high. It may be possible to meet these challenges in the coming years through new data sources and greater interdisciplinary interactions in research on human–environment systems.
Supplementary Material
Acknowledgments
The authors are grateful to two anonymous reviewers for helpful comments. This research was supported by the Natural Sciences and Engineering Research Council of Canada and the James S. McDonnell Foundation.
Footnotes
This paper results from the Arthur M. Sackler Colloquium of the National Academy of Sciences, “Coupled Human and Environmental Systems,” held March 14–15, 2016, at the National Academy of Sciences in Washington, DC. The complete program and video recordings of most presentations are available on the NAS website at www.nasonline.org/Coupled_Human_and_Environmental_Systems.
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1604978113/-/DCSupplemental.
References
- 1.Liu J, et al. Complexity of coupled human and natural systems. Science. 2007;317(5844):1513–1516. doi: 10.1126/science.1144004. [DOI] [PubMed] [Google Scholar]
- 2.Berkes F, Folke C. Linking social and ecological systems for resilience and sustainability. In: Berkes F, Folke C, editors. Linking Social and Ecological Systems: Management Practices and Social Mechanisms for Building Resilience. Vol 1. Cambridge Univ Press; Cambridge, UK: 1998. pp. 13–20. [Google Scholar]
- 3.Berkes F, Folke C, Colding J. Linking Social and Ecological Systems: Management Practices and Social Mechanisms for Building Resilience. Cambridge Univ Press; Cambridge, UK: 2000. [Google Scholar]
- 4.Liu J, et al. Coupled human and natural systems. Ambio. 2007;36(8):639–649. doi: 10.1579/0044-7447(2007)36[639:chans]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 5.Turner BL, et al. A framework for vulnerability analysis in sustainability science. Proc Natl Acad Sci USA. 2003;100(14):8074–8079. doi: 10.1073/pnas.1231335100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Figueiredo J, Pereira HM. Regime shifts in a socio-ecological model of farmland abandonment. Landscape Ecol. 2011;26(5):737–749. [Google Scholar]
- 7.Filatova T, Polhill G. Shocks in coupled socio-ecological systems: What are they and how can we model them? In: Seppelt R, Voinov AA, Lange S, Bankamp D, editors. International Congress on Environmental Modelling and Software, Managing Resources of a Limited Planet iEMSs. The International Environmental Modelling & SoftwareSociety; Manno, Switzerland: 2012. pp. 2619–2630. [Google Scholar]
- 8.An L. Modeling human decisions in coupled human and natural systems: Review of agent-based models. Ecol Model. 2012;229:25–36. [Google Scholar]
- 9.Nelson KC, Brummel RF, Jordan N, Manson S. Social networks in complex human and natural systems: The case of rotational grazing, weak ties, and eastern us dairy landscapes. Agr Hum Val. 2014;31(2):245–259. [Google Scholar]
- 10.Sivapalan M, Blöschl G. Time scale interactions and the coevolution of humans and water. Water Resour Res. 2015;51(9):6988–7022. [Google Scholar]
- 11.Calvo-Alvarado J, McLennan B, Sánchez-Azofeifa A, Garvin T. Deforestation and forest restoration in Guanacaste, Costa Rica: Putting conservation policies in context. Forest Ecol Manag. 2009;258:931–940. [Google Scholar]
- 12.Mather A, Fairbairn J. From floods to reforestation: The forest transition in Switzerland. Environ Hist. 2000;6:399–421. [Google Scholar]
- 13.de Deus Medeiros J, Savi M, de Brito BFA. Seleção de áreas para criação de unidades de conservação na floresta ombrófila mista [Selection of areas for the creation of protected areas in the mixed rain forest] Biotemas. 2005;18(2):33–50. [Google Scholar]
- 14.Kangas J, Niemeläinen P. Opinion of forest owners and the public on forests and their use in Finland. Scand J Forest Res. 1996;11(1–4):269–280. [Google Scholar]
- 15.Davis A, et al. A Forestry Program for Oregon: Oregonians Discuss Their Opinions on Forest Management and Sustainability. A Quantitative Research Project. Davis, Hibbitts and McCaig; Portland, OR: 2001. [Google Scholar]
- 16.Lambin EF, Meyfroidt P. Land use transitions: Socio-ecological feedback versus socio-economic change. Land Use Pol. 2010;27(2):108–118. [Google Scholar]
- 17.Ludwig D, Mangel M, Haddad B. Ecology, conservation, and public policy. Annu Rev Ecol Syst. 2001;32:481–517. [Google Scholar]
- 18.Drazin PG. Nonlinear Systems. Vol 10 Cambridge Univ Press; Cambridge, UK: 1992. [Google Scholar]
- 19.Dakos V, Carpenter SR, van Nes EH, Scheffer M. Resilience indicators: Prospects and limitations for early warnings of regime shifts. Philos Trans R Soc B Biol Sci. 2015;370(1659):20130263. [Google Scholar]
- 20.Scheffer M, Carpenter SR, Dakos V, van Nes EH. Generic indicators of ecological resilience: Inferring the chance of a critical transition. Annu Rev Ecol Evol Syst. 2015;46:145–167. [Google Scholar]
- 21.Scheffer M, et al. Early-warning signals for critical transitions. Nature. 2009;461(7260):53–59. doi: 10.1038/nature08227. [DOI] [PubMed] [Google Scholar]
- 22.Lindenmayer DB, Hobbs RJ, Likens GE, Krebs CJ, Banks SC. Newly discovered landscape traps produce regime shifts in wet forests. Proc Natl Acad Sci USA. 2011;108(38):15887–15891. doi: 10.1073/pnas.1110245108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Scheffer M, Hirota M, Holmgren M, Van Nes EH, Chapin FS. Thresholds for boreal biome transitions. Proc Natl Acad Sci USA. 2012;109(52):21384–21389. doi: 10.1073/pnas.1219844110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Trumbore S, Brando P, Hartmann H. Forest health and global change. Science. 2015;349(6250):814–818. doi: 10.1126/science.aac6759. [DOI] [PubMed] [Google Scholar]
- 25.Boyd WE. Social change in late Holocene mainland SE Asia: A response to gradual climate change or a critical climatic event? Quat Int. 2008;184(1):11–23. [Google Scholar]
- 26.Streeter R, Dugmore A. Late-Holocene land surface change in a coupled social–ecological system, southern Iceland: A cross-scale tephrochronology approach. Quat Sci Rev. 2014;86:99–114. [Google Scholar]
- 27.Flenley JR, King SM. Late quaternary pollen records from Easter Island. Nature. 1984;307:47–50. [Google Scholar]
- 28.Majumder MS, Cohn EL, Mekaru SR, Huston JE, Brownstein JS. Substandard vaccination compliance and the 2015 measles outbreak. JAMA Pediatr. 2015;169(5):494–495. doi: 10.1001/jamapediatrics.2015.0384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Filatova T, Polhill JG, van Ewijk S. Regime shifts in coupled socio-environmental systems: Review of modelling challenges and approaches. Environ Model Softw. 2016;75:333–347. [Google Scholar]
- 30.Sugiarto HS, Chung NN, Lai CH, Chew LY. Socioecological regime shifts in the setting of complex social interactions. Phys Rev E. 2015;91(6):062804. doi: 10.1103/PhysRevE.91.062804. [DOI] [PubMed] [Google Scholar]
- 31.Sugiarto HS, Chew LY, Chung NN, Lai CH. New Developments in Computational Intelligence and Computer Science. Institute for Natural Sciences and Engineering; Montclair, NJ: Complex social network interactions in coupled socio-ecological system: Multiple regime shifts and early warning detection. [Google Scholar]
- 32.Oraby T, Thampi V, Bauch CT. The influence of social norms on the dynamics of vaccinating behaviour for paediatric infectious diseases. Proc R Soc Lond B Biol Sci. 2014;281(1780):20133172. doi: 10.1098/rspb.2013.3172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lade SJ, Tavoni A, Levin SA, Schlüter M. Regime shifts in a social-ecological system. Theor Ecol. 2013;6(3):359–372. [Google Scholar]
- 34.Ludwig D, Walker B, Holling CS. Sustainability, stability, and resilience. Conserv Ecol. 1997;1(1):7. [Google Scholar]
- 35.Stokols D, Lejano RP, Hipp J. Enhancing the resilience of human-environment systems: A social ecological perspective. Ecol Soc. 2013;18(1):7. [Google Scholar]
- 36.Dearing JA, et al. Safe and just operating spaces for regional social-ecological systems. Global Environ Change. 2014;28:227–238. doi: 10.1016/j.scitotenv.2018.10.118. [DOI] [PubMed] [Google Scholar]
- 37.Horan RD, Fenichel EP, Drury KL, Lodge DM. Managing ecological thresholds in coupled environmental–human systems. Proc Natl Acad Sci USA. 2011;108(18):7333–7338. doi: 10.1073/pnas.1005431108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Crépin AS, Biggs R, Polasky S, Troell M, de Zeeuw A. Regime shifts and management. Ecol Econ. 2012;84:15–22. [Google Scholar]
- 39.van Nes EH, Scheffer M. Implications of spatial heterogeneity for catastrophic regime shifts in ecosystems. Ecology. 2005;86(7):1797–1807. [Google Scholar]
- 40.Martín PV, Bonachela JA, Levin SA, Muñoz MA. Eluding catastrophic shifts. Proc Natl Acad Sci USA. 2015;112(15):E1828–E1836. doi: 10.1073/pnas.1414708112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dakos V, et al. Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS One. 2012;7(7):e41010. doi: 10.1371/journal.pone.0041010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Scheffer M, et al. Anticipating critical transitions. Science. 2012;338(6105):344–348. doi: 10.1126/science.1225244. [DOI] [PubMed] [Google Scholar]
- 43.Wang R, et al. Flickering gives early warning signals of a critical transition to a eutrophic lake state. Nature. 2012;492(7429):419–422. doi: 10.1038/nature11655. [DOI] [PubMed] [Google Scholar]
- 44.Zhang K, et al. Poverty alleviation strategies in eastern China lead to critical ecological dynamics. Sci Total Environ. 2015;506:164–181. doi: 10.1016/j.scitotenv.2014.10.096. [DOI] [PubMed] [Google Scholar]
- 45.Boettiger C, Ross N, Hastings A. Early warning signals: The charted and uncharted territories. Theor Ecol. 2013;6(3):255–264. [Google Scholar]
- 46.Hastings A, Wysham DB. Regime shifts in ecological systems can occur with no warning. Ecol Lett. 2010;13(4):464–472. doi: 10.1111/j.1461-0248.2010.01439.x. [DOI] [PubMed] [Google Scholar]
- 47.Dakos V, Van Nes EH, D’Odorico P, Scheffer M. Robustness of variance and autocorrelation as indicators of critical slowing down. Ecology. 2012;93(2):264–271. doi: 10.1890/11-0889.1. [DOI] [PubMed] [Google Scholar]
- 48.Boettiger C, Hastings A. Tipping points: From patterns to predictions. Nature. 2013;493(7431):157–158. doi: 10.1038/493157a. [DOI] [PubMed] [Google Scholar]
- 49.Suweis S, D’Odorico P. Early warning signs in social-ecological networks. PLoS One. 2014;9(7):e101851. doi: 10.1371/journal.pone.0101851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Richter A, Dakos V. Profit fluctuations signal eroding resilience of natural resources. Ecol Econ. 2015;117:12–21. [Google Scholar]
- 51.Kareva I, Berezovskaya F, Castillo-Chavez C. Transitional regimes as early warning signals in resource dependent competition models. Math Biosci. 2012;240(2):114–123. doi: 10.1016/j.mbs.2012.06.001. [DOI] [PubMed] [Google Scholar]
- 52.Satake A, Rudel TK. Modeling the forest transition: Forest scarcity and ecosystem service hypothesis. Ecol Appl. 2007;17(7):2024–2036. doi: 10.1890/07-0283.1. [DOI] [PubMed] [Google Scholar]
- 53.Innes C, Anand M, Bauch CT. The impact of human-environment interactions on the stability of forest-grassland mosaic ecosystems. Sci Rep. 2013;3:2689. doi: 10.1038/srep02689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.May RM. Uses and abuses of mathematics in biology. Science. 2004;303(5659):790–793. doi: 10.1126/science.1094442. [DOI] [PubMed] [Google Scholar]
- 55.Noy-Meir I. Stability of grazing systems: An application of predator-prey graphs. J Ecol. 1975;63(2):459–481. [Google Scholar]
- 56.Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge Univ Press; Cambridge, UK: 1998. [Google Scholar]
- 57.Bauch CT. Imitation dynamics predict vaccinating behaviour. Proc R Soc Lond B Biol Sci. 2005;272(1573):1669–1675. doi: 10.1098/rspb.2005.3153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Fishburn PC. 1970. Utility theory for decision making (DTIC document). Technicalreport (Research Analysis Corporation, Wiley, New York)
- 59.Smith JM. Evolution and the Theory of Games. Cambridge Univ Press; Cambridge, UK: 1982. [Google Scholar]
- 60.Henderson KA, Anand M, Bauch CT. Carrot or stick? Modelling how landowner behavioural responses can cause incentive-based forest governance to backfire. PLoS One. 2013;8(10):e77735. doi: 10.1371/journal.pone.0077735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Barlow LA, Cecile J, Bauch CT, Anand M. Modelling interactions between forest pest invasions and human decisions regarding firewood transport restrictions. PLoS One. 2014;9(4):e90511. doi: 10.1371/journal.pone.0090511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Bauch CT, Bhattacharyya S. Evolutionary game theory and social learning can determine how vaccine scares unfold. PLoS Comput Biol. 2012;8(4):e1002452. doi: 10.1371/journal.pcbi.1002452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bolsinger CL, Waddell KL. Area of Old-Growth Forests in California, Oregon, and Washington. US Department of Agriculture, Forest Service, Pacific Northwest Research Station; Portland, OR: 1993. [Google Scholar]
- 64.Hastings A. Complex interactions between dispersal and dynamics: Lessons from coupled logistic equations. Ecology. 1993;74(5):1362–1372. [Google Scholar]
- 65.Capasso V, Serio G. A generalization of the Kermack-McKendrick deterministic epidemic model. Math Biosci. 1978;42(1):43–61. [Google Scholar]
- 66.Rand D, Keeling M, Wilson H. Invasion, stability and evolution to criticality in spatially extended, artificial host-pathogen ecologies. Proc R Soc Lond B Biol Sci. 1995;259(1354):55–63. [Google Scholar]
- 67.Pagnutti C, Bauch CT, Anand M. Outlook on a worldwide forest transition. PLoS One. 2013;8(10):e75890. doi: 10.1371/journal.pone.0075890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Durrett R, Levin S. The importance of being discrete (and spatial) Theor Popul Biol. 1994;46(3):363–394. [Google Scholar]
- 69.Salathé M, Bonhoeffer S. The effect of opinion clustering on disease outbreaks. J R Soc Interface. 2008;5(29):1505–1508. doi: 10.1098/rsif.2008.0271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Salathé M, Khandelwal S. Assessing vaccination sentiments with online social media: Implications for infectious disease dynamics and control. PLoS Comput Biol. 2011;7(10):e1002199. doi: 10.1371/journal.pcbi.1002199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Towers S. Mass media and the contagion of fear: The case of Ebola in America. PLoS One. 2015;10(6):e0129179. doi: 10.1371/journal.pone.0129179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wang Z, Andrews MA, Wu ZX, Wang L, Bauch CT. Coupled disease–behavior dynamics on complex networks: A review. Phys Life Rev. 2015;15:1–29. doi: 10.1016/j.plrev.2015.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.