Scaling theory for quasibrittle structural failure

Abstract

This inaugural article has a twofold purpose: (i) to present a simpler and more general justification of the fundamental scaling laws of quasibrittle fracture, bridging the asymptotic behaviors of plasticity, linear elastic fracture mechanics, and Weibull statistical theory of brittle failure, and (ii) to give a broad but succinct overview of various applications and ramifications covering many fields, many kinds of quasibrittle materials, and many scales (from 10^–8 to 10⁶ m). The justification rests on developing a method to combine dimensional analysis of cohesive fracture with second-order accurate asymptotic matching. This method exploits the recently established general asymptotic properties of the cohesive crack model and nonlocal Weibull statistical model. The key idea is to select the dimensionless variables in such a way that, in each asymptotic case, all of them vanish except one. The minimal nature of the hypotheses made explains the surprisingly broad applicability of the scaling laws.

Discovery of the concept of stress and strength by Galileo (1) may, in retrospect, be regarded as the first scaling theory of solid mechanics. This theory, now known to apply only to elastoplastic behavior, captures the fact that, under controlled load P, geometrically similar structures of different sizes D fail at the same nominal stress σ_N, defined as the maximum stress in the structure (if no stress singularities exist) or simply as σ_N = P/D² or P/bD for three- or two-dimensional scaling (b = structure thickness). Any departure from such scaling came to be known as the “size effect.”

About 350 years ago, Mariotte (2) pointed out that a size effect must arise because the local material strength is random and its minimum encountered in a structure decreases with D. Nevertheless, proper mathematical formulation of this idea had to wait until 1939. That year, Weibull (3) experimentally demonstrated that σ_N for brittle structures has the probability distribution that came to bear his name, although already in 1928 this distribution was derived by Fischer and Tippett (4) as the only possible limiting distribution with a threshold for the minimum of a set of n independent random variables for n → ∞. The tail of this distribution is a power law, from which Weibull deduced that the statistical size effect is also a power law, the exponent of which is a function of the coefficient of variation ω of material strength.

For half a century afterward, whenever a size effect was observed, it was generally attributed to Weibull theory (3, 5, 6), which was amply confirmed for fatigued metals and fine-grained ceramics. However, beginning with studies of concrete for nuclear reactors during 1970–1985, it gradually transpired that Weibull theory does not apply to materials now termed “quasibrittle” (7–9). These are materials in which the fracture process zone (FPZ) is not negligible compared with the cross-section dimension D (and may even encompass the entire cross section).

Depending on the scale of observation or application, quasibrittle materials include concrete, fiber composites, toughened ceramics, rigid foams, nanocomposites, sea ice, consolidated snow, rocks, mortar, masonry, fiber-reinforced concretes, stiff clays, silts, grouted soils, cemented sands, wood, paper, particle board, filled elastomers, various refractories, coal, dental cements, bone, cartilage, biological shells, cast iron, and modern tough alloys. In these materials, the FPZ (the length of which is usually 5–50 times the dominant material inhomogeneity size) undergoes softening damage such as microcracking; it represents almost the entire nonlinear zone at the crack tip, and the transverse stress declines gradually along the FPZ length (9–13). In ductile fracture of metals, by contrast, the FPZ is essentially a point within a large nonlinear zone undergoing plastic yielding rather than damage. The FPZ length can vary enormously; it is typically ≈50 cm in normal concretes, 5 cm in high-strength concretes, 10 μm to 1 mm in fine-grained ceramics, 10 nm in a silicon wafer, 100 m in a mountain mass intersected by rock joints, 1–10 m in an Arctic sea ice floe, and ≈20 km in the ice cover of Arctic Ocean (consisting of thick floes a few kilometers in size, connected by thin ice). If the FPZ is negligible compared with D, a quasibrittle material becomes perfectly brittle, i.e., follows linear elastic fracture mechanics (LEFM). Thus, concrete is quasibrittle on the scale of normal beams and columns but perfectly brittle on the scale of a dam. Arctic Ocean cover, fine-grained ceramic, or nanocomposite are quasibrittle on the scale of 10 km, 0.1 mm, or 0.1 μm but brittle on the scale of 1,000 km, 1 cm, or 10 μm, respectively.

Scaling Laws and Their Asymptotic Support

Asymptotics of Energetic Size Effect. First, let us show an elementary explanation of the nonstatistical size effect in a very specific situation (14). Consider rectangular panels of different sizes under initially uniform uniaxial tension σ_N (Fig. 1a) and assume that their failure modes are similar, which means that a₀/D = constant at maximum load P_max (a₀ = crack length excluding the FPZ). Formation of a crack relieves the stress, and thus releases strain energy, approximately from the shaded triangles on the crack flanks, limited by lines of some slope k emanating from the middle of the FPZ. To determine k, one would need to solve the boundary value problem of elasticity, but for us it suffices to know that k is constant for similar panels of different sizes D. The potential energy (ends being fixed) is 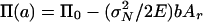where Π₀ = constant and A_r = area of the triangles = ka² (a = a₀ + c_f ≈ equivalent crack length, c_f = constant ≈ half length of the FPZ; Fig. 1a). The supports being fixed, the fracture can grow if the rate of energy release, –∂Π/∂a, is equal to the energy dissipation rate bG_f (G_f = fracture energy of material). Solving σ_N from this condition, one obtains the classical energetic size effect law for failures with large cracks or notches (14) (Fig. 1 e and j–p):

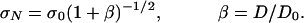[1]

D₀ = c_f(D/a₀) and σ₀ = (EG_f/kc_f)^1/2 are constants (independent of D). The size-effect law in Eq. 1 applies to many geometries. It was verified experimentally and justified theoretically for a surprisingly broad range of many different materials and structures (9, 12–23). The law was derived by asymptotic approximations of equivalent LEFM (9, 15, 18, 24), of the cohesive crack model (9, 12) and of J-integral (25) and was verified by numerical simulations with the crack band model, nonlocal-damage model, and various types of random-particle or lattice models. Another nonstatistical scaling law of broad applicability was later found for failures at crack initiation (9, 12, 13, 17, 26–32).

Fig. 1.

Explanation of the causes and trends of size effect and documentation of its experimental support and engineering application. (a and b) Size-effect sources in notched and unnotched beam. (c) Stress-separation curve. (d–i) Size-effect laws. (j–q) Type 1 and 2 size-effect laws compared with tests of various materials (referenced in refs. 9, 12, and 13). (r) Universal size-effect law. (s and t) Example of Malpasset Dam and its size effect.

It will now be shown that both scaling laws follow logically from the general asymptotic properties of quasibrittle fracture if one exploits the asymptotic matching philosophy well known from fluid mechanics (33–36). Although the asymptotic matching properties of the size-effect laws were recently highlighted (12, 13, 37–39), a systematic matching procedure was not used and will be presented here.

As a compromise between reality and simplicity, quasibrittle fracture may be described by the cohesive (or fictitious) crack model, originated by Barenblatt (40) and extended by others (9, 41–44). The FPZ at the crack front (Fig. 1 a, e, and o) is modeled as a fictitious line crack transmitting cohesive (crack-bridging) stresses σ = f_tϕ(w̄); w̄ = wf_t/G_f = dimensionless opening; w = crack opening (separation); f_t = tensile strength of material; ϕ(w̄) = monotonically decreasing (softening) function (Fig. 1c), assumed to have a finite initial slope; 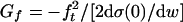= area under the initial tangent of σ (w)-curve (Fig. 1c); G_f is called the initial fracture energy, to be distinguished from the usual fracture energy 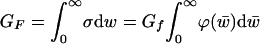= total area under the complete σ(w)-curve (Fig. 1c) = critical energy flux into the FPZ in infinite body (41). By definition, ϕ(0) = 1 and ϕ′(0) = –1/2.

Depending on the first two nonzero terms of the asymptotic expansions in powers of D and D^–1, there exist three and only three types of size effect (12, 13, 37):

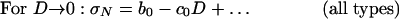[2]

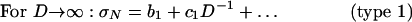[3]

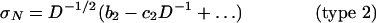[4]

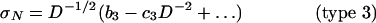[5]

where b₀, c₀,..., c₃ are positive constants determined by structure geometry (sections 2.12 and 9.4 and equations 9.61, 9.39, and 9.73 in ref. 12). Type 1 (Fig. 1d) occurs if the geometry is such that P_max is reached at crack initiation from the FPZ at a smooth surface, i.e., as soon as the FPZ is fully formed; type 2 (Fig. 1e) occurs if there is a large notch or preexisting stress-free (fatigued) crack and if the geometry is positive (12), i.e., such that P_max occurs while the FPZ is still attached to the tip; and type 3 occurs if a large crack can grow stably prior to P_max [negative geometry (12)]. The size-effect types 1 and 2 are very different, but types 2 and 3 are quite similar and hardly distinguishable in fracture testing (Fig. 1e). Eq. 2 was derived by perturbation analysis of the elastic boundary value problem (12, 13, 37). Eqs. 3–5 were derived from equivalent LEFM and verified by asymptotic expansions based on the smeared-tip method (12, 13, 15, 45).

The first terms in Eqs. 2–5 represent power-law scaling. Transition from one power law to another is normally handled by renormalization group transformation (34). This transformation, however, merely identifies the intersection of adjacent power laws, relating one power law to another. It does not describe the gradual transition between them, which can be very broad, often spanning 3 or 4 orders of magnitude. Thus, the second asymptotic terms are important, too.

Asymptotics of Energetic-Statistical Size Effect. In Weibull theory, the failure probability at a continuum point is assumed to be a function of the stress at that point. However, for heterogeneous (quasibrittle) materials, one must introduce a nonlocal generalization in which it is assumed that the probability of failure at a given point of the macroscopic smoothing continuum is a function of the average strain in a certain neighborhood of that point, the size of which is a material property (46). This hypothesis, which was shown to give good agreement with experimental observations (29–32), has the nonlocal damage model as its deterministic limit and permits dealing with failures occurring not only at crack initiation (type 1) but also after large crack growth (types 2 and 3). Numerical simulations as well as asymptotic approximations of nonlocal Weibull theory (46) have shown that, in quasibrittle failures, material randomness does not appreciably affect the mean energetic size effect except for large structures failing at crack initiation. Therefore, the asymptotic properties in Eqs. 2–5 apply to the mean σ_N, except that Eq. 3 for asymptotic type 1 size effect must be modified:

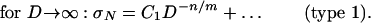[6]

Here m = Weibull modulus and n = number of dimensions in which the structure is scaled (n = 1, 2, 3); typically, m = 10–40 and n/m « 1. Eq. 6 means, not surprisingly, that Weibull size effect must apply for failures at crack initiation if the FPZ is negligible compared with D.

Asymptotic Matching Law for Type 2 or 3 Scaling. The general approximate size-effect law can be derived by combining dimensional analysis with asymptotic matching. From the Π-theorem of dimensional analysis (33, 34), two special size effects can be readily proven: (i) if the failure depends on f_t (dimension N/m²) but not G_f, then there is no size effect, i.e., σ_N = constant (this is so for all elastoplastic failures); (ii) if the failure depends on G_f (dimension J/m²) but not on f_t, then there is a size effect of the type σ_N ∝ D^–1/2 (this is so for LEFM if the cracks or notches are geometrically similar). Nothing more can be deduced from dimensional analysis alone.

One can, however, deduce more information after considering the physical meaning of the material characteristic length governing the FPZ size, 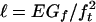(47). The FPZ length and width for D → ∞ are ηℓ and η′ℓ where η and η′ are constants of the order of 1 depending on microstructure characteristics (the parameter l_e = G_f/E is also a length but is irrelevant for failure because it controls the ratio of deformation to stress intensity factor K_I in LEFM). Depending on the ratio D/ℓ, two asymptotic cases may be distinguished (Fig. 1 e and j–p). (i) When D/ℓ → 0, the body is much smaller than a fully developed FPZ. Thus, G_f cannot matter. Therefore, the case of no size effect, σ_N = constant, is the small-size asymptote. (ii) When D/ℓ → ∞, the FPZ becomes a point in dimensionless coordinates and the stress field approaches a singularity. Thus, f_t cannot matter. Therefore, the LEFM scaling, σ_N ∝ D^–1/2, is the large-size asymptote of quasibrittle failure [which is represented by a straight line of slope –1/2 in the plot of log σ_N versus log D (Fig. 1 e and j–p)]. For the intermediate sizes, the size-effect curve may be expected to be a gradual transition between these two asymptotes. It will now be shown that the approximate form of this transition can be deduced after noting how the asymptotes are approached, i.e., by exploiting the higher-order asymptotic terms in Eqs. 2 and 4.

Examining the formulation of the boundary value problem with cohesive crack to dimensionless variables, one concludes that [if the structure shape, a₀/D and curve ϕ(w̄) are fixed] σ_N depends on only three parameters, f_t, D and K_c, where K_c = (EG_f)^1/2 = mode I fracture toughness for plane strain, E = Young's modulus [for plane stress, E needs to be everywhere in this article replaced by E′ = E/(1 – ν²); ν = Poisson ratio]. Thus, there are four governing parameters, σ_N, D, f_t, and K_c. Because they involve two independent physical dimensions (length and force), the Π-theorem (33, 34) implies that there can be only 4 – 2, i.e., two independent dimensionless parameters, Π₁ and Π₂.

So, the equation governing failure may be written as F(Π₁, Π₂) = 0, where function F is assumed to be sufficiently smooth. Although many diverse choices of Π_i (i = 1, 2) are possible, the key idea proposed here is to make a choice for which, in each asymptotic case, all Π_i vanish except one. If consideration is limited to dimensionless monomials, this can be most generally achieved by choosing

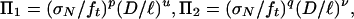[7]

where p, q, u, and v are four unknown real constants. Indeed, if we let Π₁ = 0 correspond to D → 0, then F(0, Π₂) = 0, which implies that Π₂ = constant or 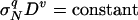for D → 0, which must be the case of no size effect; hence, v = 0. If we let Π₂ = 0 correspond to D → ∞, then F(Π₁, 0) = 0, which implies that Π₁ = constant or 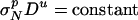, or σ_N ∝ D^–u/p for D → ∞, which must be the LEFM scaling; hence, u/p = 1/2 or u = p/2. To find p and q, we truncate the Taylor series expansion of F after the linear terms:

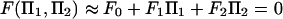[8]

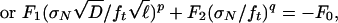[9]

where F₁ = [∂F/∂Π₁]₀ and F₂ = [∂F/∂Π₂]₀ (evaluated at Π₁ = Π₂ = 0) and F₀ = F(0, 0) (F₀, F₁, F₂ ≠ 0). For general p and q, the last equation cannot be solved explicitly for σ_N, but it can for D:

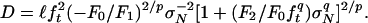[10]

This may be compared with the inverse of the large-size asymptotic expansion (Eq. 4), which has the form

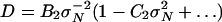[11]

for σ_N → 0 (B₂, C₂ = positive constants). Evidently, matching of the first two terms of this expansion requires p = q = 2. Then, Eq. 9 can be solved for σ_N. This yields, and verifies, the size-effect law (Eq. 1) (Fig. 1 e and j–p) in which σ₀ = f_t(–F₀F₂)^–1/2 and D₀ = ℓF₂/F₁. For D → 0, Eq. 1 has the approximation

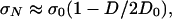[12]

which verifies that the form of the second term of small-size expansion (Eq. 2) can be matched, too. Thus, Eq. 1 is the simplest formula for type 2 size effect that can match four asymptotic terms, two for D → 0 and two for D → ∞. [However, if not only the form of the second-order terms but also the values of all four coefficients b₀, c₀, b₂, and c₂ are given, a slightly more general formula with four adjustable parameters is needed (48).]

More complex formulas of the same asymptotic accuracy, but more flexible in data fitting, can be obtained by replacing Eq. 7 with dimensionless polynomials (or other monotonic functions of Π₁ and Π₂). Such formulas can make a significant difference only if the size effect needs to be modeled for a size range exceeding ≈1½ orders of magnitude of D. Their merit is that they can capture a spectrum of fracture energies (12, 49), each of which is associated with a different order of magnitude of D.

The type 3 size-effect formula ensues similarly. The result is

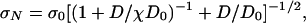[13]

where σ₀, D₀, and χ = constants (Fig. 1e). To ensure monotonicity, χ ≥ 1 (12, 37).

Asymptotic Matching Law for Type 1 Scaling. Failures at macrocrack initiation from a smooth surface need a somewhat different approach. They can be treated as a limit case of finite crack for a₀ → 0 (12, 15, 28), but because the energy release rate at crack initiation is zero, it is easier to analyze the stress redistribution caused by a finite FPZ that releases energy and must occur before a macrocrack can initiate. The nonstatistical type 1 size effect (also called, albeit not quite accurately, the strain-gradient effect) can be instructively explained by the flexural test of a beam (Fig. 1 b and q) (26). G_f is here irrelevant for P_max, and what matters is the thickness, λℓ, of the boundary layer of cracking (λ being a constant of the order of 1, depending on microstructure properties). P_max occurs roughly when the average of the elastically calculated flexural stress σ over the thickness of the boundary layer equals f_t, i.e., when k_MMc/I = f_t, in which I = bh³/12, c = D/2 – λℓ/2, M = k_ML(σ_NbD) = bending moment, L = beam span, and k_M = constant for geometrically similar beams. Solution yields 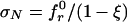, where ξ = λℓ/D and 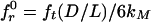(26). This approximation is second-order accurate for ξ « 1 or D » ℓ but unacceptable for smaller D because it jumps to negative σ_N. To get acceptable approximation of the same second-order accuracy in D^–1, set (1 – ξ)^–1 ≈ (1 + rξ)^1/r (r = constant ≠ 0); this gives the deterministic type 1 size effect (Fig. 1d):

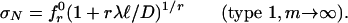[14]

For general dimensional analysis, we need a slightly different procedure than for type 2. Consider the deterministic type 1 first (m → ∞). Because, according to Eqs. 2 and 3, both asymptotes in the plot of log σ_N vs. log D are horizontal, the curve in Fig. 1d must have an inflexion point. This postulating suggests the existence of what is called an “intermediate asymptote” (34), which consists of some unknown power law. Because it separates the large-size and small-size asymptotics, we now try to match the large-size asymptotic terms alone and choose the large-size asymptote to correspond to Π₁ = 0, i.e., to F(0, Π₂) = 0. This means that Π₂ = constant for D → ∞, and thus v = 0 in Eq. 7. The linear approximation (Eq. 8) cannot in general be solved for σ_N, but it can for D:

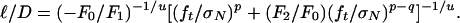[15]

The large-size expansion may be generalized as σ_N = (b₁ + rc₁D^–1 +...)^1/r, without contradicting Eq. 3 (r = arbitrary constant ≠ 0). The inverse expansion is 1/D = (–b₁ + σ^r +...)/rc₁, and matching of Eq. 15 obviously requires u =–1 and p = q = –r in Eq. 7. So Π₁ = (f_t/σ_N)^rℓ/D and Π₂ = (f_t/σ_N)^r. Now Eq. 8 can be solved for σ_N. This yields, and thus verifies, Eq. 14, in which λ = F₁/rF₂ and .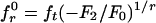

For the statistical case (m < ∞), we again choose the large-size asymptote to correspond to Π₁ = 0, Π₂ = constant. To match Eq. 6, σ_N = C₁D^–n/m ∝ f_t(D/ℓ)^–v/q; thus, v/q = n/m. Not to loose the deterministic limit, we keep p = q = –r and u = –1. Eq. 8 can now be solved for σ_N, which leads to the mean type 1 energetic-statistical size effect (Fig. 1 d and q),

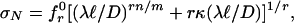[16]

where 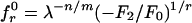, κ = λ^rn/m–1F₁/F₂r, and r is a parameter of the order of 1, sensitive to structure geometry.

Eq. 16, however, violates the small-size asymptotics in Eq. 2, and therefore must be modified further, but without affecting the first two large-size asymptotic terms. To bridge the small-size and intermediate asymptotes, we could engage in similar arguments as we did for bridging the large-size and intermediate asymptotes. Suffice to say, the complete law for the mean-size effect of type 1 (Fig. 1d), matching the small-size asymptotics in Eq. 2, is obtained by replacing λℓ/D in Eq. 16 with θ (39):

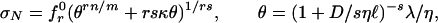[17]

where η = positive constant of the order of 1 and s may be taken as 1. Note that if we let η « D/ℓ « λ, or λ/η → ∞, Eq. 17 converges to the intermediate asymptote, which is given by the power law σ_N = s₀(κrη₀ℓ)^1/r D^–1/r and coincides with the small-size asymptote of Eq. 16 as well as with the large-size asymptote of 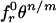. The physical reason for the existence of an intermediate asymptote is that normally the size of averaging domain in nonlocal Weibull theory (approximately the FPZ width) is much smaller than the FPZ length (39). Eq. 17 is supported by finite element simulations with nonlocal Weibull theory as well as test data from 10 different labs [all combined in one dimensionless plot in Fig. 1q (29–31)]. However, test data for concrete and composites show that the D values for which the difference between Eqs. 16 and 17 is significant are less than the material inhomogeneities, which means that Eq. 16 should mostly suffice in practice.

For bending of laminates or unreinforced concrete beams, the Weibull statistical component in Eq. 16 or 17 is usually insignificant for normal sizes (30, 50). It becomes significant only for bending fracture of very large structures such as arch dams.

Bridging of LEFM and Plasticity. To identify the size-effect parameters, one needs to anchor them to LEFM for D → ∞ and to plasticity for D → 0. In LEFM, the dimensionless energy release function g(α) characterizes the effect of structure geometry; it is defined as g(α) = k²(α), where α = a/D = relative length of crack or notch and 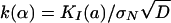. The tip α of an equivalent LEFM crack is placed into the middle of the FPZ, and the LEFM relation σ_N = [EG_f/Dg(α)]^1/2 is expanded into Taylor series in θ = α – α₀ = c_f/D about the initial relative length α₀ of crack or notch, which is assumed to be the same for different D. Depending on which terms of this series vanish (first, second, or neither), and making sure that σ_N for D → 0 is finite (as required by plasticity), one obtains type 1 and 2 size-effect Eqs. 1 and 17. However, their parameters are now expressed in terms of g(α), which introduces the effect of structure geometry [similar formulas ensue more rigorously by the smeared-tip method, in which a cohesive crack is regarded as a superposition of infinitely many LEFM cracks with continuously distributed tips and infinitely small K_I (12)]. For type 2, the relation σ_N = [EG_f/Dg(α)]^1/2 with g(α) ≈ g(α₀) + g′(α₀)c_f/D yields Eq. 1 with

[18]

where 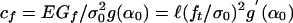≈ half of FPZ length at P_max (ref. 48, Eq. 13) (c_f depends on geometry but not on D); and β = D/D₀ = (D/c_f)g(α₀)/g′(α₀) = B²g(α₀)(D/ℓ) is called the brittleness number, because it characterizes proximity to the brittle behavior of LEFM, even for different geometries (18, 51); B is a geometry parameter of the order of 1, computed as if the crack were filled with a plastic “glue” (48).

Type 2 size effect has also been described in terms of equivalent 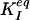, evaluated from tests as if c_f were 0, using LEFM; from Eq. 1 we have 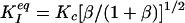(18, 51).

Eq. 16 for type 1 size effect (typical of flexure of unnotched unreinforced beams) can be obtained as the limit case of equivalent LEFM when α₀ → 0. Because g(0) = 0, one has 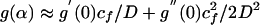. If (as usual) g″(0) < 0, the second-order approximation leads to Eq. 16, in which 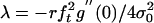, 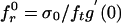(12, 28).

Universal Size-Effect Law. The size-effect that bridges types 1 and 2 (i.e., for short notches or short cracks comprised within the boundary layer) is more complex. Using similar asymptotic matching procedures, one can construct the universal size-effect law (17). Fig. 1r shows a plot of its formula (38) matching all the seven asymptotic terms in Eqs. 2 and 4, and in Eq. 6 for the statistical case (with finite m).

Scaling of Probability Density Distribution of Failure Load. Structures must typically be designed for failure probabilities p_f of the order of 10^–7. Such a low probability can be assessed only theoretically, taking into account the size effect on the probability density function (pdf) of σ_N, based on the nonlocal Weibull theory (39). For D → 0, failure is nonpropagating and must occur nearly simultaneously along the entire failure surface. Thus, the pdf of σ_N must be Gaussian (except in far-off tails), as deduced from Daniels' fiber bundle model (52) (Fig. 1f Upper Left). With increasing D, the asymptotic size effect on the mean strength is nil, and the coefficient of variation (CoV) asymptotically decreases as D^–1/2. For D → ∞, the pdf must be Weibull, corresponding to the weakest-link chain model (Fig. 1f Right), which implies a size-independent CoV. The gradual transition of pdf from Gaussian to Weibull, exemplified by various load-sharing models (53, 54), can be obtained by asymptotic matching (39) and calibrated by a chain-of-bundles model (Fig. 1f Center) (31).

Scaling for Interacting Fractures. Some failures require several fractures to form at different places. For example, statically indeterminate reinforced concrete beams or frames will collapse only after several critical cross sections (Fig. 1 h and i) develop fractures due to bending (either at the tensioned face or, if reinforced for tension, at the compressed face). For not too large D, the cohesive fractures in different cross sections develop simultaneously (Fig. 1h), causing a complex size effect. For D → 0, the behavior tends to be quasiplastic (Fig. 1g) with no size effect. For large enough D, the fractures occur in sequence (note the spikes in Fig. 1i), and then only one of them governs P_max (12, 13).

Some Generalizations. In compression fracture, e.g., kink bands in fiber composites, the softening curve of σ versus w may terminate with a finite residual stress σ_R. In that case, Eq. 1 must be replaced by

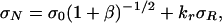[19]

(k_r = constant), which can be deduced from the J-integral (25). G_f now represents the area between curve σ(w) and line σ = σ_R. Eqs. 2–5 and 7–12 remain valid if σ_N is replaced by σ_N – k_rσ_R.

Shear fracture of mode II or III can be analyzed similarly, with G_f replaced by the shear fracture energy.

Conspectus of Applications and Ramifications

Now that the general theory has been expounded, various applications and ramification will be reviewed succinctly. There is no room for complete references; they are found in refs. 9, 12, and 13.

Standards for Material Fracture Testing. Expressing the size effect in Eq. 1 with 18 by means of function g(α) brings about the advantage that, by measuring the maximum loads for not-too-small notched specimens of different sizes (and possibly also different geometries), one can identify the mean and CoV of G_f, c_f, and ℓ (9, 12, 18, 24, 51) [this became a standardized testing method (55)]. The data fitting can be reduced to linear regression with slope 1/G_f and intercept c_f. The G_f thus obtained is the so-called initial fracture energy (48) (Fig. 1c) (roughly, G_f ≈ 0.4 G_F for concrete, although the scatter is large). The reason why the size-effect method yields G_f rather than G_F is that the cohesive stresses σ at P_max are everywhere in the FPZ of test specimens (as well as not-too-large structures) on the initial tangent (and not on the long tail, Fig. 1c) of the softening curve, exceeding f_t/3 everywhere (48, 56, 57) (which explains why G_f, rather than G_F, must be used in Eqs. 7–13).

Recent work led to a more convenient (zero-brittleness) version of the size-effect method of G_f testing (48), in which it suffices to measure the maximum loads of only one notched specimen of a small size and one small unnotched specimen [except for statistics, this method is equivalent to the measurement of initial slope (57)]. The unnotched specimen permits determining the zero-size limit σ₀ (27) of notched specimen strength, because for D → 0, failure is independent of G_f. For D → 0, the size-effect method based on equivalent LEFM requires a certain geometry-dependent correction, given by parameter B defined below Eq. 18 and computed from the cohesive crack model (48).

Measuring the type 2 size effect, one can also deduce the resistance curve (R curve), describing how the apparent fracture energy (determined as in LEFM) varies with the crack extension from a notch. The R curve is the envelope of the family of fracture equilibrium curves for various D, and using this property one can derive from Eq. 1 an expression for the R curve (9, 18, 24).

Compression Fracture and Concrete Columns. Compression failure of concrete and other particulate composites is normally caused by a band of compression splitting cracks, propagating either in the direction of compression or inclined to it. The former is preferred (because extension of the existing axial microcracks requires less energy than formation of new ones). However (similar to Fig. 1a), the inclined transverse propagation causes an asymptotically quadratic increase of energy release with fracture growth, whereas the axial propagation causes a linear increase. Therefore, the former must cause size effect, and the latter must not. So, there must exist a certain critical structure size above which the size effect will favor the inclined propagation. This behavior explains the size effect observed in concrete columns (9, 12, 13, 58) and large compression test specimens (59). The strain energy, and thus the size effect, is greater as the concrete columns are made more slender.

Stable growth of a tensile crack may provoke fracture under compressive stresses parallel to the tensile crack. This is so, e.g., for diagonal shear failure of reinforced concrete beams (60) (in which the size effect is due to compression fracture) and partly for compression punching of concrete slabs. However, for a dipping crack in gravity dam, running in compression direction, failure is caused not by compression but by a flexural crack branch through the ligament. Thus, compression fracture displays a rich palette of large-crack size effects.

Sea Ice Fracture. Size effects in sea ice have long been denied, because normal-size tests could not verify them. In retrospect, the reason was that brine voids, channels and pockets, thermal cracks, bottom roughness, and snow drifts cause the characteristic length of sea ice to be quite large: ℓ ≈ 2–10 m for horizontal and ≈0.5 m for vertical propagation of fracture (12, 25, 61). However, recent Arctic Ocean field tests of floating notched ice specimens of sizes up to 80 × 80 × 1.8 m, organized by Dempsey et al. (22), have established that, on the large scale, Eq. 1 is indeed followed, as predicted by both analytical and numerical studies of vertical penetration and of forces exerted against obstacles by moving ice (61). Eq. 1 explains why the forces measured on oil platforms are ≈1.5 orders of magnitude less than predicted by standard elastoplastic software.

Long cracks in the Arctic Ocean cover tend to run straight through thick ice floes rather than circuitously through thin ice between them. To explain this curious observation, it was shown (62) that the temperature drop ΔT needed to cause horizontal propagation of long flexural cooling cracks over the Arctic Ocean exhibits anomalous asymptotic scaling ΔT ∝ D^–3/8 rather than D^–1/2 (D = ice thickness). The reason is that the characteristic flexural wavelength L of a floating plate is proportional to D^3/4 rather than D, which means that ΔT ∝ L^–1/2, and D needs to be replaced by L in Eq. 1.

Failure of Fiber Composites. Similar to concrete or ice, this is another field in which size effects have generally been ignored in practice. However, tests (12, 25, 50, 63–65) motivated by new interest in building large ship and aircraft parts almost entirely with polymer composites clearly indicate a strong size effect, unobservable on the normal laboratory scale. For notched specimens, or structures in which a large crack or damage zone develops before P_max, the type 2 size-effect law (Eq. 1) was shown to apply (63), but the expressions for D₀ and σ₀ are complicated by material orthotropy and irregular or star-like shape of a large FPZ. Compression failure due to fiber kinking (with microbuckling) also follows type 2 size effect law (Eq. 1) but with a modification: σ_N must be replaced by σ_N – σ_r, where σ_r = residual compressive stress across the propagating kink band, equal to about a half of the initial compression strength (25). This was deduced from the compressive cohesive crack model for kink band using perturbation analysis of the J integral for the energy flux into the FPZ of kink band and was verified by tests of size effect in compression failure of unidirectional carbon–epoxy and carbon–PEEK (poly-ether-ether-keton) composites.

Fiber-reinforced concretes and polymers with short fibers exhibit more complex size effects, different for two local peaks on the load-deflection curve: one peak for matrix fracture and another for fracture and frictional pullout of fibers from the crack faces.

The size effect observed in flexural failure of laminates (66, 67) has long been attributed to pure Weibull statistical theory. The existing size-effect data alone can of course be fitted by that theory, but it has been neglected to check the corresponding CoV of strength, which would have to match Weibull theory but does not. Weibull moduli m obtained from size-effect data for various lay-ups of the same prepregs vary immensely (from 4 to 40), but this corresponds to CoV = 23% and 4%, respectively, both of which are totally unrealistic, thus ruling out pure Weibull size effect (50). The mean size-effect data can be matched consistently with the type 1 size-effect law (Eq. 16), in which the statistical part is irrelevant (equal to 1) for normal situations (thickness < 5 cm) and can matter only for much thicker laminates.

Foams, Sandwich Structures, and Composite Beams. Vinyl foam typically used for sandwich plates is normally thought to be ductile (68), but tests and simulations reveal a strong type 2 size-effect if the foam has a notch or damaged zone (64, 69–71). So, size effect must naturally be expected in sandwich plates with foam core, as indicated by preliminary tests. However, the size effect is complicated by core indentation, skin wrinkling, and delamination buckling.

Hierarchical Size Effects in Composite Structures. In a large steel–concrete composite beam, the connectors do not fail simultaneously, as plastic limit analysis dictates, but in sequence, similar to a propagating crack. Of course, size effect ensues. But the pullout of the connectors themselves from concrete slab also exhibits a size effect, amplifying the first. The result is a size “super effect,” such that σ_N ∝ D^–3/4 for D → ∞ (12, 13, 72).

Ceramics, Rocks, and Masonry. Testing of ceramics (e.g., refs. 18 and 73) shows them to be quasibrittle and exhibit a size effect of type 1 or 2 but on a smaller scale (ℓ from 0.1 to 10 mm). The same applies to intact rocks (24, 74). ℓ and D₀ are roughly proportional to the grain size (and can differ by as much as 100:1 between marble and breccia, e.g.). In rock masses, however, the dominant heterogeneity is not the grain size but the spacing of rock joints, typically ≈10 m. Accordingly, one must expect the characteristic length ℓ for size effect on the sliding of a mountain that consists of jointed rock to be of the order of 100 m. However, the rock excavation scale in normal construction is generally too small for significant size effect of this kind.

Masonry is also quasibrittle, with ℓ of the order of 1 m, which may help to explain the collapses of ancient massive towers in Italy, after about seven centuries of placid existence. The critical time is set by long-term drying of thick walls, causing shrinkage, which leads to compression failure of cladding, assisted by size effect (D. Ferretti and Z.P.B., unpublished results).

Breakout of Boreholes in Rock and Mining Excavations. The breakout of deep boreholes under remote compressive stress σ_N exhibits size effect as a function of borehole diameter D. There may be a residual stress σ_r, and it was shown that σ_N – σ_r asymptotically approaches either D^–1/2 or D^–2/5 (the anomalous exponent –2/5 arises if the spacing of axial splitting cracks around the borehole is not dictated by grain size but is free to minimize σ_N) (75). The explosive breakout of mining stopes doubtlessly exhibits a similar size effect.

Triggering of Snow Avalanches and Landslides. Dry snow-slab avalanches are triggered as mode II (shear) fractures in a weak layer at the slab base. The cohesive crack model leads to a type 2 size effect of slab thickness D but with a modification: the size effect depends on preexisting frictional stress in a weak layer and is offset by an effect of D (or snow weight) on fracture energy and residual shear stress. The theory correlates with hundreds of avalanche observations (21).

Structures with Finite Angle Notches. The power λ(γ) of the elastic stress singularity at finite-angle notches is known to decrease as the notch angle, 2γ, increases (76). However, P_max of a body with such a notch must be determined not from the singularity but from the analysis of a cohesive crack emanating from the notch tip. For γ → 0, the type 2 size effect must be approached: for γ → π, the type 2 size effect must disappear; and for D → ∞, Williams' (76) stress field must be approached for any γ. From these asymptotic conditions, one can deduce (by similar asymptotic matching as above) the size-effect formula

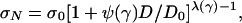[20]

where functions ψ(γ) and λ(γ) are taken from ref. 76. This formula agrees with finite element solutions for a cohesive crack emanating from the notch as well as with tests (38).

Fatigue, Rate Effect, and Dynamics. The classical Paris–Erdogan law for increments of crack length a per cycle, Δa/ΔN ∝ (CΔK_I)ⁿ, requires a size-effect correction of C if the FPZ is not negligible (ΔK_I = amplitude of cyclic K_I, and n = constant of the order of 10). Based on Eq. 1, it was shown that C = (1 + D₀/D)^–1/2 (9, 12, 13). Under monotonic or sustained loads, viscoelastic behavior of the material causes the FPZ to shorten, which makes the size effect and brittleness for slow or long-time loading greater than for fast or short-time loading (77). For very fast loading, the size effect is significantly modified by rate dependence of the softening stress-separation law of cohesive cracks (77). In dynamics, any type of viscosity η_v implies a characteristic length, ℓ_v = η_v/vρ, and then t_ch = ℓ/v becomes a characteristic time for developing size effect (v = wave velocity and ρ = mass density).

Size-Effect Simulation with the Cohesive Crack Model. Finite element computations of size effect with the cohesive crack model used to require step-by-step computation of the entire loading process for each size (43). However, the size-effect curve can be computed directly after conversion to an eigenvalue problem (12, 13, 78, 79). One must reformulate the problem in dimensionless variables, choose a series of relative crack lengths α_i (i = 1, 2,...), and then search for size D for which the condition dσ_N/dα = 0 is satisfied. This leads in dimensionless coordinates to a homogeneous Fredholm integral equation with D as the first eigenvalue. The load P_max corresponding to each α_i can then be accurately evaluated after integrating the eigenvector.

Size-Effect Simulation by Crack Band, Nonlocal, and Discrete Models. The theoretical length of a fully developed FPZ, as well as its width, may in some applications be much larger than the structural cross-section size D. In that case, typical for concrete and geotechnical engineering and often composites as well, the FPZ volume needs to be subdivided by finite elements, and the constitutive model must capture gradual strain softening of the material due to distributed damage. However, in the absence of countermeasures, the structural tangent stiffness matrix of such a model is not positive-definite. The result is ill conditioning of the boundary value problem, excessive strain localization into a set of measure zero, pathological zero-dissipation failure, spurious mesh sensitivity, and false size effect. The proper countermeasure is some form of nonlocal continuum concept (80), involving a material characteristic length ℓ. This is achieved by the nonlocal concept of damage (81) and its diverse refinements (82) [including statistical (31)], in which the nonlocal inelastic strain (or its parameter) at a continuum point is averaged over a zone of a certain characteristic size equal roughly to the FPZ width.

Frequently for large structures, the FPZ width need not be subdivided into finite elements, and then the simplest approach is the crack band model (8, 10), now widely used in industry and specialized commercial software (sbeta, diana, and atena). In that model, the postpeak portion of the softening constitutive law is scaled according to the finite element width so as to ensure correct energy dissipation. For localizing deformation, both the crack band and nonlocal models are approximately equivalent to the cohesive crack model. The long-standing challenge of a realistic three-dimensional constitutive model for softening damage in the FPZ has been met for concrete-like composites with the microplane model (83, 84). A more realistic nonlocal model requires capturing the tensorial interactions of microcracks of various orientations, with their spatial decay, and distinguishing between the shielding and amplification zones of each microcrack (85). Even better is direct simulation of the coarse microstructure by a random particle or lattice model (86).

Stochastic Finite Element Methods (SFEMs). Computing loads with required failure probability p_f ≤ ≈10^–7 is a challenge that cannot be met by the existing standard SFEMs, because they can capture only low-order statistical moments and not the far-off pdf tail. To meet this challenge, Weibull statistical size effect must ensue from SFEM for D → ∞ if the structure fails at crack initiation (32, 39). The existing standard SFEMs do not pass this check. As a remedy, the probabilistic theory of extreme values must be embedded in the SFEM in some way. This can be done by subdividing the structure into many domains scaled up with the structure size, in each of which the material strength limit is scaled down (according to the stability postulate of extreme value statistics) as a function of domain size (31).

Grim Example: Malpasset Dam. Collapse of this record-thin arch dam in 1959 flooded the town of Fréjus (founded by Caesar), killing almost 400 inhabitants. The identified direct cause (slipping of gneiss in abutment; Fig. 1s) is undisputable; however, according to scaling law (Eq. 16), the tolerable displacement of abutment would today be 51% smaller than considered in design in 1951 (30) (and doubtless still smaller if the pdf tail at p_f ≈ 10^–7 were properly taken into account). The scatter of energetic statistical size effect when the dam is scaled by various ratios is documented in Fig. 1t by computations of M. Vořechovský at Northwestern University (unpublished data) using a Weibull-adapted crack band model (31). Their mean matches Eq. 16 perfectly. Because this law can be calibrated by deterministic computations alone, the use of SFEM, extremely demanding computationally, can be skipped in practice.

Challenge for Concrete Design Codes. With many thousands of different structures designed annually, structural engineering (unlike aeronautical engineering) is a field that cannot get by without a simple design code. However, codes are approved by broad society committees and thus are notoriously difficult to update. Nevertheless, the size effect, with probabilistically justified safety provisions, must eventually be introduced into all the code articles guarding against brittle failures of various types (numbering ≈20) (60).

Scaling of Metal Plasticity at a Micrometer Scale. Free-standing metallic thin films with a thickness of ≈1 μm exhibit under pure tension a strong size effect and stable strain softening similar to concrete on a meter scale (Z.P.B., Z. Guo, and H. Espinosa, unpublished data). The cause is that, on the face that was in contact with substrate, there exists an epitaxially induced boundary layer of much elevated yield strength, which acts in the manner of a type 1 size effect. Moreover, in bending, torsion, and indentation tests, the yield strength is increased due to geometrically necessary dislocations associated with plastic strain gradients. Asymptotic scaling analysis analogous to the present one points out a way to improve the strain-gradient theory (13, 87) and explains the effect of particle size in metal–matrix nanocomposites.

Closing Comments

Even if the size effect per se is not the analyst's objective, the knowledge of size effect, or scaling, helps in obtaining analytical failure predictions in general. For the actual size of interest, a direct analytical solution may be next to impossible. However, by scaling the structure down to a vanishing size or up to an infinite size, one gets a problem of plasticity or LEFM, each of which is much easier. Knowing these asymptotic solutions, an approximate analytical solution for the actual size can then be obtained by asymptotic matching. It is for this reason that the size effect is the key problem for all quasibrittle failures.

Fracture scaling often interacts with spatial, temporal, and thermal scaling of mass transport and chemical processes. An example is the modification of size effect due to shrinkage stresses and microcracking caused by drying of concrete (56), which evolves initially as a square root of both depth and time, and the half-time of which scales as structure thickness square. Processes of material deterioration include microfracturing due to expansion of reacting particles of various sizes (e.g., alkali-silica reaction or sulphate attack in cements). Typically, particle reactivity goes up when the particle size decreases, but this is offset by the fact that the particle pressure required to fracture the matrix increases (88). Such phenomena, however, are beyond the scope of this overview, and so are the polemics on a possible role of crack fractality (20).

Further opportunities abound. One is bone, the microstructure of which is sure to cause quasibrittle behavior. Hardly explored from the present viewpoint are biological shells, wood, paper, particle board, stiff clays, silts, coal, super-strength alloys, and most materials on approach to nanoscale. It is doubtless much fertile ground lies beyond our horizon.