Cell size and growth regulation in the Arabidopsis thaliana apical stem cell niche

Significance

How does a cell decide when to divide or initiate DNA replication? How does it regulate its own growth? These fundamental questions are not well understood in most organisms; this lack of understanding is particularly true for multicellular eukaryotes. Following classical studies in yeast, we have quantified the key aspects of cell growth and division dynamics in the Arabidopsis apical stem cell niche. Our results disprove various theories for plant stem cell size/cell cycle regulation, such as that cell cycle progression is triggered when a prefixed critical size is attained, and constitute the necessary first step in the development of integrative mechanistic theories for the coordinated regulation of cell cycle progression, cell growth, and cell size in plants.

Abstract

Cell size and growth kinetics are fundamental cellular properties with important physiological implications. Classical studies on yeast, and recently on bacteria, have identified rules for cell size regulation in single cells, but in the more complex environment of multicellular tissues, data have been lacking. In this study, to characterize cell size and growth regulation in a multicellular context, we developed a 4D imaging pipeline and applied it to track and quantify epidermal cells over 3–4 d in Arabidopsis thaliana shoot apical meristems. We found that a cell size checkpoint is not the trigger for G2/M or cytokinesis, refuting the unexamined assumption that meristematic cells trigger cell cycle phases upon reaching a critical size. Our data also rule out models in which cells undergo G2/M at a fixed time after birth, or by adding a critical size increment between G2/M transitions. Rather, cell size regulation was intermediate between the critical size and critical increment paradigms, meaning that cell size fluctuations decay by ∼75% in one generation compared with 100% (critical size) and 50% (critical increment). Notably, this behavior was independent of local cell–cell contact topologies and of position within the tissue. Cells grew exponentially throughout the first >80% of the cell cycle, but following an asymmetrical division, the small daughter grew at a faster exponential rate than the large daughter, an observation that potentially challenges present models of growth regulation. These growth and division behaviors place strong constraints on quantitative mechanistic descriptions of the cell cycle and growth control.

How cells coordinate growth and division to achieve a particular cell size remains a fundamental question in biology. Our understanding of this basic property of cells is limited, in part, by the lack of quantitative data on cellular growth and size kinetics over multiple generations, especially in higher eukaryotes (1). Classical studies of cell size homeostasis focused on whether division occurred upon reaching a critical size or after a fixed time period has elapsed (2, 3). However, time-lapse studies of single-celled organisms spanning a range of bacteria (4–7) and the yeast Saccharomyces cerevisiae (8) have recently indicated that cell size is regulated by the addition of a fixed volume increment between divisions. Identification of the size regulation behavior constrains the set of feasible molecular scenarios for how growth and division are coordinated with the cell cycle (8–10). In multicellular tissues, the loss of growth and division/cell cycle coordination could have an impact on the organism’s development, yet, to the best of our knowledge, cell growth and size kinetics have never before been measured over generations in a tissue context. The experimental challenges are particularly acute because interdivision times are often on the order of tens of hours, cells have a diversity of shapes necessitating digital reconstruction in three dimensions to measure size accurately, and tissues are often difficult to access for imaging while keeping the organism alive. Further, the assumption, central to previous quantitative studies, of a fixed environment in which homeostasis is achieved, is generally invalid in multicellular tissues, where patterns of cellular differentiation can modulate growth and division.

The Arabidopsis thaliana shoot apical meristem (SAM) is a multicellular tissue whose central zone harbors stem cells that proliferate throughout the plant’s life span, dividing in-plane to produce the epidermis of all above-ground organs. As cells proliferate radially outward from the SAM’s central zone into the peripheral zone, they remain fixed in position relative to one another, experience a gradient of the stem cell reporter CLAVATA3, initiate developmental programs, increase their growth rates, and decrease their interdivision times (11–16). These tissue-level growth kinetics are common to several plant species (13, 16, 17). Current models of the SAM and other tissues have assumed that cells trigger cytokinesis upon reaching a critical size (18–20). SAM cells recover their normal mean size following a genetically induced transient size increase, indicating some degree of size regulation (21), although whether size is regulated by the critical size, critical increment, or some other rule remains untested. Further, it is not known if size regulation acts upon cell volume, surface area [as reported for fission yeast (22)], or some other metric (e.g., anticlinal surface area). Moreover, whether size regulation is dependent on cellular parameters such as cell shape or growth rate, tissue-level properties such as cell–cell contact topology, or position within the SAM has not been determined.

The rule for cell size regulation, together with growth kinetics over the cell cycle, determines a cell’s interdivision time, and hence impact on the durations of its cell cycle phases. At least in some environmental conditions, various bacteria (23, 24) and budding yeast (8, 25, 26) grow at constant rates per unit size (constant relative growth rates) throughout the cell cycle, and metazoan lymphoblasts (27) and human osteosarcoma cells (28) grow at constant relative rates during certain cell cycle phases, whereas fission yeast has been reported to show bilinear growth (two distinct phases of a constant absolute growth rate) (29). In plant tissues where wall–wall contacts between cell neighbors impose additional growth constraints compared with single cells, constant relative growth rates have been tacitly assumed (12, 14, 30), but this assumption and whether growth rate varies through the cell cycle have not been tested experimentally.

Here, we develop a pipeline for high-throughput quantification of the size of epidermal cells in tissues of the A. thaliana SAM while tracking their growth over multiple generations. We applied this pipeline to characterize growth kinetics and to determine the nature of size regulation in the multicellular SAM context. Our data revealed that cells regulate their size by a mode intermediate between critical size and critical increment independent of position within the tissue, and that cell growth kinetics vary according to asymmetrical division of the mother cell.

Results

Neither a Cell Size Nor an Interdivision Time Checkpoint Is the Trigger for the G2/M Transition or Cell Division.

Using our 4D quantification pipeline, we tracked 1,013 complete cell cycles between cell birth and division within the epidermal (L1) cell layer of the central zone over 3–4 d among SAMs grown on naphthylphthalamic acid (NPA), which inhibited the initiation of floral primordia (31), and in 16-h light/8-h dark cycles (Fig. 1 A–D and Movies S1 and S2). The central zone is defined to be <30 μm from the center of the SAM (Fig. 1C); the CLAVATA3 signal is maximum at the center and decreases to ∼0 over this range (Movies S1 and S2). The mean interdivision time was 21–31 h among SAMs, which is similar to a previous time-lapse imaging study of SAMs not grown on NPA (15). Our data confirmed reported distributions of L1 cell neighbor numbers, outer periclinal wall areas, and the linear relation (Lewis’ law) between number of neighbors and outer periclinal wall area (32–35) (Fig. 1E and SI Appendix, Figs. S1 and S2 and Table S1). Our data also confirmed the power-law scaling of cell volume ∼ (anticlinal wall area)^1/2 (Fig. 1E) that is expected, given the in-plane growth of L1 cells (SI Appendix, Text S1). In all SAMs (n = 6), cell volume and total surface area in the central zone did not vary with radial distance from the SAM center, whereas the proportions of surface area allocated to the outer periclinal and anticlinal walls increased and decreased, respectively (Fig. 2A and SI Appendix, Figs. S3–S7), demonstrating spatial variation of these size metrics and of mean cell shape. This result demonstrates that cell growth rate, which increases with distance from the SAM center, can be up-regulated independent of mean cell volume and surface area.

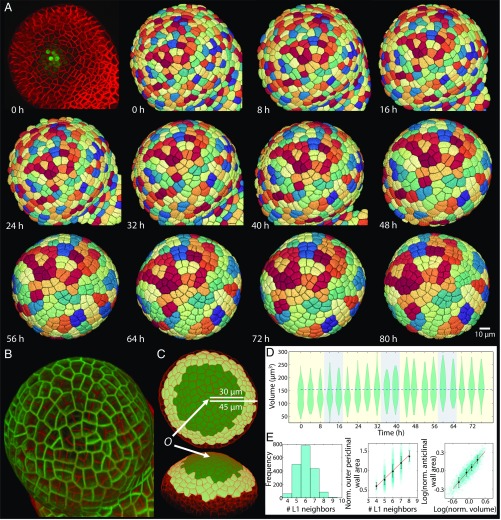
Fig. 1.

Four-dimensional pipeline for single-cell quantification and lineage tracking over multiple cellular generations to characterize cell growth and size kinetics. (A) Time-lapse confocal stacks were acquired for each SAM every 4 h for 0 to ∼80 h (every 8 h is shown). Plants were grown on NPA to inhibit growth of floral primordia that would have obstructed time-lapse imaging. The membrane reporter pUBQ10::acyl-YFP (red in top left panel) permitted accurate cellular segmentations and tracking using the MARS/ALT software (Materials and Methods), as well as quantification of cell size metrics. Cells are colored according to lineage, demonstrating that lineage tracking is ∼100% accurate. A CLAVATA3 nuclear-bound reporter (green in top left panel) permitted nuclear segmentations. (B) Snapshot of SAM 1 at 48 h with all L1 division planes formed between 24 h and 48 h colored in red. (C) Cells within 30 μm of the center of the SAM, defined by O where O corresponds to the peak of CLAVATA3 expression, which coincides with lowest cellular growth rates, are regarded as the central zone and are included in the analysis; for sister asymmetry statistics, cells within 45 μm of the SAM’s center are included in the analysis. (D) Distributions of L1 central zone cell volumes at each time point over the ∼3-d time lapse, with light/dark cycles shaded in yellow/blue for SAM 3. The blue dashed line shows the time-averaged mean of cell volumes. There was a shift-up in volume after ∼36 h of imaging (SI Appendix, Fig. S9). (E) Distribution of the number of L1 neighbors surrounding a cell (Left) and the linear relationship between the number of L1 neighbors (N_neigh) and outer periclinal wall area (A_op), N_neigh ≈ −0.15 + 0.2 A_op, (Center) are in agreement with previously published data (SI Appendix, Table S1). (Right) Scaling between cell volume and anticlinal wall area is V ∼ A_a^0.5, as demonstrated by the slope of 0.5 for log(V/mean(V)) vs. log(A_a/mean(A_a)); this scaling relationship is expected, given the in-plane growth and division of L1 cells (SI Appendix, Text S1). In each panel, data from all time points have been amalgamated for SAM 3 (n = 1,867) and black dots and error bars show medians and interquartile ranges, respectively. The corresponding data for other SAMs are provided in SI Appendix, Fig. S1 and Table S1. norm., normalized.

Fig. 2.

G2/M transition and division are not triggered when the cell reaches a critical size, when the cell adds a critical increment, or when a specific time period has elapsed. (A) Although mean cell volume remained constant across the SAM, cell outer periclinal and anticlinal wall areas increased and decreased with distance from the SAM’s center, respectively. Data points are colored according to cell volume. (B) Normalized cell birth volume (V_b/μ_V^t) was positively correlated with normalized division volume (V_d/μ_V^t) with a slope of f ≈ 0.5, whereas normalized birth volume was negatively correlated with normalized volume increment (Δ/μ_V^t). Further, normalized birth volume was negatively correlated with interdivision time (T/μ_T). (C) Asymmetry in sister-cell birth sizes [α_b = (S_b − S^sis_b)/(S_b + S^sis_b)] correlated positively with the asymmetry in sister-cell division sizes [α_d = (S_d − S^sis_d)/(S_d + S^sis_d)] for outer periclinal wall areas (A_op; R = 0.46, P = 10⁻²²; n = 415) and anticlinal wall areas (A_a; R = 0.55, P = 10⁻³⁴; n = 415). Similarly, the asymmetry in sister birth sizes correlated negatively with both the asymmetry in sister size increments (α_b vs. α_Δ: R = −0.48, P = 10⁻²⁵ for outer periclinal walls; R = −0.47, P = 10⁻²³ for anticlinal walls) and interdivision times (α_b vs. α_T: R = −0.77, P = 10⁻⁸² for outer periclinal walls; R = −0.79, P = 10⁻⁹¹ for anticlinal walls) (SI Appendix, Table S5). In each panel, red lines show least-square linear fits; black error bars show medians and interquartile ranges; and N, R, and P give the sample size, the Pearson correlation coefficient, and the corresponding P value, respectively.

The methods used to deduce whether cells divide at a critical size, after a specific time period has elapsed, or after adding a critical increment rely on the assumption of homeostasis, and variations in mean cell size in space or time can create correlations among cell cycle variables that lead to erroneous conclusions about size regulation (SI Appendix, Fig. S8). Thus, to infer the mode of SAM cell size regulation correctly, given the spatiotemporal variability in cell size measurements, it was critical to devise cell cycle statistics that do not vary in space or time. First, because cell volumes in the L1 central zone did not vary with space (SI Appendix, Fig. S3) but increased marginally (∼20%) during the time lapse (SI Appendix, Fig. S9), we normalized cell volumes (V) at time t by the average volume of L1 central zone cells (μ_V^t) at time t. Second, we quantified sister-cell asymmetries as the differences between sister size metrics normalized by their sum; for example, the asymmetry in anticlinal wall area A_a is α_b = (A_a,b − A_a,b^sis)/(A_a,b + A_a,b^sis), where A_a,b and A_a,b^sis are the anticlinal wall areas at birth of two sister cells. Because a sister pair is born and divides at approximately the same position and time, these sister size asymmetry statistics have no spatiotemporal variation (SI Appendix, Figs. S10–S14 and Table S2).

In each SAM, for cells that were tracked over a complete cell cycle, both birth volume (V_b) and normalized birth volume (V_b/μ_V^t) were positively correlated with division volume (V_d) and normalized division volume (V_d/μ_V^t), respectively (with division being defined by the appearance of a new cell membrane/wall; for each plant, n = 100–296 cell cycles; P ∼ 10⁻¹⁶–10⁻⁴ in SI Appendix, Table S3 and P = 10⁻⁴¹ and 10⁻⁵⁶ for nonnormalized and normalized pooled data in Fig. 2B). These correlations argue against an absolute cell volume checkpoint triggering division. Because our data show that G2/M occurs ≈40 min before division (SI Appendix, Table S4), whereas the mean interdivision time is 21–31 h (SI Appendix, Table S1), division events are essentially concurrent with G2/M, so G2/M also cannot be triggered by a cell volume checkpoint. Our sister size asymmetry statistics corroborate this result for total wall area, and outer periclinal, inner periclinal, and anticlinal wall areas (n = 415 sister pairs that underwent complete cell cycles that began <45 μm from the SAM center; P < 10⁻²¹ in Fig. 2C and SI Appendix, Table S5). Moreover, the strong negative correlations between birth volume and volume increment and between normalized birth volume and normalized volume increment (P = 10⁻⁶⁴ for pooled data in Fig. 2B and SI Appendix, Table S3), indicate that plant stem cells do not add a fixed size between divisions; this result was again corroborated for wall surface areas by sister size asymmetry statistics (P < 10⁻²² in Fig. 2C and SI Appendix, Table S5). Thus, no critical size or critical increment checkpoint is imposed at G2/M or division.

Furthermore, in each SAM, strong negative correlations were observed between normalized birth volume and normalized interdivision time (T/μ_T, where μ_T is the mean interdivision time across a SAM) (P = 10⁻¹¹⁴ for pooled data, Fig. 2B), and between sister size asymmetry at birth (α_b) and interdivision time asymmetry, α_T = (T − T^sis)/(T + T^sis) (P < 10⁻⁶⁶ in Fig. 2C and SI Appendix, Table S5). Thus, there is not an interdivision time checkpoint triggering the G2/M transition, indicating that cells do not simply grow for a fixed period between divisions. Because the durations of our experiments are finite, spanning the mean interdivision time by approximately threefold (SI Appendix, Table S1), cells with shorter interdivision times are inevitably overrepresented at the end of the experiment (SI Appendix, Fig. S15). To address this potential source of bias, we verified that the statistics were unaffected after recomputation using only data from cells born in the first half of the experiment (SI Appendix, Table S6). Taken together, our data reveal that neither division nor the G2/M transition is triggered by the cell reaching a critical size, adding a critical increment, or after a critical time has elapsed since birth.

Cells Grow at a Constant Rate per Unit Size, with the Smaller Sister from an Asymmetrical Division Growing at a Higher Relative Rate than the Larger Sister.

We next computed statistics to reveal the nature of cell growth kinetics over the cell cycle. Averaged over the sample, the absolute growth rate of cell volume (dV/dt × μ_T/μ_b, where μ_b is the mean birth volume) increased by a factor of ∼1.8 over the first 80% of the cell cycle, whereas the relative growth rate (growth rate per unit volume, dV/dt × μ_T/V) remained nearly constant with a slight reduction within the final 20% of the cell cycle (Fig. 3A), indicating that volume grows at a rate proportional to volume through >80% of the cell cycle. This result continued to hold when the spatiotemporal growth rate variation across the SAM (SI Appendix, Fig. S16) was taken into account (SI Appendix, Fig. S17). Next, we determined the growth kinetics of different components of the cell wall. The planar growth of epidermal cells and their slow rates of shape change over the cell cycle necessitate power-law scalings among cell volume and wall area measurements (SI Appendix, Table S7). Such scalings combine with constant volumetric relative growth rates to predict that cells grow in proportion to their size, whether size is measured by volume, anticlinal wall area, periclinal wall area, or total wall area; this prediction was confirmed by our wall area measurements (SI Appendix, Text S1 and Fig. S18). Finally, we quantified how nuclear volume changes with cell size: The nuclear-localized CLAVATA3 reporter pCLV3::dsRED-N7 permitted the segmentation of nuclei within the approximately six to nine central cells positioned <8 μm from the SAM center (SI Appendix, Supplemental Materials and Methods). These data show that nuclei grew continually throughout the cell cycle and scaled approximately proportionally with cell volume (Fig. 3 B and C), occupying 30 ± 7% of cell volume.

Fig. 3.

Cells grow at a rate proportional to their size, and nuclei grow continually through most of the cell cycle. (A) Absolute volumetric growth rate increased by ∼1.8-fold over the first 80% of the cell cycle, whereas the volumetric relative growth rate remained constant throughout the cell cycle at the expected value of ln(2) (green horizontal line) for V/μ_V^t (n = 4,299). Cell cycle stage is defined as time from birth of a cell, t, divided by its cell cycle duration, T. Growth rates during mitosis/new cell wall formation are omitted. (B) Nuclear volume was approximately proportional to cell volume as it varied over an approximately twofold range [red line corresponds to y = x; a least-square linear fit gives nuclear volume/mean(nuclear volume) = 0.86 × cell volume/mean(cell volume) + 0.13]. The plot includes data from all time points and all cells within a radius of 8 μm (n = 726): The CLAVATA3 signal diminished with distance from the SAM center, rendering nuclear volume segmentations inaccurate beyond ∼8 μm (Movies S1 and S2 and SI Appendix, Fig. S23). Black error bars show medians and interquartile ranges. (C) Nuclei grew continually throughout the cell cycle, so that the average nuclear volume/cell volume ratio remained approximately constant at ∼30%. Each plot includes data from all completed cell cycles that began within a radius of 8 μm (n = 332).

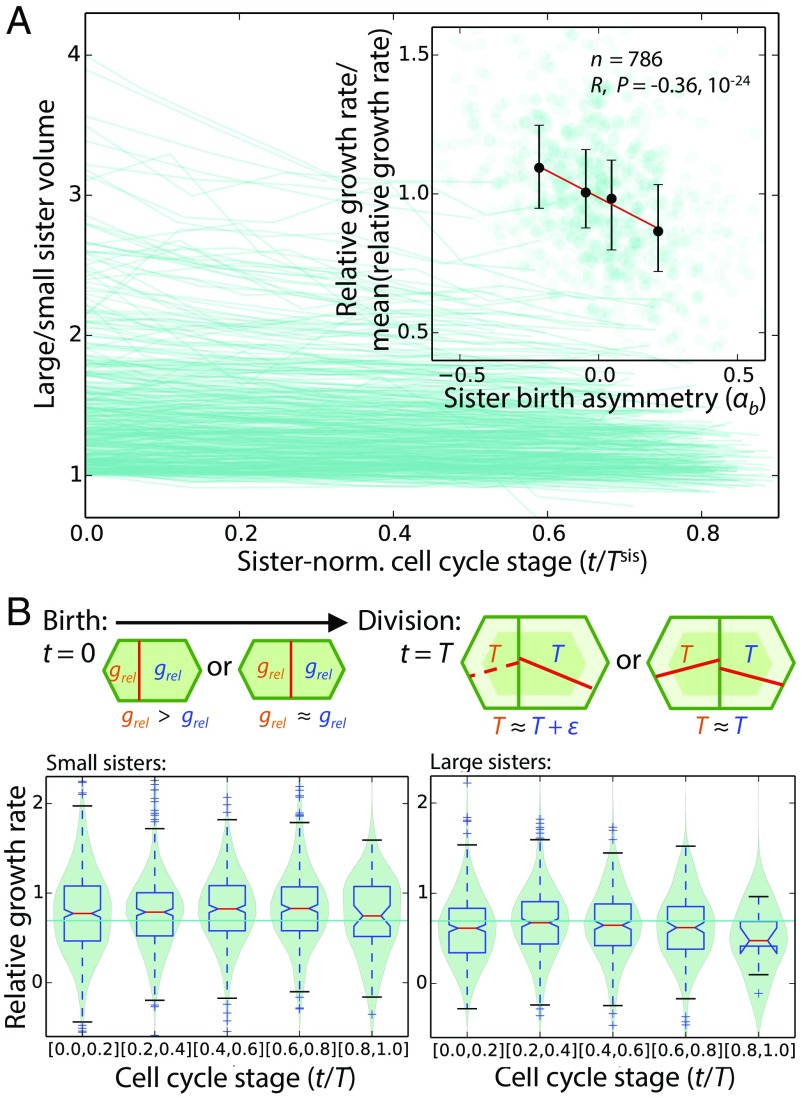
We noticed that following asymmetrical divisions, the ratio of large/small daughter cell sizes decreased over the course of the cell cycle (Fig. 4A and SI Appendix, Table S8). This decrease occurred because the small sister grew at a faster relative rate than its larger sister (Fig. 4B). Division volume asymmetry, defined by (V_b − V_b^sis)/(V_b + V_b^sis), was strongly correlated with both cell birth volume (R = 0.87, P = 10⁻²⁴²) and the normalized difference between a cell’s volume and the cell volume of its nonsister neighbors, defined by (V − V^ns-neigh)/(V + V^ns-neigh), where V^ns-neigh is the mean volume of nonsister neighbors (R = 0.47, P = 10⁻²⁸⁰; SI Appendix, Fig. S19). To determine whether the difference in relative growth rates between sister cells is driven by a dependence on birth volumes, on cells having differently sized neighbors, or on division asymmetry of mother cells, we first restricted our analysis to cells generated by symmetrical divisions [cells with |(V_b − V_b^sis)/(V_b + V_b^sis)| ≤ 0.11, to include ∼50% of data in the analysis] and found that relative growth rate then did not depend significantly on birth volume (Kruskal–Wallis: H = 3, P = 0.4) or on the relative sizes of nonsister neighbors (Kruskal–Wallis: H = 5, P = 0.14) (SI Appendix, Fig. S20 and Table S8). Second, we determined that the dependence of relative growth rates on asymmetrical divisions persisted when the data were restricted to either cells of intermediate birth volumes (H = 73, P = 10⁻¹⁵ for |V_b/mean(V_b) − 1| ≤ 0.16, to include ∼50% of data) or cells with sizes similar to the average size of their nonsister neighbors [H = 43, P = 10⁻⁹ for |(V − V^ns-neigh)/(V + V^ns-neigh)| ≤ 0.11, to include ∼50% of data] (SI Appendix, Fig. S20 and Table S8). In sum, there is no dependence of relative growth rate on either birth volume or the volume difference between a cell and its nonsister neighbors for cells generated by symmetrical divisions, whereas for cells born close to the average volume, the dependence of relative growth rate on asymmetrical division of the mother cell is strong; these data indicate that the difference in sister-cell relative growth rates is driven primarily by the asymmetrical division, and, consequently, there is a negative correlation between asymmetrical division and relative growth rate and between cell birth size and relative growth rate. Results for inner and outer periclinal wall areas were similar, but for anticlinal and total wall areas, the relative growth rate no longer depended significantly on asymmetrical division after the analysis was restricted to data subsets as described above (SI Appendix, Table S8).

Fig. 4.

Smaller daughters grow at a faster rate per unit size than their larger sisters following asymmetrical divisions. (A) Ratio of large to small sister-cell volumes decreased over the course of the cell cycle among mother cells that divided asymmetrically (time since birth, t, is normalized by the average of sister interdivision times, T^sis). (Inset) Degree of asymmetrical division, α_b = (V − V^sis_b)/(V_b + V^sis_b), was negatively correlated with the cell’s average relative growth rate over its cell cycle (black error bars show medians and interquartile ranges, red line is least-square linear fit to the medians). (B) Smaller sisters born of an asymmetrical division (α_b ≤ −0.11; n = 1,586) grew at an above-average constant relative rate throughout their cell cycle, whereas larger sisters (α_b ≥ 0.11; n = 1,054) grew at a below-average constant relative rate; the schematic illustrates that this growth pattern results in sisters having more similar interdivision times.

Beyond the position dependence of relative growth rates as cells proliferate away from the central zone, we found no evidence that relative growth rates are inherited from mother to daughter cells (SI Appendix, Fig. S21), although it is possible that noise in our data precludes detection of such an inheritance. We could discern no strong and consistent impact across the SAMs of light/dark cycling on growth rates or division patterns (Movies S3 and S4 and SI Appendix, Fig. S22); this observation may be due either to the frequent interruptions of the light/dark cycles during image acquisition or to the suppression of signaling responses to light that are partly mediated by auxin (36), and thus may be partly suppressed in NPA-grown plantlets. Regardless, our data indicate that the difference in relative growth rates between sister cells resulted from asymmetrical divisions, and, because the small sister grew more between divisions than the large sister, the higher relative growth rate of the small sister resulted in more similar sister interdivision times (Fig. 4B).

Size Regulation in the SAM Is Cell-Autonomous Rather than Position-Dependent.

In a multicellular tissue, it is feasible that the mode of cell size regulation varies according to interactions between neighboring cells or when cells are subject to a chemical/hormonal gradient. For single-celled organisms in homeostatic environments, the various modes of size regulation can all be captured by a single equation:

$$V_d=f\hspace{0.17em}{V}_b+{\mathit{\mu }}_b\left(2-f+Z\right),$$ [1]

where Z is Gaussian noise with mean 0 and SD (4σ_d² − f²σ_b²)^1/2; where σ_b and σ_d are the coefficients of variation of V_b and V_d, respectively; and f defines the mode of cell size regulation. The expression f = 0 gives division size = V_d = constant + noise, which corresponds to the critical size mode; f = 1 gives size increment = V_d − V_b = constant + noise, which corresponds to the critical increment mode; and f = 2 gives interdivision time = μ_T × log₂(V_d/V_b) (given that cells grow at a constant relative rate) = μ_T × log₂(2 + μ_b/V_b × Z) ≈ constant + noise, which corresponds to specific time mode (4, 37). The finding that cell volume grows at a constant relative rate implies that cell volume increases exponentially with time, so V(t) = V_b e^{g t} where, necessarily, g = ln2/μ_T because, in homeostatic environments, cells double their volume, on average, over a cell cycle. Our pooled data from all SAM cells tracked over a complete cell cycle and from sister-cell pairs tracked over a complete cell cycle both give f ≈ 0.5 (Fig. 2B and SI Appendix, Text S2 and Tables S3 and S5). Therefore, plant stem cells regress to their mean target size over several generations, with fluctuations decaying to one-fourth of their initial value over one cell cycle on average: Subtracting the mean cell size at division (2 μ_b) from either side of Eq. 1 with f = 0.5 gives that (fluctuation away from mean division size) = (V_d − 2 μ_b) = 0.5 (V_b − μ_b) = 0.5 × (fluctuation away from mean birth size); because cells divide in half, on average, to produce newborn cells in the next generation, therefore (fluctuation away from mean birth size in the next generation) = 0.25 × (fluctuation away from mean birth size). This rate is intermediate between the critical increment and critical size modes: The same calculation shows that for critical size (f = 0), fluctuations decay to 0 within one generation, whereas for critical increment (f = 1), fluctuations decay to one-half of their initial value within one generation.

To establish whether the relation V_d ≈ 0.5 V_b + μ_b × (1.5 + noise) is robust and independent of cells’ spatiotemporal positions, we removed 50% of the data at random or according to whether cells are born (i) early/late during the time lapse, (ii) small/large compared with the mean birth size, (iii) during light or dark periods, (iv) in the inner/outer region of the central zone, (v) with comparatively small/large neighboring cells, or (vi) with a comparatively small/large number of L1 neighbors. In all cases, there is little effect on f (SI Appendix, Table S6). Through this inspection, we excluded several phenomenological hypotheses that may have accounted for f ≈ 0.5. For example, if cell division were triggered once cells attained both a critical size and a critical increment where the critical increment (μ_b) is approximately half of the critical size (2 × μ_b), then small cells (V_b < μ_b) would, on average, reach the critical increment first; thus, they would divide upon reaching a critical size, giving f ≈ 0, whereas large cells (V_b > μ_b) would reach the critical size first and then divide upon reaching a critical increment, giving f ≈ 1, thus accounting for f ≈ 0.5 across the whole population. However, there was no such trend in our data (Fig. 2B and SI Appendix, Table S6). Similarly, division is not triggered when cells attain either a critical size or a critical increment; then small cells (V_b < μ_b) would give f ≈ 1, whereas large cells (V_b > μ_b) would give f ≈ 0. If a subset of cells divided at a particular point in the light/dark cycle according to a circadian rhythm, then cells born at this point would divide after a specific time had elapsed, giving f ≈ 2; again, no such trend is apparent in our data (Fig. 2B and SI Appendix, Table S6). Furthermore, we could discern no clear cell division spatial pattern or tendency for synchronization from movies of different SAMs (Movies S3 and S4). Because asymmetrical division of the mother cell affects relative growth rate of the two daughter cells (Fig. 4B), we assessed whether size regulation depends on division asymmetry. When our data were split according to whether cells were born of a symmetrical or asymmetrical division, we again obtained f ≈ 0.5 (SI Appendix, Table S6).

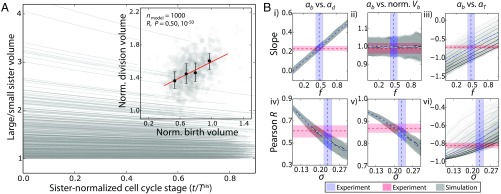
The fact that f does not vary with cell position within the meristem’s central zone, the size of neighboring cells, or other spatial variables suggested a cell-autonomous mode of size regulation. To test this hypothesis further, we compared our experimental data with simulations of cell size kinetics parameterized by Eq. 1, with all simulation parameters prescribed by our experimental measurements and with cells growing at constant relative rates that depend on mother-cell division asymmetry (SI Appendix, Text S3). All statistics were closely recapitulated, with no fitting parameters (Fig. 5 and SI Appendix, Table S9). The close agreement between our simulations and experiments indicates that a cell-autonomous mode of G2/M regulation is consistent not only with the mean trends (Fig. 5 B, i–iii) but also with most of the variability (Fig. 5 B, iv–vi) in our data. The simulation noise value of ∼0.23 indicates that ∼60% of cells miss their target mean division size (≈0.5V_b + 1.5μ_b) by <12%, in approximate agreement with previous noise measurements for single-celled organisms (6); this plausible degree of size regulation and the frequency of asymmetrical division together account for the variability in cell size (compare Fig. 2B with Fig. 5A, Inset). Further, the dependence of relative growth rate on asymmetrical division of the mother cell was sufficient to account for the quantitative dependencies among cell cycle variables determined by birth volume and interdivision time (Fig. 5 B, iii and vi).

Fig. 5.

Our experimental data are consistent with cell-autonomous growth and size regulation in the SAM, with no apparent dependence on cell position. (A) Simulation with no free parameters closely recapitulated all experimental data. In the simulation, division size depended on birth size according to Eq. 1 and cells grew exponentially in proportion to their size over the cell cycle, with smaller sisters growing at a faster relative rate than their larger sister; parameters were set to their experimentally measured values [compare Fig. 4A (main panel and Inset) with Fig. 2B and SI Appendix, Text S3 and Table S9], and the sample size, n_model, was set close to the sample size of the experimental data. (B) Simulation recapitulated experimentally measured fitted slopes (i–iii) and Pearson R values (iv–vi) only when simulation parameters were set close to their experimentally measured values. Experimentally measured medians and 90% confidence intervals are shown by dashed lines and shaded regions for fitted slopes and Pearson R values in red and for simulation parameters f (size regulation rule) and σ (noise) in blue (SI Appendix, Text S3). The effect of varying the strength of growth rate dependence on asymmetrical division, g_asym, is shown in each panel by different gray shades (g_asym = −0.03 to 0.1 × i, i = 0, …, 8 increases with opacity of gray; shaded regions, which are overlapping in i, ii, iv, and v, show 90% confidence intervals from simulations). The discrepancies between simulated and experimental Pearson R values indicate that the experimentally measured noise (σ) may be overestimated by ∼10%. These plots show that our experimental data and simulations are nontrivially consistent with one another.

Discussion

In this study, we have refuted the long-standing unexamined assumption that epidermal cells in the SAM undergo G2/M and divide at a critical size, or after a fixed time period has elapsed (Fig. 2 B and C). Instead, cells follow a size regulation rule that is intermediate between dividing at a critical size and adding a critical increment, causing cell size fluctuations from the mean to decay by ∼75% in one generation. Cells in the SAM experience molecular gradients, alter growth rates depending on position, and are subject to cell–cell contact constraints, yet our analyses indicate that the size regulation rule persists independent of position within the tissue or cell–cell contact topologies. In other eukaryotes, both G1/S and G2/M are subject to size checkpoints (2, 38, 39). Cell size and ploidy increase together when the endocycle, which bypasses mitosis, is implemented in A. thaliana sepals (40) and other differentiated tissues or by blocking division with the microtubule inhibitor oryzalin (13), indicating that the trigger for G1/S may affect regulation of the cell size/ploidy ratio rather than cell size per se (41). Our results indicate that in the SAM, where cells are diploid, G1/S is not triggered by the attainment of a critical size or critical cell size/ploidy ratio, because such regulation would contradict the positive correlations between birth and division sizes (Fig. 2 B and C).

We showed that during the cell cycle, cells expand continually at a rate proportional to their size at least until the final <20% of their cell cycle, with nuclei also growing continually at a similar rate until mitosis (Fig. 3 B and C). Because in Arabidopsis shoot apices G1, S, and G2, phases have been reported to last for ∼50%, ∼25%, and ∼15% of the cell cycle (42), our data imply that nuclei grow through each of these phases, as in other organisms (43, 44). Following an asymmetrical division, the small daughter grew at a faster rate per unit size than the large daughter (Fig. 4 A and B). Although it is challenging to infer dependences from these data due to the tight correlations among variables, the simplest interpretation of our analyses (SI Appendix, Fig. S20) is that the difference in per unit size growth rates between sisters is driven primarily by the asymmetrical division of the mother cell rather than by other size-related metrics with which asymmetrical division is correlated. This phenomenon is not straightforwardly accounted for by a cell wall growth rate that depends on elastic stress or strain of the wall, a mechanism that partially controls growth rate and is modulated by turgor (45–48). How this sister-cell growth heterogeneity can be integrated with the report that growth heterogeneity is induced by neighbor interactions (30) is a future challenge. A feasible mechanism features a master regulator of growth with the following dynamics: (i) its concentration is fixed through the cell cycle and is proportional to the per unit size growth rate; (ii) upon mitosis, the growth regulator is degraded or synthesized to attain a specific concentration; and (iii) upon division, the regulator is partitioned equally in number between the two daughters perhaps via titration against DNA (41). Such a mechanism would impart a higher concentration of the master regulator to the smaller sister.

Molecular mechanisms regulating cell size in budding and fission yeast have recently been characterized. In fission yeast, the peripheral membrane protein kinase cdr2p has been reported to regulate cell surface area to a critical value at G2/M (22). In the SAM, our data show that cell surface area and volume are regulated by a mode intermediate between critical size and critical increment. In budding yeast daughter cells, through cyclin-dependent kinase (CDK)/cyclin activity inhibition, the transcriptional inhibitor Whi5 controls cell size at G1/S via a dilution process whereby Whi5 is synthesized at a roughly constant rate through S/G2/M, which lasts for an approximately fixed time, and is then diluted out by growth during G1, triggering S-phase when it falls below a specific concentration (49). This or a similar mechanism can potentially implement the critical increment mode of size regulation (8). Such a diluter mechanism may account for a regulatory mode that is intermediate between critical increment and critical size as identified in this study, but with modification such as inhibitor degradation during the cell cycle. A. thaliana has no structural whi5 or cdr2p homologs, but the A. thaliana homolog of human retinoblastoma (RBR1) plays a functional role that is similar to Whi5 (50, 51). It would be informative to quantify the spatiotemporal dynamics of RBR1 through the cell cycle. Because it is feasible that different cellular components are subject to different size regulatory rules, a second scenario that could account for size regulation intermediate between critical size and critical increment is that the cytoplasm grows to a critical size, whereas the nucleus adds a critical increment. Single-cell tracking experiments can again be used to establish the growth and size kinetics of different cellular components and key growth regulators such as ribosomes.

Cell size has important physiological implications, determining both the surface area/volume ratio and the ratio of cytoplasm/DNA, thereby likely impacting nutrient uptake rates, protein concentrations, and transcription frequencies. Cell size and growth rates vary strongly within a plant according to tissue and developmental stage, particularly among cells that follow terminal differentiation paths, such as guard cells and pavement cells. Growth and size are evidently regulated in coordination with the cell cycle. The array of cyclins and the two types of CDKs of A. thaliana and their multiple levels of regulation indicate that cell cycle control, as well as its interplay with developmental signals, is complex (52). However, results in yeast suggest that the underpinning molecular features of CDK/cyclin-dependent cell cycle progression are surprisingly simple (53), and the role of CDKs/cyclins is broadly conserved among eukaryotes (52). Our methodology is potentially transferrable not only to other A. thaliana tissues and cell cycle fluorescent reporters but also to other plant species, and thus should be able to illuminate features of cell size, growth, and cell cycle control in different multicellular contexts, perhaps identifying conserved strategies for linking together these controls. The regulation of cell size is a fundamental challenge for all organisms, and its study can ultimately provide insight into the control of multiple processes essential to life.

Materials and Methods

Construction of a YFP Plasma Membrane Marker and Other Transgenic Lines.

DNA containing the coding sequence for YFP was amplified by PCR using primers attb1-mYfwd (5′-AAAAAGCAGGCTATGGGAGGATGCTTCTCTAAGAAGGTGAGC) and attb2-YFPrev (5′-AGAAAGCTGGGTTTACTTGTACAGCTCGTCCATGCCGAGAGTG).

The total reaction volume was 50 μL. The forward primer contains a short sequence encoding a motif that is acylated in plant cells (54). Both primers contain a portion of the attB gateway sites. Amplification conditions were 96 °C for 1 min followed by 25 cycles of 96 °C for 30 s, 54 °C for 55 s, and 72 °C for 30 s, and a final elongation of 72 °C for 30 s. After checking for products on a gel, 5 μL of the PCR was used in a second reaction (40 μL total) containing primers B1 adapt (5′-GGGGACAAGTTTGTACAAAAAAGCAGGCT) and B2 adapt (5′-GGGGACCACTTTGTACAAGAAAGCTGGGT).

Amplification conditions were 95 °C for 2 min followed by five cycles of 94 °C for 30 s, 48 °C for 30 s, and 72 °C for 1 min; 20 cycles of 94 °C for 30 s, 55 °C for 30 s, and 72 °C for 1 min; and a final elongation of 72 °C for 1 min. Products were PCR-purified (Qiagen) and then used in a one-tube format Gateway reaction as per the manufacturer’s instructions, with the destination vector pUB-DEST containing the UBQ10 promoter upstream of the Gateway site (55). The resulting vector, pUBQ10::acyl-YFP, was transformed into A. thaliana Col-0 containing pPIN1::PIN1-GFP (56, 57). The pUBQ10::acyl-YFP/pPIN1::PIN1-GFP plants were taken to the second filial (F2) generation and crossed with pCLV3::dsRED-N7 (58), a nuclear-localizing reporter for CLAVATA3 expression. This cross was taken to the F3 generation, yielding pUBQ10::acyl-YFP/pPIN1::PIN1-GFP/pCLV3::dsRED-N7 A. thaliana seeds. The pUBQ10::acyl-YFP reporter localized strongly and uniformly to cell membranes; it was stably expressed without cellular internalization and without affecting plant growth or development. These features permitted the accurate segmentation and tracking of cells. The reporter pCLV3::dsRED-N7, a nuclear-localized CLAVATA3 reporter, identified the stem cell niche’s center and, in a subset of SAM cells, enabled nuclear volume quantification (59) (SI Appendix, Supplemental Materials and Methods). The pPIN1::PIN1-GFP reporter was not analyzed as part of this study.

Plant Growth Conditions.

NPA-treated pUBQ10::acyl-YFP/pPIN1::PIN1-GFP/pCLV3::dsRED-N7 A. thaliana Col-0 plants were grown on plates with Arabidopsis medium supplemented with 10 μM NPA (31) at 20 °C with 16 h of light per day. These plants were later selected for imaging between 24 and 28 d after germination. NPA was used to inhibit organ formation (31) without substantially slowing proliferation in the SAM’s central zone (15) so that time-lapse images could be acquired without dissection, and therefore with minimal disturbance to cell proliferation.

Time-Lapse Image Acquisition and Quantification.

NPA-grown plantlets with naked, organ-free meristems were selected and gently transferred to lidded boxes measuring 5 × 5 × 3 cm³ containing room-temperature Arabidopsis medium supplemented with 10 μM NPA to a depth of ∼1 cm. Plantlets were screened for the expression of pUBQ10::acyl-YFP, pPIN1::PIN1-GFP, and pCLV3::dsRED-N7 using confocal microscopy, and then left to recover for 12 h in the same 16/8-h light/dark cycle. All three reporters were expressed in each of SAMs 2–6; SAM 1 expressed only pUBQ10::acyl-YFP and pPIN::PIN1-GFP. Confocal z-stacks were acquired every 4 h for 3–3.5 d at a resolution of 0.22 × 0.22 × 0.26 μm³ per voxel using a 63×/1.0 N.A. water immersion objective; excitation wavelengths of 488 nm and 561 nm; the corresponding dichroic filters; and a precalibrated spectral unmixing that enabled accurate separation of the YFP, GFP, and RFP signals. The confocal scan speed was no more than 9, and line averaging was set to 2. Each z-stack took ∼10 min to acquire. At the end of each high-z-resolution z-stack acquisition, a second low-z-resolution z-stack was rapidly acquired over ∼10 s with a z-step of 5–6 μm (to enable correction of a major artifact, a stretching in the z-direction owing to growth/movement in the stem during image acquisition; SI Appendix, Supplemental Materials and Methods). Data on cell size and growth kinetics were extracted by application of our 4D cellular quantification and tracking pipeline using MARS/ALT software (60) (SI Appendix, Supplemental Materials and Methods and Movies S5–S7).

Statistical Analysis, Modeling, and Simulations.

Cellular quantification and tracking data were analyzed with Python 2.7 scripts using the NumPy and SciPy libraries and StatsModels package. Simulations were performed based on a generalization of the models originally proposed (4, 37); simulations are detailed in SI Appendix, Text S3.