Climatic and evolutionary drivers of phase shifts in the plague epidemics of colonial India

Significance

Whereas pathogens are a well-known selective pressure on host immunity, few empirical examples illustrate the coupled dynamics of transmission and evolution. After the arrival of plague in colonial India, a plague-resistant rat phenotype was reported to have become prevalent in the subcontinent’s hardest hit cities. Capitalizing on archival data from these investigations, we identify the evolution of resistance in rats as a driver of observed shifts of seasonal outbreaks in concert with the flea lifecycle and its climatic determinants. Disentangling climatic and evolutionary forcing, our findings—based on century-old observations and experiments by the Indian Plague Commission—substantiate the rapid emergence of host heterogeneity and show how evolutionary responses can buffer host populations against environmentally forced disease dynamics.

Abstract

Immune heterogeneity in wild host populations indicates that disease-mediated selection is common in nature. However, the underlying dynamic feedbacks involving the ecology of disease transmission, evolutionary processes, and their interaction with environmental drivers have proven challenging to characterize. Plague presents an optimal system for interrogating such couplings: Yersinia pestis transmission exerts intense selective pressure driving the local persistence of disease resistance among its wildlife hosts in endemic areas. Investigations undertaken in colonial India after the introduction of plague in 1896 suggest that, only a decade after plague arrived, a heritable, plague-resistant phenotype had become prevalent among commensal rats of cities undergoing severe plague epidemics. To understand the possible evolutionary basis of these observations, we developed a mathematical model coupling environmentally forced plague dynamics with evolutionary selection of rats, capitalizing on extensive archival data from Indian Plague Commission investigations. Incorporating increased plague resistance among rats as a consequence of intense natural selection permits the model to reproduce observed changes in seasonal epidemic patterns in several cities and capture experimentally observed associations between climate and flea population dynamics in India. Our model results substantiate Victorian era claims of host evolution based on experimental observations of plague resistance and reveal the buffering effect of such evolution against environmental drivers of transmission. Our analysis shows that historical datasets can yield powerful insights into the transmission dynamics of reemerging disease agents with which we have limited contemporary experience to guide quantitative modeling and inference.

Innate resistance is critically advantageous to host species facing virulent pathogens that represent endemic or epidemic disease threats. However, the ability to mount strong immune defenses can incur significant physiological costs. A central principle in disease ecology, this evolutionary tradeoff implies that environmental factors determining the exposure of hosts to pathogens concurrently drive the selection—or counterselection—of disease resistance (1–3). Understanding how environment impacts the coupled dynamics of transmission and evolution is critically important amid global climatic and environmental changes affecting the distribution, emergence, and reemergence of pathogens (4, 5).

Numerous examples of immune heterogeneity in wild plant and animal hosts document the existence of innate resistance in the context of pathogen-mediated selection (6–11). That the physiological basis of such resistance incurs a cost is predicted by ecological theory (12–15), shown in laboratory measurements (16–19), and exemplified by the natural selection of susceptibility in resistant host populations that have been removed from pathogen exposure (20, 21). Despite these direct findings regarding expansion of resistance in a host population, in few instances has it been possible to provide insight into the coupled trajectories of transmission, evolutionary dynamics, and their environmental drivers (22). In a model system of the plankton species Daphnia dentifera and its parasite Metschnikowia bicuspidata, environmental factors affecting transmission intermittently alter the intensity of selection for resistance, in turn impacting the size and timing of recurrent epidemics (23–25). In a rare example from vertebrates, the intensity of seasonal myxomatosis epidemics in Australia predicted year to year variation in the susceptibility of wild rabbits (26) in a broader context of decades-long selection for resistance (12).

For zoonotic disease agents, knowing how environment and host evolution factor into transmission dynamics is of immediate public health relevance. Responses of the black rat (Rattus rattus) to the plague-causing bacterium Yersinia pestis present one of the most important and best studied cases for understanding disease-mediated selection of host immunity. R. rattus is encountered in sylvatic and urban settings, serving as a both a wildlife plague reservoir and the host that propagates bubonic plague epidemics affecting humans. In areas of Madagascar, where sylvatic R. rattus populations function as the primary plague reservoir (27), variable innate susceptibility to Y. pestis infection is associated with resistance alleles that have undergone intense selection over a century of plague exposure (28–30). Historical human bubonic plague epidemics have been associated with the introduction of Y. pestis to previously unexposed commensal rat populations. However, little is known regarding the dynamics and epidemiological impact of host evolution among rats during such incursions (31, 32). From a public health perspective, understanding plague ecology among commensal rats is important because of the contemporary reemergence (33) and unrivaled historical impact of plague: Y. pestis epidemics decimated medieval Europe and Mediterranean classical civilization (34–36), disrupted trade and geopolitics in the late Victorian British empire (37), and may have driven major population movements and admixture throughout Bronze Age Eurasia (38, 39).

Endemic present day Y. pestis in most world regions radiated from China in a late nineteenth century expansion known as the third plague pandemic, which brought the disease to port cities of every continent by 1901 via maritime trade networks (40, 41). Historical investigations undertaken in the decade after the introduction of plague to colonial India documented the expansion of a heritable, plague-resistant phenotype among urban R. rattus: in dose escalation studies of experimental plague infection carried out across Indian cities, the prevalence of rats resisting plague infection increased in association with the local severity of recent plague epidemics (42, 43). Recognizing that “it would be an extraordinary coincidence if plague had visited just those places where the rats were naturally most immune to the disease and spared those with the most susceptible rat populations,” Victorian era investigators from the Indian Plague Commission suggested an evolutionary basis for resistance patterns, reasoning that “the one per thousand or ten thousand of the rat population … which lived through a severe epidemic would quickly give rise to a highly resistant race” (42). Datasets gathered by the Plague Commission provide an opportunity to investigate this century-old hypothesis.

Distinct temporal epidemic patterns in several cities monitored by the Plague Commission could afford insight into environmental and ecological factors influencing the urban transmission cycle—including the relation of host evolution to disease dynamics. Despite an absence of effective interventions to control transmission in colonial India (44, 45), seasonal epidemics gradually shifted from recrudescing in phase with cool temperatures to appearing later in the year amid concomitant declines in plague mortality (46, 47). Stable weather patterns in Indian cities did not comport with long-term shifts in epidemic timing and severity. Plague incidence also did not follow multiannual cycles associated with sea surface temperature anomalies and other climatic phenomena. Acquired immunity in individuals within the host population similarly does not provide a good explanation for this observation, because the one-year interepidemic period generally exceeds the lifespan of wild rats (48).

Dampened or delayed seasonal outbreaks of numerous infectious diseases have previously been attributed to declining host birth rates (49–52). Although similar reductions in the rat populations of Indian cities were not observed (53–55), increases in the resistance of the rat population as a consequence of plague-mediated selection effectively serve to reduce the recruitment of susceptible hosts. To determine the underlying cause for the shift of seasonal epidemics, we modeled the contributions of host selection and climate to plague dynamics in Indian cities based on analyses of historical experimental and epidemiological data. We assessed whether the ascendance of a resistant rat population amid intense natural selection buffered climatically driven increases in transmission to susceptible hosts and contributed to the lagging pattern of epidemics. Our findings provide evidence to resolve the longstanding mystery surrounding the impacts of evolutionary selection on India’s plague epidemics and advance quantitative approaches that integrate evolutionary and environmental factors in infectious disease epidemiology.

Materials and Methods

Modeling Transmission and Evolutionary Dynamics.

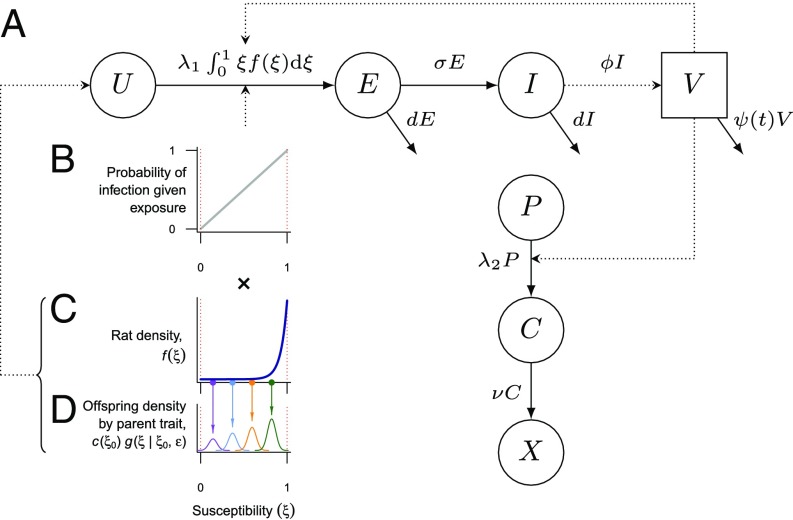
We explored the contributions of climatically forced vector mortality and selection for host resistance using a trait-based mathematical model coupling bubonic plague transmission with phenotypic evolution of a rat host population. The model was informed by previous models of rat and flea population dynamics contributing to the transmission of the disease (56–58), but tailored to address climatic determinants of transmission, to include explicit evolutionary mechanisms, and to incorporate the fitness consequences (59) associated with host selection (Fig. 1). Our model specifies a scaled population of uninfected rats (U) with a parameter 0 ≤ ξ ≤ 1 that quantifies the susceptibility of a rat to plague infection such that $U={\displaystyle {\int }_0^{1}f\left(\xi \right)d\xi }$, where f(ξ) is the density of uninfected rats with susceptibility ξ. This susceptibility represents the conditional probability of a rat becoming infected given the bite of an infectious flea, and its quantitation as a continuous variable is motivated by historical findings defining resistance in terms of an escalating inoculum Y. pestis dose necessary to cause infection (42). The model then tracks the densities of rats becoming infected and transitioning through exposed incubating (E) and infectious (I) states at rates described by the coupled differential equations $E\prime ={\lambda }_1{\displaystyle {\int }_0^1\xi f\left(\xi \right)d\xi }-(d+\sigma )E$ and $I\prime =\sigma E-\left(\mu +d\right)I$.

Fig. 1.

Schematic of compartmental transmission and susceptibility trait model structure. (A) Compartmental model for plague transmission among R. rattus. Uninfected rats (U) acquire infection at a rate determined by the applicable force of infection (λ₁) and their susceptibility (ξ; B and C) and progress through exposed incubating (E) and infectious (I) states, shedding infected fleas (V) in the latter state. From a total susceptible human population (P), individuals progress to an incubation and disease stage (C) before death (X). Arrows indicate changes in epidemiological status over time. (B) The probability of infection given exposure is directly determined by the susceptibility trait ξ. (C) The density of rats with susceptibility ξ (here, an example distribution is plotted) is multiplied by the susceptibility at each point to determine the transition rate to exposed incubating (E) and (D) subjected to Gaussian parent–offspring dispersion, so that each parent rat with susceptibility ξ₀ contributes to new generations, with offspring susceptibility drawn from normal distributions with mean ξ₀ and variance ε² to yield a new density of rats with susceptibility ξ. In the evolutionary model, the total density of offspring per member of the parent generation is scaled by the parent reproductive fitness value c(ξ₀).

The total scaled population of rats N = U + E + I and transition rates among states are governed by data-driven estimates (Table 1). Natural mortality occurs at the rate d. The force of infection λ₁ quantifies the rate that new infections occur among wholly susceptible rats (when ξ = 1). Rats progress from an incubation period to become infectious to fleas at the rate σ, and death by infection or other causes occurs at the total rate μ + d (Table 1). Historical observations showed that declines in the rat population during India’s epidemics were associated with increased rates of pregnancy among female rats (55). Therefore, we modeled births at the net rate b(1 – NK^–1) to allow reductions relative to the maximal rate b as the population approaches its carrying capacity (K = 1).

Table 1.

Estimated parameters by city

Parameter	Definition	Value*	Source
ξ	Probability of a rat acquiring plague from bite of infected flea	0–1	Scaling factor
1/σ	Mean incubation period in rats	3 d	Ref. 60
1/μ	Mean time to plague-induced mortality	2.6 d	Ref. 60
b	Maximal rat birth rate (per rat, per day, log10)	−1.532 to –1.325
1/d	Mean rat lifespan without plague infection	180 d	Refs. 55 and 61
K	Rat population carrying capacity	1	Scaling factor
ι	Fecundity reduction for a fully resistant rat (reference fully susceptible)	23.3–23.6%	Estimated
ε	SD of offspring susceptibility (reference parent susceptibility)	0.001–0.1	Varied
ϕ	Flea shedding rate from rats	1	Scaling factor
1/ψ	Mean survival of foraging fleas under observed temperatures	1.9–2.8 d	Estimated
α	Mean to peak amplitude of seasonal variation in flea mortality	9.1–17.5%	Estimated
ω	Calendar day of longest flea lifespan	Varies by city	Estimated
1/ν	Mean duration of incubation and illness in humans	10 d	Ref. 62
h	Flea searching efficiency (log10)	−7.34 to –9.70	Estimated
β	Flea–rat contact rate	0.233–0.288	Estimated

^*Presented values from estimated parameters describe the range inferred across all three cities, from the lowest 2.5 percentile to the highest 97.5 percentile of prediction intervals, for the model with host evolution. Posterior distributions are presented in Table S1, and estimates for the model without evolution are in Table S2.

Because resistance to Y. pestis is likely governed by multiple loci (28–30), we modeled phenotypic selection of the susceptibility trait. Given historical (42, 43, 63) and contemporary evidence (27, 28, 64) for counterselection of resistance in the absence of plague, we also model a fecundity trait c(ξ) = 1 – ι(1 – ξ) that quantifies the reproductive capacity of a rat as a life history tradeoff associated with resistance. The value 1 – ι is then the relative fecundity of a wholly resistant rat compared with a wholly susceptible rat. Changes in the density of rats with susceptibility ξ follow

$$\frac{\text{d}}{\mathrm{d}t}f\left(\xi \right)=b\left(1-{N\mathit{K}}^{-1}\right){{\displaystyle \int }}_0^{1}c\left({\xi }_0\right)f\left({\xi }_0\right)g\left(\xi |{\xi }_0,{\mathit{ϵ}}^2\right)d{\xi }_0-\left(\xi {\lambda }_1+d\right)f\left(\xi \right),$$ [1]

where ξ₀ measures susceptibility in the parent generation. The function g(ξ|ξ₀, ε²) describes the distribution of susceptibility among offspring of parents with susceptibility ξ₀, which we model as Gaussian with variance ε² and mean ξ₀ (65):

$$g\left(\xi |{\xi }_0,{\mathit{ϵ}}^2\right)={\left(2{\mathit{ϵ}}^2\pi \right)}^{\frac{1}{2}}\hspace{0.17em}\text{exp}[-\frac{1}{2}{\left(\xi -{\xi }_0\right)}^2{\mathit{ϵ}}^{-2}]$$ [2]

for 0 < ξ < 1. Because ξ = 0 and ξ = 1 are bounds that represent the extreme cases where an exposed rat is guaranteed to resist or acquire infection, respectively, we model g(0|ξ₀, ε²) = Φ(ξ|ξ₀, ε²) and g(1|ξ₀, ε²) = 1 – Φ(ξ|ξ₀, ε²), respectively, for the Gaussian cumulative distribution function Φ. The fecundity trait c(ξ) conveys a cost associated with resistance that prevents the accumulation of fully resistant rats in the absence of transmission.

During illness, rats shed ϕ^–1 infected fleas (V) daily before dying at a seasonally forced rate ψ(t), such that $V\prime =\varphi I-\psi \left(t\right)V$. This seasonal forcing reflects experimental evidence that the survival of infected fleas foraging for new hosts is temperature-dependent (46, 66). We model intraannual variation around the mean death rate as

$$\psi \left(t\right)=[1+\alpha \hspace{0.17em}\text{cos}\hspace{0.17em}\left(2\pi t-\omega \right)]\overline{\psi },$$ [3]

with a characteristic amplitude α and phase ω, where t indexes time across the calendar year. We model the population of infected humans (C) as $C\prime ={\lambda }_{2}P\left(t\right)-\nu C$, where P(t) is the total population of the city at a particular time, and individuals experience incubation and illness over—on average—ν^–1 days. Human deaths (X), therefore, accumulate at the rate $\widehat{X}\prime =\nu C$. To account for the human population at risk for plague, we interpolate the populations of the cities between census estimates accounting for growth and plague mortality in the intervening years. For each city and each time interval t_n to t_{n + 1}, we model population growth as

$$\widehat{P}\left(t_{n+1}\right)=P\left(t_n\right){\mathrm{e}}^{r(t_{n+1}-t_n)}-[X\left(t_{n+1}\right)-X\left(t_n\right)],$$ [4]

where X(t_n) supplies observed cumulative plague deaths to the relevant time point. In common with previous models (56, 57) and empirical evidence (67), we account for fleas’ host preference in modeling the rates that rats (λ₁) and humans (λ₂) acquire infection. Defining h as a measure of the efficiency with which fleas identify their preferred rat hosts, new infections occur in rats at the rate ${\lambda }_1=\beta \left(1-{\mathrm{e}}^{-hN}\right)V$, whereas the remaining fleas, having resorted to feeding on humans, cause infections at the rate ${\lambda }_2={\mathrm{e}}^{-hN}V$.

Historical Observations.

Epidemiological, clinical, and scientific investigations were undertaken by the Indian Plague Commission through the 1900s and 1910s (www.ncbi.nlm.nih.gov/pmc/journals/336/). We compiled historical epidemiological, meteorological, and experimental datasets from these reports to parameterize the model. The Indian Plague Commission aggregated plague mortality data from vital statistics of colonial municipalities and presidencies, providing time series of plague deaths, which we used to evaluate disease dynamics within cities. We examined plague transmission in three cities from geographically distinct regions of the subcontinent with seasonal plague epidemics and extensive epidemiological data of plague mortality. Mumbai (1891 population: 821,764) was India’s largest and first affected city, experiencing 146,000 deaths over the 16 y after the introduction of plague in 1896. The second largest city in India at this time, Kolkata (1901 population: 682,305) experienced cases beginning in 1899, with plague mortality records over the years 1900–1909 indicating 53,856 deaths in that period (68). The smaller city of Belagavi (1901 population: 26,237) experienced 11,725 deaths between plague’s appearance in late 1897 and local extinction in 1906 (46, 69).

Two sets of experiments undertaken by the Plague Commission yielded insights into the potential impacts of climatic and evolutionary factors on transmission dynamics. One experiment monitored the survival of starved rat fleas (Xenopsylla cheopis) exposed to differing ambient temperatures to assess environmentally forced flea survival as a cause for the seasonal pattern of plague epidemics in Indian cities. Fleas died more rapidly at higher temperatures across the investigated range from 15 °C to 40 °C (66). Subsequent experiments by plague investigators in Egypt reproduced these results (70). We modeled this differential death rate as the principal environmental driver based on the Commission’s findings that temperature did not impact flea fecundity or hatching (66) or Y. pestis virulence and transmissibility (46). Ecological surveys undertaken in numerous cities further reported that urban rats’ behavior and abundance did not vary with respect to season or other environmental influences aside from plague incidence (46).

A second experiment conducted by the Indian Plague Commission (42) examined susceptibility to plague in R. rattus and Rattus norvegicus captured across numerous Indian cities. Rats were inoculated s.c. with Y. pestis harvested from spleens of infected rats and subsequently monitored for illness and mortality. Experiments were repeated on roughly 100 rats from each city, with the inoculum dose ranging from 10⁻² to 2 mg spleen tissue. For rats from cities where no plague cases had been observed and those from Chennai (Madras), where transmission was not sustained after a single epidemic, mortality was nearly 100% at the lowest challenge doses. In contrast, certain rats from Mumbai, Pune, and other heavily plague-affected cities experienced mortality only after high-dose Y. pestis exposures. Resistance was inferred to be heritable, because progeny of rats that had survived plague epidemics, bred in captivity and previously unexposed to plague, likewise showed lower susceptibility to disease and mortality after Y. pestis exposure (42, 43). More recent findings substantiate the genetic basis of resistance in R. rattus (28–30). In a subsequent series of experiments examining infection on the basis of Y. pestis isolation from rats’ blood, resistance was shown to prevent the onset of infection rather than merely reduce the severity of symptoms among infected rats (46). The existence of such innate resistance has been confirmed more recently by experimental assays in R. rattus from plague-endemic areas that do not experience infection, disease, or seroconversion after Y. pestis exposure (27, 64, 71).

Datasets and Parameterization.

We inferred model parameters in a Bayesian framework. The posterior probability (P) is $\text{P}\left(\theta |X,Y\right)\propto {\displaystyle {\prod }_i{L}_1\left(X_i|{\theta }_i\right)L_2\left(Y|{\theta }_i\right)H\left({\theta }_i\right)},$ where θ_i = {b_i, β_i, h_i, α_i, ω_i, ι} is a vector of model parameters to be fitted for each city I, and the fitness cost ι is conserved among rats across all cities. For clarity, we have partitioned the likelihood function into two parts: L₁ and L₂. L₁ is a function of plague mortality time series data X_i and is obtained by evaluating

$$L_1\left(X_i|{\theta }_i\right)={\displaystyle \prod }_j\frac{{\lambda }_j^{[X_i\hspace{0.17em}\left({\tau }_j\right)-X_i\left({\tau }_{j-1}\right)]}{\mathrm{e}}^{-{\lambda }_j}}{[X_i\left({\tau }_j\right)-X_i\left({\tau }_{j-1}\right)]!},$$ [5]

where deaths between times τ_{j – 1} and τ_j follow a Poisson distribution with ${\lambda }_j={\displaystyle {\int }_{{\tau }_{j-1}}^{{\tau }_j}{\widehat{X}}_i\left(t\right)dt}$ for the state variable ${\widehat{X}}_i$ describing human deaths in city i. The second component of the likelihood, L₂, is a function of data from the experimental datasets showing the effect of temperature on flea survival and composed of the Gaussian density function

$$L_2\left(Y|{\theta }_i\right)=\frac{1}{{\sigma }_{{\delta }_i,W}^2\sqrt{2\pi }}\exp \left(\frac{-{\left({\delta }_E-{\delta }_{i,W}\right)}^2}{2{\sigma }_{{\delta }_{i,W}}^2}\right),$$ [6]

with mean and variance parameters δ_i,W and ${\sigma }_{{\delta }_{i,W}}^2$, respectively. Parameters δ_E and δ_i,W describe the change in flea (X. cheopis) death rates associated with increasing temperature in experimental data and the wild in each city i. We obtained δ_E by regressing observed flea death rates (Y; log-transformed) against exposure temperatures (log-transformed) from Plague Commission experiments documenting the death rates of starved, foraging fleas in experimental enclosures kept at 60 °F, 70 °F, and 101 °F (16 °C, 21 °C, and 38 °C). Similarly, we obtain δ_i,W and its sampling variance ${\sigma }_{{\delta }_{i,W}}^2$ by regressing the time series of model-predicted flea death rates ψ_i(t) (Eq. 3) against the time series of temperatures, W_i(t), observed within a city. Such data were reported for Mumbai, Belagavi, and Kolkata at means of daily observations aggregated at biweekly, weekly, and monthly intervals, respectively (46, 53, 55); for regression models measuring δ_i,W, the response variable was the mean estimated death rate across corresponding time intervals.

The prior probability density for the parameters is H(θ_i). The component prior probability densities for β_i, h_i, α_i, ω_i, and ι were flat, truncated at a lower bound of zero for parameters representing or modifying rates (β_i and α_i). For b_i, the upper bound of the rat birth rate, we used an informative, univariate prior distribution formulated to account for the maximal offspring produced per rat based on the incidence of pregnancy and number of embryos per rat litter. Field investigations undertaken by the Plague Commission (55) provided data on the prevalence of pregnancy in Mumbai rats (χ), which we modeled as beta distributed with parameters α = 742 (the number identified to be pregnant) and β = 1,235 (the number identified not to be pregnant). Field observations supplied the mean (μ) and variance (σ²) in the duration of pregnancy (κ) in rats (72), which we modeled as gamma distributed with parameters α = μ²σ^–2 = 484 and β = μσ^–2 = 22. We used a previously reported (73) empirical distribution of the number of embryos per litter in rats (η) (Table S3). Obtaining 100,000 sampled values of the maximal birth rate (χκ^–1)η, where each parameter {χ, κ, η} was drawn from its respective distribution independently, we constructed a continuous density function via Gaussian smoothing kernels (74). We used this empirical distribution to characterize the prior probability for proposals of b_i during Markov Chain Monte Carlo (MCMC) sampling. Values of the remaining parameters (d, μ, σ, and ν) were specified as reported published studies and provided to our model as best point estimates (Table 1).

Table S3.

Frequency distribution of rat embryos per litter

Embryos	Frequency
1	2
2	2
3	9
4	19
5	34
6	52
7	75
8	118
9	131
10	121
11	84
12	73
13	30
14	17
15	4
16	2
17	2

Census observations supplied population data used to account for changes in city populations. Data were available for the years 1891, 1901, 1906, and 1911 in Mumbai; 1891, 1901, and 1911 in Kolkata; and 1891, 1901, and 1909 in Belagavi (69, 75–78). Defining P(t₀) and P(t_F) as the starting and ending populations over any interval, respectively, we solved for r over the intervening years by minimizing the objective function ${\left(\widehat{P}\left(t_F\right)-P\left(t_F\right)\right)}^2$, evaluating $\widehat{P}\left(t_F\right)$ via a least squares fit to the discretized exponential growth represented in Eq. 4.

We applied MCMC sampling using the Metropolis–Hastings algorithm (79) to evaluate likelihoods of parameter sets and provide posterior distributions. Posterior distributions were accumulated over the course of proposing updates to one parameter, chosen at random, and saving the state of the chain at every 20th iteration to reduce autocorrelation.

Information Criterion.

To assess support for the hypothesis that rodents underwent selection for Y. pestis resistance, we compared the fit of the model including resistant rodents with a special case of the same model where no phenotypic variation occurred (ε = 0, ξ = 1) based on the Widely Applicable Information Criterion (WAIC), a Bayesian generalization of the Akaike Information Criterion (80, 81). We compared information criterion-based weights (82) of the null model (M₀) and the model incorporating evolution (M_A) as $w_A=\exp [-\left({\text{WAIC}}_A-{\text{WAIC}}_0\right)/2]$. We calculated WAIC = –2(m – p_WAIC), where $m={\displaystyle {\sum }_{j=1}^n\log \left(S^{-1}{\displaystyle {\sum }_{s=1}^{S}P\left({\theta }^S|X,Y\right)}\right)},$ $p_{\text{WAIC}}={\displaystyle {\sum }_{j=1}^n{V}_j^S\log \left[P\left({\theta }^S|X,Y\right)\right]}$, j indexes 1 … n plague mortality observations, and s indexes 1 … S random draws from the posterior distribution.

Simulation.

To provide descriptions of the stochastic dynamic epidemics predicted by our model under the constraint of the historical data, we executed the τ-leap algorithm, approximating exponentially distributed interevent waiting times.

Sensitivity Analyses.

Because the genetic basis of plague resistance in rats is not precisely known, the value of ε—the SD in offspring susceptibility relative to the parent phenotype—cannot be verified against empirical data. We ascertained the robustness of our inferences by conducting sensitivity analyses, wherein we fitted the model under values of ε spanning three orders of magnitude.

Results

Our model recapitulates the observed shifts in magnitude and timing of epidemic peaks after Y. pestis introduction in each of the three cities. Whereas plague deaths achieved their maximum in Mumbai and Kolkata in February and April, respectively, during the first years of transmission, the timing of the annual peak shifted 2 mo later to April and June in the two cities, respectively, over the ensuing decade (Figs. 2 and 3). These changes in timing coincided with decreases in the size of seasonal epidemics. The introduction of plague to Belagavi in 1897 prompted an aberrant pattern of peaks of incidence occurring in closer succession, shifting from November to August to June over the first 3 y of transmission (Fig. 4). These temporal shifts rapidly aligned the initiating phases of the epidemics more closely with decreases in temperature from their annual maximum in April (Fig. 5); then, over subsequent years, epidemics decreased in size and peaked in later months, as in Mumbai and Kolkata.

Fig. 2.

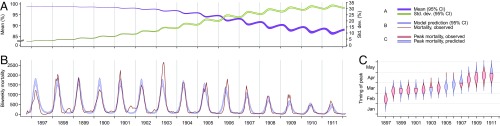
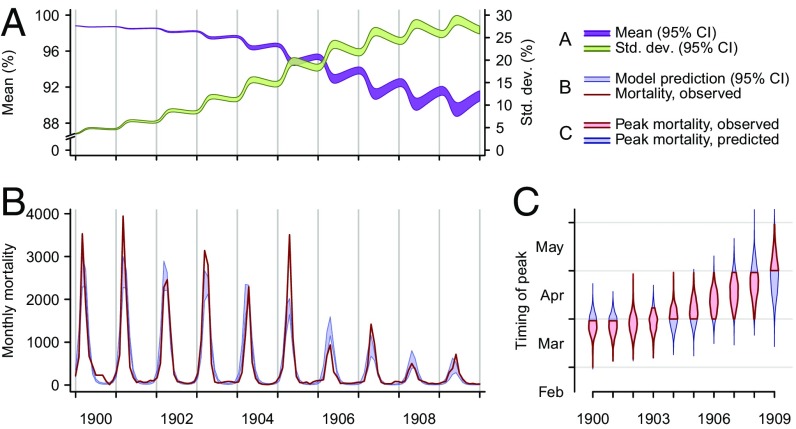
Epidemic dynamics in Mumbai. (A) Model-predicted mean susceptibility in the population [purple band, 95% credible interval (CI)] undergoes seasonal decreases along the course of the epidemic, and the SD of susceptibility in the population (green band, 95% CI) increases as the density of rats with susceptibility lower than one increases. (B) Model-predicted (blue band, 95% CI) and observed (red line) plague mortality cycles seasonally, decreasing as the mean susceptibility in the population decreases. (C) Model-predicted posterior probability density (blue violin plot) and observed (red interval) timing of peak mortality. As a consequence of the evolution of resistance, the timing of annual maxima in plague mortality shifts. Bands and violin plots are part of the range across 2,000 stochastic simulations.

Fig. 3.

Epidemic dynamics in Kolkata. (A) Model-predicted mean susceptibility in the population [purple band, 95% credible interval (CI)] undergoes seasonal decreases along the course of the epidemic, and the SD of susceptibility in the population (green band, 95% CI) increases as the density of rats with susceptibility lower than one increases. (B) Model-predicted (blue band, 95% CI) and observed (red line) plague mortality cycles seasonally, decreasing as the mean susceptibility in the population decreases. (C) Model-predicted posterior probability density (blue violin plot) and observed (red interval) timing of peak mortality. As a consequence of the evolution of resistance, the timing of annual maxima in plague mortality shifts. Bands and violin plots are part of the range across 2,000 stochastic simulations.

Fig. 4.

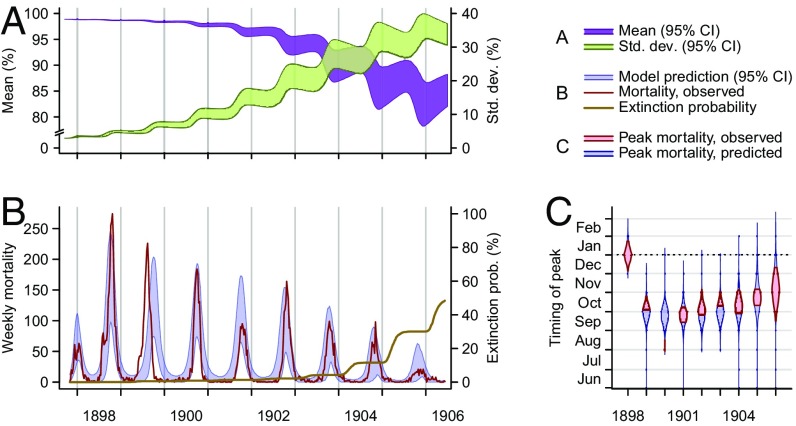
Epidemic dynamics in Belagavi. (A) Model-predicted mean susceptibility in the population [purple band, 95% credible interval (CI)] undergoes seasonal decreases along the course of the epidemic, and the SD of susceptibility in the population (green band, 95% CI) increases as the density of rats with susceptibility lower than one increases. (B) Model-predicted (blue band, 95% CI) and observed (red line) plague mortality cycles seasonally, decreasing as the mean susceptibility in the population decreases. The model-generated cumulative probability for plague extinction (brown line) increases near the end of the epidemic. The last season of epidemic disease in Belagavi was the 1905–1906 season. (C) Model-predicted posterior probability density (blue violin plot) and observed (red interval) timing of peak mortality. The epidemic in Belagavi began out of phase and rapidly adjusted to the season, a pattern the model recapitulates. Bands and violin plots represent central tendencies of the range across 2,000 stochastic simulations, discarding 968 simulations in which extinction occurred.

Fig. 5.

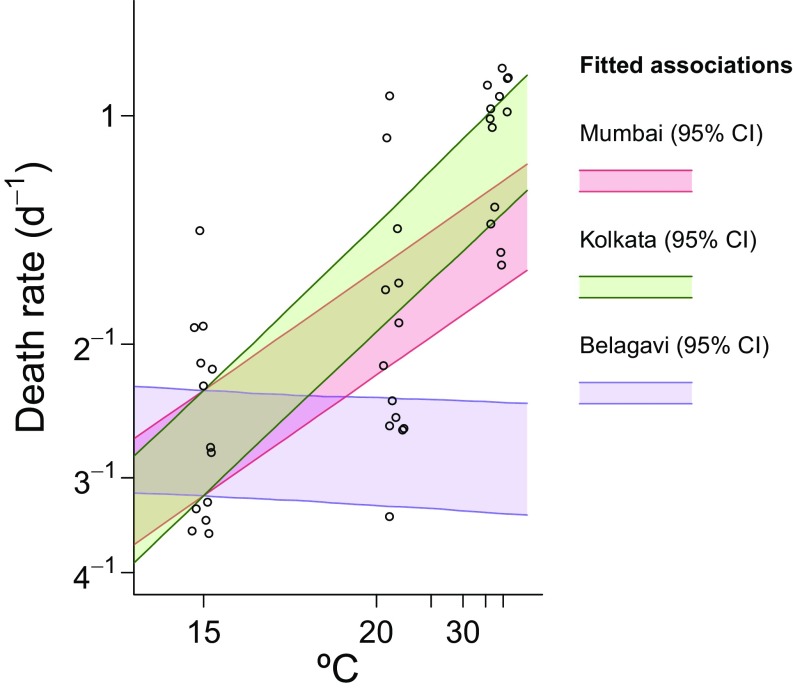
Model output regarding environmental forcing. Ninety-five percent credible intervals (CI) for the model-fitted lifespans of fleas across the seasons are plotted against ranges of temperatures reported in (A) Mumbai, (B) Kolkata, and (C) Belagavi. Plotted slopes from cities are adjusted for observed baseline differences in flea survival in the wild and under experimental conditions, which lead to distinct intercepts in regression models for (D) model-fitted relations between flea death rates and temperature, plotted against experimental data (points) showing flea survival at temperatures of 15 °C, 21 °C, and 38 °C. Points are jittered along the x axis from the original temperatures to avoid superimposition.

Our model addressed the impact of host evolution and climatic forcing by incorporating phenotypic selection of a susceptibility trait and temperature-associated seasonal variation in death rates of the rat flea. Whereas resistance-associated fecundity costs kept polymorphism in the susceptibility of rats to a minimum before plague introduction, expansions of resistance in the rat population impacted seasonal dynamics of plague after the disease was introduced. Over successive years, epidemics triggered by seasonal increases in the availability of fleas came to be limited by the declining susceptibility of a host population undergoing plague-mediated selection. In this way, the evolution of resistance buffered the nonlinear effect of increased flea survival on epidemic propagation, resulting in slower spread among susceptibles and in turn, later-peaking and smaller seasonal epidemics.

The model also succeeded in replicating climatically driven shifts observed over the years 1897–1900 in Belagavi and in the epidemics of 1897 and 1898 in Mumbai (Figs. 2 and 4). During warmer conditions, when fleas were expected to have their shortest lifespan (Fig. 5) (66), estimated R₀ values remained above 1.0 for all cities (Table S4), so that conditions were conducive to transmission, regardless of the season when plague was introduced. Whereas the initial epidemics in Belagavi and Mumbai were thus expected to commence consequent to Y. pestis introduction, temperature-associated forcing permitted our model to reproduce shifts, bringing the recrudescence of plague in these cities into phase with the cool season, when fleas were inferred to survive longest (Fig. 5).

Table S4.

Basic reproductive number (R₀) by city

Value	Mumbai	Kolkata	Belagavi
Annual mean	1.660 (1.653–1.667)	1.274 (1.263–1.286)	1.630 (1.599–1.662)
Annual minimum	1.519 (1.513–1.526)	1.085 (1.076–1.096)	1.413 (1.385–1.439)
Annual maximum	1.829 (1.822–1.837)	1.543 (1.530–1.557)	1.923 (1.887–1.961)

We derive R₀ based on an equilibrium phenotypic distribution in the absence of plague transmission, f*(ξ), obtained by simulating the demographic dynamics of a disease-free population. The corresponding density of all rats is N*. Accounting for variation in the lifespan of the rat flea, the basic reproductive number $R_0\left(t\right)=\beta \frac{\varphi }{\mu +d}\frac{1-e^{-h{N}^{\ast }}}{\psi \left(t\right)}{\displaystyle {\int }_0^1\xi \frac{f^{\ast }\left(\xi \right)}{N^{\ast }}}d\xi$. Values are presented as medians of the posterior distributions. Parentheses surround 95% prediction intervals.

In our model, ecological competition among heterogeneously susceptible rats was mediated in large part by transient dynamics unfolding during and between seasonal plague epidemics. Seasonally forced transmission prevented the population from stabilizing at an equilibrium distribution of susceptibility after plague introduction. The model instead predicted low-amplitude cyclical variation in the susceptibility of the population (Figs. 2, 3, and 4), mirroring historical observations from rats in colonial India (42). This behavior reflects the opposing evolutionary pressures on parents and their offspring in the context of seasonal plague epidemics: because the interepidemic period exceeded the expected lifespan of wild rats, most offspring of resistant rats that had survived an epidemic would receive no direct benefit from their costly genetic inheritance. We estimated that a fully resistant rat would produce, on average, 23.5% fewer offspring than its fully susceptible counterpart, a moderate cost that proved robust with estimated values of 22.9–37.6% in sensitivity analyses, wherein the SD of susceptibility between offspring and parents ranged from 0.1 to 10% (Table S5).

Table S5.

Maximum a posteriori parameter estimates according to heritability of parental susceptibility phenotype

Parameter and definition	ε = 0.001	ε = 0.005	ε = 0.01*	ε = 0.02	ε = 0.10
ι
Fecundity reduction for a fully resistant rat (reference fully susceptible)	0.229	0.231	0.235	0.271	0.376
b
Maximal rat birth rate (log10)
Mumbai	0.024	0.027	0.029	0.031	0.027
Kolkata	0.391	0.045	0.048	0.051	0.037
Belagavi	0.029	0.033	0.036	0.040	0.036
β
Flea–rat contact rate
Mumbai	0.284	0.284	0.286	0.295	0.350
Kolkata	0.232	0.233	0.234	0.246	0.295
Belagavi	0.279	0.280	0.282	0.286	0.317
h
Flea searching efficiency (log10)
Mumbai	−9.744	−9.744	−9.748	−9.745	−10.312
Kolkata	−9.644	−9.644	−9.620	−9.726	−10.289
Belagavi	−7.256	−7.256	−7.252	−7.207	−7.187
α
Seasonal amplitude (flea death rate)
Mumbai	0.092	0.092	0.092	0.101	0.094
Kolkata	0.172	0.172	0.173	0.176	0.151
Belagavi	0.153	0.153	0.153	0.166	0.169
ω
Day of longest flea survival
Mumbai	January 15	January 15	January 15	January 15	January 15
Kolkata	February 7	February 7	February 7	February 7	February 7
Belagavi	August 4	August 4	August 4	August 4	August 4

^*Posterior distributions for the model fitted with ε = 0.01 are presented in Table S1.

Whereas seasonal plague epidemics continued well into the 20th century in Mumbai and Kolkata (63, 83), transmission extinguished locally in Belagavi after the 1905–1906 epidemic (69). Stochastic realizations of our model similarly show plague persistence in Mumbai and Kolkata, while reproducing the extinction of plague from Belagavi by a median date of January 23, 1907. In contrast, a deterministic formulation of our model permits transmission to continue indefinitely in all three cities with an annual seasonal cycle. A smaller total rat population size in Belagavi, compared with the two larger cities, increases the potential for stochastic dynamics to bring about complete elimination.

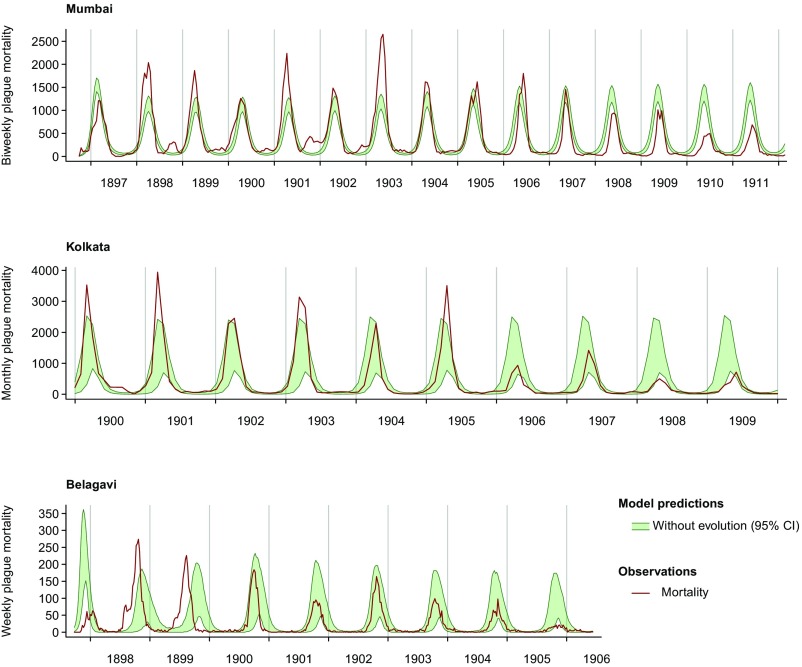
Although our model incorporating the evolution of resistance provided good fit to the timing and size of peak incidences, it was unable to reproduce long-term observed trends in the timing and size of epidemics when fitted without permitting evolution of resistance (Fig. S1). Comparing model fit with and without evolutionary forcing by WAIC, the model including evolutionary forcing was favored over the null model by a factor greater than 10¹⁰ (Table S6). Accounting for host evolution also assisted the model in adeptly capturing climatic forcing of vector survival (Fig. 5 and Fig. S2). Fitted associations between modeled variation in flea survival and observed temperature closely reproduced experimental estimates of the impact of temperature on survival of rat fleas (Fig. 5), supporting the historical hypothesis that this mechanism was the primary driver of seasonal epidemic dynamics (46, 66, 84). The model also captured transmission heterogeneities across cities resulting from climatic differences. Mumbai, which had the lowest-amplitude seasonal variation in temperature among the cities, had correspondingly lower mean to peak variation in flea death rates (9.1–9.3%) than Kolkata (17.1–17.5%) and Belagavi (15.0–15.6%). Comparing models based on the likelihood component L₂(Y|θ), which conveyed the impact of temperature on flea survival in India, the model accounting for host evolution also provided greater concordance between inferred forcing and experimental data (Table S7).

Fig. S1.

Epidemic dynamic predictions of the model without evolution by city. Epidemic trajectories [95% credible intervals (CI)] are plotted from 1,000 simulations sampling from the posterior distribution of model parameters.

Table S6.

WAIC and model weights

Geographic analysis	WAIC with evolution	WAIC without evolution	ΔWAIC*	Relative model weight with evolution
Three cities, pooled	54,692.8	111,208.7	−56,515.9	exp(28,258.0)
City-specific analyses
Mumbai	33,757.7	69,333.7	−33,576.0	exp(17,788.0)
Belagavi	9,054.9	11,247.9	−2,193.0	exp(1,096.5)
Kolkata	11,880.2	27,316.3	−15,436.1	exp(7,718.1)

^*Difference is calculated between WAIC with and without evolution as described in the text.

Fig. S2.

Environmental forcing of flea survival in the model without evolution. Ninety-five percent credible intervals (CI) for the model-fitted relations between flea death rates and temperature are plotted, adjusting for differences among intercepts (baseline) in flea survival across cities and in the experiment to account for shorter observed flea survival under experimental conditions. Points represent experimental data and are jittered along the x axis from the original temperatures (16 °C, 21 °C, and 38 °C) to avoid overplotting. The model fitted without accounting for evolution provides poorer fit to experimental data compared with the model fitted with direct evolutionary mechanisms (Tables S6 and S7).

Table S7.

Maxima of component likelihoods

Likelihood component	Log L2(Y|θ) with evolution	Log L2(Y|θ) without evolution	Relative likelihood (model with evolution)
L1(Y|θ)	−26,371.9	−51,280.5	exp(24,908.6)
L2(Y|θ)	−22.5	−772.4	exp(749.9)

Discussion

Our modeling substantiates the evolution of resistance among commensal rats in the context of intense plague-mediated selection as reported in historical investigations of the Indian Plague Commission. In particular, we have shown that observed seasonality in outbreaks can be explained by the sensitivity of flea lifespan to temperature and that resulting variation in the population of fleas—coupled with the expansion of plague-resistant R. rattus phenotypes—can explain otherwise unaccounted for changes in seasonal epidemic dynamics seen across India’s cities. Our results provide a mechanistic understanding of the ecological buffering of climatic factors driving plague transmission. In this regard, accurate inference of climatic drivers of seasonal epidemics depends on incorporating reductions in the recruitment of susceptible hosts as a consequence of plague-mediated selection. Our results show the degree to which ecological factors mediating the spread of infectious diseases and environmental drivers of transmission must be jointly understood to anticipate the impact of either on disease dynamics. Accounting for the empirically shown impact of temperature on flea survival permitted us to distinguish the contribution of evolution to changes in the temporal signature of epidemics in Indian cities, yielding inferences about plague dynamics that could not be achieved from analyses of the underlying experimental or epidemiological datasets alone. Changes in the timing of epidemics—and the role of temperature in triggering the onset of epidemics rather than their peak—obscure direct correlations between climate and incidence in India’s plague epidemics. Although numerous studies have investigated such temporal associations between human plague incidence and weather (85–89), a mechanistic understanding of how environmental forcings are buffered through ecological systems is critical for projecting how current or future climatic conditions will impact local transmission intensity or alter the latitudinal and altitudinal range where plague occurs. Such determinations are of current priority for researchers and policymakers amid concern about the impact of climate change on the distribution of plague (90) and other vector-borne and zoonotic diseases (5).

In addition to the insights gained in understanding the climatic drivers of plague, heterogeneities in host susceptibility have implications for public health objectives surrounding disease control. Existing animal-based plague surveillance programs monitor die offs and seroprevalence in rodent populations for early warning signs of the disease’s incursion (91, 92). However, expansions of resistance among hosts during epizootics could offset population declines and diminish the utility of serology as a marker for local plague transmission (27, 64, 71, 93). The diverse mammal species that may serve as plague hosts further complicate surveillance and control strategies. In the western United States, prairie dogs show no resistance to plague, despite longstanding prevalence of the disease and its devastating impact on their populations (31, 94). Our modeling supports theoretical insights (56–58) as well as historical (42) and contemporary evidence (95) that disease-mediated selection rapidly alters the distribution of susceptibility of rats, thereby impacting epidemic dynamics. In addition to improving our understanding of the mechanism of innate resistance, characterizing the genetic basis of this trait may afford novel tools for animal-based plague surveillance. Minute geographic and temporal variation in the innate susceptibility of R. rattus to plague suggests that resistance alleles may offer a sensitive and specific target for animal-based surveillance, with the potential to elucidate spatiotemporal patterns of plague transmission (27–30). Coupling such molecular surveillance data with climatic determinants of transmission would augment detection and forecasting ability, laying the foundation for inferring the possible timing and extent of local disease spread.

The empirical observation of host immune heterogeneity across diverse taxa raises the question of what ecological circumstances allow polymorphisms to persist as opposed to driving immune phenotypes to fixation (12). This uncertainty was noted by scientists of the Indian Plague Commission, who—despite recognizing plague-mediated selection as a factor in the evolution of resistance—could not account for the tendency for resistance to persist within cities during nonepidemic seasons, while disappearing from cities after the extinction of plague transmission (42). The existence of physiological tradeoffs associated with the ability of an organism to resist infection has since become a central principle in disease ecology (3). In the context of such costs, numerous lines of theoretical inquiry predict transmission to drive the persistence of polymorphisms in innate resistance; other immune phenotypes, such as the ability to tolerate infection or develop adaptive responses, are expected to achieve fixation (13, 96). These contrasting trajectories are theorized to arise from distinct ecological contexts, which favor innate resistance against pathogens that are virulent and likely to be encountered at most once in a host’s lifetime (12–15). Such conditions are met in the urban plague ecology of colonial India and supported the persistence of polymorphisms in our model in agreement with the findings of historical investigations (42). More recently, field studies have shown similar local persistence of resistance polymorphisms among R. rattus inhabiting plague foci in Madagascar, Asia, and Hawaii (27, 31, 64, 71, 94).

Notwithstanding these lines of theoretical support, a limitation to the interpretation of our analysis is that biological mechanisms underlying innate Y. pestis resistance in R. rattus remain poorly understood. We modeled resistance based on observations that rats evading disease in India also lacked culturable Y. pestis in their bloodstream, which would be necessary to infect fleas (46, 60). Such resistance in R. rattus has been called on to explain the ability of individual rats to remain asymptomatic and seronegative after Y. pestis exposure (64), in particular in Madagascar, where R. rattus serves as the primary host of Y. pestis (27, 71). Phylogenetic evidence for the recent colonization of Madagascar by R. rattus from India suggests that determinants of Y. pestis resistance among Madagascar rats may have been shared by rats involved in the third plague pandemic in India (97). Tolerant phenotypes that render Y. pestis infection asymptomatic or reduce the severity of plague have also been described in some gerbils, marmots, voles, and other rodents and small mammals. In contrast to a role of resistant hosts in reducing transmission rates, tolerant host species might play a dominant role in transmission as reservoirs of latent infection (98, 99). The matching of lagged and attenuated epidemics to our model would, accordingly, result from a resistant phenotype reducing transmission. Our findings justify a hypothesis of lower fecundity among resistant rats as a life history tradeoff that prevents the persistence of high levels of resistance in the absence of plague. Although reproductive function is among the most studied fitness costs in the context of immunity, an organism’s predisposition to reallocate reserves from anabolic processes to acute-phase immune responses may be associated with additional physiological compromises affecting metabolism, growth, and longevity (3). Such traits could also provide a mechanistic basis for counterselection of resistance in our model.

Despite considerable attention to the evolutionary impact of pathogens on hosts in ecology, longitudinal studies documenting the inextricably linked dynamics of transmission and pathogen-mediated evolutionary selection—and their environmental dependence—have been constrained to a narrow set of systems (22–26, 59). Aided by rich datasets describing epidemiological dynamics, selection, and environmental drivers of transmission, our modeling links Victorian era observations to the longstanding mystery of what caused reductions in epidemic magnitude during the third plague pandemic in India. Our results indicate that host evolution dampens and delays seasonal epidemics of plague in a manner similar to how vaccination and declining birth rates—among other processes reducing the recruitment of susceptible hosts—have impacted the timing, magnitude, and frequency of seasonal epidemics of pediatric infections, such as measles, pertussis, and rotavirus (49–52). The collection and maintenance of longitudinal data on the incidence of such diseases have been instrumental in showing the fundamental link between host recruitment rates and transmission dynamics. These circumstances merit consideration in the context of zoonoses, such as plague, for which modern surveillance data are, in some cases, disseminated at prohibitively coarse spatiotemporal scales for similar analyses (100).

To explain broad trends toward later and smaller epidemics in Indian cities, we represented transmission using a simplified model that does not account for all sources of regional and interannual heterogeneity impacting the dynamics, timing, and size of plague epidemics. For instance, our statistical framework addresses temperature as a correlate of flea survival, although other associated environmental factors may also have contributed to the longer survival of rat fleas under cool experimental and field conditions in India (46, 55, 66). Although data characterizing these factors may further refine the modeled seasonal forcing, such extensions would not alter the basic dynamics of our model, whereby lengthened flea survival during the cool season triggers epidemic recrudescence.

Our consideration of host resistance is motivated by cross-sectional differences in the susceptibility of rats to plague across Indian cities as well as subtler seasonal variation within cities. Although historical investigations did not yield detailed longitudinal data on the population dynamics of resistant and susceptible rats, a time series of infectious dose determinations within cities would provide a direct basis for inference of how resistance expanded. Remarkably, we find that a single, moderate fitness cost is sufficient to explain complex plague dynamics observed across the three cities. This finding also accounts for the low historical prevalence of resistance among rats from cities without plague, supporting the hypothesis that host selection was a key determinant of changes in the timing and severity of epidemics across all cities.

The unparalleled historical human impact of Y. pestis, the increasing epidemiological burden of plague and other rodent-borne zoonoses throughout the developing world (33, 101, 102), and lingering concerns over bioterrorist uses of plague (103) invoke the importance of understanding the transmission dynamics of Y. pestis outside its typical sylvatic niche. The singularly extensive epidemiological and experimental data gathered by the Indian Plague Commission have provided a rare opportunity to reveal the coupling of human, environmental, and ecological factors that represent drivers of urban bubonic plague in one of its most recent and severe episodes. The stark heterogeneity in the susceptibility of rats to plague across Indian cities only one decade after the initial incursion of disease in the subcontinent (42, 43) underscores the potentially rapid impact of host evolution on disease dynamics. Primary datasets gathered during historical outbreaks—like those gathered in current outbreaks—play a key role in revealing the sometimes deadly ecology of emerging and reemerging pathogens.

Table S1.

Estimated parameters by city

Parameter	Definition	Mumbai*	Kolkata*	Belagavi*
b	Maximal rat birth rate (log10)	−1.536 (–1.541 to –1.532)	−1.315 (–1.325 to –1.306)	−1.449 (–1.459 to –1.438)
ι	Fecundity reduction for a fully resistant rat (reference fully susceptible)†	23.5% (23.4–23.6%)
α	Mean to peak amplitude of seasonal variation in flea mortality	9.2% (9.1–9.3%)	17.3% (17.1–17.5%)	15.3% (15.0–15.6%)
ω	Calendar day of longest flea lifespan	January 15 (January 15 to January 15)	February 7 (February 7 to February 7)	August 4 (August 4 to August 4)
h	Flea searching efficiency (log10)	−9.748 (–9.787 to –9.700)	−9.620 (–9.701 to –9.559)	−7.25 (–7.335 to –7.166)
β	Flea–rat contact rate	0.286 (0.285–0.288)	0.234 (0.233–0.236)	0.282 (0.278–0.286)

^*Values are presented as medians of the posterior distributions. Parentheses surround 95% prediction intervals.

^†A single cost is estimated for all three cities. Sensitivity analyses refitted parameter sets considering differing heritability of the parental susceptibility phenotype (Table S5).

Table S2.

Estimated parameters by city (model without evolution)

Parameter	Definition	Mumbai*	Kolkata*	Belagavi*
b	Maximal rat birth rate (log10)	−1.76 (–1.77 to –1.76)	−1.31 (–1.34 to –1.29)	−1.86 (–1.86 to –1.85)
β	Flea–rat contact rate	0.331 (0.329–0.334)	0.222 (0.220–0.224)	0.432 (0.425–0.439)
h	Flea searching efficiency (log10)	−11.22 (–11.29 to –11.13)	−10.03 (–10.11 to –9.94)	−8.83 (–8.93 to –8.72)
α	Seasonal amplitude (flea death rate)	0.0626 (0.0617–0.0634)	0.177 (0.173–0.180)	0.115 (0.114–0.117)
ω	Day of longest flea survival	November 8 (November 8 to November 8)	February 23 (February 23 to February 23)	April 17 (April 17 to April 17)

^*Values are medians of the posterior distributions. Parentheses surround 95% prediction intervals.