Coordination vs. voluntarism and enforcement in sustaining international environmental cooperation

Abstract

The fates of “transboundary” environmental systems depend on how nation states interact with one another. In the absence of a hegemon willing and able to coerce other states into avoiding a “tragedy of the commons,” shared environments will be safeguarded if international cooperation succeeds and degraded or even destroyed if it fails. Treaties and related institutions of international law give form to these efforts to cooperate. Often, they implore states to act in their collective (as opposed to their national) interests. Sometimes, they impel cooperating states to punish free riders. A few agreements coordinate states’ behavior. Here, I present simple game-theoretic models showing whether and how treaties and related institutions can change incentives, aligning states’ self-interests with their collective interests. I show that, as a general matter, states struggle to cooperate voluntarily and enforce agreements to cooperate but that they find it relatively easy to coordinate actions. In some cases, the need for coordination is manifest. In other cases, it requires strategic thinking. Coordination may fall short of supporting an ideal outcome, but it nearly always works better than the alternatives.

Today, all individuals live within, and nearly all affiliate with, a state, of which there are about 200 worldwide. States are “coercion-wielding organizations” (1), and the ones that possess “domestic sovereignty” (2) use their formidable legislative and regulatory powers to correct “market failures,” including abuses of the environment, within their borders (the greatest human misery is to be found in the “failed” states). Unfortunately, the oceans, atmospheric fluxes, and many rivers, lakes, and ecosystems spill over “national” borders, making it impossible for states to remedy transboundary and global environmental problems independently. To remedy such problems, states must act collectively. There is no World State.

Failure to control climate change at the global level has stimulated interest in “polycentric governance,” a system “characterized by multiple governing authorities at different scales rather than a monocentric unit” (ref. 3, p. 552). Such behavior is generally to be welcomed given that action on the global scale is limited, just as adaptation to climate change is to be welcomed given that little if anything is being done globally to limit emissions. However, neither fallback can fully substitute for global collective action to limit emissions. Rather than consider only the alternatives to multilateral cooperation, we also need to figure out how to make global collective action more effective (4, 5). Up to now, negotiators have perceived climate change to be a classic cooperation game, requiring that states either negotiate national reductions in emissions in the hope that these can be enforced or pledge to reduce their emissions voluntarily in the hope that a spirit of cooperation will displace the historical tendency toward self-interest. Neither approach has worked so far. Might a different approach work better?

Clues to how to make multilateral cooperation effective are to be found in the relatively few instances in which it has worked spectacularly in the past. Two examples stand out: the eradication of smallpox, achieved in 1980 after a decade-long intensified global effort (6), and protection of the stratospheric ozone layer, which thanks to the Montreal Protocol, is now showing signs of recovery (7). Why did global collective action succeed in these cases? As I shall explain later, smallpox eradication was inherently different from the classic cooperation problem, whereas the Montreal Protocol transformed protection of the ozone layer into a different kind collective action problem. Whether by chance or design, cooperation in both cases involved coordination.

Here, I explain why the international system struggles to overcome free riding in the classic cooperation game but excels at coordinating actions that can achieve the same ends. The implication is that negotiators should pursue agreements that ask countries to do what they are good at doing and not do what they are bad at doing. In the case of climate change, countries should do more than implement the new Paris Agreement; they should also develop complementary coordination agreements.

Prisoners’ Dilemma Game

“The tragedy of the commons,” the archetypal account of how humans can mess up the environment, is sometimes portrayed as a prisoners’ dilemma (8). In the classic prisoners’ dilemma, there are two players, each with a binary choice to cooperate (C) or defect (D). Let ${\pi }_i$ denote player i’s payoff (i = 1, 2). In a prisoners’ dilemma, ${\pi }_i\left(D;C\right)>{\pi }_i\left(C;C\right)>{\pi }_i\left(D;D\right)>{\pi }_i\left(C;D\right)$. In words, taking as given how the other player chooses, each player is better off playing defect than cooperate (moreover, this ordering of payoffs applies no matter how the other player chooses, making defect a dominant strategy), but both players are better off when they both play cooperate than when they both play defect (meaning that the Nash equilibrium is inefficient).

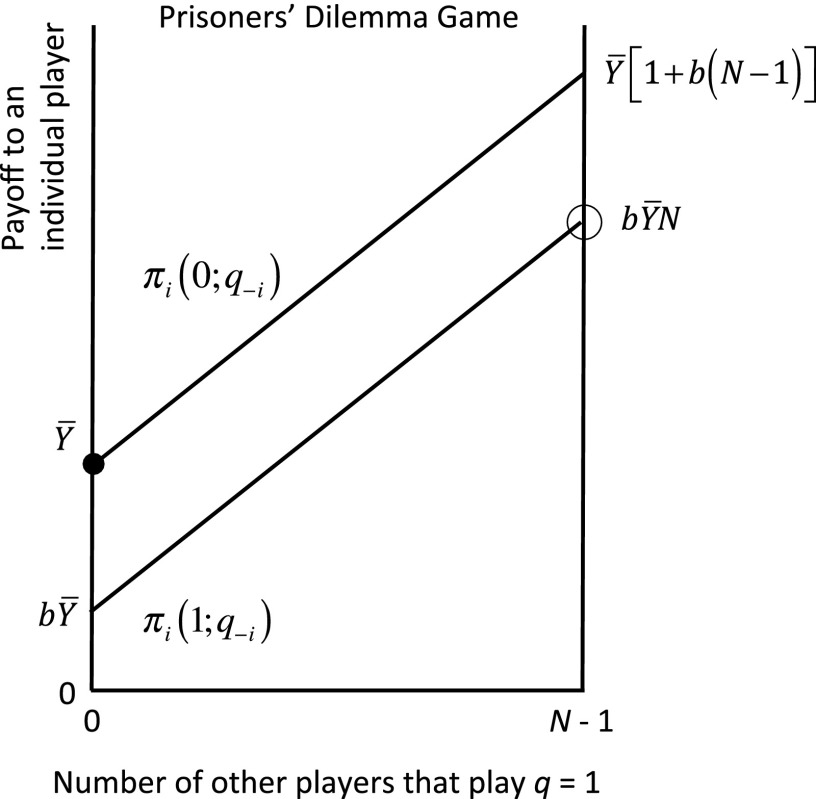
The two-player game is easily extended to N ≥ 2 players (although the prisoners’ metaphor ceases to apply when N > 2). Suppose that these countries are symmetric, meaning that they face the same choices and have the same (linear) payoff functions. Every country i (now i = 1, …, N) must choose $q_i=\left\{\mathrm{0,1}\right\}$ to maximize ${\pi }_i=\overline{Y}\left[b\left(q_i+q_{-i}\right)+1-q_i\right]$, where $\overline{Y}$ is a scaling parameter (its purpose will be explained later), $\overline{Y}\left(b-1\right)$ is the net benefit to i of cooperating (that is, playing q_i = 1), and $q_{-i}={\displaystyle {\sum }_{j,j\ne i}{q}_j}$ denotes, from i’s perspective, the number of other countries that play cooperate (that is, the number of players $j,\hspace{0.17em}j\ne i$ that choose q_j = 1 rather than q_j = 0). Finally, assume bN > 1 > b > 0. Then, for the special case in which N = 2, we have ${\pi }_i\left(0;1\right)=\overline{Y}\left(b+1\right)>{\pi }_i\left(1;1\right)=2b\overline{Y}>{\pi }_i\left(0;0\right)=\overline{Y}>$ ${\pi }_i\left(1;0\right)=b\overline{Y}$, a ranking of payoffs that defines the two-player prisoners’ dilemma.

The symmetric N-player game is illustrated (using the graphical approach devised in ref. 9) in Fig. 1. The vertical axis shows country i’s payoff, and the horizontal axis shows the number of other countries that play cooperate. The straight lines rising to the northeast thus show the payoff that country i obtains by playing q_i = 1 (lower line) or q_i = 0 (upper line). In Fig. 1, each player i is better off playing q_i = 0, irrespective of what the other players do (making play $q_i=0\forall i$ the Nash equilibrium of this game, indicated by the black circle in Fig. 1), but all players together are better off when every player i plays q_i = 1 (making $q_i=1\forall i$ the “full cooperative” outcome of this game shown by the open circle in Fig. 1).

Fig. 1.

In this prisoners’ dilemma/public goods game, there is a unique Nash equilibrium at which all players play defect/contribute nothing.

Public Goods Game

A related but somewhat different representation of the classic cooperation game is the (linear) public goods game, known as a voluntary contribution mechanism in the experimental economics literature, in which N players, each with an endowment worth $\overline{Y}$ (a dollar amount), may choose to contribute some or all of their endowment to supply a public project [that is, every country i chooses $Y_i\in \left[0,\overline{Y}\right]$ to maximize ${\pi }_i\left(Y_i;Y_{-i}\right)=\left(\overline{Y}-Y_i\right)+b\left(Y_i+Y_{-i}\right)$, where $Y_{-i}={\displaystyle {\sum }_{j,j\ne i}{Y}_j}$]. Here, the marginal cost of a contribution is one (assuming that contributions must be in whole-dollar increments), and the marginal benefit to any individual player of contributing is b. Assuming bN > 1 > b > 0, it is easy to see that the group does best when everyone contributes their entire endowment to the public project but that, taking the contributions of others as given, individual players do best when they contribute nothing—that is, when they “free ride.” The symmetric public goods game is identical to the prisoners’ dilemma shown in Fig. 1, assuming that the players face the binary choice of whether to play $Y_i=0\hspace{0.17em}\text{or}\hspace{0.17em}{Y}_i=\overline{Y}$ (this explains why I included a scaling parameter in my depiction of the prisoners’ dilemma).

As summarized in Table 1, the symmetric N-player prisoners’ dilemma and public goods games (referred to hereafter as different depictions of a “classic dilemma game”) share the following features: in both games, (i) there exists a unique Nash equilibrium, (ii) the players have dominant strategies, (iii) the Nash equilibrium is inefficient, and (iv) the Nash equilibrium is symmetric. What makes these games fascinating—and frustrating for the players who play them—is that self-interest makes each player want to defect, and yet, every player knows that, if all players behave in this way, they will all lose.

Table 1.

Equilibrium properties of various games

Equilibrium properties			Coordination
	Dilemma/public goods	Treaty/chicken	Weakest link	Catastrophe avoidance	Trade restrictions
Unique?	Yes	Yes	No	No	No
Dominant strategy?	Yes	No	No	No	No
First best efficient?	No	No	Yes	Possibly	Yes
Intermediately efficient?	No	Yes	No	Possibly	No
Symmetric?	Yes	No	Yes	Probably	Yes

It is probably because of this clash in interests that, in experiments, people play these games differently; some people choose to cooperate, and some choose not to cooperate. When the public goods game is played only once, players, on average, contribute around one-half of their endowments—a behavior that contrasts with the theory (10). The players who cooperate are not true altruists; true altruists should play the same way irrespective of how they expect others to play, and there is little evidence for this behavior. Instead, it seems that the players who cooperate in the classic two-player prisoners’ dilemma game do so in the expectation that the other player will cooperate (11). Similarly, the players who cooperate in the N-player public goods game exhibit a willingness to contribute provided that others contribute and (in the one-shot context) have an expectation that at least some of the other players will cooperate (12). In both games, the players have dominant strategies as regards their payoffs (point ii above) but not (as revealed by how they play) as regards their utilities.

If the public goods game is played a finite number of times, some players—the “conditional cooperators”—typically cooperate, at least partially, in the early rounds. Over time, however, cooperation generally declines (10). This decline arises partly because conditional cooperators reciprocate less than one for one (for example, if others contributed five on average in the previous round, a conditional cooperator might contribute only four in the next round), but it is also because of the presence of free riders (12). When some players do not contribute at all, a behavior that starts out seeming semicooperative can move quickly in the direction of the Nash equilibrium. Initially, behavior is asymmetric; over time, it becomes more symmetric (as in point iv above).

Another important observation is that, in theory, the precise value of b, which in the public goods game, represents the marginal per capita return to contributing to the public good, should not affect behavior, and yet, in experiments, free riding is observed to decrease as b increases (10). Essentially, behavior appears more cooperative when a player benefits more from his or her own provision of the public good. This result means that incentives do affect behavior, just not in the same way as suggested by the theory.

Institutions

People cooperate more effectively with the aid of institutions, which may be defined as “the rules of the game in a society or, more formally, … the humanly devised constraints that shape human interaction” (ref. 13, p. 3). Institutions enable the players to come to an agreement about what they should do collectively and what each of them should do individually, including any sharing of the costs of cooperation. Institutions also specify if and how such agreements are to be enforced.

Which institutions to use? Thomas Hobbes (ref. 14, p. 128) believed that, to overcome collective action failures, a sovereign authority, a visible power, was needed to keep people “in awe, and tye them by feare of punishment to the performance of their Covenants…” Such an authority, he reasoned, could acquire its power by either “Naturall force” or men agreeing “amongst themselves, to submit to [the authority] voluntarily…,” in which case the sovereign would be a “Common-wealth by Institution” (ref. 14, p. 132). Garrett Hardin (ref. 15, p. 1247) similarly believed that overcoming the tragedy of the commons required “mutual coercion, mutually agreed upon by the majority of the people affected.”

If this view were correct, we should expect collective action at the global level to be elusive, for there is no global sovereign, no World State. However, is the apparatus of a state really needed to correct collective action failures? Elinor Ostrom (8) has shown that, as regards local commons problems, the outcomes realized in the absence of external intervention may be much better than indicated by analytical solutions to the prisoners’ dilemma and may even be superior to top-down governance when the latter is prone to corruption and related failures. However, context matters, and Ostrom et al. (16) give reasons for why success at the local level may not scale up to the global commons. Global collective action, according to Ostrom et al. (16), involves many more players (at least if the unit of analysis is taken to be the individual), representing a greater diversity of cultures. The rules of the game also differ at this level compared with the local one. The “basic collective choice rule for global resource management,” Ostrom et al. (ref. 16, p. 282) note, requires “voluntary assent to negotiated treaties.”

This last point is critical. To Hobbes (ref. 14, p. 133), “[a] Common-wealth is said to be Instituted, when a Multitude of men do Agree, and Covenant, every one, with everyone,” that “every one, as well as he that Voted for it, as he that Voted against it, shall Authorise all the Actions and Judgements, of that [sovereign], as if they were his own…” In a democracy, the minority is bound by the decisions made by a majority. The international system of interacting sovereign states is designed very differently. States may form agreements, but such agreements apply only to the states that consent to be bound by them.

There are, to be sure, exceptions, but these exceptions only prove the rule. Under the United Nations Charter, for example, the Security Council is accorded special powers pertaining to “international peace and security,” and in recent years, beginning with Resolution 1373 (adopted in the wake of the September 11, 2001 terrorist attacks), the Security Council has imposed obligations on all United Nations members. It might, thus, seem that the Security Council has assumed the role of “World Legislature” (17), but the effect of these resolutions depends on whether they are enforced, and enforcement must be done by individual states or states acting collectively; the United Nations lacks its own enforcement capability. Another apparent exception is the European Union. Under the Treaty of Maastricht, certain decisions (including those relating to the environment) are made by a qualified majority vote. However, to become law, this treaty had to be approved unanimously by all members. More importantly, participation in the European Union remains voluntary. Dissatisfied members can always withdraw, as the United Kingdom now seems destined to do. As well, the mere threat of withdrawal can impel the other members to renegotiate their relationship. Agreements among states must be self-enforcing.

Treaty Game

Can a self-enforcing treaty change behavior? Let us see.

Suppose that N ≥ 2 countries play either the prisoners’ dilemma or the public goods game described earlier, with $k\in \left\{2,\mathrm{...},N\right\}$ of these countries forming an agreement and the other $N-k$ countries choosing not to participate. What can we expect these countries to do? How will k be determined? To answer these questions, we need to add structure to the games studied previously (18). Suppose then that the game is played in stages. In stage 1, in accordance with the (legal) principle of sovereign equality, every country chooses to be a signatory or nonsignatory to the agreement. In stage 2, signatories choose what they will do together (if they play the prisoners’ dilemma, they must choose $q_i\in \left\{\mathrm{0,1}\right\}$; if they play the public goods game, they must choose $Y_i\in \left[0,\overline{Y}\right]$). Finally, in stage 3, nonsignatories, exercising their sovereignty, choose what they will do individually.

Of course, countries need to know what they are signing up to before they decide whether to join an agreement. It thus makes sense to assume that, when the players make their choices in stage 1, they will anticipate (correctly) how the game will be played subsequently. Derivation of the equilibrium, thus, requires solving the game backward.

In stage 3, nonsignatories face precisely the same situation as in the game without an agreement, and therefore, we know that they will play q_i = 0 or Y_i = 0.

In stage 2, parties to the agreement take k as given (k is determined in stage 1) and therefore, will choose q_i in the prisoners’ dilemma and Y_i in the public goods game to maximize their collective payoff. As long as bk < 1, the parties cannot do better than to play q_i = 0 in the prisoners’ dilemma and $Y_i=0$ in the public goods game, but when bk > 1, it will pay these same players to play q_i = 1 and $Y_i=\overline{Y}$ in these games, respectively. This result means that the participants will design their treaty to say that all parties must play q_i = 1 or $Y_i=\overline{Y}$ depending on the game being played, provided that the agreement enters into force, and that the agreement will enter into force if and only if $k\ge \widehat{k}$, where $\widehat{k}$ is the smallest integer greater than $1/b$. It is important to emphasize that all treaties are designed in this way. All treaties say what the parties must do, and they all specify a minimum participation level for entry into force. In this game, these critical features of a treaty are determined endogenously.

In stage 1, each player will take the participation decisions of the other players as given. Plainly, if $\widehat{k}-2$ or fewer other countries participate in the agreement, a country cannot lose by joining, for the agreement then will not enter into force and the country will, therefore, be free to act as it pleases. By contrast, if $\widehat{k}$ or more other countries participate in the agreement, a country will lose by joining. The country will lose because, by joining, the country will have to play q_i = 1 or $Y_i=\overline{Y}$, and yet, its participation will not alter how other countries behave. However, if precisely $\widehat{k}-1$ other countries participate in the agreement, then a country will be strictly better off for joining. The country will be better off because at this participation level, a country that joins the agreement triggers its entry into force, making it necessary for this country and all of the other parties to play q_i = 1 or $Y_i=\overline{Y}$. In equilibrium, we can thus expect that there will be precisely $k^{\ast }=\widehat{k}$ parties, each playing q_i = 1 or $Y_i=\overline{Y}$, with the $N-k^{\ast }$ nonparties each playing q_i = 0 or Y_i = 0. In both the prisoners’ dilemma and the public goods game, nonparties free ride on the parties’ efforts to cooperate.

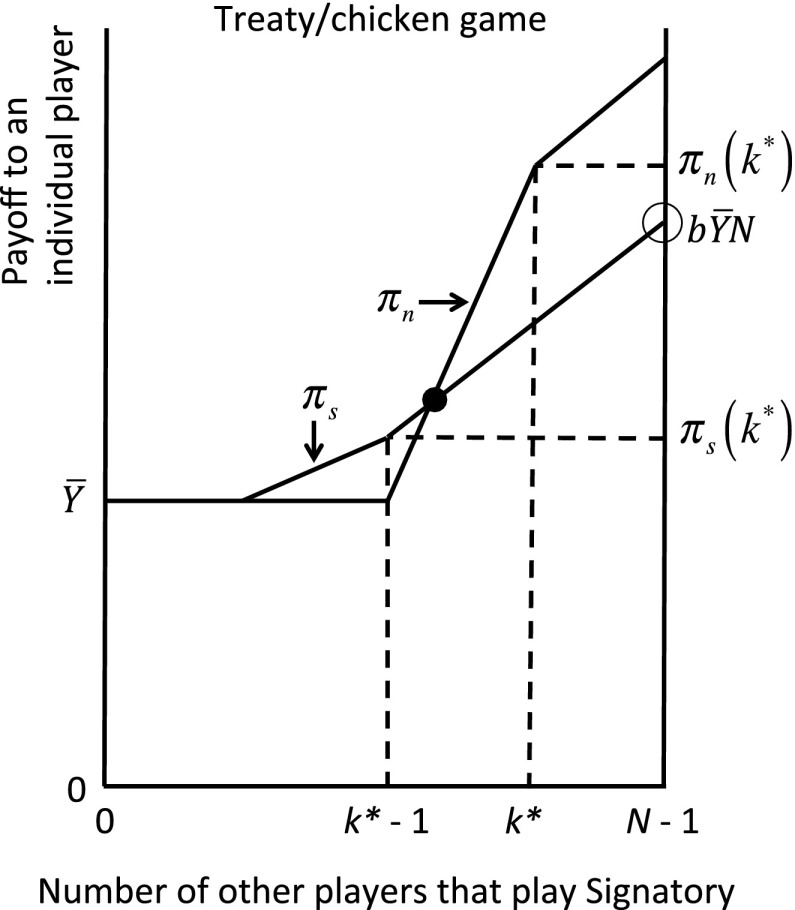
The equilibrium of this game has the following features: given the behavior of all of the other countries, no signatory can gain by withdrawing from the agreement, and no nonsignatory can gain by acceding to it; the signatories collectively cannot gain by renegotiating their agreement; and no nonsignatory can gain by changing how it behaves. The underlying game is the classic dilemma game, but the treaty transforms the game, making the players behave differently. In particular, treaty participation is a “chicken” game. Fig. 2 provides an illustration. In Fig. 2, the players have a binary choice, to be a signatory (subscript s) or a nonsignatory (subscript n), with the payoff curves for both choices reflecting the equilibrium behavior associated with the stages 2 and 3 games.

Fig. 2.

In this treaty participation game, there is a unique Nash equilibrium at $k^{\ast }$. Here, nonsignatories do better than signatories, as in a chicken game.

In this transformed game, as summarized in Table 1, (i) there is a unique Nash equilibrium; (ii) the players do not have dominant strategies; (iii) the Nash equilibrium is of intermediate efficiency, meaning that it improves on the noncooperative outcome but falls short of the ideal full cooperative outcome; and (iv) the Nash equilibrium is asymmetric. Every player is better off with the agreement than without it, but all players together would be even better off if they all cooperated. In addition, although no player has an incentive to deviate, given how all of the other players have chosen to play, each player would rather be a nonsignatory than a signatory (which is why the game is called chicken). In the dilemma game, every player free rides. In the treaty game, only some do.

How much better is the equilibrium in the treaty game compared with that in the dilemma games? The answer depends on the parameter values. For the public goods game, for example, the aggregate payoff is $\overline{Y}N$ without an agreement and $k^{\ast }\left(b\overline{Y}{k}^{\ast }\right)+\left(N-k^{\ast }\right)\left(\overline{Y}+b\overline{Y}{k}^{\ast }\right)$ with the self-enforcing agreement. Taking the difference, the aggregate gain from having the agreement is $\overline{Y}{k}^{\ast }\left(bN-1\right)$. If $1/b$ is close in value to N, and N is large, k* will be large as well. However, in this case, $bN-1$ will be close to zero, and the gain to cooperation will be very small. If $1/b$ is very small relative to N, and N is large, the term $bN-1$ will be large, but of course, k* will then be small. As one of the multiplicands increases, the other one must fall, and therefore, an agreement helps relatively little, irrespective of the participation level that it is able to sustain, as long as N is large.

Why not set the minimum participation level higher than k*? The reason is that stage 2 would then require that these signatories play $q_i=1$ or $Y_i=\overline{Y}$, and such behavior could not be enforced by credible punishments (when k > k*, it would not pay the remaining signatories to stop cooperating in the event that one country should withdraw from the agreement). This point is also taken up in the next two sections.

In an experiment testing this theory, with choices being made over 10 rounds (but with each subject’s actual payoff depending only on how the game is played in just 1 of these rounds chosen at random), participation does not differ significantly from k* (19). (The experiment assumes that the cost of contributing to the public good is quadratic rather than linear, which implies k* = 3 for any N. In this experiment, over time, the coalition size settles out to a level of 3.2 on average, although n = 10.) Compared with behavior in the absence of the treaty, average contributions and payoffs are no higher in the early rounds but improve slightly in later rounds when the coalition size approximates the theoretical prediction.

Repeated Games

The so-called “folk theorems” of repeated games tell us that, provided discount rates are sufficiently low, any feasible outcome can be supported as a subgame perfect Nash equilibrium of the infinitely repeated game. In particular, the efficient outcomes in the prisoners’ dilemma and public goods games can be supported by a strategy of reciprocity. From this perspective, when cooperation fails, the reason must be that the players somehow “selected” the wrong equilibrium. Experimental evidence shows that equilibrium selection can be difficult (20), but here, I focus on a different explanation for why cooperation can fail.

The reason that a treaty is unable to sustain an efficient outcome in a one-shot game is the assumption that the parties act so as to maximize their collective payoff both on and off the equilibrium path. In the context of the public goods game, this assumption means that, when k = k*, the parties to the agreement cannot do better collectively than to play (dropping subscripts) $Y=\overline{Y}$ and that, when k = k* − 1, the parties to this agreement (which is not an equilibrium agreement) cannot do better collectively than to play Y = 0. It is this drop in provision by parties from $Y=\overline{Y}$ to $Y=0$ that enforces participation at the level k*.

Why not require that all countries contribute $\overline{Y}$ when $k=N$ and that none do so when $k=N-1$ (or less)? If the agreement were written in this way, and the players were committed to carrying out this agreement, then full cooperation could be sustained. However, commitment is not available simply for the asking (21). If a country were to decide not to participate in this agreement, and it was in the collective interests of the remaining N – 1 countries to play $Y=\overline{Y}$ rather than $Y=0$, then this group of countries would be shooting itself in the foot by carrying out the threat to punish. Only for $k\le k^{\ast }$ is it collectively rational for the parties to an agreement to play $Y=0$ in the event of a unilateral defection.

This result is for the one-shot game. For a repeated game, collective rationality implies that an agreement must be “renegotiation-proof” (22), meaning that it must not be possible for the players to do better collectively by renegotiating their agreement when they are in either a cooperative (equilibrium) phase or a punishment (out of equilibrium) phase, responding to a previous deviation. This concept is very different from that of a subgame perfect equilibrium (the concept that underpins the folk theorems), which is about individual rationality only. Collective rationality limits the size of punishments (reductions in the provision of the public good) that are credible and therefore, sustains less cooperation.

The one-shot and repeated game models both have their strengths and weaknesses. The one-shot model tells us how the participation level will be determined but assumes full compliance. The repeated game model tells us whether compliance can be enforced but takes the participation level as given. Combining both approaches, it can be shown that the binding constraint on international cooperation is the enforcement of participation (18). To see why, note that, when Canada was on course to overshoot its allowed emission level under the Kyoto Protocol (a behavior that was surely because of the agreement not being self-enforcing), it had two options. It could remain in the agreement and thus violate the customary law that international agreements should be kept, or it could withdraw from the agreement and thus free itself from the legal obligation to comply. Not surprisingly, Canada chose to withdraw from the agreement.

In the run up to the latest climate negotiations in Paris, a number of countries insisted that the agreement had to be “legally binding.” This feature by itself, however, cannot be relied on to change behavior. If a country prefers to be free from a treaty’s obligations, it can simply choose not to participate—or withdraw from the agreement at a later date.

Consensus Treaties

The theory outlined above puts credibility above all other considerations. Another thing countries care about, however, is “fairness.” In the above model, parties to an agreement make a sacrifice that benefits all of the players, even the ones that free ride. However, can countries be relied on to play in this way? An experiment on institution formation, not unlike the theory outlined previously but involving only four players, finds that players are more inclined to support agreements involving all players compared with agreements involving only a subset of players (23).

To incorporate a concern for “fair” participation in an international agreement, we can suppose that participation must be full for reasons of fairness and that contribution levels are chosen subject to the constraint that they can be enforced by punishments that are credible given the priority accorded to fairness. In this case, free riding will not be eliminated but displaced (18), being expressed through incomplete provision rather than incomplete participation. Every country will participate and agree to do something, but no country will agree to contribute as much as required to support full cooperation. Instead of a few countries (as will be the case for the previous model when k* is small relative to N) doing a lot, a lot of countries will do very little.

The Paris Agreement has been cheered for giving expression to the principle that all countries should contribute to the collective goal of limiting emissions. However, countries were only willing to participate, because they could choose their pledges unilaterally—and on the understanding that fulfillment of these would be voluntary. Stabilizing atmospheric concentrations of greenhouse gases will require much deeper cooperation.

Punishments Reconsidered

The difficulty with the dilemma game is enforcement. Players will free ride when they can get away with it, and cooperators will be reluctant to punish this behavior when doing so means that they hurt themselves in the process.

This prediction is in theory. Experiments reveal more complex behavior. People will punish others for violating a norm, even when doing so harms their direct self-interests, provided that the punishments are highly efficient in the sense that they are much more costly to the players on the receiving end than the players who impose them (24). Other experiments show that, when punishments are less efficient (as they are in the theory), they tend not to be imposed (25). Moreover, although punishments may increase contributions, they may not make the group better off (25). The punishments must be imposed to cause contributions to increase, and punishments are costly to both the players who impose them and those on the receiving end. Furthermore, the experiment in ref. 24 assumes that there can be no retaliation. In experiments in which every player can punish any player, retaliation is common (26). Indeed, free riders will even punish cooperators strategically to discourage them from punishing free riders in the future (26). Free riding is bad, but unrestrained punishment can be worse.

The punishments discussed thus far are of material consequence. What about punishments of a more psychological or sociological nature? Some experimental studies suggest that “naming and shaming” may influence behavior (examples are in refs. 27 and 28). However, it is unclear whether these findings are sensitive to context. The only detailed analysis in international relations suggests that, at least for the case of human rights policies, naming and shaming have a limited effect and may even be counterproductive (29).

The Paris Agreement on climate change is about to put naming and shaming to a new test. The agreement’s one real innovation over previous climate treaties is to embed voluntary contribution making within a framework of “pledge and review.” Under this arrangement, every country should be able to see whether other countries’ pledges are comparable with their own, whether the totality of all such pledges suffices to meet the collective target, and in the years to come, whether countries’ actual contributions meet or fall short of their pledges.

Will Paris change behavior? It will take at least a decade to know (the pledges are for 2025 and 2030). Even after the data are in, we will not be able to tell if the arrangement had an effect, for we will never be able to observe the “counterfactual”—what countries would have done in the absence of pledge and review. The great advantage of experiments is that they provide the needed counterfactual. In a recent experiment on avoiding uncertain “catastrophic” climate change, Barrett and Dannenberg (30) find that pledge and review causes groups to increase their target (much as the parties agreed in Paris to hold temperature “well below 2 °C above pre-industrial levels,” whereas previously, they had agreed only to hold temperature change to “below 2 degrees Celsius”) and that the higher group target causes countries to increase their pledges (just as the pledges submitted for Paris exceed those made previously) but that the effect on contributions is small and lacks clear statistical significance (30). We find no evidence that pledge and review is harmful to cooperation, but we also find little evidence that it is particularly helpful. Multilateral efforts to limit climate change will need to go beyond pledge and review.

Weakest Link Game

The eradication of smallpox is perhaps the greatest achievement of international cooperation in human history, saving millions of lives in developing countries and sparing all countries from having to administer a costly and risky vaccine (6). Eradication is an exacting goal, intolerant to the slightest misstep. A disease can only be eradicated if it has been eliminated everywhere on Earth at the same time. If just one country failed to eliminate smallpox, all countries would have remained at risk and therefore, would have had to continue to vaccinate. Eradication is a “weakest link” game (31). The last case of endemic smallpox occurred in Somalia, making this country the weakest link.

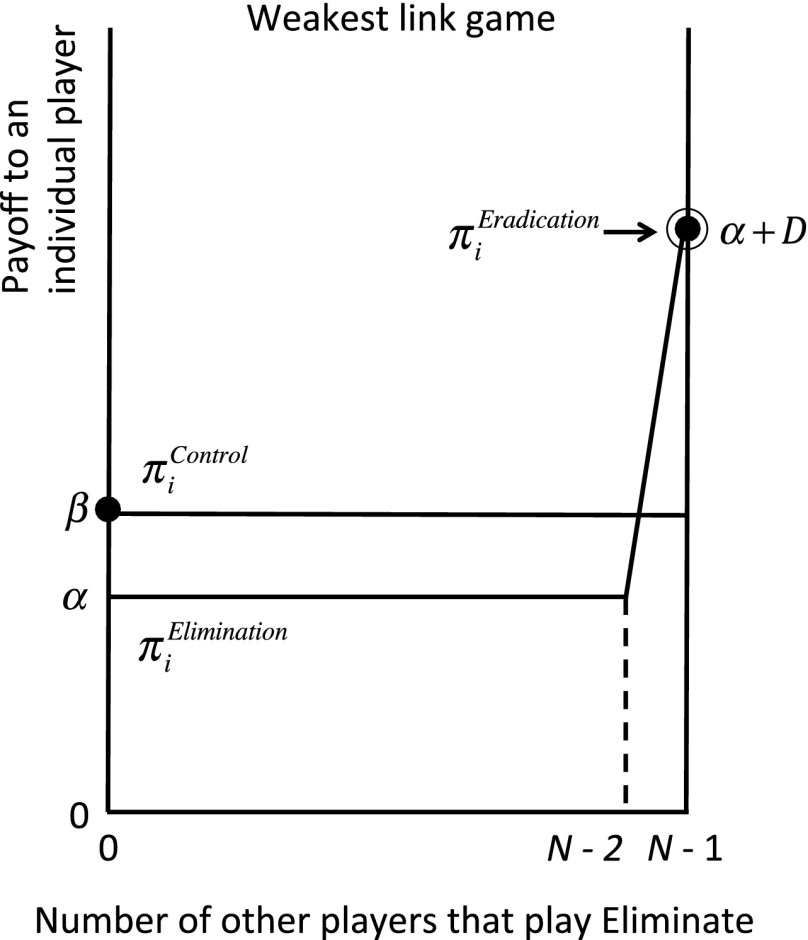
Although the eradication game can be derived using basic epidemiological relationships (32), here I offer a simplified version. The game is static (one shot) and symmetric (all countries have the same choices and payoff functions). Every country i chooses a vaccination level $v_i\in \left[\mathrm{0,1}\right]$ in the knowledge that there exists a critical vaccination level, $\overline{v}>0$, such that, for $v_i<\overline{v}$, the disease remains locally endemic and for $v_i\ge \overline{v}$, the disease is eliminated within country i; herd immunity implies $\overline{v}<1$. Let $v_{-i}^{\min }=\min \left(v_1,\mathrm{...},v_{i-1},v_{i+1},\mathrm{...},v_N\right)$ represent the smallest level of population immunity for any country other than i. Taking this value as given, country i aims to maximize ${\pi }_i\left(v_i;v_{-i}^{\min }\right)=f\left(v_i\right)+g\left(v_{-i}^{\min }\right)$, where f, the payoff to controlling the disease, is a strictly concave function and where $g\left(v_{-i}^{\min }\right)=0\hspace{0.17em}\text{if}\hspace{0.17em}{v}_{-i}^{\min }<\overline{v}$ and $\text{g}\left(v_{-i}^{\min }\right)=D\hspace{0.17em}\text{if}\hspace{0.17em}{v}_{-i}^{\min }\ge \overline{v}$. Here, D > 0 represents the “dividend” to eradication. Let ${\widehat{v}}_i$ denote the level of control that is optimal given that $v_{-i}^{\min }<\overline{v}$, yielding i the payoff ${\pi }_i^{Control}\left(\widehat{v};v_{-i}^{\min }<\overline{v}\right)=f\left(\widehat{v}\right)=\beta$, and let the payoff to local elimination be ${\pi }_i^{\mathit{Elimination}}\left(\overline{v};v_{-i}^{\min }<\overline{v}\right)=\alpha$. Because $\widehat{v}$ is optimal, we know that $\beta >\alpha$. Finally, we have ${\pi }_i^{Eradication}\left(\overline{v};v_{-i}^{\min }=\overline{v}\right)=\alpha +D$.

The eradication game is shown in Fig. 3, assuming $\alpha +D>\beta$. No country wants to eliminate the pathogen as long as it continues to circulate outside of the country’s borders. However, should every other country eliminate the disease, each country wants to do so, ensuring that the disease is eradicated. Control and elimination require recurring intervention, and the values $\alpha$ and $\beta$ should, therefore, be interpreted as annual values. Eradication, by contrast, is permanent (barring any risk of reintroduction). The dividend D can be calculated by putting a value on the deaths, illnesses, and vaccination costs avoided every year as a consequence of eradication (relative to optimal control), discounting these to the present, and then adding up this long series of values. For smallpox, the dividend was huge, implying a benefit:cost ratio [approximated in Fig. 3 by the ratio $D/\left(\beta -\alpha \right)$] in excess of 100:1 (33).

Fig. 3.

In this weakest link game, there are two Nash equilibria, and one of which yields a higher payoff for achieving eradication.

The weakest link game is a type of coordination game. In a coordination game, there exists a multiple of (pure strategy) Nash equilibria, and the players must coordinate to choose the same strategy. In the eradication game, one of these Nash equilibria is efficient, sustaining a first best outcome and thus, making eradication a first best coordination game. As summarized in Table 1, in such games, (i) there exist two (pure strategy) Nash equilibria, (ii) the players do not have dominant strategies, (iii) one of the Nash equilibria (for the eradication game, the one in which the disease is eradicated) sustains a first best, and (iv) both Nash equilibria are symmetric.

What is special about this game is not only that all players want to achieve the same goal but that each of them has an incentive to play its full part in achieving the shared goal, provided each is assured that all of the other players will play their full part.

Smallpox was in many ways uniquely suited to eradication (6), but related efforts testify to the powerful incentives to supply this kind of public good. Rinderpest, a cattle disease, was declared eradicated in 2011, and type 2 wild poliovirus was declared eradicated in 2015 (vaccine-derived type 2 polio continues to circulate). Today, the effort to eradicate the two other wild polioviruses (and all circulating vaccine-derived polioviruses) continues, although the original plan was to interrupt transmission by 2000. The campaign to eradicate Guinea worm, first launched in 1980, also continues to receive strong support. Unfortunately, both efforts also continue to encounter new problems. Being a weakest link game, even the smallest disruption can ensure that eradication remains just out of reach.

Catastrophe Avoidance Game

In the eradication game, countries must cooperate to reap a dividend. In the dangerous climate change game, by contrast, countries must cooperate to avoid a catastrophic loss—such as would result should the world cross “tipping points” for major geophysical systems, like the polar ice sheets (34).

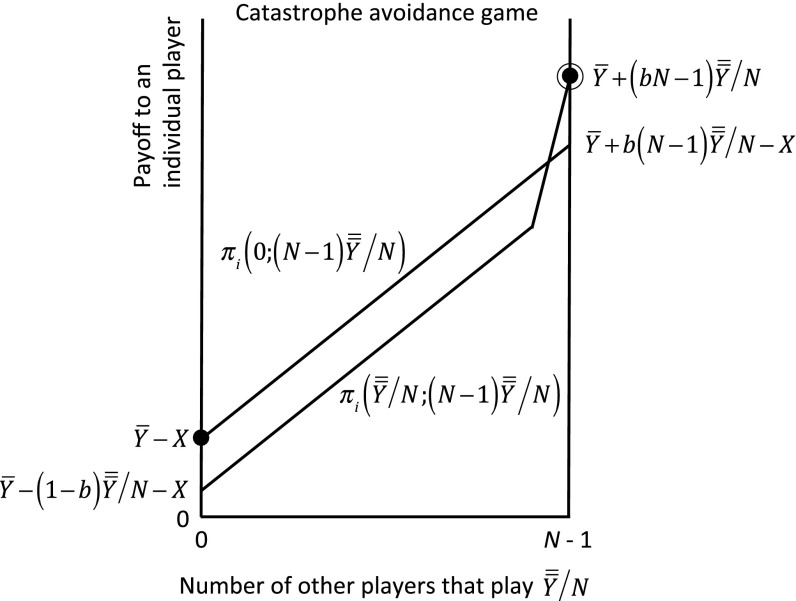
To see how the threat of crossing a dangerous threshold affects behavior, let us modify the public goods game very slightly and suppose that player i’s payoff is ${\pi }_i\left(Y_i;Y_{-i}\right)=\overline{Y}-Y_i+b\left(Y_i+Y_{-i}\right)-X$ for $Y_i+Y_{-i}<\overline{\overline{Y}}$ and ${\pi }_i\left(Y_i;Y_{-i}\right)=\overline{Y}-Y_i+b\left(Y_i+Y_{-i}\right)$ for $Y_i+Y_{-i}\ge \overline{\overline{Y}}$, with $bN>1>b>0$ as before and $\overline{Y}N\ge \overline{\overline{Y}}$ (avoiding catastrophe is feasible). Here, $\overline{\overline{Y}}$ is the threshold for a catastrophic regime shift, and X is the impact (an economic value) of crossing the threshold. Assuming that the burden of avoiding the threshold for catastrophe is shared evenly, player i will get ${\pi }_i\left(\overline{\overline{Y}}/N;\left(N-1\right)\overline{\overline{Y}}/N\right)=\overline{Y}-\overline{\overline{Y}}/N+b\overline{\overline{Y}}$. If i deviates, it will want to choose $Y_i=0$ and therefore, will get ${\pi }_i\left(0;\left(N-1\right)\overline{\overline{Y}}/N\right)=\overline{Y}+b\left(N-1\right)\overline{\overline{Y}}/N-X$. Not deviating will thus be a Nash equilibrium provided $X\ge \left(1-b\right)\overline{\overline{Y}}/N$. Let us assume that this last condition is satisfied (that is, X is truly catastrophic). Then, the catastrophe avoidance game looks very much like the weakest link game (Fig. 4).

Fig. 4.

In this catastrophe avoidance game, there are two Nash equilibria, with selection of the better one, on the right, requiring coordination.

There are, however, differences. First, if $\overline{Y}>\overline{\overline{Y}}/N$, the mutually preferred Nash equilibrium will be inefficient (in the symmetric equilibrium in which catastrophe is avoided, every country contributes less than its full endowment, although all countries together would be better off if every country contributed $\overline{Y}$). Second, provided $\overline{Y}\gg \overline{\overline{Y}}/N$, there may exist Nash equilibria in which some players contribute and some do not or some contribute more than others. That is, there may exist multiple asymmetric equilibria. Disease eradication is different. To achieve zero cases globally, each country must achieve zero cases locally. For a problem like avoiding catastrophic climate change, however, countries must decide which of them should contribute and by how much they should contribute. These differences may explain why the decision to eradicate a disease can be made by a unanimous resolution adopted by the World Health Assembly, whereas the decision to avoid “dangerous” climate change requires a treaty (treaties tolerate nonparticipation in excess of the minimum participation level). Third and perhaps most importantly, the threshold for eradicating a disease is certain (zero cases everywhere), whereas for most environmental issues of interest, the threshold for catastrophe, $\overline{\overline{Y}}$, is very uncertain.

If $\overline{\overline{Y}}$ is certain, then as shown above, catastrophe avoidance will be a coordination game. If the threshold is (sufficiently) uncertain, however, catastrophe avoidance will be a classic dilemma game (35). To see why, suppose that $\overline{\overline{Y}}$ is uncertain and distributed uniformly on the interval $\left[{\overline{\overline{Y}}}_{\min },{\overline{\overline{Y}}}_{\max }\right]$ with ${\overline{\overline{Y}}}_{\max }\le \overline{Y}$. Then, it will pay the group collectively to contribute ${\overline{\overline{Y}}}_{\max }$ so as to avoid any chance of catastrophe (this result will be true even without appealing to the “precautionary principle”). Provided that the players can communicate, it is likely that they will agree that each country should contribute its “fair share,” making ${\overline{\overline{Y}}}_{\max }/N$ the obvious “focal point” (21). When it comes to deciding how to behave, however, every country will know that, if it contributes a little less than ${\overline{\overline{Y}}}_{\max }/N$, the chances are low that this deviation will trigger a catastrophe. Moreover, each country will suffer only 1/Nth of the total consequence should catastrophe occur. Therefore, all players will be tempted to contribute less than ${\overline{\overline{Y}}}_{\max }/N$, making catastrophe virtually certain. This remarkably clear theoretical result has been strongly confirmed by how people play this game in experiments (36). When the threshold is certain or uncertainty about the threshold is very, very small, people are able to coordinate to avoid a catastrophic outcome. When uncertainty about the threshold is a little larger, efforts to cooperate fail, making it virtually inevitable that the critical threshold will be crossed. For climate change, thresholds are not only uncertain, but their probability distributions are substantially unknown (37). An experiment similar to the one noted above finds that this “ambiguity” effect lowers contributions even more and causes contributions to be more erratic (38).

Of course, the impact, X, of crossing a critical threshold will also be uncertain. Taking the melting of polar ice as an example, we do not know precisely by how much sea level will rise, how long the process will take, or how easy it will be to adapt to sea level change. However, theory (35) and experimental evidence (39) strongly suggest that uncertainty about this value has no effect on behavior (obviously, the expected value of the impact does matter). It is only uncertainty about the threshold that changes behavior. Unfortunately, tipping points for the climate are very inherently uncertain (34). Smallpox eradication had features that helped collective action. Climate change has features that make collective action very difficult.

Treaty Game Incorporating Trade Restrictions

Although stratospheric ozone is also prone to tipping, “the non-linear behavior of lower-stratospheric ozone loss was not even a consideration in the discussions that led to the CFC ban…” (ref. 40, p. 116). Indeed, negotiators did not even establish a global goal for limiting loss of column ozone levels. They merely set about trying to limit the production and consumption of ozone-depleting chemicals. Because this approach worked, however, “[s]tratospheric ozone depletion was properly dealt with well before crossing the boundary that would trigger an abrupt change of global proportions…” (40). Without deliberately trying to avoid a threshold, collective action succeeded in avoiding a threshold anyway.

The agreement that brought about this outcome—the Montreal Protocol—succeeded, because it changed incentives. Rather than just ask countries to limit chlorofluorocarbons (CFCs), Montreal made it in the interests of states to phase out CFCs. Crucially, the agreement banned trade between parties and nonparties in the controlled substances and products containing these substances. Elsewhere, I have shown how a trade ban can change incentives (18). Here, I sketch the critical mechanisms.

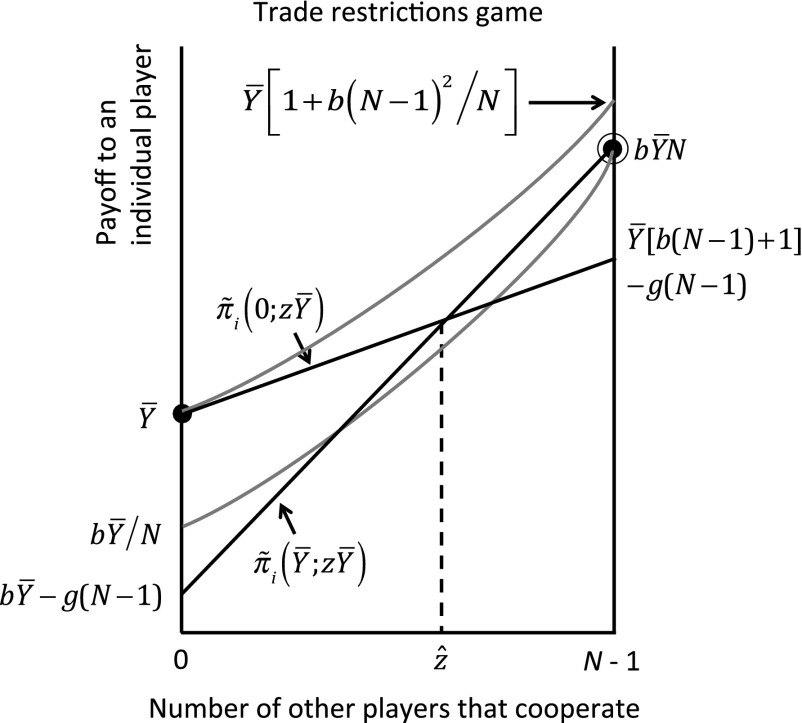
Thanks to the World Trade Organization, the status quo regime approximates “free trade.” Free trade brings many benefits, but it also results in “leakage,” the tendency, when only a subset of countries limits emissions, for emissions to increase in other countries. Assume that each player can either contribute zero or the maximum amount $\overline{Y}$. If z other players contribute $\overline{Y}$, player i gets the payoff ${\pi }_i\left(\overline{Y};z\overline{Y}\right)=b\overline{Y}\left(z+1\right)\left[1-l\left(\overline{Y};z\overline{Y}\right)\right]$ if it also contributes $\overline{Y}$ and ${\pi }_i\left(0;z\overline{Y}\right)=b\overline{Y}z\left[1-l\left(0;z\overline{Y}\right)\right]+\overline{Y}$ if it contributes zero. Here, l denotes the leakage rate: the increase in the emissions by third parties caused by a given reduction in emissions by a subset of other countries. Assume that leakage can be represented by the linear functions $l\left(\overline{Y};z\overline{Y}\right)=\theta \left[1-\left(z+1\right)/N\right]$ and $l\left(0;z\overline{Y}\right)=\theta \left(1-z/N\right)$. The gray lines in Fig. 5 trace out these two payoff functions, assuming $\theta =1$. Trade gives some curvature to the payoff functions but leaves their relative positioning unchanged compared with the classic dilemma game.

Fig. 5.

The gray lines show the public goods game played against the background of free trade. The black lines show the same game subject to a trade ban. In this game, there is a tipping point at $\widehat{z}$ and Nash equilibria at either end, with the equilibrium supported by a trade ban being preferred by all of the players.

Although a ban on trade in CFCs between parties and nonparties would eliminate leakage, it would also result in a loss in the gains from trade. Assuming a linear relation once again, and letting $-g$ denote the loss to any country not allowed to trade with any one of the other countries, country i’s payoff under a trade ban is ${\stackrel{\sim }{\pi }}_i\left(\overline{Y};z\overline{Y}\right)=b\overline{Y}\left(z+1\right)-g\left[N-\left(z+1\right)\right]$ if i contributes and ${\stackrel{\sim }{\pi }}_i\left(0;z\overline{Y}\right)=b\overline{Y}z+\overline{Y}-gz$ if i does not contribute. It is easy to show that this transformed game has a tipping point at $\widehat{z}=\left[\overline{Y}\left(1-b\right)+g\left(N-1\right)\right]/2g$ and that this point will be “interior” provided $\overline{Y}\left(1-b\right)\le g\left(N-1\right)$, making this a coordination game. Fig. 5 illustrates these payoffs. The gray lines in Fig. 5, as noted before, represent the underlying game; the black lines in Fig. 5 depict the game transformed by the trade restriction.

It should now be clear how to write the treaty. The treaty should (i) require that parties contribute $\overline{Y}$ each, (ii) ban trade between parties and nonparties, and (iii) enter into force only if at least $\widehat{k}$ countries ratify the agreement, where $\widehat{k}$ is at least as large as the smallest integer greater than $\widehat{z}$.

The threat to restrict trade transforms the game, but is the threat credible? To be credible, it must be the case that, should any country choose not to participate, the remaining $N-1$ countries will be better off when they ban trade with this country than when they continue to trade with it. Again, it is a simple matter to show that the cooperating countries are at least as well off carrying out their threat than not banning trade provided $b\overline{Y}\theta \left(N-1\right)/N\ge g$. Somewhat ironically, leakage, which is normally thought of as being detrimental to cooperation, is essential to sustaining cooperation in this coordination game.

In this game, as shown in Table 1, (i) there exist two Nash equilibria (in pure strategies), (ii) the players do not have dominant strategies, (iii) one of the Nash equilibria is first best efficient (a point to which I shall return later), and (iv) both Nash equilibria are asymmetric. In this game, there is no conflict.

Concluding Thoughts

Countries find it difficult to cooperate voluntarily. They also find it difficult to enforce agreements to supply a public good. By contrast, they find coordination relatively easy.

Coordination requires a pull: countries must believe that they will be better off if they coordinate. It also requires a push: countries must understand that, if most other countries coordinate, those that do not will be worse off. This latter incentive has been missing from all of the climate agreements.

Outside of issues like eradication, the need for coordination can be hidden from the negotiators’ view. Worse, for climate change, the options for coordination are more constrained than they were for protecting the ozone layer. Still, such options should be pursued, particularly because they would complement (and certainly not undermine) implementation of the Paris Agreement. Indeed, one such effort is already underway—negotiation of an amendment to the Montreal Protocol to phase down hydrofluorocarbons (HFCs). HFCs are harmless to the ozone layer and therefore, would not normally be controlled by this agreement. However, HFCs are a potent greenhouse gas, and the Kyoto Protocol failed to limit them. For reasons explained here, Montreal’s strategic approach will almost surely work better. Negotiators would do well to look for other opportunities to coordinate actions to limit climate change.