Covariation of axon initial segment location and dendritic tree normalizes the somatic action potential

Significance

Neurons generate highly reliable and temporally precise action potentials with a spatial onset in the axon initial segment. The axon initial segment location relative to the soma is, however, highly variable across neurons within the same cell class. Here, we experimentally and theoretically investigated the structure–function relationship of axon distances in neocortical pyramidal neurons. We discovered a scaling principle between the size of the dendritic tree and the axon distance supported by the cable properties and electrophysiological recordings. The work reveals that axons are not randomly positioned but covary with dendrites normalizing the somatic action potential in the face of diverse cellular morphologies.

Abstract

In mammalian neurons, the axon initial segment (AIS) electrically connects the somatodendritic compartment with the axon and converts the incoming synaptic voltage changes into a temporally precise action potential (AP) output code. Although axons often emanate directly from the soma, they may also originate more distally from a dendrite, the implications of which are not well-understood. Here, we show that one-third of the thick-tufted layer 5 pyramidal neurons have an axon originating from a dendrite and are characterized by a reduced dendritic complexity and thinner main apical dendrite. Unexpectedly, the rising phase of somatic APs is electrically indistinguishable between neurons with a somatic or a dendritic axon origin. Cable analysis of the neurons indicated that the axonal axial current is inversely proportional to the AIS distance, denoting the path length between the soma and the start of the AIS, and to produce invariant somatic APs, it must scale with the local somatodendritic capacitance. In agreement, AIS distance inversely correlates with the apical dendrite diameter, and model simulations confirmed that the covariation suffices to normalize the somatic AP waveform. Therefore, in pyramidal neurons, the AIS location is finely tuned with the somatodendritic capacitive load, serving as a homeostatic regulation of the somatic AP in the face of diverse neuronal morphologies.

The axon initial segment (AIS) specifies in vertebrate neurons a single domain for the final integration of synaptic input and the initiation of action potentials (APs) (1, 2). To rapidly produce large inward and outward currents mediating the AP, the AIS contains a complex arrangement of cytoskeletal and transmembrane proteins clustering high densities of voltage-gated sodium (Nav) and potassium (Kv) channels in the axolemma (2–4). Although the composition of ion channels is critical for initiation and regulation of firing patterns, there are emerging insights that the AIS is not operating in isolation but is also subject to activity-dependent changes in size and location constrained by the local dendritic branch geometry and the passive cable properties (5–7). Experimental studies linking changes in AIS length and neuronal output showed that an increased length facilitates AP generation (6, 8). In these cases, the net increased excitability is a logical consequence of the larger Nav conductance. However, predicting the impact of AIS location on neuronal output is more complex. Experimental studies showed that an activity-dependent distal shift of the AIS is associated with decreased AP output (5). In contrast, model simulations showed that shifting the AIS distally promotes excitability (9). One of the critical factors influencing AIS excitability is the large somatodendritic membrane area acting as current sink for sodium current generated in the AIS (10–12). In this view, a distal anatomical location of the AIS increases electrical compartmentalization and facilitates axonal AP generation. Indeed, the local depolarization in the AIS is proportional to the axial resistance between the soma and the AP initiation site, which increases with distance from the soma (11). However, increasing the distance between soma and AIS will be unfavorable for synapse to spike coupling, because it increases voltage attenuation and thereby, reduces the possibility for synaptic potentials to cross the AP threshold in the AIS (13). Furthermore, pyramidal neurons require axonal APs to rapidly depolarize the soma and activate somatic voltage-gated Nav channels to produce the dendritic back-propagating AP (14, 15).

In view of the importance of AIS location in neuronal excitability, it is striking that the reported intercellular variability within neuron cell types is large. In 50 to 70% of dopaminergic and GABAergic neurons of the substantia nigra, the axon arises from dendrites, even up to ∼260-µm distance from the soma (16–18). In fact, an axon origin from a dendrite is even a defining feature of some hippocampal interneurons (19, 20). Furthermore, about 30 to 60% of the pyramidal neurons in the hippocampus have an axon emerging from a basal (or sometimes, an apical) dendrite up to ∼40-µm distance from the soma (20, 21), and also, in the neocortex, axons have been observed to emerge from basal dendrites (19, 22, 23). Here, we investigated whether AIS location plays a functional role in neocortical pyramidal neuron excitability. We found that AIS distance from the soma but not length strongly and inversely correlates with the dendritic morphology and follows the theoretical relationship predicted by cable theory when resistive coupling between the soma and axon adjusts a longitudinal current that normalizes somatic AP generation. The large intercellular variation in AIS location thus reflects structural homeostatic scaling to normalize the somatic AP in the face of diverse morphologies of dendritic trees.

Results

Thick-Tufted Layer 5 Neurons Have Diverse Axonal Origins.

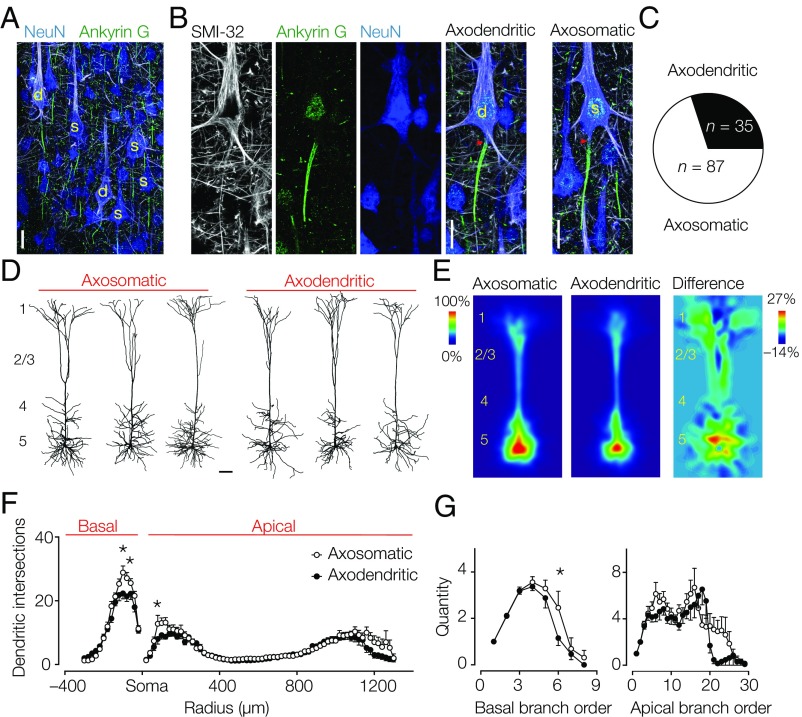
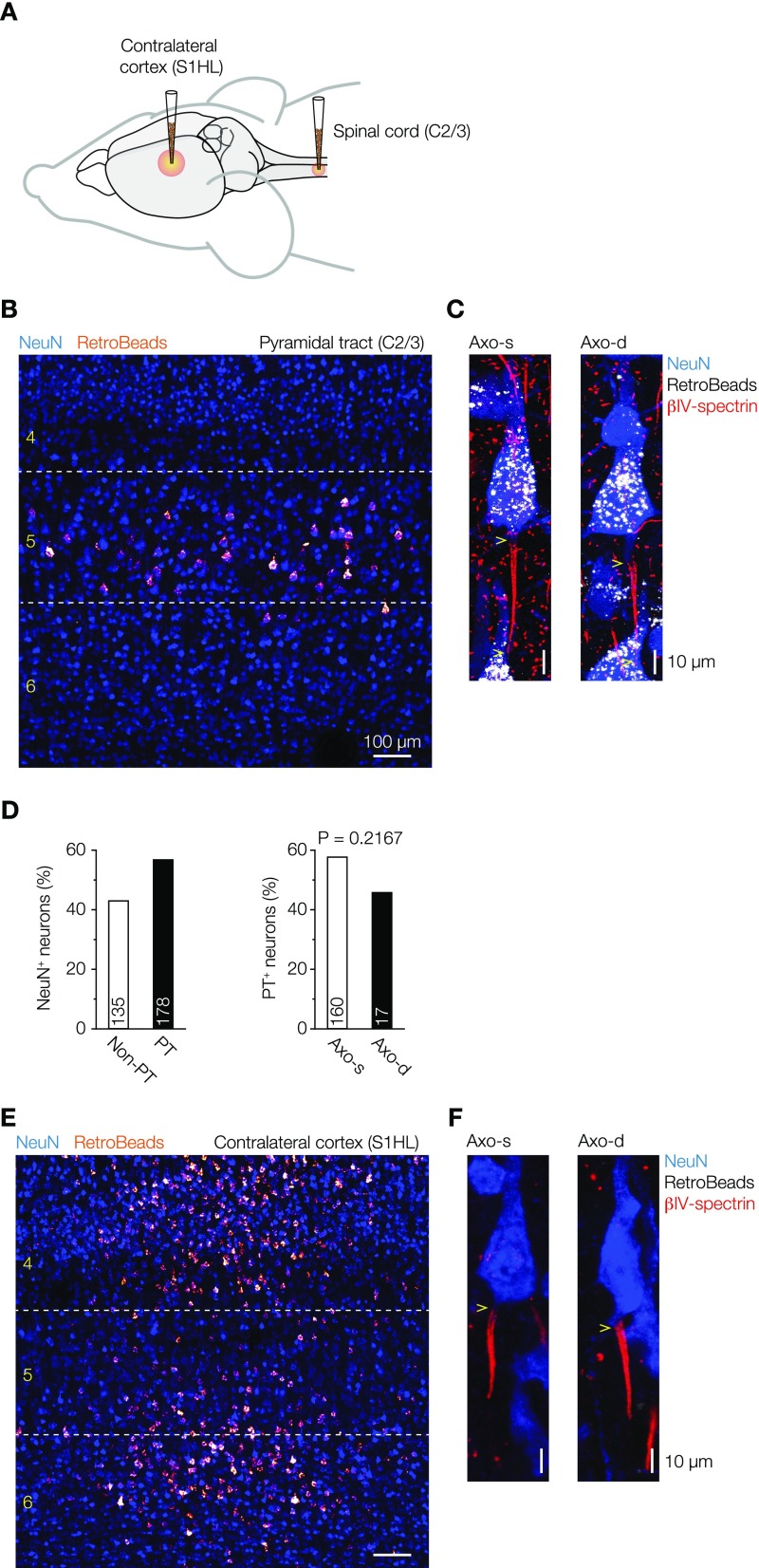
To characterize the diversity in axon locations in layer 5 pyramidal neurons, we colabeled tissue sections containing the primary somatosensory hind limb region from adult Wistar rats with Gp-anti–NeuN, a somatodendritic marker, Rb–anti-Ankyrin G, an AIS marker, and M-anti–SMI-32 (Sternberger monoclonal-incorporated antibody 32), a neurofilament marker, for type 1 (thick-tufted) layer 5 neurons (24) (Fig. 1A). SMI-32⁺ primary axons could be observed emanating from either the soma or a basal dendritic branch (Fig. 1B). Population analysis (n = 7 animals; two to three sections per animal) showed that neurons with an axon origin from a dendrite, hereby referred to as “axodendritic” neurons, constitute one-third of the population of SMI-32⁺ neurons (Fig. 1C). The large fraction of pyramidal neurons with an axon starting from a basal dendrite may indicate that they represent a distinct subtype. Based on electrophysiological and anatomical features, two major types of layer 5 pyramidal neurons have been identified: intracortically (corticocortical) projecting slender tufted layer 5 neurons and subcortically [corticosubcortical (CS)] projecting thick-tufted layer 5 neurons (24–26). Although SMI-32 typically labels thick-tufted layer 5 neurons, they may be further divided into subpopulations (24, 25). To test whether axodendritic and axosomatic neurons project to different targets, we injected fluorescent retrograde beads in the spinal cord (C2/3) (Fig. S1). Fluorescent retrobeads were localized exclusively in the somata of superficial and deep layer 5 neurons in the somatosensory and motor cortices. From a total of 313 analyzed neurons, 178 were back-labeled with fluorescent retrobeads. Within the population of layer 5 neurons with identified axon origin (somatic or dendritic), 58% of the axosomatic neurons projected to C2/3 (n = 160 of 277) compared with 46% of the axodendritic neurons (n = 17 of 37; Fisher’s exact test, P = 0.2167) (Fig. S1), indicating equal subcerebral targeting of both subtypes. Next, we made whole-cell recordings from visually identified pyramidal layer 5 neurons and filled them with biocytin for posthoc immunofluorescence using βIV-spectrin to identify the axon location (n = 38 cells; 27 animals). Similarly, a large fraction of neurons was axodendritic (50%; n = 19 of 38). The dendritic organization of both subtypes showed that apical dendrites branched extensively in layer 1, consistent with a CS cell type (Fig. 1D, Fig. S2, and Table S1). Interestingly, quantitative analysis showed that the sum of dendritic branches was smaller in the basal region of the axodendritic neurons (Fig. 1E and Table S1). This difference was further supported by a Sholl analysis revealing that the density of basal dendrites was significantly lower in axodendritic neurons (two-way ANOVA, P < 0.05, n = 26) (Fig. 1F). Additional comparison of branches as a function of distance from the soma showed that axodendritic neurons have fewer (basal and apical) dendritic sections within a proximal region of 100–200 µm from the cell body and a lower complexity of both basal and apical dendritic sections (Fig. 1 F and G). Taken together, these results indicate that the subcellular axon origin is not associated with a specific subtype but is associated with quantitative differences in the dendritic tree.

Fig. 1.

Axodendritic layer 5 pyramidal neurons are abundant in the neocortex and characterized by a smaller dendritic tree. (A) z-Projected confocal scan of a triple-immunofluorescence labeling for NeuN (somatodendritic marker; blue), Ankyrin G (an AIS marker; green), and SMI-32 (type 1 pyramidal cell marker; white). SMI-32⁺ neurons with identified axon location are indicated (yellow). (Scale bar: 25 µm.) (B, Left) Single fluorescence channels and merged image of an axodendritic neuron. (B, Right) Merged scan of an axosomatic neuron. Red arrowheads indicate the start of the AIS. d, Axodendritic; s, axosomatic. (Scale bar: 20 µm.) (C) Axodendritic neurons constitute one-third of the SMI-32⁺ neurons (28.7%; 35 of 122). (D) Representative examples of 3D reconstructed dendritic trees of axosomatic and axodendritic neurons. (Scale bar: 100 µm.) (E) Average heat maps of (Left) axosomatic (n = 13) and (Center) axodendritic (n = 13) neurons. (Right) Note the higher density of basal dendrites in the subtracted heat map. (F) Sholl plot of axosomatic (○) and axodendritic (●) neurons at 20-µm intervals. Two-way repeated measures ANOVA interaction P = 0.0651, intersections P < 0.0001, and subtype P < 0.0001. Bonferroni’s posthoc test. Error bars represent SEM. *P < 0.05. (G) Axodendritic neurons possess lower branch order of the basal dendrites. Basal branch order: two-way ANOVA interaction P = 0.3468, branch order P < 0.0001, and subtype P = 0.030. Bonferroni’s posthoc test. Apical branch order: two-way ANOVA interaction P = 0.0165, branch order P < 0.0001, and subtype P = 0.0016. Error bars represent SEM. *P < 0.05.

Fig. S1.

Labeling of layer 5 pyramidal cells by fluorescent retrograde beads injections into the spinal cord and contralateral cortex hemisphere. (A) Schematic representation of fluorescent retrograde beads injection sites. (B) Overview confocal image of the somatosensory cortex in a parasagittal section showing the spinal cord-injected retrograde beads labeling of pyramidal neurons after retrograde transport (bright red). Sections where colabeled with NeuN (blue) to reveal cortical layer identification. Neurons projecting to the spinal cord were back-labeled and restricted to layer 5. (C) Confocal images of axosomatic and axodendritic layer 5 pyramidal neurons showing labeling with fluorescent retrobeads (white) and immunolabeling for NeuN (blue) and βIV-spectrin (red). Yellow arrows indicate the origin of the AIS. (D) Bar plots quantifying the percentage of layer 5 pyramidal neurons projecting to the spinal cord. Fisher’s exact test. PT, pyramidal tract. (E) Overview confocal image of the retrograde labeling of contralaterally projecting neurons in the somatosensory cortex. Although primary cortical areas have very few callosal connections (46), some contralateral-projecting neurons with small somata were found in the primary S1HL. (Scale bar: 100 μm.) (F) Large layer 5 pyramidal neurons were not back-labeled for retrobeads injected at the contralateral cortex hemisphere. Axo-d, axodendritic; Axo-s, axosomatic.

Fig. S2.

Dendritic morphology of thick-tufted layer 5 neurons. Dendritic gallery of 13 reconstructed axodendritic (A) and 13 axosomatic (B) thick-tufted layer 5 pyramidal neurons.

Table S1.

Dendritic tree properties

Coupling type	Sum of dendritic nodes	Sum of dendritic length (µm)	Sum of dendritic area (µm2)	Apical dendritic nodes	Apical dendritic length (µm)	Apical dendritic area (µm2)	Basal dendritic nodes	Basal dendritic length (µm)	Basal dendritic area (µm2)
Axodendritic (n = 13)	69 ± 5	14,722 ± 717	57,572 ± 2,430	43 ± 3	9,404 ± 474	41,316 ± 1,772	26 ± 3	5,319 ± 279	16,257 ± 923
Axosomatic (n = 13)	83 ± 5	16,090 ± 719	65,696 ± 2,590	51 ± 3	10,239 ± 523	44,528 ± 2,266	31 ± 2	5,851 ± 276	19,211 ± 3,648
Two-tailed unpaired t test (P)	0.0537	0.1907	0.0314	0.0539	0.2483	0.2758	0.1361	0.1874	0.0413

Morphological parameters of 3D reconstructed neurons. All data are presented as mean ± SEM.

The Dendritic Morphology Scales Specifically with AIS Distance.

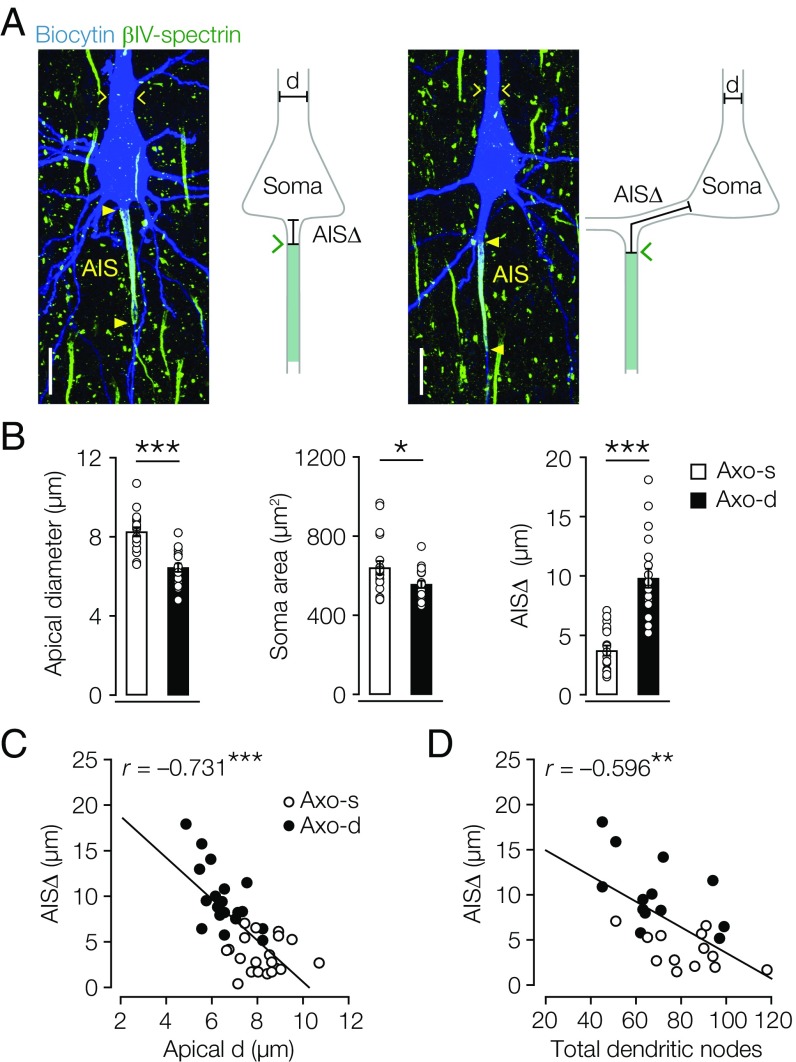
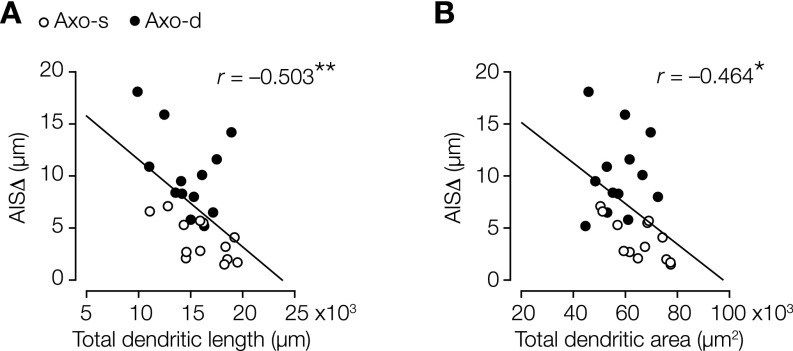
Salient characteristics of axodendritic layer 5 neurons were their relatively narrow diameter of the proximal apical dendritic trunk (Fig. 2 A and B and Table S2) and smaller somatic cross-sectional area (Fig. 2 A and B and Table S2), consistent with their reduced dendritic organization (Fig. 1 E and F). To obtain a single measure for AIS location, we determined the AIS distance (AISΔ) as the linear path length from the base of the soma to the start of the dense expression of either βIV-spectrin or Ankyrin G (Fig. 2A). In contrast to previous observations in mouse hippocampal pyramidal neurons (21), we never detected Ankyrin G or βIV-spectrin immunofluorescence signals in the dendritic branches connecting the axon, suggesting that AISΔ accurately reflects the anatomical distance from the soma. In axodendritic neurons, AISΔ was significantly more distal compared with axosomatic neurons (Fig. 2 A and B and Table S2). The size of the AIS compartment was, however, constant; neither AIS length nor the 2D area were different between subtypes (Table S2). Interestingly, specifically, the AISΔ inversely and strongly correlated with the apical dendrite diameter (Fig. 2C and Table S3). A correlation between the axonal and dendritic organization was further corroborated when plotting AISΔ against the total number of dendritic nodes (Fig. 2D and Table S3) and the total dendritic length as well as the total dendritic area (Fig. S3). In contrast, neither AIS length nor the area correlated with apical dendritic diameter (Table S3). These findings suggest that, in the population of thick-tufted layer 5 neurons, the AISΔ is fine-tuned with the anatomical organization of dendrites.

Fig. 2.

Dendritic morphology correlates with AIS distance. (A, Left) z-Projected confocal images of filled axosomatic and axodendritic layer 5 neurons (blue) overlaid with βIV-spectrin (green). (A, Right) Schematic with AISΔ indicating the linear path from soma base to start of βIV-spectrin expression. Yellow closed arrowheads indicate start and end of the βIV-spectrin immunofluorescence signal; yellow open arrows indicate apical dendrite diameter. d, Apical diameter. (Scale bar: 20 µm.) (B) Axodendritic neurons possess smaller apical dendritic diameter and somata but longer AISΔ. Two-way unpaired student’s t test. Axodendritic, n = 19; axosomatic, n = 19. Error bars represent SEM. Axo-d, axodendritic; Axo-s, axosomatic. *P < 0.05; ***P < 0.00001. (C) Correlation analysis between AISΔ and apical dendrite diameter. Pearson’s test; n = 38. ***P < 0.0001. (D) Correlation analysis between AISΔ and total sum of dendritic nodes. Pearson’s test; n = 26. **P = 0.001.

Table S2.

Morphological properties of the perisomatic domain

Coupling type	Cortical depth (µm)	Soma area (µm2)	Apical diameter (µm)	AIS distance (µm)	AIS length (µm)	AIS area (µm2)	AIS/soma ratio
Axodendritic	1,206 ± 35 (n = 18)	556.7 ± 184 (n = 19)	6.44 ± 0.2 (n = 19)	9.8 ± 0.79 (n = 19)	46.5 ± 1.3 (n = 19)	102.4 ± 4.4 (n = 19)	0.19 ± 0.01 (n = 19)
Axosomatic	1,227 ± 32 (n = 17)	640.2 ± 35.8 (n = 19)	8.25 ± 0.2 (n = 19)	3.71 ± 0.42 (n = 19)	45.7 ± 1.0 (n = 19)	108.8 ± 4.1 (n = 19)	0.18 ± 0.01 (n = 19)
Two-tailed unpaired t test (P)	0.7689	0.0388	<0.00001	<0.00001	0.6195	0.3110	0.4074

Parameters of the neuronal perisomatic morphology measured from z-projected confocal stacks. Soma area and AIS area refer to the 2D cross-sectional area estimated by using the polygon selection tool (FIJI). All data are presented as mean ± SEM (n).

Table S3.

Correlation analysis between AIS distance and neurophysiological parameters from recorded control neurons

Parameter	AISΔ	AIS L	AIS A	RMP	RIN	AP ITH	AP VTH	First dVm/dt	Second dVm/dt	AP amp.	AP H-W	ADP A	ADP amp.	Rheo base	APTrain VTH	Soma A	Apical d	Total dend. nodes	Total dend. L
AIS L
r	0.236
P	0.153
AIS A
r	−0.060	0.713**
P	0.720	0.000
RMP
r	−0.085	0.385*	0.372*
P	0.648	0.032	0.039
RIN
r	−0.062	0.114	−0.175	0.286
P	0.729	0.521	0.322	0.119
AP ITH
r	−0.335	−0.494**	−0.219	−0.462**	−0.598**
P	0.053	0.003	0.213	0.009	0.000
AP VTH
r	−0.332	0.107	0.194	0.668**	0.235	0.008
P	0.055	0.547	0.272	0.000	0.182	0.965
First dVm/dt
r	−0.232	−0.122	−0.182	0.254	0.215	−0.071	0.323
P	0.187	0.492	0.304	0.168	0.223	0.688	0.063
Second dVm/dt
r	0.062	−0.312	−0.528**	0.094	0.234	−0.113	−0.030	0.488**
P	0.726	0.072	0.001	0.615	0.182	0.526	0.868	0.003
AP amp.
r	0.008	−0.192	−0.338	−0.170	0.187	−0.163	−0.389*	−0.032	0.460**
P	0.966	0.277	0.051	0.360	0.289	0.358	0.023	0.859	0.006
AP H-W
r	−0.123	0.011	0.110	0.138	0.227	−0.139	0.045	−0.374*	−0.235	0.209
P	0.488	0.953	0.536	0.460	0.197	0.432	0.799	0.029	0.182	0.235
ADP A
r	−0.161	−0.550**	−0.506**	−0.421*	−0.191	0.619**	−0.086	−0.085	0.104	0.164	0.335
P	0.362	0.001	0.002	0.018	0.279	0.000	0.628	0.635	0.560	0.353	0.052
ADP amp.
r	−0.020	−0.274	−0.231	−0.124	−0.308	0.415*	0.026	0.052	0.067	−0.093	0.361*	0.799**
P	0.911	0.122	0.196	0.513	0.082	0.016	0.888	0.775	0.710	0.607	0.039	0.000
Rheo base
r	−0.117	−0.112	0.091	−0.308	−0.742**	0.728**	−0.020	0.055	−0.182	−0.316	−0.373*	0.216	0.259
P	0.511	0.529	0.610	0.092	0.000	0.000	0.912	0.758	0.304	0.069	0.030	0.220	0.145
APTrain VTH
r	−0.148	−0.143	−0.014	0.419*	−0.010	0.209	0.657**	0.359*	0.028	−0.504**	−0.088	0.140	0.287	0.168
P	0.404	0.420	0.939	0.019	0.956	0.236	0.000	0.037	0.873	0.002	0.622	0.429	0.105	0.343
Soma A
r	−0.060	0.120	0.340*	0.007	−0.416*	0.401*	0.134	−0.039	−0.229	−0.454**	−0.091	0.052	0.236	0.429*	0.263
P	0.718	0.472	0.037	0.968	0.014	0.019	0.451	0.827	0.194	0.007	0.607	0.771	0.186	0.011	0.134
Apical d
r	−0.731**	−0.062	0.199	0.177	−0.041	0.327	0.488**	0.134	−0.204	−0.308	0.117	0.088	0.032	0.214	0.284	0.188
P	0.0001	0.712	0.230	0.341	0.816	0.059	0.003	0.449	0.246	0.076	0.510	0.621	0.859	0.225	0.103	0.259
Total dend. nodes
r	−0.596**	−0.371	−0.280	−0.235	0.171	0.493*	0.104	−0.167	−0.139	0.199	0.242	0.529**	0.143	0.093	−0.170	−0.160	0.392*
P	0.001	0.062	0.166	0.293	0.424	0.014	0.630	0.436	0.518	0.351	0.255	0.008	0.516	0.666	0.427	0.435	0.048
Total dend. L
r	−0.503*	0.067	0.023	−0.268	0.123	0.228	0.006	−0.233	−0.045	0.364	0.164	0.126	−0.256	0.018	−0.395	−0.209	0.261	0.699**
P	0.009	0.745	0.912	0.228	0.566	0.284	0.976	0.273	0.835	0.080	0.443	0.558	0.238	0.932	0.056	0.306	0.197	0.0001
Total dend. A
r	−0.464*	0.325	0.252	−0.028	0.010	0.102	0.144	−0.072	−0.120	0.059	−0.115	−0.159	−0.350	0.231	−0.259	−0.069	0.321	0.392*	0.732**
P	0.017	0.105	0.214	0.902	0.965	0.635	0.502	0.737	0.575	0.784	0.591	0.457	0.102	0.278	0.222	0.737	0.110	0.048	0.0001

Pearson’s correlation coefficients (r) and P values are shown for all combinations. ADP A, afterdepolarization area; ADP amp., afterdepolarization amplitude; AIS A, AIS area; AIS L, AIS length; AP amp., AP amplitude; apical d, apical diameter; AP I_TH, AP current threshold; AP_Train V_TH, AP train voltage threshold; AP V_TH, AP voltage threshold; R_IN, input resistance; soma A, soma area.

^*P < 0.05.

^**P < 0.01.

Fig. S3.

AISΔ scales with dendritic length and dendritic area. (A) Correlation analysis between AISΔ, length, and total dendritic length. Pearson correlation test; n = 26. **P = 0.009. (B) Correlation analysis between AISΔ, length, and total dendritic area. Pearson correlation test; n = 26. Axo-d, axodendritic; Axo-s, axosomatic. *P = 0.017.

Somatodendritic Capacitive Load Predicts Axonal Coupling Resistance.

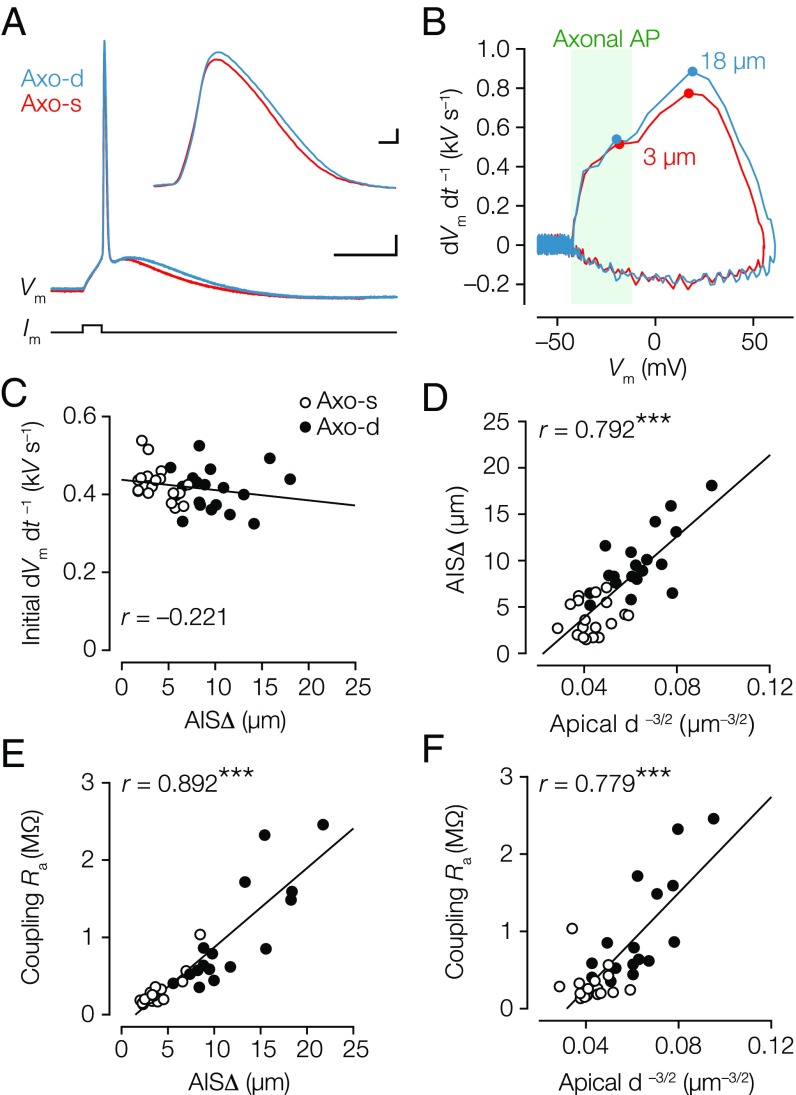
To examine whether AISΔ, ranging from 1.5 to 20 µm, impacts neuronal excitability, we examined the somatically recorded AP properties. The first rate of rise (dV_m dt ^–1) component of the somatic AP reflects the axonal axial current charging the somatodendritic capacitor (14). If the local somatodendritic capacitance is constant, dV_m dt ^–1 is expected to vary as a function of AISΔ because of the axial resistance ($R_a$). In striking contrast to the predictions, the first peak in the dV_m dt ^–1 showed no difference between the subtypes (Fig. 3 A–C, Fig. S4, and Table S4), and did not correlate with AISΔ (Fig. 3C). Similarly, the second, somatic component was also not different (Table S4). Also, the onset rapidness, defined as the slope of a linear fit to the AP phase plot (dV_m dt ^–1 vs. V_m; with units of milliseconds^–1), was not different (∼78 ms^–1) (Table S4). Theoretical work predicts that increasing AISΔ is associated with a more hyperpolarized AP voltage threshold (11). Although AP voltage threshold was significantly more hyperpolarized in axodendritic neurons (∼3 mV, P = 0.0005) (Table S4), it did not correlate with AISΔ (r = –0.332, P = 0.055) (Table S3). The AP voltage threshold rather correlated with the apical dendritic diameter (r = 0.488, P = 0.003) (Table S3), and the larger apical dendritic diameter (capacitive load) required larger current amplitudes to reach threshold compared with axodendritic neurons (P = 0.0095) (Table S4). Taken together, AISΔ alone does not explain differences in spike generation.

Fig. 3.

Similarity in AP waveform but inverted correlation between AIS distance and dendritic diameter. (A) Overlaid voltage traces of somatic APs (blue, axodendritic; AISΔ = 18 µm; red, axosomatic; AISΔ = 3 µm). (Scale bar: 10 ms, 10 mV.) (Inset) Somatic APs plotted on an expanded timescale. (Scale bar: 0.1 ms, 10 mV.) (B) Corresponding phase plots of the APs shown in A. (C) The first peak in the dV_m dt^–1 did not correlate with AISΔ. Pearson’s test (P = 0.203); n = 36. Axo-d, axodendritic; Axo-s, axosomatic. (D) Correlation plot showing AISΔ scales with apical $d^{-3/2}$. Pearson’s test; n = 38. ***P < 0.0001. (E) AISΔ distance is linearly related to coupling R_a. Pearson’s test; n = 33. ***P < 0.0001. (F) Correlation of apical $d^{-3/2}$ vs. coupling R_a. Pearson’s test; n = 33. ***P < 0.0001.

Fig. S4.

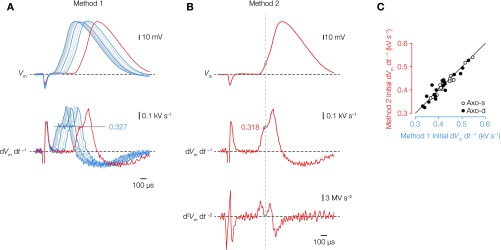
Identification of the peak in the first temporal derivative. (A, Upper) Several overlaid voltage waveforms of individually evoked APs from a layer 5 neuron with a 3-ms direct current injection. (A, Lower) Voltage first time derivative (dV_m dt^–1) from the same traces. The first peak amplitude reflects the current flow from the axonal during onset of the somatic voltage waveform (47, 48). In method 1, the initial peak of dV_m dt^–1 was the average of four to five individually measured peaks (black dotted line). (B) Red voltage trace from A including the second time derivative (d²V_m dt^–2). To test the robustness of peak measurements in method 1, we identified the temporal location of the local minimum in second time derivative (gray dotted line and gray circle), which corresponds to the peak in first time derivative (gray dotted line and gray circle). (C) Plot of the initial dV_m dt^–1 dataset analyzed using two different methods described in A and B. The data indicate a strong overlap in both methods not deviating from unity (line; Pearson’s r = 0.9; n = 36). Axo-d, axodendritic; Axo-s, axosomatic.

Table S4.

AP properties

Coupling type	AP ITH (nA)	AP VTH (mV)	First dVm dt–1 (V s–1)	Second dVm dt–1 (V s–1)	dVm dt–1 delay (µs)	AP onset rapidness (ms–1)	AP amplitude (mV)	AP half-width (µs)	ADP area (V s)	ADP amplitude (mV)
Axodendritic	1.8 ± 0.1 (n = 19)	−50.8 ± 0.6 (n = 19)	411.9 ± 12.6 (n = 19)	651.6 ± 20.4 (n = 19)	102.3 ± 3.6 (n = 19)	76.8 ± 4.5 (n = 19)	102.2 ± 0.9 (n = 19)	518.0 ± 11.7 (n = 19)	237.6 ± 21.7 (n = 19)	−4.0 ± 0.8 (n = 19)
Axosomatic	2.3 ± 0.1 (n = 17)	−47.6 ± 0.6 (n = 17)	429.7 ± 11.2 (n = 17)	633.4 ± 17.1 (n = 17)	93.8 ± 5.3 (n = 17)	78.4 ± 4.2 (n = 17)	99.6 ± 1.0 (n = 17)	510.9 ± 9.2 (n = 17)	251.0 ± 17.2 (n = 17)	−3.2 ± 0.7 (n = 17)
Two-tailed unpaired t test (P)	0.0095	0.0005	0.2986	0.5002	0.1916	0.8869	0.0505	0.6366	0.6337	0.5499

AP parameters are from recorded neurons. All data are presented as mean ± SEM (n). ADP, afterdepolarization; AP I_TH, AP current threshold; AP V_TH, AP voltage threshold.

If the maximal Nav conductance (${\overline{g}}_{Na}$) within the AIS is constant, the axial current should theoretically be larger with a more proximal AIS location. Because the somatodendritic capacitance (C_m) acts as a current sink, the axial current $I_{axon}$ should flow toward the soma and leave the neuron as capacitive current: $I_{axon}$ = C_m × dV_m dt ^–1. Based on these concepts, we hypothesized that the larger capacitance of axosomatic neurons is matched with the larger axial current expected for more proximal AIS locations. This idea is supported by the observation that apical dendrites in the axosomatic neurons are, on average, ∼2 µm larger in diameter (Fig. 2 A and B) and strongly correlated with the AISΔ (Fig. 2C and Table S3). It may be predicted that AISΔ is inversely proportional to the capacitance of a characteristic length of apical dendrite, which scales as $d^{-3/2}$, where $d$ is the apical dendritic diameter. Indeed, correlation of the transformed geometrical data showed that AISΔ is well-predicted by apical $d^{-3/2}$ (Fig. 3D). To examine more closely the relationship with resistive coupling $\left(R_a\right)$, we determined for each cell the specific coupling $R_a$ based on the 3D reconstructions assuming a specific intracellular cytoplasmic resistance $(R_i$) of 150 Ω cm (Materials and Methods). Interestingly, there was a strong linear relationship between $R_a$ and AISΔ (Fig. 3E), suggesting that branch diameters are not greatly different between the subtypes. Next, using the coupling $R_a$ estimates, we tested whether apical $d^{-3/2}$ is a predictor for $R_a$ and found a significant linear relationship (Fig. 3F). These data suggest that resistive coupling increases with smaller dendritic capacitance to reduce $I_{axon}$ during spike initiation and that the scaling of coupling $R_a$ with dendrites is independent of a somatic or dendritic origin of the axon.

Biophysical Analysis of Dendritic and Axonal Tuning of the Somatic AP.

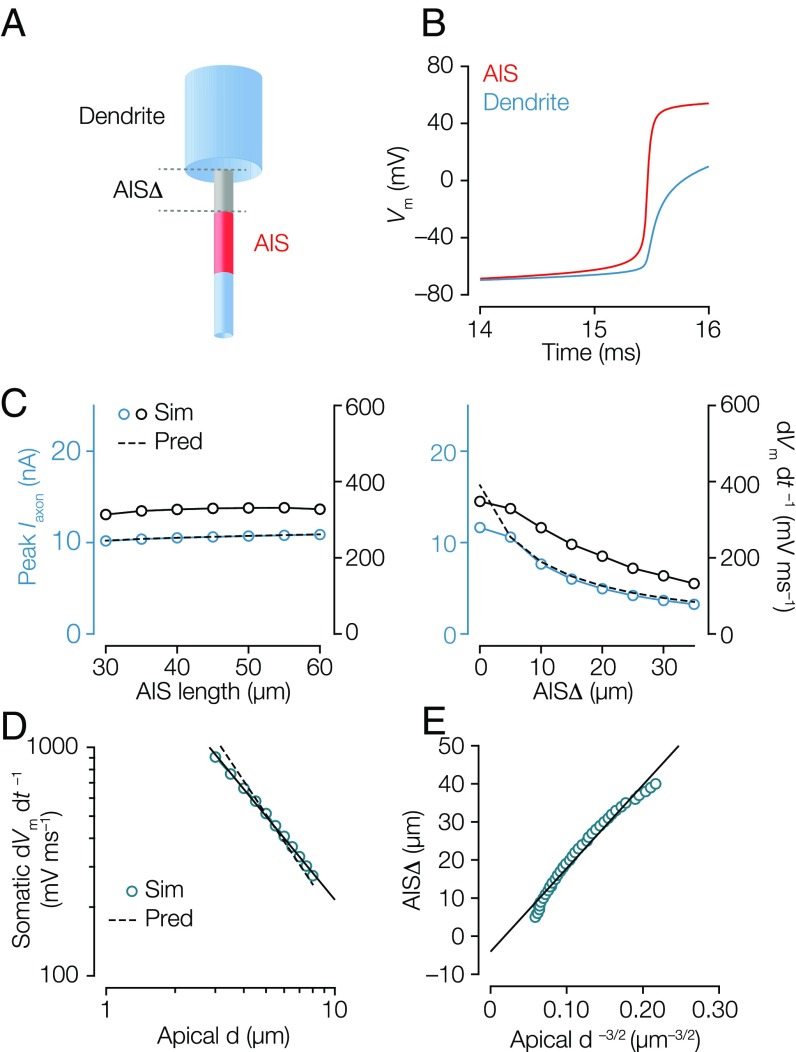
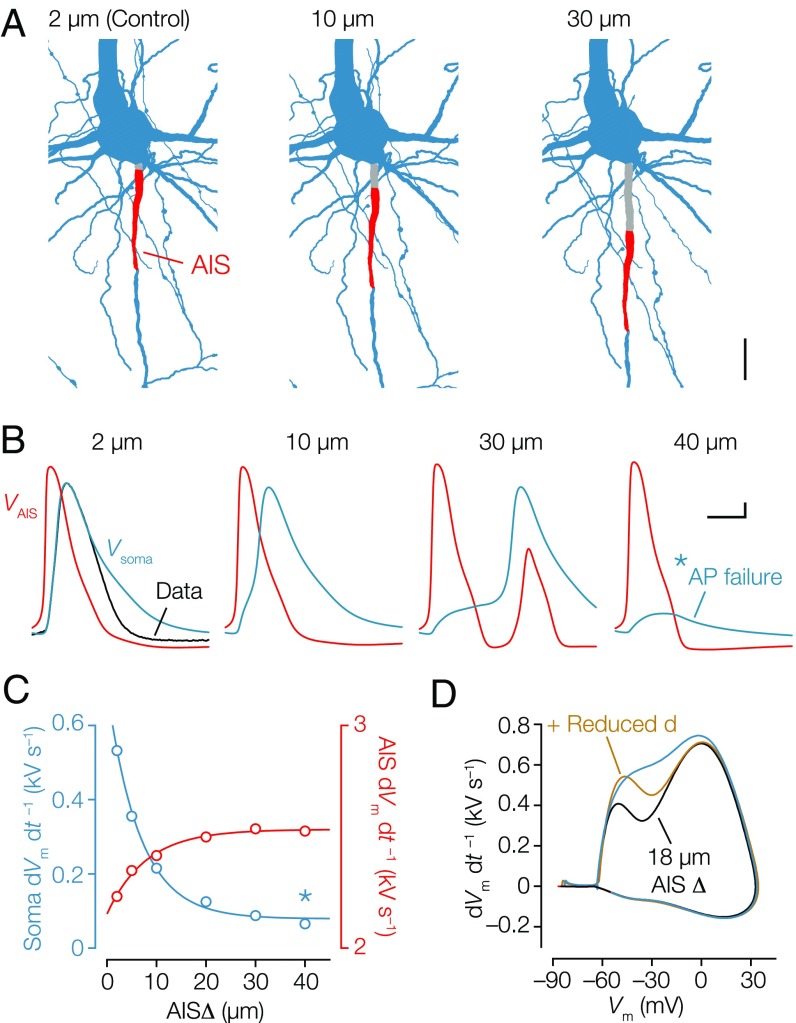
To understand how AISΔ influences the capacitive depolarization of the somatodendritic membrane by the axonal AP, we examined a simple biophysical model consisting of a cylindrical axon (diameter of 1.5 µm) connected to a larger cylindrical somatodendritic compartment (diameter of 6 µm and length of 500 µm) (Fig. 4A). Kv channels, somatodendritic Nav conductance, and the inactivation component of Nav channels were excluded (11). When Nav channels open, the membrane potential in the AIS rises toward the sodium reversal potential ($E_{Na}$) (Fig. 4B). Because there were no Nav channels between soma and AIS in the model, this region should be mostly resistive (resistance $R_a$). Therefore, the axonal current should be $I_{axon}=(E_{Na}-V_s)/R_a$, where $V_s$ is the somatic voltage. We assumed that $V_s$ remains far from $E_{Na}$ and close to spike threshold during the initial rise of the somatic AP owing to the large somatodendritic capacitance (more precisely, $V_s$ rises from spike threshold to somatic threshold, both well below $E_{Na}$). This simplified account indicated that $I_{axon}\propto 1/R_a$, and because resistance is linearly proportional to the path length (Fig. 3E), it follows that $I_{axon}\propto 1/\left(\text{AIS}\mathrm{\Delta }\right)$. A more precise analysis yields $I_{axon}\propto 1/(\text{AIS}\mathrm{\Delta }+\delta )$, where $\delta$ is a positive shift calculated from the parameters (Fig. S5 and SI Materials and Methods). $I_{axon}$ must charge a large cylindrical somatodendritic compartment with a dendritic diameter ($d$). The voltage response of a cylinder to a current scales with diameter as $d^{-3/2}$ (27). Therefore, for the voltage response at the soma to be independent of the diameter, AISΔ must scale as $d^{-3/2}$ (Materials and Methods and Fig. S5). As predicted, peak $I_{axon}$ and dV_m dt ^–1 do not depend on leak currents (Fig. S5) or AIS length in the range tested but are inversely related with AISΔ (Fig. 4C). In general, our theoretical analysis predicts that initial dV_m dt ^–1 should scale with dendritic diameter as $d^{-3/2}$, and we found numerically and theoretically that those scaling factors were well in line with the experimentally observed relationship (Fig. 4D). Finally, is the covariation between dendrites and axons sufficient to tune the somatic AP? To test this idea, we varied the dendritic diameter between 2 and 8 µm in the model and tuned the AISΔ so as to obtain a constant somatic dV_m dt ^–1 of 350 V s^–1. The results from the numerical simulation (Fig. 4E) agreed well with this prediction and showed that the AISΔ and the dendritic size interact as observed experimentally (compare with Fig. 3D).

Fig. 4.

Numerical simulations predict that dendritic scaling with AIS distance normalizes the somatic AP. (A) Illustration of the simplified conductance-based model of a pyramidal neuron with cylindrical dendrite/axon (blue) and AIS (red). AISΔ (gray) is 5-µm and 45-µm long (diameter of 1.5 µm). Nav (m¹) channels do not inactivate, and Kv channels are not included. (B) Voltage waveforms of the AIS (red) and soma (blue; interface of axon and dendrite) during AP initiation. Note the lack of repolarization in the simple model. (C, Left) Somatic I_axon and dV_m dt^–1 were independent of AIS length. (C, Right) Somatic I_axon and dV_m dt^–1 showed a strong dependence on AISΔ. (D) Somatic dV_m dt^–1 plotted against apical diameter (d) in log–log scale (blue circles). The correlation is fitted with a power law function with exponential of −1.22 (black line) compared with the theoretical prediction of –1.5 (black dashed line). (E) Combination of C, Right and D. AISΔ was adjusted to obtain a constant somatic dV_m dt^–1 of 350 V s^–1 for dendrite diameters between 2.0 and 8.0 µm and plotted as a function of $d^{-3/2}$ (blue circles). The line represents the linear regression of the data.

Fig. S5.

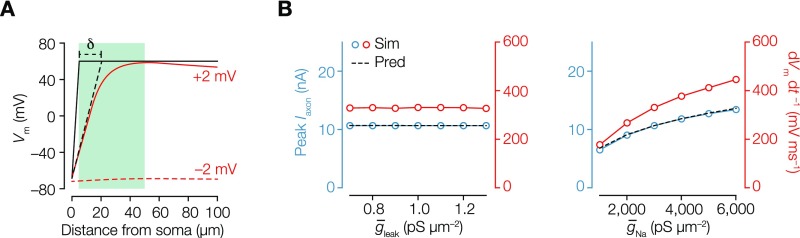
Role of voltage-gated channels in a biophysical simple model of AP initiation. (A) Voltage traces along the axon when the soma is voltage-clamped 2 mV below (red dashed line) and above (red line) the AP threshold. The black line is the theoretical voltage profile obtained if the AIS Nav channels clamp the membrane at E_Na. The difference in axial current between this profile and the simulation is equivalent to shifting AISΔ by a few micrometers ($\delta$). The voltage-clamp situation is used as the basis of theoretical predictions, where $I_{axon}$ at the soma is calculated. An analytical expression for the peak axonal current as a function of biophysical parameters was generated for the case where the soma is voltage-clamped by making the approximation that all Na_V channels are open and that leak currents are negligible. The analytical expression predicted that $I_{axon}\propto 1/(\text{AIS}\mathrm{\Delta }+\delta )$, where $\delta$ is a shift that decreases with increasing ${\overline{g}}_{Na}$. It is then expected that $I_{axon}$ measured in voltage clamp is proportional to dV_m dt^–1 in current clamp. We compared this expression with numerical simulations and the maximum somatic dV_m dt^–1 in a current-clamp simulation. (B, Left) $I_{axon}$ in voltage clamp (left axis; blue) and maximum somatic dV_m dt^–1 (right axis; red) in current clamp plotted against leak conductance (${\overline{g}}_{leak}$), showing that leak channels have no impact. The black dashed line indicates the theoretical prediction. (B, Right) Somatic $I_{axon}$ and dV_m dt^–1 plotted against Nav conductance density (${\overline{g}}_{Na}$). As expected, peak $I_{axon}$ and dV_m dt^–1 did not depend on leak conductance density (${\overline{g}}_{leak}$), because ${\overline{g}}_{leak}$ is small relative to ${\overline{g}}_{Na}$ (left axis). Both increase with sodium conductance density but in a sublinear way.

Geometry of the Somatodendritic Compartment Normalizes the Consequence of Axon Coupling to the Dendrite.

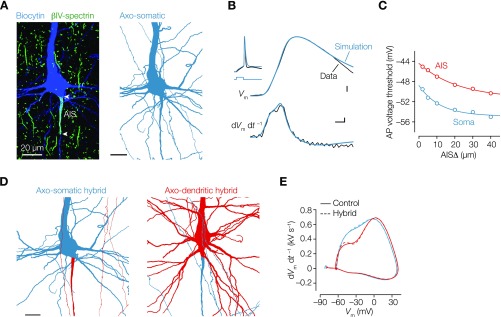
Next, to test how dendrites and AISΔ interact in neurons with complex morphologies and the presence of voltage-gated channels, we created a conductance-based multicompartmental model based on an axosomatic layer 5 pyramidal neuron (Materials and Methods and Fig. 5A). Based on the βIV-spectrin immunofluorescence signal, the AISΔ (2.1 µm) and AIS length (39.5 µm) were precisely implemented in the model (28) (Fig. S6). To test the role of $R_a$ in the optimized model, we fixed the diameter of the section representing AISΔ to 2 µm and varied the segment length between 2 and 40 µm (Fig. 5 B and C). The critical role of AISΔ was evident by the steep hyperpolarization of the voltage threshold (Fig. S6) and the decrease of the initial dV_m dt ^–1 of the model APs (Fig. 5C) in similar magnitude as predicted with the simplified biophysical model (Fig. 4C). With an AISΔ of 30 µm, the initial dV_m dt ^–1 reduced substantially, causing a temporal delay in the onset of the somatic AP and producing, subsequently, AP reflection in the axon. With an AISΔ of 40 µm, the somatic AP failed (Fig. 5 B and C). Increasing AISΔ thus facilitates axonal output but negatively impacts the antidromic AP. Finally, to test whether the reduction of $I_{axon}$ with distal AIS positions can be accounted for by reducing the somatodendritic capacitive load, we positioned the AIS at ∼18 µm from the soma. The AIS shift reduced the initial rising phase of the somatic AP by ∼179 V s^–1 (Fig. 5D), in line with the expected increase in resistive coupling (Fig. 4C). Furthermore, in agreement with the numerical and theoretical predictions, when the somatic and apical dendritic diameters were reduced by 30% (reflecting the average dendritic diameter of axodendritic neurons) (Fig. 2B), the initial peak in the dV_m dt ^–1 increased selectively and reached approximately similar amplitude compared with the control AP (Fig. 5D). Together, these simulations with realistic morphologies show that covariation of dendritic geometry and AIS distance suffices to tune the somatic AP.

Fig. 5.

Dendritic morphology and AIS distance in a realistic compartmental model normalize the somatic AP. (A) Part of the morphological reconstruction encompassing soma, proximal basal and apical dendrites (blue), and the AIS (red) used in compartmental modeling. The AISΔ of 2 µm represents the control morphology. Alternative models were made with increasing AISΔ (gray). (Scale bar: 20 µm.) (B) Simulation of single APs at the soma (blue) overlaid with the experimentally recorded AP as constraint (black) and corresponding simulated AP waveform in the distal AIS (red). Somatic and AIS APs for different AISΔ values. Note the failure of somatic (but not axonal) AP generation with a 40-µm AISΔ. (Scale bar: 0.1 ms, 10 mV.) (C) First dV_m dt^–1 of the somatic APs (blue) and the peak dV_m dt^–1 of the AIS AP (red). Data series are fitted with single exponential functions. *Somatic AP failure. (D) Phase plot of the simulated APs showing how adjusting AISΔ to 18 µm reduced the first dV_m dt^–1 by ∼179 V s^–1. Decreasing the somatodendritic compartment by 30% sufficed to recover the amplitude in the first dV_m dt⁻¹.

Fig. S6.

Compartmental modeling shows that geometrical normalization is independent of axon type. (A, Left) Confocal scan of the neuron used for the computational model. (A, Right) Part of the 3D reconstruction of the same axosomatic neuron (blue). (Scale bar: 20 µm.) (B) Overlaid and aligned AP voltage waveforms from the experimental data (black) of the same neuron shown in A and simulated AP voltage waveform (blue) for (Upper) voltage vs. time and (Lower) time derivative vs. time. The compartmental model was based on the experimentally identified AISΔ of 2.1 µm and length of 39.5 µm. To match the experimentally recorded AP waveform, ${\overline{g}}_{Na}$ in the AIS and somatodendritic membrane were adjusted (${\overline{g}}_{Na}$ AIS: 14,250 pS µm^–2; ${\overline{g}}_{Na}$ soma: 525 pS µm^–2). Inset shows a 3-ms, 2.1-nA current step and voltage responses. (Scale bars: 0.1 ms, 10 mV, 0.1 kV s^–1.) (C) Voltage threshold of somatic (blue) and AIS (red) APs generated from neurons with increasing AISΔ. Consistent with electrical compartmentalization and increased axial resistance when placing the AIS further from the soma, the local AIS AP rise time increased, and the voltage threshold, as measured at the soma, decreased (from –49.6 to –54.6 mV). Data series are fitted with single exponential function. (D) Finally, to exclude that regulation of $I_{axon}$ in the axodendritic and axosomatic occurs at the level of conductance densities or other cell-specific detailed morphological differences in their axons, we generated hybrid models. We optimized a morphologically realistic axodendritic neuron to the experimentally recorded somatic AP (full red; ${\overline{g}}_{Na}$ AIS: 14,350 pS µm^–2 ; ${\overline{g}}_{Na}$ soma: 600 pS µm^–2) and subsequently, exchanged its axon (red) with the axon of the optimized axosomatic layer 5 pyramidal neuron (blue) and vice versa. (E) Phase plots of simulated APs from control models (solid lines) and hybrid models (dashed lines). Note how the AP waveform is independent of the axon morphology.

SI Materials and Methods

In Vitro Slice Preparation.

Male or female Wistar rats (5–10 wk of age) were deeply anesthetized by isoflurane inhalation and quickly decapitated. Brain hemispheres were both removed, and parasagittal brain slices (300 µm) were prepared from S1 cortex, using a vibratome (1200S; Leica Microsystems B.V.). Throughout the slice preparation, the brain was maintained in ice-cold artificial cerebrospinal fluid (ACSF) consisting of 125 mM NaCl, 25 mM NaHCO₃, 3 mM KCl, 1.25 mM NaH₂PO₄, 25 mM glucose, 1 mM CaCl₂, and 6 mM MgCl₂ [pH 7.4; oxygenated with 95% O₂/5% CO₂ (vol/vol)]. After cutting, slices were transferred to a holding chamber filled with oxygenated ACSF maintained at 35 °C for 45 min and thereafter, stored at room temperature (RT).

Whole-Cell Recordings.

Slices were transferred to an upright microscope (BX51WI; Olympus Nederland B.V.) equipped with oblique illumination optics (WI-OBCD; N.A. 0.8). The microscope bath was perfused with oxygenated [95% O₂/5% CO₂ (vol/vol)] ACSF consisting of 125 mM NaCl, 25 mM NaHCO₃, 3 mM KCl, 1.25 mM NaH₂PO₄, 25 mM glucose, 2 mM CaCl₂, and 1 mM MgCl₂. Current-clamp whole-cell recordings were made from visualized layer 5 pyramidal neurons with Dagan BVC-700A Amplifiers (Dagan Corporation). Whole-cell patch pipettes were made from borosilicate glass (Harvard) pulled to an open-tip resistance of 5–6 MΩ. Pipettes were filled with 130 mM K-gluconate, 20 mM KCl, 4 mM Mg-ATP, 0.3 mM Na-GTP, 10 mM Hepes, and 10 mM Na₂-phosphocreatine (pH 7.4 adjusted with KOH, 280 mOsmol kg⁻¹), to which 8–10 mg mL⁻¹ biocytin and/or 100–200 µM Alexa Fluor salts (488 or 594; Invitrogen B.V.) were added. Unless otherwise stated, all chemicals were obtained from Sigma-Aldrich. All data were obtained at 32 °C (±1 °C). APs were evoked by brief (3-ms) current injections perithreshold (range = 1–3 nA) to minimally charge the dendritic membrane and temporally isolate the voltage waveform of the axosomatic AP from the current injection during the falling phase of the membrane transient. Voltage was analog low pass-filtered at 10 kHz (Bessel) and digitally sampled at 100 kHz using an analog–digital converter (ITC-18; HEKA Elektronik GmbH) and data acquisition software AxoGraph (v. 1.5.4; Molecular Devices Co.). Access resistance was, on average, ∼20 MΩ for somatic recordings and fully compensated using bridge balance and capacitance neutralization. Recordings were aborted if the access resistance exceeded 30 MΩ. All AP properties were determined from AP threshold, defined as the voltage at which the AP depolarization rate approximates 50 V s^–1 (29).

Morphological Reconstruction of Thick-Tufted Layer 5 Neurons.

Immediately after recording, slices were transferred to a fixative of 0.1 M PBS (pH 7.4) containing 4% (wt/vol) paraformaldehyde for 20–25 min. Brain slices were then blocked with 5% (wt/vol) BSA, 5% (vol/vol) normal goat serum (NGS), and 2% (vol/vol) Triton X-100 diluted in PBS for 2 h at RT. Slices were subsequently incubated with Rb-anti–βIV-spectrin (1:200; gift from M. N. Rasband, Baylor College of Medicine, Houston), fluorophore-conjugated streptavidin (1:500; Invitrogen B.V.), 5% (wt/vol) BSA, 5% (vol/vol) NGS, and 2% (vol/vol) Triton X-100 diluted in PBS overnight at RT. Slices were washed in PBS, incubated in secondary antibodies (1:500) for 2 h at RT, and washed again to visualize the immunoreaction. Sections were then mounted on glass slides and coverslipped in Vectashield (Vector Laboratories). The 2D cell body area was estimated by outlining the soma area with the polygon selection tool (FIJI) from distance-calibrated z-projected confocal stacks acquired from acute brain slices. Apical dendritic diameter was measured as an average of five equally spaced (5 µm) diameter estimations starting from 5 µm from the soma edge using the line selection tool (FIJI).

For morphological reconstruction of the dendritic trees, tile scan images of biocytin-labeled neurons were collected with a Leica TCS SP5 II (DMI6000 CFS; acquisition software Leica Application Suite AF v. 2.6.3.8173) or SP8X (DM6000 CFS; acquisition software Leica Application Suite AF v. 3.2.1.9702) confocal laser-scanning microscope (Leica Microsystems GmbH). Confocal images were acquired at 2,048 × 2,048 pixels (1.0-µm z step) using a 40× (N.A. 1.3; 0.75–1.0 digital zoom) oil-immersion objective. To avoid bleed through between emission wavelengths, automated sequential acquisition of multiple channels was used and saved as uncompressed LIF format. The 3D reconstructions of the dendritic structures were performed by computerized tracing using Neurolucida (v.10; MBF Bioscience Inc.). To examine the accuracy with 1.0-µm z-step optical sections, we additionally scanned regions with 0.5- and 0.25-µm z steps and reconstructed the somatodendritic morphology in all three scans. Quantitative comparison of the total surface area showed an ∼96% accuracy with z steps of 1.0 µm.

Heat maps of reconstructed thick-tufted layer 5 pyramidal neurons were made by normalizing the size of each neuron to the total cortical depth and converting Neurolucida reconstructions into uncompressed black and white TIFF images using Adobe Illustrator (Adobe Systems Inc.). Then, the following bitmap manipulations were done using FIJI (ImageJ) graphic software (v1.47; NIH). Cell bodies were centered at the medial lateral axis. Binary images were Gaussian filtered to a radius of 100 pixels (∼50 µm). The contrast of each cell’s Gaussian blur filtered image was adjusted to make the highest pixel intensity for the image the maximum value possible before averaging the images for each neuron. These group average images were then adjusted for contrast to make the highest pixel intensity for the image the maximum value possible (38). The color lookup table used was FIJI’s physics.

Retrograde Fluorescent Tracer Injection.

Green or red fluorescent retrograde beads (Retrobeads IX; Lumafluor Inc.) were used to identify a subpopulation of cortical layer 5 pyramidal cells based on their axonal targets. For spinal cord injections (n = 2), young adult rats (4–5 wk old) were anesthetized with i.m. injection of ketamine (0.1 mL 100 g^–1), xylazine (0.05 mL 200 g^–1), and distilled H₂O (1:1:2 volume ratio) and placed in stereotaxic stage. Incision in the cervical region was made; laminectomy at level cervical C3 and C4 was preformed, and subsequently, the dura matter was opened. Immediately after laminectomy, the retrograde dye was carefully injected using glass pipette (∼15-µm-diameter tip). Each animal received three injections (3 × 1 µL; dorsal and lateral finiculi) at depth of 0.8 mm from the dorsal surface of the spinal cord using pressure injections with a syringe pump (injection rate: 250 nL min^–1; Harvard Apparatus Inc.). For cortical injections (n = 2), young adult rats (4–5 wk old) were head-fixed in a stereotaxic stage and anesthetized with isoflurane (5% induction; 2.0–2.5% maintenance), and a microdrill was used to create a small craniotomy (2-mm-diameter circle). We injected 250 nL (volume rate: 23 nL s^–1) fluorescent beads into the primary somatosensory cortex (S1HL; n = 2; –2.04 mm posterior to bregma, 2.6 mm lateral of sagittal suture, 1-mm deep) (39) using the Drummond Nanoject Volume Injector (Drummond Scientific Co.). The micropipette was kept in place for 5–10 min before retraction. About 3–5 d were used to permit adequate retrograde transport of the fluorescent beads to the pyramidal somata before processing the tissue for fluorescent immunohistochemistry. For immunolabeling, 150-µm-thick parasagittal sections were colabeled for guinea pig anti-NeuN (1:1,000; EMD Millipore) and Rb-anti–βIV-spectrin.

Quantification of Retrobead-Labeled Neurons.

Quantification of double-labeled neurons was restricted to the S1HL for both contralateral cortex- and spinal cord-projecting neurons. At least four to five cortical sections for each injection paradigm were selected that contained numerous fluorescent back-labeled pyramidal neurons within S1HL. All layer 5 pyramidal neurons per section that contained fluorescent microspheres were examined by sequential z-stack (50–60 µm) acquisition of multiple channels of an area of 554 × 554 µm spanning layer 2/3 to layer 6 with a laser-scanning confocal microscope (Leica SP8 X DM6000 CFS) at 2,048 × 2,048-pixel resolution (1.0-µm z step; bit depth = 8) using a 20× (N.A. 0.75; ×1 digital zoom) oil-immersion objective. All layer 5 pyramidal neurons per section containing dense fluorescent microspheres were examined individually for immunolabeling and axon coupling by alternating the fluorescence channels in FIJI (ImageJ) graphic software (v1.47; NIH). This study is based on the examination of 784 layer 5 pyramidal neurons. An average of ∼60 neurons per layer 5 subpopulation were counted for each section (n = 14 sections; n = 4 rats) used.

Compartmental Modeling.

For conductance-based multicompartmental simulations, we used a biocytin-filled thick-tufted rat layer 5 pyramidal axosomatic neuron (cell ID 2014_01_28_#1) scanned at 2,048 × 2,048-pixel resolution with confocal microscopy using 1-µm z steps (Leica SP8) and 3Dly reconstructed with Neurolucida (v.10, MicroBrightField) and imported into the NEURON simulation environment (v. 7.3) (40). Both the AIS and nodal domains were carefully incorporated into the model as distinct sections, with the width and length values based on the precise location of βIV-spectrin (2.1 µm). Cytoplasmic resistance (R_i) was set to 150 Ω⋅cm throughout all compartments. The resting membrane potential (RMP) was adjusted with e_pas to –80 mV, and temperature was set nominally at 33 °C. Throughout the somatodendritic and nodal compartments, the membrane resistance (R_m) was set to 25 kΩ⋅cm² and capacitance (C_m) 1.0 µF⋅cm^–2. Myelination of internodal sections was represented by increasing internodal R_m to 100 kΩ⋅cm² and decreasing C_m to 0.25 µF⋅cm^–2. Nav conductance was implemented by two separate eight-state allosteric models developed for the soma and the axon (41) and distributed linearly decreasing in density along the somatodendritic axis and locally increasing in peak densities in the AIS as described previously (42, 43). Nav peak conductance values used were 525 pS⋅µm^–2 in the soma, 20 pS⋅µm^–2 in dendrites, 40 pS⋅µm^–2 in the internodal membrane, 4,000 pS⋅µm^–2 in the nodes, and 14,250 pS⋅µm^–2 at the peak density in the AIS. Potassium (K⁺) and calcium-dependent K⁺ conductance were distributed as described recently (model accession no. 144526; ModelDB). Kv7 peak conductance was set at 150 pS⋅µm^–2 in nodes of Ranvier and at the end of the AIS, 15 pS⋅µm^–2 in axon collaterals and the internodes, and 5 pS⋅µm^–2 in dendrites (43). The K⁺ and Na⁺ equilibrium potentials were set to –85 and +55 mV, respectively. The hyperpolarization-activated cation channel model was exponentially increasing in the apical dendrites (44) but uniform in the axon (1.0 pS⋅µm^–2). The final input resistance of the model neuron was 18.6 MΩ (22.7 MΩ experimentally). Segment length was adjusted to be below 10% of the alternating current length constant, λ_AC, at 3 kHz for each section. Because we were primarily interested in the rising phase of the AP, simulations were performed with integration time steps (dt) of 2 µs. To compare the simulations with electrophysiological recordings, simulated traces were filtered at 10 kHz and resampled at 100 kHz. Simulated APs were evoked with a 3-ms, 2.1-nA current injection (2.5 nA experimentally). For the hybrid model simulations, we used 3D-reconstructed thick-tufted rat layer 5 pyramidal axodendritic neuron with βIV-spectrin–based AISΔ of 11.6 µm (cell ID 2014_11_24_#3). RMP was adjusted with e_pas to –89.5 mV, and membrane parameters were set to previously described values. Nav peak conductance values used in the soma and AIS were 600 and 14,350 pS⋅µm^–2, respectively. Final input resistance of the model neuron was 20.7 MΩ (20.6 MΩ experimentally), and APs were simulated with a 3-ms, 1.8-nA current injection (2.1 nA experimentally).

Numerical Simulations of the Simplified Model.

All simulations were performed with the Brian Simulator with temporal resolution of 0.015 ms and spatial resolution of 1 µm (45). The neuron model used in the simulations consists of a cylindrical somatodendritic compartment of diameter of 6 µm and length of 500 µm attached to a thinner cylinder (diameter = 1.5 µm and length = 300 µm) representing the axon. The specific membrane capacitance is C_m = 0.9 µF⋅cm^–2, and the leak conductance density (${\overline{g}}_{leak}$) was set to 1 pS⋅µm^–2, giving a membrane time constant τ_m = 9 ms. Intracellular resistivity is R_i = 150 Ω⋅cm, and the leak reversal potential is E_Leak = −80 mV. Only Nav channels and leak channels were included, because we focus on spike initiation. Kv channels and inactivation of Nav channels are not considered. Unless otherwise stated, the AIS starts at 5 µm away from the soma and is 45-µm long, in line with experimental observations (Results). Nav channels are uniformly distributed in the AIS, and the Na current is defined by the following equations:

$$I_{Na}={\overline{g}}_{Na}m(E_{Na}–V),$$

$${\tau }_m\frac{dm}{dt}=m_{\infty }\left(V\right)–m,$$

and

$$m_{\infty }\left(V\right)=\frac{1}{1+exp\left(\frac{V_{\frac{1}{2}}–V}{k_a}\right)},$$

where E_Na = 60 mV, k_a = 6 mV, V_1/2 = −30 mV, and τ_m = 50 µs. The peak Na conductance density is ${\overline{g}}_{Na}$ of 3,000 pS µm^–2. Note that, to reduce the complexity, the current equation (I_Na) uses m¹. Furthermore, there are no Nav channels in the soma, because they are not involved in spike initiation. The model is simulated in somatic current clamp and somatic voltage clamp. In current clamp, a 1-ms current step is injected at the soma (i.e., at the junction between the somatodendritic cylinder and the axonal cylinder). The maximum of the first time derivative of the voltage is recorded at the soma (red axis in Fig. S4 B and C). In voltage clamp, the voltage at the soma is successively clamped at values between −80 and −30 mV, with steps of 0.0025 mV. The threshold for spike initiation is defined as the lowest value of the somatic voltage for which one-half of the Nav channels at the AIS end are open. The axonal current is measured at the beginning of the AIS at a potential 0.2 mV above the threshold (blue axis in Fig. S4 B and C).

Resistive Coupling of AIS and Soma.

The soma and AIS are electrically coupled by the resistive characteristics of the axon region between the two sites. For a cylindrical axon, the axial resistance is proportional to length. For an axon with nonuniform diameter d(y), where y is distance from soma, this resistance is

$$R_a=\frac{4R_i}{\pi }\underset{0}{\overset{x}{{\displaystyle \int }}}\frac{1}{d{\left(y\right)}^2}dy,$$

where x is AIS distance, and R_i = 150 Ω⋅cm is intracellular resistivity.

Analytical Calculation of Axonal Current.

We calculate the axonal current invading the soma at AP initiation in the following simplified model: the soma is clamped at voltage V_s, the axon is a cylinder of diameter d_AIS, Nav channels are uniformly distributed along the AIS with conductance density g and are all open, and capacitive currents are neglected. Under these assumptions, voltage is a linear function of distance x in the resistive part of the axon between soma (x = 0) and AIS (x = Δ). In the AIS, the cable equation is a linear second-order ordinary differential equation:

$$r_{a}V″=-\pi d_{AIS}g(E_{Na}-V),$$

where the derivative is with respect to x, and

$$r_a=\frac{4R_i}{\pi d_{AIS}^2}$$

is axial resistance per unit length. The AIS is defined as the region between x = Δ and x = Δ + L. The two boundary conditions are given by (i) somatic voltage clamp:

$$V\left(0\right)=V_s$$

and (ii) axial current vanishes at AIS end:

$$V\prime (\mathrm{\Delta }+L)=0.$$

Because voltage is linear between x = 0 and x = Δ, the first boundary condition can be replaced by

$$V\left(\mathrm{\Delta }\right)=V_s+V\prime \left(\mathrm{\Delta }\right)\mathrm{\Delta }.$$

We solve this differential equation analytically, and we calculate the axonal current flowing into the soma as

$$I=\frac{V\left(\prime 0\right)}{r_a}=\frac{V\prime \left(\mathrm{\Delta }\right)}{r_a}.$$

We obtain the following expression:

$$I=\frac{E_{Na}-V_s}{r_a(\mathrm{\Delta }+\delta )},$$

where $\delta$ is a shift equal to

$$\delta =\frac{\sqrt{\frac{d_{AIS}}{g{R}_i}}}{2\tanh \sqrt{\frac{4R_i}{d_{AIS}}g}L}.$$

For large AIS length and conductance density, this shift is close to

$$\delta \approx \frac{1}{2}\sqrt{\frac{d_{AIS}}{g{R}_i}}.$$

Therefore, axonal current scales as 1/(Δ + $\delta$). The voltage response of a cylindrical dendrite of diameter d depends linearly on the current and scales with $d^{-3/2}$ (27):

$$V\propto \frac{d^{-\frac{3}{2}}}{\mathrm{\Delta }+\delta }.$$

Therefore, normalizing the voltage response requires

$$\text{AIS}\mathrm{\Delta }=k·d^{-\frac{3}{2}}-\delta ,$$

where k is a proportionality factor.

Statistics.

Statistical differences between groups were tested with MatLab R2014a (8.3.0.523; MathWorks) or GraphPad Prism (v.6.0h; GraphPad Software) using a cutoff significance level (P) of 0.05. Correlation coefficients were determined using IBM SPSS (v.23; IBM Co.).

Discussion

In this study, we identified that a large fraction of adult thick-tufted rat layer 5 pyramidal neurons has an axon emanating from a basal dendrite (Fig. 1). These observations are in line with earlier reports using Golgi staining or EM from layer 2/3 or 5 pyramidal cells in a range of different cortical areas and species (19, 22, 23) or in hippocampal pyramidal neurons (20, 21) and support the notion that variation in axon location is a common principle of the cellular architecture of pyramidal cells. Cable theory predicts that the axial resistance between the AIS and the soma has a strong impact on spike initiation (11). Although the resistive coupling values across the population spanned more than one order of magnitude (from ∼0.1 to 2.5 MΩ) (Fig. 3), we surprisingly could not identify a functional impact of AISΔ on somatically recorded AP properties (Table S3). To achieve uniform APs at the soma, our theoretical analyses and compartmental simulations predict that AISΔ should be inversely related with the local somatodendritic capacitance. The anatomical properties of layer 5 pyramidal neurons were well in line with these theoretical predictions and revealed a strong correlation, with the correct order of magnitude, with the apical dendrite diameter and number of dendritic nodes (Fig. 2 and Table S3). These experimental results support the theory of resistive coupling (11), predicting that the main determinants of the first component of the somatic AP are local geometry and intracellular resistivity.

Scaling of AIS location with somatodendritic morphology may be a general feature of neurons. For example, in midbrain dopaminergic neurons, axons often emanate from a dendrite that is larger in diameter (16–18). In these cells, the dendritic APs are electrically isolated during synaptic potentials and often characterized by temporal imprecision, failure, reverberation, and/or reflection (18). Because dopaminergic cells release neurotransmitter from somatodendritic sites, it is thought that dendritic origin of the AIS facilitates somatodendritic autoinhibition (18). In other cell types, the AIS location is linked to unique electrical computations. For example, in auditory neurons in chicks, the AIS distance, ranging between 0- and 50-µm distance, is adapted to enable frequency tuning (6, 13). Consistent with predictions from axial resistive coupling, the distal AIS position in these cells is characterized by smaller somatic AP amplitudes but with the distinct advantage of axonal AP output being phase-locked to higher input frequencies in the kilohertz range. Uncoupling the axon from charging the soma in some cell types, thus, benefits local axonal computations.

In pyramidal neurons, however, the AIS not only integrates incoming synaptic inputs and transforms them into output patterns but at the same time, plays a critical role in the antidromic direction to depolarize the somatodendritic membrane capacitance with sufficient magnitude and speed to activate the somatic Nav channels initiating the back-propagating spike (15, 29, 30). These observations of invariable somatic APs are in agreement with recordings in hippocampal CA1 pyramidal neurons with AIS distances ranging between ∼1.0 and 20 µm showing little, if any, difference in the somatic AP (21). In that study, it was shown that axon coupling to basal dendrites facilitates synapse-evoked dendritic spike generation in the axon-carrying dendrite (21). Although we did not examine the presence of local basal dendritic spikes, our integrated electrophysiological and morphological approach suggests that the anatomical arrangement may rather serve geometrical homeostasis, normalizing the amplitude and rise time of the somatic AP. Back-propagating APs are implicated in a wide range of dendritic computations (31), acting as a retrograde signal for nonlinear integrative functions in the dendritic branches of cortical pyramidal neurons (32–34). Tuning the position of the axon and local dendritic area may ensure amplitude and temporal fidelity of the back-propagating spike during its transition from the axon to the soma and dendritic branches.

The cellular and molecular mechanisms tuning the somatodendritic geometry together with the axon location remain to be determined. During the first weeks of development, when the dendritic tree rapidly expands, the AIS also shifts from its distal site to a more proximal location near the soma (35) and dynamically changes in length (36). One mechanism identified for activity-dependent changes in AIS location includes the Ca²⁺ influx from L-type Ca²⁺ channels subsequently activating the cytosolic signaling pathways, including the Ca²⁺-calmodulin–sensitive phosphatase calcineurin (37). Such a molecular mechanism may also be suitable to link local somatodendritic Ca²⁺ elevations with cytoskeletal organization along the axon. This hypothesis remains to be established and would require simultaneous morphological analysis of dendrites and axons. The finding of a structural homeostatic scaling between axons and dendrites in pyramidal neurons may also have implications for the interpretation of activity-dependent relocation of the AIS along the longitudinal axis of the axon (5). Rather than reducing intrinsic excitability, our modeling predicts that shifting the AIS alone distally would weakly promote axonal firing (Fig. 5), consistent with theoretical and modeling results (9, 11). Furthermore, our results indicate that, in cortical pyramidal cells, the anatomical location of the AIS is to a large degree covarying with the local somatodendritic membrane area, ensuring the generation of uniform somatic APs in the face of highly variable dendritic loads.

Materials and Methods

All animal experiments were done in compliance with the European Communities Council Directive of November 24, 1986 (86/609/EEC) and were reviewed and approved by the animal welfare and ethics committee (DEC) of the KNAW under protocol number NIN 11.70. All details for electrophysiological recordings, numerical simulations, biophysical modeling, and compartmental NEURON modeling are described in SI Materials and Methods.