Estimating uncertainty in respondent-driven sampling using a tree bootstrap method

Significance

Some hidden or hard-to-reach populations of interest to researchers are difficult to study with standard statistical methods because there is not a reliable list of members from which samples can be drawn. Respondent-driven sampling (RDS) is a common way to reach members of these populations by allowing a small number of respondents to recruit further respondents in the target population from their personal contacts. However, estimates derived from RDS are known to have a high degree of uncertainty, for which current methods do not fully account. We present a method that overcomes this problem and allows for better statistical inference from RDS data.

Abstract

Respondent-driven sampling (RDS) is a network-based form of chain-referral sampling used to estimate attributes of populations that are difficult to access using standard survey tools. Although it has grown quickly in popularity since its introduction, the statistical properties of RDS estimates remain elusive. In particular, the sampling variability of these estimates has been shown to be much higher than previously acknowledged, and even methods designed to account for RDS result in misleadingly narrow confidence intervals. In this paper, we introduce a tree bootstrap method for estimating uncertainty in RDS estimates based on resampling recruitment trees. We use simulations from known social networks to show that the tree bootstrap method not only outperforms existing methods but also captures the high variability of RDS, even in extreme cases with high design effects. We also apply the method to data from injecting drug users in Ukraine. Unlike other methods, the tree bootstrap depends only on the structure of the sampled recruitment trees, not on the attributes being measured on the respondents, so correlations between attributes can be estimated as well as variability. Our results suggest that it is possible to accurately assess the high level of uncertainty inherent in RDS.

Researchers are often interested in studying hidden or hard-to-reach populations. These populations might be very small relative to the general population, or inclusion in these populations might carry a social stigma or other privacy concerns that make them hard to access. For example, HIV research often targets high-risk groups such as injecting drug users (IDUs), men who have sex with men, and female sex workers. Unfortunately, these groups are difficult to sample from because they lack a reliable sampling frame on which to base traditional sampling methods, and if a study restricts itself to only the most accessible members of a population, biases are likely to result.

Respondent-driven sampling (RDS) combines a nonprobabilistic chain-referral or snowball design with a statistical model that allows for estimation and inference of population parameters (1–3). According to White et al. (4), RDS had been used in over 460 studies in 69 countries as of 2015. The RDS process begins with the initial selection of a first wave of participants called seeds, who may be selected nonrandomly from the hidden population by convenience sampling. These participants are given uniquely numbered recruitment coupons and tasked with recruiting the next wave from people whom they know in the target population, usually with financial incentives. When this next wave of individuals returns with the coupons, they are in turn tasked with recruiting an additional wave, and this process continues until the desired sample size is met or no further recruits appear. This process makes use of the social network underlying the hidden population while reducing privacy concerns that might result from asking respondents directly for a list of contacts. Also, the use of numerous recruitment waves reduces the dependence of the overall sample on the initial convenience sample.

Several statistical approaches have been proposed to control for the biases associated with chain-referral methods. In his original papers on RDS, Heckathorn (1, 2, 5) described the sampling process and used the principles of network homophily and reciprocity between network connections to devise methods for estimating the prevalence of attributes in the population. Using Markov chain theory, Salganik and Heckathorn (6) showed that these RDS estimates were asymptotically unbiased under assumptions about the sampling process and the underlying social network. Li and Rohe (7) recently extended these limit-theorem results to include cases with multiple referrals. Salganik (8) also devised a bootstrap method for estimating the sampling variance of these estimates based on the differing referral patterns of respondents with various attributes, and Yamanis et al. (9) modified this method to respect the observed branching structure of the sample. Volz and Heckathorn developed a Hansen–Hurwitz type estimator corresponding to RDS and used the existing theory about those estimators to also estimate its variability (3). Gile and coworkers (10, 11) proposed estimators that either liken RDS to a probability proportional to size without replacement-sampling design or attempt to leverage properties of a working network model, with both methods allowing for bootstrap estimates of uncertainty. Crawford et al. (12) also proposed a method that leverages properties of the underlying graph but further included information from the order and timing of recruitment in their model.

Despite recent advances, quantifying the potentially large uncertainty associated with the RDS process remains a largely open problem. Goel and Salganik (13) performed simulations on known network populations and showed that this variability was much higher than previously thought, often 5–10 times or more greater than the standard simple random-sampling process (13). As a result, naive use of statistical inference would result in confidence intervals that are misleadingly narrow. The researchers also found that even confidence intervals derived from methods tailored to RDS failed to achieve coverage rates close to the methods’ advertised values.

We introduce a tree bootstrap method for estimating the uncertainty in the RDS process. We test the tree bootstrap method against commonly used existing methods in two simulation studies that mirror ones performed by Goel and Salganik (13), and we apply our method to RDS data collected from hidden populations of IDUs in Ukraine.

Methods

The recruitment process underlying RDS involves complicated social dynamics that would be difficult to model. Therefore, much of the literature on the properties of RDS estimators relies on a set of simplifying assumptions. We will assume here that (i) the social network is finite and connected; (ii) network connections are reciprocal, not directed; (iii) recruits accurately report their network degree; (iv) recruitment coupons are distributed uniformly at random to neighbors in the network; and (v) individuals may be recruited into the sample more than once (3, 5, 6). In practice, not all of these assumptions are realistic. Specifically, RDS is usually performed without replacement, disallowing the same individual from being recruited more than once. See Results for a discussion of how this violation affects estimation from an RDS sample.

Under these assumptions, RDS is equivalent to a random walk on the underlying social network. Hence, RDS can be modeled by a first-order Markov chain on the space of network nodes, having a stationary distribution proportional to the degrees of the nodes (6). That is, the probability that an individual is recruited into the sample is proportional to the number of connections that individual has within the network. From this, it follows that the Volz–Heckathorn estimator for the mean $\mu$ of an attribute $x$ in the population can be developed by weighting sampled individuals inversely proportional to their degree. Thus, we have

$${\widehat{\mu }}_{\text{VH}}=\frac{{\sum }_{i=1}^n\frac{x_i}{d_i}}{{\sum }_{i=1}^n\frac{1}{d_i}},$$ [1]

where $x_i$ is the value of the attribute in individual $i$ and $d_i$ is the network degree of individual $i$ (3). When the $x_i$ take on binary 0-1 values indicating the presence or absence of an attribute, then ${\widehat{\mu }}_{\text{VH}}$ estimates the prevalence of the attribute in the population. An additional assumption that the initial recruits, or seeds, were selected with probability proportional to their degree is often included to ensure that the Markov chain begins at its stationary distribution (6). With this assumption, the estimator is unbiased, but even without this assumption, it is still asymptotically unbiased (3).

Because RDS produces samples that are not independent, estimating the variance of and constructing confidence intervals for the Volz–Heckathorn estimator ${\widehat{\mu }}_{\text{VH}}$ is not straightforward. Furthermore, the nature of the dependence within samples is defined by the underlying social network, most of which is unobserved. A number of methods for estimating the uncertainty of RDS estimates have been developed. Volz and Heckathorn suggested a variance estimator for ${\widehat{\mu }}_{\text{VH}}$ that invokes the standard theory of Hansen–Hurwitz estimators (3). Salganik (8) proposed a bootstrap procedure that splits the sample into groups based upon the attribute value of their recruiter and iteratively resamples from these groups accordingly. Both of these methods attempt to leverage the Markovian properties of the RDS recruitment process. However, the methods both assume that these properties hold even when the individuals are grouped by their attribute values, which is not ensured by the theory. Gile (10) treated RDS similarly to a probability proportional to size without replacement design and developed an alternative to the Volz–Heckathorn estimator with weights that are no longer simply proportional to network degree.

The method of uncertainty estimation for RDS that we introduce is both simple to implement and outperforms other methods in simulation studies. The major difference between the methods mentioned above and the one we propose is that previous methods focus heavily on the status of the observed attribute. Instead, we suggest ignoring the attribute status and focusing solely on the structure of the RDS recruitment trees, which allows us to take advantage of the primary source of the dependence within samples, namely the underlying social network.

Tree Bootstrap.

Our method is essentially a multilevel bootstrap procedure applied within the hierarchical framework of the RDS recruitment trees. To draw a bootstrap sample from a set of observed trees, the initial step is to resample with replacement from the seeds of the trees. Next, from each of those seeds, we resample with replacement from their recruits, creating the second level of the bootstrap sample trees. From each of these new recruits, we then resample with replacement from their recruits to create a third level. This process continues iteratively until no further recruits are available. From the resulting bootstrap sample trees, any statistic of interest, such as the Volz–Heckathorn estimator, can be computed. By taking multiple bootstrap samples, the sampling distribution of the statistic can then be estimated from the observed RDS trees in a way that respects the dependence within the sample (14, 15). This is similar to what happens with other well-known techniques for resampling from correlated data, such as the block bootstrap methods for time series or spatial data, except that in our case, the structure of the dependence comes from the RDS recruitment process instead of proximity in time or space (16, 17). We note that due to the asymmetries of the observed RDS trees, the tree bootstrap produces resamples that vary in size. To alleviate any bias that may result from this variation, any inference based upon the bootstrap distribution of a statistic should be weighted by the effective relative sample sizes (e.g., ${\sum }_{i}1/d_i$ for the Volz–Heckathorn estimator).

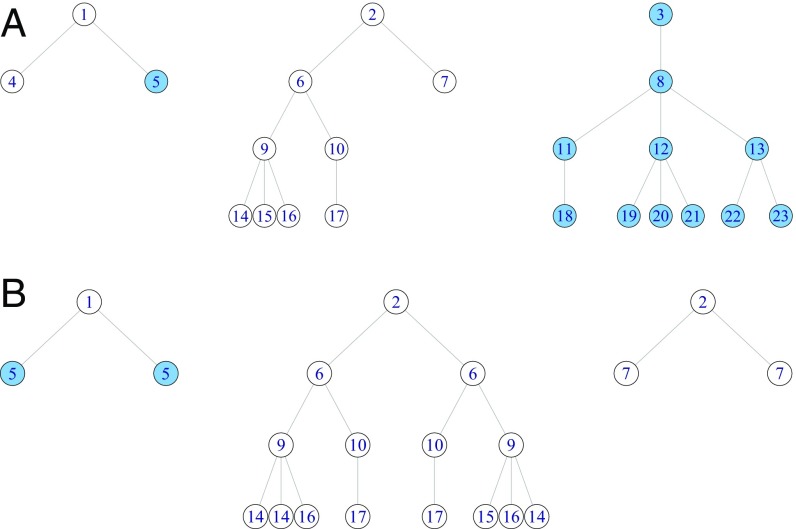
Fig. 1B shows an example of a bootstrap sample drawn from the observed trees in Fig. 1A. Note that seed 2 was selected twice in the initial resampling step, whereas seed 3 was not selected, but the resampled trees resulting from the two copies of seed 2 are quite different due to the further recruits that were selected in later steps. Also note that although the individuals are shaded according to their attribute value, these values do not affect the resampling procedure. However, variability in the sampling distribution of statistics involving the attribute values will be represented in the changing structure of the resampled bootstrap trees. In fact, we can see from this example that the substantial attribute homophily observed in Fig. 1A will result in a higher degree of variability in attribute statistics when using the tree bootstrap method than we would expect if we used a standard bootstrap method.

Fig. 1.

(A) Example of an RDS recruitment tree. (B) Resample taken from the RDS recruitment tree by the tree bootstrap method. Individuals are shaded according to their attribute value.

Data.

Project 90.

Our first dataset comes from the Colorado Springs Project 90 study, which was funded by the Centers for Disease Control and Prevention to investigate the affect of network structure on HIV transmission among a population of high-risk heterosexuals. From 1988 to 1992, researchers conducted interviews with 595 sex workers, paying and nonpaying partners of sex workers, IDUs, and sexual partners of drug users, and a network was constructed based upon a complete enumeration of participants’ social, sexual, and/or drug contacts (18–20). There was a total of 5,492 individuals in the network, but we will focus only on the largest connected component, consisting of 4,430 individuals and 18,407 edges. For each individual, 13 different attributes were measured, including demographic factors and other factors of interest such as whether the individual is a sex worker, pimp, or sex worker client.

We used the Project 90 data to develop a simulation study by simulating RDS recruitment trees from the network using the following process: (i) 10 seeds are selected at random from the network with probability proportional to their degree; (ii) with probabilities 1/3, 1/6, 1/6, or 1/3, respectively, each recruit successively selects 0, 1, 2, or 3 new recruits uniformly at random from their neighbors in the network; and (iii) recruitment continues until the RDS contains 500 individuals. For our initial simulation study, all sampling was done with replacement, so the standard RDS assumptions hold. This process mimics that found in Goel and Salganik’s assessment of RDS using the same Project 90 data (13). However, to account for how RDS is usually implemented in practice, we also conducted a second simulation study in which sampling was performed without replacement. It should be noted that although these are simulation studies from a network, the network itself was not simulated. Instead, only the RDS recruitment process was simulated from a preexisting network.

Add Health.

Our second dataset is from the National Longitudinal Study of Adolescent Health (Add Health), a nationally representative longitudinal study of adolescents in grades 7–12 to investigate the effect of social environments and behaviors in adolescence on health and achievement outcomes in young adulthood. We used only the initial wave of sampling from the 1994 to 1995 school year in which researchers administered in-school questionnaires to 90,118 students attending 84 pairs of middle and high schools chosen to be representative of US schools with respect to region of the country, urbanism, school type, ethnicity, and school size (21, 22). Social networks were mapped based upon nominations of up to five male and five female friends from each respondent’s school pair. The largest connected components of these school networks consist of a total of 72,262 individuals and 258,688 edges and range in size from 25 to 2,539 students, with a median of 753. For each individual, 46 different attributes were measured, including demographic factors, family status factors such as whether their mother or father live at home, and involvement in various school activities including sports teams and clubs. Our simulation study using the Add Health data were performed for each of the 84 school pairs in the same manner as described above for the Project 90 data.

Ukraine IDU.

These data were collected in 2011 from IDUs in major Ukrainian cities. Rates of HIV in Ukraine were among the highest in Eastern Europe at the time, and the epidemic had continued to grow despite comprehensive efforts to slow transmission of the disease, especially among IDUs (23). In an effort to track trends in HIV prevalence and understand behavioral patterns that affect the spread of the disease, sentinel surveillance of IDUs was conducted through the administration of behavioral surveys using RDS methodology. In each of 26 targeted cities, between 2 and 6 seed respondents were selected nonrandomly based on prespecified criteria. Each respondent then recruited up to 3 additional respondents until between 200 and 500 total IDUs were surveyed, with the target sample size being higher in cities with higher HIV prevalence (24). We will focus on four attributes measured by the behavioral survey in each city: (i) hospitalization to state drug treatment in-patient clinics during 2010; (ii) participation in the state substitution maintenance therapy (SMT) program; (iii) registration at nongovernmental organizations (NGO) that provide HIV prevention services; and (iv) use of HIV rapid tests distributed by NGOs that provide HIV prevention services. All our analyses are secondary data analyses of data collected by other organizations. The data we obtained included no personal identifiers of any kind.

Results

Project 90.

From each of 1,000 simulated respondent-driven samples from the Project 90 data, we used multiple existing methods to infer the population proportions for each of the 13 attributes using confidence intervals. Because these true population proportions are known from the data, we can use these inferences to compare the coverage probabilities of the confidence intervals derived from the different methods. If we estimate 95% confidence intervals from the simulated samples, then for each attribute, we would expect these confidence intervals to cover the true population proportion in approximately 95% of the samples.

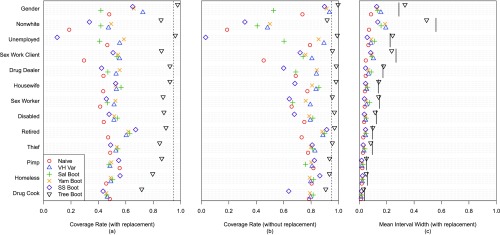
Fig. 2A shows the resulting coverage probabilities of the 95% confidence intervals as estimated by the following methods: (i) the naive proportion variance estimator; (ii) the Volz–Heckathorn variance estimator; (iii) the Salganik bootstrap; (iv) the Yamanis bootstrap; (v) the Gile successive-sampling bootstrap; and (vi) the tree bootstrap. Bootstrap confidence intervals were computed using the percentile method. For each attribute, the tree bootstrap method hewed much closer to the expected 95% coverage probability than any of the alternative methods, which rarely achieved more than 70% coverage. The tree bootstrap provided well-calibrated inference for attributes with very high design effects, such as whether an individual was nonwhite or a sex worker client. The estimated design effects for these attributes are about 60 and 30, respectively (13), where the design effect is defined as the ratio of the variance of the RDS estimator to that of the estimator from a simple random sample. Thus, if the design effect is 10, then the precision of an estimate from an RDS of size 500 is equivalent to that of a simple random sample of size 50.

Fig. 2.

Estimating population proportions via RDS with the Project 90 data. Coverage probabilities and widths of 95% confidence intervals estimated by the following methods: (i) the naive proportion variance estimator; (ii) the Volz–Heckathorn variance estimator; (iii) the Salganik bootstrap; (iv) the Yamanis bootstrap; (v) the Gile successive-sampling bootstrap; and (vi) the tree bootstrap. For the coverage probabilities and widths in A and C, sampling was performed with replacement, and for the coverage probabilities in B, sampling was performed without replacement. Attributes are in decreasing order of prevalence in the network. The dashed vertical black lines in A and B are at 0.95, so that for a perfectly calibrated method, the symbol would lie on the line. The short black lines in C are the expected 95% interval widths based on 10,000 simulated samples.

Fig. 2C shows the mean widths of these 95% confidence intervals for each attribute (80% intervals are shown in SI Appendix, Fig. S1). To form a basis of comparison, we generated 9,000 additional samples and then calculated the expected widths of the intervals using the 2.5th and 97.5th percentiles of the sampling distribution across all 10,000 simulated samples. The average widths of the tree bootstrap confidence intervals were much closer to the expected values than those from the other methods. Even when estimating the proportions of nonwhites and sex worker clients, the tree bootstrap method inferred confidence intervals wide enough on average to accommodate their high design effects.

In contrast to the assumptions underlying the statistical models commonly used for RDS, RDS is usually carried out by sampling without replacement. In practice, respondents are generally not allowed to recruit individuals who have already been included in the sample. This can affect the sampling process because the underlying social network is reduced by the removal of nodes as the sampling continues, and it has been observed that the resulting RDS estimates can be biased (10, 25). As a result, we repeated the simulation study under the assumption that sampling was performed without replacement. Fig. 2B shows the coverage probabilities of these 95% confidence intervals as estimated by the same methods as before. The tree bootstrap method still had coverage at least equal to the nominal 95% in almost all cases, and indeed its coverage was better (i.e., closer to the nominal level) than when sampling was with replacement. The other methods still had coverage substantially below the nominal level in most cases. As when sampling with replacement, only the tree bootstrap captured the large variability inherent in these samples when estimating attributes with high design effects, such as the proportions of nonwhites or sex worker clients.

Add Health.

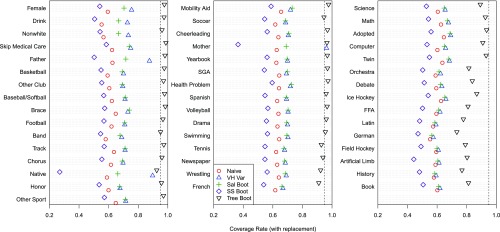
We inferred population proportions using confidence intervals for each of the 84 school pairs and 46 attributes in the Add Health data in each of 1,000 simulated respondent-driven samples. Fig. 3 shows the resulting mean coverage probabilities across the school pairs of 95% confidence intervals as estimated by the following methods: (i) the naive proportion variance estimator; (ii) the Volz–Heckathorn variance estimator; (iii) the Salganik bootstrap; (iv) the Gile successive-sampling bootstrap; and (v) the tree bootstrap. The Salganik and Gile successive bootstrap methods had much longer computation times than the other methods due to the presence of 46 attributes. This result illustrates a benefit of the tree bootstrap method not being attribute-based: inference about any number of attributes can be carried out from a single bootstrap sample.

Fig. 3.

Estimating population proportions via RDS with the Add Health data. Mean coverage probabilities of 95% confidence intervals across the 84 school pairs estimated by the following methods: (i) the naive proportion variance estimator; (ii) the Volz–Heckathorn variance estimator; (iii) the Salganik bootstrap; (iv) the Gile successive-sampling bootstrap; and (v) the tree bootstrap. Sampling was performed with replacement, and attributes are in decreasing order of mean prevalence over the 84 networks. The dashed vertical black lines are at 0.95, so that for a perfectly calibrated method, the symbol would lie on the line.

As with the Project 90 simulation study, the tree bootstrap method provided intervals with coverage probabilities closer to the nominal 95% than the alternatives, which usually achieved around 60–80% coverage (80% intervals in SI Appendix, Fig. S2). Again, the tree bootstrap provided reasonably well-calibrated inference regardless of the magnitudes of the design effects for the attributes. The results when sampling is without replacement are shown in SI Appendix, Figs. S3 and S4.

Ukraine IDU.

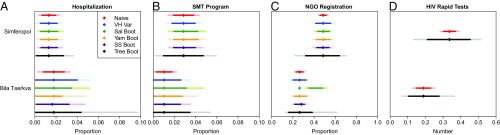
We applied the tree bootstrap method to the RDS data collected from IDUs in 26 Ukrainian cities. Fig. 4 A–D shows the resulting 80 and 95% confidence intervals obtained from this method, along with various others. The results for two selected cities are shown in Fig. 4; the remaining results are in SI Appendix, Tables S1–S4.

Fig. 4.

Ukrainian IDU data: estimates of the proportion of IDUs hospitalized to state drug treatment in-patient clinics during 2010 (A), the proportion of IDUs who participated in the state SMT program (B), the proportion of IDUs registered at NGOs that provide HIV prevention services (C), and the average number of HIV rapid tests distributed by NGOs that are used by each registered IDU (D). The figures show 80% (dark) and 95% (light) confidence intervals obtained from the naive proportion variance estimator, the Volz–Heckathorn variance estimator, and the tree bootstrap for two Ukrainian cities, Simferopol and Bila Tserkva.

Fig. 4 A and B give estimates for the proportion of IDUs hospitalized to state drug treatment in-patient clinics during 2010 and the proportion who participated in the state SMT program, respectively. As expected from the simulation study, the interval estimates from the tree bootstrap methods were generally wider than those from the alternative methods. For example, the upper limits of the 95% interval estimates from Bila Tserkva in Fig. 4A were 5.2 and 4.7% when using Salganik’s and Gile’s methods but 9.7% when using the tree bootstrap, nearly twice as high. Given previous results in this paper and related literature, we expect that the tree bootstrap more closely represented the true variability of the RDS estimators.

Fig. 4C gives estimates for the proportion of IDUs registered at NGOs that provide HIV prevention services, and Fig. 4D gives estimates for the average number of HIV rapid tests distributed by these NGOs that are used by each registered IDU. Again, we see that the tree bootstrap provided wider interval estimates that are more likely to cover the true values than the other methods. The interval estimates from Simferopol in Fig. 4C are around three times wider for the tree bootstrap method than for the others, with the 95% interval stretching from 22 to 70%.

Fig. 4D shows estimated means of the average number of HIV rapid tests distributed by NGOs that are used by each registered IDU. Our tree bootstrap method requires no additional modifications to handle cases where the object of inference is a count. Other currently available methods have not been adapted to discrete counts or continuous outcomes, which would be difficult because most methods rely on transitions from a finite number of discrete states.

Discussion

Previous work has indicated that although the Volz–Heckathorn estimator can correct for much of the bias introduced by the RDS process, estimating the process’s variance is much harder (13). Previous statistical inferences from RDS can be misleading when design effects often reduce effective sample sizes by a factor of 10 or more. We have shown here that existing methods for variance estimation such as the Volz–Heckathorn variance estimator, the Salganik bootstrap, and the Gile successive-sampling bootstrap can fail to fully capture the variability in RDS estimates.

Our tree bootstrap method can produce interval estimates that are able to account for the high variability of the RDS process, even when the design effects are very large. The tree bootstrap intervals tend to be slightly conservative, but we have shown that their widths are not excessive compared with what should be expected from RDS. In many applications, this slight conservatism may be preferable to the overly narrow intervals that other methods provide. In some cases, the tree bootstrap yields interval estimates that are too wide for practical use, but this probably indicates a very large design effect and low effective sample size, suggesting that the RDS data are not of much value in these cases. Thus, our methods may also help diagnose situations where RDS is not of much use.

In the tree bootstrap, the resampling is performed with respect only to the structure of the RDS recruitment tree and not to the attributes measured on the respondents. Thus, estimates from any number of attributes can be derived from a single bootstrap sample. This is not the case for the other methods we examined, each of which requires an independent analysis for each attribute of interest. This makes the tree bootstrap more efficient computationally and also means that we can estimate not only the variances of the estimates of each attribute but also the covariances between these estimates. This could be useful in a capture–recapture design in which multiple capture sources are compared with a single RDS recapture sample because, in this case, good population size estimation would rely on estimating the dependence between the capture sources within the recapture sample.

The tree bootstrap is based on resampling through the tree structure while ignoring the attributes, and this may be what drives the method’s success. Previous methods, including the Volz–Heckathorn variance estimator and the Salganik bootstrap, effectively model RDS as a first-order Markov process on the set of attribute states. Although it is true that RDS is a first-order Markov process on the nodes in the underlying social network, this characteristic no longer holds when the nodes are aggregated by attribute status, which leads to bias in the estimation of sampling variance (26). On the other hand, the tree bootstrap method can be viewed as a resampling of paths down the observed RDS tree. Because entire paths from root to leaf are resampled together, transitions of length greater than one are considered, and we are able to escape the first-order Markov approximation. Further study of the theoretical properties of the tree bootstrap would be worthwhile.

Conclusion

We have introduced the tree bootstrap method for estimating uncertainty in samples derived from RDS. Unlike previous methods, the tree bootstrap can capture the large variability inherent in the RDS process, even in extreme cases. This method allows us to construct calibrated interval estimates, avoiding the overly narrow intervals that existing methods provide. We hope that this method removes one of the major obstacles facing the practical application of RDS to the study of hidden and hard to reach populations. An R package to implement the method called RDStreeboot is publicly available from CRAN, at https://CRAN.R-project.org/package=RDStreeboot.