Unified framework for information integration based on information geometry

Significance

Measuring the degree of causal influences among multiple elements of a system is a fundamental problem in physics and biology. We propose a unified framework for quantifying any combination of causal relationships between elements in a hierarchical manner based on information geometry. Our measure of integration, called geometrical integrated information, quantifies the strength of multiple causal influences among elements by projecting the probability distribution of a system onto a constrained manifold. This measure overcomes mathematical problems of existing measures and enables an intuitive understanding of the relationships between integrated information and other measures of causal influence such as transfer entropy. Inspired by the integration of neural activity in consciousness studies, our measure should have general utility in analyzing complex systems.

Abstract

Assessment of causal influences is a ubiquitous and important subject across diverse research fields. Drawn from consciousness studies, integrated information is a measure that defines integration as the degree of causal influences among elements. Whereas pairwise causal influences between elements can be quantified with existing methods, quantifying multiple influences among many elements poses two major mathematical difficulties. First, overestimation occurs due to interdependence among influences if each influence is separately quantified in a part-based manner and then simply summed over. Second, it is difficult to isolate causal influences while avoiding noncausal confounding influences. To resolve these difficulties, we propose a theoretical framework based on information geometry for the quantification of multiple causal influences with a holistic approach. We derive a measure of integrated information, which is geometrically interpreted as the divergence between the actual probability distribution of a system and an approximated probability distribution where causal influences among elements are statistically disconnected. This framework provides intuitive geometric interpretations harmonizing various information theoretic measures in a unified manner, including mutual information, transfer entropy, stochastic interaction, and integrated information, each of which is characterized by how causal influences are disconnected. In addition to the mathematical assessment of consciousness, our framework should help to analyze causal relationships in complex systems in a complete and hierarchical manner.

Quantitative assessment of causal influences among elements in a complex system is a fundamental problem in many fields of science, including physics (1), economics (2), gene networks (3), social networks (4), ecosystems (5), and neuroscience (6). There have been many previous attempts to quantify causal influences between elements in stochastic systems. Information theory has played a pivotal role in these endeavors, leading to various measures, including predictive information (7), transfer entropy (8), and stochastic interaction (9). Drawn from consciousness studies involving measurement of integration of neural activity (10, 11), the mathematical concept of integrated information is also useful as a framework for analyzing causal relationships in complex systems with multiple elements.

Recent research suggests that the brain loses the ability to integrate information when consciousness is lost during dreamless sleep (12), general anesthesia (13), or vegetative states (14), suggesting that quantifying integration of information can serve as a neurophysiological marker of consciousness (10, 11, 15). The integrated information theory (IIT) of consciousness (16, 17) proposes a measure of integration called integrated information that quantifies multiple causal influences among elements of a system. Integrated information is theoretically motivated by the holistic property of consciousness experienced as a unified whole that is irreducible into separate parts or experiences. Whereas the original motivation for integrated information is intended to elucidate the neural substrate of consciousness, it can in principle be applied to many research fields.

Despite its broad potential impact, the application of integrated information (16, 18) to experimental data is severely limited (19, 20) due to the original measure’s derivation under restricted conditions, wherein the probability distribution of past states in a system is assumed to be uniform, variable discrete (18). In an effort to broaden the applicability, several measures have been proposed under general conditions (9, 19, 21). However, these proposed measures are limited by mathematical problems. Quantification of a pairwise causal influence from one element to another can be achieved with existing measures, but to quantify multiple causal influences among many parts poses the problems of overestimation and confounding noncausal influences. To overcome these problems, we propose a unified framework for quantifying causal influences based on information geometry (22). The measure we propose, called “geometric integrated information” ${\mathrm{\Phi }}_G$, overcomes the described difficulties, provides geometric interpretations of existing measures, and elucidates the relationships among the measures in a hierarchical manner. The mathematical solution we derive should have broad utility in elucidating complex systems.

Three Postulates on Strength of Influences

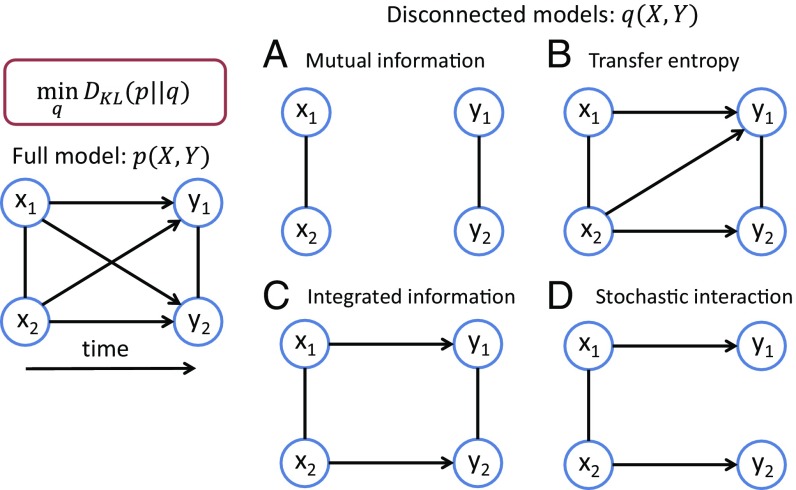
We propose a unified theoretical framework for quantifying the strength of spatiotemporal influences based on three postulates. Let us consider a stochastic dynamical system in which the past and present states of the system are given by $X=\{x_1,x_2,\mathrm{\cdots },x_N\}$ and $Y=\{y_1,y_2,\mathrm{\cdots },y_N\}$, respectively, where $N$ is the number of elements in the system. Information about $X$ is integrated by influences among elements and transmitted to $Y$. The spatiotemporal influences of the system are fully characterized by the joint probability distribution $p(X,Y)$. We call $p(X,Y)$ a “full model”. In a dynamical system characterized by $p(X,Y)$, there are three different types of influences. Influences between elements at the same time (called equal-time influences) can be quantified by analyzing only the marginal distributions $p(X)$ or $p(Y)$. Influences across different time points (called across-time influences) can be further divided into those among different units (cross-influences) and those within the same unit (self-influences). The across-time influences can be quantified from the conditional probability distribution $p(Y|X)$. They are also known as causal influences (2, 8), in the sense of causality that is statistically inferred from conditional probability distributions although it does not necessarily mean actual physical causality (23). Here, we use the term causality in this context and focus on quantifying causal influences.

For quantifying causal influences (both self- and cross-influences) among elements of $X$ and $Y$, consider approximating the probability distribution $p(X,Y)$ by another probability distribution $q(X,Y)$ in which the influences of interest are statistically disconnected. We call $q(X,Y)$ a “disconnected model.” The strength of influences can be quantified by to what extent the corresponding disconnected model $q(X,Y)$ can approximate the full model $p(X,Y)$. The goodness of the approximation can be evaluated by the difference between the two probability distributions $p(X,Y)$ and $q(X,Y)$. Minimizing a difference between $p(X,Y)$ and $q(X,Y)$ corresponds to finding the best approximation of $p(X,Y)$ by a disconnected model $q(X,Y)$. From this reasoning, we propose the first postulate as follows.

Postulate 1. Strength of influences is quantified by a minimized difference between the full model and a disconnected model.

The second postulate is used to define a disconnected model. Consider partitioning the elements of a system into $m$ parts, $X=\{X_1,X_2,\mathrm{\cdots },X_m\}$ and $Y=\{Y_1,Y_2,\mathrm{\cdots },Y_m\}$, where $X_i$ and $Y_i$ contain the same elements in a system. To avoid the confounds of noncausal influences, we should minimally disconnect only the influences of interest without affecting the rest. To define such a minimal operation of statistically disconnecting influences from $X_i$ to $Y_j$, we propose the second postulate as follows.

Postulate 2. A disconnected model, where influences from $X_i$ to $Y_j$ are disconnected, satisfies the Markov condition $X_i\to {\stackrel{\sim }{X}}_i\to Y_j$, where ${\stackrel{\sim }{X}}_i$ is the complement of $X_i$ in $X$; that is, ${\stackrel{\sim }{X}}_i=X-X_i$.

The Markov condition $X_i\to {\stackrel{\sim }{X}}_i\to Y_j$ means that $X_i$ and $Y_j$ are conditionally independent given ${\stackrel{\sim }{X}}_i$,

$$q(X_i,Y_j|{\stackrel{\sim }{X}}_i)=q(X_i|{\stackrel{\sim }{X}}_i)q(Y_j|{\stackrel{\sim }{X}}_i).$$ [1]

Under the Markov condition, there is no direct influence from $X_i$ on $Y_j$ given the states of the other elements ${\stackrel{\sim }{X}}_i$ being fixed.

The third postulate defines the measure of a difference between the full model and a disconnected model, which is denoted by $D[p:q]$. There are many possible ways to quantify the difference between two probability distributions (22, 24). We consider several theoretical requirements that the measure of difference should satisfy to have desirable mathematical properties (details in Supporting Information): (i) $D[p:q]$ should be nonnegative and becomes 0 if and only if $p=q$, (ii) $D[p:q]$ should be invariant under invertible transformations of random variables, (iii) $D[p:q]$ should be decomposable, and (iv) $D[p:q]$ should be flat. We can prove that the only measure that satisfies all of the theoretical requirements is the well-known Kullback–Leibler (KL) divergence (22). Thus, we propose the third postulate as follows.

Postulate 3. A difference between the full model and a disconnected model is measured by KL divergence.

Taken together, the strength of causal influences from $X_i$ to $Y_j$, $ci[X_i\to Y_j]$, is quantified by the minimized KL divergence,

$$ci[X_i\to Y_j]=\underset{q(X,Y)}{min}{D}_{KL}[p(X,Y)||q(X,Y)],$$ [2]

under the constraint of the Markov condition given by Eq. 1.

A Unified Derivation of Existing Measures

In this section, we derive existing measures from the unified framework and provide the interpretations of them.

Total Causal Influences: Mutual Information.

First, consider quantifying the total strength of causal influences between the past and present states. From the operation of disconnections given by Eq. 1, the influences from all elements $X$ to $Y$ are disconnected by forcing $X$ and $Y$ to be independent,

$$q(X,Y)=q(X)q(Y).$$ [3]

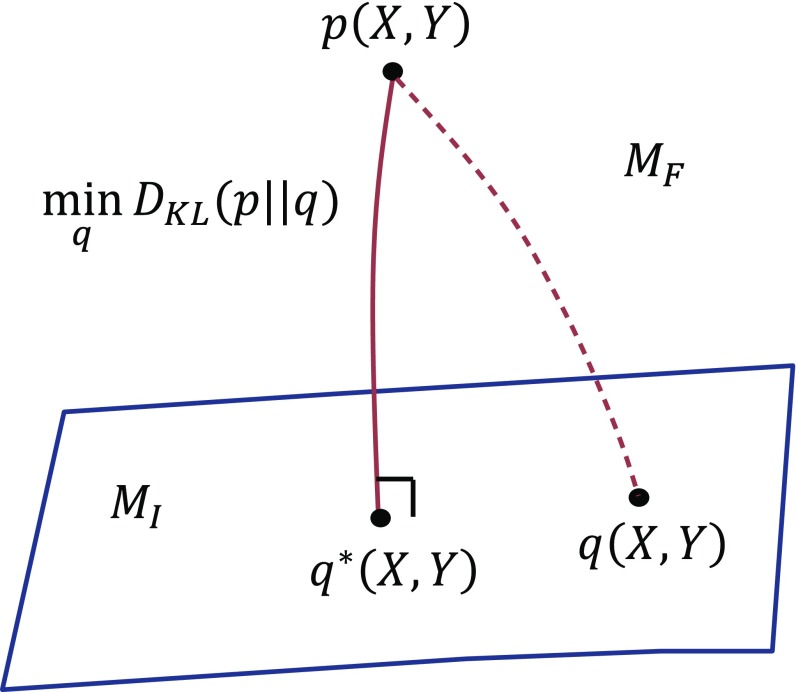
The disconnected model is graphically represented in Fig. 1A. To introduce the perspective of information geometry, consider a manifold of probability distributions ${\mathcal{M}}_F$, where each point in the manifold represents a probability distribution $p(X,Y)$ (a full model). Consider also a manifold ${\mathcal{M}}_I$ where $X$ and $Y$ are independent, which means that there are no causal influences between $X$ and $Y$. A probability distribution $q(X,Y)$ (a disconnected model) is represented as a point in the manifold ${\mathcal{M}}_I$. In general, the actual probability distribution $p(X,Y)$ is represented as a point outside the submanifold ${\mathcal{M}}_I$ (Fig. 2). The difference between the two probability distributions is quantified by KL divergence,

$$D_{KL}[p(X,Y)||q(X,Y)]=\sum _{X,Y}p(X,Y)\log \frac{p(X,Y)}{q(X,Y)}.$$ [4]

Fig. 1.

(A–D) Minimizing the Kullback–Leibler (KL) divergence between the full and the disconnected model leads to various information theoretic quantities: (A) mutual information, (B) transfer entropy, (C) integrated information, and (D) stochastic interaction. Constraints imposed on the disconnected model are graphically shown.

Fig. 2.

Information geometric picture for minimizing the KL divergence between the full model $p(X,Y)$, which resides in the manifold ${\mathcal{M}}_F$, and the disconnected model $q(X,Y)$, which resides in the manifold ${\mathcal{M}}_I$. $q^{\ast }(X,Y)$ is the point in ${\mathcal{M}}_I$ that is closest to $p(X,Y)$.

We consider finding the closest point $q^{\ast }$ to $p$ within the submanifold ${\mathcal{M}}_I$, which minimizes the KL divergence between $p(X,Y)$ and $q(X,Y)\in {\mathcal{M}}_I$ (Fig. 2). This corresponds to finding the best approximation of $p(X,Y)$. The minimizer of KL divergence is derived by orthogonally projecting the point $p(X,Y)$ to the manifold ${\mathcal{M}}_I$ according to the projection theorem in information geometry (22) (Supporting Information). In the present case, $p$, the closest point $q^{\ast }$, and any point $q$ in ${\mathcal{M}}_I$ form an orthogonal triangle. Thus, the following Pythagorean relation holds: $D(p||q)=D(p||q^{\ast })+D(q^{\ast }||q)$. From the Pythagorean relation, we can find that the KL divergence is minimized when the marginal distributions of $q^{\ast }(X,Y)$ over $X$ and $Y$ are both equal to those of the actual distribution $p(X,Y)$; i.e., $q^{\ast }(X)=p(X)$ and $q^{\ast }(Y)=p(Y)$. The minimized KL divergence is given by

$$\underset{q}{min}{D}_{KL}[p||q]=H(Y)-H(Y|X),$$ [5]

$$=I(X;Y)$$ [6]

where $H(Y)$ is the entropy of $Y$, $H(Y|X)$ is the conditional entropy of $Y$ given $X$, and $I(X;Y)$ is the mutual information between $X$ and $Y$. From the derivation, we can interpret the mutual information between $X$ and $Y$ as the total causal influences between $X$ and $Y$. The mutual information between the present and past states can be also interpreted as the degree of predictability of the present states given the past states and has been termed as predictive information (7).

Partial Causal Influences: Conditional Transfer Entropy.

Next, consider quantifying a partial causal influence from one element to another in the system. From the operation of disconnections in Eq. 1, a partial causal influence from $x_i$ to $y_j$ is disconnected by $q$, satisfying

$$q(x_i,y_j|{\stackrel{\sim }{x}}_i)=q(x_i|{\stackrel{\sim }{x}}_i)q(y_j|{\stackrel{\sim }{x}}_i),$$ [7]

where ${\stackrel{\sim }{x}}_i$ is the past states of all of the variables other than $x_i$. Under the constraint, the KL divergence is minimized when $q(X)=p(X)$, $q(y_j|X)=p(y_j|{\stackrel{\sim }{x}}_i)$, and $q({\stackrel{\sim }{y}}_j|X,y_j)=p({\stackrel{\sim }{y}}_j|X,y_j)$ (Supporting Information). The minimized KL divergence is found to be equal to the conditional transfer entropy,

$$\underset{q}{min}{D}_{KL}[p||q]=H(y_j|{\stackrel{\sim }{x}}_i)-H(y_j|X),$$ [8]

$$=TE(x_i\to y_j|{\stackrel{\sim }{x}}_i),$$ [9]

where $TE(x_i\to y_j|{\stackrel{\sim }{x}}_i)$ is the conditional transfer entropy from $x_i$ to $y_j$ given ${\stackrel{\sim }{x}}_i$. Thus, we can interpret the conditional transfer entropy as the strength of the partial causal influence from $x_i$ to $y_j$.

A Measure of Integrated Information

Integrated information is defined as a measure to quantify the strength of all causal influences among parts of the system. In the case of two units, integrated information should quantify both of the causal influences from $x_1$ to $y_2$ and from $x_2$ to $y_1$. It aims to quantify the extent to which the whole system exerts synergistic influences on its future more than the parts of a system independently do and, thus, irreducibility of the whole system into independent parts (16). Accordingly, integrated information is theoretically required that it should be nonnegative and upper bounded by the total causal influences in the whole system, which is the mutual information between the past and present states $I(X;Y)$ in our framework as shown above (20). Based on Postulates 1–3, we uniquely derive a measure of integrated information by imposing the corresponding constraints, which naturally satisfies the theoretical requirement.

Consider again partitioning a system into $m$ parts. By applying the operation in Eq. 1 for all pairs of $i$ and $j$ ($\ne i$), we can find that all causal influences among the parts are disconnected by the condition

$$q(Y_i|X)=q(Y_i|X_i)(\forall i).$$ [10]

To quantify integrated information, we consider a manifold ${\mathcal{M}}_G$ constrained by Eq. 10. Note that within ${\mathcal{M}}_G$, the present states in a part $Y_i$ directly depend only on the past states of itself, $X_i$, and thus the transfer entropies from one part $X_i$ to all of the other parts $Y_j$ ($j\ne i$) are 0. Now we propose a measure of integrated information, called geometric integrated information ${\mathrm{\Phi }}_G$, as the minimized KL divergence between the actual distribution $p(X,Y)$ and the disconnected distribution $q(X,Y)$ within ${\mathcal{M}}_G$:

$${\mathrm{\Phi }}_G=\underset{q\in {\mathcal{M}}_G}{min}{D}_{KL}[p||q].$$ [11]

The manifold ${\mathcal{M}}_G$ formed by the constraints for integrated information (Eq. 10) includes the manifold ${\mathcal{M}}_I$ formed by the constraints for mutual information (Eq. 3); i.e., ${\mathcal{M}}_I\subset {\mathcal{M}}_G$. Because minimizing the KL divergence in a larger space always leads to a smaller value, ${\mathrm{\Phi }}_G$ is always smaller than or equal to the mutual information $I(X;Y)$:

$$0\le {\mathrm{\Phi }}_G\le I(X;Y).$$ [12]

Thus, ${\mathrm{\Phi }}_G$, uniquely derived from Postulates 1–3, naturally satisfies the theoretical requirements as integrated information.

Comparisons with Other Measures

The Sum of Transfer Entropies.

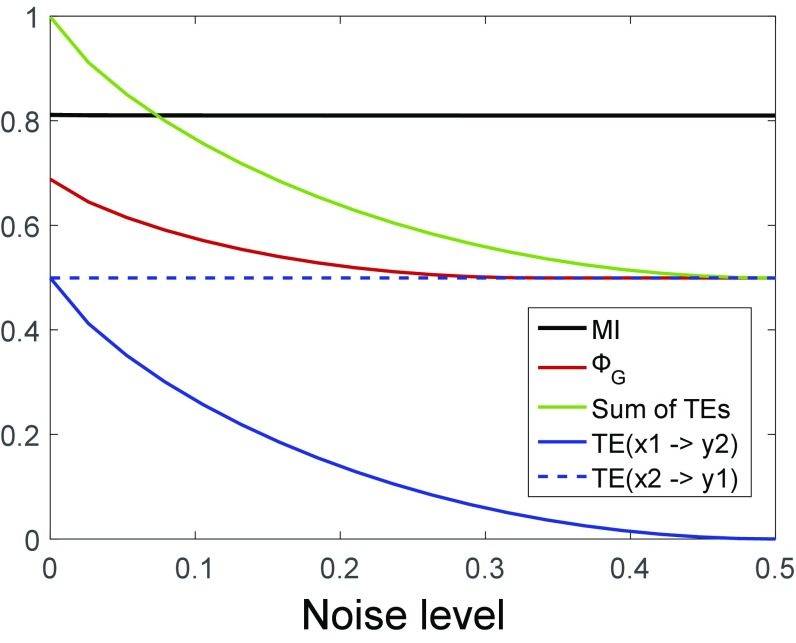
For simplicity, consider a system consisting of two variables (Fig. 1). Conceptually, a measure of integrated information should be designed to quantify the strength of two causal influences from $x_1$ to $y_2$ and from $x_2$ to $y_1$ (Fig. 1C). Because each causal influence is quantified by the transfer entropy, $TE(x_1\to y_2|x_2)$ or $TE(x_2\to y_1|x_1)$, one may naively think that the sum of transfer entropies can be used as a valid measure of integrated information and may be the same as ${\mathrm{\Phi }}_G$. In contrast with this naive intuition, the sum of transfer entropies is not equal to ${\mathrm{\Phi }}_G$ and moreover, it can exceed the mutual information between $X$ and $Y$, which violates the important theoretical requirement as a measure of integrated information (Eq. 12). When there is strong dependence between $y_1$ and $y_2$, simply taking the sum of transfer entropies leads to overestimation of the total strength of causal influences. An extreme case where such overestimation occurs is when $y_1$ and $y_2$ are copies of each other.

As a simple example, consider a system consisting of two binary units, each of which takes one of the two states, $0$ or $1$. Assume that the probability distribution of the past states of $x_1$ and $x_2$ is a uniform distribution; i.e., $p(x_1,x_2)=1/4$. The present state of unit $1$, $y_1$, is determined by the AND operation of the past state $x_1$ and $x_2$, that is, $y_1$ becomes 1 if both $x_1$ and $x_2$ are 1, and it becomes 0 otherwise. On the other hand, $y_2$ is determined by a “noisy” AND operation where the state of $y_2$ flips with certain probability $r$; i.e., $p(y_2=1)=1-r$ if $(x_1,x_2)=(\mathrm{1,1})$ and $p(y_2=1)=r$ if $(x_1,x_2)=(\mathrm{0,0}),(\mathrm{0,1}),(\mathrm{1,0})$, where $r$ determines the noise level. As the noise level of the noisy AND operation decreases, the dependence between $y_1$ and $y_2$ gets stronger. When there is no noise, i.e., $r=0$, $y_1$ and $y_2$ are completely equal. We varied the strength of dependence by changing the noise level and calculated transfer entropies and ${\mathrm{\Phi }}_G$ (see Supporting Information for the computation of ${\mathrm{\Phi }}_G$ in the binary case) (Fig. 3). As the noise level decreases, the transfer entropy from $x_1$ to $y_2$ increases but the mutual information stays the same because $y_2$, which is a noisy AND gate, does not add any additional information about the input $X$ above the information already provided by $y_1$, which is the perfect AND gate. When the noise level is low and thus the dependence between $y_1$ and $y_2$ is strong, the sum of transfer entropies exceeds the amount of mutual information.

Fig. 3.

Comparison between integrated information and the sum of transfer entropies (TE). A system consists of two binary units whose states are determined by an AND gate and a noisy AND gate. When the noise level of the noisy AND gate is low and thus the dependence between the units is strong, the sum of transfer entropies (green line) exceeds the mutual information (black line) whereas integrated information ${\mathrm{\Phi }}_G$ (red line) is always less than the mutual information. Each transfer entropy (blue solid and dotted lines) is always less than or equal to ${\mathrm{\Phi }}_G$.

On the other hand, ${\mathrm{\Phi }}_G$ never exceeds the amount of mutual information (Fig. 3). ${\mathrm{\Phi }}_G$ avoids the overestimation by simultaneously evaluating the strength of multiple influences. In contrast, the sum of transfer entropies separately quantifies causal influences by considering only parts of the system. For example, when the transfer entropy from $x_1$ to $y_2$ is quantified, $y_1$ is not taken into consideration, which leads to the overestimation. To accurately evaluate the total strength of multiple influences, we need to take a holistic approach as we proposed to do with ${\mathrm{\Phi }}_G$. The flaw of the simple sum of transfer entropies illuminates the limitation of the part-based approach and the advantage of the holistic approach.

A related quantity with the sum of transfer entropies has been proposed as causal density (21). Originally, causal density was proposed as the normalized sum of the conditional Granger causality from one element to another (21). Because transfer entropy is equivalent to Granger causality for Gaussian variables (25), the normalized sum of the conditional transfer entropies can be considered as a generalization of causal density. Although a simple sum of Granger causality or transfer entropies is easy to evaluate and would be useful for approximately evaluating the total strength of causal influences, we need to be careful about the problem of overestimation.

Stochastic Interaction.

Another measure, called stochastic interaction (9), was proposed as a different measure of integrated information (19). In the derivation of stochastic interaction, Ay (9) considered a manifold ${\mathcal{M}}_S$ where the conditional probability distribution of $Y$ given $X$ is decomposed into the product of the conditional probability distributions of each part (Fig. 1D):

$$q(Y|X)=\prod _{i=1}^{m}q(Y_i|X_i).$$ [13]

This constraint satisfies the constraint for the integrated information (Eq. 10). Thus, ${\mathcal{M}}_S\subset {\mathcal{M}}_G$. In addition to that, this constraint further satisfies conditional independence among the present states of parts given the past states in the whole system $X$:

$$q(Y|X)=\prod _{i=1}^{m}q(Y_i|X).$$ [14]

This constraint corresponds to disconnecting equal-time influences among the present states of the parts given the past states of the whole in addition to across-time influences (Fig. 1D). On the other hand, the constraint in Eq. 10 corresponds to disconnecting only across-time influences (Fig. 1C).

The KL divergence is minimized when $q(X)=p(X)$ and $q(Y_i|X_i)=p(Y_i|X_i)$ (9). The minimized KL divergence is equal to stochastic interaction $SI(X;Y)$:

$$\underset{q}{min}{D}_{KL}[p||q]=\sum _{i}H(Y_i|X_i)-H(Y|X),$$ [15]

$$=SI(X;Y).$$ [16]

In contrast to the manifold ${\mathcal{M}}_G$ considered for ${\mathrm{\Phi }}_G$, the manifold ${\mathcal{M}}_S$ formed by the constraints for stochastic interaction (Eq. 13) does not include the manifold ${\mathcal{M}}_I$ formed by the constraints for the mutual information between $X$ and $Y$ (Eq. 3). This is because not only causal influences but also equal-time influences are disconnected in ${\mathcal{M}}_S$ (Fig. 1D). Stochastic interaction can therefore exceed the total strength of causal influences in the whole system, which violates the theoretical requirement as a measure of integrated information (Eq. 12). Notably, stochastic interaction can be nonzero even when there are no causal influences, i.e., when the mutual information is 0 (20). To summarize, stochastic interaction does not purely quantify causal influences but rather quantifies the mixture of causal influences and simultaneous influences.

Analytical Calculation for Gaussian Variables

Although we cannot derive a simple analytical expression for ${\mathrm{\Phi }}_G$ in general, it is possible to derive it for Gaussian variables. In this section, we analytically compute ${\mathrm{\Phi }}_G$ when the probability distribution of a system $p(X,Y)$ is Gaussian. We also show a close relationship between the proposed measure of integrated information ${\mathrm{\Phi }}_G$ and multivariate Granger causality. Consider the following multivariate autoregressive model,

$$Y=AX+E,$$ [17]

where $X$ and $Y$ are the past and present states of a system, $A$ is the connectivity matrix, and $E$ is Gaussian random variables with mean $0$ and covariance matrix $\mathrm{\Sigma }(E)$, which are uncorrelated over time. The multivariate autoregressive model is the generative model of a multivariate Gaussian distribution. Regarding Eq. 17 as a full model, we consider the following as a disconnected model:

$$Y=A\prime X+E\prime .$$ [18]

The constraints for ${\mathrm{\Phi }}_G$ (Eq. 10) correspond to setting the off-diagonal elements of $A\prime$ to 0:

$$A_{ij}^{\prime }=0\left(i\ne j\right).$$ [19]

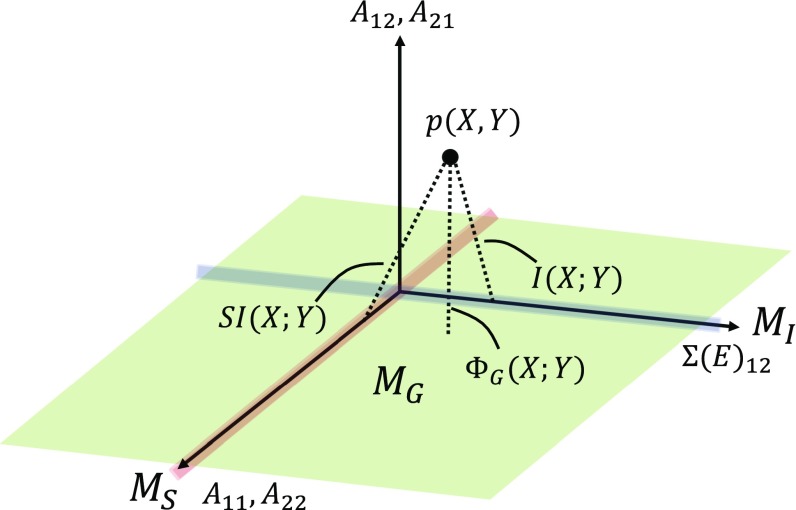
It is instructive to compare this with the constraints for the other information theoretic quantities introduced above: the constraints for mutual information (Fig. 1A), transfer entropy from $x_1$ to $y_2$ (Fig. 1B), and stochastic interaction (Fig. 1D). They correspond to $A\prime =0$, ${A\prime }_{21}=0$, and the off-diagonal elements of $A\prime$ and $\mathrm{\Sigma }{(E)}^{\prime }$ being 0, respectively. Fig. 4 shows the relationship between the manifolds formed by the constraints for mutual information ${\mathcal{M}}_I$, stochastic interaction ${\mathcal{M}}_S$, and integrated information ${\mathcal{M}}_G$. We can see that ${\mathcal{M}}_I$ and ${\mathcal{M}}_S$ are included in ${\mathcal{M}}_G$. Thus, ${\mathrm{\Phi }}_G$ is smaller than $I(X;Y)$ or $SI(X;Y)$. On the other hand, there is no inclusion relation between ${\mathcal{M}}_I$ and ${\mathcal{M}}_S$.

Fig. 4.

Relationships between manifolds for mutual information ${\mathcal{M}}_I$ (gray line), stochastic interaction ${\mathcal{M}}_S$ (orange line), and integrated information ${\mathcal{M}}_G$ (green plane) in the Gaussian case. ${\mathcal{M}}_I$ is the line where $A=0$, ${\mathcal{M}}_S$ is the line where $\mathrm{\Sigma }{(E)}_{12}$ and $A_{12},A_{21}$ are 0, and ${\mathcal{M}}_G$ is the plane where $A_{12},A_{21}$ are 0.

By differentiating the KL divergence between the full model $p(X,Y)$ and a disconnected model $q(X,Y)$ with respect to $\mathrm{\Sigma }{{(X)}^{\prime }}^{-1}$, $A\prime$, and $\mathrm{\Sigma }{{(E)}^{\prime }}^{-1}$, we can find the minimum of the KL divergence, using the following equations (details in Supporting Information):

$$\mathrm{\Sigma }{(X)}^{\prime }=\mathrm{\Sigma }(X),$$ [20]

$${(\mathrm{\Sigma }(X)(A-A\prime )\mathrm{\Sigma }{(E)}^{\prime -1})}_{ii}=0,$$ [21]

$$\mathrm{\Sigma }{(E)}^{\prime }=\mathrm{\Sigma }(E)+(A-A\prime )\mathrm{\Sigma }(X){(A-A\prime )}^T.$$ [22]

By substituting Eqs. 20–22 into the KL divergence, we obtain

$${\mathrm{\Phi }}_G=\frac{1}{2}\log \frac{|\mathrm{\Sigma }{(E)}^{\prime }|}{|\mathrm{\Sigma }(E)|}.$$ [23]

$|\mathrm{\Sigma }(E)|$ is called the generalized variance, which is used as a measure of goodness of fit, i.e., the degree of prediction error, in multivariate Granger causality analysis (26, 27). In the Gaussian case, ${\mathrm{\Phi }}_G$ can be interpreted as the difference in the prediction error on comparison of the full and the disconnected model, in which the off-diagonal elements of $A\prime$ are set to 0. Thus, ${\mathrm{\Phi }}_G$ is consistent with multivariate Granger causality based on the generalized variance. ${\mathrm{\Phi }}_G$ can be rewritten as the difference between the conditional entropy in the full model and that in the disconnected model,

$${\mathrm{\Phi }}_G=H(q(Y|X))-H(p(Y|X)).$$ [24]

For comparison, mutual information, transfer entropy, and stochastic interaction are given as $I(X;Y)=\frac{1}{2}\log \frac{|\mathrm{\Sigma }(X)|}{|\mathrm{\Sigma }(E)|}$, $TE(x_i\to y_j|x_j)=\frac{1}{2}\log \frac{\mathrm{\Sigma }{(E)}_{jj}^{\ast }}{\mathrm{\Sigma }{(E)}_{jj}}$, $SI(X;Y)=\frac{1}{2}\log \frac{\mathrm{\Sigma }{(E)}_{11}^{\ast }\mathrm{\Sigma }{(E)}_{22}^{\ast }}{|\mathrm{\Sigma }(E)|}$, where $\mathrm{\Sigma }{(E)}_{jj}^{\ast }$ ($j=\mathrm{1,2}$) is the covariance of the conditional probability distribution $p(y_j|x_j)$.

Hierarchical Structure

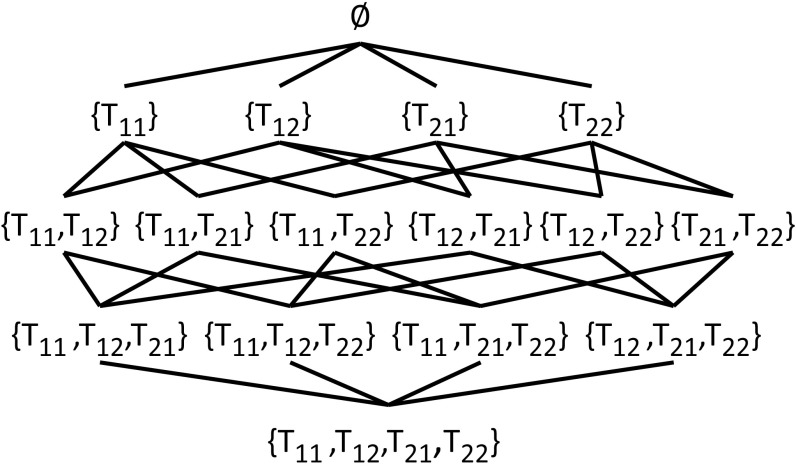
We can construct a hierarchical structure of the disconnected models and then use it to systematically quantify all possible combinations of causal influences (28). For example, in a system consisting of two elements, there are four across-time influences, $x_1\to y_1$, $x_1\to y_2$, $x_2\to y_1$, and $x_2\to y_2$, which are denoted by $T_{11}$, $T_{12}$, $T_{21}$, and $T_{22}$, respectively. Although we consider only the cross-influences, $T_{12}$ and $T_{21}$ for transfer entropy and integrated information, we can also quantify self-influences $T_{11}$ and $T_{22}$ by imposing the corresponding constraints, such as $q(y_1|x_1,x_2)=q(y_1|x_2)$ and $q(y_2|x_1,x_2)=q(y_2|x_1)$, respectively. A set of all possible disconnected models forms a partially ordered set with respect to KL divergence between the full and the disconnected models (Fig. 5). If a given disconnected model is related to another one with a removal or an inclusion of an influence, the two models are connected by a line in Fig. 5. From Bottom to Top in Fig. 5, information loss increases as more influences are disconnected. Note that there is no ordering relationship between the disconnected models at the same level of the hierarchy. In Fig. 5, Top, all four influences are disconnected, and thus information loss is maximized, which corresponds to the mutual information $I(X;Y)$. The hierarchical structure generalizes related measures mentioned in this article and provides a clear perspective on the relationship among different measures.

Fig. 5.

A hierarchical structure of the disconnected models where across-time influences are broken in a system consisting of two units. All possible combinations of influences retained in the disconnected model are displayed. If two models are related with the addition or removal of one influence, they are connected by a line. The KL divergence between the full and the disconnected model increases from Bottom to Top.

Discussion

In this paper, we proposed a unified framework based on information geometry, which enables us to quantify multiple influences without overestimation and confounds of noncausal influences. With the framework, we uniquely derived the measure of integrated information, ${\mathrm{\Phi }}_G$. Moreover, our framework enables the complete description of causal relationships within a system by quantifying any combination of causal influences in a hierarchical manner as shown in Fig. 5. We expect that our framework can be used in diverse research fields, including neuroscience (29, 30), where network connectivity analysis has been an active research topic (31), and in particular consciousness researchers (32–34) because information integration is considered to be a key prerequisite of conscious information processing in the brain (10, 11).

To apply the measure of integrated information in real data, we need to resolve several practical difficulties. First, the computational costs increase exponentially with the system size. Thus, some way of approximating data is necessary. As we showed in this paper, the Gaussian approximation enables us to analytically compute integrated information, allowing us to compute integrated information in a large system (Eqs. 20–23). However, in real world systems, including brains, nonlinearity can be often significant and the Gaussian approximation may poorly fit to data. In such cases, transforming time series data into a sequence of discrete symbols can result in more accurate approximation (34, 35). Our measure of integrated information can be computed in such discrete distributions as shown in Supporting Information. Second, we need to find an appropriate partition of a system, which is an important problem in IIT (16). The computational costs for finding the optimal partition also exponentially increase. To overcome this difficulty, some effective optimization method needs to be used, possibly methods from discrete mathematics.

From a theoretical perspective, we could consider replacing Postulates 2 and 3 with different ones as interesting future research. As for Postulate 2, which defines the operation of disconnecting causal influences, we can use the interventional formalism (23, 36), which quantifies causal influences based on mechanisms of a system rather than observation of the system. As for Postulate 3, which defines the difference between the full model and a disconnected model, we can replace the KL divergence with other measures (24), such as the optimal transport distance, a.k.a, earth mover’s distance, which is considered to be important in IIT (17) and also has been shown to be useful in statistical machine learning (37). Our framework based on information geometry can be generally used for deriving different measures of causal influences from such different postulates and for analyzing the different geometric structures induced by them.

Manifold of Probability Distributions

Information geometry deals with a manifold of probability distributions and elucidates geometry in the manifold. Each point in the manifold represents a particular probability distribution. For example, consider a discrete probability distribution $p(x)$ where $x$ is a discrete random variable taking $n+1$ different values $x=\{\mathrm{0,1},\mathrm{\cdots },n\}$. Let $p_i$ be the probability that $x$ takes the value $i$,

$$p_i=\text{Prob}[x=i],\hspace{1em}i=\mathrm{0,1},\mathrm{\cdots },n.$$ [S1]

Because the sum of probabilities has to be 1,

$$\sum _{i=0}^n{p}_i=1,$$ [S2]

the probability distribution is parameterized by a vector of $n$ probabilities

$$\xi =(p_1,p_2,\mathrm{\cdots },p_n).$$ [S3]

Thus, the set of all possible probability distributions $p(x)$ forms an $n$-dimensional manifold. The vector of $n$ probabilities, $\xi$, is considered as a coordinate of the manifold. This manifold is called the probability simplex and is denoted by $S_n$.

Another example is a univariate Gaussian distribution,

$$p(x;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{(x-\mu )}^2}{2{\sigma }^2}\right),$$ [S4]

where $x$ is a random continuous variable, $\mu$ is the mean, and ${\sigma }^2$ is the variance. A Gaussian distribution is specified by two variables, $\mu$ and $\sigma$. Thus, a set of Gaussian distribution forms a two-dimensional manifold parameterized by $\mu$ and $\sigma$. The coordinate system of the manifold is $\xi =(\mu ,\sigma )$.

Discrete probability distributions and a Gaussian distribution belong to a broad class of probability distributions called an exponential family. The probability distributions included in the exponential family are written in the form

$$p(x,\xi )=\exp \left(\sum _{i=1}^n{\xi }_i{h}_i(x)+k(x)-\psi (\xi )\right),$$ [S5]

where $h_i(x)$ and $k(x)$ are functions of a random variable $x$ and $\psi (\xi )$ is the normalization factor. A set of $n$ parameters $\xi =({\xi }_1,{\xi }_2,\mathrm{\cdots },{\xi }_n)$ specifies the probability distributions. Thus, the exponential family of probability distributions forms an $n$-dimensional manifold with the coordinate system $\xi$.

Requirements for a Measure of Difference

As detailed in the main text, we postulated that the strength of influences is quantified by a minimized difference between the full model $p$ and a disconnected model $q$, which is denoted by $D[p:q]$. There are many possible ways to quantify a difference between probability distributions (22, 24). We consider four theoretical requirements that should be satisfied by the measure of a difference so that the measure has desirable mathematical properties. We can prove that the only measure of a difference that satisfies all four requirements is the Kullback–Leibler (KL) divergence.

The first requirement is as follows.

Requirement 1. $D[p(x):q(x)]$ should be a divergence.

A divergence, $D[P:Q]$, is a quantity that measures a degree of separation between two points $P$ and $Q$, satisfying the following criteria:

• i)$D[P:Q]\ge 0$.
• ii)$D[P:Q]=0$ if and only if $P=Q$.
• iii)
  When $P$ and $Q$ are sufficiently close, by denoting their coordinates by ${\xi }_P$ and ${\xi }_Q={\xi }_P+d\xi$, the Taylor expansion of $D$ is written as

  $$D[{\xi }_P:{\xi }_Q]=\frac{1}{2}\sum g_{ij}({\xi }_P)d{\xi }_{i}d{\xi }_j+\mathcal{O}(|d\xi {|}^3),$$ [S6]

  and matrix $G=\left(g_{ij}\right)$ is positive definite.

The first and second criteria are considered as the minimum requirements so that the quantity can be interpreted as a measure of the separation between two points. A divergence is a weaker notion than a distance because it does not satisfy the axioms of distance; i.e., a divergence is not symmetric, $D[P:Q]\ne D[Q:P]$, and does not satisfy the triangle inequality. When the third criterion is satisfied, a manifold $\mathcal{M}$ determined by the positive-definite matrix $g_{ij}$ is said to be Riemannian. As explained in the previous section, a probability distribution of the full model and a disconnected model can be represented as a point in the manifold of probability distributions, $S_n$. We consider the two points corresponding to the full model and a disconnected model as $P$ and $Q$, respectively.

The second requirement is as follows.

Requirement 2. $D[p(x):q(x)]$ should be invariant under invertible transformations of random variables.

$D[p(x):q(x)]$ should be invariant when a random variable $x$ is transformed by an invertible function $y=k(x)$, where $x$ and $y$ are one-to-one mapping. When $x$ and $y$ are one-to-one mapping, there is no information loss due to the transformation of variables. Invariance is also a necessary condition because the measure of a difference should not depend on a particular choice of variables but rather should be invariant under such lossless transformations of variables,

$$D[p(x):q(x)]=D[p(y=k(x)):q(y=k(x))].$$ [S7]

We can arbitrarily make countless invariant divergences. In general, when a certain invariant divergence, $D_{in}[p:q]$, is given, $g(D_{in}[p:q])$ is also an invariant function where $g$ is an arbitrary monotonic function that satisfies $g(0)=0$ and $g\prime (0)>0$. To resolve such arbitrariness, the third requirement is necessary.

Requirement 3. $D[p(x):q(x)]$ should be decomposable.

When a divergence can be written in an additive form of component-wise divergences for some function $d$,

$$D[p:q]=\sum _{i=0}^{n}d(p_i,q_i),$$ [S8]

it is said to be decomposable. It has been proved that an invariant and decomposable divergence is uniquely written in the form (22)

$$D[p:q]=\sum _{i=0}^n{p}_{i}f\left(\frac{q_i}{p_i}\right),$$ [S9]

where $f$ is a differentiable convex function satisfying

$$f(1)=0.$$ [S10]

This type of divergence is called $f$ divergence.

There still remains an arbitrariness in the choice among the $f$-divergence functions. The arbitrariness can be resolved by the requirement of flatness in the manifold of probability distributions.

Requirement 4. $D[p(x):q(x)]$ should be flat.

A divergence induces a Riemannian metric and a dual pair of affine connections coupled by the metric. It is said to be “flat” when it induces a flat structure in the underlying manifold where its dual curvatures are 0. The dually flat manifold has useful properties as it can be considered as a generalization of a Euclidean space. Importantly, information geometry shows that the generalized Pythagorean theorem and the related projection theorem hold in a dually flat manifold. These theorems play pivotal roles in this paper as we show below, as well as in many applications in various fields including statistics, machine learning, and information theory because the minimization of the divergence can be easily solved by these theorems. As we quantify causal influences as the minimized divergence, this property is beneficial for our purpose.

With the requirement of dual flatness, the divergence is now uniquely determined and is found to be the well-known KL divergence (22),

$$D_{KL}[p(x)||q(x)]=\sum _{x}p(x)\log \frac{p(x)}{q(x)}.$$ [S11]

To summarize, the KL divergence is the only divergence that is invariant, decomposable, and flat, satisfying all of the theoretical requirements for a measure of difference with the desired mathematical properties. Thus, as in Postulate 3 in the main text, we propose that the difference between the full model and a disconnected model should be quantified by the KL divergence.

Pythagorean Theorem

As stated in the previous section, the KL divergence induces a dually flat structure in the manifold of probability distributions. A dually flat manifold can be considered as a generalization of Euclidian space. In a dually flat manifold, a generalized Pythagorean theorem holds. Let us consider three points (probability distributions) $p$, $q$, and $r$ in a dually flat manifold. When the dual geodesic connecting $p$ and $q$ is orthogonal to the geodesic connecting $q$ and $r$, the following Pythagorean theorem holds:

$$D_{KL}[p(x)||r(x)]=D_{KL}[p(x)||q(x)]+D_{KL}[q(x)||r(x)].$$ [S12]

Here, the term “geodesic” does not mean the shortest path connecting two points. It is used to mean a straight line connecting two points. The geodesic connecting $q$ and $r$ is represented as

$${\theta }_{qr}=(1-t){\theta }_q+t{\theta }_r,$$ [S13]

where ${\theta }_q$ and ${\theta }_r$ represent the positions of $q$ and $r$, respectively, in a coordinate system $\theta$. Its tangent vector is given by

$$\frac{d{\theta }_{qr}}{dt}={\theta }_r-{\theta }_q.$$ [S14]

In a dually flat manifold, there is a dual coordinate system ${\theta }^{\ast }$ that is coupled with $\theta$ via Legendre transformation. The dual geodesic connecting $p$ and $q$ is represented as

$${\theta }_{pq}^{\ast }=(1-t){\theta }_p^{\ast }+t{\theta }_q^{\ast },$$ [S15]

where ${\theta }_p^{\ast }$ and ${\theta }_q^{\ast }$ represent the positions of $p$ and $q$, respectively, in the dual coordinate system ${\theta }^{\ast }$. Its tangent vector is given by

$$\frac{d{\theta }_{pq}^{\ast }}{dt}={\theta }_q^{\ast }-{\theta }_p^{\ast }.$$ [S16]

That the two geodesics are orthogonal means that the two tangent vectors (Eqs. S14 and S16) are orthogonal,

$$\frac{d{\theta }_{pq}^{\ast }}{dt}\cdot \frac{d{\theta }_{qr}}{dt}=0,$$

$$({\theta }_q^{\ast }-{\theta }_p^{\ast })\cdot ({\theta }_r-{\theta }_q)=0.$$

It can be shown that the above equation representing the relationship of the orthogonal triangle is equivalent to the Pythagorean relation in Eq. S12 (22).

Projection Theorem and Pythagorean Relations

We consider minimizing the KL divergence between the full model $p$ and a disconnected model $q$ under constraints

$$D_{KL}[p||q^{\ast }]=\underset{q\in {\mathcal{M}}_D}{min}{D}_{KL}[p||q],$$ [S17]

where $q^{\ast }$ is the minimizer of the KL divergence and ${\mathcal{M}}_D$ is a submanifold where the constraints are satisfied. According to the projection theorem in information geometry, the closest point $q^{\ast }$ can be found by orthogonally projecting the point $p$ to the submanifold ${\mathcal{M}}_D$. The orthogonal projection means that the dual geodesic connecting $p$ and $q^{\ast }$ is orthogonal to any tangent vector in ${\mathcal{M}}_D$ at the intersection. If the submanifold ${\mathcal{M}}_D$ is flat, the dual geodesic connecting $p$ and $q^{\ast }$ is orthogonal to geodesics connecting $q^{\ast }$ and any point $q\in {\mathcal{M}}_D$. In a flat submanifold, any geodesic connecting any two points in the submanifold is included in the submanifold. Thus, the three points $p$, the closest point $q^{\ast }$, and any point $q$ $\in {\mathcal{M}}_D$ form an orthogonal triangle. As explained in the previous section, the following Pythagorean relation holds for the orthogonal triangle:

$$D_{KL}[p||q]=D_{KL}[p||q^{\ast }]+D_{KL}[q^{\ast }||q].$$ [S18]

Total Causal Influences: Mutual Information

Total causal influences can be quantified by minimizing the KL divergence under the constraint where the past and future states of a system $X$ and $Y$ are independent. The constraint is given by

$$q(X,Y)=q(X)q(Y).$$ [S19]

As explained in the previous section, the Pythagorean relation (Eq. S18) holds because the submanifold determined by the constraint is flat. From the Pythagorean relation, we have

$$\begin{array}{c}{D}_{KL}[p||q]-(D_{KL}[p||q^{\ast }]+D_{KL}[q^{\ast }||q])=0,\\ \sum _{X,Y}(p(X,Y)-q^{\ast }(X,Y))\log \frac{q^{\ast }(X,Y)}{q(X,Y)}=0,\\ \sum _X(p(X)-q^{\ast }(X))\log \frac{q^{\ast }(X)}{q(X)}+\sum _Y(p(Y)-q^{\ast }(Y))\log \frac{q^{\ast }(Y)}{q(Y)}=0.\end{array}$$ [S20]

From Eq. S20, we find that $q^{\ast }(X)$ and $q^{\ast }(Y)$ must be equal to the marginal distributions of $p(X,Y)$ over $X$ and $Y$, respectively:

$$\begin{array}{c}{q}^{\ast }(X)=p(X),\\ q^{\ast }(Y)=p(Y).\end{array}$$

The minimized KL divergence is given by

$$\underset{q(X,Y)}{min}{D}_{KL}(p||q)=\sum _{X,Y}p(X,Y)\log \frac{p(X,Y)}{p(X)p(Y)},=H(X)+H(Y)-H(X,Y),=I(X;Y),$$

where $H$ is the entropy and $I(X;Y)$ is the mutual information between $X$ and $Y$.

Partial Causal Influences: Transfer Entropy

Partial causal influences from one element to another can be quantified by minimizing the KL divergence under the constraint where $x_i$ and $y_j$ are conditionally independent given the past states of a system that excludes only $x_i$. The constraint is given by

$$q(y_j|X)=q(y_j|{\stackrel{\sim }{x}}_i),$$ [S21]

where ${\stackrel{\sim }{x}}_i$ is the past states of a system except for $x_i$. The constraint disconnects the causal interaction from $x_i$ to $y_j$. Under the constraint, the disconnected model $q(X,Y)$ is expressed as

$$q(X,Y)=q({\stackrel{\sim }{y}}_j|y_j,X)q(y_j|X)q(X),=q({\stackrel{\sim }{y}}_j|y_j,X)q(y_j|{\stackrel{\sim }{x}}_i)q(X),$$

where ${\stackrel{\sim }{y}}_j$ is the present states of a system except for $y_j$. The KL divergence between $p$ and $q$ can be decomposed into the following three KL divergences,

$$D_{KL}(p(X,Y)||q(X,Y))=D_{KL}(p(X)||q(X))+D_{KL}(p(y_j|X)||q(y_j|X))+D_{KL}(p({\stackrel{\sim }{y}}_j|X,y_j)||q({\stackrel{\sim }{y}}_j|X,y_j)).$$ [S22]

When we minimize the KL divergence in Eq. S22, we can separately minimize the three KL divergences. Because the constraint does not affect the first term and the third term, we can easily find that the first term and the third term are minimized (become 0) when $q(X)$ and $q({\stackrel{\sim }{y}}_j|X,y_j)$ are equal to the corresponding distributions $p(X)$ and $p({\stackrel{\sim }{y}}_j|X,y_j)$, respectively. Thus, the minimization of the KL divergence in Eq. S22 is simply expressed as

$$\underset{q(X,Y)}{min}{D}_{KL}(p(X,Y)||q(X,Y))=\underset{q(y_j|X)}{min}{D}_{KL}(p(y_j|X)||q(y_j|X)).$$ [S23]

We can find the minimizer of the KL divergence by using the Pythagorean relation because the submanifold determined by the constraint in Eq. S21 is flat. From the Pythagorean relation, we have

$$\sum _{X,y_j}(p(X,y_j)-q^{\ast }(X,y_j))\log \frac{q^{\ast }(y_j|X)}{q(y_j|X)}=0,\sum _{{\stackrel{\sim }{x}}_i,y_j}p({\stackrel{\sim }{x}}_i)(p(y_j|{\stackrel{\sim }{x}}_i)-q^{\ast }(y_j|{\stackrel{\sim }{x}}_i))\log \frac{q^{\ast }(y_j|{\stackrel{\sim }{x}}_i)}{q(y_j|{\stackrel{\sim }{x}}_i)}=0,$$ [S24]

where the relation that $q^{\ast }(X)=p(X)$ is used. From Eq. S24, we find that

$$q^{\ast }(y_j|{\stackrel{\sim }{x}}_i)=p(y_j|{\stackrel{\sim }{x}}_i).$$ [S25]

The minimized KL divergence is calculated as

$$\underset{q(X,Y)}{min}{D}_{KL}(p(X,Y)||q(X,Y))=\sum _{X,y_j}p(X,y_j)\log \frac{p(y_j|X)}{p(y_j|{\stackrel{\sim }{x}}_i)},=H(y_j|{\stackrel{\sim }{x}}_i)-H(y_j|X),=TE(x_i\to y_j|{\stackrel{\sim }{x}}_i),$$

where $H(y_j|{\stackrel{\sim }{x}}_i)$ [or $H(y_j|X)$] is the conditional entropy given ${\stackrel{\sim }{x}}_i$ [or $X$] and $TE(x_i\to y_j|{\stackrel{\sim }{x}}_i)$ is the conditional transfer entropy from $x_i$ to $y_j$ given ${\stackrel{\sim }{x}}_i$.

Integrated Information

We propose to quantify integrated information as the minimized KL divergence,

$${\mathrm{\Phi }}_G=\underset{q}{min}{D}_{KL}(p||q),$$ [S26]

under the constraint

$$q(Y_i|X)=q(Y_i|X_i)\left(\forall i\right),$$ [S27]

where $X_i$ and $Y_i$ represent the past and present states of the elements in the $i$th subsystem, respectively. In general, it is difficult to analytically solve the minimization of the KL divergence under the above constraints unlike in the case of mutual information or transfer entropy. Note that the submanifold determined by the constraints is not flat and thus the Pythagorean relation in Eq. S18 does not hold. We need to numerically solve the constrained minimization of KL divergence by using optimization methods such as Newton’s method.

Integrated Information for Discrete Variables

In the following, we show how to compute ${\mathrm{\Phi }}_G$ when the states of units are represented by discrete variables. As the simplest case, we consider a system consisting of two binary units whose states are $0$ or $1$. Generalization to the other cases is quite straightforward although computations are more complicated. In the case of two units, the constraints for integrated information are given by

$$q(y_1|x_1,x_2)=q(y_1|x_1),$$ [S28]

$$q(y_2|x_1,x_2)=q(y_2|x_2).$$ [S29]

Under the constraint, the disconnected model $q(X,Y)$ is expressed as

$$q(X,Y)=q(y_2|x_1,x_2,y_1)q(y_1|x_1,x_2)q(X),=q(y_2|x_1,x_2,y_1)q(y_1|x_1)q(X),$$

where we used the first constraint (Eq. S28). We cannot further simplify $q(y_2|x_1,x_2,y_1)$ by using the second constraint (Eq. S29). Thus, we need to introduce the Lagrange multipliers for the second constraint. Note that as we are currently considering the binary variables, the second constraint is equivalent to the constraint

$$q(y_2|x_1=0,x_2)-q(y_2|x_1=1,x_2)=0.$$ [S30]

With the method of Lagrange multipliers, the Lagrangian is given by

$$\mathcal{L}=D_{KL}(p||q)+\rho (\sum _{X}q(X)-1)+\sum _{x_1}\lambda (x_1)(\sum _{y_1}q(y_1|x_1)-1)+\sum _{x_1,x_2,y_1}\mu (x_1,x_2,y_1)(\sum _{y_2}q(y_2|x_1,x_2,y_1)-1)+\sum _{x_2}\beta (x_2)(q(y_2=1|x_1=0,x_2)-q(y_2=1|x_1=1,x_2)),$$ [S31]

where $\rho$, $\lambda (x_1)$, $\mu (x_1,x_2,y_1)$, and $\beta (x_2)$ are Lagrange multipliers. The constraint in Eq. S30 is imposed on only one of the states of $y_2$ (we set $y_2=1$ without loss of generality) because the constraint for the other state of $y_2$, i.e., $q(y_2=0|x_1=0,x_2)-q(y_2=0|x_1=1,x_2)=0$, is automatically satisfied due to the constraint of ${\sum }_{y_2}q(y_2|x_1,x_2,y_1)=1$.

The disconnected model $q(X,Y)$ that minimizes the KL divergence can be found by differentiating the Lagrangian with respect to $q(X)$, $q(y_1|x_1)$, and $q(y_2|x_1,x_2,y_1)$ and setting the partial derivatives to 0,

$$\frac{\partial \mathcal{L}}{\partial q(X)}=-\frac{p(X)}{q(X)}+\rho =0,$$ [S32]

$$\frac{\partial \mathcal{L}}{\partial q(y_1|x_1)}=-\frac{p(y_1,x_1)}{q(y_1|x_1)}+\lambda (x_1)+\beta (x_2){(-1)}^{x_1}q(y_2=1|x_1,x_2,y_1)=0,$$ [S33]

$$\frac{\partial \mathcal{L}}{\partial q(y_2|x_1,x_2,y_1)}=-\frac{p(x_1,x_2,y_1,y_2)}{q(y_2|x_1,x_2,y_1)}+\mu (x_1,x_2,y_1)+\beta (x_2)y_2{(-1)}^{x_1}q(y_1|x_1)=0.$$ [S34]

From the first equation (Eq. S32), we can simply find that

$$q(X)=p(X).$$ [S35]

However, the other two equations cannot be analytically solved. Thus, to find the solutions of the above equations, we need to resort to a numerical method. When we computed ${\mathrm{\Phi }}_G$ in a system consisting of two binary units in Fig. 3 of the main text, we used Newton’s method.

Integrated Information for Gaussian Variables

When the probability distributions are Gaussian distributions, ${\mathrm{\Phi }}_G$ can be analytically computed. For simplicity, we consider partitioning a system into individual elements, meaning that there are $N$ subsystems, each subsystem containing only one unit. The constraints are expressed as

$$q(y_i|X)=q(y_i|x_i)(\forall i).$$ [S36]

Consider the following multivariate autoregressive model,

$$Y=AX+E,$$ [S37]

where $X$ is the past state of a system, $Y$ is the present state of a system, $A$ is the connectivity matrix, and $E$ is Gaussian random variables, which are uncorrelated over time. The multivariate autoregressive model is the generative model of a multivariate Gaussian distribution. The joint probability distribution of $X$ and $Y$ is expressed as

$$p(X,Y)=\exp \left\{-\frac{1}{2}\left(X^T\mathrm{\Sigma }{(X)}^{-1}X+{(Y-AX)}^T\mathrm{\Sigma }{(E)}^{-1}(Y-AX)-\psi \right)\right\},$$ [S38]

where $\mathrm{\Sigma }(X)$ and $\mathrm{\Sigma }(E)$ are the covariance matrices of $X$ and $Y$, respectively. We consider combining $X$ and $Y$ and define a new vector $Z$,

$$Z=\left(\begin{array}{c}\hfill X\hfill \\ \hfill Y\hfill \end{array}\right).$$ [S39]

Then, the joint probability distribution of $X$ and $Y$ is rewritten as

$$p(Z)=\exp \left\{-\frac{1}{2}\left(Z^T\mathrm{\Sigma }{(Z)}^{-1}Z-\psi \right)\right\},$$ [S40]

where the covariance matrix of $Z$ is given by

$$\mathrm{\Sigma }(Z)=\left(\begin{array}{cc}\hfill \mathrm{\Sigma }(X)\hfill & \hfill \mathrm{\Sigma }(X)A^T\hfill \\ \hfill A\mathrm{\Sigma }(X)\hfill & \hfill \mathrm{\Sigma }(E)+A\mathrm{\Sigma }(X)A^T\hfill \end{array}\right),$$ [S41]

and the inverse of $\mathrm{\Sigma }(Z)$ is given by

$$\mathrm{\Sigma }{(Z)}^{-1}=\left(\begin{array}{cc}\hfill \mathrm{\Sigma }{(X)}^{-1}+A^T\mathrm{\Sigma }{(E)}^{-1}A\hfill & \hfill -A^T\mathrm{\Sigma }{(E)}^{-1}\hfill \\ \hfill -\mathrm{\Sigma }{(E)}^{-1}A\hfill & \hfill \mathrm{\Sigma }{(E)}^{-1}\hfill \end{array}\right).$$ [S42]

Similarly, the joint probability distributions in the disconnected model are given by

$$q(X,Y)=\exp \left\{-\frac{1}{2}\left(X^T\mathrm{\Sigma }{{(X)}^{\prime }}^{-1}X+{(Y-A\prime X)}^T\mathrm{\Sigma }{{(E)}^{\prime }}^{-1}(Y-A\prime X)-\psi \prime \right)\right\},$$ [S43]

$$=\exp \left\{-\frac{1}{2}\left({Z^{\prime }}^T\mathrm{\Sigma }{{(Z)}^{\prime }}^{-1}Z\prime -\psi \prime \right)\right\},$$ [S44]

where $\mathrm{\Sigma }{(X)}^{\prime }$ and $\mathrm{\Sigma }{(E)}^{\prime }$ are the covariance matrices of $X$ and $Y$ in the disconnected model, respectively, and $A\prime$ is the connectivity matrix in the disconnected model. The constraints in Eq. S36 correspond to setting the off-diagonal elements of $A\prime$ to 0:

$${A\prime }_{ij}=0(i\ne j).$$ [S45]

The KL divergence between the full model and a disconnected model is given by

$$D_{KL}(p||q)=\frac{1}{2}(\log \frac{|\mathrm{\Sigma }{(Z)}^{\prime }|}{|\mathrm{\Sigma }(Z)|}+Tr(\mathrm{\Sigma }(Z)\mathrm{\Sigma }{{(Z)}^{\prime }}^{-1})-2N),$$ [S46]

where $N$ is the number of variables in $X$ or $Y$ and $2N$ is the total number of variables in $X$ and $Y$. The determinant of $\mathrm{\Sigma }(Z)$ can be calculated as

$$|\mathrm{\Sigma }(Z)|=|\mathrm{\Sigma }(X)||\mathrm{\Sigma }(E)+A\mathrm{\Sigma }(X)A^T-A\mathrm{\Sigma }(X)\mathrm{\Sigma }{(X)}^{-1}\mathrm{\Sigma }(X)A^T|,$$ [S47]

$$=|\mathrm{\Sigma }(X)||\mathrm{\Sigma }(E)|.$$ [S48]

Thus, the KL divergence is rewritten as

$$D_{KL}(p||q)=\frac{1}{2}(\log \frac{|\mathrm{\Sigma }{(X)}^{\prime }|}{|\mathrm{\Sigma }(X)|}+\log \frac{|\mathrm{\Sigma }{(E)}^{\prime }|}{|\mathrm{\Sigma }(E)|}+Tr(\mathrm{\Sigma }(Z)\mathrm{\Sigma }{{(Z)}^{\prime }}^{-1})-2N).$$ [S49]

The trace of $\mathrm{\Sigma }(Z)\mathrm{\Sigma }{{(Z)}^{\prime }}^{-1}$ is calculated as

$$Tr(\mathrm{\Sigma }(Z)\mathrm{\Sigma }{{(Z)}^{\prime }}^{-1})=Tr(\mathrm{\Sigma }(X)\mathrm{\Sigma }{{(X)}^{\prime }}^{-1}+\mathrm{\Sigma }(X)({A^{\prime }}^T-2A^T)\mathrm{\Sigma }{{(E)}^{\prime }}^{-1}A\prime +(\mathrm{\Sigma }(E)+A\mathrm{\Sigma }(X)A^T)\mathrm{\Sigma }{{(E)}^{\prime }}^{-1}).$$ [S50]

The derivatives of the KL divergence with respect to the components of $\mathrm{\Sigma }{(X)}^{\prime -1}$, $A\prime$, $\mathrm{\Sigma }{(E)}^{\prime -1}$ can be calculated as

$$\frac{\partial D_{KL}}{\partial \mathrm{\Sigma }{(X)}_{ij}^{\prime -1}}=\mathrm{\Sigma }{(X)}_{ji}-\mathrm{\Sigma }{(X)\prime }_{ji},$$ [S51]

$$\frac{\partial D_{KL}}{\partial {A\prime }_{ii}}={(\mathrm{\Sigma }(X)(A\prime -A)\mathrm{\Sigma }{{(E)}^{\prime }}^{-1})}_{ii},$$ [S52]

$$\frac{\partial D_{KL}}{\partial \mathrm{\Sigma }{(E)}_{ij}^{\prime -1}}=\mathrm{\Sigma }{(E)}_{ji}-\mathrm{\Sigma }{(E)\prime }_{ji}+{((A-A\prime )\mathrm{\Sigma }(X){(A-A\prime )}^T)}_{ji},$$ [S53]

where we used

$$\frac{\partial |A|}{\partial A_{ij}}=|A|A_{ji}^{-1}.$$ [S54]

Thus, the KL divergence is minimized when

$$\mathrm{\Sigma }{(X)}^{\prime }=\mathrm{\Sigma }(X),$$ [S55]

$${(\mathrm{\Sigma }(X)(A-A\prime )\mathrm{\Sigma }{{(E)}^{\prime }}^{-1})}_{ii}=0,$$ [S56]

$$\mathrm{\Sigma }{(E)}^{\prime }=\mathrm{\Sigma }(E)+(A-A\prime )\mathrm{\Sigma }(X){(A-A\prime )}^T.$$ [S57]

By substituting Eqs. S55 and S57 into Eq. S50, we find that the trace of $\mathrm{\Sigma }(Z)\mathrm{\Sigma }{{(Z)}^{\prime }}^{-1}$ is $2N$,

$$Tr(\mathrm{\Sigma }(Z)\mathrm{\Sigma }{{(Z)}^{\prime }}^{-1})=2N.$$ [S58]

Thus, the minimized KL divergence, ${\mathrm{\Phi }}_G$, is simply written as

$${\mathrm{\Phi }}_G=\frac{1}{2}\log \frac{|\mathrm{\Sigma }{(E)}^{\prime }|}{|\mathrm{\Sigma }(E)|}.$$ [S59]