Molecular dimension explored in evolution to promote proteomic complexity

Abstract

The architecture of present-day protein interaction networks depends on how protein associations evolved. Here, we explore how and why evolution-related mutations influence protein structure to promote protein associations, and thereby network development. We specifically address two questions: (i) How can protein folds remain conserved while proteins accommodate new binding partnerships as genes duplicate? (ii) What is the structural/molecular basis for hub proteins being the most likely to acquire new connections? The answers stem from the examination of the structure wrapping, or protection from water attack. Wrapping is shown to be a crucial consideration in the exploration and evolution of proteomic interactivity.

Protein folds tend to be evolutionarily conserved. Thus, to assess the impact of evolutionary change (1), a concept finer than the fold is needed. Here we address the question: what molecular changes does evolution explore to promote interactome complexity (2, 3)? The connectivity of a folding domain was recently shown to correlate statistically with its number of dehydrons (4, 5), or deficiently packed backbone hydrogen bonds (4–10). This finding now enables us to elucidate the molecular mechanism underlying the evolution of protein interaction networks, which has thus far been an open problem (2, 3, 11–15). Describing this mechanism requires an understanding of the impact of evolutionary change on protein structure. Because the fold appears to be conserved across distant homologous sequences (16), we need to identify another molecular dimension (6) that evolution must explore to modulate the extent of protein interactivity.

By studying the evolution of the yeast proteomic network (11, 12), we now report how new binding partnerships are promoted by relaxing the structure packing. The rate of accretion of packing defects or, equivalently, of protein connectivities is determined at times of species divergence. For any folding domain, we find an autocatalytic build-up of packing defects that ultimately yields a scale-free network (2, 13). This finding is intuitively appealing because mutations are more likely to produce new dehydrons in deficiently wrapped proteins and are likely to have a smaller impact on better wrapped proteins.

Because gene duplication is the dominant means of creating new genes and fostering the evolution of complex organisms (17, 18), it has been argued that it must guide the evolution of network complexity (2). Thus, because a hub protein is more likely than any other to interact with a gene prone to undergo duplication, it becomes a node prone to acquire new connections, in accord with the “rich-get-richer” accretion scenario (2). Nevertheless, this picture has several shortcomings. (i) Often, as a gene is duplicated, one copy retains the function while the other accumulates mutations eventually leading to the creation of a new function (17, 18). Thus, if a protein is originally capable of binding to a gene product, it would have to also coevolve with the gene replica to accommodate the new binding partnership. (ii) Often, a folding domain is monomeric in some organisms but becomes multimeric as a result of gene duplication, as with human hemoglobin (18). This change implies that the protein must have evolved from being monomeric to encompass quaternary interactions (6), as needed to promote allostericity and regulation, but retained the original fold for functional reasons. (iii) Often, gene duplication is partial or internal (17, 18), making it unclear how this process may foster new connectivities.

To address these problems, we need to examine the impact of evolutionary change on protein structure and its ramifications on network architecture. Molecular changes preserving the fold must eventually follow gene duplication events to accommodate new binding partnerships. Thus, although the fold is conserved across species, its wrapping or extent of intramolecular dehydration of backbone hydrogen bonds is not (5, 6). This phenomenon leads to changes in the number of binding partnerships as needed to correct intramolecular deficiencies (5, 6). Such associations are enabled because underwrapped backbone hydrogen bonds, or dehydrons (10), are sticky for hydrophobes. Their adhesiveness results from the strengthening and stabilization of the electrostatic interaction as it becomes dehydrated. Dehydrons are adhesive because removing exogenous water from their surroundings decreases charge screening and destabilizes the nonbonded state by hindering the hydration of the amide and carbonyl (7–10).

Here we report on how mutations influencing wrapping affect network evolution. As protein structures become more underwrapped, they also become more reliant on binding partnerships (7, 9), in turn fostered by the stickiness of the wrapping defects, and this interdependence increases the network complexity.

For instance, the pea (Lupinus luteus) leghemoglobin (19) [Protein Data Bank (PDB) ID 1GJD] is monomeric, whereas human hemoglobin (PDB ID 1BZ0) is tetrameric as a result of gene duplication (6, 18). The individual β-subunit in human hemoglobin is more loosely packed than the pea leghemoglobin (Fig. 1), exhibiting three dehydrons at the quaternary structure interfaces (6). On the other hand, leghemoglobin is perfectly wrapped, in consonance with its monomeric native state.

Fig. 1.

Illustrative comparative analysis of the wrapping of backbone hydrogen bonds of pea leghemoglobin (A) and human hemoglobin β-subunit (B). The chain backbone is represented as a virtual-bond polygonal joining α-carbons. Dehydrons computed following ref. 10 are indicated as green segments joining nonadjacent α-carbons, whereas properly desolvated backbone hydrogen bonds are shown as gray segments. Whereas the pea folding domain is a perfect wrapper of its backbone and is monomeric, the tetrameric human ortholog possesses the dehydrons associated with pairs (5,9), (90,94), and (90,95). The first dehydron is adjacent to E6, the sickle-cell anemia mutation site, and is located at the protein–protein interface Glu-6-(Phe-85, Leu-88) in the deoxy fiber. The other two dehydrons are determinants of the quaternary organization (6, 10).

Methods

Ortholog Identification. Orthologs of yeast proteins are identified in the organisms specified below by following the double-query procedure, a bidirectional best-hit method (20). Thus, psi-blast (21) is first used in a database similarity search on the entire proteome of the chosen organisms with a yeast protein serving as a query. Sequences with at least 50% identity in alignment are selected. Once the best hit has been found, it is used as a query protein to search for similarities in the yeast proteome. If the best hit happens to be the yeast protein used originally as query, both proteins are regarded as orthologs arising from a common ancestor.

Structure-Based Identification of Dehydrons. To identify the dehydrons in a domain fold, multidomain chain or protein complex in one-chain or multiple-chain PDB entries, we adopt the following premises (4–10): The extent of intramolecular hydrogen-bond desolvation in monomeric structure is quantified by determining the number of nonpolar carbonaceous groups within a desolvation domain. This domain is defined as two intersecting balls of fixed radius centered at the α-carbons of the hydrogen bonded residues. The statistics of hydrogen-bond wrapping vary according to the desolvation radius adopted, but the tails of the distribution invariably single out the same dehydrons in a given structure over a 6.0–7.4 Å range for the choice of desolvation radius. Here, the value 6.2 Å was adopted for consistency.

In most (≈92% of PDB entries) stable protein folds, the backbone hydrogen bonds are wrapped on average by ρ = 26.1 ± 7.5 nonpolar groups (or 14.0 ± 3.7 if we count only side-chain groups and exclude those from the hydrogen-bonded residue pair), with ρ as our measure of the extent of wrapping of the bond. Dehydrons are then defined as hydrogen bonds in the tails of the distribution, i.e., with <12 nonpolar groups in their desolvation domains (their ρ-value is, at most, two Gaussian dispersions below the mean). Dehydrons are the dominant factors driving association in 38% of the PDB complexes (the density of dehydrons at protein–protein interface is >3/2 that of the average density of individual monomeric partners). Furthermore, dehydrons constitute a significant factor (interface dehydron density larger than average) in 92.9% of all PDB complexes (7).

Sequence-Based Identification of Dehydrons. Our analysis would be severely constrained if we were limited to structural databases. We have found a relationship between wrapping and a structural parameter that can be directly and reliably predicted from sequence: the propensity for inherent structural disorder in any region of a domain fold (22–25). The latter parameter is assessed with a high degree of accuracy by the program pondr-vlxt, a neural-network predictor of native disorder (22) that takes into account residue attributes such as hydrophilicity, aromaticity, and their distribution within the window interrogated. Thus, a disorder score λ_D, with 0 ≤ λ_D ≤ 1, is assigned to each residue within a sliding window. This value represents the predicted propensity of the residue to be in a disordered region, with λ_D = 1, in case of absolute certainty. The score λ_D = 0 indicates absolute certainty that the residue is part of an ordered region. Only 6% of >1,100 nonhomologous PDB proteins give false positive predictions of disorder in sequence windows of ≥40 amino acids. Even this 6% of false positives is an overestimation, because many disordered regions in monomeric chains become ordered upon ligand binding or in crystal contacts. The correlation between propensity for disorder and wrapping implies that it is possible to predict dehydrons directly from sequence. It would suffice to determine the pondr-generated pattern corresponding to each of the desired features. The correlation between pondr-vlxt score at a particular residue site and the extent of wrapping, ρ, of the hydrogen bond engaging that residue (if any) is shown in Fig. 2. The strong correlation shown in Fig. 2 implies that we can infer the existence of dehydrons from the pondr-vlxt score with 94% accuracy in regions with a disorder score (λ_d) >0.35, provided that such regions are flanked by well wrapped regions (λ_d < 0.35) to ensure the actual existence of structure.

Fig. 2.

Correlation between the pondr-vlxt disorder score (1 = native structural disorder, 0 = order) at a residue and the extent of wrapping of the backbone hydrogen bond engaging that particular residue.

The correlation implies that the propensity to adopt a natively disordered state becomes pronounced for proteins that, because of their chain composition, cannot fulfill the minimal wrapping requirement for the protection of their backbone hydrogen bonds. This minimal requirement dictates that at least seven nonpolar groups should wrap each backbone hydrogen bond.

It might appear surprising that a predictor of a three-dimensional attribute, the dehydron, could be inferred from sequence, especially because structure cannot be inferred from sequence. However, the disorder score is obtained by using a learning strategy that incorporates sequence windows in its training set together with the structural context in which such windows occur. Thus, if the window is wide enough, few spatial contexts may be compatible with the window structure, and this information is subsumed in the training set for the disorder predictor.

Fig. 2 shows the dispersion in the linear correlation between predicted disorder score within a structured region and extent of wrapping of the hydrogen bonds. We examined 2,806 nonredundant nonhomologous PDB domains (10) and obtained the disorder score from pondr-vlxt (22, 23) on each individual residue at the center of a sequence window of length 41 residues. Residues from the set of PDB structures have been independently grouped according to the extent of wrapping of the backbone hydrogen bond engaging them. Thus, 45 bins of 400 residues each have been constructed, because 52 is the maximum number of nonpolar groups in the desolvation domain of a backbone hydrogen bond reported in the PDB and no hydrogen bond in the PDB is protected by fewer than seven nonpolar groups. The average pondr-vlxt score has been determined for each bin (square in Fig. 2). The error bars in Fig. 2 represent the dispersion of disorder scores within each bin. Notice the highly significant correlation, except at ρ = 7, 8, when the scant wrapping makes the structural attribution dubious for the monomeric state (10). No ρ value of <7 is found in the PDB. Thus, lower wrapping signals disordered regions. Obviously, the disorder score for such regions is 1. The data at first sight seem to imply that pondr-based dehydron predictions might actually correspond to hydrogen bonds lying within an 8- to 17-wrapping range. However, >98% of the PDB hydrogen bonds are either well wrapped (ρ > 19) or dehydrons (ρ < 12), with <2% marginally wrapped hydrogen bonds (12 < ρ < 19) (10). Thus, the pondr-based inference of dehydrons is in fact quite accurate (>95%) because of the relative paucity of marginally wrapped hydrogen bonds, which would lie within the dispersion range in the correlation shown in Fig. 2.

A caveat to this methodology arises because the PDB is a database biased toward ordered proteins (highly disordered chains are unlikely to crystallize, although there are conspicuous exceptions, such as PDB ID code 1JFW, which crystallizes with virtually no secondary structure). However, the disorder contribution to the PDB is large enough to make the PDB a reliable training set for disorder prediction using machine learning techniques and the annotated SwissProt sequence database as the testing set (22–25).

Results

To establish the molecular basis for network evolution, we need to assess the impact of germ-line mutation on interactivity. The effect cannot be too severe: distortion or loss of protein structure typically introduces a phenotype too grossly changed to become inheritable (1). However, wrapping may be affected, as the statistics shown in Fig. 3 reveal. Amino acid substitution alters the number of nonpolar groups within the desolvation domain of backbone hydrogen bonds, and in so doing affects their wrapping. Substitution of a good wrapping residue for a poor wrapper (i.e., G, A, S, T, N, or D), or vice versa, affects the sensitivity to water removal around the hydrogen bonds protected by the residue (26).

Fig. 3.

Statistics on the impact of mutations on the wrapping, and thereby on the interactivity (7, 10), of proteins reported in the PDB. A repository of mutations is constructed for each type of substitution (SNPs, evolution-related and disease-related) and the mutations are distributed in five classes or “structural impact groups” (A–E), according to their effect on the wrapping of the protein. The 12,099 SNPs with allelic frequency higher than 1% occurring in coding regions for PDB proteins were exhaustively extracted from the National Center for Biotechnology Information (NCBI) database of genetic variation (dbSNP) (26). A repository of identical size was constructed by considering naturally occurring amino acid substitutions across homologous proteins by using proteins reported in PDB as reference (see Methods). Finally, an exhaustive repository of 1,811 germ-line disease-related mutations on human proteins reported in PDB was extracted from OMIM, the Online Mendelian Inheritance in Man database (27). The structural impact of mutation is divided in five categories: A, the substitution does not alter the dehydron pattern of the protein; B, the substitution does not affect the dehydron pattern but affects the wrapping of specific hydrogen bonds by reducing in at least three the number of surrounding nonpolar groups, thus making the structure wrapping susceptible to subsequent mutations; C, the substitution preserves the preexisting dehydrons, but adds new ones as the protein-coding gene undergoes duplication concurrently with the mutation in the original gene; D, the substitution does not preserve preexisting dehydrons; E, the substitution decreases the wrapping of specific hydrogen bonds below the threshold of seven nonpolar surrounding groups required to preserve the integrity of the structure (4, 5, 7).

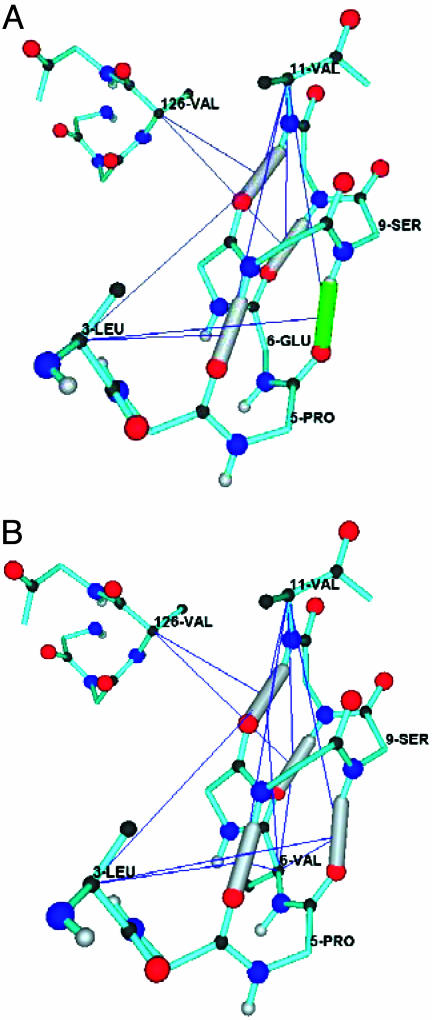
Nonsynonymous single-nucleotide polymorphisms (SNPs) (27) occurring in protein-coding regions do not affect the wrapping enough to change dehydrons (Fig. 3). Evolutionary change, i.e., amino acid substitution in homologous proteins, tends to conserve preexisting dehydrons (4, 5) while forming new ones (6) to foster further connectivity concurrently with gene duplication events. On the other hand, disease-related mutations do not tend to conserve dehydrons (Fig. 3) (see www.ncbi.nlm.nih.gov/omim). This situation is illustrated by the E6V sickle-cell anemia mutation in the β-subunit of human hemoglobin. This substitution increases the wrapping of the (P5,S9)-dehydron in the β-subunit (6, 10) as shown in Fig. 4.

Fig. 4.

Impact of disease-related mutation on the wrapping of protein structure. Detail of the wrapping of backbone hydrogen bonds displaying the (P5,S9)-dehydron in wild-type human hemoglobin β-subunit (A) and the well wrapped (P5,S9)-hydrogen bond in the sickle-cell anemia mutant (B). The protein backbone is represented in atomic detail, with well wrapped amidecarbonyl hydrogen bonds shown as gray tubes and dehydrons shown in green. A thin line from the α-carbon of a residue to the center of a hydrogen bond indicates that the residue is a wrapper of the bond: at least one nonpolar group in its side chain is contained in the desolvation domain of the hydrogen bond. (A) Wrapping pattern for wild type with (P5,S9)-dehydron. (B) Wrapping pattern for E6V mutant, which does not conserve the (P5,S9)-dehydron, turning it into a well wrapped hydrogen bond because of the desolvating contribution from V6.

Structural databases are underreported. Therefore, a molecular-based analysis of the evolution of network complexity requires an alternative, supplementary means to identify dehydrons. Thus, one can use a sequence-based predictor of dehydrons in folding domains by relating wrapping to propensity for native disorder (22–25), as shown in Fig. 2. The disorder score used here is an attribute of sequence and essentially measures the extent to which a protein fails to pack well enough to protect the backbone hydrogen bonds from water attack (Methods). Thus, the “twilight zone” between order and disorder (approximately, the range 0.33 ≤ λ_d ≤ 0.49) corresponds with 91% probability to the wrapping range 7 ≤ ρ ≤ 12. The dehydrons lie precisely in this ρ range. For the chosen desolvation radius, there is no hydrogen bond in the PDB with fewer than seven nonpolar wrapping groups (5). Note that the criteria used here and in refs. 22–25 have very different bases, so the comparison, though persuasive, must be interpreted with caution.

We now turn to the evolution of network connectivities, and introduce an operation that we call “trimming.” The trimming of a present-day protein network for a particular species is a reduction in the number of nodes, retaining only those that represent common ancestral proteins at the time of divergence of another species. To understand the evolution of connectivities, the network of protein–protein interactions in Saccharomyces cerevisiae inferred from two-hybrid experiments (11) was trimmed at different evolutionary times according to the following steps.

1. Orthologs for each of the 6,294 yeast proteins were searched following the double-query criterion (Methods) in three organisms with relatively small proteomes, the bacteria Escherichia coli, the plant Arabidopsis thaliana, and the fission yeast Schizosaccharomyces pombe, with times of divergence from yeast estimated at 4, 1.58 ± 0.9, and 1.14 ± 0.8 gigayears (1 gigayear = 10⁹ years), respectively (28).

2. Each yeast protein is placed in one of four ancestry groups, according to the number of organisms that contain orthologs of the protein. Thus, the presumed oldest yeast proteins have orthologs in the other three organisms (group 4), whereas the youngest do not have orthologs in any of the other three species (group 1); group 2 contains proteins with orthologues in yeast and fission yeast, and group 3 contains proteins with orthologues in yeast, fission yeast, and A. thaliana.

3. The yeast network is trimmed at each divergence time point, retaining only the nodes that subsequently branch into the orthologs. This procedure is justified insofar as ortholog proteins have evolved from a common ancestor.

The extent of overall wrapping deficiency, r, of a protein is given as a density, and computed as the number of dehydrons (9, 10) per 100 backbone hydrogen bonds. Fig. 5A shows the extent of overall wrapping deficiency of proteins in each of the four ancestry groups. To display the data, proteins have been lumped into their structural (SCOP) superfamilies (29). Fig. 5A reveals that the presumed evolutionary age of proteins correlates significantly with their extent of overall wrapping deficiency. We may conclude that, within a 21% confidence band in the r value, the oldest proteins in the network are also those with the highest densities of dehydrons, the proteins whose structural integrity requires the highest number of binding partnerships. Those proteins in particular belong mainly to two SCOP families, the P loop NTP hydrolases and the ARM repeat. Because r is a linear marker for interactivity (6), Fig. 5A shows that evolutionary age correlates significantly with network centrality, as it should, because regions relevant to interactivity are expected to be conserved.

Fig. 5.

Correlation between underwrapping and ancestry of structural superfamilies and their time evolution. (A) Extent of overall wrapping deficiency of yeast domain folds versus the ancestry of the proteins. The overall wrapping deficiency r, defined as number of dehydrons per 100 backbone hydrogen bonds, is inferred from sequence (Methods), except for domains reported in the PDB (e.g., the yeast Hsp90 chaperone, or the yeast cellular prion protein). The ancestry group of a protein is determined by the number of organisms (from a group of four) containing orthologs of the protein, as indicated in main text. The symbol 〈r〉 indicates average over all yeast proteins in a SCOP superfamily. The open squares represent the average 〈r〉 over each ancestry group, whereas the filled squares represent averages over individual SCOP superfamilies represented in an ancestry group. The wrapping deficiency r value dispersions over all proteins in an ancestry group are shown as error bars. Ancestry group 1 comprises 4,913 yeast proteins and 161 SCOP superfamilies; group 2 comprises 1,149 proteins and 41 SCOP superfamilies; group 3 comprises 175 proteins and 6 SCOP superfamilies; and group 4 comprises 57 proteins and 2 SCOP superfamilies. Selected families are plotted for each ancestry group. Listed in decreasing dehydron density, they are as follows: group 4: P loop NTP hydrolases (signal transduction), ARM repeat; group 3: protein kinases (PK), phospholipase C/P1 nucleases, class II aaRS biotin synthetases; group 2: Rossman fold domains, NAD(P) binding, trypsin-like serine proteases, EF-hand; group 1: nucleotidyl transferases. The figure reveals a significant correlation between ancestry and wrapping deficiency, thereby implying a relationship between centrality and age, as wrapping is a structural marker for interactivity (5). (B) Dependence of the average number of wrapping defects on evolutionary time for selected SCOP superfamilies in yeast belonging to ancestry groups 2, 3, and 4. The exponential time dependence is indicative of an autocatalytic rate of accretion of dehydrons or, equivalently, of connectivities (4), supporting the “rich gets richer” scenario of network evolution. The phospholipase C/P1 nucleases from ancestry group 3 have a relatively low intercept, only slightly above the intercept for the Rossman domain, belonging to group 2. This is compatible with the large dispersion in wrapping deficiency within the ancestry families, as shown in A.

The average overall wrapping deficiency of individual SCOP families has been plotted over evolutionary time in Fig. 5B. These results were obtained by trimming the yeast network at the mean estimated times of divergence of the four organisms, as indicated above. Only those nodes corresponding to proteins that yield orthologs in the organisms evolving after a divergence time are retained. The node connectivities in the trimmed network are determined and converted into the r values of the corresponding proteins. This procedure allows us to reconstruct the ancestral network for protospecies that branched progressively into the four chosen organisms. Converting connectivities into r values requires multiplication of the former by the conversion factor 1.2 (with ± 0.18 uncertainty) (4, 5).

For all 210 SCOP superfamilies represented in yeast, the 〈r〉 values obtained by converting present-day connectivities (12, 30) coincides to within 4–9% with the values obtained directly by the sequence-based wrapping predictor described in Methods.

The results shown in Fig. 5B illustrate, for a few structural superfamilies, a general rate law of evolution of network complexity: the accumulation of dehydrons, or equivalently, of connectivities on a node increases quasi-exponentially in evolutionary time, with a single exponential factor α = 0.195 ± 0.07 per gigayear for any protein. Thus, the rate of accumulation of connectivities w(t) = dx/dt is given as w(t) = αζn(t) = αx(t), where x(t) and n(t) are the number of preexisting connections and dehydrons, respectively, on the node-protein, and ζ = 1.2 ± 0.18 is the conversion factor described above. The dispersion in slope over all SCOP superfamilies represented in yeast is 0.195 ± 0.09 per gigayear.

Thus, evolutionary mutations are less likely to occur in highly connected proteins because their dehydrons determine interactions and hence are conserved. However, mutations in such systems, when they occur, are likely to lead to new dehydrons. On the other hand, mutations in proteins on the network's periphery are more frequent but less likely to produce new dehydrons.

These figures on the evolutionary kinetics of connectivity accumulation must be regarded with caution. Although no quantitative studies exist at present, the bidirectional best-hit method used in this work probably works best at detecting orthologs in highly conserved proteins that interact with many partners, but will likely perform more poorly on proteins with few binding partnerships and, therefore, with higher amino acid variability. Furthermore, being based on a single criterion like sequence divergence, the evolutionary dates adopted here are only approximate, and thus not fully reliable (28).

Discussion

In studying the evolution of proteomic networks, we have found an autocatalytic law of accretion of proteomic connectivities and found the evolutionary latitude that enables proteins to become more interactive while preserving their fold. The law yields a scale-free network (2, 13) because it implies that the probability of acquiring new connections is proportional to the number of preexisting connections. Furthermore, the results reveal how an increase in network connectivity may be achieved while preserving the functionally relevant folds: it occurs by means of enhancing the underwrapping of the backbone hydrogen bonds by mutations that selectively reduce the number of nonpolar groups on side chains. The partial exposure of a hydrogen bond upon mutation, turning it into a dehydron in a monomer, both implies and necessitates the formation of a new connectivity, often with another protein. A mutation is likely to have a higher impact on wrapping, turning a hydrogen bond into a dehydron, if the underlying structure is already poorly wrapped. This is the case because the hydrogen bond affected by the mutation is likely to have been marginally wrapped even before the mutation occurred. In other words, defectively packed proteins have a high wrapping susceptibility to mutation. These results provide the molecular basis for a “rich-get-richer” accretion scenario governing the formation of scale-free proteomic networks (2, 13).