Abstract
The aim of this study was to investigate the changes in the relationships between repeated sprint ability (RSA) and anthropometric measures as well as fitness qualities in soccer players. Twenty-one professional soccer players performed several anthropometric and physical tests including countermovement vertical jumps (CMJs), a straight-line 30 m sprint (T30), an RSA test (6 x 20 + 20 m with 20 s recovery), a progressive isoinertial loading test in a full squat, a Yo-Yo Intermittent Recovery Test Level-1 (YYIRT-1) and a 20 m shuttle run test (20mSRT). The mean (RSAmean), the fastest (RSAbest), each single sprint time, and the percentage in a sprint decrease (%Dec) in the RSA test were calculated. RSAbest correlated significantly with RSAmean (r = .82) and with all single sprints (p < 0.05), showing a downward trend as the number of sprints performed increased. No significant relationship was observed between the %Dec and RSA performance. CMJs and the T30 also showed a correlation with RSA performance, whereas lower limb strength did not show any relationship with RSA performance. RSAmean showed significant (p < 0.05) relationships with body mass (r = .44), adiposity (r = .59) and the YYIRT-1 (r = -.62), increasing as the number of repeated sprints increased. The 20mSRT showed minimal relationships with RSA performance. In conclusion, maximal sprint capacity seems to be relevant for the RSA performance, mainly in the first sprints. However, high intermittent endurance capacity and low adiposity might help enhance the RSA performance when increasing the number of repeated sprints.
Keywords: anthropometrics, repeated explosive efforts, strength, sprinting, intermittent endurance, soccer
Introduction
Soccer is a sport with high-intensity actions of variable length and duration, interspersed with recovery periods, most of which last longer than 60 s (Carling et al., 2012). Usually, a shorter recovery time (≤20 s) is more frequent for central-midfielders, but this information may vary depending on the soccer team or the league competition (Carling et al., 2012). Although the total distance covered by each player has remained relatively constant over the last few years, the demand of physical efforts has increased due to greater high-intensity running and longer sprinting distance covered during matches (Barnes et al., 2014). Consequently, due to both these efforts and the fatigue suffered by the player towards the end of the match, and temporarily after high-intensity periods (Bradley & Noakes 2013), the ability to repeatedly produce maximal sprints with brief recovery periods (RSA) might be a relevant aptitude in soccer players (Rampinini et al., 2007).
Therefore, several researchers have tried to determine the factors of RSA performance in soccer players (Chaouachi et al., 2010; da Silva et al., 2010; Lopez-Segovia et al., 2015). It is suggested that a high muscle mass percentage and low adiposity are likely to be beneficial to physical performance of soccer players (Arnason et al., 2004). However, the relationships between anthropometrics and RSA performance have been little studied (Brocherie et al., 2014; Buchheit & Mendez-Villanueva 2014). Buchheit and MendezVillanueva (2014) showed that changes in the sum of 7 skinfolds were negatively related to the changes in the mean time of the RSA test (RSAmean), and did not correlate with changes in the fastest sprint times (RSAbest). These results could indicate that the negative effect of adiposity on RSA performance might be increased through sprint repetitions. However, to our knowledge, the relationships between the different anthropometric variables and RSA performance through sprint repetitions have not been investigated yet.
The relationship between VO2max and RSA performance has been widely investigated (Aziz et al., 2000; Castagna et al., 2007; Dupont et al., 2005, 2010). However, a previous study (da Silva et al., 2010) reported that RSA was more strongly correlated with the velocity at which VO2max was attained rather than the commonly measured VO2max. Low-moderate relationships (r = -0.05 to -0.71) between RSAmean and more functional endurance tests have been observed (da Silva et al., 2010; Dupont et al., 2005). The number and length of the sprints, the recovery time between sprints as well as the methodology used to determine maximal aerobic capacity (field vs. laboratory tests) or the type of the endurance test performed (continuous vs. intermittent) might influence the magnitude of these relationships (Aziz et al., 2007; Balsom et al., 1992). To our knowledge, no previous study has analyzed the influence of a continuous vs. intermittent endurance test on RSA performance. Besides, the low-moderate relationships observed between soccer player´s endurance capacity and RSA performance suggest that factors others than aerobic fitness such as anaerobic performance might explain RSA performance in soccer players (Aziz et al., 2007; Castagna et al., 2007). In this regard, previous studies have underlined significant relationships between RSA and vertical jump performance (r = .35 to .81) (Dawson et al., 1993; Stojanovic et al., 2012; te Wierike et al., 2014; Tonnessen et al., 2011). Furthermore, the maximal sprinting speed has shown a great influence on RSAbest(Lopez-Segovia et al., 2015) and RSAmean (Chaouachi et al., 2010; Dardouri et al., 2014; Dawson et al., 1993) suggesting that speed is the main predictor of overall repeated-sprint performance (Buchheit and Mendez-Villanueva, 2014). On the other hand, although the magnitude of force generated during dynamic muscle contractions is related to sprint performance (Comfort et al., 2014; Lopez-Segovia et al., 2014; Wisloff et al., 2004), the relationship between muscle strength and RSA performance has received little attention (Lopez-Segovia et al., 2014; Lopez-Segovia et al., 2015). To our knowledge, only one study (Lopez-Segovia et al., 2015) showed a significant relationship (p < .05) between muscle strength and RSAmean (r = -.52), RSAbest (r = -.76), and the mean of the first three sprint times (r = -.64); however, this relationship tended to disappear as the number of sprints performed increased. Thus, although many investigations have focused on the determinant factors of RSA performance in soccer players (Chaouachi et al., 2010; da Silva et al., 2010; Lopez-Segovia et al., 2015), and neuromuscular performance has been shown to be decisive for RSA (Mendez-Villanueva et al., 2008), little is known about the evolution of the determinant factors when increasing the number of sprints performed in an RSA test. Consequently, the aim of the present study was to analyze the relationships between RSA and lower body strength, maximal sprinting speed, jumping ability, endurance capacity (intermittent and continuous), and anthropometric measures in professional soccer players. We hypothesized that a soccer player’s lower limb strength would explain much of the performance in the first sprints, whereas aerobic capacity and adiposity would have more influence on the performance when the number of sprints increased.
Material and Methods
Participants
Twenty-one highly trained soccer players (age 24.3 ± 4.6 yr, body height 1.74 ± 0.07 m, body mass (BM) 73.1 ± 8.1 kg, fat mass (FM) 11.4 ± 1.5%, muscle mass (MM) 48.7 ± 1.8%) from a professional Moroccan soccer club volunteered to participate in this study. Typical weekly training for this team included: specific soccer training (5 sessions), physical conditioning (3-4 sessions, of which 2 consisted of strength training) and competitive play (1 game per week), totaling approximately 16 h per week on average. All players had completed strength-training programs in the past and were familiarized with the testing exercises. Once informed about the purpose, testing procedures and potential risks of the investigation, all subjects gave their voluntary written consent to participate. The present investigation was approved by the Research Ethics Committee of the Pablo de Olavide University, and conducted in accordance with the Declaration of Helsinki.
Procedures
A cross-sectional experimental design was used to analyze the relationships between RSA performance and fitness indicators such as sprint and jump ability, leg strength, endurance and anthropometric variables. All the tests were completed at the end of the preseason (September) and were carried out on three consecutive weeks at least 48 hours after the most recent game. The tests were conducted at the same time of the day. During the first testing session, a battery of tests was performed in the following order: 1) 30 m running sprints; 2) countermovement vertical jumps (CMJs); 3) an RSA test. During the second testing session, the players completed a progressive isoinertial loading test in a full squat. The third session included the Yo-Yo Intermittent Recovery Test Level 1 (YYIRT-1), and the fourth one consisted of a 20 m shuttle run test (20mSRT). Anthropometric assessment was made during the familiarization sessions.
Measures
Anthropometric Dimensions
Height measurements were taken during maximal inspiration with precision of 0.5 cm using a stadiometer (Quirumed®, Valencia, Spain); BM was determined using a calibrated digital scale (Quirumed®, Valencia, Spain) with the subjects wearing only underwear; and skinfold thickness was measured at 6 sites (triceps, subscapular, supraespinale, abdominal, anterior thigh, and mid leg) using Holtain skinfold calipers (Holtain T/W Skinfold Caliper®, Dyfed, UK). All measurements were made in duplicate by the same trained operator. When the difference between the two measured values was less than 5%, the average value of both measurements was used for further analysis. When the difference exceeded 5%, we performed a third measure and the average value of the three measurements was used. The bone diameters (biepicondyle of the humerus and the bicondyle of the femur) were measured with a pachymeter (Holtain Bicondylar Caliper®, Dyfed, UK), and for muscle perimeters a measuring-tape (Harpenden Anthropometric Tape®, Holtain, Dyfed, UK) was used. The body fat percentage was estimated using the Yuhasz equation (1974) [Percent Fat (%) = (tricipital + subscapular + suprailiac + abdominal + front thigh + medial calf skinfolds x 0.1051) + 2.585]. Fat mass (FM) was calculated as BM · Percent Fat · 100-1, and lean body mass (LBM) was determined as BM – FM (Heyward and Wagner, 2004). Muscular Mass (MM) was estimated using the Matiegka (1921) equation[MM (kg) = BM – (FM + Bone Mass + Residual Mass)]. Percent MM was calculated as MM · BM-1 · 100.
Sprint test
The subjects had to sprint twice for 30 m indoors, with 3 minutes rest in-between. The starting position was standardized, with the starting line placed 1 m behind the first time gate. The photocell gates (Racetime2®, Microgate, Bolzano, Italy) were placed at the start and at 30 m. A standardized warm-up protocol was conducted before assessment. The subjects were required to perform the tests as fast as possible. The best performance was recorded for further analysis.
Jump test
Five maximal CMJs, with one-minute rest in-between were performed. CMJ height was registered, the highest and lowest values were discarded, and the resulting average value was kept for analysis. Jump height was determined with an infrared timing system (Optojump®, Microgate, Bolzano, Italy).
Repeated sprint ability test (RSA)
The RSA test consisted of six 40 m (20 + 20 m with 1800 turns) shuttle sprints separated by 20 s of passive recovery. An adaptation of the test previously validated by Impellizzeri et al. (2008) was used, consisting in rounding a cone instead of touching a line with the foot. The players started from 1 m behind the starting line, sprinted for 20 m, rounded a cone and came back to the starting line as fast as possible. During the 20 s of passive recovery the subjects remained standing and they were alerted 5 seconds before the following sprint. The performance variables used were: the best maximal repeated shuttle sprint time (20 + 20 m) (as the players’ reference performance) (RSAbest), the single time of each of the six sprints (RSA1, RSA2, RSA3, RSA4, RSA5 and RSA6), the average time obtained from the six repeated sprints (RSAmean), and the percentage in a sprint decrease (%Dec) calculated according to the following formula: (RSAmean/RSAbest x100) – 100 (Rampinini et al., 2007). Sprint times were recorded using photocell gates (Microgate, Bolzano, Italy).
Yo-Yo Intermittent Recovery Test Level 1
This test consisted of 2 x 20 m shuttle runs at increasing speeds, with 10 s of active recovery in-between. The test was carried out indoors and the subjects were guided by a beep signal. The test ended when the subjects were no longer able to reach the finish line at the beep signal on two consecutive occasions. The total distance covered (m) was recorded as the final result of the test (Krustrup et al., 2003).
20 meter shuttle run test
This test required participants to run back and forth on a 20 m course, touching the 20 m line at the same time as the pre-recorded audio signals were emitted. The initial speed was 8.5 km·h-1 and increased by 0.5 km·h-1 each minute. The test finished when the participant could no longer follow the pace. The total distance covered (m) was recorded as the final result of the test (Leger et al., 1988). The test took place on an indoor court.
Isoinertial progressive loading test
A Smith machine (Multipower Fitness Line®, Peroga, Murcia, Spain) was used for the isoinertial test. The players performed a full squat from an upright position, descending at a controlled velocity and getting up at maximal velocity. The initial load was set at 20 kg and was progressively increased by 10 kg up to the lifting velocity <1 m·s-1 (Gonzalez-Badillo et al., 2015; Lopez-Segovia et al., 2015). The subjects performed 3 repetitions with each load, and the best repetition (fastest mean propulsive velocity) was considered for subsequent analysis (Sanchez-Medina et al., 2010). The inter-set recovery time was 4 min. The load that elicited a ~1.00 m·s-1 velocity relative to BM (V1-load) was used to assess strength performance. This load was chosen as it is considered a sufficiently high velocity that represents medium loads (Conceicao et al., 2015). Thus, it might represent the behavior of the force-velocity relationship. Furthermore, this load had been used as a reference to schedule a resistance training program (Alvarez-San Emeterio et al., 2011) and to analyze the relationships between lower limb strength and RSA performance (Lopez-Segovia et al., 2014; Lopez-Segovia et al., 2015). The warm-up consisted of 5 min of joint mobilization exercises, followed by two sets of six repetitions (3 min rest) with 20 kg. A dynamic measurement system (T-Force System®, Ergotech, Murcia, Spain) was used to register velocity.
Statistical Analysis
Data are expressed as mean ± standard deviation (SD). The distribution of each variable was verified by the Shapiro-Wilk normality test. Test-retest reliability was measured by the coefficient of variation (CV) and intraclass correlation coefficients (ICC, 95%CI), calculated with the one-way random effects model. Linear regression analysis with Pearson’s coefficients (r) and 90% confidence intervals (90%CI) was used to calculate the relationships between the performance variables analyzed. A comparison was made between the best (n = 11) and the worst (n = 10) players in RSAbest, %Dec, T30, and YYIRT-1 to analyze the influence of these variables on RSA performance. For this analysis, the median value of each variable was used for dividing the group into best and worst players. A factorial ANOVA with repeated measures with Bonferroni’s post-hoc comparisons was used to compare the differences between groups in RSAmean and in each single repeated-sprint. The level of statistical significance was set at p ≤ 0.05. In addition to null hypothesis testing, data were assessed for clinical significance using an approach based on the magnitude of change (Hopkins et al., 2009). The standardized differences between groups (ES, 90% confidence limit) were calculated using pooled SD. For between-groups comparison, the probabilities of greater (i.e., greater than the smallest worthwhile change [0.2 x between subjects SD, based on the Cohen d principle]), similar or smaller differences between the groups were calculated. Quantitative chances of better or poorer effect were assessed qualitatively as follows: <1%, almost certainly not; 1 to 5%, very unlikely; 5 to 25%, unlikely; 25 to 75%, possibly; 75 to 95%, likely; 95 to 99%, very likely; and <99%, almost certainly (Hopkins et al., 2009). If the chances of having better and poorer performances were both >5%, the true difference was assessed as unclear (Hopkins et al., 2009). Inferential statistics based on interpretation of magnitude of effects were calculated using a purpose-built spreadsheet for the analysis of controlled trials (Hopkins 2006). The rest of statistical analyses were performed using SPSS software version 18.0 (SPSS Inc.®, Chicago, IL).
Results
The mean values and SD of the different variables assessed are shown in Table 1. Test-retest reliability for both T30and CMJ measured by the CV was 0.8% and 3.1%, respectively; while the ICC (95%CI) was 0.98 [0.95-0.99] and 0.98 [0.96-0.99], respectively.
Table 1.
Values in selected neuromuscular performance variables
| RSAmean (s) | RSAbest (s) | %Dec (%) | T30 (s) | V1-load | CMJ (cm) |
|---|---|---|---|---|---|
| 7.60 ± 0.17 | 7.36 ± 0.18 | 3.3 ± 1.5 | 4.27 ± 0.15 | 0.81 ± 0.14 | 33.6 ± 3.6 |
| RSA1 (s) | RSA2 (s) | RSA3 (s) | RSA4 (s) | RSA5 (s) | RSA6 (s) |
| 7.39 ± 0.18 | 7.44 ± 0.20 | 7.56 ± 0.20 | 7.65 ± 0.19 | 7.75 ± 0.23 | 7.80 ± 0.20 |
| YYIRT-1 (m) | 20mSRT (m) | ||||
| 1558 ± 362 | 1981 ± 309 | ||||
Data are mean ± SD, n = 21 RSAmean: mean sprint time of the six sprints; RSAbest: the best time of the six sprints %Dec: percent sprint decrement for the six sprints T30m: 30 m sprint time; V1-load: the load which participants were able to elicit ~1.00 m·s-1 velocity relative to body mass; CMJ: countermovement jump height;RSA1: first sprint time of the six repeated sprints; RSA2: second sprint time of the six repeated sprints; RSA3: third sprint time of the six repeated sprints; RSA4: fourth sprint time of the six repeated sprints; RSA5: fifth sprint time of the six repeated sprints; RSA6: sixth sprint time of the six repeated sprints YYIRT-1: Yo-Yo Intermittent Recovery Test Level 1; 20mSRT: 20 meter Shuttle Run Test
RSAmeancorrelated significantly with RSAbest(r = .82 [.70, .94], p < .001) and with all single sprints (r = .71 to .92, p < .001) of the RSA test. RSAbestalso correlated significantly with all single sprints (p < 0.01 - 0.05), although it showed a downward trend as the number of sprints performed increased (from r = .87 [.78; .96] for RSA1 to r = .59 [.35; .83] for RSA6). No significant relationship was observed between the %Dec and any of RSA performance variables analyzed (Table 2).
Table 2.
Relationships (90% confidence intervals) between different variables of repeat sprint ability
| RSAbest | %Dec | RSA1 | RSA2 | RSA3 | RSA4 | RSA5 | RSA6 | |
|---|---|---|---|---|---|---|---|---|
| RSAmean | .82[.70;.94]*** | .21[-.14;.56] | .71[.53;.89]*** | .90[.83;.97]*** | .92[.86;.98]*** | .92[.86;.98]*** | .91[.85;.97]*** | .86[.76;.96]*** |
| RSAbest | -.38[-.69;-.07] | .87[.78;.96]*** | .87[.78;.96]*** | .67[.47;.87]** | .69[.50;.88]** | .62[.39;.85]** | .59[.35;.83]** | |
| %Dec | -.36[-.68;-.04] | -.02[-.39;.35] | .34[.01;.67] | .31[-.02;.64] | .40[.09;.71] | .38[.07;.69] |
RSAmean: mean sprint time of the six sprints; RSAbest: the best time of the six sprints; %Dec: the percentage in a sprint decrement for the six sprints RSA1: first sprint time of the six repeated sprints; RSA2: second sprint time of the six repeated sprints; RSA3: third sprint time of the six repeated sprints; RSA4: fourth sprint time of the six repeated sprints; RSA5: fifth sprint time of the six repeated sprints; RSA6: sixth sprint time of the six repeated sprints
*Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.01.
RSAmean showed significant relationships (p < .05) with BM (r = .44 [.14, .74]) and FM (r = .59 [.35, .83]). FM and BM showed significant relationships with almost all repeated sprints. These relationships were higher as the number of sprints performed increased (Table 3). However, MM did not have a significant relationship with any of the RSA performance variables analyzed. A significant relationship was observed between RSAmean and the CMJ (r = -.45 [-.74; -.16], p < .05), whereas V1-load did not show a significant relationship with any of the different measures of RSA performance. The T30 showed significant correlations with all RSA variables except for the %Dec. In addition, the YYIRT-1 presented a significant relationship with RSAmean (r = -.62 [-.85; -.39], p < .05) and with almost all single sprints, with an upward trend as the number of sprints increased (from r = -.11 for RSA1 to r = -.70 for RSA6). The 20mSRT showed minimal or no relationships with RSA performance variables (Table 3).
Table 3.
Relationships (90% confidence intervals) between different RSA variables and endurance, acceleration, jump ability strength and anthropometry measures
| BM | FM | MM | V1-load | CMJ | T30 | YYIRT-1 | 20mSRT | |
|---|---|---|---|---|---|---|---|---|
| RSAmean | .44[.14;.74]* | .59[.35;.83]** | -.40[-.71; .09] | -.24[-.59;.11] | -.45[-.74; .16]* | .66[.45;.87]** | -.62[-.85; .39]* | -.39[-.70; .08] |
| RSAbest | .24[-.11;.59] | .30[-.03;.63] | -.35[-.67; .03] | -.30[-.63;.03] | -.36[-.68; .04] | .55[.59;.81]* | -.40[-.71; .09] | -.03[-.40;.34] |
| %Dec | .30[-.03;.63] | .42[.12;.72] | -.05[-.42;.32] | -.12[-.48;.24] | -.11[-.47;.25] | .13[-.23;.49] | -.39[-.70; .08] | -.56[-.81; .31]* |
| RSA1 | .13[-.23;.49] | .24[-.11;.59] | -.43[-.73; .13] | -.21[-.56;.14] | -.37[-.69; .05] | .48[.20;.76]* | -.11[-.47; .25] | .20[-.15;.55] |
| RSA2 | .37[.05;.69] | .54[.28;.80]* | -.32[-.65;.01] | -.34[-.67; .01] | -.55[-.81; .29]** | .62[.39;.85]** | -.54[-.80; .28]* | -.42[-.72; .12] |
| RSA3 | .30[-.03;.63] | .45[.16;.74]* | -.29[-.63;.05] | -.03[-.40;.34] | -.28[-.62;.06] | .51[.24;.78]* | -.53[-.79; .27]* | -.42[-.72; .12] |
| RSA4 | .45[.16;.74]* | .55[.29;.81]** | -.27[-.61;.07] | -.16[-.52;.20] | -.38[-.69; .07] | .51[.24;.78]* | -.60[-.84; .36]** | -.55[-.81; .29]** |
| RSA5 | .44[.14;.74]* | .63[.41;.85]** | -.38[-.69; .07] | -.32[-.65;.01] | -.47[-.76; .18]* | .61[.38;.84]** | -.70[-.89; .51]***** | -.42[-.72; .12] |
| RSA6 | .54[.28;.80]** | .59[.35;.83]** | -.39[-.70; .08] | -.11[-.47;.25] | -.26[-.60;.08] | .66[.45;.87]** | -.70[-.89; .51]***** | -.44[-.74; .14]* |
RSAmean: mean sprint time of the six sprints; RSAbest: the best time of the six sprints; %Dec: the percentage in a sprint decrement for the six sprints RSA1: first sprint time of the six repeated sprints; RSA2: second sprint time of the six repeated sprints; RSA3: third sprint time of the six repeated sprints; RSA4: fourth sprint time of the six repeated sprints; RSA5: fifth sprint time of the six repeated sprints; RSA6: sixth sprint time of the six repeated sprints BM: Body mass; FM: Percentage of fat mass; MM: Percentage of muscle mass V1-load: the load which participants were able to elicit ~1.00 m·s-1 velocity relative to body mass; CMJ: countermovement jump height; T30m: 30 m sprint time YYIRT-1: Yo-Yo Intermittent Recovery Test Level 1; 20mSRT: 20 meter Shuttle Run Test
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.05.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.001, n = 21
Denotes significance at p ≤ 0.01.
Denotes significance at p ≤ 0.05.
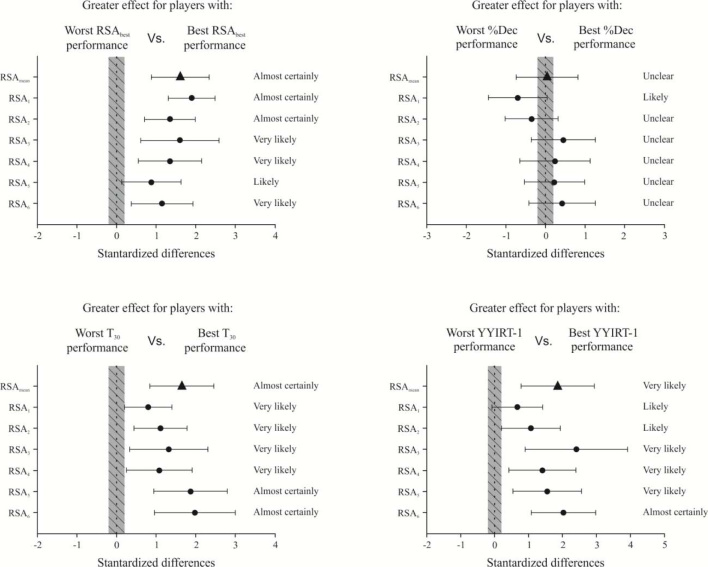
The fastest players in RSAbest (7.22 ± 0.10 s) were significantly (p < .001 - .05) faster in RSAmean and in all single sprints than the slowest players (7.51 ± 0.09 s, Figure 1A). The differences in RSAmean and all single sprints were unclear in almost all RSA performance variables between best (2.2 ± 0.7%) and worst (4.6 ± 1.0%) players in the %Dec (Figure 1B). The fastest players in the T30 (4.16 ± 0.08 s) were significantly (p < .05 – .01) faster in RSAmean and in all single sprints than the slowest players in the T30 (4.40 ± 0.07 s, Figure 1C). The players with greater YYIRT-1 performance (1835 ± 235 m) showed greater (p < .05 - .01) performance in both RSAmean and almost all single sprints than players with lower YYIRT-1 performance (1264 ± 174 m, Figure 1D).
Figure 1.
Differences (90% confidence intervals) in RSA performance between the best (n = 11) and the worst (n = 10) players in the best sprint time in the RSA test (RSAbest), percent sprint decrement in the RSA test (%Dec), 30 m sprint time (T30), and Yo-Yo Intermittent Recovery Test Level 1 (YYIRT-1). RSA performance was determined by the mean sprint time of the six sprints (RSAmean) and the single time of each of the six sprints (RSA1, RSA2, RSA3, RSA4, RSA5, and RSA6). Shaded areas represent trivial differences.
Discussion
The main findings of the present study were that 1) RSA performance, determined by RSAmean and each single sprint, was greatly related to RSAbest, and this association decreased as the number of sprints performed increased (from r = .87 for RSA1 to r = .59 for RSA6); 2) BM and adiposity seemed to negatively influence RSAmean, enhancing this association when increasing the number of repeated sprints; 3) strength performance in a full squat was not a predictor of RSA performance while jumping and maximal sprinting speed seemed to positively influence RSA performance; and 4) the intermittent endurance test (YYIRT-1) showed a greater correlation with RSA performance than the continuous endurance test (20mSRT). According to the results of this study, a better performance in both straight or shuttle sprints (T30 and RSAbest) and intermittent endurance test (YYIRT-1), as well as low levels of adiposity might contribute to RSA performance.
The results of the present study suggest that RSAmean has common factors with the CMJ (r = -.45) and maximal sprint speed (r = .66), whereas muscle strength assessed by full squat exercise, does not show any correlation with RSA performance. In line with our results, two studies have observed significant relationships (r = .63 to .75, p < 0.05) between maximal sprint speed and RSAmean (Dardouri et al., 2014; Ingebrigtsen et al., 2014), whereas a vertical jump has shown a lower relationship (r = -.35 to -.74) with RSAmean (Stojanovic et al., 2012; te Wierike et al., 2014); however, these studies used basketball players, which might hamper the comparisons between the obtained results. Maximal sprint speed was expected to have a greater effect on RSA performance than jumping height, as both tests require the same ability (running sprint). The impact of maximal sprinting speed on RSAmeanis likely to be dependent on the RSA protocol (Buchheit and Mendez-Villanueva, 2014); nonetheless, our results suggest that both coaches and conditioning professionals should try to attain high levels of acceleration and maximal sprint speed in the development of RSA among soccer players.
The relationship between endurance capacity and RSA performance has been previously widely studied (Aziz et al., 2000; Castagna et al., 2007; Dupont et al., 2005, 2010); however, to our knowledge, no previous studies have focused on the association between intermittent vs. continuous endurance tests and RSA performance. Regarding the endurance tests performed, the YYIRT-1 showed a significant relationship with RSAmean, whereas the 20mSRT did not show any significant relationship with RSAmean (Table 3). The greater relationships observed between YYIRT-1 and RSA performance would suggest that the intermittent endurance test might be a more specific test, and has more influence on the ability to repeat sprints. Recently, Gibson et al. (2013) also showed similar relationships between endurance performance (YoYo test) and RSAmean (r = -.71). On the other hand, YYIRT-1 and RSA performance tended to show enhanced relationships as the number of sprints increased (from r = -.11 for RSA1to r = -.70 for RSA6). Lopez-Segovia et al. (2015) observed that performance in the first sprints was mainly explained by soccer player’s strength and sprint capacity; in contrast, when the number of sprints increased, the performance was more related to endurance. Consequently, our results suggest that the ability to perform endurance intermittent efforts is a key factor to attain greater RSA performance, increasing with sprint repetitions.
With regard to anthropometry, MM showed a non-significant moderate relationship with RSAmean(r = -.40), whereas FM showed a potential negative influence on RSAmean (r = .44, p < .05) and almost all single sprints (Table 3). This finding means that subjects with higher FM needed longer time to complete the RSA test, and vice versa. In this line, Buchheit and MendezVillanueva (2014) showed that changes in RSAmean were correlated with changes in the sum of 7 skinfolds, but this relationship was not observed for RSAbest, which could mean that the negative effect of adiposity on RSA performance might increase along with sprint repetitions. Likewise, Brocherie et al. (2014) observed that the subjects with a higher muscle index and muscular cross-sectional areas exhibited greater RSAmean performance (r = .53); inversely, soccer players with a lower adipose index had greater performance during the RSA test (r = -.33). Therefore, in support of the previous authors, we suggest that the higher FM would be expected to place an additional mechanical load; additionally, a new finding is that this association increases with sprint repetitions (from r = .24 for RSA1 to r = .59 for RSA6).
The results of the current study suggest that RSAmean is related to RSAbest (r = .82) and all single repeated sprints (r = .71 to .92; Table 2). This finding is in line with previous studies (Chaouachi et al., 2010; Dupont et al., 2010; Gibson et al., 2013), whereas other authors did not observe any significant correlation between these two variables (Dupont et al., 2005; Lopez-Segovia et al., 2015). In these two studies, significant relationships between the %Dec and RSAmean (r = .55 to .71) were observed (Dupont et al., 2005; Lopez-Segovia et al., 2015). However, in the present study, the %Dec did not show a significant relationship with RSAmean (r = .21). These differences might be explained by a greater number of sprints and active recovery performed in those studies (Dupont et al., 2005; Lopez-Segovia et al., 2015). This fact might have induced a greater sprint decrease in those studies (Dupont et al., 2005; Lopez-Segovia et al., 2015) than the %Dec reported in the present study (5.8 - 8.6% vs. 3.3%, respectively); and, therefore, a lower relationship between RSAbest and RSAmean. On the other hand, this study shows significant correlations between RSAbest and all single repeated sprints, and that this correlation decreases as the number of sprints performed increases (from r = .87 for RSA1 to r = .59 for RSA6). These findings are in accordance with those of Lopez-Segovia et al. (2015) who reported an almost perfect correlation (r = .93) between RSAbest and the mean of the first three sprints, although this relationship disappeared for the subsequent sprints. These results also show that the performance in the first sprints is strongly associated with the maximal sprint capacity. By contrast, when the number of repeated sprints increases, the performance might be explained by other factors such as intermittent endurance capacity. This was shown in the present study by the enhancement in the magnitude of the relationships between the YYIRT-1 and sprint time as the number of sprints increased (from r = -.11 for RSA1 to r = -.70 for RSA6).
Typically, three variables have been used to describe the performance in RSA (RSAmean, RSAbest, and %Dec). Although the %Dec has been considered the most valid and reliable method to quantify fatigue in tests of RSA, it has shown inconsistent test-retest reliability (Glaister et al., 2008). Some authors (Bishop et al., 2011) suggest that the RSA performance is better described by the RSAmean, with or without a low %Dec. Our findings reinforce this hypothesis, since when the subjects were divided according to their performance in different tests, the players that attained greater performance in a straight or shuttle sprint (RSAbest and T30) and in intermittent endurance capacity (YYIRT-1) achieved greater RSA performance (Figure 1). However, the players who had a less %Dec (2.2 ± 0.7%) did not achieve greater performance neither in RSAmean nor in any of the single sprints compared to players who performed a greater %Dec (4.6 ± 1.0%) (Figure 1). Furthermore, players who experienced a greater %Dec showed likely (87/10/3%) greater performance in RSA1 than those who got a less %Dec. Thus, the %Dec should be interpreted cautiously, since a smaller %Dec may be associated with smaller amounts of work performed during the initial sprints (Hamilton et al., 1991). Consequently, RSAmean and single repeated-sprint times should be used in order to determine RSA performance.
As limitation, we could not perform a direct assessment of maximal oxygen uptake, as well as the fat mass and muscle mass using technology such as Dual Energy X-ray Absorptiometry (DEXA). Furthermore, correlations do not necessarily imply cause and effect. Therefore, the interpretation of the possible mechanisms that result in performance enhancement should be cautious.
In conclusion, the performance in the first sprints during an RSA test is mainly explained by the maximal sprint capacity. However, when the number of repeated sprints increases the performance should be explained by other factors such as intermittent endurance capacity and adiposity levels. The results of the present study can contribute to raising awareness about determinant factors of RSA. These findings have important practical implications for coaches and conditioning professionals, who should aim at high levels of maximal sprint speed in the development of RSA in soccer players, since maximal sprint speed seems to explain the performance in the first repeated sprints. On the other hand, high levels of intermittent endurance capacity and low adiposity levels have a significant impact on RSA performance when the number of sprints increases.
Authors submitted their contribution to the article to the editorial board.
References
- Alvarez-San Emeterio C, Antunano NP, Lopez-Sobaler AM, Gonzalez-Badillo JJ. Effect of strength training and the practice of Alpine skiing on bone mass density, growth, body composition, and the strength and power of the legs of adolescent skiers. J Strength Cond Res. 2011;25:2879–2890. doi: 10.1519/JSC.0b013e31820c8687. [DOI] [PubMed] [Google Scholar]
- Arnason A, Sigurdsson SB, Gudmundsson A, Holme I, Engebretsen L, Bahr R. Physical fitness, injuries, and team performance in soccer. Med Sci Sports Exerc. 2004;36:278–285. doi: 10.1249/01.MSS.0000113478.92945.CA. [DOI] [PubMed] [Google Scholar]
- Aziz AR, Chia M, Teh KC. The relationship between maximal oxygen uptake and repeated sprint performance indices in field hockey and soccer players. J Sports Med Phys Fitness. 2000;40:195–200. [PubMed] [Google Scholar]
- Aziz AR, Mukherjee S, Chia MY, Teh KC. Relationship between measured maximal oxygen uptake and aerobic endurance performance with running repeated sprint ability in young elite soccer players. J Sports Med Phys Fitness. 2007;47:401–407. [PubMed] [Google Scholar]
- Balsom PD, Seger JY, Sjodin B, Ekblom B. Maximal-intensity intermittent exercise: effect of recovery duration. Int J Sports Med. 1992;13:528–533. doi: 10.1055/s-2007-1021311. [DOI] [PubMed] [Google Scholar]
- Barnes C, Archer DT, Hogg B, Bush M, Bradley PS. The evolution of physical and technical performance parameters in the english premier league. Int J Sports Med. 2014;35:1095–1100. doi: 10.1055/s-0034-1375695. [DOI] [PubMed] [Google Scholar]
- Bishop D, Girard O, Mendez-Villanueva A. Repeated-sprint ability - part II: recommendations for training. Sports Med. 2011;41:741–756. doi: 10.2165/11590560-000000000-00000. [DOI] [PubMed] [Google Scholar]
- Bradley PS, Noakes TD. Match running performance fluctuations in elite soccer: indicative of fatigue, pacing or situational influences? J Sports Sci. 2013;31:1627–1638. doi: 10.1080/02640414.2013.796062. [DOI] [PubMed] [Google Scholar]
- Brocherie F, Girard O, Forchino F, Al Haddad H, Dos Santos GA, Millet GP. Relationships between anthropometric measures and athletic performance, with special reference to repeated-sprint ability, in the Qatar national soccer team. J Sports Sci. 2014;32:1243–1254. doi: 10.1080/02640414.2013.862840. [DOI] [PubMed] [Google Scholar]
- Buchheit M, Mendez-Villanueva A. Changes in repeated-sprint performance in relation to change in locomotor profile in highly-trained young soccer players. J Sports Sci. 2014;32:1309–1317. doi: 10.1080/02640414.2014.918272. [DOI] [PubMed] [Google Scholar]
- Carling C, Le Gall F, Dupont G. Analysis of repeated high-intensity running performance in professional soccer. J Sports Sci. 2012;30:325–336. doi: 10.1080/02640414.2011.652655. [DOI] [PubMed] [Google Scholar]
- Comfort P, Stewart A, Bloom L, Clarkson B. Relationships between strength, sprint, and jump performance in well-trained youth soccer players. J Strength Cond Res. 2014;28:173–177. doi: 10.1519/JSC.0b013e318291b8c7. [DOI] [PubMed] [Google Scholar]
- Conceicao F, Fernandes J, Lewis M, Gonzalez-Badillo JJ, Jimenez-Reyes P. Movement velocity as a measure of exercise intensity in three lower limb exercises. J Sports Sci. 2015:1–8. doi: 10.1080/02640414.2015.1090010. [DOI] [PubMed] [Google Scholar]
- Chaouachi A, Manzi V, Wong del P, Chaalali A, Laurencelle L, Chamari K, Castagna C. Intermittent endurance and repeated sprint ability in soccer players. J Strength Cond Res. 2010;24:2663–2669. doi: 10.1519/JSC.0b013e3181e347f4. [DOI] [PubMed] [Google Scholar]
- da Silva JF, Guglielmo LG, Bishop D. Relationship between different measures of aerobic fitness and repeated-sprint ability in elite soccer players. J Strength Cond Res. 2010;24:2115–2121. doi: 10.1519/JSC.0b013e3181e34794. [DOI] [PubMed] [Google Scholar]
- Dardouri W, Selmi MA, Sassi RH, Gharbi Z, Rebhi A, Yahmed MH, Moalla W. Relationship Between Repeated Sprint Performance and both Aerobic and Anaerobic Fitness. J Hum Kinet. 2014;40:139–148. doi: 10.2478/hukin-2014-0016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson B, Fitzsimons M, Ward D. The relationship of repeated sprint ability to aerobic power and performance measures of anaerobic work capacity and power. Aust J Sci Med Sport. 1993;25:88–93. [Google Scholar]
- Dupont G, McCall A, Prieur F, Millet GP, Berthoin S. Faster oxygen uptake kinetics during recovery is related to better repeated sprinting ability. Eur J Appl Physiol. 2010;110:627–634. doi: 10.1007/s00421-010-1494-7. [DOI] [PubMed] [Google Scholar]
- Dupont G, Millet GP, Guinhouya C, Berthoin S. Relationship between oxygen uptake kinetics and performance in repeated running sprints. Eur J Appl Physiol. 2005;95:27–34. doi: 10.1007/s00421-005-1382-8. [DOI] [PubMed] [Google Scholar]
- Gibson N, Currie J, Johnston R, Hill J. Relationship between measures of aerobic fitness, speed and repeated sprint ability in full and part time youth soccer players. J Sports Med Phys Fitness. 2013;53:9–16. [PubMed] [Google Scholar]
- Glaister M, Howatson G, Pattison JR, McInnes G. The reliability and validity of fatigue measures during multiple-sprint work: an issue revisited. J Strength Cond Res. 2008;22:1597–1601. doi: 10.1519/JSC.0b013e318181ab80. [DOI] [PubMed] [Google Scholar]
- González-Badillo JJ, Pareja-Blanco F, Rodríguez-Rosell D, Abad-Herencia JL, del Ojo-López JJ, SánchezMedina L. Effects of velocity-based resistance training on young soccer players of different ages. J Strength Cond Res. 2015;29:1329–1338. doi: 10.1519/JSC.0000000000000764. [DOI] [PubMed] [Google Scholar]
- Hamilton AL, Nevill ME, Brooks S, Williams C. Physiological responses to maximal intermittent exercise: differences between endurance-trained runners and games players. J Sports Sci. 1991;9:371–382. doi: 10.1080/02640419108729897. [DOI] [PubMed] [Google Scholar]
- Heyward VH, Wagner DR. Applied body composition assessment. Champaign, IL: Human Kinetics;; 2004. [Google Scholar]
- Hopkins WG. Spreadsheets for analysis of controlled trials, with adjustment for a subject characteristic. Sportscience. 2006;10:46–50. [Google Scholar]
- Hopkins WG, Marshall SW, Batterham AM, Hanin J. Progressive statistics for studies in sports medicine and exercise science. Med Sci Sports Exerc. 2009;41:3–13. doi: 10.1249/MSS.0b013e31818cb278. [DOI] [PubMed] [Google Scholar]
- Impellizzeri FM, Rampinini E, Castagna C, Bishop D, Ferrari Bravo D, Tibaudi A, Wisloff U. Validity of a repeated-sprint test for football. Int J Sports Med. 2008;29:899–905. doi: 10.1055/s-2008-1038491. [DOI] [PubMed] [Google Scholar]
- Ingebrigtsen J, Brochmann M, Castagna C, Bradley PS, Ade J, Krustrup P, Holtermann A. Relationships between field performance tests in high-level soccer players. J Strength Cond Res. 2014;28:942–949. doi: 10.1519/JSC.0b013e3182a1f861. [DOI] [PubMed] [Google Scholar]
- Krustrup P, Mohr M, Amstrup T, Rysgaard T, Johansen J, Steensberg A, Pedersen PK, Bangsbo J. The yo-yo intermittent recovery test: physiological response, reliability, and validity. Med Sci Sports Exerc. 2003;35:697–705. doi: 10.1249/01.MSS.0000058441.94520.32. [DOI] [PubMed] [Google Scholar]
- Leger LA, Mercier D, Gadoury C, Lambert J. The multistage 20 metre shuttle run test for aerobic fitness. J Sports Sci. 1988;6:93–101. doi: 10.1080/02640418808729800. [DOI] [PubMed] [Google Scholar]
- Lopez-Segovia M, Dellal A, Chamari K, Gonzalez-Badillo JJ. Importance of muscle power variables in repeated and single sprint performance in soccer players. J Hum Kinet. 2014;40:201–211. doi: 10.2478/hukin-2014-0022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Segovia M, Pareja-Blanco F, Jimenez-Reyes P, Gonzalez-Badillo JJ. Determinant factors of repeat sprint sequences in young soccer players. Int J Sports Med. 2015;36:130–136. doi: 10.1055/s-0034-1385880. [DOI] [PubMed] [Google Scholar]
- Matiegka J. The testing of physical efficiency. Am J Phys Anthropol. 1921;4:223–230. [Google Scholar]
- Mendez-Villanueva A, Hamer P, Bishop D. Fatigue in repeated-sprint exercise is related to muscle power factors and reduced neuromuscular activity. Eur J Appl Physiol. 2008;103:411–419. doi: 10.1007/s00421-008-0723-9. [DOI] [PubMed] [Google Scholar]
- Pyne DB, Saunders PU, Montgomery PG, Hewitt AJ, Sheehan K. Relationships between repeated sprint testing, speed, and endurance. J Strength Cond Res. 2008;22:1633–1637. doi: 10.1519/JSC.0b013e318181fe7a. [DOI] [PubMed] [Google Scholar]
- Rampinini E, Bishop D, Marcora SM, Ferrari Bravo D, Sassi R, Impellizzeri FM. Validity of simple field tests as indicators of match-related physical performance in top-level professional soccer players. Int J Sports Med. 2007;28:228–235. doi: 10.1055/s-2006-924340. [DOI] [PubMed] [Google Scholar]
- Sanchez-Medina L, Perez CE, Gonzalez-Badillo JJ. Importance of the propulsive phase in strength assessment. Int J Sports Med. 2010;31:123–129. doi: 10.1055/s-0029-1242815. [DOI] [PubMed] [Google Scholar]
- Stojanovic MD, Ostojic SM, Calleja-Gonzalez J, Milosevic Z, Mikic M. Correlation between explosive strength, aerobic power and repeated sprint ability in elite basketball players. J Sports Med Phys Fitness. 2012;52:375–381. [PubMed] [Google Scholar]
- te Wierike SC, de Jong MC, Tromp EJ, Vuijk PJ, Lemmink KA, Malina RM, Elferink-Gemser MT, Visscher C. Development of repeated sprint ability in talented youth basketball players. J Strength Cond Res. 2014;28:928–934. doi: 10.1097/JSC.0000000000000223. [DOI] [PubMed] [Google Scholar]
- Tonnessen E, Shalfawi SA, Haugen T, Enoksen E. The effect of 40-m repeated sprint training on maximum sprinting speed, repeated sprint speed endurance, vertical jump, and aerobic capacity in young elite male soccer players. J Strength Cond Res. 2011;25:2364–2370. doi: 10.1519/JSC.0b013e3182023a65. [DOI] [PubMed] [Google Scholar]
- Wisloff U, Castagna C, Helgerud J, Jones R, Hoff J. Strong correlation of maximal squat strength with sprint performance and vertical jump height in elite soccer players. Br J Sports Med. 2004;38:285–288. doi: 10.1136/bjsm.2002.002071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuhasz MS. Physical Fitness Manual. London Ontario,University of Western Ontario. 1974 [Google Scholar]