Performance Assessment in Water Polo Using Compositional Data Analysis

Abstract

The aim of the present study was to identify groups of offensive performance indicators which best discriminated between a match score (favourable, balanced or unfavourable) in water polo. The sample comprised 88 regular season games (2011-2014) from the Spanish Professional Water Polo League. The offensive performance indicators were clustered in five groups: Attacks in relation to the different playing situations; Shots in relation to the different playing situations; Attacks outcome; Origin of shots; Technical execution of shots. The variables of each group had a constant sum which equalled 100%. The data were compositional data, therefore the variables were changed by means of the additive log-ratio (alr) transformation. Multivariate discriminant analyses to compare the match scores were calculated using the transformed variables. With regard to the percentage of right classification, the results showed the group that discriminated the most between the match scores was “Attacks outcome” (60.4% for the original sample and 52.2% for cross-validation). The performance indicators that discriminated the most between the match scores in games with penalties were goals (structure coefficient (SC) = .761), counterattack shots (SC = .541) and counterattacks (SC = .481). In matches without penalties, goals were the primary discriminating factor (SC = .576). This approach provides a new tool to compare the importance of the offensive performance groups and their effect on the match score discrimination.

Introduction

Water polo is a sport with a growing worldwide interest, particularly for research purposes, with a noticeable increase in the number of recent publications (Prieto et al., 2013). The available research has tried to identify the performance characteristics of the game for both men´s and women´s competitions (Escalante et al., 2011, 2012; Lupo et al., 2010, 2012). The main aim of the performance analysis is to identify the strengths and weaknesses of the water polo teams in order to improve their performance (Carling et al., 2005, 2009). Notational analysis is a method of registering and analysing the dynamics of a complex situation in a sporting context (Hughes and Franks, 2004), which collects performance indicators. A performance indicator is a selection, or combination, of action variables that aims to define some or all the aspects of a performance. Clearly, to be useful, performance indicators should relate to a successful performance or outcome (Hughes and Bartlett, 2002). The performance characteristics of the water polo players are related to the success of the winning teams in short term competitions (Escalante et al., 2011, 2012, 2013; Lupo et al., 2014) such as the Olympic Games, World Championships and European Championships. In men´s games, eight game-related statistics i.e. shots, extra player shots, 5 m shots and assists (offensive efficiency), blocked shots, goalkeeper-blocked shots, goalkeeper-blocked extra player shots and goalkeeper-blocked 5 m shots (defensive efficiency) were considered (Escalante et al., 2011) to distinguish between winning and losing teams in the final phase of the 2008 Olympic Games held in Beijing. In other studies, the offensive performance indicators i.e. centre goals, power play goals, counterattack goals, assists, offensive fouls, steals, blocked shots and won sprints, as well as defensive indicators i.e. goalkeeper-blocked shots, goalkeeper-blocked inferiority shots and goalkeeper-blocked 5 m shots (Escalante et al., 2013) were used to distinguish between performances in international championships and their relationship with the phases of competition. The losing teams performed more even actions, whereas winning teams performed more counterattacks (Lupo et al., 2012). Power play actions were more frequent in closed games than unbalanced games (Lupo et al., 2012). A margin of victory (balanced with a ≤ 3 goals difference and unbalanced with a > 3 goals difference) has been introduced to minimize the effect of the situational nature inherent in other teams (Lupo et al., 2012), as a measurement of match outcomes in performance analysis. On the other hand, performance in a regular water polo season has been analysed by different authors (García et al., 2015; Lupo et al., 2010; Prieto et al., 2013) by examining the offensive performance indicators that discriminate between match scores. The favourable games had averages that were significantly higher for counterattacks and counterattack shots, goals and shots from zone 5 and 6, whereas unfavourable games had significantly higher averages in even attacks and even shots, no goal shots and shots originated from zone 3 and 4 (García et al., 2015). However, considering the joint influence of all variables in the same group on the match score would be problematic because the sum of the variables is 100%. For example, the group “Attack outcome” includes such variables as “Goals”, “No goal shots”, “Exclusions achieved”, “Penalties achieved”, “Offensive fouls” and “Lost possessions”. Since one and only one of these six “Attack outcomes” can occur, the sum of the parts is 100%. Compositional data are multivariate data in which the components represent some part of a whole. They are usually recorded in a closed form, accruing to a constant (e.g. one if measured in parts per unit or 100 if measured in percentages). Such data are widespread in the geosciences and other disciplines. Compositional data are characterised by particular and important numerical properties that have major consequences for any statistical analysis (Pawlowsky-Glahn and Egozcue, 2006). In chemistry, compositional data are frequently used to reflect elemental concentrations as percentages, as the sum of the concentrations is 100% (Pesenson et al., 2015). Considering that the variables of each group of offensive performance indicators in the present study had a constant sum which equaled 100%, we used appropriated statistical techniques for compositional data. To the best of our knowledge, very few references on compositional data in sport sciences may be found (Liu, 2004; Li and Liu, 2004; Shimizu et al., 2014). The aim of the present study was to identify the groups of offensive performance indicators that discriminated between match scores (favourable, balanced or unfavourable), taking into account the nature of compositional data during a regular season in the Spanish Water Polo League. These performance indicators can be of great interest for coaches and players due to their usefulness for training plans and the direction of competitions.

Material and Methods

Participants

A notational analysis was performed on 88 men´s water polo matches (2 samples per match, in total 176 samples) played by 10 teams from the first Spanish water polo division during 3 seasons (2011-2014). This sample represents 22.2% of all the matches played in this water polo division. The results of 88 matches were: 41 favourable matches, 94 balanced matches and 41 unfavourable matches.

Measures

The independent variables were the offensive performance indicators as showed in Table 1. They were selected in agreement with elite managers and following a revised bibliography. These indicators had been used before by other researchers (Escalante et al., 2012; Hraste et al., 2010; Lupo et al., 2011, 2014). Moreover, they were clustered in five groups: “Attack Situation”, “Shot Situation”, “Outcome”, “Zone” and “Flakes” (Table 1). The dependent variable in this study was the match score (unfavourable, balanced and favourable). In relation to the match score, we considered a balanced score (≤ 3 goals difference), and an unfavourable or favourable score (> 3 goals difference).

Table 1.

List of performance indicators clustered in five groups

Groups	Performance indicator	Definition
	AT	Total attacks
Attacks in relation to the	PATI (ATI)	Percentage of even attacks with respect to total attacks (count of even attacks)
different playing situations (“Attack	PATS (ATS)	Percentage of power play attacks with respect to total attacks (count)
Situation”)	PATCO (ATCO)	Percentage of counterattacks with respect to total attacks (count)
	PATPE (ATPE)	Percentage of penalty attacks with respect to total attacks (count)
Shots in relation to the	L	Total shots
different playing	PLI (LI)	Percentage of even shots with respect to total shots (count)
situations	PLSU (LSU) PLCO (LCO)	Percentage of power play shots with respect to total shots (count) Percentage of counterattack shots with respect to total shots (count)
(“Shot Situation”)	PLPE (LPE)	Percentage of penalty shots with respect to total shots (count)
	PG (G)	Percentage of goals with respect to total attacks (count)
	PLS (LS)	Percentage of no goal shots with respect to total attacks (count)
Attacks outcome	PEXP (EXP)	Percentage of exclusions achieved with respect to total attacks (count)
(“Outcome”)	PPEN (PEN)	Percentage of penalties achieved with respect to total attacks (count)
	PFO (FO)	Percentage of offensive fouls with respect to total attacks (count)
	PPERD (PERD)	Percentage of lost possessions with respect to total attacks (count)
	PL1 (L1)	Percentage of shots originated from zone 1 with respect to total shots (count)
	PL2 (L2)	Percentage of shots originated from zone 2 with respect to total shots (count)
Origin of shots (see Figure	PL3 (L3)	Percentage of shots originated from zone 3 with respect to total shots (count)
1) (“Zone”)	PL4 (L4)	Percentage of shots originated from zone 4 with respect to total shots (count)
	PL5 (L5)	Percentage of shots originated from zone 5 with respect to total shots (count)
	PL6 (L6)	Percentage of shots originated from zone 6 with respect to total shots (count)
	PLD (LD)	Percentage of drive shots with respect to total shots (count)
Technical execution of	PL1F (L1F)	Percentage shots after 1 flake with respect to total shots (count)
shots (“Flakes”)	PL2F (L2F)	Percentage of shots after 2 flakes with respect to total shots (count)
	PLM2F (LM2F)	Percentage of shots more than 2 flakes with respect to total shots (count)

Procedures

The matches were recorded by a video camera positioned at the side of the pool, at the level of the midfield line. A match analysis system (LongMatch, System version 0.20.8, Barcelona, Spain) was used for the notational analysis.

The inspection and its related search were made by the same researcher to avoid bias. The quality of the data was evaluated using the Kappa Cohen index. We randomly selected three matches which were observed with a lapse of time; the Kappa index was 0.97.

Statistical analysis

Considering that the variables of each group (Table 1) had a constant sum which was equal to 100%, the data were compositional. Based on previous studies with compositional data (Aitchison, 1986), the variables of each composition were changed using log-quotient transformation between the parts (specifically, additive log-ratio (alr) transformation). For example, in the group “Attack Situation”, the variables PATI, PATS, PATCO and PATPE were transformed into: log(PATS/PATI), log(PATCO/PATI) and log(PATPE/PATI). PATI was chosen as the common denominator due to its highest variance and mean. Discriminant analyses were applied to the transformed variables in order to identify the offensive performance indicators which discriminated between the favourable, balanced and unfavourable scores; thus, two discriminant functions were obtained. Indicators with structure coefficients (SC1, SC2) values ≥0.30 were considered relevant when their SC belonged to a significant discriminant function. The eigenvalue, the canonical correlation index, the Wilk´s lambda and the percentage of right classification were used to measure discriminant power. The homogeneity assumption was evaluated with the Box´s M test. To deal with the problem of essential zeros in the variable PATPE, two analyses were conducted: for matches with penalties and for matches without penalties. For groups “Shot Situation” and “Outcome”, we followed the same methods to transform and to deal with the zeros. The groups “Zone” and “Flakes” needed only one analysis with all the matches due to the non-essential zeros. Furthermore, a final discriminant analysis was applied to the independent variables with the SC > 0.30 obtained in the previous analyses. The log-transformation improved the normality of the variables, allowing the use of models that assumed normality, like the discriminant analysis. All statistical analyses were performed using SPSS software release 18.0 (SPSS Inc., Chicago, IL, USA).

Results

The results of the discriminant analyses are presented in Table 2, for each group (Table 1) with alr transformed variables. Taking into account all measures of discriminant power (percentage of right classification is specifically shown), in matches with penalties, the group “Outcome” qualified the most (60.4% for the original sample and 52.2% for cross-validation), followed by the group “Shot Situation” (51.1% for original sample and 46.8% for cross-validation), “Attack Situation” (49.5% for original sample and 40.4% for cross-validation), “Flakes” (49.1% for original sample and 44.1% for cross-validation) and “Zone” (43.7% for original sample and 37.3% for cross-validation). In matches without penalties, the results were similar. Moreover, with regard to the first discriminant function (the only significant one), Table II shows that out of 11 variables corresponding to groups “Attack Situation”, “Outcome” and “Shot Situation”, only 4 had the SC ≥ 0.30 in matches with penalties and out of 8 variables corresponding to groups “Attack Situation”, “Outcome” and “Shot Situation”, only 6 variables showed the SC ≥ 0.30 in matches without penalties. The groups “Zone” and “Flakes” had 7 variables with a relevant SC (≥ 0.30).

Table 2.

Discriminant analyses between the match score for each group with log-transformed variables (matches with penalties (^P) and without penalties (^S)) * p < .05; ** p < .01; ***p < .001

	Structure coefficients		Eigenvalue				Wilk´s Lambda				Box	% Original sample	% Cross-validation
	SC1	SC2	Eigenvalue		Can.	Corr.	Wilks´s Lambda		Sig.		Sig.	TOTAL	TOTAL
log(PATS/PATIP)	.344	.907
log(PATS/PATIP)	.992		.265	.005	.457	.067	.787	.995	.001**	.807	.831	49.5	40.4
log(PATS/PATIP)
log(PATPE/PATIP)
log(PATS/PATIS)	.939	-.344	.138	.002	.349	.042	.877	.998	.065	.729	.541	39.4	38.0
log(PATCO/PATIS)	.634	.773
log(PG/PLSP)	.884
log(PEX/PPLSP)		.382
log(PPEN/PLSP)			.682	.070	.637	.256	.556	.934	.000***	.163	.798	60.4	52.5
log(PFO/PLSP)		.991
log(PPER/PLSP)
log(PG/PLSS)	.926
log(PEXP/PLSS)	.614	.649	.688	.067	.639	.250	.555	.937	.000***	.213	.855	66.2	58.1
log(PFO/PLSP)
log(PPER/PLS)		.604
log(PLSU/PLI )		.704
log(PLCO/PLIP)	.997		.392	.024	.531	.152	.702	.977	.000***	.352	.533	51.1	46.8
log(PLPE/PLIP)		.809
log(PLSU/PLIS)	.662	.750	.358	.000	.513	.014	.736	1.000	.001**	.909	.699	50.0	47.1
log(PLCO/PLIS)	.827	-.562
log(PL1/PL6)	.391	.508
log(PL2/PL6)	.728	.584
log(PL3/PL6)	.680		.197	.032	.406	.175	.810	.969	.001**	.373	.387	43.7	37.3
log(PL4/PL6)	.784	.317
log(PL5/PL6)		.794
log(PL1F/PLD)	.481	.872
log(PL2FPLD)	.851		.133	.025	.342	.156	.861	.976	.017*	.279	.492	49.1	44.4
log(PLM2F/PLD)	.639

Table 3 presents the results of discriminant analysis of those variables with the SC ≥ 0.30 obtained in previous analyses in matches with penalties and without penalties. For the matches with penalties, the discriminant functions classified correctly 73.3% (original sample) and 63.3% (cross-validation) of the match score. In this discriminant analysis, only the first discriminant function was significant and the variables that had higher discriminatory power were log(PG/PLS) (SC = .735), log(PLCO/PLI) (SC = .483) and log(PATCO/PATI) (SC = .391). For matches without penalties, the discriminant functions classified correctly 91.9% (original sample) and 43.2% (cross-validation) of the match score. In this discriminant analysis the variable that had higher discriminatory power was log(PG/PLS) (SC = .576).

Table 3.

Results of a discriminant analysis of the variables that were significant in the previous analysis * p < .05; ** p < .01; ***p < .001

	MATCHES WITH PENALTIES		MATCHES WITHOUT PENALTIES
	Structure coefficients		Structure coefficients
	SC1	SC2	SC1	SC2
log(PATS/PATI)				.513
log(PATCO/PATI)	.391			.476
log(PG/PLS)	.735		.576
log(PEXP/PLSS)				.416
log(PLSU/PLIS)				.397
log(PLCO/PLI)	.483
log(PL1/PL6)		.393
log(PL2/PL6)		.755		.400
log(PL3/PL6)		.534
log(PL4/PL6)		.393
log(PL1F/PLD)		.334
log(PL2F/PLD)		-.333
log(PLM2F/PLD)
Box´s M	174.768 (p = .319)		-
Eigenvalue	1.496	.108	2.968	.380
Canonical	.774	.312	.865	.525
Correlation Index
Wilk´s Lambda	.362	.903	.183	.725
Chi Square	83.402	8.410	47.607	9.013
Df	22	10	26	12
Sig	.000***	.589	.006**	.702
	% Correct	% Correct	% Correct	% Correct
	Classification	Classification	Classification	Classification
	(Original sample)	(Cross-validation)	(Original sample)	(Cross-validation)
% unfavourable	81.8	68.2	90.9	54.5
% balanced	65.1	53.5	90.5	38.1
% favourable	80.0	76.0	100	40.0
% classification	73.3	63.3	91.9	43.2

Figure 1.

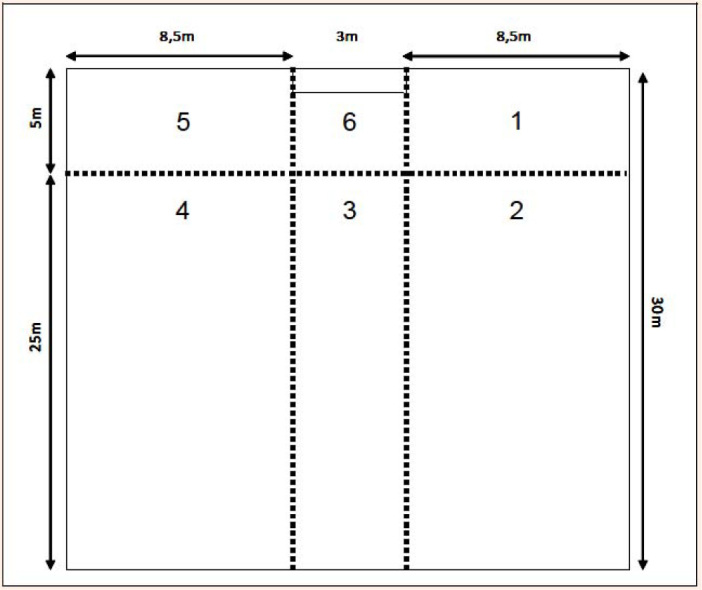
Schema of the division of the court according to 6 zones (Lupo et al., 2012)

Discussion

The aim of the present study was to identify groups of offensive performance indicators which best discriminated between the match scores (favourable, balanced or unfavourable) in water polo. Although summative season long performance comparisons between teams may be considered limited by different authors (Lago, 2009; Prieto et al., 2013; Tucker et al., 2005), studies of this type can provide general values that aid our understanding of water polo and could establish the norms according to which training sessions are structured (García et al., 2015; Lago and Lago, 2010).

We used the offensive performance indicators transformed with alr transformation within each group, as their sum was 100%. To our knowledge, the present paper was the first to assess the impact of the offensive performance indicators on match scores in water polo using compositional data analysis.

The results of the initial discriminant analyses identified “Outcome” as the most discriminatory group, followed by the groups “Shot Situation”, “Attack Situation”, “Flakes” and “Zone”, respectively. In the final discriminant analysis, only three variables (log(PG/PLS), log(PATCO/PATI), log(PLCO/PLI)) were found to discriminate teams in relation to match scores in matches with penalties, and one variable (log(PG/PLS)) in matches without penalties. In line with the present results, it was found (García et al., 2015) that the variable “goal”, within the group “Outcome”, had the greatest discriminatory power between the match scores, together with the variables related to a playing situation: counterattack, even and power play, within the groups “Shot Situation” and “Attack Situation”. The same variables (goal and playing situation: even, counterattack and power play) were also shown to be one of the most potent discriminant indicators between successful and unsuccessful teams in different championship phases (Escalante et al., 2013). Equally, the winning teams made a higher number of counterattacks in women´s international championships (Escalante et al., 2012). Also the winning teams had low frequencies in even attacks and high frequencies in counterattacks during matches with an unbalanced match score (> 3 goals of difference) (Lupo et al., 2014). In other team sports such as handball, several papers have shown the importance of the counterattack (Bilge, 2012; Foretic et al., 2010). Moreover, the present study showed, as a further result, the importance of the exclusion and power play actions in matches without penalties. The effectiveness of power play shots was a performance indicator which discriminated between winning and losing teams in the final phase of the 2008 Olympic Games held in Beijing (Escalante et al., 2011). Again exclusion was a performance indicator that differentiated between women and men (Escalante et al., 2011), reflecting greater aggressiveness of men in competition. These performance indicators, i.e. goal and exclusion, belong to the group “Outcome”, which was the most discriminating group between match scores in this study. Although there are few studies that have analysed the discriminant power of different groups, the variables of the “Outcome” group (goal, exclusion) were selected as relevant in other studies which compared water polo game-related statistics considering match scores (Escalante et al., 2011, 2013; García et al., 2015; Lupo et al., 2012). The groups “Shot Situation” and “Attack Situation” reinforce the results obtained by other researches (García et al., 2015), where the counterattack and even were elements differentiating between the match scores. However, the groups “Flakes” and “Zone” had the lowest discriminatory power, maybe because they are groups including more specific variables.

Some authors (García et al., 2013) concluded that winning and losing teams had approximately the same opportunities to play with a numerical advantage, which is in line with our results regarding matches with penalties. Nevertheless, our results of compositional data which selected matches without penalties, go one step beyond, showing the importance of performance indicators related to numerical inequality (exclusion, power play attacks and shots).

The number of penalties is a common performance indicator in strong teams with a favourable match score. Therefore, by selecting only matches without penalties, we eliminated many of the matches with a favourable score (a decreased number of goals, counterattacks, attacks and shots), so this may be a possible explanation of the increase of discriminatory power of other performance indicators (exclusion and power play actions and shots) considering scores in matches without penalties.

Taking into account the right percentages of classification, our results using compositional data (73.3% original sample and 63.3% cross-validation) are more accurate compared to the results by García et al. (2015) who used untransformed variables (72.2% original sample and 61.9% cross-validation).

Concerning the limitations of the current study, two aspects should be underlined. Firstly, although the sample was the largest compared with other research conducted so far including analysis of these characteristics in water polo, the sample was not random, because of the difficulty of achieving the matches’ recordings. This generated an unbalanced design of the match scores (favourable, balanced or unfavourable). Secondly, despite the compositional data analysis is more appropriate statistically, its interpretation may be less understandable for coaches and water polo players.

As practical implications, the coaches should enhance the skills of the counterattack and reinforce withdrawal in defense. In addition, they should take into account that the power play actions are a key factor in balanced matches. Following this advice, the teams will have more possibilities to obtain a favourable outcome.

Authors submitted their contribution to the article to the editorial board.