Mating patterns and rates of biological invasion

Invasive nonnative plants are in the news because of their dramatic effects on our national agriculture, aquaculture, rangelands, water supplies, and other important resources (1, 2). Invasive plants also cause the decline of local biodiversity worldwide, with clear effects on native species and ecosystems (3, 4). For economic and ecological reasons, these invaders have been a primary focus of conservation and restoration efforts, although control programs seldom have the resources to keep up with the spread of new invaders (5). One of the conundrums of controlling invasive plants is that eradication is feasible only very early on, before a species has become widespread. However, a new nonnative plant is unlikely to attract attention or funding when it is only found here and there, especially when its populations are growing slowly and therefore seem to pose little immediate threat. Initially slow “lag phases” in population growth are suspected to be common in invasions (e.g., ref. 6), yet evidence that they occur has been mostly anecdotal. Demonstrating the occurrence of lag phases has been impeded by the nature of exponential growth. When numbers are small, population growth can be imperceptible, even if the growth rate is quite large. A lag phase implies that the rate itself increases over time. We need hard evidence that rates of population growth change over time, along with experiments to reveal the mechanism behind that change. In this issue of PNAS, Davis et al. (7) demonstrate that a lack of sexual partners results in a lag in the spread of an important weedy grass invading mudflats on the northwest coast of North America.

An “Ecosystem Engineer”

Some invaders cause major structural changes to a landscape; in effect, they create a fundamentally new ecosystem in the invaded region. Although it is a valued native component of coastal vegetation on the eastern seaboard, Spartina alterniflora (cordgrass) is an invasive and damaging “ecosystem engineer” in Willapa Bay, WA. This meadow-forming grass traps sediments in tidal mudflats, changes local hydrology by creating high zones and deep channels, and eliminates native eelgrass beds and saltmarsh vegetation (Fig. 1). Spartina invasion causes a dramatic degradation of the wildlife habitat value of tidal mudflats and marshlands of the Washington coast, which are a key resource for shorebirds, migrating ducks and geese, juvenile fish, and invertebrates. At the same time, by eliminating tidal mudflats Spartina threatens the $16 million oyster industry in Willapa Bay. Spartina was first introduced to Willapa Bay in the 1890s, but in 1982 it still occupied only 400 acres. Spread increased alarmingly in the last two decades (Fig. 2). Previous explanations for this apparently increasing rate of invasion have included adaptive evolution by the plant and/or El Niño climatic events (8), although the biological mechanism for the phenomenon remained unresolved.

Fig. 1.

S. alterniflora invasion into Willapa Bay, WA, where open mudflats and marsh lands are being converted into thick Spartina meadows. Photograph courtesy of H. G. Davis, University of California, Davis.

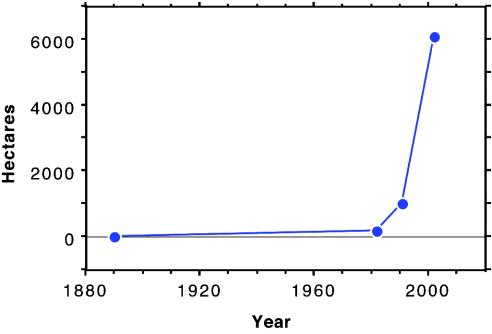
Fig. 2.

The pattern of invasion of S. alterniflora in Willapa Bay from 1894 to 2002 shows a long period of very slow growth, followed by extremely rapid increase in the 1980s and 1990s (data from Washington State Department of Ecology, www.ecy.wa.gov/programs/sea/coast/plants/spartina.html).

Understanding Rates of Invasion Through Mathematics

To understand rates of invasion, biologists turn to mathematical models. The desire to estimate and predict rates of invasive spread from biological parameters such as population growth and dispersal has resulted in a fruitful collaboration between mathematics and biology for several decades (9–13). Mathematical models of invasion may take the form of reaction–diffusion equations, integro–difference equations, or spatially explicit simulations that allow for the inclusion of greater biological detail. These models have provided answers to why some species spread extremely rapidly whereas others do not, how the environment may influence rates of spread, and how long-distance dispersal events (e.g., a fly carried along on the family vacation) drive invasion rates. One important insight from mathematical approaches is that invasion can be slowed by an Allee effect, when populations grow more slowly at low densities (14). We have long recognized the importance of Allee effects in the conservation of organisms that have small populations, like grizzly bears. However, Allee effects may also slow the early stages of biological invasions (15–17). With an Allee effect, the introduced species increases very slowly at first until it builds up a large enough population size, at which point there is a rapid escalation of spread. Allee effects could be one explanation for lag phases.

Pollen Limitation and the Allee Effect

For invading plants, factors that influence seed production can greatly affect how fast populations spread. Work on animal-pollinated plants has shown that reproduction and invasion may be limited by pollination (18–20). Recent studies highlight a number of unresolved questions about the role of mutualistic interactions between plants and insects in plant invasions. For example, do established nonnative pollinators such as the European honey bee facilitate the invasion of nonnative plants (e.g., refs. 18, 19, and 21)? Do invasive plants show adaptive evolution to particular local pollinators (or vice versa)? Should we expect successful invaders to be independent of such interactions altogether (for example, showing high rates of asexual reproduction or self-fertilization), or to evolve reduced reliance on pollinators (22)?

Two aspects of the study by Davis et al. (7) are unique and make this work particularly exciting. First, whereas we know a lot about pollen limitation of animal-pollinated species (23), surprisingly few studies have been done on pollen limitation of wind-pollinated plants like Spartina. The assumption has been that wind-pollinated species produce more than enough pollen to go around. By doing clever field experiments, Davis et al. demonstrated that reproductive success in these grasses was highly variable and influenced primarily by the amount of pollen available to the plant.

Second, in this and another paper (24), Davis and colleagues showed that pollen limitation and reproductive success were strongly influenced by the density of plants. That is, Spartina demonstrated a powerful Allee effect. Isolated individuals at the edge of the invasion front were strongly pollen limited, whereas individuals in meadows surrounded by other Spartina plants were not. Pollen in the air, as well as pollen received by receptive female flowers, varied greatly over short distances across the landscape and was driven by whether plants had immediate neighbors. Models based on these empirical results (25) show that the effects of density on reproduction can have dramatic implications for biological invasions and their control.

As the subject of a major National Science Foundation biocomplexity grant, S. alterniflora has recently gained “model system” status in the field of invasion biology, with a large team of researchers using ecological and genetic approaches to piece together the puzzle of a dramatic ecological phenomenon. Studies of reproductive biology placed in a demographic and ecological context, like that of Davis et al. (7), can provide us with insights into the important biological drivers of major landscape change.