Domain swapping is a consequence of minimal frustration

Abstract

The same energy landscape principles associated with the folding of proteins into their monomeric conformations should also describe how these proteins oligomerize into domain-swapped conformations. We tested this hypothesis by using a simplified model for the epidermal growth factor receptor pathway substrate 8 src homology 3 domain protein, both of whose monomeric and domain-swapped structures have been solved. The model, which we call the symmetrized Gō-type model, incorporates only information regarding the monomeric conformation in an energy function for the dimer to predict the domain-swapped conformation. A striking preference for the correct domain-swapped structure was observed, indicating that overall monomer topology is a main determinant of the structure of domain-swapped dimers. Furthermore, we explore the free energy surface for domain swapping by using our model to characterize the mechanism of oligomerization.

It is now well established that proteins are minimally frustrated (1). The minimal frustration principle states that naturally occurring proteins have been evolutionarily designed to have sequences that achieve efficient folding to a structurally organized ensemble of structures with few traps arising from discordant energetic signals (2–7). A recent computational survey has reported that proteins that associate by means of traditional binding modes also have funnel-like energy landscapes designed to have specific binding (8). Domain swapping is an unconventional mechanism of oligomerization in which the structural elements, or “domains,” of individual monomers are interchanged between identical partners by recruiting interactions that are crucial for stabilizing the protein in its monomeric form (9, 10). When domain swapping occurs, noncovalent interactions between the swapping region and the rest of the monomer are broken and replaced by nearly the same interactions with the other monomer(s). Is domain swapping a sign of frustration? To answer this question, we are led to ask whether domain-swapping proteins have evolved such that the same energy landscape that determines their folding into monomeric conformations also determines which way(s) they will domain-swap into oligomeric conformations. Currently, ≈60 proteins have been identified as domain-swapped complexes. The phenomenon has been proposed to play a role in aggregation, misfolding, and the regulation of function, but its biological implications are still unclear (11–17).

By avoiding frustrating conflicts between different energetic biases, proteins have evolved to have a funneled energy landscape that optimizes native structure-seeking interactions while selecting against interactions leading to traps (18, 19). A funneled landscape reduces the highly intractable problem of configurational search through traps to a much smaller parallel search of the configuration space. Once the energetic frustrations associated with conflicting interactions have been minimized, the topology of protein becomes the key determinant of the folding mechanism, encoding the interplay between stabilizing free energies and chain entropy. Structure-based Gō-type minimalist models containing attractive native interactions and repulsive nonnative interactions correspond to perfectly funneled energy landscapes. Such models have impressively reproduced the experimentally observed folding mechanism of many single-domain proteins (6, 20). The quantitative form of minimal frustration of proteins has been successfully used to improve protein structure prediction energy functions (21) and for protein design (22). Because proteins carry out their function while interacting with other cellular components, one may also ask not only whether proteins have evolved to fold efficiently but also whether proteins may be optimized for selective binding. Recently, the formation of various homodimers was studied by using perfectly funneled energy landscapes reproducing the mechanisms found in the laboratory (23, 24). These results indicate that the dimer native topology, by encoding a funneled landscape, becomes a major determinant for binding mechanisms for proteins whose binding is required for function.

What determines the mechanism of domain-swapping proteins? Is native topology a sufficient predictor? The monomeric and dimeric structures of a domain-swapping protein are expected to be comparable in energies per molecule because the contacts are largely conserved between the structures (11). The transition from monomers to a domain-swapped dimer must couple with at least partial unfolding to allow the swapping region to be exchanged. The energetic cost of breaking and replacing the swapping region interactions, which typically represent a large portion of the total contacts within the monomer, leads to a high-energy barrier separating the monomeric and domain-swapped dimeric conformations (9, 10, 16, 25). Thus, it may be surprising that any protein would undergo such a large barrier transition. The domain-swapping mechanism has been recently studied for bovine seminal RNase (26), which forms two different quaternary structures: a swapped dimer and an un-swapped dimer that has a much smaller interface. It was shown that a coupling between folding and binding is more likely for the domain-swapped dimer of bovine seminal RNase than for the dimer with no swapping. The kinetic accessibility of the domain-swapped dimer significantly decreases when the competition between the two forms is introduced, reflecting that the interchange requires crossing a high barrier.

Several previous studies have searched for distinguishing features common among domain-swapping proteins. However, there does not appear to be any sequence homology or secondary structure similarity that is found in all domain-swapping proteins (12). Are there local signals for swapping? In some cases, proline residues are found in the hinge loop, suggesting their possible importance (14, 27), but there are many examples of domain-swapping proteins with no prolines in the hinge loop. Thus a unifying explanation for how proteins domain-swap has been elusive. In this present study, our goal is to determine whether the monomeric protein topology alone is sufficient for predicting how a protein will form complexes by means of the domain-swapping mechanism. To address this issue, we applied an extension of the usual Gō-type model, which we called the symmetrized Gō-type potential, to epidermal growth factor receptor pathway substrate 8 (Eps8) src homology 3 (SH3) domain (28), a small domain-swapping protein. The model is based exclusively on the N native interactions that exist in the monomeric structure. In the symmetrized Gō-type potential for a domain-swapped dimer, the same native contacts that define the N intramolecular noncovalent interactions in the native monomeric conformation also define 2N possible intramolecular interactions and 2N possible intermolecular noncovalent interactions, resulting in 4N total represented. It immediately follows that such a potential has the possibility of many topological traps and does not have a perfectly funneled energy landscape, as does the traditional Gō-type model for monomeric proteins (6, 20). There is frustration between the choice of whether to make any contact internally or with a corresponding partner's amino acid residue. The definition of the symmetrized Gō-type potential alone provides no information that would bias one swapping region over another. In principle, any region can swap, and nothing precludes the possibility of even multiple swapping regions, allowing for numerous traps. Only if an inherent bias towards a single, intertwined conformation exists can we say that there exists instructions encoded in the monomer topology on how to domain-swap into an oligomer.

Model and Methods

Symmetrized Gō-Type Hamiltonian. Here we introduce a symmetrized Gō-type potential for a two-chain protein. This model is based on the traditional Gō-type potential, a simplified C^α protein model. The potential is largely defined by attractive native interactions and repulsive nonnative interactions, as well as the backbone geometry, which reflects a perfectly funneled energy landscape with no energetic frustration for the monomer such that it will fold into only its native conformation. In the symmetrized Gō-type potential, the native contacts in the monomeric structure serve to define both the intrachain interactions and the interchain interactions. As illustrated by the cartoon depicted in Fig. 1c, for each intrachain interaction between residues i and j in chain A (i′ and j′ in chain B), the corresponding interchain interaction between residues i and j′ (and i′ and j) also exists.

Fig. 1.

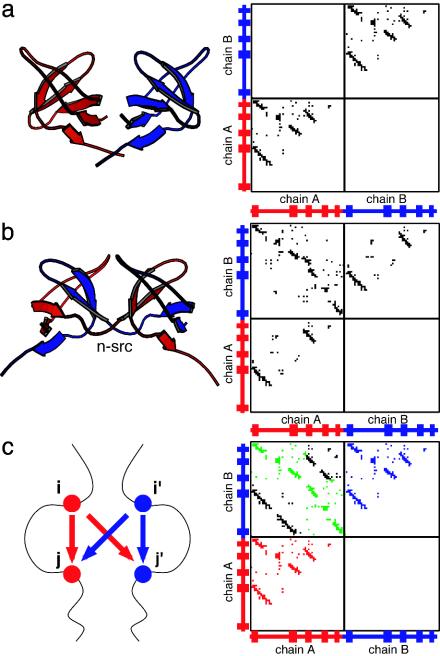
Contact maps for Eps8 SH3 domain and the symmetrized Gō -type model. (a) The structure and contact map of MSH3 [Protein Data Bank (PDB) ID 1I0C] of Eps8. (b) The structure and contact map of DSH3 (PDB ID 1I07) of Eps8. (c) A schematic illustration for the symmetrized Gō -type model and the corresponding contact map for the two-chain system (see text for details). In this symmetrized Gō -type model contact map, red and blue represent all of the intrachain contacts for chains A and B, respectively. Green represents the native interchain contacts that are found in the domain-swapped structure of DSH3. Black represents the nonnative interchain contacts that are not found in the domain-swapped structure of DSH3. The structures were created with molscript (36).

The energy function of the symmetrized Gō-type potential for the two-chain (chain A and chain B) protein with configuration Γ is as follows:

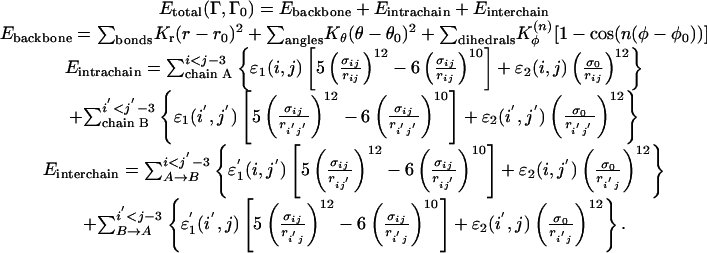[1]

The local backbone interaction E_backbone applies to both chain A and chain B; K_r, K_θ, and K_φ are the force constants of the bond, angle, and dihedral angle, respectively. Note that r₀, θ₀, and φ₀ are the corresponding values taken from the native monomeric configuration Γ₀ only. The contact interactions, E_intrachain and E_interchain, contain Lennard–Jones 10–12 terms for the nonlocal “native” intrachain and interchain contacts and short-range repulsive terms for “nonnative” pairs.

As a starting point for the energy function, we chose K_r = 100ε, K_θ = 20ε, 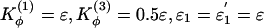, and ε₂ = 0.001ε. σ_ij is equal to the distance between the pair of residues (i, j) in the native monomeric configuration and σ₀ = 1 (in units of r₀ = 3.8Å) for all nonnative residue pairs.

We performed molecular dynamics simulations with the replica exchange method by periodically exchanging configurations that were running at a sequence of temperatures (29–31). A wide range of temperatures was chosen to ensure sufficient sampling from folded to unfolded states and to provide reasonable overlap of energy histograms of neighboring pairs. All replica exchange simulations started from the native monomeric configurations. We imposed an interchain constraint E_constraint = K(R – R₀)² for the center-of-mass distance of the two chains R with a target distance R₀ to restrict the sampling of our simulations to a configuration space where domain swapping could be observed. We also performed sets of 50 runs of simulated annealing to sample more thoroughly the conformational space (for details, see the supporting information, which is published on the PNAS web site).

The SH3 Domain from Eps8. For illustration, we chose an SH3 domain of the epidermal growth factor receptor pathway substrate 8 (Eps8), which has been observed in both the monomeric and dimeric domain-swapped conformations (28). The monomeric SH3 (MSH3) of Eps8 is a relatively small protein, formed by two orthogonal β-sheets connected by a hinge named the n-src loop (Fig. 1a). The dimeric SH3 (DSH3) is formed by domain swapping, in which a part of secondary structure is exchanged between two protein chains. (Fig. 1b). The two structures have essentially identical secondary and tertiary structures, except for the n-src loop, which has a closed form in the MSH3 and an open form in the domain-swapped DSH3.

To construct the symmetrized Gō-type potential for this protein, we determined the native contacts of MSH3 by using csu (Contacts of Structural Units) software (32). The list of the native contacts in the monomeric conformation was used as a template for all intrachain and interchain interactions as follows. For each intrachain interaction between residues i and j in chain A (i′ and j′ in chain B), we allowed interchain interactions by introducing the same interactions between residues i and j′ (i′ and j). The symmetrized contact map, illustrating the interactions represented in the symmetrized Gō-type potential for Eps8 SH3, is shown in Fig. 1c. Note that the map of interchain contacts includes both those that are found in the dimer x-ray structure (we call these “native interchain contacts”) and those not observed in the dimer (“nonnative interchain contacts”).

Results and Discussion

By using the symmetrized Gō-type potential, we are now able to determine how domain-swapping proteins undergo a transition from a monomeric to a domain-swapped conformation. The environment of a given residue is largely the same in monomeric or domain-swapped configurations, justifying our symmetrization of the intrachain interactions to form the interchain interactions. A consequence of defining such a symmetrized energy function is that there exist competing energetic and topological states (“topological frustration”). There is no a priori guarantee that a single, intertwined oligomer structure will be predicted by the symmetrized Gō-type potential; nor is there a guarantee that it will have the same domain-swapped structure found in nature. Unlike the intrachain interactions, which yield a perfectly funneled energy landscape for the monomer, the interchain interaction leads to “ruggedness” for the dimer in that there exist favorable interactions that are not found in the domain-swapped structure. If a bias exists toward a single, stable domain-swapped conformation, it must be determined strictly from the energy landscape that folds the protein into a monomeric conformation.

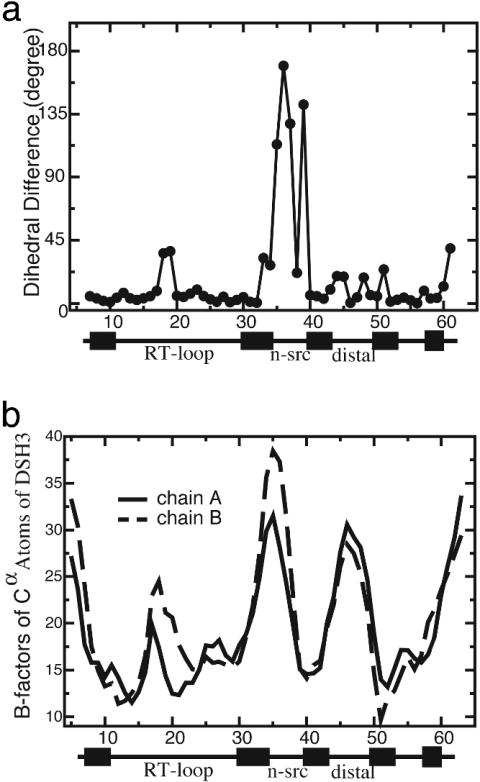
Modeling a Frustrated Flexible n-src Hinge Region. There exists a very high energetic barrier for dimerization via domain swapping because it is involved in a large conformational change which occurs at the n-src loop (Fig. 1). In the “vanilla” version of the present model, all of the dihedrals are energetically biased to be those obtained from the monomeric conformation. The dihedral angle difference for Cα atoms between MSH3 and DSH3 clearly shows a large conformational change localized at the n-src loop where domain swapping occurs (Fig. 2a). The hinge region, the n-src loop, is a priori biased to remain in the monomeric conformation and not convert to the dimer.

Fig. 2.

The flexibility of the n-src hinge loop. (a) The dihedral angle difference for C^α atoms between MSH3 and DSH3 shows that the large conformational change for domain swapping is located at the flexible n-src loop (residues 35–39). (b) Higher thermal B-factors for C^α atoms in the n-src and distal loops of DSH3 [Protein Data Bank (PDB) ID 1I07].

To quantify the significance of frustration in the hinge region of the dimer, we first performed replica exchange molecular dynamics simulations. The simulations were carried out with the interchain center-of-mass constraint of 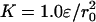and R₀ = r₀. Even with the frustrated hinge, the native-like domain-swapped structures are rather well represented and stable. The symmetrized Gō landscape favors the native interchain contacts rather than those not seen in the experimental dimer structure (see the supporting information). Topological trap states (i.e., structures that appreciably involve contacts that are nonnative but allowed by the symmetrized Gō model) exist, but are found to occur in low frequency.

To effectively account for the conformational change energetics at the hinge region, we first introduced a flexible n-src loop by turning off the dihedral terms in the n-src loop (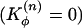). Therefore, this loop can rotate in any orientation and freely access the monomeric and dimeric configurations. This flexibility of the n-src loop is also consistent with the observed thermal B-factors in DSH3 (Fig. 2b). We found that allowing the n-src loop to be flexible stabilizes the domain-swapped dimeric configuration by eliminating most of the trap states (as reflected by the low probability of forming nonnative interchain contacts) and removing the bias that favors the monomeric configuration (Fig. 3a).

Fig. 3.

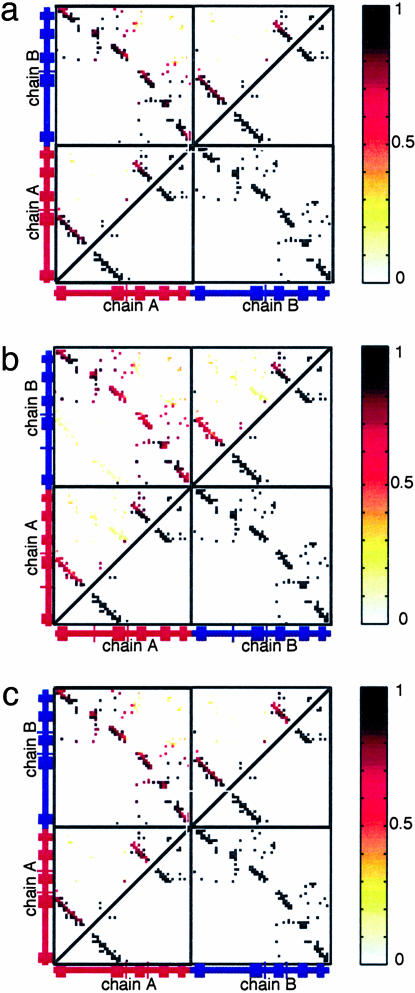
Symmetrized Gō -type model with flexible loops. Shown is the contact probability map for Q_interchain > 100 (above diagonal line) and symmetrized contact map (below diagonal line) for the flexible n-src loop only (a), the flexible (partly) RT and n-src loops (b), and the flexible n-src and distal loops (c).

To determine whether the local properties of the loop determine the swapped structure, we also allowed the other loops (specifically the RT and distal loops) to be flexible (Fig. 3 b and c). The contact probability map for the case of the flexible RT and n-src loops shows that the native domain-swapped dimer is still the most dominant (Fig. 3b), which is also true for the case of flexible distal and n-src loops (Fig. 3c), but when all loops were flexible more trap states were found. Nevertheless, Fig. 3 shows that the domain-swapped conformation actually observed in the dimer crystal structure was clearly the most represented.

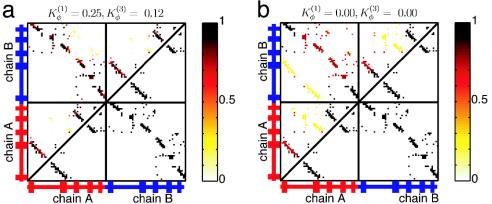
Monomer Topology Determines Domain-Swapped Structures. Because the introduction of flexible loops does not dictate which part of the protein becomes the hinge, we took the further, more radical, step of relaxing all of the dihedral force constants throughout the entire protein. No longer is secondary structure strongly funneled in this model. By relaxing the dihedral force constants, the main determinant of the swapped structure becomes the topology derived from the monomeric structure. When we performed simulated annealing after reducing the dihedral force constant by a factor of 4, we obtained four trajectories that resulted in the correctly swapped conformation (Fig. 4a). The remaining 46 trajectories resulted in monomeric configurations. During the transition, topological traps were sampled but were found to be unstable. So the symmetrized Gō energy landscape was not only successful in consistently obtaining the experimentally observed conformation, but the simulations show that the topological traps were actually avoided during the transition. When we deleted all of the dihedral terms (not just those at the hinge), we still found three natively swapped structures and only one of the nonnatively swapped structures (Fig. 4b).

Fig. 4.

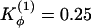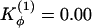Symmetrized Gō -type model with relaxed dihedral force constants. Contact probability map for Q_interchain > 77 (above diagonal line) and contact map of the natively domain-swapped dimer (below diagonal line) from sets of simulated annealing molecular dynamics simulations. (a) Changes to the dihedral force constants and . (b) and .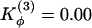

We also applied the symmetrized Gō-type potential, designed for domain-swapping proteins, to a protein that has not been found to yield unique domain-swapped dimers in nature. We applied the same protocol used for simulated annealing of Eps8 to chymotrypsin inhibitor 2 (CI2). To date, there is no detectable evidence of domain-swapping of CI2 in its wild-type form. We note, however, that artificial insertion of a long glutamine repeat does lead to domain swapping (33). In our simulated annealing runs of CI2 in its wild-type form, we found not a unique structure but rather multiple, distinct sets of dimeric conformations. Of particular note is a structure that was not intertwined at all, but was still domain-swapped (see the supporting information). However, the interchain interactions that were introduced by the symmetrized Gō-type potential produce an extended interface that binds the monomers. The existence of multiple distinct ensembles of dimeric conformations that are found to be stable implies a competition between these multiple dimeric states.

The monomer topology, rather than special features of the n-src loop, determines which of the domain-swapped dimeric structures will form. However, the yield of domain-swapped structures is, as we shall see, sensitive to the properties of the loop, which is consistent with the observed effects of mutations in the hinge region of p13suc1 (14). Mutations can affect the equilibrium and kinetics of swapping, yet the actual structure of the domain-swapped dimer is determined by the monomer topology.

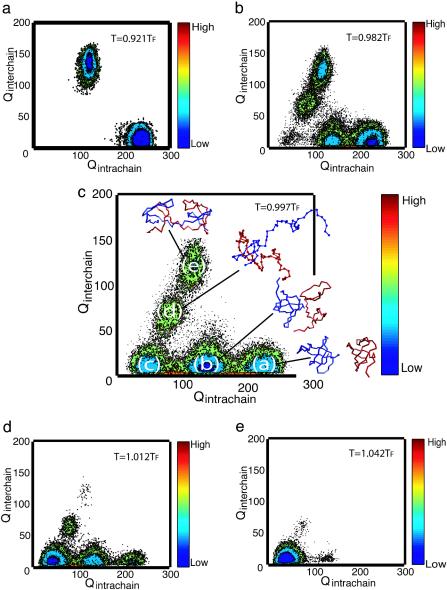
Mechanism of Domain Swapping. The model with the flexible hinge loop has a lower energetic barrier from the one in which the hinge dihedral energy must be frustrated to swap. The lower barrier allows enhanced sampling of swapping transition state configurations, so the symmetrized Gō-type potential with the flexible n-src loop allows us to investigate the mechanism of domain swapping. Fig. 5 shows the free energy surfaces at various temperatures as a function of Q_intrachain and Q_interchain, the number of intrachain contacts and interchain contacts. These free energy surface maps are calculated by using F = –k_BTlogP(Q_intrachain, Q_interchain), where P(Q_intrachain, Q_interchain) is the probability distribution of the intrachain and interchain contact formation. At a very low temperature, T = 0.921T_F (Fig. 5a), where T_F is the folding temperature (k_BT_F/ε = 1.324), there exists two basins corresponding to the native-like monomeric and domain-swapped conformations. The replica exchange method enables us to find domain-swapped dimers even at low temperatures, whereas the regular constant temperature simulation yields monomeric conformations only. As the temperature increases, the two most probable ensembles of native-like structures tend to unfold (Fig. 5b). When T approaches T_F (Fig. 5c), five dominating free-energy minima are observed with typical structures shown in Fig. 5c. These minima can be identified as native monomers (Fig. 5ca), partially unfolded monomers (Fig. 5cb), unfolded monomers (Fig. 5cc), partially folded or open-ended domain-swapped dimers (where approximately half of each monomer forms interchain contacts with its partner and the rest remains unfolded) (Fig. 5cd), and domain-swapped dimers (Fig. 5ce). We infer that in this case the most favorable mechanism of domain swapping is native monomers ⇋ partially folded monomers ⇋ unfolded monomers ⇋ open-end domain-swapped dimers ⇋ domain-swapped dimers. At higher temperatures, unfolded structures become populated on the surface (Fig. 5 d and e).

Fig. 5.

Free energy landscapes for domain swapping as a function of Q_intrachain and Q_interchain at five temperatures of an eight-replica simulation with the interchain center-of-mass constraint 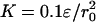and R₀ = 0.1r₀.

The importance of unfolded states is shown in Fig. 5c. These unfolded states serve as free energy traps in the process of dimerization at the folding temperature. Thus, the native monomers unfold first and then form domain-swapped dimers. This result agrees with the experimental observation that domain swapping takes place from the unfolded state in many proteins, such as human prion and p13suc1 (14, 25, 34, 35). When proteins are unfolded, the competition between the intrachain and interchain interactions will lead proteins to monomeric or dimeric configurations, respectively.

In our simulations, the intermediate states, which resemble open-ended domain-swapped dimers (Fig. 5cd), are obligatory for monomers to access the domain-swapped form because the intermediate state is located midway between the unfolded state and the native-like domain-swapped dimeric state on the free energy surface shown in Fig. 5c. Under certain conditions, such as an increase of protein concentration, these intermediates can be populated. As protein concentration is further increased, the interchain interactions will dominate over the intrachain interactions, and protein aggregates could be thus formed from the templates of the intermediates. The partially folded intermediates thus serve as “templates” for self-assembled aggregates.

Conclusions

We have introduced and implemented the symmetrized Gō-type potential to study the mechanism of domain swapping, by using Eps8 SH3 domain as a test case. The observation of the formation of the native-like domain-swapped dimer demonstrates that single-domain proteins are evolutionarily designed for efficient folding but can also lead to specific structures from oligomerization by means of domain swapping. The domain-swapped dimer actually observed in nature was found to be the most populated and the most stable in our simulations. The success of the symmetrized Gō-type model in predicting the domain-swapped structure indicates that the overall monomeric topology, rather than local signals in the hinge regions, determines where domain swapping can occur.