Abstract
Electrical conductivity and permittivity of biological tissues are important diagnostic parameters and are useful for calculating subject-specific specific absorption rate distribution. On the other hand, water proton density also has clinical relevance for diagnosis purposes. These two kinds of tissue properties are inevitably associated in the technique of electrical properties tomography (EPT), which can be used to map in vivo electrical properties based on the measured B1 field distribution at Larmor frequency using magnetic resonance imaging (MRI). The signal magnitude in MR images is locally proportional to both the proton density of tissue and the receive B1 field; this is a source of artifact in receive B1-based EPT reconstruction because these two quantities cannot easily be disentangled. In this study, a new method was proposed for simultaneously extracting quantitative conductivity, permittivity and proton density from the measured magnitude of transmit B1 field, proton density-weighted receive B1 field, and transceiver phase, in a multi-channel radiofrequency (RF) coil using MRI, without specific assumptions to derive the proton density distribution. We evaluated the spatial resolution, sensitivity to contrast, and accuracy of the method using numerical simulations of B1 field in a phantom and in a realistic human head model. Using the proposed method, conductivity, permittivity and proton density were then experimentally obtained ex vivo in a pork tissue sample on a 7T MRI scanner equipped with a 16-channel microstrip transceiver RF coil.
Index Terms: Electrical Properties, Proton Density, Proton Density Imaging, B1-mapping, Electrical Properties Tomography, EPT, magnetic resonance imaging (MRI), Quantitative magnetic resonance imaging
I. Introduction
The generation of MRI (magnetic resonance imaging) signal involves a series of tissue properties. Among them, one class relates to the MRI-visible nuclear spins, such as proton density and relaxation times (e.g. T1, T2, and T2*), and another defines the distribution of the radiofrequency (RF) magnetic field inside the object, such as the electrical conductivity, permittivity and magnetic permeability. Using MRI, quantitative parametric mapping of various types of tissue properties can provide insight into the fundamental aspects of tissue for both research and medical purposes.
Recently, there has been an increasing interest toward quantitatively imaging, in vivo, the electrical properties (EP) of biological tissues, including conductivity (σ) and permittivity (ε), using so-called electrical properties tomography (EPT) technique, based on the RF field (or B1 field) measured during an MRI scan [1]–[11]. The electrical properties of tissue depend on multiple factors, such as water content, ion concentration, protein and fat composition, that can be significantly altered under pathological conditions. For example, substantial variations of EP at Larmor frequencies of water proton have been reported in various types of tumors, when compared with normal tissues [12]–[14], suggesting that EPT may have the potential to be a noninvasive diagnostic tool in oncology.
Quantitative mapping of MRI-visible proton density (ρ) is also a topic of great interest for several reasons. First of all, the coupling between ρ and receive B1 field need to be disentangled in order to implement EPT algorithms involving receive B1 field. Based on certain assumptions to reduce ρ bias on receive B1 field, utilizing both transmit ( ) and receive B1 ( ) fields, several EPT techniques [8]–[11], [15] have been proposed to quantitatively calculate the unknown absolute B1 phase to overcome the limitation of half-transceiver-phase estimation at higher field strength [2], [5]; more recently, a gradient-based EPT algorithm demonstrated high quality in vivo images of human brain with high spatial resolution and reduced sensitivity to noise [15]. However, those EPT methods are sensitive to the experimental scenario where the utilized assumptions to remove ρ bias are not valid. Secondly, quantitative calculation of the specific absorption rate (SAR) requires without ρ bias [9], [16]. Calculation of SAR involves derivative on both and . Careful calibration of magnitude and mapping of ρ are needed to assure SAR calculation accuracy. Thirdly, quantitative mapping of ρ can provide clinically relevant information in pathological conditions that are associated with changes in tissue water homeostasis, such as multiple sclerosis [17], brain ischemia [18], brain tumor [19] or interferon treatment of liver metastases [20].
In order to derive quantitative ρ-map, other contributing sources of MRI signal modulation have to be minimized or removed. These include the relaxation times (T1, T2 and T2*), B0 field distortion, and inhomogeneity of and . Whereas B0 and can readily be measured, spatial variation of is particularly challenging to be disassociated from ρ. One solution, using transceiver RF coils, is based on the reciprocity theorem [21], assuming identical or symmetric profiles between and [9], [10], [15], with the former being readily measured using various B1-mapping techniques [22]–[24]. However, as the field strength increases, this assumption generally does not hold because of the reduced wave length at higher frequencies. Meanwhile, the distribution of B1 field strongly correlates with the imaged objects so that it becomes increasingly inaccurate to predict the receive B1 profiles for a specific coil based on measurements obtained in a homogeneous phantom [19]. Another way for extracting ρ is based on the unified segmentation approach [25] to remove the residual inhomogeneity of identified as the bias field map [26], [27]. Although this approach improves the reconstruction accuracy compared to the reciprocity-based method, it may fail in presence of abnormal morphologies such as brain tumors [26], [28]. The third strategy to quantify ρ exploits the observation of linear relationship between 1/T1 and 1/ρ [28]–[30]. However, reconstruction errors again manifest themselves when brain diseases or injuries involving hemorrhagic, protein, fatty or calcification components are present with T1-hyperintense images [31].
In this study, we proposed a novel method to quantitatively calculate the electrical properties (σ and ε) and ρ at the same time. The measured and ρ-weighted were taken as inputs into Maxwell’s equations, which describe the RF wave propagation in a sample carrying specific distribution of electromagnetic properties. Proton density was calculated as a scaling factor of . The method was evaluated using simulated B1 field in a digital phantom and in a realistic human head model. Experiments were performed to validate the proposed approach in a phantom including pork tissue on a 7T MRI scanner.
II. Theory
During MRI scans, the induced time-varying B1 field can be described by the time-harmonic Maxwell’s equations at Larmor frequency. Combining Ampere’s and Faraday’s Law of Maxwell’s equations, assuming the magnetic permeability of biological tissue to be equal to that of free space, and ignoring the Bz component which does not contribute to MRI signal, the relationship between the electrical properties and B1 field in the rotating coordinates can be written as [15]
| (1) |
and
| (2) |
where ω denotes the angular Larmor frequency of protons, μ0 the magnetic permeability of free space, εc ≡ ε − iσ/ω the complex permittivity including both conductivity σ and permittivity ε, and g+ and g− represent correspondingly g+ = gx + igy and g+ = gx − igy. Here, g ≡ (gx, gy, gz) is a gradient vector equal to ∇lnεc.
Using MRI, the measured B1 components include the magnitude , ρ-weighted magnitude , and image phase Θ. The image phase Θ is a summation of transceiver phase θ between a transmit and a receive channel and the background phase, which can be induced by B0 inhomogeneity, magnetic susceptibility, chemical shift, RF signal pathway delay, etc. Spatially variable background phase components can be imaged using B0-mapping techniques with multiple echo times (TE) while the RF signal pathway delay only contributes a spatially constant zero-order phase, which is eliminated in the differential operation in EPT.
The relative phase between arbitrary transmit or receive channels can be calculated as the difference of Θ related to corresponding transmit or receive channels. Taking transmit channel n as the reference channel, denoting its unknown absolute transmit B1 phase as ϕn, the transmit and receive B1 fields can be written as
| (3) |
where includes the measured and relative phase ϕrnj of transmit channel #j, is a complex field with a ρ-weighted magnitude of receive channel #k and transceiver phase θnk, and γ ≡ 1/ρ denotes a correcting factor to account for the unknown ρ.
Taking (3) into (1) and (2), they can be transformed into the forms of unknowns and measured components as
| (4) |
and
| (5) |
where the unknowns are ∇ϕn, ∇lnγ, g, and εc. As we can see in (4) and (5), besides the first order components of the unknowns, there are second order polynomial or derivatives of the unknowns, and the complex permittivity εc is combined with the higher order terms. To derive a solution of ∇ϕn, ∇lnγ and g, we combined their high order polynomial and derivative and εc in (4) and (5) and treated it as a new independent variable. With measured and of at least four transmit and receive channels, ∇ϕn, ∇lnγ and g can be derived by solving a set of linear equations. Final maps of εc and ρ can be calculated from the gradient g and ∇lnγ using the finite difference method, with at least one seed point providing a priori ρ and absolute value of εc as introduced in [15].
The reconstructed EP or ρ were evaluated using relative error (RE) and correlation coefficient (CC) as defined in (6) according to the corresponding ground true maps.
| (6) |
where vi is the value of reconstructed image on pixel i and vti the ground true value.
III. Methods
A. Simulation of B1 Field
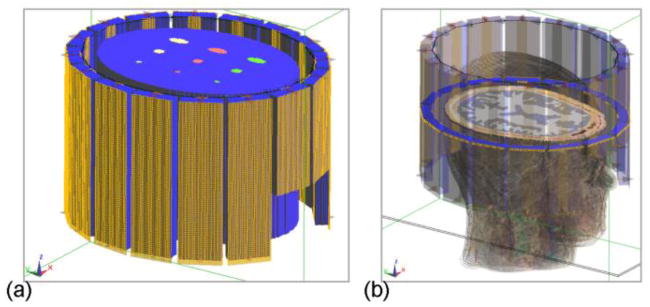
Electromagnetic fields, including B1, were simulated to evaluate the proposed method based on the finite-difference time-domain (FDTD) technique using SEMCAD X (Schmid & Partner Engineering, Zurich, Switzerland). In the simulation, a model of the 16-channel microstrip RF array coil [32] used in the following experiment was loaded with either a digital phantom (Fig. 1a) or the realistic Duke head model (Fig. 1b) from Virtual Family (IT’IS Foundation, Zurich, Switzerland). The models were discretized into voxels of 1.5×1.5×2 mm3 in size. The z-axis is defined parallel to the head-foot direction. The tuning/matching circuits and the decoupling capacitors of the coil model were replaced with 50Ω port in the FDTD simulation, and the resultant S-parameters were transferred into Advanced Design System (ADS) (Agilent Technologies, Santa Clara, CA, USA) where the coil was tuned, matched and decoupled at 298 MHz by optimizing the S-parameters. The final B1+ and B1− fields of the sixteen channels at 298 MHz were calculated based on the 50Ω port signal in the circuit simulation in ADS and the port signal and field maps in the 3D simulation in SEMCAD X [33], [34]. Values of ρ in cerebrospinal fluid (CSF), gray matter (GM) and white matter (WM) in the Duke head model were set to 1, 0.8 and 0.65, respectively [35], and 1 for other tissues.
Fig. 1.
Simulation setup of a sixteen-channel microstrip RF coil loaded with a digital phantom (a) or the Duke head model (b) in which a cross-section of the brain is shown.
In the phantom simulation study, the effective spatial resolution and sensitivity for reconstructing EP and ρ were evaluated. An elliptic cylinder was used as the outer compartment with dimensions set approximately about the overall size of a human head, with a length of 16 cm, a major axis of 20 cm and a minor axis of 15 cm. The electrical properties of the cylinder were chosen as the average of human brain tissue at 298 MHz [36], with σ=0.55 S/m and ε=52 ε0. Inside the cylinder, as shown in Fig. 1, circular cylinders with diameters of 5 mm and 10 mm, and elliptic cylinders with a major axis of 20 mm and minor axis of 10 mm were included, organized on a 3 × 3 Cartesian grid with their longitudinal axis parallel to the z axis and their lengths being 16 cm. The three rows, carrying 3 different shapes each, were given the following pairs of (conductivity, relative permittivity): (0.61 S/m, 57), (0.83 S/m, 65) and (1.1 S/m, 72), and the corresponding ρ values were 1.1, 1.25 and 1.5, respectively, normalized to the value of ρ in the background (outer compartment).
The impact of noise was evaluated by adding independent and identically distributed random Gaussian noise, separately to the real and imaginary parts of the simulated complex and fields. The standard deviation of the Gaussian noise was determined to be 2% of the average magnitude of the corresponding B1 field inside the object, resulting in an equivalent signal-to-noise (SNR) ratio of 50. When noise addition was applied, the data was smoothed, before further calculation, using a 3D Gaussian filter with a standard deviation of 1.2 voxels and a kernel size of 5 voxels in all three dimensions.
The input RF power to each channel was normalized to 1 W by taking into account the reflected power. The peak transmit B1 magnitude of a single channel inside the object is about 0.8 μT. The standard deviation of the added Gaussian noise is 1.4 nT for the phantom model and 1.3 nT for Duke head model.
B. Experiments
1) Phantom preparation
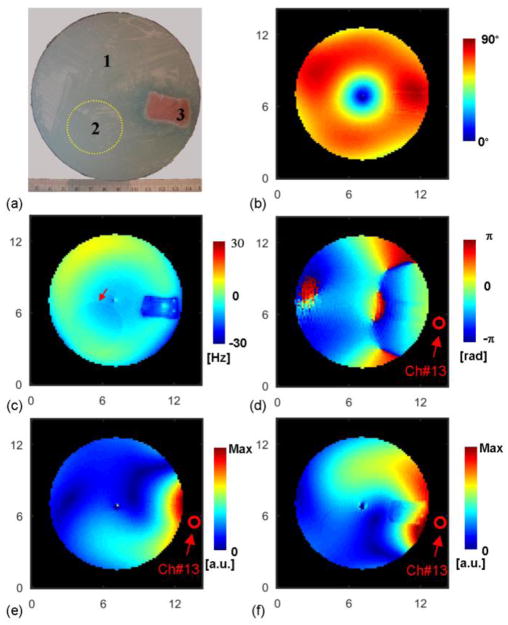
A phantom containing two compartments of different saline gel solutions and one inclusion of pork muscle tissue was built as shown in Fig. 4a. The outer diameter of the phantom was 12 cm. The main body (compartment #1) of the phantom was filled with a gel solution including Agar, NaCl, CuSO4·5H2O and deionized water with a mass ratio of 1.2:0.27:0.1:100. The electrical properties, measured with an Agilent 85070E dielectric probe and E5061B network analyzer (Agilent Technologies, Santa Clara, CA, USA) at 300 MHz, were σ=0.639±0.003 S/m and ε=79.1±0.1ε0, where ε0 is the vacuum permittivity. A small balloon (compartment #2), positioned inside the main body as shown in Fig. 4a, was filled with a gel solution including Agar, NaCl, CuSO4·5H2O and deionized water with a mass ratio of 1.2:0.45:0.1:100, and the measured electrical properties were σ=0.939±0.004 S/m and ε=78.1±0.5 ε0. A block of fresh pork muscle (compartment #3), with measured electrical properties of σ=1.38±0.04 S/m and ε=71.3±0.8 ε0, was also immersed in the gel. MR experiments began less than 30 minutes after building the phantom to minimize diffusion of ion from meat into gel, which may change the conductivity distribution.
Fig. 4.
Experimental condition. (a): Photograph of a cross section of the phantom showing pork muscle and a small spherical compartment of gel as indicated by the yellow dash circle. (b): Measured flip angle distribution in CP2+ B1 shimming configuration. (c): Measured ΔB0 field map in Hz. Red arrow indicates the boundary of the small gel compartment. (d): Measured image phase distribution using channel #13 for both transmission and reception. (e): Measured magnitude of transmit B1 field of channel #13. (f): Measured proton density-weighted magnitude of receive B1 field of channel #13. The axis unit is cm.
2) B1-mapping procedures
The measured B1-related components included , the image phase Θjk using transmit channel #j and receive channel #k, and the background ΔB0 map. A sixteen-channel transceiver microstrip RF coil [32] was used in the experiment. First of all, a B1-shimming configuration was applied in the CP2+ mode [37], providing strong around the periphery of the phantom, and the resultant flip angle (FA) map was imaged using the Actual Flip-angle (AFI) technique (maximum FA≈90°) [23]. With one channel transmitting at a time, a series of small-flip-angle (FA<10°) GRE (gradient-recalled echo, 10 averages) sequence was employed to calculate the magnitude after the GRE images were normalized by the sine of the measured AFI map [38]. The image phase Θjk was acquired from another scan, in the same single-channel-transmit mode, with a larger flip angle (maximum FA≈30°, 3 averages). In the same B1-shimming mode as the AFI scan, the ρ-weighted magnitude was acquired using a GRE scan (maximum FA≈90°, TE=3.1 ms and TR=8 s, 2 averages) and removing the sine of FA from the measured images. The ΔB0 map was calculated by taking the phase difference of a GRE scan at two TEs which were separated by 5.08 ms. All imaging sequences employed a voxel size of 1.5×1.5×3 mm3, and 12 contiguous slices (thickness = 3 mm) were acquired in total.
3) Data preprocessing
The relative transmit B1 phase map ϕrnj between channel #j and a reference channel #n was derived from all receive channels, calculated as with where Ijk and Ink are the MRI images received on channel #k when transmit channels #j and #n are used, respectively. The transceiver phase θnk was derived from the image phase Θnk after · ΔB0-induced phase ϕΔB0=γg·ΔB0·TE (with γg the gyromagnetic ratio and TE the echo time) was removed. The resultant complex relative transmit B1 field and ρ-weighted receive B1 field were smoothed using a Gaussian filter with a standard deviation of 1.2 voxels and kernel of 5 voxels in all three directions.
IV. Results
A. Simulations
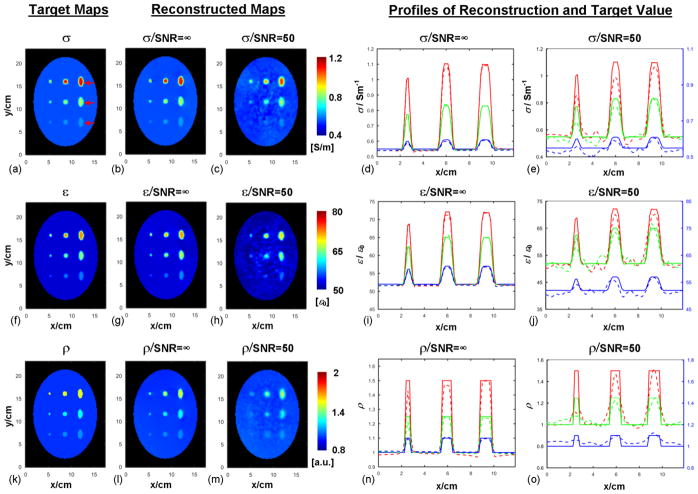
Results of reconstructed EP and ρ of the phantom model are compared with the corresponding target maps as shown in Fig. 2. The target distributions of EP are calculated based on Ampere’s Law from simulated electromagnetic field data. A seed point at the center of the phantom was utilized. As can be seen, under the noise-free condition in Fig. 2b, g and l, both EP and ρ were accurately reconstructed in comparison with the target distribution. The REs and CCs of the reconstructed maps under the noise-free condition were REσ=0.9% / CCσ=99.7%, REε=0.7% / CCε=99.0% and REρ=2.1% / CCρ=94.3%. The line profiles extracted from the reconstructed results, shown in Fig. 2d, i and n, reveal a high consistency between reconstruction and ground true values, and indicate that objects with a diameter as small as 5 mm and contrast ratio as low as 10% relative to the surrounding region could still be clearly detected.
Fig. 2.
From left to right: (a), (f) and (k): Target maps of conductivity (σ), permittivity (ε) and proton density (ρ). Red arrows in (a) indicate the positions of the line profiles shown in the reconstruction plots. (b,) (g) and (l): Reconstructed σ, ε and ρ distribution in the absence of noise, respectively. (c), (h) and (m): Reconstructed σ, ε and ρ distribution when random noise was added into simulated B1 field, respectively. (d), (i) and (n): Line profiles of reconstructed σ, ε and ρ in the absence of noise, respectively. (e), (j) and (o): Line profiles of reconstructed σ, ε and ρ in the noise condition, respectively. The profiles of the bottom line are plotted based on the right y-axis for improved visualization. Red, green and blue lines represent the top, middle and bottom arrows shown in (a), respectively, with solid lines for target value and dashed lines for reconstructed results.
The results of reconstructed EP and ρ, when noise (SNR=50) was included, are shown in Fig. 2c, e, h, j, m and o. It can be seen that, overall, there is a good agreement between reconstructed maps and target distribution, and shaped compartments that are larger than 5mm or with a contrast higher than 10% are clearly identified, even though fluctuation resulting from the noise addition is observed, especially between the inserted compartments. We notice that the peak values of reconstructed EP and ρ inside the cylindrical objects under the noise condition are mostly lower than the target peak values. This phenomenon is partially due to the effect of applied Gaussian filter and can be confirmed in reconstructed EP and ρ using filtered noise-free field data (results not shown). The REs and CCs for the reconstruction with added noise are REσ=4.5%/CCσ=93.6% and REε=2.6%/CCε=88.4%, and REρ=3.9%/CCρ=81.5%, respectively. It can also be seen in Fig. 2c, h and m, that the shaped compartments with only 10% contrast and 5 mm in diameter become difficult to be distinguished from the background due to the combined effect of added noise and applied Gaussian filter. Similar observations can be made for the corresponding line profiles as a function of compartment size and contrast in Fig. 2e, j and o.
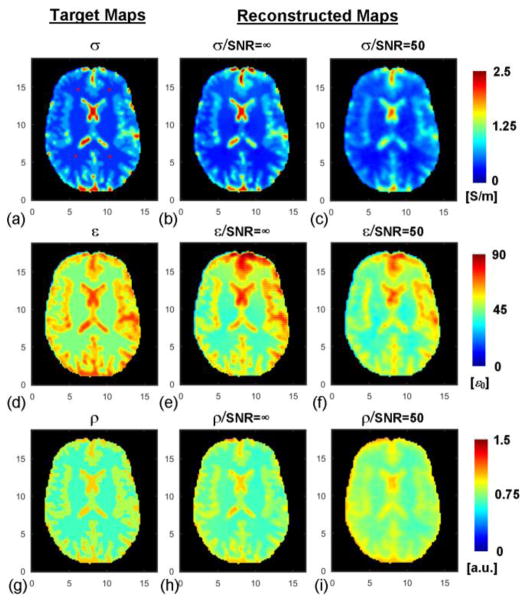
Using the realistic Duke head model, the reconstructed maps of EP and ρ are shown in Fig. 3. The REs and CCs for the reconstructed EP and ρ in different brain regions are presented in Table I. It can be observed that under the noise-free condition, the reconstructed EP and ρ values were highly consistent with the target distribution. When noise was added, the reconstructed maps were still fairly consistent with the target maps, however they appear blurred due to the applied Gaussian filter, which is needed to mitigate the magnification of noise by Laplatian operator.
Fig. 3.
Duke head model and reconstruction results. From left to right: target distribution of conductivity (a), permittivity (d) and proton density (g) of the model; reconstructed conductivity (b), permittivity (e) and proton density (h) in the absence of noise; reconstructed conductivity (c), permittivity (f) and proton density (i) when noise was added. Red “*” in (a) represent the location of four seed points. The axis unit is cm.
TABLE I.
Evaluation of Reconstructed EP And Proton Density Using Duke Head Model
| REs | SNR=∞ | SNR=50 | |
|---|---|---|---|
| GM | σ | 14.8% | 20.1% |
| ε | 11.0% | 14.5% | |
| ρ | 5.4% | 9.1% | |
|
| |||
| WM | σ | 14.5% | 15.1% |
| ε | 10.6% | 11.1% | |
| ρ | 5.2% | 15.2% | |
|
| |||
| CSF | σ | 14.7% | 28.8% |
| ε | 14.3% | 17.9% | |
| ρ | 6.8% | 10.0% | |
|
| |||
| Total (REs/CCs) | σ | 14.7%/0.96 | 23.0%/0.91 |
| ε | 11.4%/0.95 | 13.9%/0.93 | |
| ρ | 5.5%/0.95 | 9.9%/0.88 | |
B. Experiments
Figure 4b–f show the experimental phantom with several measured parametric maps. In the CP2+ B1-shimming mode, the transmit B1 field (Fig. 4b) is boosted around the circumference of the phantom (constructive interferences) whereas destructive interferences result in a region devoid of transmit B1 field at the center of the phantom, which was excluded in the reconstruction algorithm. Over a fraction of its circular path, the boundary between the inserted balloon and the surrounding gel phantom can easily be followed as shown by the red arrow in the B0 map (Fig. 4c). Fig. 4f clearly demonstrates the impact of proton density in the ρ-weighted magnitude of receive B1, with sharp discontinuity in the corresponding map at the boundary between pork and gel.
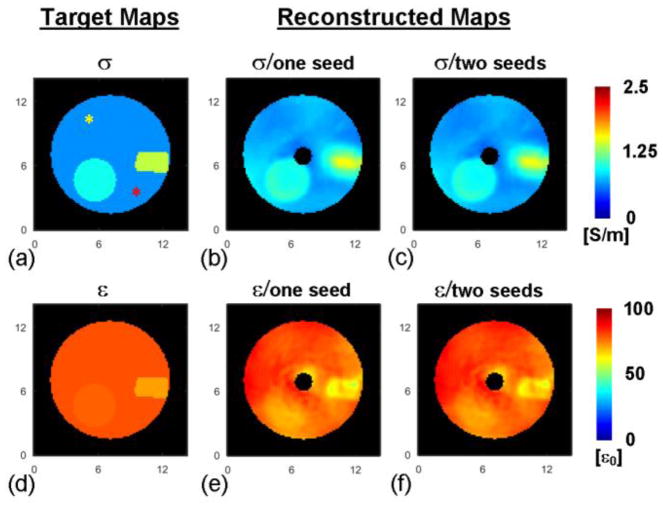
The reconstructed EP maps are shown in Fig. 5 in comparison with the target maps based on the probe-measured values. Note that in the reconstructed maps (Fig. 5b, c, e and f), the black circle in the center represents the region devoid of B1+ field that was excluded from the reconstruction. The reconstruction results of EP using either one or two seed points in compartment #1 are shown in Fig. 5b and e, and Fig. 5c and f, respectively. The results are consistent to each other regarding the selection of seed points. The reconstructed EP values using different seed points, summarized in Table II, are in good agreement with the probe measurement. The three phantom compartments are clearly identified in the reconstructed maps, with a sharp delineation of the boundary between the balloon and the cylinder. On the other hand, the boundary between pork and gel in the conductivity map is blurred, possibly because of diffusion of conducting ions into the gel in which the pork is exposed. The latter explanation is consistent with the sharper edge preserved in the permittivity map, since permittivity is less sensitive to the ion diffusion process.
Fig. 5.
Left: drawings of the three phantom compartments with conductivity (a) and permittivity (d) values as measured with a probe. Yellow and red asterisks in (a) indicate the seed points. Middle: reconstructed conductivity (b) and permittivity (e) maps using one seed point located at the yellow asterisk in (a). Right: reconstructed conductivity (c) and permittivity (f) maps using two seed points in (a). The axis unit is cm.
TABLE II.
Reconstructed EP In The Phantom
| EP a | Reconstruction (one seed) | Reconstruction (two seeds) | Probe measurement | |
|---|---|---|---|---|
| #1 | σ | 0.77±0.17 | 0.74±0.17 | 0.64 |
| ε | 77.2±5.4 | 78.3±5.3 | 79.1 | |
|
| ||||
| #2 | σ | 0.98±0.04 | 0.95±0.04 | 0.94 |
| ε | 74.2±4.5 | 75.6±4.5 | 78.1 | |
|
| ||||
| #3 | σ | 1.28±0.16 | 1.26±0.16 | 1.38 |
| ε | 64.7±3.5 | 66.6±3.5 | 71.3 | |
Units of σ and ε are S/m−1 and ε0, respectively.
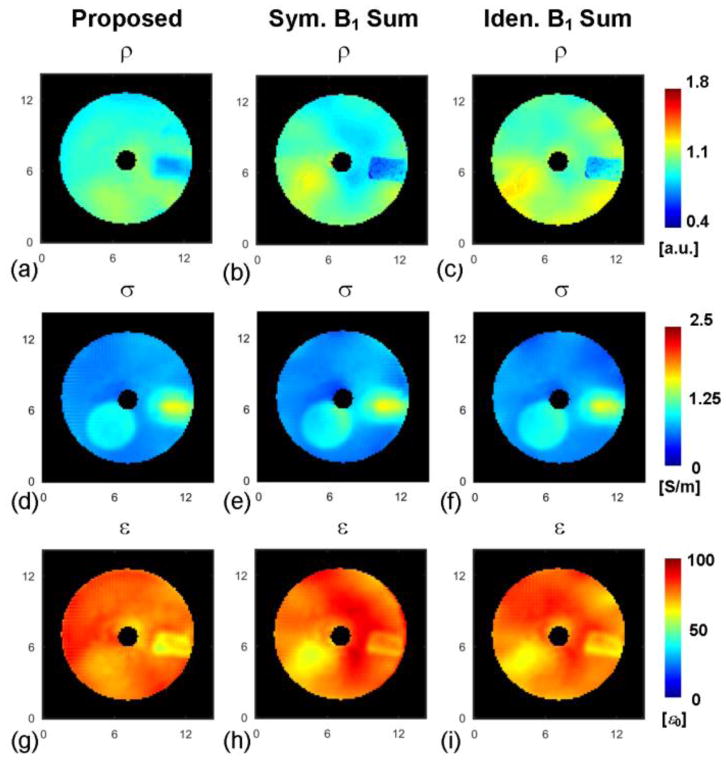
The reconstructed ρ in the phantom using the proposed method is shown in Fig. 6a, with calculated values that are comparable for the gel compartments #1 (0.98±0.08) and #2 (1.07±0.04), which is expected since only the NaCl concentration was slightly changed between the two gels. The value of reconstructed ρ is 0.85±0.05 within the pork. We were not able to independently measure the actual ρ distribution in the pork tissue for assessing the accuracy of the reconstructed ρ results. However, an indirect evaluation consists in applying the calculated ρ value to EPT reconstruction methods, which implicitly rely on unbiased maps, and evaluating the corresponding calculated EP. In the present case we followed this approach using the gradient-based EPT (gEPT) algorithm [15]. We also compared two additional methods for estimating ρ that are based on some B1-pattern assumptions: one assumes an approximate mirroring symmetry between the sum of transmit B1 magnitude and that of receive B1 magnitude through all channels in a transceiver coil symmetrical about the y-axis: [10], [15], while the other assumes an approximate identity between the two sums under the same coil geometry assumptions [9], [39]. As can be seen in Fig. 6b and c, the estimated ρ distributions based on B1-pattern assumptions result in larger spatial deviations of ρ inside each phantom compartment (ρ should be homogeneous in compartment #1 as well as in compartment #2). Similarly, the reconstructed EP maps as shown in Fig. 6e and h and Fig. 6f and i, which were obtained using the gEPT algorithm and estimated ρ from B1-pattern assumptions, clearly depict larger EP erroneous deviations than the reconstructed EP maps using gEPT and calculated ρ with the proposed method (Fig. 6d and g). This is especially noticeable in the permittivity maps. These findings are supported by the quantitative evaluation of the reconstructed EP using REs and CCs as shown in Table III. The larger impact of ρ on permittivity results is consistent with the theoretical analysis that indicates that permittivity is more closely related than the conductivity to the magnitude of B1 field [5].
Fig. 6.
Reconstructed proton density and its effect on the accuracy of EP reconstruction using the gradient-based EPT (gEPT) algorithm. Top: reconstructed proton density using the proposed method (a), assuming symmetric B1 pattern (b) or assuming identical B1 pattern (c). Middle: reconstructed conductivity (d)–(f) using gEPT algorithm and estimated proton density corresponding to (a)–(c), respectively. Bottom: reconstructed permittivity (g)–(i) using gEPT algorithm and estimated proton density corresponding to (a)–(c), respectively. The axis unit is cm.
TABLE III.
Evaluation of Reconstructed EP Using Gradient-based EPT And Differently Derived Proton Density.
| Calculated ρ | S.B.-ρ | I.B.-ρ | ||
|---|---|---|---|---|
| RE | σ | 15% | 18% | 15% |
| ε | 6% | 9% | 8% | |
|
| ||||
| CC | σ | 0.82 | 0.77 | 0.82 |
| ε | 0.6 | 0.17 | 0.35 | |
S.B.-ρ: Estimated ρ assuming symmetric B1 pattern
I.B.-ρ: Estimated ρ assuming identical B1 pattern
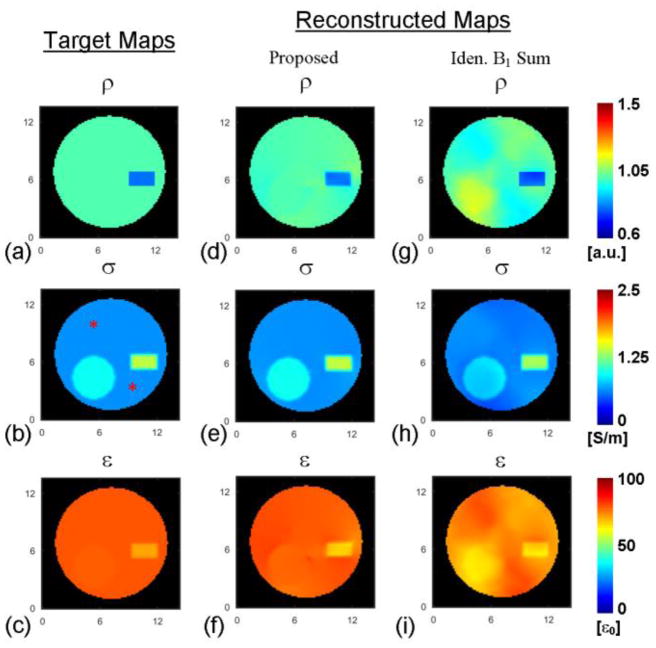
In Fig. 6, one can observe the deleterious consequences, on gEPT based EP reconstruction, of inaccurate ρ estimation derived from B1-pattern assumptions (resulting in inaccurate receive B1 magnitude maps). It can be noticed that errors spatially proprogate not only near boundaries but also in homogeneous regions. The impact on EP reconstruction of ρ estimation inaccuracy was further investigated in a simulation study with a model reproducing the tissue phantom and the RF coil. Probe-measured electrical properties (listed in Table II) of phantom compartments were assigned to the simulation model. The proton density of the model was taken as the calculated value: 0.85 for “meat” and 1 for the rest. The results are shown in Fig. 7. By visual inspection, the reconstructed ρ using the proposed method is consistent with the target ρ map while the B1 pattern-based ρ estimation (assuming ) shows obvious errors. The error pattern in Fig. 7g is similar to that in Fig. 6c. Meanwhile, the reconstructed EP results in Fig. 7e and f, using ρ calculated with the proposed method, indicate much higher fidelity than those in Fig. 7h and i obtained using the B1-pattern approach, especially in reconstructed ε. The REs and CCs of the reconstructions are REρ=1.5%/CCρ=0.92, REσ=1.7%/CCσ=0.99 and REε=2.0%/CCε=0.84 based on the proposed approach, and REρ=5%/CCρ=0.66, REσ=9.9%/CCσ=0.95 and REε=8.8%/CCε=0.43 based on the B1-pattern assumption.
Fig. 7.
Reconstructed proton density and its effect on the accuracy of EP reconstruction using the gradient-based EPT (gEPT) algorithm in a phantom-mimicking simulation study. Images in each column represent (a–c) target maps of ρ, conductivity (σ) and permittivity (ε), (d–f) reconstruction of ρ based on the proposed method, and reconstructions of σ and ε using gEPT algorithm and the reconstructed ρ in (d), (g–i) reconstruction of ρ assuming identical B1 summation pattern, and reconstruction of σ and ε using gEPT algorithm and the estimated ρ in (g). The symbol “*” indicates seed points. The axis unit is cm.
V. Discussions
In this study, for the first time, quantitative ρ distribution was rigorously calculated based on measurable B1 information in MRI, along with the electrical properties. Different from other approaches exploiting various assumptions such as the B1 reciprocity [9], [10] or the 1/ρ-1/T1 relationship [28], [29], the proposed method calculates ρ by solving the Maxwell’s equations involving transmit and receive B1 field, exploiting the multiple channels available in a transceiver array. The method was first evaluated using simulated B1 field, and the results showed strong similarity between, on the one hand, the reconstructed ρ and electrical properties and, on the other hand, their target values. The method was further validated using a physical multi-compartment phantom on a 7T MRI scanner. The experimental results demonstrated accurate EP reconstruction, based on B1 measurements, when compared with direct dielectric probe measurement. Significant improvement in ρ estimation was found with the proposed method compared with B1 pattern-based approaches.
Compared to a previously proposed gradient-based EPT (gEPT) technique [15], which has been shown to provide improved robustness against noise and increased performance near tissue boundaries, the major advantage of the proposed method is that it aims at rigorously calculating ρ from the measured B1 information. It expands the generality of the gEPT method, and it is independent of particular geometric assumptions about the object or the coil for ρ estimation that typically tempt to fail at higher field. At the same time, quantitative ρ map is estimated and can be useful for understanding lesions causing tissue’s water content change. The resultant unbiased magnitude of receive B1 field is also desirable for accurate estimation of SAR [9], [16], which is an important safety concern at high field. As can be seen in (4) and (5), in order to calculate ρ, the transceiver phase for each pair of transmit and receive channels is utilized together with the magnitude and as input. As a common approach in EPT studies [5], [8], [9], [40], utilizing the transceiver phase requires removal of background phase resulting from inhomogeneous B0 field distribution, susceptibility-induced B0 distortion, chemical shift and eddy current induced phase accumulation. On the other hand, EPT methods, such as gEPT, using only relative B1 phase between individual channels [10], [11], [15], are insensitive to possible residual background phase. As suggested by our results in Fig. 6, an optimized strategy could consist of applying the calculated ρ distribution to the gEPT algorithm, thereby taking advantage of the robustness of the relative phase measurement offered by the latter.
Similar to several other EPT techniques[8]–[11], [15], the method proposed in this study relies on using data from multiple RF channels to derive multiple unknowns related to absolute B1 phase, EP and ρ. In principle, at least four transmit channels are needed to derive the gradient of absolute B1 phase based on (4); likewise, at least four receive channels are needed to calculated ρ-related gradient in (5). Considering the wider availability of eight-channel rather than sixteen-channel RF systems, we have also evaluated (data not shown) in simulations the proposed method using only eight equally distributed RF coil elements (based otherwise on the same structure as that of the sixteen-channel coil), loaded with the Duke head model. These simulation results were highly similar to those shown in Fig. 3 with sixteen channels. With only four evenly distributed channels, however, the results were pejoratively affected by the overall limited B1 spatial coverage provided by only 4 channels to an object with the size of a human head. A particular case may be considered for 1.5 or 3T scanners. Indeed, on the clinical scanners (≤ 3 T), multi-channel transmit resources are most often not available, however, standard clinical scanners are typically equipped with multiple receive channels (32 channels are very common). Thus, one potential strategy with these single-channel transmit systems would be to first estimate the absolute B1 phase of the quadrature birdcage volume RF coil (almost universally used for RF transmission on clinical systems) by using the latter in transceiver mode [2], [6]. Then, in a second step, ρ could be calculated using the multiple receive channels and the estimated B1 phase by solving (5). Note that, at such lower field (≤ 3 T) both the phase assumption and B1 pattern-based ρ estimation may be more readily valid. Therefore, their respective accuracy and advantage for estimating ρ would need to be further investigated.
The sensitivity and spatial resolution for detecting contrast in both EP and ρ were evaluated in the simulation study as shown in Fig. 2. It can be seen that down to the relative contrast ratio of 10%, the proposed method is able to detect small regions (<5 mm) of different EP, at a much smaller spatial scale than that of the wavelength (≈14 cm) of the probing RF field. We attributed these performances to the high spatial resolution obtained in MRI acquisitions, which is a general advantage of the EPT technology, and to the enhanced near-boundary performance and noise robustness of the proposed algorithm in which spatial gradient of EP is integrated to derive the final EP maps. Due to the noise-reduction spatial filter, the effective resolution of the reconstructed EP and ρ maps is less than that of actual MRI images, with an evident smoother appearance for the results obtained with experimental data as well as for those obtained in simulation studies when noise addition is performed. This points towards the need for exploring, in future studies, fast and unbiased B1 mapping techniques to achieve high SNR in the measured B1 data in order to reduce or alleviate the use of spatial filters.
In this study, the EP and ρ values of the seed points were assumed to be known in order to calculate the final maps using the corresponding gradient. A frequent approach in semi-quantitative MRI or spectroscopy consists in normalizing metabolites or ρ in various tissues by comparison to the value of a reference tissue such as ventricular CSF for intra-cerebral studies. Similarly, in the current study an arbitrary value of ρ can be assigned to a seed point. However, there is a growing interest in the absolute values of EP, and it may be impractical under some in vivo conditions to find seed points where absolute EP values are assumed to be known. Incorrect assignment of these seed point values can shift the global reconstructed maps. As can be seen in (4) and (5), although the local absolute EP value in εc can be calculated pixel-by-pixel once gradient of absolute phase, EP and ρ are determined, this local pixel-wise EP solution is subjective to error propagation during reconstruction. Recently, we have proposed an algorithm to sample useful absolute EP value in the reconstructed local EP solution [41]. The method utilized the local EP solution to provide absolute EP value reference, and at the same time, improved EP reconstruction performance using gradient g+ from measured as a global constraint. It is straightforward and expected to be more accurate to incorporate the full gradient vector g as provided in the proposed method here.
Including the proposed method, EPT algorithms concerning inhomogeneous EP distribution involve the z-component of B1 field in their equations [4], [10], [15], [40]. However, currently there are no methods to directly access the Bz component using MRI. In this study, using the longitudinal microstrip coil elements, satisfactory results were obtained by neglecting Bz near the middle session of the coil along the z-axis, following the similar strategy adopted in previous EPT studies [10], [15], [40]. This can be seen as a restrictive condition limited to certain types of coil geometry, potentially incompatible with other coil elements involving a larger Bz contribution, such as loop coils with conductors perpendicular to the z-axis. Recently, Katscher et al. proposed, in numerical simulation studies, methods for estimating Bz based on Maxwell’s equations [42], [43]. Further work is needed to determine the practical value of the proposed approach for estimating Bz in experimental studies.
As we can see in (4) and (5), assuming negligible Bz, the object for solving the equations is essentially deriving a system of nonlinear partial differential equations (PDE) involving the unknown absolute B1 phase, EP and ρ. In previous studies, various assumptions have been exploited to gauge the absolute B1 phase [2], [5] or ρ distribution [10], [15]. Assuming known absolute B1 phase, Hafalir et al. developed a linear PDE-based EPT approach (cr-MREPT) [40], and explicitly utilized the spatial relationship between the EP of different voxels, which is carried in the derivatives, to improve the results near boundaries and the robustness to overcome disruption induced by measurement noise. However, reconstruction error increased when cr-MREPT was evaluated using the estimated phase based on the half-transceiver-phase assumption. In this study, the final EP and ρ maps were derived in two steps: 1) the gradient of EP, ρ and B1 phase were calculated using multiple channels of B1 data and 2) spatial integration was carried out on the gradients to obtain the final maps. Unique solution was obtained when multiple channels of B1 data were available. Future work will explore algorithms to solve the distribution of phase, EP and ρ in the nonlinear PDEs as shown in (4) and (5) in one step. They are expected to give more robust reconstruction results by taking advantage of the spatial relationship between voxels and avoiding error propagation across steps.
VI. Conclusion
In this study, for the first time, we have developed a new method to quantitatively map proton density distribution, together with electrical properties distribution, using the B1 field information measured with an MRI scanner. The method was evaluated and validated both theoretically in simulation studies and experimentally in a physical phantom on a 7T scanner. The results demonstrated high spatial resolution and high sensitivity to contrast in reconstructed EP and ρ. The method improves the generality of EPT algorithms utilizing both transmit and receive B1 fields, devoid of specific assumptions to obtain ρ distribution which is coupled with receive B1 field in MRI measurement. Accuracy of reconstructed ρ maps was improved compared to previous estimation based on B1-pattern assumptions. This method is expected to help improve EP-based noninvasive in vivo tissue characterization and provide a new way for estimating quantitative ρ map for diagnostic and research purpose.
Acknowledgments
This work was supported in part by NIH R21 EB017069, R01 EY023101, U01 HL117664, R21 EB014353, P41 EB015894, R01 EB011551, S10 RR026783, NSF CBET-1450956, CBET-1264782, and WM KECK Foundation. Jiaen Liu was supported by a University of Minnesota Doctoral Dissertation Fellowship.
Contributor Information
Jiaen Liu, Department of Biomedical Engineering, University of Minnesota, Minnesota, 55455, USA.
Pierre-Francois Van de Moortele, Center for Magnetic Resonance Research, University of Minnesota, Minnesota, 55455, USA.
Xiaotong Zhang, Department of Biomedical Engineering, University of Minnesota, Minnesota, 55455, USA.
Yicun Wang, Department of Biomedical Engineering, University of Minnesota, Minnesota, 55455, USA.
Bin He, Department of Biomedical Engineering and Institute for Engineering in Medicine, University of Minnesota, Minnesota, 55455, USA.
References
- 1.Haacke EM, Petropoulos LS, Nilges EW, Wu DH. Extraction of conductivity and permittivity using magnetic resonance imaging. Phys Med Biol. 1991 Jun;36(6):723–734. [Google Scholar]
- 2.Wen H. Noninvasive quantitative mapping of conductivity and dielectric distributions using RF wave propagation effects in high-field MRI. Proc. SPIE; San Diego, CA, USA. 2003; pp. 471–477. [Google Scholar]
- 3.Katscher U, Voigt T, Findeklee C, Vernickel P, Nehrke K, Dossel O. Determination of Electric Conductivity and Local SAR Via B1 Mapping. IEEE Trans Med Imag. 2009 Sep;28(9):1365–1374. doi: 10.1109/TMI.2009.2015757. [DOI] [PubMed] [Google Scholar]
- 4.Zhang X, Zhu S, He B. Imaging Electric Properties of Biological Tissues by RF Field Mapping in MRI. IEEE Trans Med Imaging. 2010 Feb;29(2):474–481. doi: 10.1109/TMI.2009.2036843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Voigt T, Katscher U, Doessel O. Quantitative conductivity and permittivity imaging of the human brain using electric properties tomography. Magn Reson Med. 2011;66(2):456–466. doi: 10.1002/mrm.22832. [DOI] [PubMed] [Google Scholar]
- 6.van Lier AL, Brunner DO, Pruessmann KP, Klomp DWJ, Luijten PR, Lagendijk JJW, van den Berg CAT. B 1+ Phase mapping at 7 T and its application for in vivo electrical conductivity mapping. Magn Reson Med. 2012;67(2):552–561. doi: 10.1002/mrm.22995. [DOI] [PubMed] [Google Scholar]
- 7.Seo JK, Kim MO, Lee J, Choi N, Woo EJ, Kim HJ, Kwon OI, Kim DH. Error analysis of nonconstant admittivity for MR-based electric property imaging. IEEE Trans Med Imaging. 2012 Feb;31(2):430–437. doi: 10.1109/TMI.2011.2171000. [DOI] [PubMed] [Google Scholar]
- 8.Sodickson D, Alon L, Deniz C, Brown B, Zhang B, Wiggins G, Cho G, Eliezer N, Novikov D, Lattanzi R, Duan Q, Sodickson L, Zhu Y. Local Maxwell Tomography Using Transmit-Receive Coil Arrays for Contact-Free Mapping of Tissue Electrical Properties and Determination of Absolute RF Phase. Proceedings of the 20th Annual Meeting of ISMRM; Melbourne, Australia. 2012; p. 388. [Google Scholar]
- 9.Katscher U, Findeklee C, Voigt T. B1-based specific energy absorption rate determination for nonquadrature radiofrequency excitation. Magn Reson Med. 2012;68(6):1911–1918. doi: 10.1002/mrm.24215. [DOI] [PubMed] [Google Scholar]
- 10.Zhang X, Van de Moortele PF, Schmitter S, He B. Complex B1 mapping and electrical properties imaging of the human brain using a 16-channel transceiver coil at 7T. Magn Reson Med. 2013 May;69(5):1285–1296. doi: 10.1002/mrm.24358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu J, Zhang X, Van de Moortele PF, Schmitter S, He B. Determining electrical properties based on B(1) fields measured in an MR scanner using a multi-channel transmit/receive coil: a general approach. Phys Med Biol. 2013 Jul;58(13):4395–4408. doi: 10.1088/0031-9155/58/13/4395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Joines WT. The measured electrical properties of normal and malignant human tissues from 50 to 900 MHz. Med Phys. 1994;21(4):547–550. doi: 10.1118/1.597312. [DOI] [PubMed] [Google Scholar]
- 13.Yoo D. The dielectric properties of cancerous tissues in a nude mouse xenograft model. Bioelectromagnetics. 2004 Oct;25(7):492–497. doi: 10.1002/bem.20021. [DOI] [PubMed] [Google Scholar]
- 14.Balidemaj E, van Lier ALHMW, Crezee H, Nederveen AJ, Stalpers LJA, van den Berg CAT. Feasibility of Electric Property Tomography of pelvic tumors at 3T. Magn Reson Med. 2015 Apr;73(4):1505–1513. doi: 10.1002/mrm.25276. [DOI] [PubMed] [Google Scholar]
- 15.Liu J, Zhang X, Schmitter S, Van de Moortele P-F, He B. Gradient-based electrical properties tomography (gEPT): A robust method for mapping electrical properties of biological tissues in vivo using magnetic resonance imaging. Magn Reson Med. 2014 Sep; doi: 10.1002/mrm.25434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang X, Schmitter S, Van de Moortele PF, Liu J, He B. From Complex B1 Mapping to Local SAR Estimation for Human Brain MR Imaging Using Multi-channel Transceiver Coil at 7T. IEEE Trans Med Imaging. 2013 Mar;32(6):1058–1067. doi: 10.1109/TMI.2013.2251653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Laule C, Vavasour IM, Moore GRW, Oger J, Li DKB, Paty DW, MacKay AL. Water content and myelin water fraction in multiple sclerosis. A T2 relaxation study. J Neurol. 2004 Mar;251(3):284–293. doi: 10.1007/s00415-004-0306-6. [DOI] [PubMed] [Google Scholar]
- 18.Ayata C, Ropper AH. Ischaemic brain oedema. J Clin Neurosci. 2002 Mar;9(2):113–124. doi: 10.1054/jocn.2001.1031. [DOI] [PubMed] [Google Scholar]
- 19.Neeb H, Zilles K, Shah NJ. A new method for fast quantitative mapping of absolute water content in vivo. NeuroImage. 2006 Jul;31(3):1156–1168. doi: 10.1016/j.neuroimage.2005.12.063. [DOI] [PubMed] [Google Scholar]
- 20.Andersson T, Ericsson A, Eriksson B, Hemmingsson A, Lindh E, Nyman R, Oberg K. Relative proton density and relaxation times in liver metastases during interferon treatment. Br J Radiol. 1989 May;62(737):433–437. doi: 10.1259/0007-1285-62-737-433. [DOI] [PubMed] [Google Scholar]
- 21.Hoult DI. The principle of reciprocity in signal strength calculations—A mathematical guide. Concepts Magn Reson. 2000 Jan;12(4):173–187. [Google Scholar]
- 22.Sacolick LI, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch-Siegert shift. Magn Reson Med. 2010;63(5):1315–1322. doi: 10.1002/mrm.22357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn Reson Med. 2007 Jan;57(1):192–200. doi: 10.1002/mrm.21120. [DOI] [PubMed] [Google Scholar]
- 24.Nehrke K, Börnert P. DREAM—a novel approach for robust, ultrafast, multislice B1 mapping. Magn Reson Med. 2012;68(5):1517–1526. doi: 10.1002/mrm.24158. [DOI] [PubMed] [Google Scholar]
- 25.Ashburner J, Friston KJ. Unified segmentation. NeuroImage. 2005 Jul;26(3):839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- 26.Volz S, Nöth U, Deichmann R. Correction of systematic errors in quantitative proton density mapping. Magn Reson Med. 2012 Jul;68(1):74–85. doi: 10.1002/mrm.23206. [DOI] [PubMed] [Google Scholar]
- 27.Weiskopf N, Lutti A, Helms G, Novak M, Ashburner J, Hutton C. Unified segmentation based correction of R1 brain maps for RF transmit field inhomogeneities (UNICORT) NeuroImage. 2011 Feb;54(3):2116–2124. doi: 10.1016/j.neuroimage.2010.10.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Volz S, Nöth U, Jurcoane A, Ziemann U, Hattingen E, Deichmann R. Quantitative proton density mapping: correcting the receiver sensitivity bias via pseudo proton densities. NeuroImage. 2012 Oct;63(1):540–552. doi: 10.1016/j.neuroimage.2012.06.076. [DOI] [PubMed] [Google Scholar]
- 29.Fatouros PP, Marmarou A. Use of magnetic resonance imaging for in vivo measurements of water content in human brain: method and normal values. J Neurosurg. 1999 Jan;90(1):109–115. doi: 10.3171/jns.1999.90.1.0109. [DOI] [PubMed] [Google Scholar]
- 30.Gelman N, Ewing JR, Gorell JM, Spickler EM, Solomon EG. Interregional variation of longitudinal relaxation rates in human brain at 3.0 T: relation to estimated iron and water contents. Magn Reson Med. 2001 Jan;45(1):71–79. doi: 10.1002/1522-2594(200101)45:1<71::aid-mrm1011>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 31.Cakirer S, Karaarslan E, Arslan A. Spontaneously T1-hyperintense lesions of the brain on MRI: a pictorial review. Curr Probl Diagn Radiol. 2003 Sep;32(5):194–217. doi: 10.1016/s0363-0188(03)00026-4. [DOI] [PubMed] [Google Scholar]
- 32.Adriany G, Van de Moortele PF, Ritter J, Moeller S, Auerbach EJ, Akgün C, Snyder CJ, Vaughan T, Uğurbil K. A geometrically adjustable 16-channel transmit/receive transmission line array for improved RF efficiency and parallel imaging performance at 7 Tesla. Magn Reson Med. 2008 Mar;59(3):590–597. doi: 10.1002/mrm.21488. [DOI] [PubMed] [Google Scholar]
- 33.Kozlov M, Turner R. Fast MRI coil analysis based on 3-D electromagnetic and RF circuit co-simulation. J Magn Reson. 2009 Sep;200(1):147–152. doi: 10.1016/j.jmr.2009.06.005. [DOI] [PubMed] [Google Scholar]
- 34.Lemdiasov RA, Obi AA, Ludwig R. A numerical postprocessing procedure for analyzing radio frequency MRI coils. Concepts Magn Reson Part A. 2011 Jul;38A(4):133–147. [Google Scholar]
- 35.Just M, Thelen M. Tissue characterization with T1, T2, and proton density values: results in 160 patients with brain tumors. Radiology. 1988 Dec;169(3):779–785. doi: 10.1148/radiology.169.3.3187000. [DOI] [PubMed] [Google Scholar]
- 36.Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys Med Biol. 1996 Nov;41(11):2271–2293. doi: 10.1088/0031-9155/41/11/003. [DOI] [PubMed] [Google Scholar]
- 37.Orzada S, Johst S, Maderwald S, Bitz AK, Solbach K, Ladd ME. Mitigation of B1(+) inhomogeneity on single-channel transmit systems with TIAMO. Magn Reson Med. 2013 Jul;70(1):290–294. doi: 10.1002/mrm.24453. [DOI] [PubMed] [Google Scholar]
- 38.Van de Moortele P-F, Snyder C, DelaBarre L, Adriany G, Vaughan T, Ugurbil K. Calibration Tools for RF Shim at Very High Field with Multiple Element RF Coils: from Ultra Fast Local Relative Phase to Absolute Magnitude B1+ Mapping. Proc. Intl. Soc. Mag. Reson. Med; Berlin, Germany. 2007; p. 1676. [Google Scholar]
- 39.Van de Moortele P-F, Ugurbil K. Very Fast Multi Channel B1 Calibration at High Field in the Small Flip Angle Regime. Proc. Intl. Soc. Mag. Reson. Med; Hawaii, USA. 2009; p. 367. [Google Scholar]
- 40.Hafalir FS, Oran OF, Gurler N, Ider YZ. Convection-reaction equation based magnetic resonance electrical properties tomography (cr-MREPT) IEEE Trans Med Imaging. 2014 Mar;33(3):777–793. doi: 10.1109/TMI.2013.2296715. [DOI] [PubMed] [Google Scholar]
- 41.Liu J, Zhang X, Wang Y, Van de Moortele P-F, He B. Local Electrical Properties Tomography With Global Regularization By Gradient. Proceedings of the 23th Annual Meeting of ISMRM; Toronto, ON, Canada. 2015; p. 3297. [Google Scholar]
- 42.Katscher U, Djamshidi K. Improving B1-based SAR determination via iterative determination of missing field components. Proceedings of the 21st Annual Meeting of ISMRM; Salt Lake City, USA. 2013; p. 4410. [Google Scholar]
- 43.Katscher U, Braun M, Findeklee C, Leussler C, Graesslin I, Vernickel P, Morlock M. B1-based SAR determination for local RF transmit coils. Proceedings of the 23rd Annual Meeting of ISMRM; Toronto, ON, Canada. 2015; p. 383. [Google Scholar]