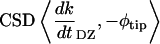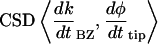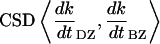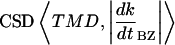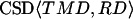Root-Gel Interactions and the Root Waving Behavior of Arabidopsis^,

Abstract

Arabidopsis roots grown on inclined agarose gels exhibit a sinusoidal growth pattern known as root waving. While root waving has been attributed to both intrinsic factors (e.g. circumnutation) and growth responses to external signals such as gravity, the potential for physical interactions between the root and its substrate to influence the development of this complex phenotype has been generally ignored. Using a rotating stage microscope and time-lapse digital imaging, we show that (1) root tip mobility is impeded by the gel surface, (2) this impedance causes root tip deflections by amplifying curvature in the elongation zone in a way that is distinctly nontropic, and (3) root tip impedance is augmented by normal gravitropic pressure applied by the root tip against the gel surface. Thus, both lateral corrective bending near the root apex and root tip impedance could be due to different vector components of the same graviresponse. Furthermore, we speculate that coupling between root twisting and bending is a mechanical effect resulting from root tip impedance.

The roots of Arabidopsis, grown on dense agarose gels, exhibit a gradient of growth behaviors that depend on the pitch of the gel's surface (Okada and Shimura, 1990; Simmons et al., 1995b; Buer et al., 2000; Migliaccio and Piconese, 2001). Generally, when the gel pitch is vertical (θ = 90°), the roots grow relatively straight; when the pitch is horizontal (θ = 0°), the roots form regular coils; and when the pitch is of intermediate angle (θ = 30°–60°), the roots grow in an oscillatory pattern commonly referred to as root waving. Root growth trajectories vary among ecotypes (Rutherford and Masson, 1996; Hashimoto, 2002). They are sensitive to exogenous or endogenous ethylene in the head space above the roots and to the concentration of Suc in the gel (Buer et al., 2003) and they depend on the kind and concentration of media salts, on the type and concentration of gel, and on the way the plates are sealed (Buer et al., 2000). Some genetic lesions are known to alter the gel pitch-dependence of the phenotype. The roots of one mutant produce tightly piled oscillations when the gel is shifted from vertical to 45° (Okada and Shimura, 1990). A similar phenotype is observed in the presence of exogenous ethylene (Buer et al., 2003). Another mutant (Okada and Shimura, 1990) will form coils at a gel pitch of 45°, as does the reduced gravitropism (rgr1) mutant of Simmons et al. (1995a).

In addition to the straight/waving/coiling phenotypes observed at different gel pitches, the roots also tend to toward the right as they grow (Migliaccio and Piconese, 2001), slanting to the right during wavy and straight growth, and turning only to the right during coiling growth (see Fig. 1A for definitions of right and left-handed twisting and bending). This bias appears to be general, except for a few reported mutants that are biased to the left (Marinelli et al., 1997; Furutani et al., 2000; Thitamadee et al., 2002). During wavy growth, a right turn is often accompanied by left-handed twisting, whereas a left turn is often accompanied by right-handed twisting, although to a lesser extent. Right-handed coiling roots always twist to the left, as do right-handed slanting roots. Okada and Shimura (1990), Simmons et al. (1995b), and Migliaccio and Piconese (2001) have argued that the correlation between twisting and turning reflects a functional or explanatory relationship to flattened versions of the spirals formed by twining vines, and that this correlation and its relationship to circumnutation constitutes the functional basis of root waving. Clearly, the underlying bending and twisting biases of the root are important to understanding the asymmetry commonly observed in slanting and coiling. However, the absence of a consistently tight correlation between twisting and bending, even during wavy growth (Buer et al., 2003), suggests that root waving is contingent upon neither an explanation of this coupling nor the asymmetries that inhere in them.

Figure 1.

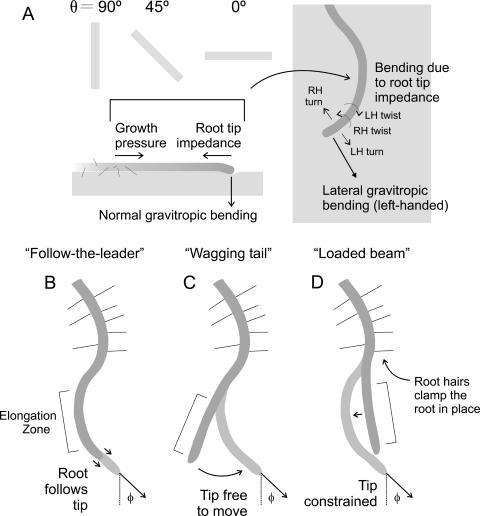
Hypothetical consequences of mechanical interactions between the root tip and gel surface. A, A schematic of the various physical forces suspected to be involved in root waving in the presence of physical interactions between the root tip and gel surface. Normal gravitropic bending could affect the magnitude of root tip impedance. Arrows over the root tip in the right panel indicate right-handed (RH) and left-handed (LH) bending and twisting. The region behind the root tip shown here has negative curvature. B, Follow-the-leader growth. The root tip prescribes the final shape of the root. C, Wagging tail growth. In the absence of friction, the root tip is free to move, and the gel surface acts simply as a two-dimensional constraint on root growth. An oscillatory pattern develops due to a lateral gravitropic over-correction or to circumnutation. D, Loaded beam growth. Surface interactions between the root tip and the gel surface impede the movement of the root tip relative to the expansion of the elongation zone. This amplifies whatever root curvature is already present behind the root tip up to the point of first root hair development. In each case (B, C, and D), φ is the angle between the direction the root tip is pointing (arrow) and the downward slope of the gel surface (dotted line), here shown as an angle of positive magnitude (i.e. to the left in the frame of reference of the root).

The central question in the study of root waving is why the root should coherently wave or coil. Why is the relatively straight growth of the root at 90° not matched by equally straight growth at 45°? And why at 0°, in the absence of any effectual lateral gravitropic bias, does the root not simply meander? While the overall downward trajectory of the root is clearly a gravitropic effect, as corroborated by studies of auxin-deficient or gravitropism-impaired mutants (Okada and Shimura, 1990; Simmons et al., 1995a; Rutherford and Masson, 1996; Mullen et al., 1998b; Rosen et al., 1999; Migliaccio and Piconese, 2001; Massa and Gilroy, 2003), why the root should turn at all—that is, what causes root tip deflection?—is still debated. A variety of deflecting forces have been proposed, including thigmotropism (Okada and Shimura, 1990), circumnutation (Simmons et al., 1995b; Rutherford and Masson, 1996; Migliaccio and Piconese, 2001), and, as mentioned above, the coupling that occasionally existed between root twisting, coiling and slanting. However, none of these studies has considered the direct physical effect that the gel could have on the growth of the root. Because the length and diameter of the root tip are small, the forces acting between the root and gel will be relatively large as compared to the bending and torsional moduli of the root (i.e. the degree of stress that must be applied to bend or twist the root a given amount; in roots, given their geometry, both of these moduli are likely to scale with the 4th power of radius). We hypothesize that root tip deflection—whether of the continuous sort as in coiling, or of the periodic sort as in waving—can be explained as the result of this physical interaction. If present, friction between the root tip and the gel surface (or root tip impedance), acting in opposition to the growth pressures produced by the root, could lead the more basal regions of the root to bend (Fig. 1A). Bending of this sort, i.e. exaggeration in root curvature due to root elongation, was previously observed by Simmons et al. (1995b), but not experimentally pursued.

Friction between the root tip and the gel would impede the normal movement of the root tip, an effect that would be enhanced by any force that drew the root tip against the gel surface, including gravitropism. This raises the intriguing possibility that both the production and correction of root tip deflections result from different aspects of the same graviresponse, parsed into its lateral and normal components (Fig. 1A). Lateral gravitropism, the more traditionally recognized component of the graviresponse in root waving studies, acts in the plane of the gel surface to maintain the root on a trajectory congruent with the downward slope of the gel surface. It will be strong—that is, it will contain more of the total bending differential imposed by the graviresponse—when the gel pitch is near vertical. Conversely, the remaining component of the graviresponse, normal gravitropism, acts to turn the root in a direction perpendicular to the plane of the gel surface. Normal gravitropic bending, and thus friction and root tip impedance, will be strongest when gel pitch is near horizontal. At a 90° pitch, then, root tip impedance will be minimal and lateral gravitropic corrections will be robust, leading to relatively straight growth along the downward slope of the gel. At a 0° pitch, on the other hand, root tip impedance will be at its maximum, while the lateral component of the graviresponse will be ineffectual, leading to bending in the root elongation zone from which the root cannot recover, i.e. coiling. At intermediate pitches, the normal and lateral components of the graviresponse will be of intermediate strength, leading to impedance-derived root tip deflections followed by lateral gravitropic corrections, and so on. This hypothesis, that gravitropism-derived root tip impedance is critical to the development of these phenotypes, is lent circumstantial support by the observation that roots will wave coherently when the gel is below the root (60° pitch), but not when the gel is above the root (120° pitch, Simmons et al., 1995b). Instead, the roots grow in an essentially straight pattern along the downward, if inverted, slope of the gel. If circumnutation alone were responsible for root tip deflections, an equal degree of root waving would be expected at both 60° and 120°.

Evaluating this root tip impedance hypothesis requires not only a demonstration of the presence of root tip-gel surface interactions, but also evidence that it is gravitropism that generates this impedance. The former can be accomplished by direct observation of the evolution of the wavy root phenotype through time. This would represent a methodological break from previous studies, which have only documented already established patterns of growth. Depending on the behavior of the root tip and the elongation zone, the root-waving phenotype could emerge in one or a combination of at least three categorically different ways. In the first (Fig. 1B, follow-the-leader growth), the entire root follows the same trajectory as the root tip. A complex growth response would be required to generate the wavy-root shape in this way, and so seems unlikely to occur. In the second (Fig. 1C, wagging tail growth), the lateral and longitudinal movement of the root tip is unimpeded, and constrained only by the two-dimensional environment imposed by hydrostatic interactions with the gel surface. Here, root waving could be due to gravitropic overshoot or circumnutation. In the third (Fig. 1D, loaded beam growth), the lateral and longitudinal movement of the root tip is impeded by the gel surface, leading to growth-induced amplification of any curvature already present in the root. If root waving were found to emerge in this way, then it would probably preclude circumnutation as the primary deflective force.

Loaded beam growth and wagging tail growth can be critically distinguished in a number of ways. First, loaded beam growth will produce curvature anywhere in the root elongation zone up to where root hairs first begin to develop, whereas wagging tail growth will produce curvature only in the distal part of the root (first 500 μm) where tropic growth responses are most highly concentrated (Mullen et al., 1998a; Massa and Gilroy, 2003). Second, unlike curvature development in wagging tail growth, we would expect curvature development in loaded beam growth to be found throughout the elongation zone and thus to be temporally and spatially separable into curvature due to root tip impedance on the one hand and curvature due to lateral gravitropic corrections on the other. Third, loaded beam growth should be accompanied by evidence of physical interactions between the root tip and gel surface, such as gel surface deformation. Finally, under loaded beam growth, root elongation rates should be higher than the rate of tip movement, whereas under wagging tail growth, root tip movement should be at least as fast as the root elongation rate, and under follow-the-leader growth, the root should elongate as fast as the root tip moves (as would be observed if the root grew in a straight line).

In this study, these possibilities are distinguished using a rotating-stage zoom microscope that houses a sterile, gel-plated Arabidopsis seedling and permits digital time lapse imaging of the root while held at a fixed pitch. Our goal is to determine first if the root tip is impeded by the gel surface and second, using spectral analysis of rates of curvature development in different parts of the root elongation zone to see if deviations in root tip angle from the downward slope of the gel surface are attributable to that impedance. In a separate experiment, but using similar methods, we confirm the results of the asymmetric gel pitch experiment of Simmons et al. (1995b), which showed that root waving intensity is greatest when the gel surface is below the root, and thus dependent upon gravitropism for its strength. The results presented here are consistent with the loaded beam model of growth, and strongly indicate the presence of root tip impedance, which is in turn amplified by normal gravitropic bending. The implications of this finding with respect to other root growth behaviors, such as root twisting, are discussed.

RESULTS

Growth Trajectories and Tip Movement

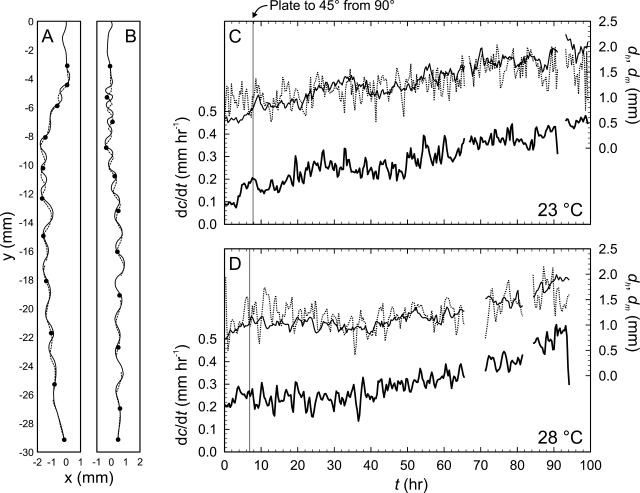
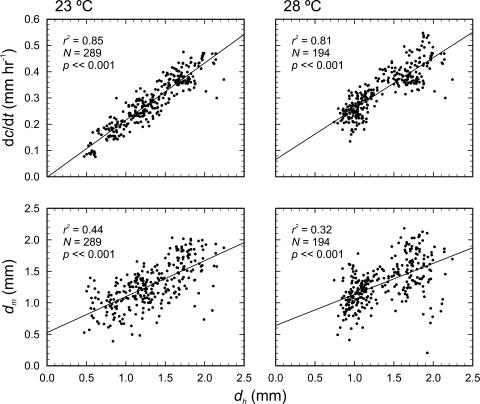
The growth of two roots was followed in detail over a period of 100 h at 0.33 to 0.5 h intervals, with one root grown at a gel surface temperature of 23°C and the other at a temperature of 28°C. In both cases, wavy growth commenced after the gels' pitch was changed from 90° to 45° (Fig. 2, A and B), and root elongation rate (dc/dt) increased with time, with the root grown at 28°C growing slightly faster at the beginning of the experiment (Fig. 2, C and D). Both the distance from the tip to the root hairs d_h and the distance from the tip to where the root stopped moving d_m increased with time. Early in the 28°C experiment (between t = 10 and 20 h), d_m was slightly higher than d_h, indicating that the root was moving despite the presence of root hairs, but otherwise d_m and d_h were weakly correlated in both roots (Fig. 3). Furthermore, dc/dt was well correlated with d_h, suggesting that dc/dt was more closely aligned with the length of the elongation zone (that is, to the amount of root that is elongating) than with the root's relative elemental growth rate (compare with Beemster and Baskin, 1998).

Figure 2.

Growth rates and the point of first root hair development in roots grown at 23°C (A and C) and 28°C (B and D) as a function of time. A and B, Final shape (solid line) and root tip pathway (dashed line) of roots grown at 23°C (A) and 28°C (B). Black circles indicate positions of the root tip at 10 h intervals starting at t = 0 h (arbitrary). Missing data reflect times when the root tip had grown outside the field of view. C and D, The root elongation rate (dc/dt, thick solid line), the distance from the root tip to first root hair development (d_h, thin solid line), and the distance from the root tip to where root ceases to significantly move (d_m, dotted line), for roots grown at 23°C (C) and 28°C (D). The vertical solid line in each panel indicates when the plate was shifted from θ = 90° to 45° (23°C, 7.9 h; 28°C, 6.9 h).

Figure 3.

d_h plotted against dc/dt and d_m at 23°C and 28°C, indicating a relationship between the length of the growth zone and its elongation rate, and between a measure of growth zone length and the point of cessation of lateral growth zone motion.

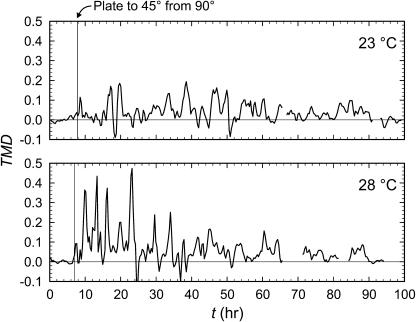
The final shape of the root did not match the trajectory of the root tip at either 23°C or 28°C (Fig. 2, A and B), immediately ruling out the follow-the-leader category of wavy root development (Fig. 1D). The root elongation rate-normalized difference between dc/dt and the rate of movement of the root tip (called the tip movement differential, or TMD) was positive in both roots (Fig. 4), implying a loaded beam mode of root waving. There were some negative excursions in TMD, indicating occasional wagging tail growth. TMD was nearly zero and relatively invariant prior to rotating the gel surface from a 90° to a 45° pitch, when it abruptly increased and thenceforth declined with time. TMD was greater at 28°C than at 23°C, but in both cases TMD varied periodically, suggesting periodic variation in root tip impedance.

Figure 4.

The tip movement differential (or TMD) at 23°C and 28°C. The vertical solid line in each panel indicates when the plate was shifted from θ = 90° to 45° (see Fig. 2). TMD reflects the degree to which root elongation exceeds root tip movement. Positive and negative values are reflective of the loaded beam and wagging tail models, respectively (Fig. 1, B and C).

Curvature Development

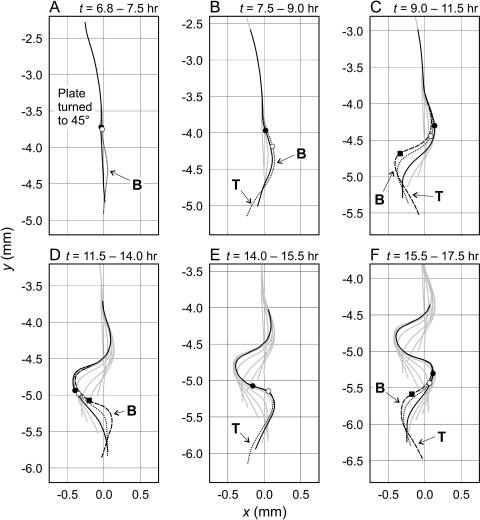
Curvature developed differently in different parts of the root and in a basally progressive manner (Fig. 5). Gel pitch was initially set to 90°, allowing the root to grow straight along the downward slope of the gel (Fig. 5A). When rotated to a pitch of 45° (at t = 6.9 h for the 28° experiment), curvature developed behind the root tip with no lateral tip movement. Because the root tip was oriented along the downward slope of the gel surface prior to shifting the gel pitch to 45°, this initial curvature cannot be attributed to a lateral gravitropic correction. As the root grew, the bend continued to develop but at a position basal of the root tip, acting to turn the root tip away from the downward slope of the gel surface (Fig. 5B). Immediately subsequent to that, the root tip and the 0.5-mm region behind it bent slightly in the opposite direction (Fig. 5B). This new curvature then underwent additional bending with little lateral tip movement, again in a basally progressive manner (Fig. 5C). The process repeated itself in opposite directions, with bending at the root tip serving to correct deviations from the vertical, and the elongation of the root accentuating this curvature and thus imposing stimulus for future lateral gravitropic bending (Fig. 5, D–F; see Supplemental Video 1 at www.plantphysiol.org).

Figure 5.

Curvature development in the root grown at 28°C between t = 6.8 and 17.5 h. At t = 6.8 h, θ was set to 45° from 90°. Root shape is given by two to three centerlines per frame (solid, dotted, and long-dashed, with increasing t). The gray lines indicate the positions of the root in the previous frames. The point at which the first root hairs were observed in each of these time intervals is given by a set of symbols (black circle, white circle, and square). Bending near the root apex (putatively tropic) is denoted by the symbol T, whereas bending throughout the root (putatively nontropic) is denoted by the symbol B. These forms of bending are distinguished by whether the section of root is near the tip and by their direction of curvature. See Supplemental Video 1 for the original time-lapse image source of this sequence.

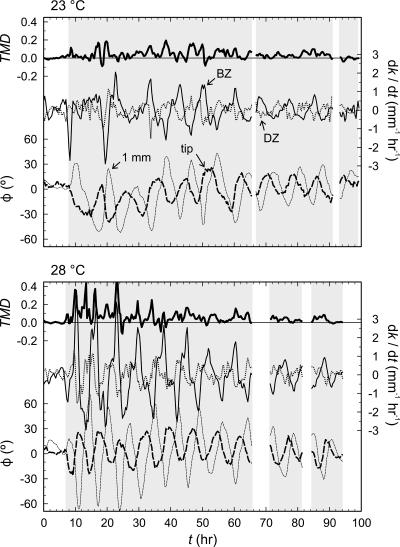
Because of the delay in the development of root curvature in the distal versus the more basal parts of the root elongation zone, curvature development (dk/dt) in the root elongation zone was measured (Fig. 6) separately for distal and basal zones (DZ and BZ, respectively). The DZ and BZ are arbitrarily delimited at a distance of 0.5 mm from the root tip, following the demarcations indicated by the work of Mullen et al. (1998a), Massa and Gilroy (2003), and others. The angle between a tangent to the centerline of the root and the downward slope of the gel surface (φ) was measured (Fig. 6) at both the root tip (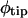) and at a point 1 mm basal of the root tip (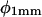). Curvature developed at a higher rate in both the distal and basal zones at 28°C than it did at 23°C, and there was a clear visual synchronization between TMD and curvature development in the basal zone (dk/dt_BZ) at 28°C. In both roots, curvature development in the distal zone (dk/dt_DZ) appeared to be inversely in phase with φ at the root tip, and while both roots exhibited the same degree of variation in variation in 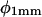was much greater at 28°C. Furthermore, 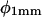and dk/dt_BZ were greater than 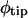and dk/dt_DZ in both roots, supporting the presence of basally progressive and amplified curvature in the root.

Figure 6.

Tip movement differential (TMD), curvature development (dk/dt) in the distal and basal zones (DZ and BZ), and root angular deviation (φ) from the downward slope of the gel at the tip and 1 mm back from the tip. Gray shading indicates temporal regions in which good spectral data can be resolved (i.e. the gel surface has been turned to 45° and the root tip is still within the field of view).

Gel Surface Deformation

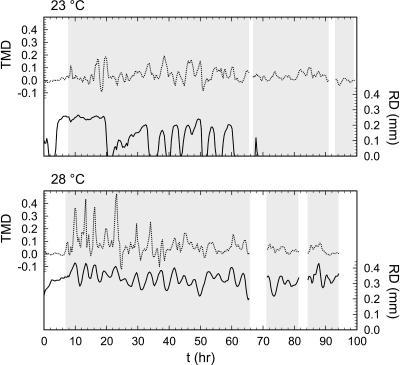
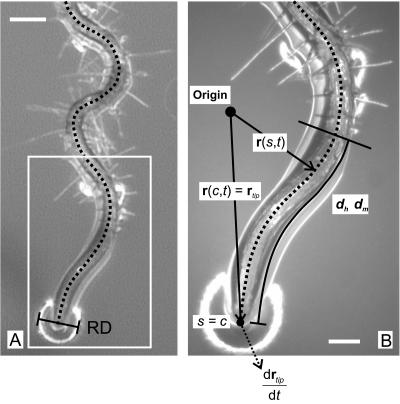
Gel surface deformation by the root tip was quantified as the reflection diameter (RD) observed around the root tip. A large reflection diameter indicated a deeper deformation of the gel surface, and thus a larger applied force. This reflection was only observed at the tip. RD appeared to be in phase with TMD, especially at 28°C (Fig. 7), but was negligible at 23°C after approximately 70 h. RD was generally higher at 28°C than at 23°C, although the absence of a light level control made direct comparison of the two problematic. In both cases RD was periodic, suggesting that the force applied by the root tip to the gel surface was, as well.

Figure 7.

TMD and tip reflection diameter (RD). Nonexistent reflections were assigned a zero RD value. See Figure 6 for relevance of gray shading, and Supplemental Video 1 for an example of variation in RD with time.

Spectral Analysis

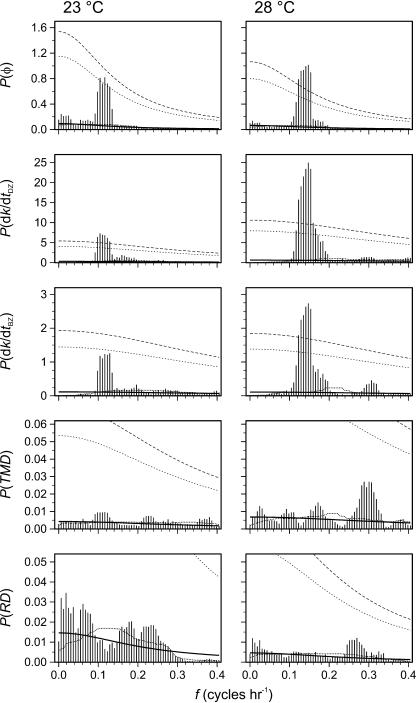
These signals were spectrally analyzed using the multiple-taper (MT) method of power spectral density estimation outlined by Thomson (1982). This method is appropriate for brief and interrupted time series, such as these. Using the MT method, it was found that the power spectral densities of φ, dk/dt_DZ, and dk/dt_BZ (Fig. 8) were clustered at frequencies of once per 7.8 to 10.2 h at 23°C, and once per 6.5 to 8.2 h at 28°C. In general, these clusters were statistically distinguishable from background red noise (χ²-test, df = 6, P < 0.05), except for dk/dt_BZ at 23°C. Some additional clustering, though not statistically significant, was observed in some of these signals at one octave above the primary cluster. The power spectral densities of TMD and RD also indicated clustering at one octave above the primary cluster frequencies, especially at 28°C, but again none was statistically significant.

Figure 8.

Spectrum estimates (vertical lines) using the multiple-taper method (Thomson, 1982), with p = 2 (df = 6), of φ, dk/dt_DZ, dk/dt_BZ, TMD, and RD at both 23°C and 28°C. The spectra are estimated using the shaded data in Figures 6 and 7, with zero padding in nonshaded regions. The background noise level is estimated using 43-bin median window filter (thin dotted line) and least-squares fit (thick solid line) of a red-noise continuous spectrum (see text for details). The 95% (thin short-dashed line) and 99% (thin long-dashed line) χ² confidence limits against the background spectra are also given.

The cross-spectral densities (CSDs) of select pairs of these signals were calculated to determine if they were correlated in magnitude and phase at different frequencies. If the CSD (a complex function) is statistically coherent at a given frequency (that is, its coherence is significantly greater than zero according to Student's t distribution), then it can be used to determine the phase shift between the signals at that frequency (Table I). The cross spectral density of curvature development in the distal zone and root tip deflection angle indicated that the two were negatively correlated and in phase, while a CSD of curvature development in the distal and basal zones indicated that the basal zone lagged by 2 to 3 h. Furthermore, change in root tip deflection angle with time was tightly in phase with curvature development in the basal zone.

Table I.

Time lags between various time series using the multi-taper cross-spectral density method (Thomson, 1982)

	T = 23°C			T = 28°C
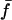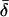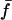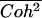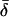	h−1		h	h−1		h
	0.12	0.92***	0.78	0.14	0.98***	0.53
	0.11	0.94***	0.20	0.14	0.95***	0.26
	0.11	0.90***	2.86	0.14	0.98***	2.08
	0.22	0.58*	0.75	0.29	0.71**	−0.23
	n/a	n/a	n/a	0.29	0.69*	−0.32

Significance level is the two-tailed probability that Coh (i.e. the square-root of Coh², here treated as a correlation coefficient) does not differ significantly from zero, as compared against the Student's t distribution (critical values of Coh², df = 6, are 0.50 for P < 0.05*, 0.70 for P < 0.01**, and 0.82 for P < 0.001***). Mean Coh² and time lag (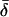) data are shown for the mean frequencies (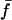) over which their corresponding CSD is of relatively high strength. By convention, the CSD of two signals, A and B, i.e. CSD〈A,B〉, at a given frequency will have a positive value of δ if A leads B.

While peak clustering in some signals might not be statistically distinguishable from noise on its own (as in the case of TMD and RD; Fig. 8), useful and statistically robust information can still be gleaned from CSDs of those signals with others of greater power (Thomson, 1982). TMD was found to be tightly in phase with excursions in dk/dt_BZ (that is, with the absolute value of dk/dt_BZ, or |dk/dt_BZ|) for both roots, and also in phase with RD at 28°C.

Gel Drying

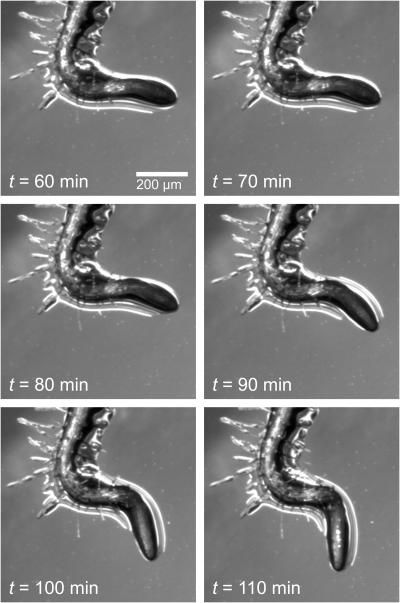
Further evidence of friction between the root tip and gel surface was provided anecdotally by observations of a root grown at 23°C on an air dried 1.2% gel surface (Fig. 9; Supplemental Video 2). Dry air was delivered to the chamber, drying the gel, and causing the root tip to visibly stick its surface from t = 60 min to t = 80 min, after which the root's graviresponse releases the tip from sticking to the gel surface. Increased root twisting is observed as the root sticks to the gel before t = 80 min and then increases dramatically as the tip is freed after t = 80 min, suggesting that torsional energy, as well as bending energy, can be stored by the root when impeded by the gel surface.

Figure 9.

Growth of a root tip over a period of 50 min on a partially desiccated 1.2% gel surface, showing the buildup of both torsional and bending stress in the root tip due to frictional resistance imposed by the gel surface. See Supplemental Video 2 for the original time-lapse images from this sequence. The time signatures in Supplemental Video 2 and this figure are synchronized.

Asymmetric Gel Surface Environments

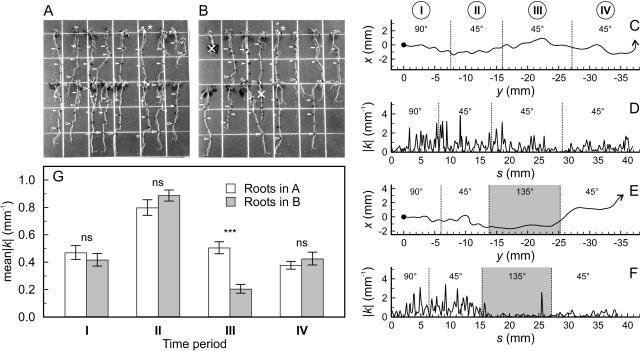
An experiment confirming the results of Simmons et al. (1995b), who showed that root waving is strongly reduced at a surface pitch of 120°, found that a change in gel surface pitch from 45° to 135° (Fig. 10) caused a statistically significant drop (P < 0.001, log-transformed one-tailed t test, n = 16, 12) in the mean absolute value of root curvature between the two angles, followed by a recovery in curvature when the gel pitch was returned to 45° (Fig. 10G). Mean absolute curvature is a good metric for root waving (or coiling) because it provides an unbiased measure of root waving intensity. Coherently waving and simply meandering roots can be clearly distinguished by the strong difference in the degree of curvature between them (Fig. 10, D and F).

Figure 10.

Root waving intensity in response to asymmetrical gel surface environments. A and B, Arabidopsis seedlings grown on sealed gel plates were first grown at a gel pitch of 90° (time period I) and then, once the roots had grown approximately 10 mm, at a 45° pitch (solid bars). After 44 additional hours (time period II), one plate (B) was shifted to a gel pitch of 135°, while the other (A) was maintained at a gel pitch of 45° (black triangles). After 44 h of growth in this configuration (time period III), the 135° plate was shifted back to 45° (white triangles), and the roots of both plates were permitted to grow for an additional 16 h before imaging (time period IV). Roots marked with an X grew abnormally and were not included in this analysis. Asterisks indicate those roots shown in C to F. C and E, Root trajectory (in [x,y] coordinates) of two roots, one grown at a consistent gel pitch of 45° (A) and the other placed temporarily at a gel pitch of 135° in time period III (B). D and F, Root curvature, k (mm⁻¹), as a function of parametric root length (s) of the roots shown in C and E, respectively. G, Mean absolute curvature (mean|k|) at different gel pitches during the growth of the roots shown in A and B. Mean curvature is statistically significantly smaller (***, P < 0.001, log-transformed one-tailed t test, n = 16 [A], n = 12 [B]) when the gel pitch is 135° than when it is 45°, and not significant (ns) when the pitches match. Error bars indicate the se of the mean.

DISCUSSION

The Potential Importance of Root-Gel Interactions

The results presented here are meant to illustrate the potential importance of the root-gel interface for root waving. It should be noted at the outset that, although some roots are known to grow in a non-straight pattern or meander across the gel surface even at 90° (Rutherford and Masson, 1996), here we mean by root waving those patterns of growth reflecting a temporally and spatially coherent oscillatory process, and indicated by a high degree of curvature. Curvature is difficult to judge visually (Silk, 1992), and although a root may appear to be waving, this meandering growth often has an order of magnitude lower curvature than the maximum curvature observed during coherent wavy growth (see Fig. 10, D and F). Nonstraight growth at any pitch could simply reflect noise in the shape of the gel surface or in the growth conditions, or in the root's inability to grow straight under all circumstances, especially when graviresponse-impaired (Mullen et al., 1998b).

Temporal data are presented for only two root growth experiments, although the same qualitative behavior has been observed in all roots examined (data not shown). Nevertheless, because each experiment contains more than one oscillatory event, there is more statistical power than the limited number of discrete experiments would suggest. Thus, the study is not meant to cover root waving exhaustively—many studies have already established its presence and some of its characteristics (Okada and Shimura, 1990; Buer et al., 2000; Migliaccio and Piconese, 2001)—but rather to explore its evolution in time. Information of the kind provided by this study is critical if we are to properly parse the different physical forces involved in root waving, as well as interpret and predict the effects of relevant genetic lesions in auxin or cell wall biochemistry (Marinelli et al., 1997; Mullen et al., 1998b; Rosen et al., 1999).

The principle difficulty associated with the interpretation of root waving is the lack of a clear framework for understanding its behavior, and a general uncertainty as to which processes to include. Circumnutation (Simmons et al., 1995b; Rutherford and Masson, 1996; Migliaccio and Piconese, 2001), thigmotropism (Okada and Shimura, 1990), phototropism (Okada and Shimura, 1992), gravitropism (Okada and Shimura, 1990; Simmons et al., 1995b), and spiralizations in root twisting and turning (Migliaccio and Piconese, 2001) have all been invoked, but until critical evidence is produced that can distinguish between them, each lays claim to plausibility, not exclusivity.

Root Tip Impedance and Gravitropism

Previous studies showing high sensitivity to plate angle, ethylene concentration, and graviresponse impairment indicate a clear corrective role for gravitropism in root waving (Simmons et al., 1995b; Mullen et al., 1998b; Buer et al., 2003). Here, we suggest that the normal component of the graviresponse—directed perpendicular to the gel surface—could generate friction between the root and gel surface, causing deviations in root tip trajectory via root tip impedance. Thus, both the correction and production of root tip deviations could be the result of the same gravitropic reaction to root tip deflection. The former, corrective role of gravitropism is a well established phenomenon. Support for the latter is 4-fold: the root tip will turn toward the gel surface if the gel pitch is nonvertical (taken as given), the root tip physically interacts with the gel surface, variation in this interaction is synchronized with change in root tip angle and in curvature in regions of the root not typically associated with the gravitropic response, and root waving is strong only when the gel surface is below the root tip.

The presence of root tip-gel interaction is documented by the positive values of TMD observed after the gel is rotated to a 45° pitch (Fig. 4), supporting the loaded beam hypothesis presented in Figure 1. At first glance, a positive TMD could be interpreted in one of two ways. Either the root tip is impeded by the gel, or the root elongation zone undergoes a complicated growth response that consistently gives the appearance of root tip immobility. The latter has some precedent; to maintain a constant hook shape and protect the emerging cotyledons and shoot apical meristem (Silk and Erickson, 1978) many hypocotyls undergo positive curvature on one side of the axis and displaced negative curvature on the other. Here, however, the restorative curvature that would be necessary in more basal parts of the root to keep the root tip stationary in the absence of friction is not possible with the root hairs holding the root in place prior to the root reversing its curvature (Figs. 2, 3, and 5). As such, we interpret the positive TMD data as evidence that tip impedance is the result of gel surface friction, and not due to an endogenous growth phenomenon like circumnutation. That the gel surface is physically capable of slowing the movement of the root tip is supported in an extreme case by the gel drying experiment (Fig. 9; Supplemental Video 2).

The physical interaction between the root tip and the gel is directly demonstrated by surface deformation around the root tip, as measured by reflection from the ring light (Fig. 7; Supplemental Video 1), showing that the root tip applies a force against the agar surface and sometimes causes it damage (see Supplemental Video 1). No significant gel surface deformations were observed at any time during the experiment except around the root tip (Fig. 7, Supplemental Video 1). Furthermore, TMD and RD data are tightly in phase at 28°C, indicating a strong relationship between root tip impedance and the force applied by the root tip against the gel surface. The presence of consistent gel surface deformation, at least at 28°C, indicates that root waving can occur even in the presence of perpetual positive pressure between the root tip and the gel. In fact, gel deformation tends to be largest when curvature development in the basal zone is at its greatest. This provides evidence against circumnutation or thigmotropism as the primary deflective force in root waving, since under those models root waving would require that the root tip be free to move (wagging tail growth), significantly reducing the positive pressure found between the gel and root tip just at the time that curvature developed in the root.

The immobility of the root tip should cause the entire elongating root to bend, up to the first root hairs, leading to a deflection in root tip direction. Curvature development in the distal zone is in phase with root tip deflection and appears to directly reflect the lateral component of the graviresponse (Table I). However, curvature development in the basal zone tends to lag curvature development in the distal zone by 2 to 3 h (Table I), a longer period of time than what is typically required to initiate gravitropic bending in Arabidopsis (Mullen et al., 1998a). Furthermore, this basal curvature develops outside the zone of maximum relative elemental growth rate (Beemster and Baskin, 1998; Mullen et al., 1998a). The observed temporal lag and spatial dislocation are similar to the stepwise growth pattern exhibited by Arabidopsis roots upon meeting a rigid obstacle, as shown by Massa and Gilroy (2003). Curvature development in the basal zone is stronger than in the distal zone (just as 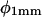is greater than 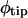; see Fig. 6), suggesting that most of the root's curvature development is nontropic. In fact, changes in root tip deflection, dφ/dt_tip and TMD are in phase with curvature development in the basal zone, not with that in the distal zone (Table I), consistent with the hypothesis that most of the root tip deflection is generated by overall root bending and not solely by tropic bending near the tip.

If normal gravitropic bending enhances root tip impedance, as implied by the synchronization between TMD, RD, and dk/dt_BZ, then inverting the gel surface should strongly reduce the intensity of root waving. This has been observed in previous work (Simmons et al., 1995b), and has been confirmed here in a more rigorous manner (Fig. 10). While this experiment alone does not conclusively demonstrate that gravitropism is sufficient to generate root tip deflections, it does indicate that normal gravitropic bending is what initiates the causal chain leading to root tip deflection. It also indicates that if circumnutation is involved in generating root tip deflections, its strength must be mediated by the graviresponse and the presence of the gel surface.

Growth Rate and Temperature Dependence of Root Waving

Differences between the two experiments as a function of temperature are not statistically resolvable. However, the strong dependence of root growth on temperature has been repeatedly observed (compare with Silk, 1992), and the results presented here are consistent with those results. Because gravitropism is a growth phenomenon and likewise temperature dependent, it is reasonable to speculate that the stronger variation observed at 28°C and the shorter temporal period of oscillation are at least partially due to the difference in the relative elemental growth rate of the root (Fig. 2). Both an increase in gravitropic sensitivity and an increase in root elongation rate, under the loaded beam hypothesis, should lead to an increase in the amplitude, or strength, of root waving. It is also possible that the increase in temperature softens the gel, increasing its deformability and its capacity to impede the root tip. Along the same lines, the drop in TMD with time (Fig. 4) comes with an increase in elongation rate (Fig. 2), which would suggest that there is a temporal reduction in the effect of the gravitropic response on root waving. We would expect the length of the elongation zone and the efficacy of the root hairs at anchoring the basal parts of the root (Figs. 2 and 3) will govern the spatial frequency of root waving by determining how much curvature will develop over the length of elongation zone at a given TMD. Critical experiments to address these possibilities have yet to be performed.

Gravitropism and Root Tip Impedance Appear Sufficient to Explain Root Waving and Coiling

We suggest that root waving consists of the following sequence of events. When the gel is placed at an intermediate pitch, root tip impedance becomes strong relative to the capacity of the root to correct deflections in root tip angle, and curvature develops up to the point of first root hair development (it is significant that at both 23°C and 28°C this initial bend is to the right). As this curvature develops, the root tip is deflected, leading to an increase in the graviresponse, which causes the root tip to correct the deflection and bend the other way, but only in the distal part of the root tip. Root tip impedance then amplifies the distal curvature created by this lateral correction into greater curvature in the basal zone, leading to an opposite root tip deflection, another opposite graviresponse, and so on.

The same logic can be applied to root coiling. The gel surface is placed horizontally, and root tip impedance amplifies any preexisting curvature in the root elongation zone. The lateral component of the graviresponse is ineffectual at a horizontal pitch—or, in the case of graviresponse impaired mutants, minimal—and cannot correct the resulting deviation. In contrast, the normal component is at its strongest, leading to increased root tip impedance, root bending, and finally coiling. Root tip impedance could be important even without strong normal gravitropic bending, as evidenced by studies of graviresponse-impaired roots (Simmons et al., 1995a; Mullen et al., 1998b), which coil even at a 45° pitch but grow relatively straight at 90°. Roots with a strongly impaired graviresponse are unable to coil at any pitch (Okada and Shimura, 1992; Bowman, 1993).

Circumnutation is an important growth phenomenon in plants but it seems to have little importance in explaining root waving. If circumnutation were strong enough to generate oscillations at a pitch of 45°, then it should also be strong enough to generate them at 135°. However, the mean curvature of roots grown at a 135° pitch is considerably lower than those grown at 45° (Fig. 10). Also, if circumnutation drove root tip deflections, then we would expect the roots to grow according to the wagging tail model, especially when the plate is inverted and there is little root tip impedance. The high degree of root tip immobility observed in this study does not bear out this prediction. While it is possible that internally derived oscillations could generate patterns similar to loaded beam growth via a complicated axial pattern of lateral growth differentials, we would then have to explain why the root tip remains immobile against the action of such strong internal forces, leading us back to root tip impedance as an important force in generating the root waving phenotype.

Coupling between Root Bending and Twisting

Although not explicitly treated in this work, much has been made of the role of root twisting in relation to root bending as an explanatory foundation for root waving (Okada and Shimura, 1990; Migliaccio and Piconese, 2001). The relationship between the two, though not always consistently observed (Buer et al., 2003), has led to speculation that root waving depends on either a gravitropism- or thigmotropism-induced circumnutational process (Simmons et al., 1995b), or that it reflects a flattened version of the spiral growth found in many growing plant axes, such as those generally observed by Darwin and Darwin (1880). The circumnutation hypothesis is lent further support by the right-handed turning bias of Arabidopsis roots, where it is common for circumnutating organs to have a directional preference.

The apparent importance of root tip impedance for root waving, as found and discussed here, leads naturally to speculation about how it could affect root bending asymmetry and the relation between bending and twisting. The initial turning tendency of Arabidopsis roots is to the right, but left and right only have meaning in the context of the gel surface. In animals, left-right asymmetry arises only when two axes—dorsal-ventral and anterior-posterior—are established. The analogous axes in this case are the basal-distal axis defined by the root's longitudinal axis and its direction of growth, and the up-down environment imposed by the gel surface. Thus, the initial turn must be somehow constrained by these axes of asymmetry to be internally biased to the right. It could be that the right handed bias in the initial turn is actually an emergent property of the left-twisting bias of the root. What determines this twisting bias is unclear. However, given that twisting is a whole-root phenomenon, the bias may emerge from the aggregate behavior of each cell in the root. During early cell expansion, the cell wall microtubules of epidermal root cells are known to be arranged in a right-handed helical manner (Liang et al., 1996). By its geometry, this right-handed arrangement would yield left-handed twisting during cell elongation (Hashimoto, 2002), which would in turn yield whole-root twisting like coils in a rope.

This left-twisting tendency could translate into a right-handed bend via the effects of root tip impedance. As the root tip is pushed along the resistive gel surface, the underlying tendency of the root to twist to the left could store torsional energy that is released only if the root turns to the right (a minimal energy configuration, one that is easily confirmed using a physical model such as a length of O-ring stock held against a rigid, frictional surface). Conversely, when the root is pushed forward in a left-handed turn, root tip impedance could cause the root to twist to the right and store torsional energy against its tendency to twist to the left. This differential in energy storage—where energy is stored in a left-handed turn and released in a right-handed turn—would explain why wavy roots turn more easily to the right than to the left, and why straight-growing and coiling roots have a right-handed bias. We present this only as a hypothesis, but it gains strength when we consider that the right-handed turning bias is only apparent when the gel is below the root (Fig. 10); that is, its emergence depends on the presence of root tip impedance. Not only the strength of root waving (Fig. 10), but also the slanting tendency of roots grown at a 60° pitch, disappears when the gel is shifted to a pitch of 120° (Simmons et al., 1995b). Interestingly, when cortical microtubule arrays are destabilized (Baskin, 2001), leading to right-handed root twisting, a common secondary effect is generate left-handed slanting, waving, and coiling (Marinelli et al., 1997; Thitamadee et al., 2002).

The coupling between root twisting and turning is not necessary to explain the fact of root waving or coiling, only their occasional lateral asymmetry. Indeed, the presence of ethylene in the headspace of the growth plate appears to remove any correlation between twisting and coiling, as well as the tendency of the root to slant to the right (Buer et al., 2000; Buer et al., 2003), even though the root continues to wave. Studies that explore the time-evolution of the root trajectory during root waving, as well as ones that look directly at the mechanics of the root tip and gel surface interaction should help to further our understanding of these important phenomena.

CONCLUSION

Direct observation of the time-evolution of root waving yields considerable insight into the processes involved. The differential between root tip movement and root elongation rate suggests that the root tip is frictionally impeded, and direct observation of gel surface deformation by the root tip shows that the root tip presses against the gel surface. Furthermore, changes in root tip deflection angle, the tip movement differential, and gel surface deformation are all well correlated and in phase with major curvature development in regions just distal of sites of root hair development, suggesting that root tip deflection is due to root tip friction. The presence of surface deformations that are in phase with high values of the tip movement differential strongly suggests that much of the friction generated at the root tip is due to downward (or normal) gravitropic bending by the root tip against the gel surface, as supported by an experiment showing a reduction in mean root curvature at an oblique (135°) gel pitch. Root waving, and by extension root coiling, could be explicable solely in terms of gravitropism and root tip impedance by the gel surface.

Given that the roots in these experiments and others are grown on a physical medium, it is natural to assume that at least part of their behavior is explicable with adequate attention to what could result from these mechanical interactions. If a growing root tip is physically impeded, then either the root will cease to grow or it will bend (see especially Massa and Gilroy, 2003). Prior studies have not adequately addressed this possibility in wavy roots. Future work using these methods, combined with direct measurements of the mechanical properties of the roots and the gel, and with studies of graviresponse mutants and of the effects of changes in various environmental conditions, will help to better outline the role of root-gel interactions in the development of root growth patterns in Arabidopsis.

MATERIALS AND METHODS

Microscope Apparatus

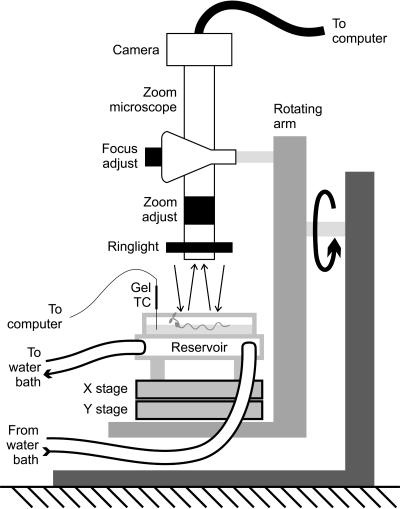
Growth conditions were selected to best mimic those used in previous studies. Special note was taken of the results of Buer et al. (2000), leading us to use a continuous supply of filter-sterilized, humidified, outside air to avoid the effects of ethylene accumulation. One-half-strength Murashige and Skoog salts were employed as the medium most commonly used in root waving studies. The roots were grown on agarose gels in a rotating, sterile, acrylic observation stage (Fig. 11) placed under four fixed overhead fluorescent cool-white lamps (20 W, 61 cm, General Electric, www.ge.com), themselves mounted on a steel pipe frame covered in opaque black felt to protect the experiments from stray light. Both the microscope and the stage were mounted on a custom built rotating arm with high-precision X-Y linear stage motion control (Newport, Irvine, CA). The stage was constructed of clear acrylic and mounted above a custom-built, acrylic-walled water reservoir connected to a circulating water bath (PolyScience, Niles, IL). The bath temperature was regulated with feedback to the circulator via an RTD probe inserted into the water reservoir below the gel, while the surface temperature of the gel was itself measured using a 30 AWG hypodermic thermocouple probe (HYP-1, OMEGA Engineering, Stamford, CT) and monitored with a datalogger (CR10X, Campbell Scientific, Logan, UT). The gel surface was regularly 3°C warmer than the water in the reservoir due to the heat generated by the overhead lights under the felt. Only gel surface temperature is reported here. The acrylic stage fit a single 100-cm diameter glass petri dish (no cover) just above the reservoir, and was fed with sterile, humidified ambient air at a rate of 800 mL min⁻¹. The air was humidified using a custom built nafion tube humidifier (MH-series, Perma Pure, LLC, Toms River, NJ). Condensation on the interior surface of the acrylic stage's cover was prevented with externally mounted resistance heaters.

Figure 11.

Custom-built experimental apparatus used in this study to permit time-lapse and temperature controlled imaging of root growth at multiple gel surface pitches. A single rotating arm contains all experimental elements, except for the overhead lamps.

Images were recorded using a monocular video zoom microscope (VZM 450i, Edmund Industrial Optics, Barrington, NJ), mounted with a monochrome CCD camera (XC-73, Sony, Japan) and microscope-mounted ring light. Image capture and light control were managed by computer via custom electronics using the Windows Beta version 4.02 of Scion Image (Scion Corporation, Frederick, MD). Images were captured once every 20 to 30 min and stored as time-stamped TIFF files. Scale was determined using a transmission stage micrometer. Focus was manually controlled using a coarse-fine control knob mounted to the rotating arm, while the zoom was controlled via the microscope itself. Between images, the ring light was turned off and the roots were illuminated only by the overhead lights. At the time of image capture, the overhead lights were turned off, the ring light turned on and allowed to stabilize for at least 10 s, an image was captured, the ring light was turned off, and the overhead lights were turned back on. This avoided unwanted phototropic effects due to light from non-vertical sources.

Growth Experiments

The roots were grown at bath temperatures of 20°C and 25°C, corresponding to gel surface temperatures of 23°C and 28°C, respectively. Three Col-0 seeds per experiment (CS1092, Arabidopsis Biological Resource Center, www.arabidopsis.org) were plated on a 1-cm thick medium composed of 1.2% (w/v) Bacto-Agar (Difco Laboratories), 1.5% (w/v) Suc, and one-half strength Murashige and Skoog basal macro- and micronutrients and vitamins (M0654, M0529, M3900, Sigma-Aldrich, www.sigmaaldrich.com). Each dish was sealed with porous surgical tape (Buer et al., 2000), stored in the dark at 4°C for 4 d, and then placed in the sterile observation stage with the cover removed. The gel pitch was set to θ = 90° (vertical) and the overhead lights to a continuous 50 μmol photons m⁻² s⁻¹. The camera was then focused on the seed, and upon germination image capture was begun. When radicle growth had reached at least 10 mm, θ was set to 45° and light level to a continuous 85 μmol photons m⁻² s⁻¹. While filming, the stage was periodically X-Y-translated to keep the root tip and most distal root hairs in frame. Gaps in the data reflect those times when the root tip grew out of frame. Image series covered a period of approximately 100 h in both experiments.

An additional experiment was performed on surgical-tape sealed plates in a germination chamber maintained at a constant temperature of 20°C, a constant light level of 85 μmol photons m⁻² s⁻¹, and with high humidity. Sterilized Col-0 seeds were plated on each of two plates. Both plates were stored in the dark at 4°C for 4 d, and then placed in the germination chamber at a 90° gel pitch until the seedlings had germinated and their roots had grown approximately 10 mm in length. Both plates were then shifted to a 45° pitch, and after 44 h, one of the plates was shifted to a 135° pitch. After an additional 44 h, the 135° plate was returned to a 45° pitch and both plates were permitted to grow for another 16 h. The roots of both plates were then photographed in detail using a camera-mounted stereomicroscope.

Image Analysis

Each captured image was registered in TIF format (640 × 480 pixels, 8-bit grayscale depth). These images were then imported into CorelDraw v10 (Corel, Ottawa, Canada) and aligned to form a progressive composite. First (Fig. 12), a single multi-node line, with approximately 100-μm node spacing, was drawn along the centerline of the root image composite from the radicle origin to the root tip. The data in this line was stored, and then the line was modified to fit the previous image in the series. This method of modifying previously drawn lines made it unnecessary to fully redraw the line for each image. An additional, straight line was drawn transversely across the root at the point on each image where root hairs first become visible. This method was time-consuming, but the lateral movement of wavy roots, and the visual artifacts they leave behind, such as gel surface damage and deformation, and root surface reflections, introduce problems that make it highly problematic to use traditional marker-based root growth measurements (Beemster and Baskin, 1998) or advanced image analysis software (van der Weele et al., 2003). Similar composites were created from the images taken of roots grown in the germination chamber and a centerline was drawn over each. The position of the root tips of each root were marked whenever the plates were shifted to different angles.

Figure 12.

Measurements of root shape. A, In each image, lines were drawn through the root's centerline and the diameter of the gel surface reflection (RD), if visible, was measured. Bar represents 200 μ. B, The root centerline was rendered as a time- and root arc length-dependent X-Y vector, r(s,t), measured from the root origin (shown here as an arbitrarily positioned point on the gel surface, but actually located at the point of radicle emergence from the seed coat). s (mm) is the arc length along the root from the root origin. c is the distance from the root origin to the root tip, or root length. The velocity of the root tip is measured as the time derivative of r at the tip. d_h and d_m are the distances from the root tip to the first observable root hairs and to where the root first becomes stationary, respectively. Bar represents 100 μm.

The nodal data from these lines were exported into a single EPS file for the entire image series (a text file), from which the X-Y coordinates of the nodes in each line could be extracted for analysis. All analyses were performed using MATLAB version 6.5 (MathWorks, Natick, MA). The data were scaled to units of mm and translated so that the origin of each line (the point of radicle emergence) had coordinates [x,y] = [0 mm, 0 mm]. Because nodes were not regularly placed along the centerline, but instead spaced to assure an accurate representation of the root trajectory with varying nodal density depending on the curvature of the root, the centerlines' nodes were splined to a common spatial resolution of 20 μm, which was close enough to minimize quadratic error in arc length measurements. Each centerline (Fig. 12) was then rendered as a parametric vector function of root arc length, s (mm), and time, t (hr):

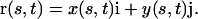(1)

Arc length was measured from the root origin (s = 0 mm) to the root tip (s = c), where c is the root length (and a function of time). The rate of increase in root length, or the elongation rate of the root, is the first derivative of c with time, or dc/dt, and the position of the root tip is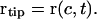

The distance between the root tip and the first appearance of root hairs, or d_h (mm), was determined by calculating the intersection between r and the transverse line earlier drawn across the root to indicate root hair position. Another metric, d_m (mm), which is the distance from the root tip to the point where the root ceases to change its position, was determined by first rendering r in terms of distance from the root tip [that is r^* = r(c − s,t)] and then determining the magnitude of its derivative with time. The point along r^* (i.e. c − s) where the rate of movement first exceeds 0.01 times the summed movement over the entire length of the root was assigned to d_m. The size of the reflection of the ring light around the root tip caused by local deformation of the gel surface, or RD (mm), was measured as the transverse diameter of the reflection (Fig. 12A).

The tip movement differential, or TMD, is the growth rate-normalized difference between the rate of elongation of the root and the magnitude of the velocity of the root tip, or:

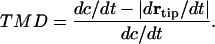(2)

Positive values of TMD signify a relatively slow root tip, and negative values signifying a relatively fast root tip.

Root curvature k (mm⁻¹) can be calculated from r, provided s is an accurate estimate of root arc length, as:

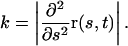(3)

The angle φ (°) at which the root deviates from the downward slope of the gel surface is given by:

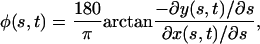(4)

where φ > 0 signifies a left turn in the frame of reference of the root, and φ < 0 signifies a right turn. This sign convention is also applied to k (even though curvature is a vector magnitude and thus conventionally non-negative), where a bend to the left indicates positive curvature.

The root elongation zone was arbitrarily split into two domains to tease apart root bending in its more basal and distal parts, following Mullen et al. (1998a) and Massa and Gilroy (2003). Here, these are called the distal and basal zones (DZ and BZ) and correspond to the first 0.5 mm of the root tip and from there to the first occurrence of root hairs, respectively. The cutoff of 0.5 mm was chosen to divide the root tip into the more rapidly elongating distal zone and the more slowly elongating basal zone. Due to the propagation of error involved in calculating a second derivative (i.e. k) on subtly varying, yet imprecise data, and because the DZ and BZ represent different material as the root grows, the time rate of change in curvature in these two domains was calculated as the change in the mean curvature over each zone, not the zonal mean of the changes in curvature at each point.

Spectral Analysis

Spectral analysis requires that the time series be evenly sampled in time. Because the degree of statistical significance assigned to the results does not depend on the sampling frequency but rather on the number of realizations of particular oscillations present in the time series, the re-sampling frequency is not critical, provided that it is sufficient to capture the major features. However, resampling requires a splining of the original time series and it is important that the resampling frequency be selected such that artifactual splining overshoot is introduced evenly throughout the resulting spectra. One way this can be done is to resample at twice or four times the underlying sampling frequency, but because the sampling rate was uneven in this study, an arbitrary resampling period of 1/π h was selected for having a value near the image sampling periods of 20 or 30 min, and for not sharing any common roots with those numbers. The data were splined using a piecewise cubic hermite interpolating polynomial, or pchip, which provides a smooth spline with little overshoot.

Some data series had central frequencies that were strongest at the oscillation frequency of the root (that is the frequency of one full oscillation of the root tip). Others (such as TMD and RD) oscillated at twice that frequency. To compare time series with common features, but which oscillated at different octaves, it was necessary to double the frequency of the more slowly oscillating series by detrending it and taking its absolute value, thereby converting negative excursions to positive ones. For example, dk/dt is compared against TMD as |dk/dt|.

Each time series was linearly detrended. Because the root occasionally grew out of the field of view, there are occasionally missing data after t equals approximately 65 h in both experiments. Missing data were replaced with zeros prior to calculating their discrete Fourier transforms. Spectral analysis was only applied to data gathered after the gel surface had been rotated from 90° to 45°.

An estimate of the power spectral density (PSD) of φ, dk/dt_DZ, dk/dt_BZ, TMD, and RD from each root was estimated using the MT method of Thomson (1982). The MT method avoids some of the spectral bias due to nonstationary data (that is, data that does not contain the same spectral information through time) and spectral leakage. It also provides a spectral estimate with a robustly calculated number of degrees of freedom that can be used in hypothesis testing. In other methods, df is set by the number of realizations of a particular oscillation in the data set, but with the MT method, df is set by the number of eigentapers used to sample the original time series. In this study, the MT method was applied using a time-bandwidth product of p = 2 (an appropriately low value for short data series such as these), from which three (K = 2p − 1) Slepian eigentapers were calculated for a total of six degrees of freedom (df = 2K). See the review by Mann and Lees (1996) for a relatively readable explanation of this method.

The background noise spectrum was assumed to be red noise, which is noise with some degree of temporal autocorrelation. Data without temporal autocorrelation is by definition white noise. The discrete red noise spectrum P_RN(f) as a function of frequency f is given for a finite data series by the following relation (Mann and Lees, 1996):

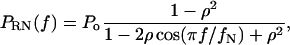(5)

where 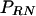is evaluated for f from 0 to the Nyquist frequency 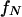to match the frequency distribution of the spectral estimate, 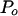is a normalization coefficient, and ρ is the lag-one autocorrelation coefficient for the signal. An initial background spectral estimate was calculated for each spectrum by applying a 43-frequency bin median filter to the PSD (following the protocol described by Mann and Lees, 1996). Values of 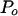and ρ were found by least-squares fit of Eq. (5) to the median filtered data (Mann and Lees, 1996). The statistical significance of any one peak was then calculated as the ratio of the power contained in that peak (i.e. the variance partitioned to that frequency) to the power contained at the frequency in the background noise estimate. This ratio was then compared to the χ² value at a given significance level with df = 6.

Cross-spectral densities (CSDs) of pairs of signals are also calculated using the MT method (Thomson, 1982). The CSD is a complex function of frequency and contains both the degree of cross-correlation and the phase angle delay between the two signals. The statistical significance of the CSD can be calculated in a way similar to the product-moment correlation coefficient by determining the coherence-squared, or Coh², between two signals, A and B:

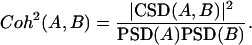(6)

If the square-root of Coh² is statistically significant (df = 6) against the Student's t distribution (determined as if Coh were a correlation coefficient), then the phase delay (δ, hr) can be accurately calculated from the CSD as the inverse tangent of the ratio of the imaginary and real part of the CSD at f, divided by 2πf. Because the CSD often contains multiple adjacent peaks (or peak clusters) with high power content, Coh² and δ are provided as the mean values corresponding to those peak clusters. A negative δ indicates that A lags B and a positive δ that it leads B.