Surface Lattice Resonances for Enhanced and Directional Electroluminescence at High Current Densities

Abstract

Hybrid photonic-plasmonic modes in periodic arrays of metallic nanostructures offer a promising trade-off between high-quality cavities and subdiffraction mode confinement. However, their application in electrically driven light-emitting devices is hindered by their sensitivity to the surrounding environment and to charge injecting metallic electrodes in particular. Here, we demonstrate that the planar structure of light-emitting field-effect transistor (LEFET) ensures undisturbed operation of the characteristic modes. We incorporate a square array of gold nanodisks into the charge transporting and emissive layer of a polymer LEFET in order to tailor directionality and emission efficiency via the Purcell effect and variation of the fractional local density of states in particular. Angle- and polarization-resolved spectra confirm that the enhanced electroluminescence correlates with the dispersion curves of the surface lattice resonances supported by these structures. These LEFETs reach current densities on the order of 10 kA/cm², which may pave the way toward practical optoelectronic devices with tailored emission patterns and potentially electrically pumped plasmonic lasers.

The nanoscale localization of electromagnetic energy through the interaction of light with metallic nanostructures has attracted significant attention over the past decade. The increased field intensity associated with plasmonic structures supporting surface plasmon polaritons (SPPs) has led to many technological advances.¹⁻³ Nevertheless, the issue of the intrinsic losses of metals is still considered as a limiting factor for maximum performance.⁴ The periodic arrangement of structures that support SPPs can be used to overcome this obstacle. When the periodicity is comparable to the wavelength of the plasmon resonances, diffractive⁵ or waveguide⁶ coupling of the scattered field by the SPPs forms new hybrid photonic–plasmonic modes. Owing to their photonic component these so-called surface lattice resonances (SLRs) or quasi-guided modes are more delocalized and long-lived and, thus, possess much higher quality factors compared to pure SPPs.⁷ More importantly, despite the more extended field profiles, the overall field intensity is even higher than for SPPs.⁸ The unique properties of SLRs have recently enabled promising achievements such as enhanced and directional light emission,⁸⁻¹⁰ strong light–matter interactions,¹¹⁻¹⁶ and lasing.¹⁷⁻²¹

Despite these intriguing phenomena, electrically driven operation of light-emitting devices involving SLRs is not a straightforward task. The main reason for this is the intrinsic sensitivity of SLRs to the surrounding environment and its dielectric constant due to their far-field nature.^8,22 Therefore, numerous practical challenges arise with regard to the incorporation of injecting electrodes, charge transport, and emissive layers without affecting the SLRs. Current reports dealing with electrically pumped devices and periodically patterned/arranged metal structures are limited to the far-field out-coupling of trapped light or its redirection in, for example, organic light-emitting diodes (OLEDs).²³⁻²⁶ In addition, integration of metallic nanostructures supporting SLRs in the transport/emissive layer of a sandwiched diode-structure is likely to drastically affect the electrical performance of the device, for example, via formation of current hot-spots or unintentional charge trapping.

In this regard, light-emitting field-effect transistors (LEFETs) may offer a vital solution to avoid any detrimental impact of SLRs on the device performance and, likewise, any destructive interference of the device electrodes with the SLRs. Ambipolar LEFETs represent a planar device architecture where holes and electrons are injected into a single charge transport and emissive layer from coplanar source and drain electrodes. Charge carrier accumulation layers are formed that create a mobile p–n junction where holes and electrons meet.²⁷ The recombination of these charges leads to light-emission from the channel area several micrometers away from the injecting electrodes, unlike in an OLED. Hence, in this configuration, the axial (out of plane) light emission and far-field coupling of the SLRs are not obscured. Our recent results on colloidal gold nanorods in polymer LEFETs have further shown that no deterioration of the electrical performance is found after their integration directly in the semiconducting layer.²⁸

With the aim to explore and verify the potential of SLRs in the LEFET geometry, we incorporate periodically arranged gold nanodisks (NDs) with square symmetry into the semiconducting channel. We demonstrate that combining SLR modes and their high local fields around the NDs with optically or electrically generated excitons in close proximity leads to an increase of light emission via the modification of the fractional local density of states and the Purcell effect. Angle- and energy-resolved electro- and photoluminescence (EL/PL) measurements confirm the dispersive emission enhancement trends associated with hybrid photonic–plasmonic modes, leading to directional light emission. The high current densities in LEFETs (on the order of 10⁴ A/cm²) may pave the way toward practical optoelectronic devices involving SLRs featuring tailored emission, polaritonic components, and possibly lasers.

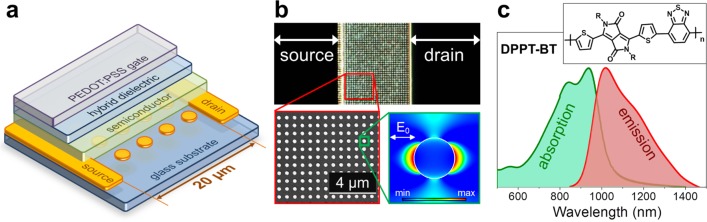
Figure 1a shows the schematic structure of a bottom-contact, top-gate ambipolar polymer LEFET. A rectangular array of 25 nm high gold NDs was fabricated by electron-beam lithography on top of a glass substrate (over a 20 × 500 μm² area). After being covered with a 1 nm layer of aluminum oxide for electrical insulation, the source-drain electrodes were patterned photolithographically around the ND array. The transistor was completed with a 40 nm thick film of a narrow bandgap semiconducting copolymer (DPPT-BT), followed by a hybrid gate dielectric (226 nm of poly(methyl methacrylate), 38 nm hafnium oxide and 5 nm aluminum oxide) and a 200 nm thick PEDOT:PSS gate electrode, deposited by aerosol jet printing. In conventional LEFETs, the gate electrode would consist of a metal such as silver or gold; however, its proximity to the ND array (∼270 nm) would destructively interfere with the SLRs. The printed PEDOT:PSS is conductive enough (sheet resistance 110–150 Ω/sq) for the necessary application of the gate potential, but the change in the refractive index is kept to a minimum by using this conductive polymer. The effective refractive index of the stack is approximately n = 1.5, mostly defined by the bottom glass, the top PMMA and PEDOT:PSS layers (see Supporting Information for more details on sample fabrication). Hence, in this optimized stack configuration, the SLRs are not negatively affected by the device geometry.

Figure 1.

(a) Schematic geometry of a top-gated light-emitting field-effect transistor (LEFET). (b; top) Dark-field optical micrograph of an LEFET under white-light illumination showing edges of source and drain electrodes and the channel filled with a periodic array of gold nanodisks with 670 nm pitch (diameter 300 nm); (bottom-left) corresponding scanning electron micrograph and (bottom-right) mode profile of supported SLRs (i.e., field intensity enhancement at λ = 1350 nm in logarithmic scale). (c) Absorption and photoluminescence spectrum of a thin film of the semiconducting polymer DPPT-BT with corresponding molecular structure.

Figure 1b (top) shows a dark-field image under white light illumination of a typical channel of the LEFET filled with a nanodisk array. The length (distance between source and drain electrode) and width of the channel are 20 and 500 μm, respectively, which is large enough to host a sufficient number of NDs, as the strength of SLRs scales with the number of interacting NDs.²⁹ We also fabricated a channel without NDs nearby in order to acquire reference data (see Supporting Information, Figure S1). The corresponding scanning electron micrograph (Figure 1b, bottom-left) shows an array of 300 nm diameter disks with square periodic arrangement and 670 nm pitch. The size of the NDs and the periodicity of the array were selected such that the final SLRs would appear in the spectral region of the luminescence of the employed semiconducting polymer DPPT-BT, that is, ∼1000–1300 nm (see Figure 1c). In our case, this requires us to vary the localized surface plasmon resonance (LSPR) of the ND (and, thus, its size) in order to overlap with the first diffraction order at λ = pitch × environment refractive index.³⁰ The simulated in-plane mode profile of the formed SLRs (at λ = 1350 nm) around the disk clearly shows that in addition to the localized fields, there are also more spatially extended features, emphasizing the photonic component of the hybrid SLRs (see Supporting Information for simulation details).^8,9 The DPPT-BT copolymer was chosen to ensure high current and exciton densities that are enabled by its high and balanced electron and hole mobilities (μ_e = 0.7 cm² V^–1 s^–1, μ_h = 0.3 cm² V^–1 s^–1).³¹

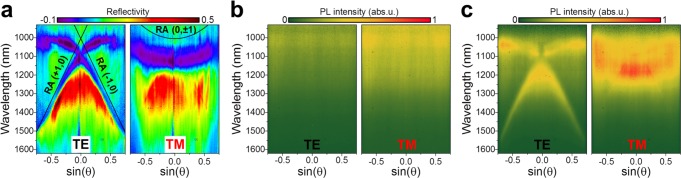
To investigate the angle and wavelength-dependent properties of the SLRs as well as their coupling with the DPPT-BT copolymer we used a Fourier-space imaging setup (see ref (8) and Supporting Information for details). This configuration enables acquisition of the wavelength and angle distribution of the collected light in a single measurement. Figure 2a shows representative reflectivity data, defined as the difference of the signals acquired from the channel with and without the ND array and normalized by the spectrum from a 100% reflecting surface illuminated with the lamp. Distinct spectral features are found for the two polarizations. First, for the transverse-electric (TE) polarized light, the optical response is dominated by the highly dispersive SLRs associated with the coupling of the LSPR with the (+1,0) and (−1,0) diffraction orders, usually called Rayleigh anomalies (RAs). Taking into account the refractive index of the environment and the array pitch, the analytical curves^8,30 for the latter are calculated and indicated by the black lines. In case of the transverse-magnetic (TM) polarization, the main spectral features are governed by the (0, ±1) RAs. It is important to emphasize that due to the Fano-like interactions of the LSPRs with RAs leading to the SLRs, the eigenvalues of the SLRs may not necessarily correlate with the wavelength positions of the observed reflectivity extrema. Moreover, as the reflectivity is the difference between scattering and absorption processes, the observed SLRs will manifest itself as minima or maxima depending on which process is dominating for a given ND array (e.g., small NDs are mostly absorptive, while the larger NDs exhibit higher scattering). Interestingly, the reflectivity data show regions with negative values, indicating that the scattering from the reference channel (without NDs) is higher than that from the one with NDs (i.e., where absorption is dominant). As for the line width (and, thus, quality) of the SLRs, the rather broad dips/peaks (here, minima of reflectivity) correspond to the strong overlap of the RAs with the LSPRs and, thus, lossy properties of the SLRs owing to the larger plasmonic character. For longer wavelengths, larger angles, and TE-polarization, this overlap is lower, and thus, more of the photonic character prevails.

Figure 2.

(a) Angle- and polarization-resolved reflectivity spectra of a nanodisk array. Analytical dependencies for Rayleigh anomalies are indicated with black lines. Corresponding photoluminescence spectra of the polymer layer without (b) and with (c) nanodisks array.

The effects of coupling between SLRs and excitons in LEFETs were first investigated by angle-dependent PL measurements under excitation with a λ = 785 nm laser from the channel without and with NDs as shown in Figure 2b and c, respectively. For the channel without ND arrays, we find that all spectra show the broad emission of the DPPT-BT without any variation with emission angle. Slight differences of the intensity for the two polarizations result from the polarized laser excitation. As for the channel with ND arrays, we can clearly see the characteristic spectral features due to the SLRs as in the case of the reflectivity, although with relatively large line widths. In order to corroborate that these low-quality resonances appear due to the large spectral overlap between the LSPRs and RAs and not because of the stack geometry of the device, we fabricated analogous devices but with a smaller overlap (ND array pitch of 830 nm and a disk diameter of 180–200 nm). In this case, the line width was as narrow as 25 nm, but at the expense of its intensity (see Supporting Information, Figure S2).

The observed spectral features are due to the increased fractional local density of states associated with the increased local fields of the SLRs, as confirmed previously via numerical simulations.⁸ The fractional local density of states, which is proportional to the power emitted in one particular direction, is closely related to the local density of states, which is the integral over all emission angles (i.e., Purcell effect).³² Integration of the acquired PL signal across all detection angles confirms that the total emitted power is also enhanced, although not as strongly as in some particular directions of emission (see Supporting Information, S3). Despite the fact that the detection and integration should be performed over the whole 4π solid angle, it is obvious that the total emitted power is higher for light emission with the ND array. The corresponding wavelength dependence of the angle-integrated PL enhancement also helps us to rule out any substantial impact by increased laser excitation, which would lead to wavelength-independent enhancement of the emission. From these observations we may conclude that the emission enhancement is due to an increased radiative decay of generated excitons and a redirected emission following the dispersion properties of the SLRs. Owing to the picosecond exciton lifetime in DPPT-BT,³¹ it would be very challenging to experimentally resolve any shortening of the lifetime caused by the Purcell effect, which would be an unambiguous proof. A possible contribution by improved outcoupling of trapped light (via the higher scattering cross-section of the SLRs) can be excluded in a thin DPPT-BT layer with preferred in-plane orientation of the copolymer backbone, which is less prone to these issues, as discussed previously.^26,28

To demonstrate the light emission properties under electrical exciton generation we performed transport measurements on the LEFET, as illustrated in Figure 3a. Upon application of drain and gate voltage (the source is grounded), electrons and holes accumulate at the semiconductor–dielectric interface. Note that in ambipolar LEFETs all injected holes and electrons recombine and thus a fixed drain current value leads to a fixed number of generated electron–hole pairs. As the PEDOT:PSS and the glass substrate are transparent in the spectral region of interest, we are able to detect emitted light either from the top or bottom (here only the upward direction is depicted for clarity). As reported recently, the presence of metal nanostructures in the channel only slightly influences the electrical performance of the device, probably by increasing the surface roughness of the semiconductor layer or by changing the exact geometry of the injecting electrode.²⁸ The transfer characteristics of LEFETs with and without the ND array in the channel, as shown in Figure 3b, again support this observation. No significant or systematic variations of the charge carrier mobilities due to the ND arrays were found (see also Supporting Information, S4 and S5, for additional comparison of electrical performance). Figure 3c shows a representative real space image of the emission zone acquired at a current density of J_ds = 6 kA/cm² (taking into account a channel width of 500 μm and an estimated accumulation layer thickness of 2 nm). Here, the observable width of the emission zone is about 1.2 μm and is limited by the emission wavelength, the collecting near-IR objective with a numerical aperture of 0.8 and the thickness of the glass substrate.

Figure 3.

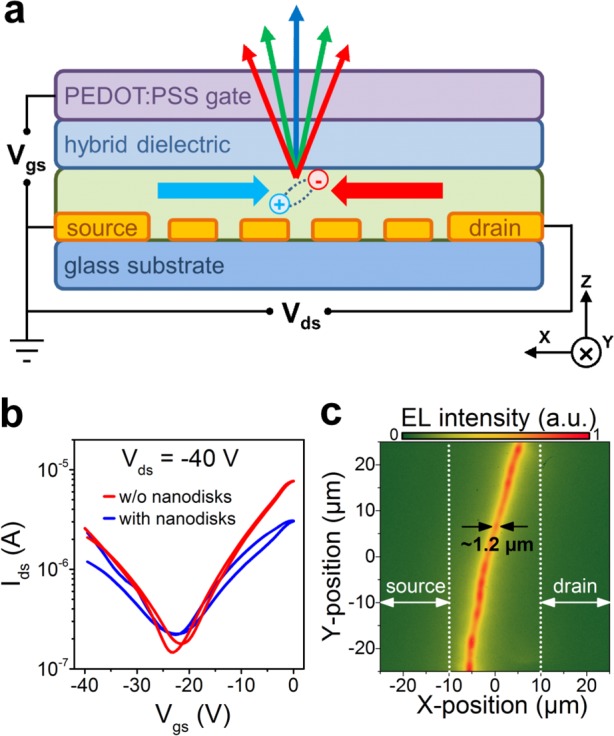
(a) LEFET operation principle with recombination and emission zone (not to scale). (b) Ambipolar transfer characteristics of LEFETs without (red curve) and with (blue) gold nanodisks array in the channel. (c) Representative planar electroluminescence image of the emission zone with respect to the electrodes.

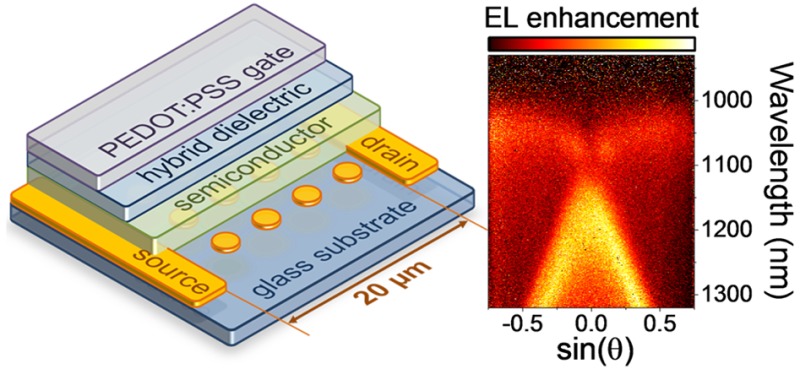
Figure 4a,b shows the angle- and wavelength-dependent emission properties of the fabricated sample under electrical (EL) and optical pumping (PL). They exhibit qualitatively the same behavior, revealing the spectral features of the SLRs. Here, we define EL and PL enhancement factors as the ratio of the signals with and without NDs for the same exciton generation conditions, that is, current density or laser power. The absolute values of enhancement for EL are lower than those for PL because the electrically generated excitons are formed only at the PMMA/DPPT-BT interface (within 1–2 nm) and thus further away from the regions of maximum local fields, while for PL, excitons are generated in the whole 40 nm layer of DPPT-BT and are hence more affected by the larger local field intensities (see Supporting Information, Figure S6, for a side view of the field intensity enhancement profiles). For even higher enhancement values, the layer thickness could be reduced and thus the distance between electrically generated excitons and regions with high local fields would be decreased. Although the intrinsic emission efficiency of the DPPT-BT is low (∼0.01%) and thus the Purcell effect can be easily demonstrated, materials with high emission efficiency could also take advantage of this configuration as the collective coupling of NDs will lead to redirection of emission as reported recently.⁹ Furthermore, the increased radiative decay rate via the Purcell effect would also offer a higher saturation threshold and thus higher maximum brightness.

Figure 4.

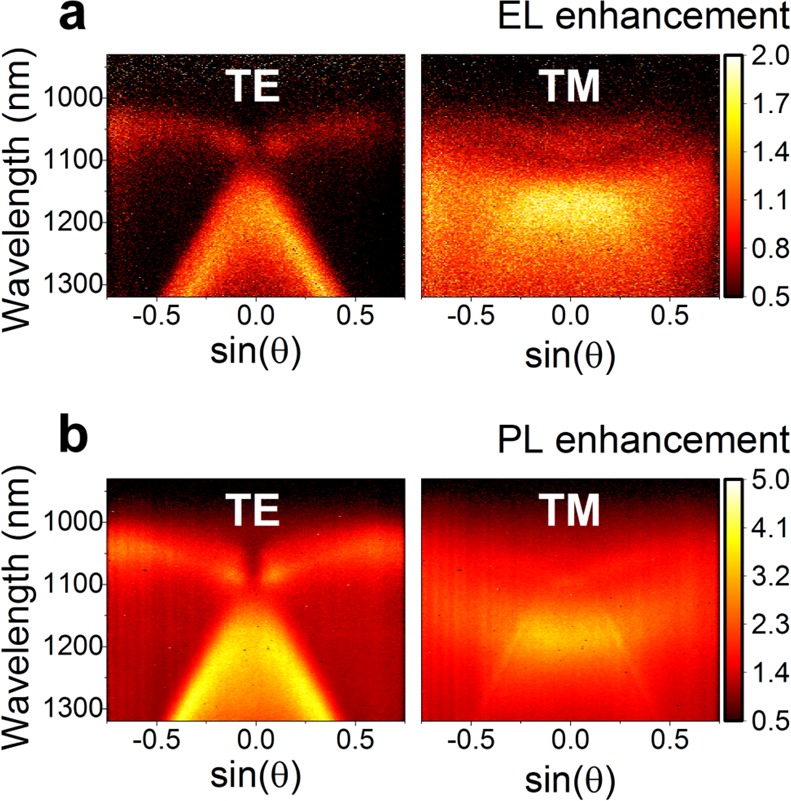
Comparison of angle- and polarization-resolved (a) electroluminescence and (b) photoluminescence enhancement spectra.

Aside from the potential of tailored emission properties for optoelectronic devices, the presented results are a significant step forward for electrically driven devices supporting SLRs. Current densities on the order of 10⁴ A/cm² are comparable to values required to reach population inversion and to compensate for loses in plasmon-assisted nanolasers.³³ Even higher current densities could be achieved by increasing the applied voltages and further reducing the gate dielectric thickness. Moreover, many different organic and inorganic semiconductors could be used as the gain and charge transport material, for example, quantum dot solids,³⁴ single-walled carbon nanotubes,³⁵ two-dimensional transition metal dichalcogenides,³⁶ perovskites,³⁷ or organic semiconductors,³⁸ that cover a spectral range from the visible to the near-infrared. Furthermore, strong plasmon-exciton coupling is feasible,^11,12,16 thus, potentially enabling electrically driven polaritonic devices and possibly plasmon-exciton polariton condensation.³⁹

In conclusion, we have demonstrated a light-emitting device geometry where plasmonic structures supporting SLRs are directly driven by electrical excitation. The integration of ND arrays in LEFETs shows their mutual compatibility in terms of charge transport properties and far-field coupling allowing for efficient SLRs. These results open the way toward electrically driven plasmon-exciton polariton devices and possibly low-threshold lasing. Finally, the high local fields also offer a robust and easy tool for tailored emission of optoelectronic devices.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsphotonics.6b00491.

• Methods: Fabrication and characterization of LEFETs, and 3D-FDTD calculations. Additional data and analysis: dark-field image of LEFETs, representative PL results of an ND array sample with 830 nm pitch, angle-integrated intensity and enhancement of PL, electrical characteristics of LEFETs with and without ND array, simulated field intensity profile (PDF).

Author Contributions

^† These authors contributed equally to this work (Y.Z. and M.H.).

The authors declare no competing financial interest.