Towards imaging the body at 10.5 tesla

Abstract

Purpose

To explore the potential of performing body imaging at 10.5T compared to 7.0T through evaluating the transmit/receive performance of similarly configured dipole antenna arrays.

Methods

Fractionated dipole antenna elements for 10.5T body imaging were designed and evaluated using numerical simulations. Transmit performance of antenna arrays inside the prostate, kidneys and heart were investigated and compared to those at 7.0T using both phase-only RF shimming and multi-spoke pulses. Signal-to-noise ratio (SNR) comparisons were also performed. A 10-channel antenna array was constructed to image the abdomen of a swine at 10.5T. Numerical methods were validated with phantom studies at both field strengths.

Results

Similar power efficiencies were observed inside target organs with phase-only shimming, but RF non-uniformity was significantly higher at 10.5T. Spokes RF pulses allowed similar transmit performance with accompanying local SAR increases of 25–90% compared to 7.0T. Relative SNR gains inside the target anatomies were calculated to be >2-fold higher at 10.5T, and 2.2-fold SNR gain was measured in a phantom. Gradient echo and fast spin echo imaging demonstrated the feasibility of body imaging at 10.5T with the designed array.

Conclusion

While comparable power efficiencies can be achieved using dipole antenna arrays with static shimming at 10.5T; increasing RF non-uniformities underscore the need for efficient, robust and safe parallel transmission methods.

INTRODUCTION

Moving to higher static magnetic field strengths (B₀) can increase the sensitivity of magnetic resonance (MR) studies, improve susceptibility contrast and increase chemical shift dispersion. Since the inception of MRI, pushing toward higher field strengths to seek answers to physiological and biological questions has been the goal of many researchers. Currently, approximately 60 ultra-high field (UHF, B₀ ≥ 7.0 tesla (7.0T)) human scanners are in operation world-wide with a majority of them being 7.0T systems (1). A number of systems that are beyond 10T are being planned or have been installed (2). Notably, the first whole-body 10.5T human scanner has recently been ramped to field and is operational. However, with the increasing field strength, electro-magnetic (EM) wavelengths inside the tissues become shorter, causing destructive transmit B₁ (B₁⁺) interferences. In addition, local specific absorption rate (SAR) increases with the field strength, a constant concern at UHF. Tackling these challenges via radiofrequency (RF) coil designs and parallel transmission (pTx) methods is an active area of research, which has shown potential for imaging several target anatomies inside the body at 7.0T (3,4).

Arrays of dipole antennae have been used increasingly for body imaging at 7.0T because of their favorable field distributions, increased power efficiency at depth and improved SAR performance (5–8). Current distribution on the coil element plays an important role in shaping the EM fields inside the so-called “near field” region; however at larger depths (i.e. outside the near-field region) where propagating EM waves become more dominant, wave propagation effects need to be considered for optimal coil design. It has been shown at 7.0T that outside the “near-field” regime, antenna elements (e.g., dipole antennae) allowing high wave propagation directivity may provide improved B₁⁺ efficiency inside the body compared to conventional coil elements (e.g., microstrip line and loop coil elements) (8,9). Because the near-field region is pushed closer to the element at 10.5T compared to 7.0T, dipole antenna elements are anticipated to have a better performance than the microstrip line and resonating loop elements for most body imaging applications.

Solely from the transmit RF management perspective, imaging the body is expected to be more challenging at 10.5T than at 7.0T, because wavelengths inside the tissue are reduced to around 9 cm. The goal of this work was to determine the main differences and major challenges for 10.5T body imaging by comparing local transceiver arrays of similar configurations to those at 7.0T. Specifically, we designed fractionated dipole antenna elements for body imaging at 10.5T using a similar methodology reported by Raaijmakers et al (10). These individual elements were used to simulate a 10-channel array for which transmit performance (i.e. power efficiency, field uniformity and RF safety) as well as receive performances inside the prostate, kidneys and heart were investigated and compared to a similar design at 7.0T. To validate the electromagnetic modeling results, the 10-channel dipole array was constructed for 10.5T and used to experimentally obtain transmit B₁⁺ and SNR measurements for comparison with similarly obtained 7.0T data in a uniform torso-sized saline phantom. Finally, MRI of the abdomen of a large swine was obtained to demonstrate the feasibility of performing body imaging studies at 447 MHz.

METHODS

Design of a fractionated dipole antenna element for 10.5 tesla

Fractionated dipole antenna elements at 10.5T were designed (10) using a finite-difference time-domain (FDTD) solver (SEMCAD X software V14.8, SPEAG, Zürich, Switzerland), for a proton Larmor frequency of 447 MHz. The dipole antenna was placed 2 cm away from the surface of a uniform rectangular phantom (dimensions: 20×20×40 cm³) of which the electrical properties mimic the human body (ε_r = 36, σ = 0.42 S/m). The basic fractionated dipole element structure used in this work consists of two arms, with each arm sectioned at two locations (Figure 1.a) where the neighboring sections on each arm are connected with identical reactive components. Our design procedure was as follows: first an approximate total length of the dipole element was determined. This was accomplished by simulating EM-field distributions inside the phantom for a range of element lengths (between 18 and 30 cm). The resulting peak 10g averaged local SAR (SAR_10g) was calculated followed by the calculation of power efficiency (i.e., B₁⁺/W^0.5) and SAR efficiency (i.e., B₁⁺/SAR_10g^0.5) inside 8 cm³ cubes located at depths of 4, 6, 8 and 10 cm. The goal was to determine a length which gave high power efficiency at depths greater than 8 cm. After the length was found, the value of the reactive components was determined. For this, another set of simulations were performed for a range of reactance values (between −60Ω (i.e. capacitive) and 120Ω (i.e. inductive)). The goal was to achieve reactance values that yielded both favorable power and SAR efficiencies at depths of 8 cm and deeper.

Figure 1.

(a) Dipole antenna elements at 7.0 T and (b) 10.5 T. (c) Anterior housing of the dipole antenna array containing six elements.

Comparison of 7.0 and 10.5 tesla dipole antennae elements

Peak local SAR and power efficiency distributions of dipole antenna elements at 10.5T were compared against fractionated dipole antenna elements previously developed by Raaijmakers et al. at 7.0T (10). Simulations were performed using an FDTD solver with the same phantom used for element length evaluations. Additionally, in each case two dipole antenna elements were placed next to each other on the rectangular phantom. Mutual coupling as a function of inter-element distance was calculated by varying the center-to-center distance between the two elements from 4 to 10 cm with 1 cm increments.

Numerical analysis of 10-channel antenna arrays on an anatomical human model

Array performances of the 7.0T and 10.5T dipole elements were investigated inside the prostate, kidneys and heart of an adult male human model (“Duke” from Virtual Family v1.0) (11) at 297.2 and 447 MHz, respectively. Ten antenna elements were placed around the pelvis, abdomen and chest of Duke for the prostate, kidney and heart simulations, respectively. A total of six simulations were performed (prostate, kidney and heart simulation locations; 7.0 and 10.5T ¹H Larmor frequencies) using correct frequency specific electrical properties (12). Conductors of the antenna elements were 2 cm away from the tissue surface and were placed at geometrically identical locations both at 7.0 and 10.5T. All elements were terminated with 50Ω voltage source ports. The entire body and the gradient shield were included in the simulations. EM-field distributions of each antenna element were computed using an FDTD solver. EM field solutions inside Duke within a 30 cm-long region centered at the antenna elements along the z-dimension were extracted. Meshing resolution within the antenna conductors and inside the 30 cm-long region where the EM-fields were extracted was ≤1 mm. The mesh resolution of the simulation was gradually coarsened outside the region of interest to accelerate computations. Mesh sizes ranged between 100–133 Million cells (120.9±12.4 Million cells). EM-field distributions were imported to MATLAB (Mathworks, Natick, Massachusetts) for post processing and analysis.

EM-field distributions were re-gridded onto a uniform 2 mm grid using nearest-neighbor interpolation. SAR Q-matrices were formed using a modified version of the N-gram averaging algorithm developed by Carluccio et al. (13). The SAR Q-matrices were further compressed into a largely reduced number of virtual observation points (VOPs) (14) which were subsequently used for pTx spoke pulse design to accelerate the estimation of peak 10g-averaged local SAR. The SAR overestimation percentage used in creating the VOPs was 5% for 10.5T and 10% for 7.0T simulations, yielding comparable absolute overestimation at both field strengths for a given target organ.

Power efficiency, field uniformity, peak local SAR and SAR efficiency metrics were used to assess the transmit performance of the antenna arrays at both field strengths targeting the prostate, kidneys and heart. Field uniformity was quantified using the coefficient of variation (CV; i.e., SD/mean) of B₁⁺ inside each target organ (i.e. prostate, kidneys, or heart). A range of phase-only shim solutions were calculated by varying the tradeoff between power efficiency and field uniformity.

Relative SNR values of the antenna arrays were numerically calculated by combining the normalized receive B₁ (B₁⁻) distributions of individual antenna elements in a root sum-of-squares (RSOS) fashion and scaling with the square of B₀ to account for the field-strength related increase in signal power (15):

$$\mathrm{S}\mathrm{N}{\mathrm{R}}_{\text{relative}}~{\left(\frac{{\mathrm{B}}_0}{7.0}\right)}^2·\sqrt{{\sum }_{\mathrm{n}=1}^{10}{\left(\frac{|{\mathrm{B}}_{1,\mathrm{n}}^{-}|}{\sqrt{{\mathrm{P}}_{\mathrm{n}}}}\right)}^2}$$ [1]

where B₀ is the field strength, $\frac{|{\mathrm{B}}_{1,\mathrm{n}}^{-}|}{\sqrt{{\mathrm{P}}_{\mathrm{n}}}}$ is the magnitude of the receive B₁ field normalized to 1 W of accepted power for the n^th antenna element.

Parallel transmission using spoke pulses

In addition to phase-only RF shimming as is typically performed at 7.0T, we designed pTx spoke pulses (16) to evaluate the performances of the 10-channel dipole arrays at 7.0T and 10.5T when exploiting parallel transmit capabilities. For each target organ (i.e., prostate, kidneys and heart), single- and 2-spoke pTx pulses were designed for slab-selective excitation targeting a uniform flip angle (FA) distribution within the region of interest (ROI) and were designed with an explicit local SAR constraint. The design problem was formulated in the image domain (17) as a constrained minimization (18,19) to seek channel-specific and spoke-specific RF weights (i.e., magnitude and phase modulations) that minimize the excitation error while satisfying a predefined local SAR limit. The excitation error was quantified in the magnitude least squares sense (20) assuming small tip angle excitation, and the peak 10 g SAR estimated by using VOPs.

To improve RF performance in the 2-spoke pulse design, the spoke positioning in the excitation k-space was determined by an additional optimization process. To have an equivalent but reduced parameter space, the first spoke was always positioned at the origin of the excitation k-space and only the placement of the second spoke was variable (21). The placement of the second spoke was tuned by an exhaustive search over a large number of candidate placements. Instead of a 2D grid restricted to the kx-ky plane, the candidate placements were predefined on a 3D grid of the excitation k-space. This was done to increase the degrees of freedom in pulse design, thereby producing more homogeneous flip angles in a 3D ROI. The gridding of the k-space was based on spherical coordinates (i.e., kr, kθ, kφ). The radius (kr) was incremented from 1/FOV to 3/FOV in steps of 0.2/FOV where FOV is the average dimension of the target organ, while the polar (kθ) and azimuthal (kφ) angles were both incremented from 0° to 180° in steps of 45°. The placement that minimized the Tikhonov regularized least squares was chosen as the best location of the second spoke and was used for the subsequent local SAR constrained 2-spoke pulse design. The resulting 3D gradient blips were similar to those associated with kT point pulses (22) which have been shown to be effective for volumetric flip angle homogenization.

In all cases, the constrained minimization pulse design was solved using “fmincon” in Matlab for which the initial point was obtained by solving a least square minimization with Tikhonov regularization (17). For all pulse designs, the nominal flip angle was set to 45 degrees where the sub-pulses consisted of a sinc waveform with a time bandwidth product of 4 and a pulse length of 1 ms. Furthermore, the local SAR was evaluated assuming a duty cycle of 10% for single-spoke and 20% for 2-spoke pulse designs.

To characterize the RF performance of the dipole arrays, the L-curve demonstrating the tradeoff between excitation fidelity and the resulting local SAR was obtained by varying the predefined local SAR limits during pulse design. Specifically, the predefined local SAR limit was varied from 1 to 20 W/kg for investigated anatomies. The excitation fidelity was evaluated using normalized root mean square error (NRMSE) of the excitation which quantifies the deviation of the resulting flip angles within the target organ from the nominal flip angles. The local SAR was calculated using the SAR Q-matrices, not the VOP’s which were only used during pulse design. In addition, the average forward total antenna array power for duty cycles of 10% and 20% were calculated for 1- and 2-spoke pulse designs, respectively. Average flip angle values inside the investigated organs were computed for the designed spoke pulses.

Implementation of 10.5 T 10-channel dipole antenna array

In order to conduct experimental studies in phantoms and in vivo, a 10-channel dipole antenna array was constructed matching that modeled in simulations. The elements of this array were etched on double-sided FR4 printed circuit boards (PCBs) (Figure 1.b). PCBs were mounted between two 9.5 mm-thick thermoplastic polyehterimide blocks (ULTEM 1000 resin, Sabic Global, Pittsfield, Massachusetts). Dipole antenna elements were initially fine-tuned on a human body at 447 MHz by adjusting their lengths and matched to better than −15 dB using first-order lattice balun networks. Two flexible fabric housings (anterior and posterior) were used to place the antenna elements around the object being imaged while maintaining a center-to-center separation of ~9 cm between neighboring elements (Figure 1.c), with the anterior housing containing 6 and the posterior housing 4 antenna elements. The 9 cm spacing was initially used to match the geometry of the 7.0T array used in previous work (10).

10.5 T MRI system properties and experimental methods

MRI experiments were conducted on a whole-body 10.5 tesla scanner (Siemens Healthcare, Erlangen, Germany), equipped with 32 receive and 16 transmit channels. Each transmit channel was driven by 2-kW power amplifiers (Stolberg HF-Technik AG, Stolberg, Germany). The 10-channel transceiver dipole antenna array was interfaced to the scanner via a 16-channel transmit/receive box (Virtumed LLC, Minneapolis, Minnesota).

Phantom validation studies

To validate numerical computations, matching experiments and simulations were performed using an ~18L torso-sized phantom (23) filled with a saline solution (4.5 g/l NaCl, 1 g/l CuSO₄), with electrical properties (ε_r = 77.8, σ = 0.82 S/m) and (ε_r = 77.5, σ = 0.85 S/m) at 7.0 and 10.5 tesla ¹H Larmor frequencies, respectively. Experiments were conducted on 7.0T and 10.5T whole-body scanners (Siemens Healthcare, Erlangen, Germany) with identical data acquisition protocols. Flip angle maps were acquired with the actual flip angle technique (24) (TR₁/TR₂/TE: 20/120/3 ms; nominal FA = 50°; voxel-size: 2×2×4 mm³; acquisition matrix: 226×226×64) and were used to calculate power efficiency distributions. SNR data were acquired using a fully-relaxed GRE sequence (TR/TE: 10000/3.1 ms; FA = 90°; voxel-size: 2×2×8 mm³; acquisition matrix: 226×226×32) followed by a noise scan with minimum TR and no RF excitation (25).

First, power efficiency distributions of single dipole antenna elements inside the phantom were measured at both field strengths, and matching simulations were performed at both ¹H Larmor frequencies. Power losses in the transmit chain (i.e. T/R switch, cable and mismatch losses) were measured and accounted for. In addition, B₁⁺ and SNR distributions of the 10-channel dipole antenna arrays were investigated on the torso phantom at both field strengths, with six elements placed anteriorly and four elements posteriorly. Phase-only efficiency shimming inside a 24×24 mm² square region approximating the size and location of the prostate was performed (26). Power efficiency and SNR distributions were calculated both experimentally and numerically with simulations closely matching experimental conditions. Power efficiency and SNR ratios between 7.0 and 10.5 tesla arrays were calculated inside centrally located cubes (24 mm edge length) and compared with experimental results to assess the accuracy of numerical simulations. Furthermore, SNR gains inside a 24×24 mm² square region were calculated for each slice to investigate the extent of SNR gains along the z-dimension of the phantom.

Imaging studies

To demonstrate the potential for imaging the body at 10.5T, the 10 channel dipole array was used to obtain renal images of a 75 kg female swine post-mortem (19 cm in the anterior-posterior dimension). To improve RF efficiency and uniformity, phase-only RF shimming targeting both kidneys was conducted prior to the anatomical image acquisitions. Both 3D gradient echo (GRE) and multi-slice fast spin-echo (FSE) images were acquired. The 3D GRE images were acquired in axial and coronal views with TR/TE = 17/2.7 ms, voxel-size = 1.2×1.2×3 mm³, FOV = 460×460×96 mm³, and total duration = 5m 14s. The multi-slice FSE image was acquired in the coronal view with TR/TE = 4000/42 ms, voxel-size = 1.8×1.8×3 mm³, FOV = 450×450×21 mm³, and duration = 1m 52s.

RESULTS

Design of a fractionated dipole antenna at 10.5 tesla

A dipole antenna length of 22 cm was identified as providing high power efficiency at depths greater than 8 cm inside the phantom compared to other investigated antenna lengths. Inductive reactance values along antenna arms tended to decrease local SAR efficiency and power efficiency close to the elements (i.e. depths <5 cm), but demonstrated improved SAR efficiency at depths greater than 8 cm. Therefore, a reactance value of ~25Ω was chosen, which is a trade-off between power and SAR efficiencies at depths greater than 8 cm. Increasing the inductance value further could significantly reduce the power efficiency of the dipole antenna. The chosen inductance value was realized by two 24 mm-wide meanders on each arm (Figure 1.b). Because of the variations between simulated and experimental loading conditions, the physically implemented dipole antenna elements were shortened to 21 cm to achieve resonance at 447 MHz.

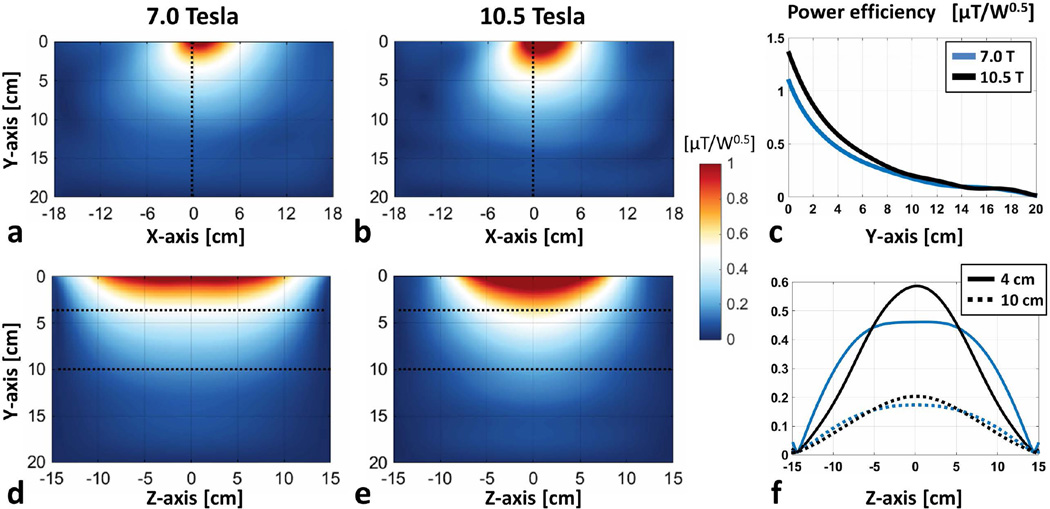
Power efficiency distributions for 7.0T and 10.5T dipole antenna elements inside a uniform phantom along axial and sagittal slices are shown in Figure 2. Due to its shorter length, the full-width half-maximum (FWHM) of power efficiency for the 10.5T antenna along the z-dimension was 28% shorter than that of 7.0T, resulting in reduced coverage at 10.5T in that dimension. The power efficiency of the 10.5T antenna was 27% and 17% higher at depths of 4 and 10 cm, respectively, with 76% higher peak 10g SAR than the 7.0T antenna.

Figure 2.

(a) Power efficiency distributions of 7.0 T and (b) 10.5 T dipole antenna elements along axial slices inside a uniform phantom are shown. (c) Power efficiency profiles along the center of the axial slices are plotted (blue: 7.0 T, black: 10.5 T). Power efficiency distributions of 7.0 and 10.5 T antennae inside sagittal slices are shown in (d) and (e), respectively. (f) Power efficiency profiles at a depth of 4 cm (solid) and 10 cm (dashed) are plotted for the 7.0 and 10.5 T antennae in blue and black, respectively.

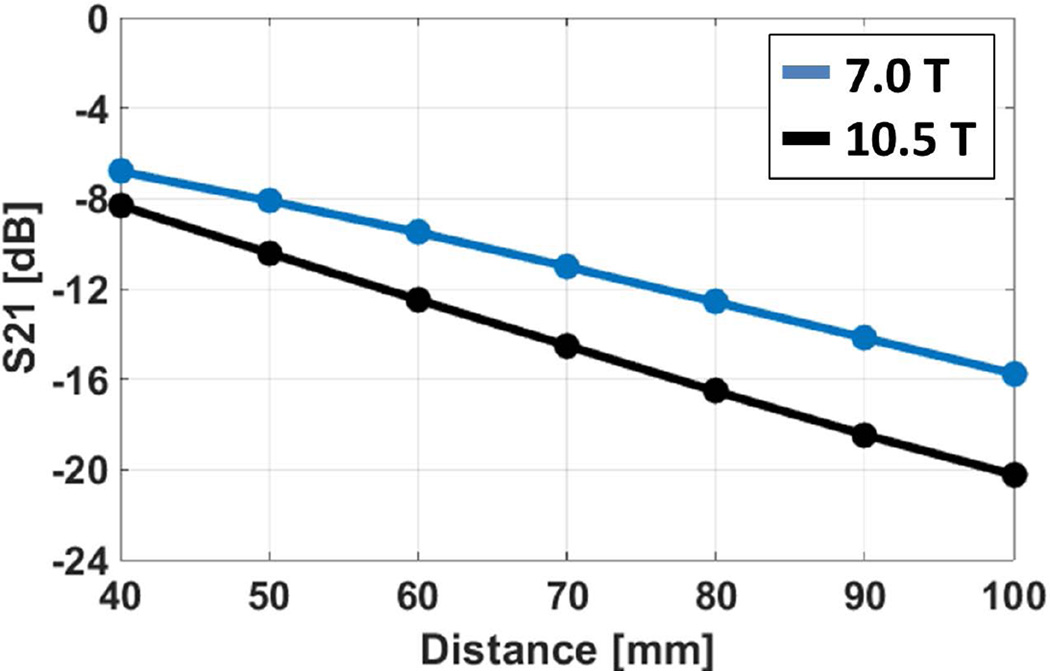
Mutual coupling between two antenna elements at various center-to-center distances are plotted in Figure 3. At a distance of 80 mm, coupling between antenna elements was −12.6 and −16.5 dB at 7.0T and 10.5T, respectively. For a target decoupling value of ≤−12 dB, 7.0T and 10.5T antenna elements could be placed at center-to-center distances of ≥ 80 and 60 mm, respectively.

Figure 3.

Amount of coupling (in dB) between neighboring antenna elements placed on a rectangular uniform phantom are plotted against their center-to-center separation distances (blue: 7.0 T, and black: 10.5 T antenna elements).

Numerical comparison of 7.0 and 10.5 T dipole antenna arrays for imaging the body

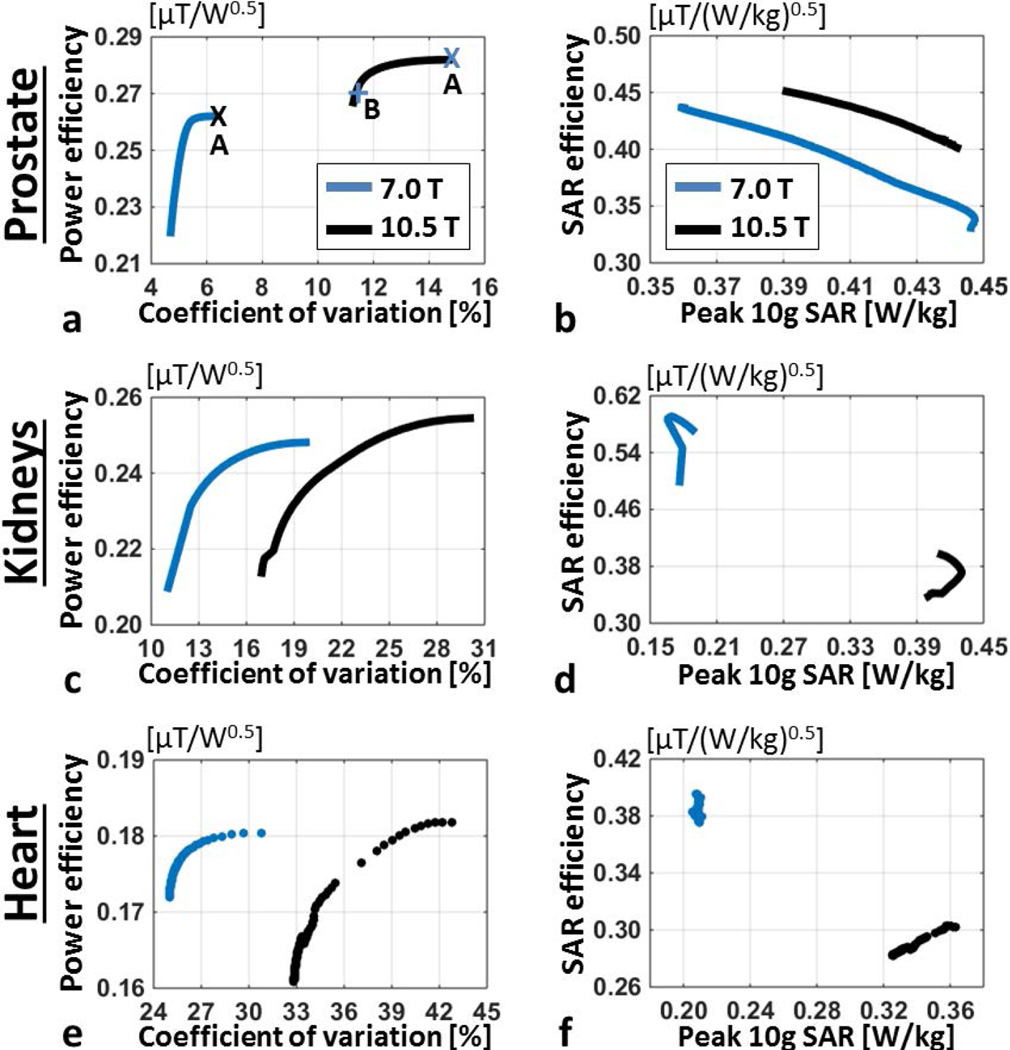
The plot of numerically computed power efficiency versus coefficient of variation (CV) inside the prostate with phase-only shimming (Figure 4.a) demonstrates that both antenna arrays can provide similar power efficiencies at their respective field strengths, however the resulting field uniformity at 7.0T is superior. Using a phase-only shim solution optimized for power efficiency at 10.5T, 133% higher CV was observed compared to an efficiency shim solution at 7.0T (Supporting Figure S1.a–b). A phase-only shim solution optimized for field uniformity at 10.5T, yielded 79% higher CV than an efficiency solution at 7.0T. SAR efficiency inside the prostate and peak 10g local SAR of the arrays are plotted in Figure 4.b, showing that the 7.0T antenna array can achieve slightly lower (~10%) SAR levels compared to 10.5T inside the prostate. Power efficiency vs CV distributions inside the kidneys and heart are plotted in Figure 4.c and e, respectively. In both organs, both antenna arrays provide similar power efficiency while field uniformity at 10.5T is poorer. SAR efficiency of the antenna arrays inside the kidneys and heart are plotted against peak 10g SAR in Figure 4.d and f, respectively. Peak SAR values of the 10.5T array are on average 130% and 62% higher than its 7.0T counterpart with kidney and heart specific shim solutions, respectively. Even though both arrays can provide similar power efficiencies, SAR efficiency of 10.5T array is lower inside the kidneys and heart by 35 and 23%, respectively, due to its higher local SAR deposition.

Figure 4.

(a) Power efficiency vs coefficient of variation of B1+ magnitude inside the prostate of Duke and (b) SAR efficiency vs peak 10g local SAR are shown for 7.0 T (blue) and 10.5 T (black) antenna arrays. Power efficiency distributions pertaining to annotated shim solutions are shown in Supporting Figure S1. (c) Average power efficiency vs its coefficient of variation inside kidneys and (e) heart are plotted. (d) SAR efficiency vs peak 10g local SAR plots for kidney and (f) heart phase-only shim solutions are displayed.

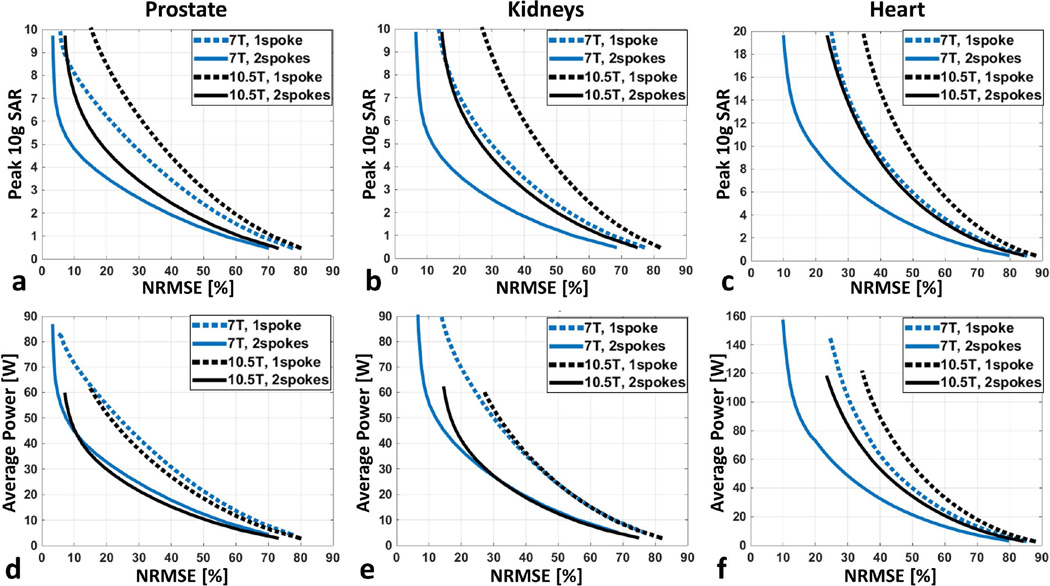
L-curves demonstrating the tradeoffs between excitation error (i.e. NRMSE) and local SAR limit for various design scenarios are plotted in Figure 5.a–c. For the same target organ and number of spokes, RF performance was worse at 10.5T where SAR increased by 25–35% for prostate, 60–80% for kidneys and 50–90% for heart when achieving comparable excitation fidelity inside the target organ. However, for kidneys and heart, designing 2-spoke pulses at 10.5T appeared to yield similar RF performance to single-spoke designs at 7.0T. For prostate, designing 2-spoke pulses at 10.5T started to outperform the single-spoke design at 7.0T. L-curves demonstrating the relation between forward antenna array power and NRMSE are shown in Figure 5.d–f. The range of average FAs achieved in the target anatomies over the range of powers applied are listed in Supporting Table S1 for the pulses designed for each target anatomy. FAs of approximately 45° are achieved at both 7.0 and 10.5T inside the prostate and kidneys, however 2-spoke pulse designs are required at 10.5T in the kidneys. Inside the heart, an average FA close to 45° is achieved only with a 2-spoke pulse at 7.0T and, given the design constraints, not achieved at 10.5T due to the local SAR limits being reached.

Figure 5.

L-curves demonstrating the tradeoff between excitation error (NRMSE) and resulting peak local SAR for 7.0 T (blue) and 10.5 T (black) arrays when designing 1-spoke (dashed) and 2-spoke (solid) pTx pulses to image (a) the prostate, (b) the kidneys and (c) the heart. The pTx pulses were designed with explicit local SAR constraint, and the L-curve per design scenario was created by varying the predefined peak 10 g SAR limit. In all cases, the nominal flip angle was 45 degrees. Note that combining 2-spoke pulse design with our 10.5T dipole array provided comparable (when imaging kidneys or heart) or even better (when imaging prostate) RF performance than single-spoke designs at 7.0T. L-curves demonstrating the tradeoff between excitation error (NRMSE) and required average total array power for 7.0 T (blue) and 10.5 T (black) arrays for 1- and 2-spoke (solid) pTx pulses to image (d) the prostate, (e) the kidneys and (f) the heart are shown.

RSOS combination of normalized receive fields from simulation on axial slices intersecting the prostate, kidneys and heart for the antenna arrays at 7.0T and 10.5T are shown in Supporting Figure S2, and mean values are listed in Table 1. Average B₁⁻ performance of the antenna arrays are within ±6% of each other. Simulated relative SNR gains at 10.5T are calculated using Eq. [1], and listed in Table 1. More than two-fold gains are anticipated at 10.5T in all imaging targets under investigation using dipole antenna arrays with the same number of channels, while excluding the field strength dependent spin relaxation effects.

Table 1.

Mean values of numerically computed receive B₁⁻ performance of antenna arrays inside the prostate, kidneys and heart are listed (distributions are shown in Supporting Figure S2). Anticipated relative SNR gains at 10.5 T compared to 7.0 T are calculated using Eq. [1] and listed along the last column.

	RSOS B1− combination [µT/W0.5]		Relative SNR gain of the 10.5 T antenna array vs the 7.0 T array
	Antenna array at 7.0 T	Antenna array at 10.5 T
Prostate	0.279	0.296	2.39
Kidneys	0.353	0.365	2.33
Heart	0.297	0.283	2.14

Phantom validation studies

Power efficiency distributions of dipole antenna elements inside the torso phantom along an axial slice intersecting the center of the elements are shown in Supporting Figure S3; with top and bottom rows depicting numerical and experimental results, respectively. Power efficiency profiles of the elements are plotted in Supporting Figure S3.c and f, respectively demonstrating good agreement between simulations and experiments. Power efficiency and SNR distributions of the 10-channel dipole antenna arrays are shown in Supporting Figure S4 and Supporting Figure S5, respectively. Top and bottom rows show numerical and experimental results, respectively; while left and right columns demonstrate the SNR distributions at 7.0T and 10.5T, respectively. Measured SNR maps fail to provide accurate results in regions of low power efficiency with the chosen shim solutions, and results are reported from inside the annotated regions where reliable RF excitation is generated. Simulated and measured power efficiency ratios for 7.0T and 10.5T inside annotated cubes are 1.00 and 1.04, respectively. SNR gains at 10.5T are 2.39- and 2.26-fold inside annotated regions from simulation and experiment, respectively. Numerical and experimental results are within 6% of each other with respect to the power efficiency and SNR investigations of the 10 channel antenna array, validating the accuracy of EM-field simulations. The 10.5T dipole antenna array provides SNR gains of >2.25-, >2- and >1.5-fold when looking at larger extents along the z-dimension of 58, 110 and 200 mm, respectively (Supporting Figure S6).

Imaging studies

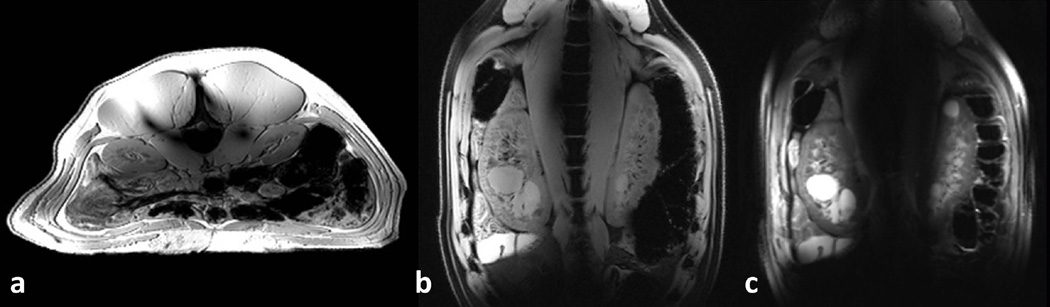
Anatomical axial and coronal GRE images inside the abdomen of a swine are shown in Figure 6.a–b, respectively, with phase-only RF shimming providing acceptable field transmission inside the kidneys. Coincidently, renal cysts were observed in the swine imaged in these studies. Coronal FSE images (Figure 6.c) show improved contrast between the cystic lesion and normal appearing renal anatomy compared to respective GRE images. In the FSE images, parts of the renal tissues and borders of the kidneys towards the middle of the coronal imaging slices were not visible due to B₁⁺ dropout in those locations.

Figure 6.

(a) Axial and (b) coronal GRE images acquired inside the abdomen of a swine with anterior-posterior dimension of 19 cm. Phase-only RF shimming inside the kidneys are used in acquisitions. (c) Coronal FSE image demonstrates good contrast between the cysts inside the kidneys, cortex and medulla. Image quality in the middle of the imaging slice is hampered due to B1+ dropoff.

DISCUSSION

We designed dipole antenna elements for imaging the body at 10.5T using a similar methodology to the one described by Raaijmakers et al (10). An array of the new elements was then compared against a similar antenna array configuration at 7.0T (10). Due to the higher Larmor frequency at 10.5T, optimized dipole antenna element lengths were shorter than similarly designed 7.0T counterparts, yielding a reduced coverage in the z-dimension. The coverage of the 10.5T antenna array was suitable for prostate imaging, however renal and cardiac imaging would benefit from coverage similar to that provided by the 7.0T array. A larger imaging FOV along z could be supported by using longer antennae with capacitive loading, by interleaving the elements along z-dimension and/or placing elements in mulitple rows (27–30). In this work, we used a similar antenna design methodology at 10.5T to that originally used for 7.0T, kept the number of antenna elements the same and placed them at identical locations at both field strengths and in all imaging locations (i.e. around the pelvis, abdomen and chest of Duke) in order to minimize the number of variables between field strengths.

Coupling between neighboring antenna elements at a given separation is lower at 10.5T, which may enable development of arrays with higher element densities and channel counts (31). Reduction in mutual coupling can be explained by the increased EM field phase variation and shortened wavelength at higher frequencies (31). Even though not explicitly investigated in this work, larger spatial phase variations at higher frequencies results in more distinct individual coil sensitivity profiles and improved parallel imaging performance at higher field strengths (32). Element count and density can also be increased by shortening the length of the antennae by using high permittivity blocks (7), by further distributing the inductance along the arms of the antenna (33,34) and by combining antenna elements with loop coils (35,36). Development and evaluation of an improved 10.5T body imaging array with higher number of channels will be the focus of future work.

Our results show that dipole antenna arrays have similar power efficiencies and peak local SAR with phase-only shimming inside the prostate, however with increased frequency and decreased wavelength, field uniformity was significantly worse at 10.5T. The SAR increase observed when achieving similar excitation errors (i.e. NRMSE) inside the investigated target organs ranged between 25 and 90%, lower than the quadratic SAR relation to B₀ (37) (i.e. 125% at 10.5T vs 7.0T), and in agreement with more recent work investigating electrodynamic constraints at higher frequencies (31,38,39).

Quadratic SNR gains with increasing B₀ were previously observed with minimally invasive monopole antennae at 3.0T and above (40,41), and here again quadratic SNR gains at 10.5T are anticipated against 7.0T in numerical simulations (i.e. ~125%, Table 1) and also measured in saline phantoms (Supporting Figure S5). It is worth noting that the smaller coverage of the 10.5T array along the z-dimension biases SNR comparisons by limiting the noise contribution from tissues outside the region of interest, especially in smaller imaging targets such as the prostate and kidneys. If the coverage of the coils were the same at both field strengths while keeping the number of elements unchanged, a more moderate supra-linear SNR gain recently reported by Pohmann et al. may be expected (42). However, dense receiver arrays as used in this previous work, are not currently available for UHF body imaging, and will need to be developed in order to realize the potential gains in SNR. Similarly, the shorter z-coverage of the 10.5T array is favorable for imaging the prostate, yielding up to 35% higher peak SAR compared to 7.0T while achieving similar transmit performance. In contrast, up to 90% more peak SAR is observed for similar transmit performance in larger organs (i.e. heart). These results underscore the importance of target specific array optimization at UHF.

In vivo studies in healthy human subjects at 10.5T will be conducted upon receiving the U.S. Food and Drug Administration (FDA) and institutional review board approvals. In the absence of running human volunteers, large swine were imaged at 10.5T post-mortem. Imaging of a live swine was not pursued because post-mortem imaging was deemed satisfactory to evaluate the EM-field behavior in vivo. RF transmit performance was sufficient to obtain acceptable image quality inside the kidneys of a swine using GRE sequences. However, achieving the desired transmit performance when performing RF pulse sequences with high levels of power deposition (i.e. FSE) at 10.5T may not be accomplished using static (26,43,44) or dynamically applied static RF shimming methods (45) inside medium- and large-sized targets. Several RF management strategies such as RF excitation using time-interleaved acquisition of modes (46), multi-spoke pulses (22,47), pTx RF pulse design (48–52), or direct signal control approaches (53–55) may be employed to overcome some of the challenges. Furthermore, incorporation of novel quantitative imaging methods that can perform in the presence of heterogeneous RF fields may alleviate the need of strict transmit field control (56). Numerical modeling, validation and real-time monitoring of RF safety (57–64) will play an important role in successful implementation of pTx methods. Even though increasing B0 and Larmor frequency poses challenges in terms of field uniformity and RF management, it also opens up new opportunities for transmit array design using higher element densities and channel counts.