Abstract
Cardiovascular simulations have great potential as a clinical tool for planning and evaluating patient-specific treatment strategies for those suffering from congenital heart diseases, specifically Fontan patients. However, several bottlenecks have delayed wider deployment of the simulations for clinical use; the main obstacle is simulation cost. Currently, time-averaged clinical flow measurements are utilized as numerical boundary conditions (BCs) in order to reduce the computational power and time needed to offer surgical planning within a clinical time frame. Nevertheless, pulsatile blood flow is observed in vivo, and its significant impact on numerical simulations has been demonstrated. Therefore, it is imperative to carry out a comprehensive study analyzing the sensitivity of using time-averaged BCs. In this study, sensitivity is evaluated based on the discrepancies between hemodynamic metrics calculated using time-averaged and pulsatile BCs; smaller discrepancies indicate less sensitivity.
The current study incorporates a comparison between 3D patient-specific CFD simulations using both the time-averaged and pulsatile BCs for 101 Fontan patients. The sensitivity analysis involves two clinically important hemodynamic metrics: hepatic flow distribution (HFD) and indexed power loss (iPL). Paired demographic group comparisons revealed that HFD sensitivity is significantly different between single and bilateral superior vena cava cohorts but no other demographic discrepancies were observed for HFD or iPL. Multivariate regression analyses show that the best predictors for sensitivity involve flow pulsatilities, time-averaged flow rates, and geometric characteristics of the Fontan connection. These predictors provide patient-specific guidelines to determine the effectiveness of analyzing patient-specific surgical options with time-averaged BCs within a clinical time frame.
Keywords: computational fluid dynamics, univentricular, patient-specific, surgical planning, boundary conditions
Introduction
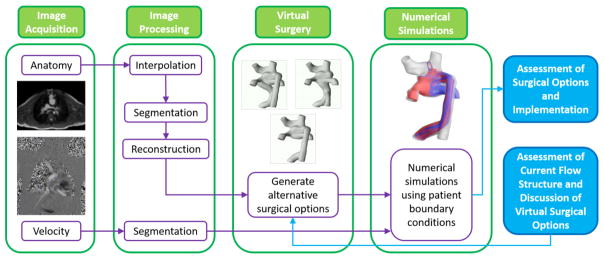
Cardiovascular flow simulation is a non-invasive high-resolution technique to augment the knowledge gained from current medical imaging and clinical measurements (Marsden and Esmaily-Moghadam, 2015). In single ventricle lesions, especially at the Fontan stage, numerical simulations have been used to understand patient hemodynamics (Khiabani et al., 2015; Marsden et al., 2007; Tang et al., 2014), test novel treatment concepts (Esmaily-Moghadam et al., 2015; Trusty et al., 2016; Yang et al., 2013), and predict surgical outcomes (de Zélicourt et al., 2011; de Zélicourt and Kurtcuoglu, 2015; Haggerty et al., 2012; Kung et al., 2013; Sundareswaran et al., 2009a). Cardiovascular simulation has become a fruitful area of translational research and has potential to impact clinical decisions, especially by assisting surgical planning (de Zélicourt and Kurtcuoglu, 2015; Fogel et al., 2013; Marsden and Esmaily-Moghadam, 2015; Marsden, 2014; Restrepo et al., 2015b). Figure 1 illustrates a standard procedure of the surgical planning for congenital single ventricle heart diseases. It consists of four steps: 1) Image Acquisition, which obtains medical images; 2) Image Processing, which reconstructs anatomy and segments blood flow velocity; 3) Virtual Surgery, which generates alternative surgical options; 4) Numerical Simulation, which conducts computational analysis for hemodynamics of the surgical options. Extensive discussions usually happen at step 3 for potential surgical options, as well as after step 5 for assessment of surgical options and implementations. In general, the timeline for surgical planning cases is around one or two weeks.
Figure 1.
A schematic drawing of standard surgical planning procedure; reproduced from (Fogel et al., 2013)
Recently, with the assistance of cardiovascular simulations, optimization techniques were introduced to seek optimal patient-specific surgical treatments (de Zélicourt et al., 2010; Marsden, 2014, 2013). A geometric robustness analysis was also developed to assess the discrepancy in surgical planning outcomes between the proposed and implemented anatomies (Restrepo et al., 2015b). However, numerous challenges limit the effectiveness and applicability of surgical planning. Major limitations include high computational cost, lack of verification, and limited validation of the current surgical planning process. In terms of the computational cost, it often takes days to finish a simulation even with modern high-performance computing power (de Zélicourt et al., 2009; Wei et al., 2014), but fast turnover time is key for surgical planning (Fogel et al., 2013). Moreover, high computational cost may prevent the clinical adoption of the previously mentioned leading-edge surgical planning techniques, (i.e. optimization of surgical treatments and geometric robustness analysis) which require many simulations.
The utilization of time-averaged flow BCs instead of pulsatile flow BCs in cardiovascular simulations is currently a viable option from a cost-standpoint for surgical planning in Fontan patients. On average, it reduces the total simulation time by 50% (Khiabani et al., 2012). Moreover, time-averaged BCs have been widely used and validated in cardiovascular simulations (de Zélicourt et al., 2009; DeGroff, 2008; Wang et al., 2007). Nevertheless, in vivo blood flow is undoubtedly pulsatile (Fogel et al., 1997). Marsden et al.(Marsden et al., 2007) first demonstrated that pulsatility could impact the numerically predicted Fontan hemodynamics. Dur et al.(Dur et al., 2012) further emphasized the importance of taking into account flow pulsatility for Fontan hemodynamic prediction by systematically analyzing the effect of pulsatile BCs using an idealized Fontan model. Therefore, it is critical to quantitatively understand the sensitivity of using time-averaged BCs in place of physiologically accurate BCs regarding key Fontan hemodynamic metrics. The findings can be used to assess the effectiveness of using time-averaged BCs for reducing computational cost, hence, enhancing the applicability and generalization of Fontan surgical planning. Previous simulations statistically (n = 35) showed good agreement between using time-averaged and pulsatile BCs in simulating Fontan hemodynamics (Haggerty et al., 2014). Additionally, a 10% discrepancy in flow energy loss through the Fontan connection between using time-averaged and pulsatile BCs was found when the weighted pulsatility of venous return flow is less than 30%. (Khiabani et al., 2012). However, these previous studies rely on small sample sizes limiting their ability to comprehensively understand the sensitivity of using time-averaged BCs on Fontan simulations at a population level. In addition, most of the previously mentioned studies focus on Fontan energetics and only marginally discussed hepatic flow distribution, which some argue is a more important Fontan hemodynamic metric for current clinical practice (de Zélicourt and Kurtcuoglu, 2015; Pike et al., 2004; Srivastava et al., 1995; Sundareswaran et al., 2009a; Yang et al., 2013).
To address these limitations, the current study carried out a systematic investigation evaluating the sensitivity of both Fontan connection power loss and hepatic flow distribution to using time-averaged BCs rather than the more physiological pulsatile BCs for a large cohort of patients. Benefiting from the large patient cohort, statistical analyses are conducted to explore potential demographic differences, as well as investigate the best predictors of sensitivity to the time-averaged BCs. These predictors can be used to estimate the patient-specific sensitivity of using time-averaged BCs. Together with the clinical time constraint, the effectiveness of employing time-averaged BCs for surgical planning can be identified.
Materials and Methods
Patient Cohort
This study was a retrospective investigation using consecutive patient data from the Georgia Tech-Children’s Hospital of Philadelphia Fontan database. Exclusion criteria include severe CMR artifacts, insufficient phase contrast data, and diagnosis of Ebstein’s anomaly. These exclusions resulted in a 101 patient study. All patients had a completed Fontan connection. Informed consent was obtained and the protocol was approved by the Georgia Institute of Technology and Children’s Hospital of Philadelphia institutional review boards. Patient demographic details are provided in Table 1. The demographic sub-divisions listed in Table 1 have been found clinically important in previous literature (d’Udekem et al., 2007; Haggerty et al., 2014; Khiabani et al., 2015, 2012; Tang et al., 2014).
Table 1.
Patient demographic information (n=101)
| Age (y) | 12.3±8.1 |
| BSA (m2) | 1.23±0.51 |
| Gender (male/female) | 67/34 |
| Bilateral/Single SVC Anatomies | 20/81 |
| IVC Connection Type (IA/EC) | 65/36 |
| HLHS/non-HLHS | 40/61 |
Data are reported as mean±standard deviation.
Anatomy and Velocity Reconstruction
Magnetic resonance imaging (MRI) data were acquired at the Children’s Hospital of Philadelphia. The MRI scans were taken under breath-held conditions and electrocardiogram gated. The transverse bright blood contiguous MRI slices were used to build isotropic voxels by using an adaptive control grid interpolation technique (Frakes et al., 2008, 2003) implemented in MATLAB (The MathWorks, Inc., Natick, MA). The regions of interest were then selected by utilizing a bouncing ball algorithm (Frakes et al., 2003). Finally, surfaces of the in vivo 3D anatomies were reconstructed with Geomagic Studio (Geomagic Inc., NC, USA). Phase contrast magnetic resonance imaging (pcMRI) was also acquired and an in-house methodology using parametric active contours with gradient vector flow was used to segment through-plane velocities to obtain vessel specific blood flow waveforms (Frakes et al., 2004; Sundareswaran et al., 2009b).
Computational Fluid Dynamics
All simulations in this study were carried out using an in-house immersed boundary (IB) method (de Zélicourt et al., 2009). The method is based on a sharp interface scheme and tailored to an unstructured Cartesian grid in order to improve computational efficiency for modeling complex Fontan anatomies. A hybrid staggered/collocated computational grid was employed based on the surface mesh generated by GAMBIT (ANSYS Inc, Lebanon, NH). The Navier-Stokes equations were solved on the staggered grid for better stability, while the boundary conditions were imposed on the collocated grid for synchronization between velocity and pressure. The convection term was discretized using the upwind scheme to further avoid solution instability. A fractional step time marching scheme was used. Overall, a second order accuracy is achieved in both time and space.
The in-house IB code has been used in a wide range of studies and possesses the ability to adequately capture unsteady flows in Fontan connection (Haggerty et al., 2014; Khiabani et al., 2015, 2012; Tang et al., 2014). The Cartesian mesh grid size was generated corresponding to 2% of the inferior vena cava (IVC) diameter. This mesh resolution has proven to yield a grid-independent solution (de Zélicourt et al., 2009). The simulations used 2000 time steps per cardiac cycle for numerical stability. All simulations in this study were run for 6 cardiac cycles in order to achieve periodic stable solutions. Parabolic velocity profiles were imposed at all inlets, and 10 mm extensions were added for flow to develop before entering the computational domain of the Fontan connection. Mean inlet boundary velocity values were taken directly from pcMRI. All outlets were extended 50 mm for both flow development and numerical stability. The outlets employed mass flow splits obtained from pcMRI measurements to ensure mass conservation. Lastly, this study assumed rigid walls and represented blood as a single phase Newtonian fluid.
Hemodynamic Metrics
Flow pulsatility is a major characteristic of flow waveforms, which we quantified with a pulsatility index (PI):
| (1) |
where Qaverage, Qmin, and Qmax were the average, minimum and maximum flow rates across the vessel over one cardiac cycle, respectively. A total weighted pulsatility index (wPI) was further defined representing an overall pulsatility level of the Fontan connection.
| (2) |
wPIinlet and wPIoutlet are weighted pulsatility indices that characterize the flow pulsatility for inlets and outlets, respectively:
| (3) |
| (4) |
where was the time-averaged flow rate of the vessel j.
In this study, two clinically important hemodynamic metrics were calculated from CFD simulations to assess sensitivity of using the time-averaged BCs: hepatic flow distribution (HFD) and indexed power loss (PL). Unbalanced hepatic flow distribution (HFD) to the lungs has been associated with pulmonary arteriovenous malformations (PAVM) in approximately 25% of patients (Pike et al., 2004; Srivastava et al., 1995). Despite numerical evidence showing energy dissipation in the Fontan connection to be a small portion of the ventricular power in two patients (Kung et al., 2013), indexed power loss is linked to limited exercise tolerance (Khiabani et al., 2015; Whitehead et al., 2007).
In simulations, HFD was defined by the percentage (%) of IVC flow to the left pulmonary artery, which is obtained by an in-house particle tracking code (35). Power loss was defined using a control volume energy analysis of the Fontan connection:
| (5) |
where ρ, p, v, and A are blood density, static pressure, velocity, and vessel area, respectively. HFD and PL were averaged over one cardiac cycle after the solution became periodically stable. Indexed power loss (iPL) was further defined as follows:
| (6) |
where is time-averaged systemic venous flow, is the time-averaged PL, and BSA is body surface area (Dasi et al., 2008).
The sensitivity of using the time-averaged BCs in this paper is defined as the discrepancy between hemodynamic metrics between simulations using the time-averaged and pulsatile BCs. The smaller the discrepancy, the less sensitive the metric is to using the time-averaged BC. The sensitivity of HFD and iPL were quantified by dHFD and diPL, respectively:
| (7) |
| (8) |
where subscripts pBC and taBC stand for the pulsatile and time-averaged boundary conditions, respectively.
Statistical Analysis
The current study employed SPSS 22 (IBM Corporation, Armonk, New York) for statistical analyses. All comparisons considered p<0.05 as significant. For normally distributed data, a paired two-tailed t test was utilized, otherwise the Mann-Whitney test was used. Pearson’s and Spearman’s correlations was utilized, for normalized and non-normalized distributions respectively, to identify significant relationships between variables. The multiple linear regression model was used with forward stepwise procedure.
Results
Cohort Results
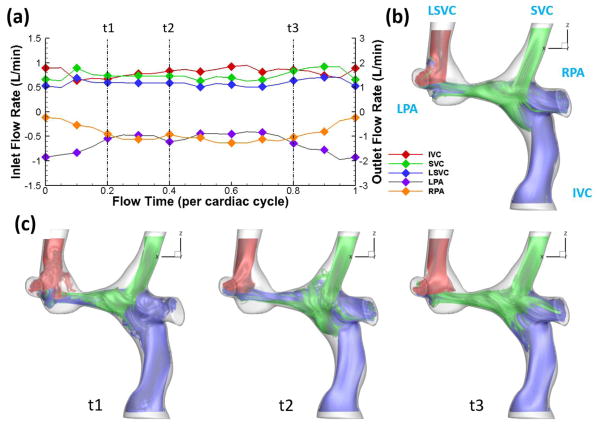
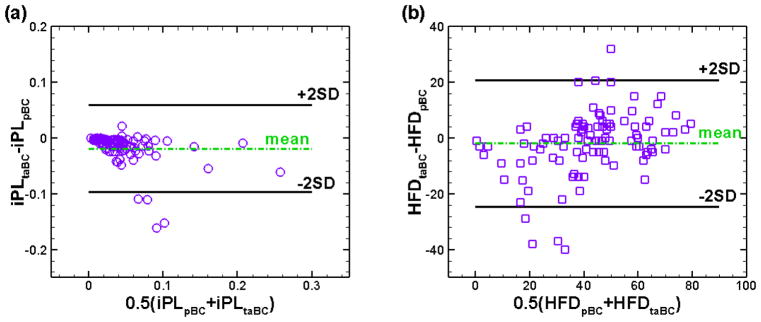
Figure 2 shows one example of the differences in flow fields throughout a cardiac cycle between simulations using time-averaged and pulsatile BCs. Bland-Altman plots of iPL and HFD for the time-averaged versus pulsatile boundary conditions are shown in Fig. 3. These analyses demonstrate a mean difference of −0.017 for iPL and −1.86% for HFD. This indicates that pulsatile indexed power loss and hepatic flow distribution were generally higher than time-averaged values for a given patient. The “2SD” lines in Fig. 3 indicate the 95% limits of agreement, which are ±22.7% for HFD and ±0.079 for iPL. Moreover, the mean values of HFD and iPL in Fig. 3 are 42.44% and 0.071, respectively. The following content focuses on the sensitivity of HFD and iPL derived from simulations using the time-averaged and pulsatile boundary conditions, which are defined as diPL and dHFD in Eqs. (7) and (8).
Figure 2.
Streamlines of a TCPC from simulations with (b) time-averaged boundary conditions and (c) pulsatile boundary conditions. Correponding flow waveforms are shown in (a).
Figure 3.
Bland-Altman comparison of (a) iPL and (b) HFD derived from simulations using pulsatile and time-averaged boundary conditions.
Factors Affecting the Sensitivity of HFD and iPL
Statistical analyses were conducted to explore primary factors affecting the sensitivity of HFD and iPL. The analyses involved demographic data presented in Table 1, flow data shown in Table 2, and geometric characteristics tabulated in Table 3. Reynolds number in Table 2 was calculated based on the IVC diameter and flow rate. Flow rates were indexed by body surface area. Vessel diameters in Table 3 were normalized by the square root of body surface area.
Table 2.
Flow data for the 101 patients
| Reynolds Number (Re) | 554±239 |
| Pulmonary Flow Distribution (%LPA) | 44±12 |
| Qivc (L/min/m2) | 1.70±0.55 |
| Qsvc (L/min/m2) | 1.02±.53 |
| Qlpa (L/min/m2) | 0.95±0.65 |
| Qrpa (L/min/m2) | 1.14±0.66 |
| Qlsvc (L/min/m2) (n = 21) | 0.68±0.35 |
| Qaz (L/min/m2) (n = 2) | 1.07±0.39 |
| Qrupa (L/min/m2) (n = 24) | 0.24±0.37 |
| iQs (L/min/m2) | 2.79±0.78 |
| wPIinlet (%) | 45±18 |
| wPIoutlet (%) | 49±26 |
| wPItotal (%) | 47±19 |
Data are reported as mean ± standard deviation.
Table 3.
Cohort Geometric Characteristics
| Vessel diameter (mm/m) | IVC | SVC | LPA | RPA | RUPA (n = 24) | LSVC (n = 21) | AZ (n = 2) |
|---|---|---|---|---|---|---|---|
| Minimum | 15.9±3.3 | 12.8±3.1 | 8.6±2.9 | 10.7±3.0 | 6.9±1.6 | 9.0±2.0 | 7.1±2.2 |
| Mean | 19.0±4.1 | 14.7±3.7 | 11.6±3.0 | 12.8±3.3 | 8.3±1.8 | 10.8±2.8 | 8.3±2.6 |
| Maximum | 22.9±5.7 | 17.6±4.5 | 17.1±5.2 | 16.5±4.7 | 10.6±3.1 | 13.4±4.9 | 12.7±3.0 |
|
| |||||||
| IVC Offset with SVC* | IVC Offset With LSVC* | ||||||
| Vessel Offsets | 0.25±0.33 | 1.55±0.93 | |||||
|
| |||||||
| IVC-SVC | IVC-LPA | IVC-RPA | SVC-LPA | SVC-RPA | LPA-RPA | ||
| Angles (°) | 133±22.5 | 109±17 | 87±15 | 106±16 | 100±13 | 107±28 | |
|
| |||||||
| IVC-LSVC | LSVC-SVC | LSVC-LPA | LSVC-RPA | ||||
| Angles (°) | 132±36 | 56±31 | 102±13 | 122±21 | |||
Values are mean ± standard deviation
normalized by mean IVC diameter
Demographic Analyses
Demographic analyses were first carried out for both dHFD and diPL corresponding to all the demographic groups listed in Table 1. No significant difference was observed for diPL between any demographic sub-groups. dHFD was found to be significantly different between single and bilateral SVC cohorts (Table 4). Therefore, for further statistical analysis, the entire cohort (n = 101) was considered for diPL calculations, while the cohort was divided into single-SVC (n = 80) and bilateral-SVC sub-groups (n=21) for dHFD analysis.
Table 4.
Statistical Analyses of Different Demographic Groups
| Demographic Groups | diPL (%) | dHFD (%) | ||
|---|---|---|---|---|
| Mean±SD | p-value | Mean±SD | p-value | |
| IA/EC | 25.5±22.3/29.5±22.5 | 0.236 | 6.7±6.4/10.0±10.9 | 0.719 |
| HLHS/non-HLHS | 26.6±19.4/27.2±24.3 | 0.610 | 7.0±8.6/8.4±8.3 | 0.173 |
| female/male | 25.6±25.5/27.6±20.7 | 0.186 | 7.3±8.4/8.1±8.4 | 0.356 |
| bilateral/single SVC(s) | 26.0±18.9/27.2±23.3 | 0.900 | 13.1±11.2/6.4±6.9 | 0.008* |
statistically significant (p < 0.05)
Best Statistical Predictors for Sensitivity of HFD and iPL
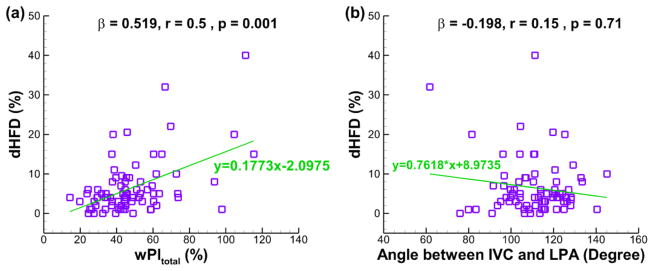
The best predictors for dHFD and diPL based on multivariate regression analyses are shown in Fig. 4–6. All variables included in these analyses were tabulated in Table 2 & 3. dHFD for the single-SVC cohort is best predicted (R = 0.54 and p < 0.001) by the wPItotal and the angle between IVC and LPA (ivc_lpa_angle):
| (9) |
Figure 4.
The best predictor of dHFD for the single-SVC cohort based on multiple regression analyses (n = 80, R = 0.54, p < 0.001): (a) wPItotal, and (b) angle between IVC and LPA. β = standardized coefficient of the multiple regression, r = partial correlation, p = significance of the partial correlation.
Figure 6.
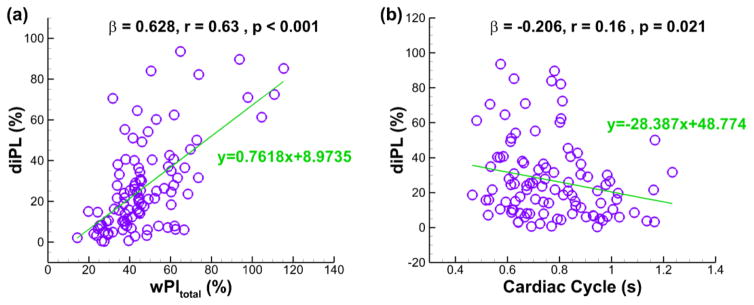
The best predictor of diPL based on multiple regression analyses (n = 101, R = 0.665, p < 0.001): (a) wPItotal, and (b) length of Cardiac Cycle. β = standardized coefficient of the multiple regression, r = partial correlation, p = significance of the partial correlation.
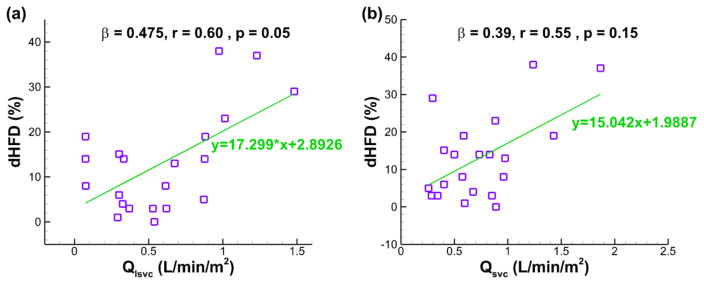
, while dHFD for the bilateral-SVC cohort is best predicted (R = 0.71 and p < 0.002) by the combination of Qlsvc and Qsvc as shown in the following equation:
| (10) |
For all 101 patients, the best statistical predictors for diPL (R = 0.665 and p < 0.001) are the wPItotal and the length of the cardiac cycle (CardiacCycle), which is the time elapsed for one heartbeat. The resulting formula is:
| (11) |
No collinearity exists between the predictors in Eqs. (9)–(11). Including additional metrics in the above equations did not increase their predictive power.
Discussion
Time-averaged BCs have been historically used in Fontan simulations for a wide range of studies. With current CFD capabilities, it may be advantageous to use time-averaged BCs to provide Fontan surgical planning results within a clinical time frame. However, the potential discrepancy between hemodynamic metrics using time-averaged and more physiological pulsatile BCs must be quantified to determine the viability of using time-averaged BC as an option to save computational costs. This study focused on two hemodynamic metrics related to patient outcomes: HFD and iPL. The Bland-Altman plots in Fig. 3 highlights that the difference of iPL and HFD were −24.3% and −4.4%, respectively, based on their mean values. The −24.3% difference in iPL indicates that the time-averaged BCs is not a good replacement of pulsatile BCs when assessing iPL. On the other hand, although the mean difference of HFD was −4.4%, the 95% limits of agreement for HFD was ±53.5%. This implies that the time-averaged BCs cannot be directly used as a surrogate of pulsatile BCs for evaluating HFD. Therefore, it is crucial to analyze and understand the patient-specific sensitivity of HFD and iPL.
Two variables, diPL and dHFD, were quantified in this study to represent the patient-specific sensitivity of iPL and HFD, respectively, when using time-averaged BCs. Overall, dHFD is 7.8±8.4% and diPL is 27.0±22.3%. It is noted that, although 50% HFD is assumed to be optimal for many previous studies (Haggerty et al., 2014; Sundareswaran et al., 2009a; Yang et al., 2013), the exact value required for preventing or alleviating PAVMs is still unknown. Clinically acceptable HFD ranges from 30% to 70% (Haggerty et al., 2012; Restrepo et al., 2015a, 2015b; Sundareswaran et al., 2009a; Trusty et al., 2016). Therefore, a 7.8% discrepancy in HFD between using the time-averaged and pulsatile BCs may not significantly affect clinical decisions based upon HFD. On the contrary, a 27.0% discrepancy may have clinical impact when using iPL as a predictor for patients’ exercise performance (Khiabani et al., 2015).
Furthermore, demographic analyses show that diPL does not vary within demographic sub-groups. On the other hand, dHFD was found to be significantly different (p=0.008) between the single SVC and bilateral SVC groups (Table 4), but all other demographic comparisons showed no statistically significant differences. Consequently, diPL multiple regression analysis incorporated all 101 patients, while the dHFD analysis was split into two groups: single SVC and bilateral SVC.
This study is the first to systematically investigate the sensitivity of HFD when using time-averaged BCs, and HFD is a very important hemodynamic metric for Fontan surgical planning. dHFD was shown to behave differently between single and bilateral SVC Fontan connections. The relations between dHFD, diPL and their predictors are summarized in Eqs. (9)–(11). Interestingly, the weighted pulsatility index was included as one of predictors for both dHFD and diPL. This is expected since more discrepancies between flow fields of using the time-averaged and pulsatile BCs were observed in the Fontan connection at a relatively high pulsatility index (Khiabani et al., 2012). Furthermore, it should be noted that the predictors for the sensitivity of using time-averaged BCs are all clinically available patient-specific variables calculated without the use of any a priori CFD simulations. Using any CFD simulation based variables as predictors would have negated the motive of reducing computational cost. For a Fontan surgical planning case, the sensitivity of using time-averaged BCs can be estimated based on Eqs. (9)–(11) as long as the clinical flows and geometric characteristics are obtained. Then, balancing the clinical time-constraint and acceptable sensitivity, the viability of using time-averaged BCs can be determined on an individual case basis.
Based on this study (Figs. 4–6), if the acceptable sensitivity is determined to be 10%, time-averaged BCs could have been used to assess HFD for 83% of the single SVC patients and 48% of the bilateral SVC patients, but could only be used to evaluate iPL for 26% of the patients. When the focus of the surgical planning is on HFD, a large portion of the cases can use time-averaged BCs to save computational cost, determined by Eqs. (9)–(11). It is worth noting that 10% is not a “gold standard” for acceptable sensitivity. Here, it only serves as an example to demonstrate how the predictors concluded in this study can be used. Clinicians and surgical planning engineers should determine the allowable sensitivity on a case-by-case basis. Nevertheless, multiple surgical options/anatomies are usually proposed throughout a surgical planning case. Often, the comparison between hemodynamic performance of proposed options is more important than the actual values of hemodynamic metrics for a given surgical option. Therefore, small errors in the hemodynamic analysis of individual proposed options may not affect the decision making process.
Limitations
Simulations in this study assumed rigid vessel walls. However, the bulk flow measurement agreement between the 4D in-vivo data and the rigid wall simulation suggests this assumption is valid (Haggerty et al., 2012; Sundareswaran et al., 2009a). Additionally, the boundary conditions used in this study were spatially averaged for each inlet and enforced as a parabolic velocity profile. Differences were demonstrated between 3D measured velocity profiles and idealized ones in simulating flow through aorta (Morbiducci et al., 2013), carotid bifurcation (Campbell et al., 2012), and TCPC (Roldán-Alzate et al., 2014). But it was suggested that, in comparison to the velocity profile, the velocity waveform has greater impact on hemodynamic metrics (Campbell et al., 2012). Hence, the assumption of idealized velocity profile should not significantly affect the conclusions of this study. Nevertheless, on-going research is being carried out to evaluate the impact of these assumptions.
Conclusion
This study comprehensively investigated the sensitivity of Fontan hemodynamic metrics when using time-averaged BCs, which is quantified by the difference between simulations using the time-averaged and pulsatile BCs. A total of 101 patients were studied, and two clinically important bulk hemodynamic metrics (HFD and iPL) were investigated. Based on the 101 patient population mean, the Bland-Altman plots present significant variations between patients when comparing resultant hemodynamic metrics by using time-averaged and pulsatile BCs. This suggests that a comprehensive understanding of the patient-specific sensitivity of using time-averaged BCs is vitally important. Statistical analysis was utilized to explore the factors affecting the patient-specific sensitivity of HFD and iPL, i.e. dHFD and diPL, respectively. To the best of our knowledge, this paper is the first to investigate dHFD and to show that dHFD for the bilateral SVC cohort is significantly larger than dHFD for the single SVC cohort (p = 0.008). On the other hand, the demographic analysis elucidated that no demographic factor included in this study influences diPL. Furthermore, multivariate regression analysis was employed to explore the best predictors of dHFD and diPL. dHFD was best predicted by the wPItotal and the angle between IVC and LPA for the single SVC cohort and by the time-averaged flow rates of SVC and LSVC for the bilateral SVC cohort. diPL is best correlated to the wPItotal and the length of the cardiac cycle. These regression equations can be used to estimate patient-specific sensitivity of the time-averaged BCs based on patient data prior to conducting simulations. The estimated sensitivity then provides a guideline for determining when the time-averaged BCs can be used to save computational time in order to meet clinical time constraints.
Figure 5.
The best predictors of dHFD for the bilateral-SVC cohort based on multiple regression analyses (n = 21, R = 0.71, p < 0.002): (a) Qlsvc, and (b) Qsvc. β = standardized coefficient of the multiple regression, r = partial correlation, p = significance of the partial correlation.
Acknowledgments
This study was supported by the National Heart, Lung, and Blood Institute Grants HL67622 and HL098252. The authors acknowledge Wenjun Wu and Abisshek Lakshman, who are undergraduate students at the Georgia Institute of Technology, for their assistance in data analysis and Luyu Zhang, who is a graduate student at Emory University for her assistance in statistical anlaysis. In addition, the authors acknowledge the use of ANSYS software which was provided through an Academic Partnership between ANSYS, Inc. and the Cardiovascular Fluid Mechanics Lab at Georgia Institute of Technology.
Abbreviations and Acronyms
- BSA
body surface area
- IA
intra-atrial
- EC
extra-cardiac
- HLHS
hypoplastic left heart syndrome
- IVC
inferior vena cava
- SVC
superior vena cava
- LSVC
left superior vena cava
- AZ
semi-azygos vein
- LPA
left pulmonary artery
- RPA
right pulmonary artery
- RUPA
right upper pulmonary artery
- Qs
total venous flow
- SD
standard deviation
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Campbell IC, Ries J, Dhawan SS, Quyyumi Aa, Taylor WR, Oshinski JN. Effect of Inlet Velocity Profiles on Patient-Specific Computational Fluid Dynamics Simulations of the Carotid Bifurcation. J Biomech Eng. 2012;134:51001. doi: 10.1115/1.4006681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- d’Udekem Y, Iyengar AJ, Cochrane AD, Grigg LE, Ramsay JM, Wheaton GR, Penny DJ, Brizard CP. The Fontan procedure: contemporary techniques have improved long-term outcomes. Circulation. 2007;116:I157–64. doi: 10.1161/CIRCULATIONAHA.106.676445. [DOI] [PubMed] [Google Scholar]
- Dasi LP, Pekkan K, Katajima HD, Yoganathan AP. Functional analysis of Fontan energy dissipation. J Biomech. 2008;41:2246–2252. doi: 10.1016/j.jbiomech.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Zélicourt DA, Ge L, Wang C, Sotiropoulos F, Gilmanov A, Yoganathan A. Flow simulations in arbitrarily complex cardiovascular anatomies - An unstructured Cartesian grid approach. Comput Fluids. 2009;38:1749–1762. doi: 10.1016/j.compfluid.2009.03.005. [DOI] [Google Scholar]
- de Zélicourt DA, Haggerty CM, Sundareswaran KS, Whited BS, Rossignac JR, Kanter KR, Gaynor JW, Spray TL, Sotiropoulos F, Fogel MA, Yoganathan AP. Individualized computer-based surgical planning to address pulmonary arteriovenous malformations in patients with a single ventricle with an interrupted inferior vena cava and azygous continuation. J Thorac Cardiovasc Surg. 2011;141:1170–1177. doi: 10.1016/j.jtcvs.2010.11.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Zélicourt DA, Marsden A, Fogel MA, Yoganathan AP. Imaging and patient-specific simulations for the Fontan surgery: Current methodologies and clinical applications. Prog Pediatr Cardiol. 2010;30:31–44. doi: 10.1016/j.ppedcard.2010.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Zélicourt Da, Kurtcuoglu V. Patient-Specific Surgical Planning, Where Do We Stand? The Example of the Fontan Procedure. Ann Biomed Eng. 2015 doi: 10.1007/s10439-015-1381-9. [DOI] [PubMed] [Google Scholar]
- DeGroff CG. Modeling the fontan circulation: Where we are and where we need to go. Pediatr Cardiol. 2008;29:3–12. doi: 10.1007/s00246-007-9104-0. [DOI] [PubMed] [Google Scholar]
- Dur O, Kocyildirim E, Soran O, Wearden PD, Morell VO, DeGroff CG, Pekkan K. Pulsatile venous waveform quality affects the conduit performance in functional and “failing” Fontan circulations. Cardiol Young. 2012;22:251–62. doi: 10.1017/S1047951111001491. [DOI] [PubMed] [Google Scholar]
- Esmaily-Moghadam M, Hsia TY, Marsden AL. The assisted bidirectional Glenn: A novel surgical approach for first-stage single-ventricle heart palliation. J Thorac Cardiovasc Surg. 2015;149:699–705. doi: 10.1016/j.jtcvs.2014.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fogel MA, Khiabani RH, Yoganathan A. Imaging for preintervention planning pre- and post-fontan procedures. Circ Cardiovasc Imaging. 2013;6:1092–1101. doi: 10.1161/CIRCIMAGING.113.000335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fogel MA, Weinberg PM, Hoydu A, Hubbard A, Rychik J, Jacobs M, Fellows KE, Haselgrove J. The nature of flow in the systemic venous pathway measured by magnetic resonance blood tagging in patients having the Fontan operation. J Thorac Cardiovasc Surg. 1997;114:1032–1041. doi: 10.1016/S0022-5223(97)70017-5. [DOI] [PubMed] [Google Scholar]
- Frakes D, Smith M, de Zélicourt D, Pekkan K, Yoganathan A. Three-dimensional velocity field reconstruction. J Biomech Eng. 2004;126:727–735. doi: 10.1115/1.1824117. [DOI] [PubMed] [Google Scholar]
- Frakes DH, Conrad CP, Healy TM, Monaco JW, Fogel M, Sharma S, Smith MJT, Yoganathan AP. Application of an adaptive control grid interpolation technique to morphological vascular reconstruction. IEEE Trans Biomed Eng. 2003;50:197–206. doi: 10.1109/TBME.2002.807651. [DOI] [PubMed] [Google Scholar]
- Frakes DH, Dasi LP, Pekkan K, Kitajima HD, Sundareswaran K, Yoganathan aP, Smith MJ. A new method for registration-based medical image interpolation. IEEE Trans Med Imaging. 2008;27:370–377. doi: 10.1109/TMI.2007.907324. [DOI] [PubMed] [Google Scholar]
- Haggerty CM, de Zélicourt Da, Restrepo M, Rossignac J, Spray TL, Kanter KR, Fogel Ma, Yoganathan AP. Comparing Pre- and Post-operative Fontan Hemodynamic Simulations: Implications for the Reliability of Surgical Planning. Ann Biomed Eng. 2012;40:1–13. doi: 10.1007/s10439-012-0614-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haggerty CM, Restrepo M, Tang E, de Zélicourt DA, Sundareswaran KS, Mirabella L, Bethel J, Whitehead KK, Fogel MA, Yoganathan AP. Fontan hemodynamics from 100 patient-specific cardiac magnetic resonance studies: A computational fluid dynamics analysis. J Thorac Cardiovasc Surg. 2014;148:1481–1489. doi: 10.1016/j.jtcvs.2013.11.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khiabani RH, Restrepo M, Tang E, De Zélicourt D, Sotiropoulos F, Fogel M, Yoganathan AP. Effect of flow pulsatility on modeling the hemodynamics in the total cavopulmonary connection. J Biomech. 2012;45:2376–2381. doi: 10.1016/j.jbiomech.2012.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khiabani RH, Whitehead KK, Han D, Restrepo M, Tang E, Bethel J, Paridon SM, Fogel Ma, Yoganathan aP. Exercise capacity in single-ventricle patients after Fontan correlates with haemodynamic energy loss in TCPC. Heart. 2015;101:139–143. doi: 10.1136/heartjnl-2014-306337. [DOI] [PubMed] [Google Scholar]
- Kung E, Baretta A, Baker C, Arbia G, Biglino G, Corsini C, Schievano S, Vignon-Clementel IE, Dubini G, Pennati G, Taylor A, Dorfman A, Hlavacek AM, Marsden AL, Hsia TY, Migliavacca F. Predictive modeling of the virtual Hemi-Fontan operation for second stage single ventricle palliation: two patient-specific cases. J Biomech. 2013;46:423–9. doi: 10.1016/j.jbiomech.2012.10.023. [DOI] [PubMed] [Google Scholar]
- Marsden A, Esmaily-Moghadam M. Multiscale Modeling of Cardiovascular Flows for Clinical Decision Support. Appl Mech Rev. 2015;67:1–11. doi: 10.1115/1.4029909. [DOI] [Google Scholar]
- Marsden AL. Optimization in Cardiovascular Modeling. Annu Rev Fluid Mech. 2014;46:519–546. doi: 10.1146/annurev-fluid-010313-141341. [DOI] [Google Scholar]
- Marsden AL. Simulation based planning of surgical interventions in pediatric cardiology. Phys Fluids. 2013;25 doi: 10.1063/1.4825031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsden AL, Vignon-Clementel IE, Chan FP, Feinstein Ja, Taylor Ca. Effects of Exercise and Respiration on Hemodynamic Efficiency in CFD Simulations of the Total Cavopulmonary Connection. Ann Biomed Eng. 2007;35:250–263. doi: 10.1007/s10439-006-9224-3. [DOI] [PubMed] [Google Scholar]
- Morbiducci U, Ponzini R, Gallo D, Bignardi C, Rizzo G. Inflow boundary conditions for image-based computational hemodynamics: Impact of idealized versus measured velocity profiles in the human aorta. J Biomech. 2013;46:102–109. doi: 10.1016/j.jbiomech.2012.10.012. [DOI] [PubMed] [Google Scholar]
- Pike NA, Vricella LA, Feinstein JA, Black MD, Reitz BA. Regression of severe pulmonary arteriovenous malformations after Fontan revision and “hepatic factor” rerouting. Ann Thorac Surg. 2004;78:697–699. doi: 10.1016/j.athoracsur.2004.02.003. [DOI] [PubMed] [Google Scholar]
- Restrepo M, Crouch AC, Haggerty CM, Rossignac J, Slesnick TC, Kanter KR, Yoganathan AP. Hemodynamic Impact of Superior Vena Cava Placement in the Y-Graft Fontan Connection. Ann Thorac Surg. 2015a;101:183–189. doi: 10.1016/j.athoracsur.2015.07.012. [DOI] [PubMed] [Google Scholar]
- Restrepo M, Luffel M, Sebring J, Kanter K, del Nido P, Veneziani A, Rossignac J, Yoganathan A. Surgical Planning of the Total Cavopulmonary Connection: Robustness Analysis. Ann Biomed Eng. 2015b;43:1321–1334. doi: 10.1007/s10439-014-1149-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roldán-Alzate A, García-Rodríguez S, Rivera L, Wieben O, Anagnostopoulos PV, Francois CJ. Hemodynamic study of TCPC using in vivo and in vitro 4D flow MRI and numerical simulation. J Cardiovasc Magn Reson. 2014;16:W39. doi: 10.1186/1532-429X-16-S1-W39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava D, Preminger T, Lock JE, Mandell V, Keane JF, Mayer JE, Kozakewich H, Spevak PJ. Hepatic Venous Blood and the Development of Pulmonary Arteriovenous Malformations in Congenital Heart Disease. Circulation. 1995;92:1217–1222. doi: 10.1161/01.CIR.92.5.1217. [DOI] [PubMed] [Google Scholar]
- Sundareswaran KS, de Zélicourt D, Sharma S, Kanter KR, Spray TL, Rossignac J, Sotiropoulos F, Fogel Ma, Yoganathan AP. Correction of Pulmonary Arteriovenous Malformation Using Image-Based Surgical Planning. JACC Cardiovasc Imaging. 2009a;2:1024–1030. doi: 10.1016/j.jcmg.2009.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sundareswaran KS, Frakes DH, Fogel MA, Soerensen DD, Oshinski JN, Yoganathan AP. Optimum fuzzy filters for phase-contrast magnetic resonance imaging segmentation. J Magn Reson Imaging. 2009b;29:155–65. doi: 10.1002/jmri.21579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang E, Restrepo M, Haggerty CM, Mirabella L, Bethel J, Whitehead KK, Fogel MA, Yoganathan AP. Geometric Characterization of Patient-Specific Total Cavopulmonary Connections and its Relationship to Hemodynamics. JACC Cardiovasc Imaging. 2014;7:215–224. doi: 10.1016/j.jcmg.2013.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trusty PM, Restrepo M, Kanter KR, Yoganathan AP, Fogel MA, Slesnick TC. A pulsatile hemodynamic evaluation of the commercially available bifurcated Y-graft Fontan modification and comparison with the lateral tunnel and extracardiac conduits. J Thorac Cardiovasc Surg. 2016;151:1529–1536. doi: 10.1016/j.jtcvs.2016.03.019. [DOI] [PubMed] [Google Scholar]
- Wang C, Pekkan K, de Zélicourt D, Horner M, Parihar A, Kulkarni A, Yoganathan AP. Progress in the CFD Modeling of Flow Instabilities in Anatomical Total Cavopulmonary Connections. Ann Biomed Eng. 2007;35:1840–1856. doi: 10.1007/s10439-007-9356-0. [DOI] [PubMed] [Google Scholar]
- Wei Z, Charlie Zheng Z, Yang X. Computation of Flow Through a Three-Dimensional Periodic Array of Porous Structures by a Parallel Immersed-Boundary Method. J Fluids Eng. 2014;136:40905. doi: 10.1115/1.4026357. [DOI] [Google Scholar]
- Whitehead KK, Pekkan K, Kitajima HD, Paridon SM, Yoganathan aP, Fogel Ma. Nonlinear Power Loss During Exercise in Single-Ventricle Patients After the Fontan: Insights From Computational Fluid Dynamics. Circulation. 2007;116:I-165–I-171. doi: 10.1161/CIRCULATIONAHA.106.680827. [DOI] [PubMed] [Google Scholar]
- Yang W, Feinstein Ja, Shadden SC, Vignon-Clementel IE, Marsden AL. Optimization of a Y-graft design for improved hepatic flow distribution in the fontan circulation. J Biomech Eng. 2013;135:11002. doi: 10.1115/1.4023089. [DOI] [PubMed] [Google Scholar]