Patient-specific CFD models for intraventricular flow analysis from 3D ultrasound imaging: comparison of three clinical cases

Abstract

Background

As the intracardiac flow field is affected by changes in shape and motility of the heart, intraventricular flow features can provide diagnostic indications. Ventricular flow patterns differ depending on the cardiac condition and the exploration of different clinical cases can provide insights into how flow fields alter in different pathologies.

Methods

In this study, we applied a patient-specific computational fluid dynamics model of the left ventricle and mitral valve, with prescribed moving boundaries based on transesophageal ultrasound images for three cardiac pathologies, to verify the abnormal flow patterns in impaired hearts. One case (P1) had normal ejection fraction but low stroke volume and cardiac output, P2 showed low stroke volume and reduced ejection fraction, P3 had a dilated ventricle and reduced ejection fraction.

Results

The shape of the ventricle and mitral valve, together with the pathology influence the flow field in the left ventricle, leading to distinct flow features. Of particular interest is the pattern of the vortex formation and evolution, influenced by the valvular orifice and the ventricular shape. The base-to-apex pressure difference of maximum 2 mmHg is consistent with reported data.

Conclusion

We used a CFD model with prescribed boundary motion to describe the intraventricular flow field in three patients with impaired diastolic function. The calculated intraventricular flow dynamics are consistent with the diagnostic patient records and highlight the differences between the different cases. The integration of clinical images and computational techniques, therefore, allows for a deeper investigation intraventricular hemodynamics in patho-physiology.

Introduction

The human cardiovascular system is thought to be optimized to provide blood to the entire body with minimal energy expenditure of the heart muscle. This is particularly visible in the in- and outflow into the left ventricle, where the genesis of a vortex in diastole enhances the ventricular filling, reducing the losses due to conversion of the kinetic energy into pressure in this phase (Martinez-Legatzpi et al., 2014). Furthermore, the vortex ameliorates the washout of the left ventricle (LV) and facilitates systolic ejection (Gharib et al., 2006). The occurrence of cardiac diseases may produce intraventricular flow features deviating from what is considered normal and optimal, reducing the cardiac function.

Various techniques are available to assess the patient’s cardiac function. The analysis of the structural cardiac components and deformation patterns (e.g. strain imaging) provide fundamental information on the kinematics and contractility of the heart. The analysis of intraventricular flow, on the other hand, may be an even more powerful indicator of abnormal cardiac phenomena, as changes in the blood flow can precede the development of noticeable structural modifications (Pedrizzetti et al., 2015(1)). Therefore, a reliable and quantitative evaluation of cardiac flow may result not only in a diagnosis of an existing status, but in its prediction, based on an abnormal or sub-optimal cardiac performance (Pedrizzetti et al., 2015 (1-2)).

Intraventricular flows can be visualized with different techniques, ranging from 4D flow Magnetic Resonance Imaging (MRI), to ultrasound Doppler, vector flow mapping techniques and ultrasound-based particle imaging velocimetry (echoPIV) among others (Sengupta et al., 2012). In recent years, the use of image-based numerical simulations is providing interesting results and insights in the intraventricular hemodynamics. The combined use of computational simulations and clinical images for research and diagnosis can provide additional information (e.g. vortex formation) and is a valuable tool to investigate the relationship between cardiac pathology and the associated abnormal flow pattern (Mittal et al., 2016, Le et al., 2012, Gharib et al., 2006). Of particular interest is the vortex structure which dominates the fluid-dynamics of the LV especially during diastole. This vortex is known to be strictly related to the LV performance and functionality (Martinez-Legazpi et al., 2014, Le et al., 2012, Kilner et al., 2000, Pedrizzetti et al., 2005). Other hemodynamic indices that have been explored include intraventricular pressure gradients (Greenberg et al., 2001). From a clinical perspective, as heart failure and cardiac dysfunction have an epidemic proportion, especially in the ageing population (Redfield et al., 2003), the assessment of intraventricular filling patterns can be used to obtain information to better identify subjects at risk for whom a tailored therapy could be required.

We developed a CFD modelling methodology which, based on patient-specific real-time transesophageal (rt-TEE) ultrasound images, allows to develop a patient-specific model of intraventricular hemodynamics. The major advantage of the use of rt-TEE ultrasound images as a starting point for a CFD model is its excellent spatial resolution, allowing for the segmentation of the valve leaflets and left ventricle. In addition, the technique is bed-side, fast and non-ionizing, and does not require any contrast agents. Different pathologies could be studied and compared in larger patient groups. At the same time, rt-TEE also has some disadvantages such as the presence of noise (compared to MRI or CT images), the relatively limited temporal resolution and possible limitations to the sector that can be imaged in case of large, dilated ventricles. In this study, the method is applied to three different pathological cases, to detect the diversity of the flow field depending on the morphology of the LV, the possible diseased mitral valve (MV) and the different contractility of the heart, with the main goal of investigating, from a computational point of view, the features of the intraventricular flows in diseased ventricles.

Materials and methods

Patients selection and ultrasound images segmentation

Three patients, scheduled for aortic or mitral valve surgery, were included in the analysis on the basis of their LV characteristics and clinical indications (Table 1). All patients underwent the routine pre-operative rt-TEE ultrasound examination. The imaging protocol was approved by the University of Pennsylvania School of Medicine Institutional Review Board and informed consent was obtained from the patients regarding the use of the imaging data for research purposes. Pre-operative rt-3D TEE gated images were acquired with an iE33 scanner (Philips Medical Systems, Andover, MA). The frame rate was 17 to 30 Hz. The images were acquired over four consecutive cardiac cycles and reconstructed into one cardiac cycle to obtain the desired full field of view, which included the LV and MV. The segmentation of the structures of interest was realized with an automatic segmentation technique, to obtain a 3D geometric model (Pouch et al., 2015). The segmentation provided two sets of triangulated surfaces, one for the LV and one for the MV, which were used as input for the CFD model.

Table 1.

clinical pre-operative indications.

	LV size	Ax1 [mm]	Ax2 [mm]	EDV [mL]	SV [mL]	EF %	Heart rate	CO [L/min]	MV regurgitation	Clinical indication	Surgical Procedure
P1	Normal	73	43	58	30	52	61 bpm	1.83	Trace	Hypokinetic walls, Concentric hypertrophy	AV Replacement
P2	Normal	81	39	55	20	36	62 bpm	1.24	Mild	Impaired relaxation	AV Replacement
P3	Dilated	105	100	250	55	22	77 bpm	4.23	Mild	Global diastolic dysfunction – Severe hypokinesis	MV repair and CAD treatment

Abbreviations: Ax₁, Ax₂: major and minor axis of the LV. EDV: end diastolic volume, SV: stroke volume, EF: ejection fraction, CO: cardiac output, AV: aortic valve, CAD: coronary artery disease.

CFD model with prescribed moving boundaries

The Navier-Stokes equations were solved with a finite volume approach and an ALE formulation where the motion of the boundaries was implemented with extensive own programming in the CFD solver in use (ANSYS Fluent 15.0, Inc., Canonsburg, PA, USA). The segmented surfaces provide the position of the MV and LV in discrete time-points of the cardiac cycle, and this information is used to prescribe their kinematics for the CFD simulation. This CFD model with moving boundaries is described in full details in the work of Bavo et al., 2016. The simulations were run on a Dell PowerEdge R620 server (2× Intel Xeon E5-2680v2 CPUs at 2.8Ghz) with eight cores used.

Boundary conditions and material properties

In this work the simulations are limited to the diastolic phase and the effect of any possible systolic flow features is neglected. As the motion of the walls is imposed as derived from the clinical images, a uniform pressure was imposed at the inlet of the atrium. No outlet was identified: during diastole the aortic valve is closed and no aortic regurgitation is modeled. Blood was considered as a homogeneous and Newtonian fluid, with standard values of density ρ (1060 kg/m³) and viscosity μ (0.0035Pa.s). To include the effects of the opening valve, the simulation was started at late systole, with the mitral valve closed and the LV in its smallest volume configuration.

Fluid-dynamics evaluation criteria

Of particular importance is the analysis of the vortex structure formation and evolution in the left ventricle, which we identified with the commonly used λ₂ criterion (Jeong et al., 1995). As small local pressure differences in the ventricular chamber have an influence on the vortex formation and efficient ventricular filling (e.g. Greenberg et al., 2001), the pressure distribution of the three cases are also analyzed. Pressure values are relative to the imposed pressure at the atrial inlet. We calculated the intraventricular pressure difference ΔP throughout diastole between the cross sections CS₁ near the base of the LV, and CS₂ near the apex (see figure 1 for the exact locations), with ΔP = pressure at base – pressure at apex. We calculated the viscous energy dissipation, derived from the Navier-Stokes equation and the conservation of energy combined with the assumption of a homogeneous, incompressible, Newtonian and isotropic fluid as:

$$\mathrm{\Phi }=2\mu \left[{\left(\frac{\partial u}{\partial y}\right)}^2+{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial w}{\partial z}\right)}^2\right]+{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}^2+{\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right)}^2$$

where μ is the fluid viscosity.

Figure 1.

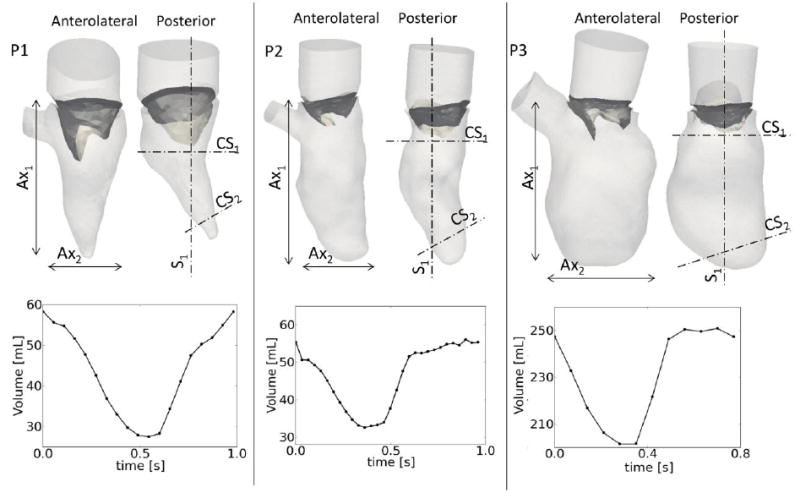
upper panel: patient geometries, showing the anterolateral and posterior walls of the LV. The dimensions of the major (Ax₁) and minor (Ax₂) axes are reported in table 1. Lower panel: LV volume curves calculated from the segmented ventricles. Sections S₁, CS₁ and CS₂ used to report relevant results in figure 2 and 3.

Results

Patient-specific data

Figure 1 displays the LV and MV geometries of the three patients, with chosen views showing the anterolateral and the posterior side of each geometry at late diastole. P1 has a moderate concentric hypertrophy, with a preserved ejection fraction (EF). The LV volume in the second patient is comparable to P1, but the ejection fraction is reduced and the ventricle has an elongated shape. The third patient has a severe ventricular dilatation, with dimensions substantially larger than the other subjects (table 1). The volume curve during the entire cardiac cycle is reported in the lower panel of figure 1 for the three cases. The remodeling and enlargement of the ventricle of P3 is evident from the volume curve and the impaired status of the heart is confirmed by an extremely low EF (22%).

The ventricles and valves for the three patients are shown for three time-points (late systole, E-peak and late diastole) in Figure 2.

Figure 2.

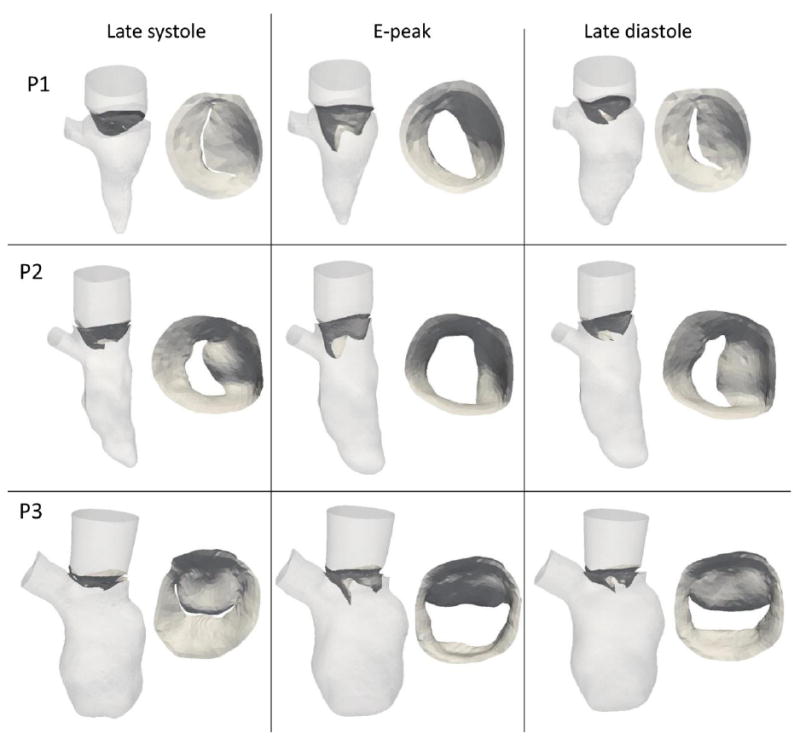
moving walls and valvular leaflets in the three patients at late systole, E-peak and late diastole.

Intraventricular flow and pressure field

Figure 3 displays the intraventricular flows and the pressure map during diastole for the three patients. Four significant time-points were selected, i.e. acceleration, peak of early filling (E-peak), deceleration, and peak of atrial filling (A-peak, if any). Data are displayed in section plane S₁ (figure 1). The volume flow rate curve, calculated at the atrial surface, is indicated on the right panel for each panel, as is the base-to-apex pressure difference.

Figure 3.

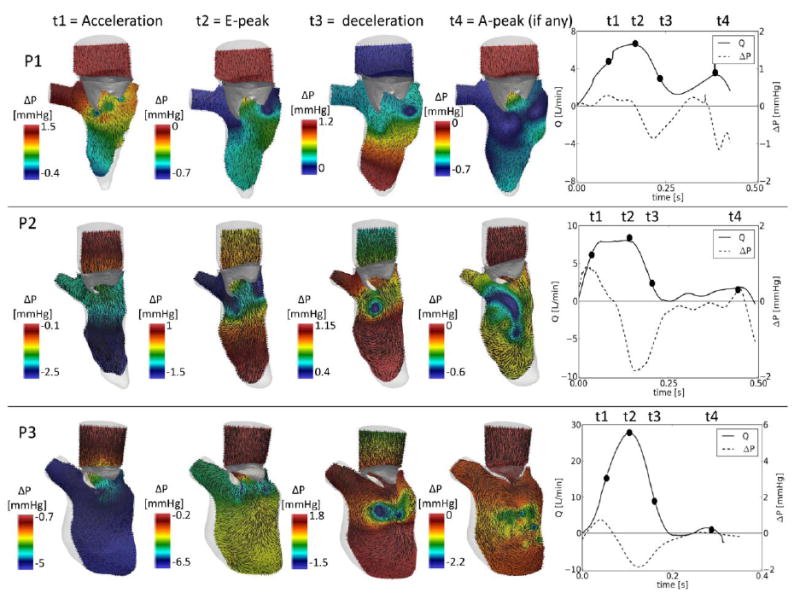
Intraventricular flow on a 2D slice and pressure variations (section S₁ indicated in fig.1) at four relevant time-points. Right panels: volume flow rate curve (solid line), calculated at the atrial inlet, intraventricular pressure gradient, calculated as the difference of the average pressure between the cross section 1 and 2 (CS₁ and CS₂) of figure 1. Note that the scale of the pressure changes in each panel.

While there was a prominent E-peak in all cases, the A-peak was present for P1 only (flow curve, solid line). The intraventricular pressure difference (dotted line, right panels of figure 1) curves show a similar trend in the three cases until the end of the E-peak, with a positive base-to-apex pressure difference driving the acceleration, and a reversed difference the deceleration of flow. In all cases, the reversed pressure difference was higher than the forward gradient, but did not exceed 2 mmHg. As P1 was the only patient with a prominent A-wave, it is also the only patient with a second positive and reversed pressure difference in late diastole.

During the acceleration phase, in the three subjects, the flow is driven into the LV. At peak filling, the recirculation of the blood becomes an important feature, especially for P1 and P2, in whom the rotational flow structures arising from the edges of the MV are asymmetric and correspond with lower pressure values. The asymmetry is due to the presence of the asymmetric valvular leaflets. In P3 this feature is less evident, due to its larger geometry and limited leaflet motion. The deceleration phase enlarged the rotational flow structures, which migrated and transport blood towards the apical regions of the LV. In this phase, the inversion of the pressure difference between the apical and the basal portion of the LV is visible in the three patients, causing the deceleration of the flow. The deceleration phase also corresponds to lower pressure zones in the central area of the LV below the valve, which are related to the vortex motion and recirculation flow path. The extension of this region varies from patient to patient. At the end of diastole, in P1 a second peak is detected in both the flow curve and in the presence of a spatially extended region of low pressures in the LV. However, the presence of an additional rotational flow is not clearly visible. In the remaining two patients the flow field becomes more chaotic and the vortical flows lose intensity.

Vortex analysis

The vortex structures are different in the three cases (Figure 4). In P1 and P2, in early diastole (acceleration) a vortex structure originates in the proximity of the valvular edges (figure 4). In P3 the vortex of the early diastole is broader than for the other subjects. At peak mitral inflow, in all the cases the vortex structure has increased its dimensions and occupies a larger portion in the LV. The spatial configuration of the vortex is influenced by the shape of the valvular leaflets: the vortices of P1 and P2 have a saddle-like shape dictated by the valve shape and assume an inclination of about 45 degrees with respect to the sagittal plane of the LV when migrating to the apex, while the poorly motile valve of P3 is not able to orient the vortex ring, which remains almost horizontal. During the deceleration phase, the vortices detach from the valvular edge and migrate to more apical regions of the LV. In P1 and P2, the main vortex impacts the anterolateral and lateral ventricular walls, respectively. Due to the impact with the wall, the vortex of P2 twists and it starts dissipating (fig. 3, t3). The motion of the vortex of P1 is less intense and the flow is more organized due to lower velocities. In contrast, the P3 vortex does not impact the dilated LV, therefore it migrates further and it shows secondary structures similar to the trailing vortex tubes reported in Le et al., 2012.

Figure 4.

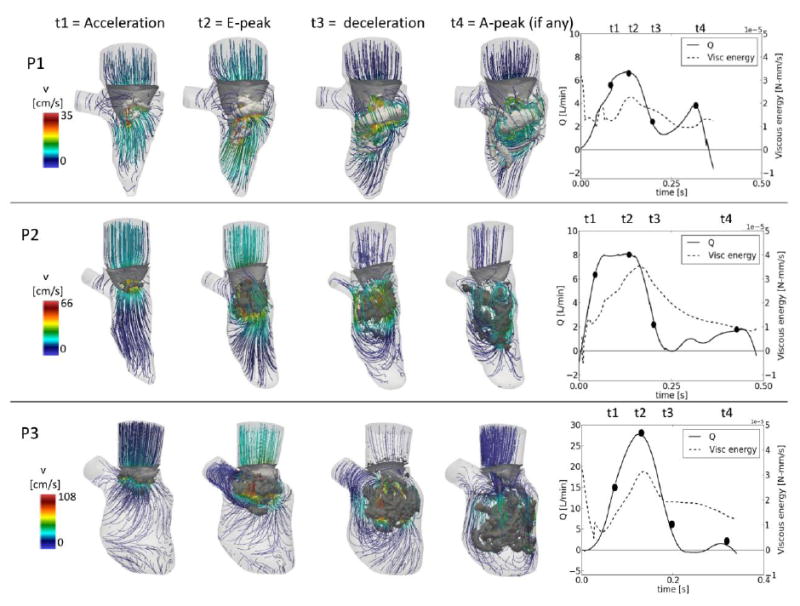
Intraventricular vortex visualization (λ₂) and velocity streamlines at four relevant time-points. Right panels: flow curve and viscous energy dissipation curve.

The velocity streamline directions are defined by the motion of the valve in the three cases. In P1, the velocity magnitude shows two maximum peaks in correspondence to the E- and A-peak of the transmitral flow. Due to the different dimensions of the three LVs, the peak velocities differ. In each case, the maximum velocity at E-peak is in agreement with the peak velocity measured with pulsed Doppler. Finally, the right panels of figure 4 display the viscous energy dissipation.

Discussion

Clinical considerations

In this work, the comparison of three different clinical cases with a computational tool allowed to detect the profound differences that exist between the intraventricular flow fields in patients with different cardiac pathologies. Even though the numerical simulation is an indirect technique to obtain the flow field, the studied cases indicate that pathology-related flow features are consistent with literature data. P1, suffering from aortic stenosis, shows hypokinesis of parts of the ventricular walls, has a preserved EF and a double-peaked-shaped transmitral flow. However, the small geometric dimensions and abnormal motility of the walls do not allow for the development of an important vortex structure and high velocity jet. The dilated ventricle of P3 offers interesting insights into the hemodynamics of dilated cardiomyopathy. As documented in Bermejo et al., 2014, the vortex structure in a dilated LV is broader than in a normal LV and it is more able to transfer the blood to the apical regions of the LV, facilitating transport and ameliorating convective pressure losses. Coherent with these findings, the vortex structures of P3 are larger and more persistent during diastole than for the other two patients. In the case of P3, the valve has a less evident influence on the flow field compared with P1 and P2. The limited motion of the leaflets does not orient the direction of the entering blood jet towards the wall of the LV and is not able to push the vortex structures to the apical regions of the LV. During the deceleration phase (t3 and t4) the vortex features are comparable to the cases reported in literature in which no valve is included in the model (Le et al., 2012). The presence of the dilated ventricle, furthermore, does not allow the vortex to impact on the walls and consequently its dissipation. Due to the absence of the A-peak vortex formation, no considerations can be made on the interaction of the first and second vortices.

Despite the presence of diastolic dysfunction, the inlet flow jet produced a vortex ring in the three patients. The formation of the vortex, its initial growth and the maximum strength reached seem not to be dependent on the size of the ventricle, but only on the diameter and the shape of the valvular orifice, which is consistent with Stewards et al., 2012. After the pinch-off of the vortex from the valvular edges, the evolution of the vortex depends on the ventricular walls, whose position and dimensions determine the impact zone (if any) and the possibility of expansion or dissipation of the vortex (Steward et al., 2012, Bermejo et al., 2014). The pressures in the ventricles are strictly connected to the vortex formation and small variations in the pressure gradients influence the velocity field and rotational flow. The correspondence of the pressure distribution and the areas where the vortex is located is in good agreement with Vierendeels et al., 2002. Local variations in the ventricular pressures are related to the vortex formation and efficiency of the heart (Greenberg et al., 2001) and the availability of pressure maps in the ventricle provides pressure information otherwise not easily measurable in the LV due to the invasiveness of these measurements. Both the shape and magnitude of the intraventricular pressure difference curves in the three cases are comparable to the invasively measured data reported in Greenberg et al., 2001. The intraventricular pressure differences are notably lower in P1, despite the fact that the ejection fraction is preserved in this patient, and that peak flows are comparable to those in P2. Intraventricular flow velocities are also significantly lower in this patient (figure 4). The trends of the energy dissipation (Fig. 4, right panels) are consistent in the three patients, with a prominent peak during the early deceleration phase of the blood. The values are lowest in P1, consistent with the visual observation (t3 in figure 4) that the vortex breakdown is more noticeable in P2 and P3 than in P1. Compared to the work of Pedrizzetti et al., 2010, the peak of dissipated energy occurs earlier in diastole in our cases. We speculate that this is due to the presence of the valve in our simulations (the valve was not modeled as a 3D object in Pedrizzetti 2010), forcing the vortex into a lower position into the LV and consequently an earlier impact (and dissipation) on the ventricular walls.

Methodological considerations

The methodology used for the CFD simulations shows several advantages over existing works, with in particular (i) the use of clinically available rt-TEE ultrasound images as the source of the motion and (ii) the direct incorporation of the patient’s 3D valve in the simulations. As shown before, the presence of the MV leaflets in the simulations is crucial, as the leaflets direct the flow and shape the vortex. A correct representation of the valvular apparatus is therefore mandatory to reproduce all features of intraventricular flow field (Bavo et al., 2016, Seo et al., 2014).

In literature, patient-specific LV geometries are commonly derived from computed tomography (CT) scans (Mihalef et al., 2011, Chnafa et al., 2014) or MR images (Seo et al., 2014, Vedula et al., 2016, Le et al., 2012). In few cases, cardiac ultrasound images are used (Lai et al., 2015). As the rt-TEE US acquisition is a routine procedure during surgery, there is a great availability of preoperative images data-sets. Due to time and space resolution issues, different techniques have been adopted to include the valve in the model. In Seo et al., 2014 and Vedula et al., 2016, the valvular shape is simplified and derived from anatomical atlases, its motion prescribed as a function of the opening angle. A more realistic valve representation is proposed in Mihalef et al 2011, based on landmark positioning on high quality CT scans. As we demonstrated, the use of rt-TEE ultrasound images, routinely acquired during most of the surgical procedures, allows to simultaneously obtain both the valve and ventricular position, avoiding the need for surrogate strategies to include the valve.

All reported works on intraventricular flows including a moving valve are based on the immersed boundary technique (at least for the valvular motion e.g. Seo et al., 2014, Mihalef et al., 2011). In contrast, the discussed model relies on the ALE approach for the solution of the Navier-Stokes equations for the entire domain, including the moving valve, demonstrating the feasibility of this approach even in presence of highly motile structures.

Limitations

Despite its aforementioned advantages over other approaches, it is clear that our methodology also suffers from limitations. On the imaging side, a major limitation is the temporal resolution of rt-TEE. As such, the model cannot provide any useful information on the timing of the cardiac cycle events. For example, no isovolumetric phases are included and the motion of the valve could be limited by the acquisition frequency. The geometries used in this work are patient-specific but do not include details such as papillary muscles and trabeculae, which have an impact on the flow field (Vedula et al., 2016). In addition to the modeling hypothesis and assumptions (e.g. Newtonian fluid), the creation of the model relies on user-dependent tasks, especially in the preprocessing phase. It is mandatory to automate some of the processing steps before the model can be more extensively used in a clinical context for medical applications. As this work was focused on the diastolic phase, only a portion of the cardiac cycle was simulated. The absence of the systolic phase in the simulation may introduce approximations in the calculated flow field, especially in the case of a regurgitant MV, in which a systolic transmitral backflow can influence the vortex formation and the ventricular hemodynamics. Future work will encompass the complete cardiac cycle.

Conclusions

In this work we comparatively studied the intraventricular flow field in three patients with various LV pathologies, making use of patient-specific 3D CFD models derived from clinical 3D ultrasound data. Our results indicate that the morphological changes due to the pathology influence the intraventricular dynamics, producing different patterns in each case. The availability of pressure maps and the vortex visualization provided important information otherwise not available from clinical measurements. The main findings are in agreement with the clinical reports of the subjects and with clinical data on the same patient category.